An adaptive mesh method for time dependent singularly perturbed differential-difference equations

P. Pramod Chakravarthy; Kamalesh Kumar

doi:10.1515/nleng-2018-0075

Article Open Access

An adaptive mesh method for time dependent singularly perturbed differential-difference equations

P. Pramod Chakravarthy and Kamalesh Kumar

Published/Copyright: September 17, 2018

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information

From the journal Nonlinear Engineering Volume 8 Issue 1

Abstract

In this paper, a time dependent singularly perturbed differential-difference convection-diffusion equation is solved numerically by using an adaptive grid method. Similar boundary value problems arise in computational neuroscience in determination of the behaviour of a neuron to random synaptic inputs. The mesh is constructed adaptively by using the concept of entorpy function. In the proposed scheme, prior information of the width and position of the layers are not required. The method is independent of perturbation parameter ε and gives us an oscillation free solution, without any user introduced parameters. Numerical examples are presented to show the accuracy and efficiency of the proposed scheme.

Keywords: Differential-difference equations; Singular perturbation; Boundary layer; Entropy; adaptive mesh; Central finite difference scheme

MSC 2010: 65L11; 65M12; 35K20

1 Introduction

Singularly perturbed partial differential equations arise in a wide variety of application fields such as biosciences, economics, material science, medicine, robotics etc. [5, 14, 20] and in the last few decades there has been a growing interest in the study of delay differential equations [3, 4, 9]. In 1965 Stein [19] proposed a mathematical model of neuronal variability to study the stochastic movement of neuron. Later he generalized the model to study the distribution of past synaptic potential amplitudes. In 1991 Musila and Lansky [13] generalised the Stein’s model and given the following mathematical model:

−∂u∂t=σ22∂2u∂x2+(μD−xτ)∂u∂x+λsu(x+as,t)+ωsu(x+is,t)−(λs+ωs)u(x,t).

Here, due to exponential decay between two consecutive jumps caused by the input processes, the first derivative term will occur. The membrane potential decays exponentially to the resting level with a membrane time constant τ and μ_D and σ are diffusion moments of Wiener process characterizing the influence of the dentritic synapses on the cell excitability. The reaction terms correspond to the superposition of excitatory and inhibitory inputs and we can assume that they are Poissonian. The excitatory input contributes to the membrane potential by amplitude a_s with intensity λ_s and similarly the inhibitory input contributes by amplitude i_s with intensity ω_s. This model makes available time evolution of the trajectories of the membrane potential.

Lange and Miura [11], studied the asymptotic analysis of singularly perturbed boundary value problems for differential-difference equations in ordinary differential equations. This study motivated many researchers to work on numerics of singularly perturbed differential-difference equations in ordinary differential equations and partial differential equations. Here we are concerned with the partial differential equations of convection-diffusion type with general shift arguments, which are singularly perturbed. It is noticeable that the behavior of the solution of singularly perturbed partial differential equations with shift arguments are essentially different from those of without shift arguments.

Ramesh and Kadalbajoo [15] proposed a numerical scheme based on classical finite differences on the Shishkin mesh for solving singularly perturbed partial differential-difference equations with small shift arguments. The method is found to be uniformly convergent with respect to the perturbation parameter. Kumar and Kadalbajoo [9] had given a B-spline collocation method on fitted mesh for solving singularly perturbed partial differential-difference equations with small shift arguments. In [9, 15], they approximated the shifted terms by Taylor series and difference schemes are applied. Such methods will work when shifts are smaller than perturbation parameter and fails in the case when shifts are bigger than perturbation parameter. Bansal et. al.[3, 4] developed parameter uniform numerical schemes to find the approximate solution of time dependent singularly perturbed convection-diffusion-reaction problems with general shift arguments in space variable, which work for small shifts as well as large shifts. Rao and Chakravarthy [16] had given a fitted numerical scheme for singularly perturbed one-dimensional parabolic partial differential equations with small shifts.

If we solve singularly perturbed partial differential equations using central finite difference scheme on a uniform mesh, it gives oscillatory solution, which shows that method is unstable. To deal with such situation, more mesh points in boundary layer region is required. To cater the need, layer adaptive meshes have been developed by Bakhvalov [2], Gartland [8] and others. A special piecewise uniform meshes have been proposed by Miller and Shishkin [12]. Shishkin meshes are used widely because of their simplicity. The major drawback of Shishkin meshes is the requirement of prior information of the location of the layer regions. To overcome this drawback, in this paper, we proposed an adaptive mesh method using the concept of entropy function for solving convection-diffusion-reaction singularly perturbed delay parabolic partial differential equations. The method is independent of perturbation parameter ε and gives us an oscillation free solution, without any user introduced parameters.

The paper is organized as follows: The problem under consideration is stated and the sufficient compatibility conditions on the initial and boundary data to guarantee the existence, uniqueness and appropriate regularity of the solutions to the problem are presented in Section 2. Numerical scheme and variable mesh algorithm is presented in Section 3. Section 4 is devoted to the stability and error analysis. To demonstrate the efficiency and applicability of the proposed numerical scheme, numerical experiments are carried out for three test problems and results are given in Section 5. The paper ends with conclusions in last section.

2 Statement of the problem

Let Ω = (0, 1), D = Ω × (0, T], for some fixed time T and Γ = Γ_l ∪ Γ_b ∪ Γ_r, where Γ_l = {(x, t) : − δ ≤ x ≤ 0, and 0 ≤ t ≤ T} and Γ_r = {(x, t) : 1 ≤ x ≤ 1 + η, and 0 ≤ t ≤ T} are the left and the right sides of the domain D and Γ_b = [0, 1].

In this paper, we consider a class of time dependent singularly perturbed partial differential difference equation with initial condition and the interval boundary conditions of the from:

∂u∂t−ε∂2u∂x2+a(x)∂u∂x+b(x)u(x,t)+c(x)u(x−δ,t)+d(x)u(x+η,t)=f(x,t),(1)

where (x, t) ∈ D,

u(x,0)=ϕb(x),∀x∈Γb=[0,1],u(x,t)=ϕl(x,t),∀(x,t)∈Γl={(x,t):−δ≤x≤0,and0≤t≤T},u(x,t)=ϕr(x,t),∀(x,t)∈Γr={(x,t):1≤x≤1+η,and0≤t≤T},(2)

where 0 < ε ≪ 1 is the singular perturbation parameter, δ, η > 0 represent the shift parameters. The functions a(x), b(x), c(x), d(x), f(x, t), ϕ_b(x), ϕ_l(x, t), ϕ_r(x, t) are assumed to be smooth and bounded functions on D, that satisfy the conditions b(x) + c(x) + d(x) ≥ α > 0 on Γ_b = [0, 1], for some constant α. When δ = η = 0, the above problem reduces to singularly perturbed partial differential equation. If a(x) ≥ β > 0, for some constant β, c(x) < 0 and d(x) < 0 for all x ∈ Γ_b = [0, 1], then the solution exhibits boundary layer along x = 1.

The problem (1) with initial condition and the interval boundary conditions (2), can be rewritten as

Lεu(x,t)=F(x,t),

where

Lεu(x,t)≡∂u∂t−ε∂2u∂x2+a(x)∂u∂x+b(x)u(x,t)+d(x)u(x+η,t),if0<x≤δ,0<t≤T,∂u∂t−ε∂2u∂x2+a(x)∂u∂x+b(x)u(x,t)+c(x)u(x−δ,t)+d(x)u(x+η,t),ifδ<x<1−η,0<t≤T,∂u∂t−ε∂2u∂x2+a(x)∂u∂x+b(x)u(x,t)+c(x)u(x−δ,t),if1−η≤x≤1,0<t≤T,(3)

and

F(x,t)=f(x,t)−c(x)ϕl(x−δ,t),if0<x≤δ,0<t≤T,f(x,t),ifδ<x<1−η,0<t≤T,f(x,t)−d(x)ϕr(x+η,t),if1−η≤x≤1,0<t≤T.(4)

The existence and uniqueness of a solution of (1) can be established under the assumption that the data are Holder continuous and also satisfy appropriate compatibility conditions at the corner points (0, 0), (1, 0), (−δ, 0), (1 + η, 0) then the required compatibility conditions are [18]

ϕb(0)=ϕl(0,0),ϕb(1)=ϕr(1,0),(5)

and

∂ϕl(0,0)∂t−ε∂2ϕb(0)∂x2+a(0)∂ϕb(0)∂x+b(0)ϕb(0)+c(0)ϕl(−δ,0)+d(0)ϕb(η)=f(0,0),∂ϕr(1,0)∂t−ε∂2ϕb(1)∂x2+a(1)∂ϕb(0)∂x+b(1)ϕb(1)+c(1)ϕb(1−δ)+d(1)ϕr(1+η,0)=f(1,0).(6)

These conditions guarantee that there exists a constant C independent of ε such that ∀ (x, t) ∈ D,

Lemma 2.1

(Maximum principle) Let the functionφ(x, t) ∈ C^2,1(D), such that 𝓛_εφ(x, t) ≥ 0 inDandφ(x, t) ≥ 0 for all (x, t) ∈ (D − D). Thenφ(x, t) ≥ 0 for all (x, t) ∈ (D).

Proof

Let there exists (x_p, t_q) ∈ D, for some positive integer p and q such that

φ(xp,tq)=min(x,t)∈D¯φ(x,t),

and also assume that φ(x_p, t_q) < 0. From our assumption it is clear that (x_p, t_q) ∉ (D − D), which implies that (x_p, t_q) ∈ D. Since at the point (x_p, t_q) function φ attains minimum, so φ_t = φ_x = 0, φ_xx ≥ 0 at point (x_p, t_q) and b(x) + c(x) + d(x) > 0, c(x) < 0 and d(x) < 0 for all x ∈ [0, 1]. Using differential operator 𝓛_ε on φ(x, t), from (3) we have for 0 < x_p ≤ δ and 0 < t_q ≤ T,

Lεφ(xp,tq)=∂φ∂t−ε∂2φ∂x2+a(xp)∂φ∂x+b(xp)φ(xp,tq) +d(xp)φ(xp+η,tq) =−ε∂2φ∂x2+b(xp)φ(xp,tq)+d(xp)φ(xp+η,tq) =−ε∂2φ∂x2+b(xp)φ(xp,tq)+d(xp)φ(xp+η,tq) +d(xp)φ(xp,tq)−d(xp)φ(xp,tq) =−ε∂2φ∂x2+(b(xp)+d(xp))φ(xp,tq) +d(xp)(φ(xp+η,tq)−φ(xp,tq)) <0,

for δ < x_p < 1 − η and 0 < t_q ≤ T

Lεφ(xp,tq)=∂φ∂t−ε∂2φ∂x2+a(xp)∂φ∂x+b(xp)φ(xp,tq) +c(xp)φ(xp−δ,tq)+d(xp)φ(xp+η,tq) =−ε∂2φ∂x2+b(xp)φ(xp,tq)+c(xp)φ(xp−δ,tq) +d(xp)φ(xp+η,tq) =−ε∂2φ∂x2+(b(xp)+c(xp)+d(xp))φ(xp,tq) +c(xp)φ((xp−δ,tq)−φ(xp,tq))+d(xp)φ((xp+η,tq)−φ(xp,tq)) <0,

for 1 − η ≤ x_p ≤ 1 and 0 < t_q ≤ T

Lεφ(xp,tq)=∂φ∂t−ε∂2φ∂x2+a(xp)∂φ∂x+b(xp)φ(xp,tq) +c(xp)φ(xp−δ,tq) =−ε∂2φ∂x2+b(xp)φ(xp,tq)+c(xp)φ(xp−δ,tq) =−ε∂2φ∂x2+b(xp)φ(xp,tq)+c(xp)φ(xp−δ,tq) +c(xp)φ(xp,tq)−c(xp)φ(xp,tq) =−ε∂2φ∂x2+(b(xp)+c(xp))φ(xp,tq)+c(xp)(φ(xp+η,tq) −φ(xp,tq)) <0,

which contradict our assumption as 𝓛_εφ(x, t) ≥ 0 in D. So we have φ(x, t) ≥ 0 for all (x, t) ∈ (D). □

Lemma 2.2

Ifu(x, t) satisfies the maximum principle then forn = 0, 1 and 2, the derivatives of the exact solutionu(x, t) of the model problem(1)satisfy the following bound

|∂nu(x,t)∂tn|≤C,(x,t)∈D¯

whereCis a generic positive constant independent ofε.

Proof

First we prove the bound for n = 0. We have,

|u(x,t)−u(x,0)|=|u(x,t)−ϕb(x)|≤Ct,∀(x,t)∈D¯ |u(x,t)|≤|ϕb(x)|+Ct,

since ϕ_b(x) ∈ C²(D) and t is bounded.

|u(x,t)|≤C1,for some constantC1.

Now we have to prove the bound for n = 1,

we have u ≡ 0 along x = 0 and x = 1, therefore u_x ≡ 0 and u_xx ≡ 0. Now for t = 0,

∂u∂t−ε∂2u∂x2+a(x)∂u∂x+b(x)u(x,0)+c(x)u(x−δ,0)+d(x)u(x+η,0)=f(x,0),

using above conditions on u, we have

∂u(x,0)∂t=f(x,0)|∂u(x,0)∂t|≤C,for some constantC.

Apply the differential operator 𝓛_ε on u_t(x, t)

Lεut(x,t)=Ft(x,t)

which implies that,

|Lεut(x,t)|=|Ft(x,t)|≤C,∀(x,t)∈D¯,

using maximum principle,

|∂u(x,t)∂t|≤C,∀(x,t)∈D¯.

Similarly one can prove the result for n = 2. □

Theorem 2.3

Forn = 0, 1, 2, 3 and 4, the derivatives of the exact solutionu(x, t) of the model problem(1)satisfy the following bound

|∂nu(x,t)∂xn|≤C(1+ε−nexp(−β(1−x)/ε)),(x,t)∈D¯

whereCis a generic positive constant independent ofε.

Proof

The proof of this theorem can be found in [3]. □

3 Numerical Scheme

In this section, we present a numerical scheme which works nicely when the delay and advance parameters are larger than perturbation parameter. To describe the method, we consider the linear singularly perturbed partial differential equation (1) subject to the initial and interval boundary conditions (2). Let the time interval [0, T] be partitioned into N equal parts with constant step size Δt. Let 0 = t₀, t₁, … t_N = T be the mesh points. Then we have t_j = jTN , j = 0, 1, …, N.

Applying backward Euler formula for time derivative in equation (1) we obtain

Uj(x)−Uj−1(x)Δt−εd2Uj(x)dx2+a(x)dUj(x)dx+b(x)Uj(x)+c(x)Uj(x−δ)+d(x)Uj(x+η)=f(x,tj),

where U^j = U(x, t_j) ⋍ u(x, t_j), for j = 1, 2, …, N.

After rearranging the terms in above equation, we get

Uj(x)Δt−εd2Uj(x)dx2+a(x)dUj(x)dx+b(x)Uj(x)+c(x)Uj(x−δ)+d(x)Uj(x+η)=f(x,tj)+Uj−1(x)Δt.(7)

This can be rewritten as

Lε∗U(x,tj)=G(x,tj)(8)

where

Lε∗U(x,tj)≡−εd2Uj(x)dx2+a(x)dUj(x)dx+(b(x)+1Δt)Uj(x)+d(x)Uj(x+η),if0<x≤δ,−εd2Uj(x)dx2+a(x)dUj(x)dx+(b(x)+1Δt)Uj(x)+c(x)Uj(x−δ)+d(x)Uj(x+η),ifδ<x<1−η,−εd2Uj(x)dx2+a(x)dUj(x)dx+(b(x)+1Δt)Uj(x)+c(x)Uj(x−δ),if1−η≤x≤1.(9)

and

G(x,tj)=f(x,tj)+Uj−1(x)Δt−c(x)ϕl(x−δ,tj),if0<x≤δ,f(x,tj)+Uj−1(x)Δt,ifδ<x<1−η,f(x,tj)+Uj−1(x)Δt−d(x)ϕr(x+η,tj),if1−η≤x≤1.(10)

3.1 Finite difference operators for a non-uniform mesh

The first order forward, backward and central difference operators in space on non-uniform mesh(adaptive mesh) points x_i are defined as

Dx+ui=ui+1−uixi+1−xi,Dx−ui=ui−ui−1xi−xi−1,andDx0ui=ui+1−ui−1xi+1−xi−1,

respectively and the second order central difference operator Dx+Dx− in space is defined as

Dx+Dx−ui=2(D+ui−D−ui)xi+1−xi−1.

Using above finite difference operators on a non-uniform mesh, we have

Lε∗U(x,tj)≡−εDx+Dx−Uj(x)+a(x)Dx0Uj(x)+(b(x)+1Δt)Uj(x)+d(x)Uj(x+η),if0<x≤δ,−εDx+Dx−Uj(x)+a(x)Dx0Uj(x)+(b(x)+1Δt)Uj(x)+c(x)Uj(x−δ)+d(x)Uj(x+η),ifδ<x<1−η,−εDx+Dx−Uj(x)+a(x)Dx0Uj(x)+(b(x)+1Δt)Uj(x)+c(x)Uj(x−δ),if1−η≤x≤1.(11)

The initial and interval boundary conditions can be rewritten as

U(x,0)=ϕb(x),x∈[0,1],U(x,tj)=ϕl(x,tj),−δ≤x≤1,j=0,1,...,N,

U(x,tj)=ϕr(x,tj),1≤x≤1+η,j=0,1,...,N.(12)

We solve (11) along with the conditions (12) using central difference scheme with minimum number of mesh points on uniform mesh in space direction. The presence of the singular perturbation parameter ε leads to occurrences of wild oscillation in the numerical solution. In order to avoid such oscillations, a large number of mesh points are required in layer region, when ε is very small. To overcome this, we generated a variable mesh using entropy function. The strategy for generating an adaptive mesh is given in the following subsection.

3.2 Mesh Selection Strategy

Now, we define, the entropy production equation by multiplying with an appropriate test function. From the theory of scalar conservation law, we know that U² is always an appropriate entropy variable and therefore 2U(x, t_j) is a suitable multiplying test function [10]. On multiplying with the test function, we obtain

Lε∗U(x,tj)∗2U(x,tj)=G(x,tj)∗2U(x,tj).(13)

After simplifying, equation (13) can be written as

−ε(Z″−2(U′2))+a(x)Z′+2(b(x)+1Δt)Z+2Uj(c(x)ϕl(x−δ)+d(x)Uj(x+η)−f(x,tj)−Uj−1(x)Δt)=0,if0<x≤δ,−ε(Z″−2(U′2))+a(x)Z′+2(b(x)+1Δt)Z+2Uj(c(x)Uj(x−δ)+d(x)Uj(x+η)−f(x,tj)−Uj−1(x)Δt)=0,ifδ<x<1−η,−ε(Z″−2(U′2))+a(x)Z′+2(b(x)+1Δt)Z+2Uj(c(x)Uj(x−δ)+d(x)ϕr(x+η)−f(x,tj)−Uj−1(x)Δt)=0,if1−η≤x≤1,

where Z = U².

The above equation can be rewritten as

−εZ″+a(x)Z′+2Uj(c(x)ϕl(x−δ)+d(x)Uj(x+η)−f(x,tj)−Uj−1(x)Δt)=−2(b(x)+1Δt)Z−2ε(U′2),if0<x≤δ,−εZ″+a(x)Z′+2Uj(c(x)Uj(x−δ)+d(x)Uj(x+η)−f(x,tj)−Uj−1(x)Δt)=−2(b(x)+1Δt)Z−2ε(U′2),ifδ<x<1−η,−εZ″+a(x)Z′+2Uj(c(x)Uj(x−δ)+d(x)ϕr(x+η)−f(x,tj)−Uj−1(x)Δt)=−2(b(x)+1Δt)Z−2ε(U′2).if1−η≤x≤1,(14)

The right-hand side of the equation (14) is considered as our entropy function and is always negative for all values x ∈ [0, 1]. As we know that, if we solve equation (11) by using central difference method, we get oscillations inside and near the boundary layer region. We calculate the discrete analogue of left hand side part in (14) using the same central difference operator by taking Zi=Ui2 , where U_i is the central difference computed solution of equation (11). If we write the right hand side part of (14) at the mesh point (x_i, t_j), as

−2(b(xi)+1Δt)(Ui+1,j.Ui−1,j)−2ε(Ui,j−Ui−1,jxi−xi−1)(Ui+1,j−Ui,jxi+1−xi),(15)

we get the positive value whenever the oscillations occur, where U_i is the central difference computed solution. To generate the variable mesh, first we calculate entropy function with minimum number of initial uniform mesh points in space direction. To handle the delay and advance terms, we construct a special mesh, so that the terms containing the shifts lie on nodal point after discretization on uniform mesh. We find out the mesh point, where the entropy is maximum and positive. We add mesh points, one to the left and other to the right side of the mesh point where entropy is maximum and positive. Now, we compute the solution with newly generated mesh points (non uniform mesh) using central difference method and check whether the entropy is positive or negative through out the interval of integration. If the entropy is positive, we pick up the mesh point where the entropy is maximum and positive and we repeat the process of adding mesh points both sides. We repeat this process till we get entropy negative through out the interval of integration.

4 Stability and Error analysis

Use the difference operators for a non-uniform mesh in (11), since h_i = x_i+1 - x_i, h_i−1 = x_i − x_i−1 and h_i + h_i−1 = x_i+1 − x_i−1. For 1 < k, l < M, we have

−ε2(D+Ui,j−D−Ui,j)xi+1−xi−1+aiUi+1,j−Ui−1,jxi+1−xi−1+(bi+1Δt)Ui,j+diUi+l,j,ifi=1,2,...,k,−ε2(D+Ui,j−D−Ui,j)xi+1−xi−1+aiUi+1,j−Ui−1,jxi+1−xi−1+(bi+1Δt)Ui,j+ciUi−k,j+diUi+l,j,ifi=k+1,k+2,...,M−l−1,−ε2(D+Ui,j−D−Ui,j)xi+1−xi−1+aiUi+1,j−Ui−1,jxi+1−xi−1+(bi+1Δt)Ui,j+diUi+l,j,ifi=M−l,M−l+1,...,M,(16)

and

Gi,j=fi,j+Ui,j−1Δt−ciϕl(i−k,j),ifi=1,2,...,k,fi,j+Ui,j−1Δt,ifi=k+1,k+2,...,M−l−1,fi,j+Ui,j−1Δt−diϕr(i+l,j),ifi=M−l,M−l+1,...,M.(17)

On rearrangement, the Equation (16)-(17) can be written as

EiUi−1,j+FiUi,j+HiUi+1,j+IiUi−k,j+JiUi+l,j=fi,j+Ui,j−1Δt,(18)

where

Ei=|−2εhi−1(hi+hi−1)−aihi+hi−1|Fi=|2εhi(hi+hi−1)+2εhi−1(hi+hi−1)+bi+1Δt|Hi=|−2εhi(hi+hi−1)+aihi+hi−1|Ii=|ci|Ji=|di|

and

|Ei|+|Hi|=2εhihi−1,

provided |a_i| ≤ 2ε/h_i−1 and |a_i| ≤ 2ε/h_i.

For i = 1, 2, …, k and j = 1, 2, …, N,

EiUi−1,j+FiUi,j+HiUi+1,j+JiUi+l,j=fi,j+Ui,j−1Δt−ciϕl(i−k,j)

|Fi|−|Ei|−|Hi|−|Ji|=|2εhihi−1+bi+1Δt|−|2εhihi−1|−di=bi+1Δt−di

since b_i > 0 and d_i < 0 on [0, 1] and Δt is step size in temporal direction. We have

|Fi|>|Ei|+|Hi|+|Ji|.(19)

For i = k + 1, k + 2, …, M − l − 1, and j = 1, 2, …, N,

EiUi−1,j+FiUi,j+HiUi+1,j+IiUi−k,j+JiUi+l,j=fi,j+Ui,j−1Δt

|Fi|−|Ei|−|Hi|−|Ii|−|Ji|=|2εhihi−1+bi+1Δt|−|2εhihi−1|−ci−di=bi+1Δt−ci−di,

since b_i > 0, c_i < 0 and d_i < 0 on [0, 1] and Δt is step size in temporal direction. We have

|Fi|>|Ei|+|Hi|+|Ii|+|Ji|.(20)

For i = M − l, M − l + 1, …, M, and j = 1, 2, …, N,

EiUi−1,j+FiUi,j+HiUi+1,j+IiUi+l,j=fi,j+Ui,j−1Δt−diϕr(i+l,j)

|Fi|−|Ei|−|Hi|−|Ii|=|2εhihi−1+bi+1Δt|−|2εhihi−1|−ci=bi+1Δt−ci

since b_i > 0 and c_i < 0 on [0, 1] and Δt is step size in temporal direction. We have

|Fi|>|Ei|+|Hi|+|Ii|,(21)

which shows that the given system is diagonally dominant. The scheme is stable and the unknown U_i.j must be solved at each time level.

Truncation error:

Let M^∗ is number of mesh interval on an adaptive mesh obtained using entropy function concept. If x_i is i^th mesh point on M^∗. We define left hand and right hand side distance by

hi−1=xi−xi−1,hi=xi+1−xi.

Using Taylors series expansion

u(xi−hi−1,tj)=u(xi,tj)−hi−1∂u(xi,tj)∂x+hi−122!∂2u(xi,tj)∂x2−hi−133!∂3u(xi,tj)∂x3+...

u(xi+hi,tj)=u(xi,tj)+hi∂u(xi,tj)∂x+hi22!∂2u(xi,tj)∂x2+hi33!∂3u(xi,tj)∂x3+...

and

u(xi,tj−Δt)=u(xi,tj)−Δt∂u(xi,tj)∂t+Δt22!∂2u(xi,tj)∂t2−Δt33!∂3u(xi,tj)∂t3+...,

using these expansions in Eq. (18), we get

(−2εhi−1(hi+hi−1)−aihi+hi−1)(u(xi,tj)−hi−1∂u(xi,tj)∂x+hi−12∂2u(xi,tj)∂x2−hi−13∂3u(xi,tj)∂x3+...)+(2εhi(hi+hi−1)+2εhi−1(hi+hi−1)+bi+1Δt)u(xi,tj)+(−2εhi(hi+hi−1)+aihi+hi−1)(u(xi,tj)+hi∂u(xi,tj)∂x+hi2∂2u(xi,tj)∂x2+hi3∂3u(xi,tj)∂x3+...)+ciu(xi−δ,tj)+diu(xi+η,tj)−1Δt(u(xi,tj)−Δt∂u(xi,tj)∂t+Δt2∂2u(xi,tj)∂t2−Δt3∂3u(xi,tj)∂t3+...)=0.

After simplification the terms, the truncation error is

T.E.=∂u(xi,tj)∂t−ε∂2u(xi,tj)∂x2+b(xi)u(xi,tj)+a(xi)∂u(xi,tj)∂x+c(xi)u(xi−δ,tj)+d(xi)u(xi+η,tj)−f(xi,tj)+a(xi)(hi−hi−1)2∂2u(xi,tj)∂x2−Δt2∂2u(xi,tj)∂t2+(−ε(hi−hi−1)3+a(xi)(hi−13+hi3)hi−1+hi)∂3u(xi,tj)∂x3+Δt26∂3u(xi,tj)∂t3,

which can further be simplified to

T.E.=a(xi)(hi−hi−1)2∂2u(xi,tj)∂x2−Δt2∂2u(xi,tj)∂t2+(−ε(hi−hi−1)3+a(xi)(hi−13+hi3)hi−1+hi)∂3u(xi,tj)∂x3+Δt26∂3u(xi,tj)∂t3,

as h_i−1, h_i → 0 and Δt → 0 the T.E. → 0, which shows that scheme is consistent and the truncation error of the scheme is of order O(h_i − h_i−1, Δt). The Lax equivalence theorem says that a finite difference approximation for a properly posed partial differential equation satisfying consistency and stability are necessary and sufficient conditions for convergence.

5 Numerical results

To demonstrate the efficiency and applicability of the proposed numerical scheme, numerical experiments are carried out for three test problems of singularly perturbed partial differential equations with large shifts parameters. The exact solution of the problems are not known, so the maximum point wise errors are calculated using the following double mesh principle [6]:

EεM∗,N=max0≤i,j≤M∗,N∣UM∗,N(xi,tj)−U2M∗,2N(x2i,tj)∣,

where U^{M^*,N}(x_i, t_j), denote the numerical solution obtained on a mesh containing M^* + 1 points in spatial direction and N + 1 points in temporal direction.

The numerical rate of convergence is calculated using the formula

RεM∗,N=log∣EεM∗,N−Eε2M∗,2N∣log⁡2.

We use the notation M, N for mesh intervals in space and time direction, on uniform mesh and M^* for final adaptive mesh intervals in space direction.

Example 5.1

[3] Consider the following singularly perturbed partial differential equation:

∂u∂t−ε∂2u∂x2+(2−x2)∂u∂x+(x+3)u(x,t)−u(x−δ,t)−2u(x+η,t)=10t2e−tx(1−x),

where (x, t) ∈ (0, 1) × (0, 3] and is subject to the following interval boundary conditions and the initial condition,

u(x,t)=0,∀(x,t)∈Γl={(x,t):−δ≤x≤0and0≤t≤T},

u(x,t)=0,∀(x,t)∈Γr={(x,t):1≤x≤1+ηand0≤t≤T},

The adaptive mesh generation with ε = 2⁻¹⁰, for this example is plotted in Figure 1. The numerical solution of the central finite difference scheme on uniform mesh and on adaptive mesh for three different time levels with ε = 2⁻¹⁴, δ = 0.2 and η = 0.4, for this example, is plotted in Figure 2a and Figure 2b. To examine the effect of shift parameters on the boundary layer behaviour of the solution, surface plot of the solution of example 5.1 for different values of ε and δ and η, using adaptive mesh is plotted in Figure 3a and Figure 3b. The maximum point wise errors and rate of convergence are presented in Table 1 for this boundary value problem for different values of perturbation parameter ε.

Fig. 1

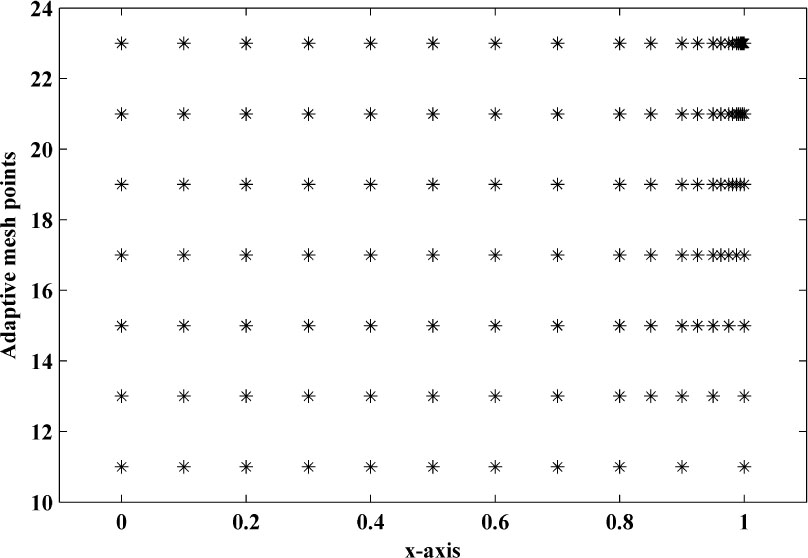
Adaptive mesh generation for example 5.1 with ε = 2⁻¹⁰, δ = 0.6, η = 0.7, M=10(initially) and N=20.

Fig. 2

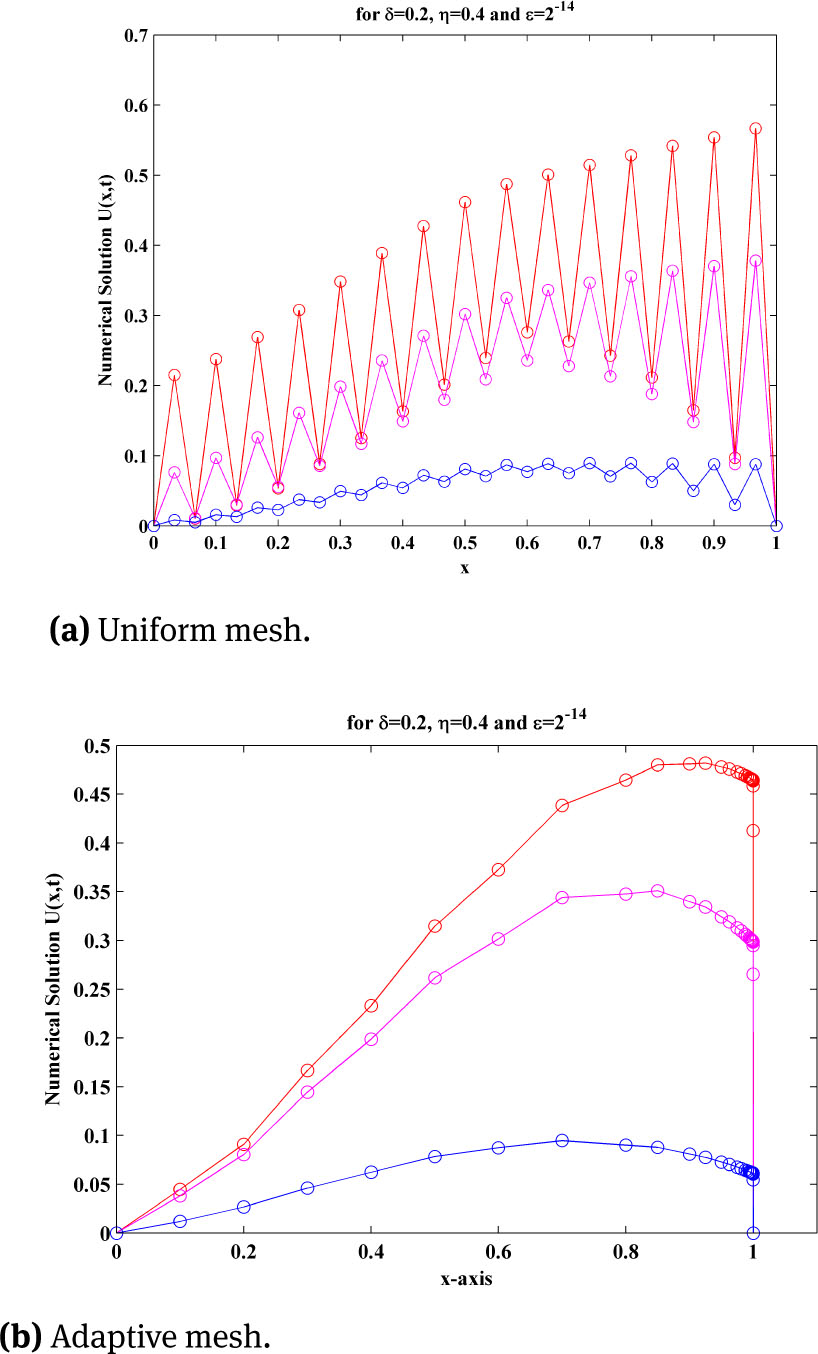
Numerical solution of example 5.1, using uniform mesh and adaptive mesh for three different time level with ε = 2⁻¹⁴, δ = 0.2, η = 0.4, M=30 and N=20.

Fig. 3

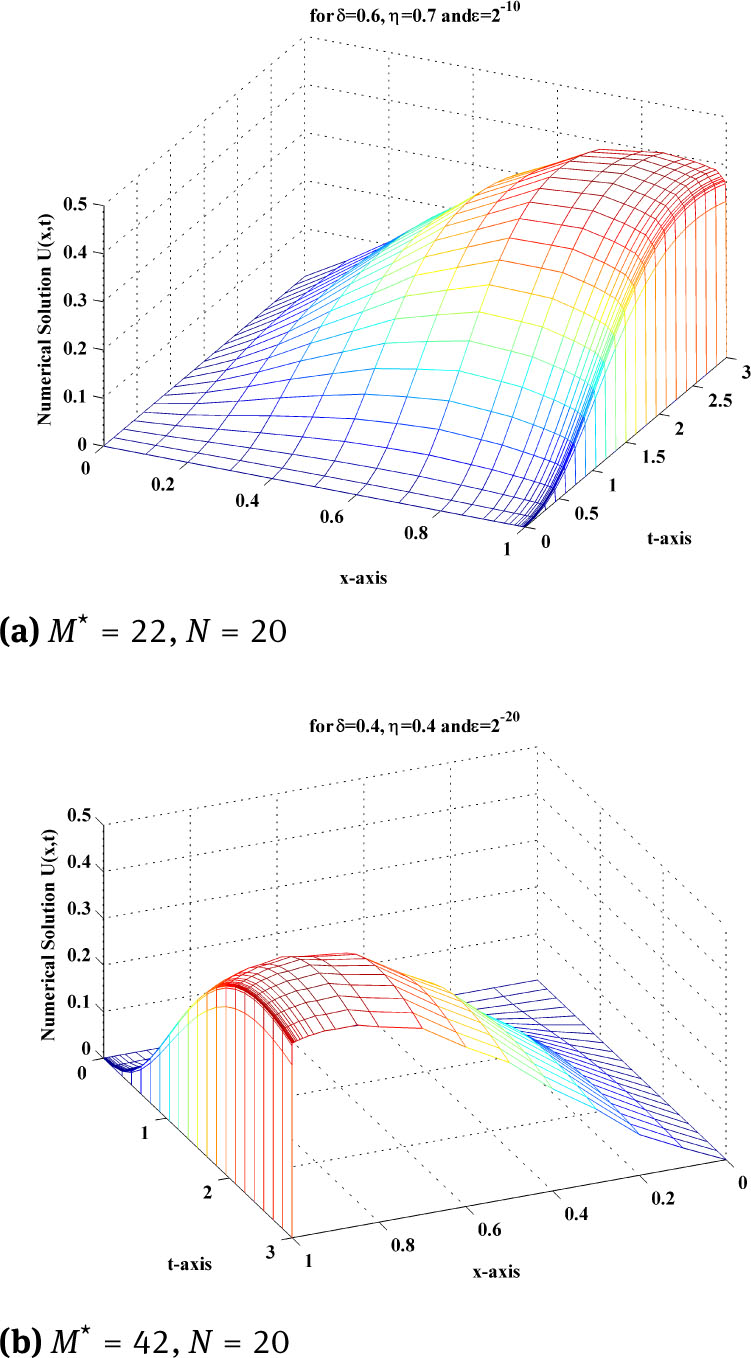
Surface plot of example 5.1, using adaptive mesh for different values of ϵ, δ and η.

Table 1

Maximum point wise errors of the solution and corresponding rate of convergence for Example 5.1 by taking δ = 0.6, η = 0.7, M=10 and N=20 for different values of ε.

ε	Generated mesh	Max. error	Rate of Convergence
	(M^*)		(R^{M^*}^,N)
2^–10	22	2.3422e-02	2.2166
2^–11	24	2.4004e-02	2.2086
2^–12	26	2.4260e-02	2.2037
2^–13	28	2.4377e-02	2.2012
2^–14	30	2.4432e-02	2.1910
2^–15	32	2.4460e-02	2.1993
2^–16	34	2.4473e-02	2.1991
2^–17	36	2.4479e-02	2.1989
2^–18	38	2.4483e-02	2.1989
2^–19	40	2.4484e-02	2.1988
2^–20	42	2.4485e-02	2.1988
2^–21	44	2.4485e-02	2.1988
2^–22	46	2.4486e-02	2.1988
2^–23	48	2.4486e-02	2.1988
2^–24	50	2.4486e-02	2.1988
2^–25	52	2.4486e-02	2.1988
2^–26	54	2.4486e-02	2.1988
2^–27	56	2.4486e-02	2.1988
2^–28	58	2.4486e-02	2.1988
2^–29	60	2.4486e-02	2.1988
2^–30	62	2.4486e-02	2.1988

Example 5.2

[3] Consider the following singularly perturbed partial differential equation:

∂u∂t−ε∂2u∂x2+(1+x+x2)∂u∂x+(1+x2)u(x,t)−(14+x22)u(x−δ,t)−14u(x+η,t)=sinπx(1−x),

where (x, t) ∈ (0, 1) × (0, 1] and is subject to the following interval boundary conditions and the initial condition,

u(x,t)=0,∀(x,t)∈Γl={(x,t):−δ≤x≤0and0≤t≤T},u(x,t)=0,∀(x,t)∈Γr={(x,t):1≤x≤1+ηand0≤t≤T},u(x,t)=0,∀x∈[0,1].

The adaptive mesh generation with ε = 2⁻²⁰, for this example is plotted in Figure 4. The numerical solution of the central finite difference scheme on uniform mesh and on adaptive mesh for three different time level with ε = 2⁻²², δ = 0.7 and η = 0, for this example, is plotted in Figure 5a and Figure 5b. To examine the effect of shift parameters on the boundary layer behaviour of the solution, surface plot of the solution of example 5.2 for different values of ε and δ and η, using adaptive mesh is plotted in Figure 6a and Figure 6b. The maximum point wise errors and rate of convergence are presented in Table 2, 3, 4 for this boundary value problem for different values of perturbation parameter ε.

Fig. 4

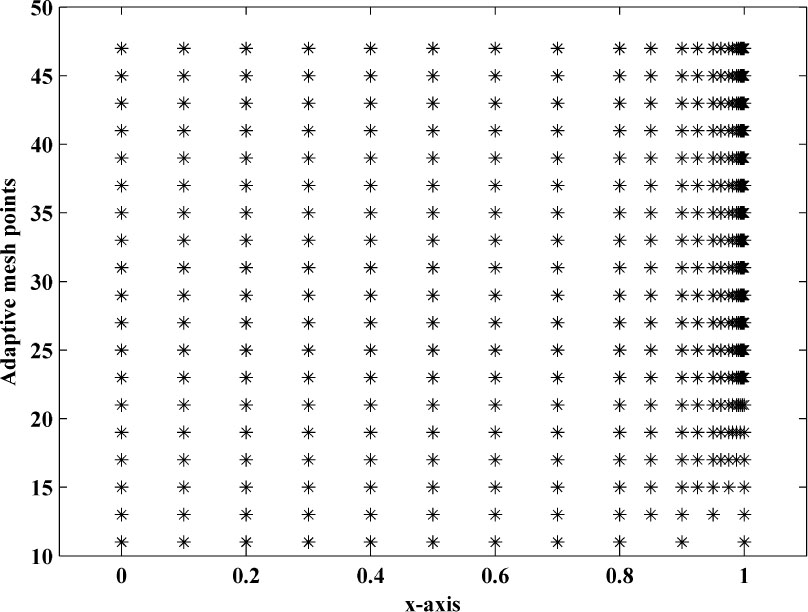
Adaptive mesh generation for example 5.2 with ε = 2⁻²⁰, δ = 0, η = 0.5, M=10(initially) and N=20.

Fig. 5

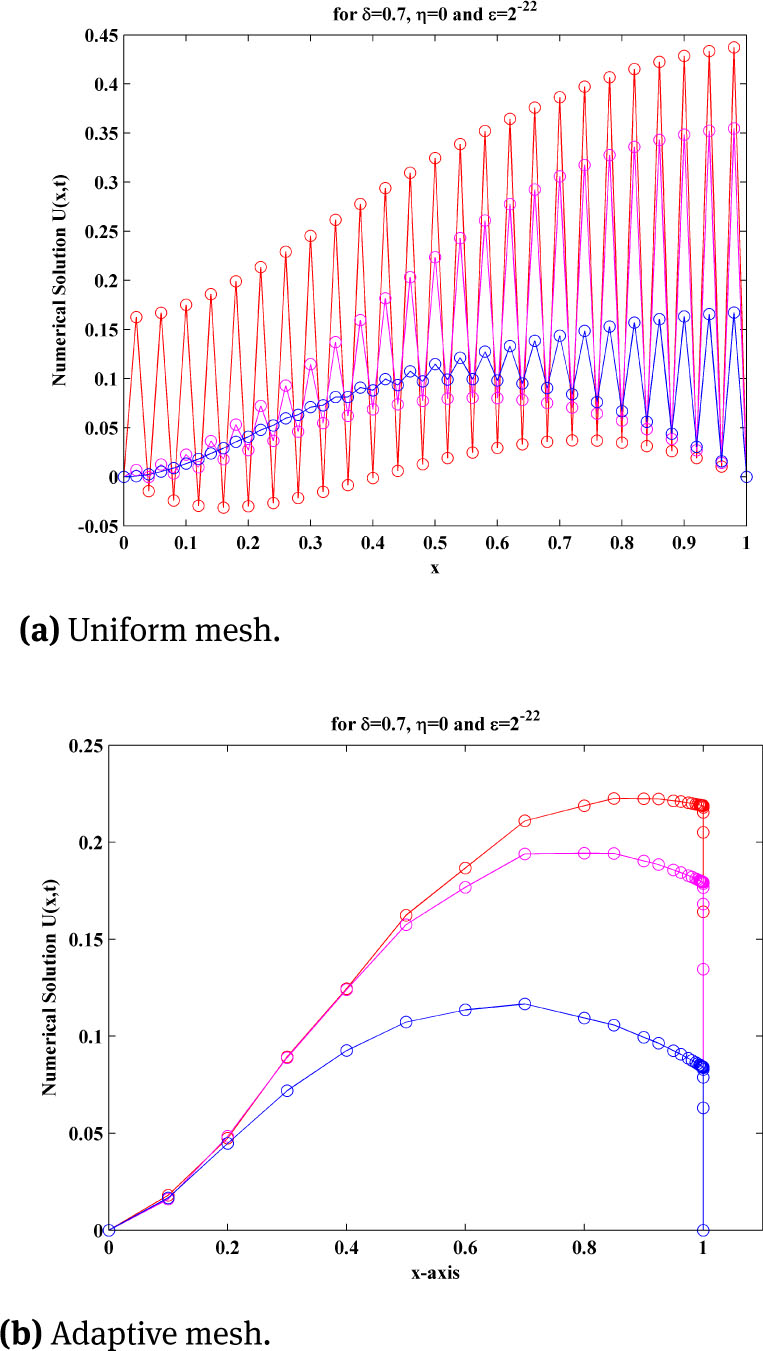
Numerical solution of example 5.2, using uniform mesh and adaptive mesh for three different time level with ε = 2⁻²², δ = 0.7, η = 0, M=50 and N=20.

Fig. 6

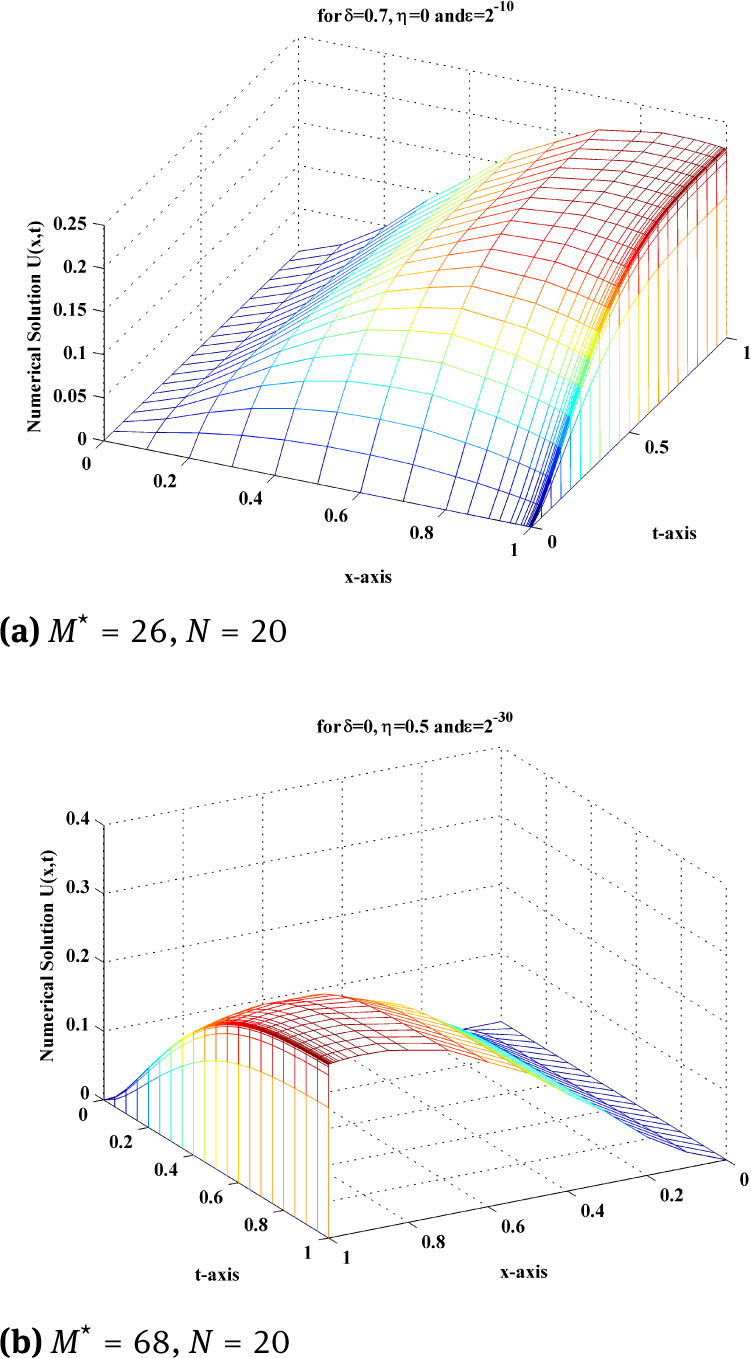
Surface plot of example 5.2, using adaptive mesh for different values of ϵ, δ and η.

Table 2

Maximum point wise errors of the solution and corresponding rate of convergence for Example 5.2 by taking δ = 0.6, η = 0.7, M=10 and N=20 for different values of ε.

ε	Generated mesh	Max. error	Rate of Convergenci
	(M^*)		(R^{M^*}^,N)
2^–10	26	1.0006e-02	1.3435
2^–15	36	1.0058e-02	1.3392
2^–20	46	1.3391e-02	1.3391
2^–25	58	1.0059e-02	1.3391
2-30	68	1.0059e-02	1.3391

Table 3

Maximum point wise errors of the solution and corresponding rate of convergence for Example 5.2 by taking δ = 0, η = 0.5, M=10 and N=20 for different values of ε.

ε	Generated mesh	Max. error	Rate of Convergence
	(M^*)		(R^{M^*}^,N)
2^–10	26	1.1246e-02	1.3077
2^–15	36	1.1300e-02	1.3033
2^–20	46	1.1302e-02	1.3031
2^–25	58	1.1302e-02	1.3031
2^–30	68	1.1302e-02	1.3031

Table 4

Maximum point wise errors of the solution and corresponding rate of convergence for Example 5.2 by taking δ = 0.7, η = 0, M=10 and N=20 for different values of ε.

ε	Generated mesh	Max. error	Rate of Convergence
	(M^*)		(R^{M^*,N})
2⁻¹⁰	26	1.0145e-02	1.3435
2⁻¹⁵	36	1.0193e-02	1.3392
2⁻²⁰	46	1.0194e-02	1.3391
2⁻²⁵	58	1.0194e-02	1.3391
2⁻³⁰	68	1.0194e-02	1.3391

Example 5.3

[3] Consider the following singularly perturbed partial differential equation:

∂u∂t−ε∂2u∂x2+(1−x22)∂u∂x+(x+6)u(x,t)−4u(x−δ,t)−u(x+η,t)=x(1−x),

where (x, t) ∈ (0, 1) × (0, 3] and is subject to the following interval boundary conditions and the initial condition,

u(x,t)=0,∀(x,t)∈Γl={(x,t):−δ≤x≤0and0≤t≤T},u(x,t)=0,∀(x,t)∈Γr={(x,t):1≤x≤1+ηand0≤t≤T},u(x,t)=0,∀x∈[0,1].

The adaptive mesh generation with ε = 2⁻³⁰, for this example is plotted in Figure 7. The numerical solution of the central finite difference scheme on uniform mesh and on adaptive mesh for three different time level with δ = 0.1 and η = 0.2, for this example, is plotted in Figure 8a and Figure 8b. To examine the effect of shift parameters on the boundary layer behaviour of the solution, surface plot of the solution of example 5.3 for different values of ε and δ and η, using adaptive mesh is plotted in Figure 9a and Figure 9b. The maximum point wise errors and rate of convergence are presented in Table 5 for this boundary value problem for different values of perturbation parameter ε.

Fig. 7

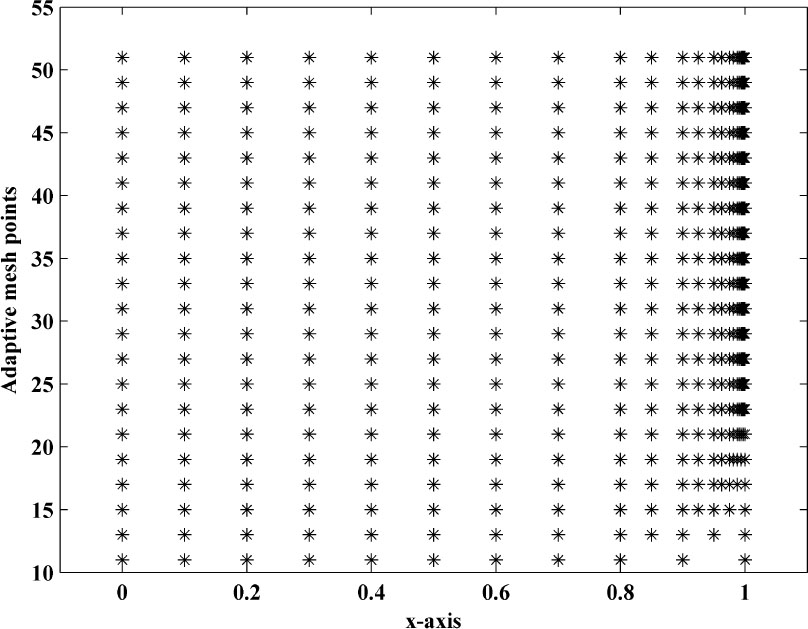
Adaptive mesh generation for example 5.3 with ε = 2⁻³⁰, δ = 0.1, η = 0.2, M=10(initially) and N=20.

Fig. 8

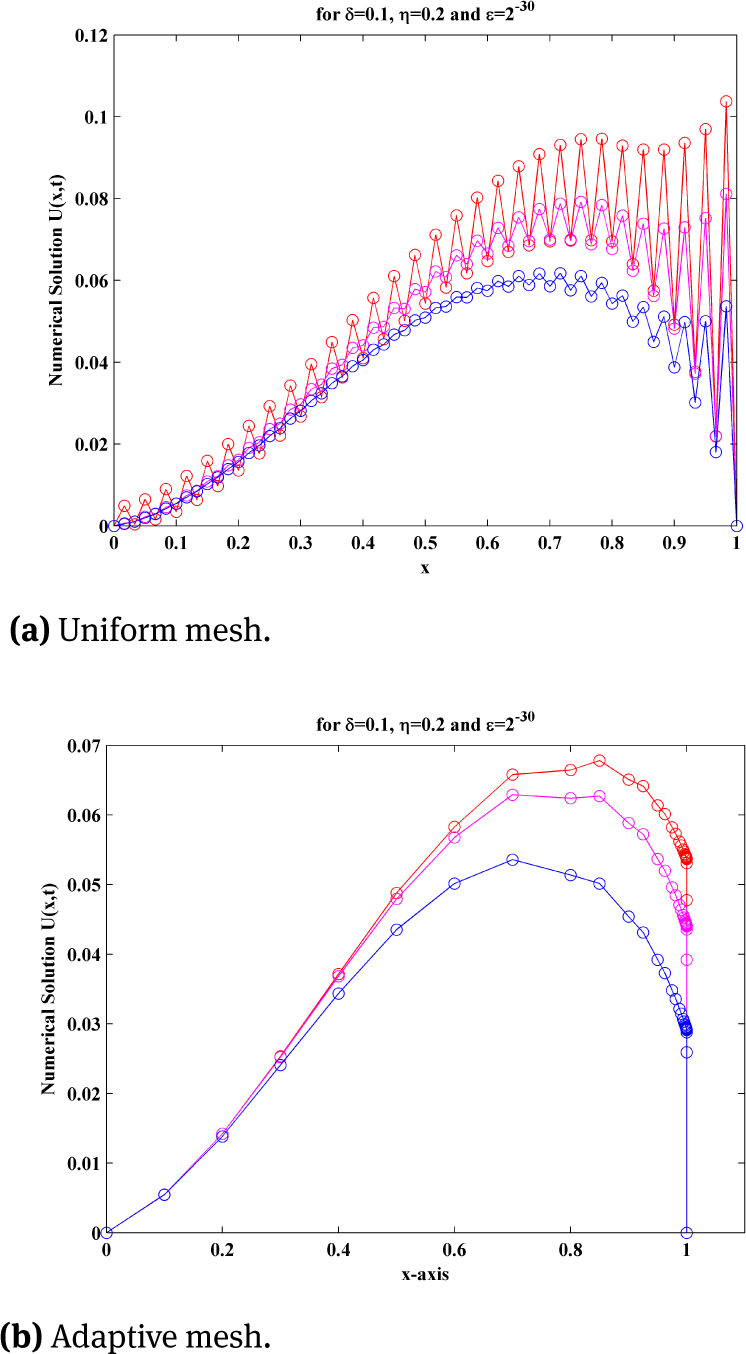
Numerical solution of example 5.3, using uniform mesh and adaptive mesh for three different time level with ε = 2⁻³⁰, δ = 0.1, η = 0.2, M=60 and N=20.

Fig. 9

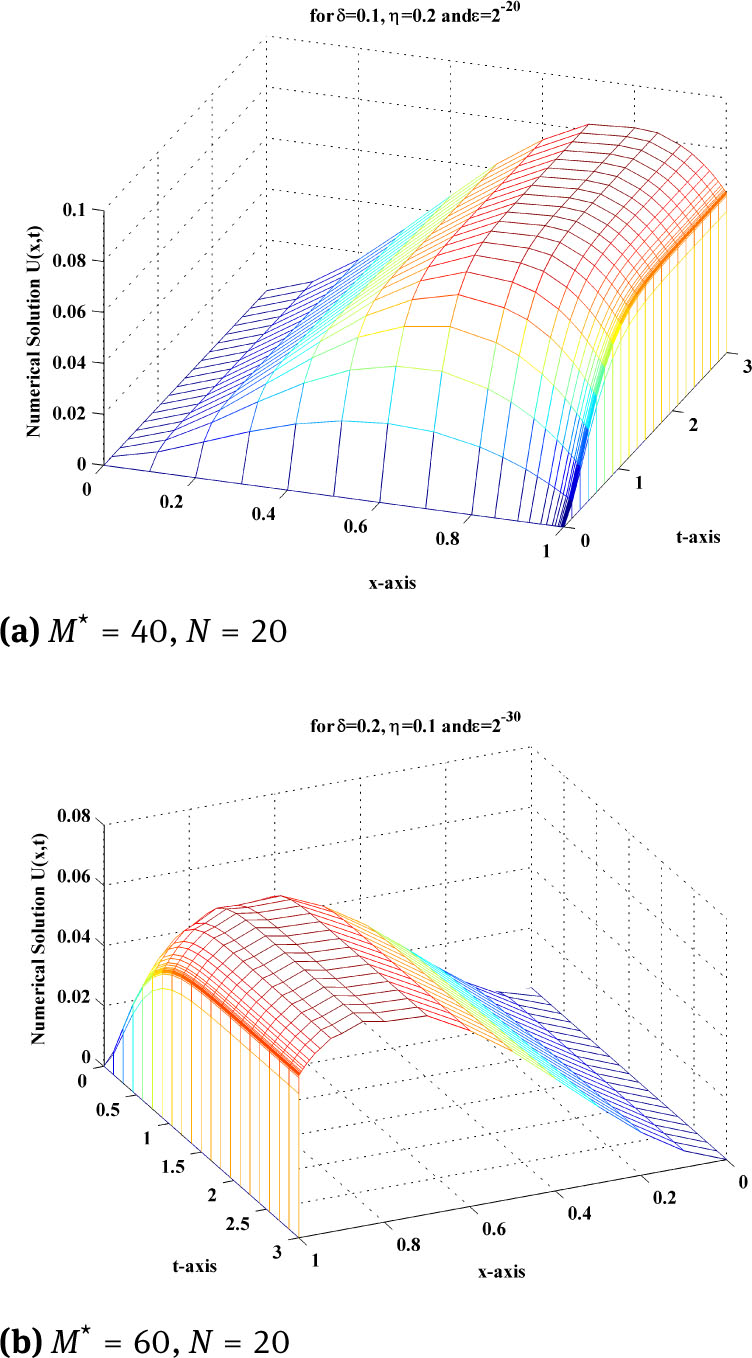
Surface plot of example 5.3, using adaptive mesh for different values of ϵ, δ and η.

Table 5

Maximum point wise errors of the solution and corresponding rate of convergence for Example 5.3 by taking δ = 0.1, η = 0.2, M=10 and N=20 for different values of ε.

ε	Generated mesh	Max. error	Rate of Convergence
	(M^*)		(R^{M^*,N})
2⁻¹⁰	20	4.0629e-03	0.7271
2⁻¹¹	22	4.1600e-03	0.7421
2⁻¹²	24	4.2101e-03	0.7483
2⁻¹³	26	4.2353e-03	0.7514
2⁻¹⁴	28	4.2479e-03	0.7533
2⁻¹⁵	30	4.2542e-03	0.7544
2⁻¹⁶	32	4.2573e-03	0.7551
2⁻¹⁷	34	4.2589e-03	0.7555
2⁻¹⁸	36	4.2597e-03	0.7557
2⁻¹⁹	38	4.2600e-03	0.7558
2⁻²⁰	40	4.2603e-03	0.7558
2⁻²¹	42	4.2604e-03	0.7559
2⁻²²	44	4.2604e-03	0.7559
2⁻²³	46	4.2604e-03	0.7559
2⁻²⁴	48	4.2604e-03	0.7559
2⁻²⁵	50	4.2604e-03	0.7559
2⁻²⁶	52	4.2604e-03	0.7559
2⁻²⁷	54	4.2604e-03	0.7559
2⁻²⁸	56	4.2604e-03	0.7559
2⁻²⁹	58	4.2604e-03	0.7559
2⁻³⁰	60	4.2604e-03	0.7559

6 Conclusions

In this work, a time dependent singularly perturbed differential-difference convection-diffusion equation is solved numerically by using an adaptive grid method. To discretize the domain, we used uniform mesh in the temporal direction and an adaptive mesh has been generated using the concept of entropy function for the spatial direction. The method is based on central finite difference scheme. It has been found that our algorithm gives oscillation free solution with a minimum no of mesh points. Numerical results are carried out to show the efficiency and accuracy of the method. From the results it can be observed that, the method converges uniformly with respect to the perturbation parameter ε. It is also observed and shown in figures that how perturbation parameter ε and shift parameters δ and η effect the boundary layer behaviour of solutions. From the numerical results, it is concluded that our adaptive mesh offers a significant advantage with compare to Bakhvalov and Shishkin meshes. The computation is simple and intuitive.

References

[1] O. Arino, M.L. Hbid, E. Ait Dads, Delay differential equations and applications, Springer, Berlin, 2006.10.1007/1-4020-3647-7Search in Google Scholar

[2] N.S. Bakhvalov, On the optimization of the methods for solving boundary value problems in the presence of boundary layers, Zh. Vychisl. Mater. Fiz. 9(1969), pp. 841–859.Search in Google Scholar

[3] K. Bansal, K.K. Sharma, Parameter uniform numerical scheme for time dependent singularly perturbed convection-diffusion-reaction problems with general shift arguments, Numer. Algor. 75(1)(2017), pp. 113–145.10.1007/s11075-016-0199-3Search in Google Scholar

[4] K. Bansal, P. Rai, K.K. Sharma, Numerical treatment for the class of time dependent singularly perturbed parabolic problems with general shift arguments, Differ. Equ. Dyn. Syst. 25(2)(2017), pp. 327–346.10.1007/s12591-015-0265-7Search in Google Scholar

[5] O. Cheng, M. Jia-qi, The nonlinear singularly perturbed problems for predator-prey reaction diffusion equation, J. Biomath. 20(2)(2005), pp. 135–141.Search in Google Scholar

[6] E.R. Doolan, J.J.H. Miller, W.H.A. Schilders, Uniform numerical methods for problems with initial and boundary layers, Boole Press, Dublin, 1980.Search in Google Scholar

[7] A. Friedman, Partial differential equations of parabolic type, Prentice-hall, Englewood Cliffs, 1964.Search in Google Scholar

[8] E.C. Gartland, Graded-mesh difference schemes for singularly perturbed two-point boundary value problems, Math. Comput. 51(184)(1988), pp. 631–657.10.1090/S0025-5718-1988-0935072-1Search in Google Scholar

[9] D. Kumar, M.K. Kadalbajoo, A parameter-uniform numerical method for time dependent singularly perturbed differential-difference equations, Appl. Math. Model. 35(6)(2011), pp. 2805–2819.10.1016/j.apm.2010.11.074Search in Google Scholar

[10] V. Kumar, B. Srinivasan, An adaptive mesh strategy for singularly perturbed convection diffusion problems, Appl. Math. Model. 39(2015), pp. 2081–2091.10.1016/j.apm.2014.10.019Search in Google Scholar

[11] C.G. Lange, R.M. Miura, Singular perturbation analysis of boundary-value problems for differential-difference equations, SIAM J. Appl. Math. 42(1982), pp.502–531.10.1137/0142036Search in Google Scholar

[12] J.J.H. Miller, E.O. Riordan and I.G. Shishkin, Fitted numerical methods for singular perturbation problems, Word Scientific, Singapore, 1996.10.1142/2933Search in Google Scholar

[13] M. Musila, P. Lansky, Generalized Stein’s model for anatomically complex neurons, BioSystems. 25(3)(1991), pp. 179–191.10.1016/0303-2647(91)90004-5Search in Google Scholar

[14] J.D. Murray, Mathematical Biology I: An Introduction, third edition, Springer-Verlag, Berlin, 2001.Search in Google Scholar

[15] V.P. Ramesh, M.K. Kadalbajoo, Upwind and midpoint upwind difference method for time dependent singularly perturbed differential-difference equations with layer behavior, Appl. Math. Comput. 202(2)(2008), pp. 453–471.Search in Google Scholar

[16] R.N. Rao, P.P. Chakravarthy, Fitted numerical methods for singularly perturbed one-dimensional parabolic partial differential equations with small shifts arising in the modelling of neuronal variability, Differ. Equ. Dyn. Syst. (2017), pp. 1–18.Search in Google Scholar

[17] H.G. Roos, M. Stynes and L. Tobiska, Numerical Methods for Singularly Perturbed Differential Equations, Springer-Verlag, Berlin, 2008.Search in Google Scholar

[18] V.A. Solonnikov, O.A. Ladyzenskaja and N.N. Ural’ceva, Linear and quasi linear equations of parabolic type, American Mathematical Society Providence, Rhode Island, 1988.Search in Google Scholar

[19] R.B. Stein, A theoretical analysis of neuronal variability, Biophys.J. 5(2)(1965), pp. 173–194.10.1016/S0006-3495(65)86709-1Search in Google Scholar

[20] J. Wu, Theory and applications of partial functional differential equations, Springer, NewYork, 1996.10.1007/978-1-4612-4050-1Search in Google Scholar

Received: 2018-05-06

Accepted: 2018-05-10

Published Online: 2018-09-17

Published in Print: 2019-01-28

This work is licensed under the Creative Commons Attribution 4.0 Public License.

Articles in the same Issue

https://doi.org/10.1515/nleng-2018-0075

Keywords for this article

Differential-difference equations; Singular perturbation; Boundary layer; Entropy; adaptive mesh; Central finite difference scheme

Creative Commons

BY 4.0