Abstract
In this article, ABAQUS finite-element software is used to establish an asphalt pavement structure model under high-temperature environment in summer. The changes in the temperature field and moisture concentration field of asphalt pavement are studied under the condition of 1-day continuous temperature change. The creep model is used to analyse the influence of ambient temperature and humidity on the rutting deformation of asphalt pavement. The results show that the maximum temperature of asphalt pavement can reach 60°C in the high-temperature environment in summer. The temperature accumulation effect causes the temperature of the middle and lower layers to increase by approximately 10°C, which easily induces rutting. Ambient humidity has a great influence on the change in moisture concentration in the upper layer. Considering the influence of ambient humidity in the high-temperature environment, the rut depth increases by 67%.
1 Introduction
As one of the most serious damage forms of asphalt pavement, rutting seriously affects the service performance and service life of asphalt pavement and has a significant influence on pavement quality. Asphalt pavement rutting factors can be divided into internal and external factors. The internal factors include aggregate properties, asphalt mixture gradation, asphalt pavement structure design, and other factors. The external factors are mainly related to ambient temperature, humidity, and load. Asphalt pavement is exposed to the natural environment for a long time, and the service environment is complex and changeable. In recent years, the harsh climate environment of extremely high temperatures in summer and increasingly common vehicle overload have accelerated the generation and development of asphalt pavement rutting.
Temperature is the main factor that affects the rutting deformation of asphalt pavement. Asphalt mixture is a temperature-sensitive material, and mechanical properties are greatly affected by temperature. As the temperature rises, the cohesion of the asphalt mixture decreases, and the strength and stiffness are reduced. In the high-temperature environment, asphalt mixtures behave as semisolid and semifluid states. Under the action of load, the asphalt mixture has flow deformation, which easily produces rutting. In order to study the development law of asphalt pavement rutting, experts and scholars at home and abroad have carried out a large number of relevant experimental research.
Lu et al. used the Hamburg rutting test to study the high-temperature stability of asphalt mixtures and found that the Hamburg rutting test can significantly distinguish the high-temperature stability of different types of asphalt mixtures [1]. Chen used the MEPDG rutting prediction model to analyse the rutting development law of combined base asphalt pavement. The results showed that temperature has a significant influence on the dynamic modulus of the mixture in each structural layer of asphalt pavement, and the maximum rutting deformation occurs in the middle surface layer [2]. Liu et al. analysed the influence of different factors on the rutting resistance of asphalt mixtures through indoor rutting tests and gray theory. The results showed that the main influencing factors of rutting resistance are the asphalt content, aggregate gradation type, and test temperature [3]. Javilla et al. conducted stress tests under different stress levels, and the results showed that load can greatly affect the generation and development of rutting [4]. Pouranian et al. studied the influence of temperature and load on asphalt pavement rutting through laboratory experiments, and the results showed that temperature has a great influence on flow-type rutting. When the temperature exceeds 40°C, the load has a significant influence on the generation and development of asphalt pavement rutting [5]. Liu et al. adopted COMSOL finite-element software to establish a concrete thermodynamic model based on hydration degree, consider the influence of temperature and moisture, and study the change of concrete temperature field, which has important guiding significance [6]. Han et al. analysed the influence of different factors on the temperature field of concrete through experiments and numerical simulation and proposed a concrete heat transfer calculation based on an electric heating system [7].
With the development and application of finite-element theory, the research and prediction of asphalt pavement rutting development by using finite-element software has gradually become the development direction of rutting research. Yang et al. considered the influence of temperature, load frequency, stress, asphalt dosage, and other factors on the dynamic modulus and established a rutting prediction model on the basis of the dynamic modulus. By comparing with measured values, it was found that the model has a higher prediction accuracy for rutting deformation of a three-layer pavement structure [8]. Zhang et al. used ABAQUS finite-element software to establish an asphalt pavement structural model and analysed the influences of environmental temperature, load, and driving speed on asphalt pavement rutting deformation. The study found that temperature has the most significant effect on asphalt pavement rutting deformation, and driving speed is the smallest [9]. Zhang considered the characteristics of asphalt pavement surface material properties changing with temperature and adopted a creep model on the basis of a continuously variable temperature field to analyse the asphalt pavement rutting development law. Research has shown that improving the deformation resistance of the middle surface layer can effectively reduce the generation and development of rutting [10]. Brehnke et al. used finite-element software to analyse and find that overload is an important reason for the generation and development of asphalt pavement rutting [11].
In summary, current research on asphalt pavement rutting mainly focuses on temperature and load without considering the influence of moisture concentration on rutting development. In addition, asphalt pavement experiences a humidity gradient of soil pavement and air during its service, which produces a humidity effect and causes water damage to asphalt pavement. In previous studies, it was generally believed that water damage comes from liquid water. The test method is to soak the specimen in liquid water and compare the wet and dry properties of the specimen before and after immersion. However, according to engineering practice, water damage also exists in arid and less rainy areas. Relevant studies in recent years have also shown that gaseous water migrates and diffuses faster in asphalt pavement and can carry a large number of water molecules into the asphalt pavement in a short time, which is an important reason for asphalt pavement water damage [12]. However, current research on asphalt pavement rutting has ignored the influence of gaseous water on rutting deformation. As a result, the calculated rutting depth of asphalt pavement is low, and the service performance of asphalt pavement is overestimated. Under the high-temperature environment, the diffusion rate of moisture inside asphalt pavement accelerates, and the influence of ambient humidity on the rutting deformation of asphalt pavement gradually increases. Therefore, considering the effect of ambient humidity on the rutting deformation of asphalt pavement can reduce the occurrence of asphalt pavement rutting disease in a humidity environment. It is important to improve the design and service life of asphalt pavement.
In order to simulate the actual service environment of asphalt pavement, this article adopts Abaqus finite-element software to establish the asphalt pavement structure model and analyse the variation law of the asphalt pavement temperature field. The moisture diffusion coefficient of pavement materials at different temperatures is obtained through a moisture diffusion test, and a simulation analysis of the moisture concentration field of asphalt pavement is conducted. The influence of temperature and moisture concentration on the rutting deformation of the asphalt pavement is analysed by introducing temperature and moisture concentration at different times.
2 Temperature field analysis
2.1 Determination of the calculation model
The article selects the asphalt pavement structure commonly used in Chinese expressways: 4 cm SBS-modified asphalt AC-13 top layer + 6 cm SBS-modified asphalt AC-20 middle layer + 8 cm base asphalt AC-25 bottom layer + 40 cm cement stabilized gravel + 20 cm graded gravel + soil base. The model size is 6 m wide and 3 m thick. The pavement structure model is shown in Figure 1.

Pavement structure finite-element model.
In this article, the same finite-element model is used for temperature field, moisture concentration field, and rutting prediction. Because the load has a great influence on the surface structure. Therefore, the load position and the surface layer structure grid are properly encrypted. The model grid division is shown in Figure 2.

Schematic diagram of model grid division.
2.2 Temperature field material parameters
According to the literature [13], the thermal physical property parameters of each structural layer of asphalt pavement are shown in Table 1.
Thermal physical parameters of pavement materials
| Parameter | Unit | Surface course | Grassroots | Subbase | Soil base |
|---|---|---|---|---|---|
| Thermal conductivity | J/(m h °C) | 4,680 | 5,616 | 5,148 | 5,616 |
| Density | kg/m3 | 2,300 | 2,200 | 2,100 | 1,800 |
| Heat capacity | — | 924.9 | 911.7 | 942.9 | 1040.0 |
| Solar radiation absorption rate | — | 0.90 | |||
| Road emissivity | — | 0.70 | |||
| Absolute zero | °C | −273 | |||
| Stefan–Boltzmann constant | J/(h m2 K4) | 2.041 × 10−4 | |||
2.3 Temperature field simulation analysis
Taking the most unfavourable temperature field in Nanchang in July as an example. According to the meteorological data, the 24 h temperature data of a day in July are selected as the boundary conditions of the temperature field simulation. Simultaneously setting 24 transient analysis steps to simulate temperature changes for 24 h a day. Considering the influence of solar radiation, temperature, and convective heat exchange, pavement effective radiation on the asphalt pavement temperature field. Among them, solar radiation, temperature, and convective heat exchange are approximated by equations (1) and (2), respectively. In ABAQUS, the FILM subroutine (which defines the temperature and convective heat exchange) and the DFLUX subroutine (which defines the solar radiation) are, respectively, called to achieve this. The road emissivity is 0.81.
where
where
As well as the accumulation effect of temperature, the temperature data under the same conditions were cycled for 7 days to extract the temperature variation data of each structural layer, as shown in Figure 3.
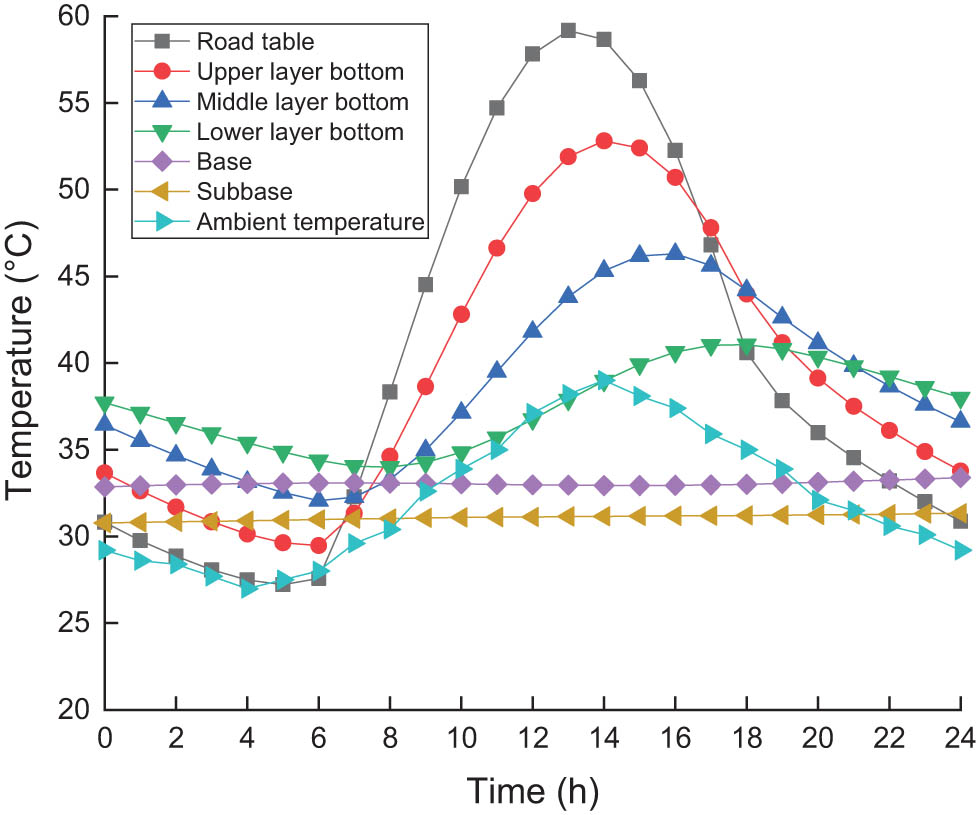
Temperature change curve of each structure layer of asphalt pavement.
As shown in Figure 3, the influence of ambient temperature on the asphalt pavement temperature gradually weakens with increasing depth of the structural layer, and the temperature of the base layer basically remains stable. The temperature of each structural layer of asphalt pavement changes periodically. With the increase in the structure layer depth, the temperature of each layer gradually lags behind the ambient temperature, and the road surface reaches the highest temperature at approximately 14 o’clock. After 7 days of temperature cyclic loading, the initial temperature of each structural layer is higher than the ambient temperature, and the middle and lower layer temperature is increased by approximately 10°C. The temperature accumulation effect needs to be taken into account under persistent hot weather conditions in summer.
Figure 4 shows the heat flow distribution cloud map of asphalt pavement along the depth direction at different moments (HLF2 is positive, which means that the asphalt pavement is exothermic). Affected by solar radiation, asphalt pavement is in an exothermic state at 6:00 AM and 6:00 PM and in an endothermic state at 12:00 noon.

Heat flow distribution cloud diagram of asphalt pavement at different times. (a) 6:00, (b) 12:00, and (c) 18:00.
Figure 5 shows the asphalt pavement temperature field at different times (unit: °C). From Figure 5, the asphalt pavement continuously absorbs heat during the day under the action of solar radiation, which causes the temperature of each structure layer to rise. The temperature of asphalt pavement is decreased due to the exothermic effect of each structure layer. The asphalt pavement experiences three processes of cooling–warming–cooling in 1 day, and the temperature difference of the road surface reaches 30°C in 1 day, which has a great influence on the performance of the asphalt mixture. After 1 day of temperature change, the highest temperature of asphalt pavement appears in the middle and lower layers, which is mainly because the temperature of the asphalt pavement's upper layer is greatly affected by environmental temperature change. The surface of asphalt pavement is heated rapidly by absorbing heat, and the surface of the pavement is in direct contact with the environment at night, which leads to the temperature of the structure layer being higher than the surface temperature.

Temperature nephogram of asphalt pavement at different times. (a) 6:00, (b) 12:00, (c) 14:00, (d) 18:00, (e) 20:00, and (f) 24:00.
3 Humidity field analysis
Inside the asphalt pavement, water mainly migrates and diffuses in gaseous form. In this section, based on the temperature field, the influence of ambient humidity on the performance of asphalt pavement is considered, and the variation law of the moisture concentration field in asphalt pavement is analysed.
3.1 Moisture movement type in asphalt pavement
Inside asphalt pavement, moisture movement can be classified into two types: accumulated moisture movement and penetrating moisture movement. In the early stage of asphalt pavement construction, after high-temperature rolling, it is generally believed that there is no moisture within the asphalt mixture. At this time, moisture diffused and accumulated from the air and subgrade to the asphalt surface until the moisture concentration reached dynamic equilibrium. As the moisture concentration in the soil foundation tends to be saturated, moisture constantly diffuses from the soil foundation to the asphalt surface layer. After the accumulation in the surface layer reaches equilibrium, moisture is diffused into the air through the asphalt surface layer, which is called penetrating moisture diffusion. The above two types of moisture diffusion exist simultaneously during the service life of asphalt pavement. In the early stage of service, the accumulation type of moisture diffusion dominates and gradually changes to the penetration type of moisture diffusion.
This section mainly studies the penetrating moisture diffusion after the moisture concentration reaches equilibrium inside asphalt pavement. First, the moisture diffusion coefficient of asphalt pavement material is determined by the test, and the parameters required for finite-element analysis are obtained by fitting the test results. Then, the mass diffusion module is selected in ABAQUS finite-element software to analyse the moisture concentration field.
3.2 Measurement of moisture diffusivity
3.2.1 Test materials
The AC-13C and AC-20C asphalt mixes selected SBS-modified asphalt and diabase aggregate, and AC-25C selected 70# matrix asphalt and limestone aggregate. The asphalt was tested according to the relevant test specifications [14], and the test results were all in line with the specifications. The results are listed in Table 2. The test results of the asphalt mixture ratio are shown in Figures 6–8.
Test results of asphalt materials
| Pilot projects | Unit | Test values | |
|---|---|---|---|
| SBS modified asphalt | 70# matrix asphalt | ||
| Density (15°C) | g/cm3 | 1.035 | 1.032 |
| Penetration (25°C) | 0.1 mm | 55.4 | 67.0 |
| Ductility (5°C) | cm | 28.5 | — |
| Ductility (10°C) | cm | — | 22.5 |
| Dynamic viscosity coefficient | °C | 65.9 | 49.2 |

Grading curve of the AC-13C asphalt mixture.
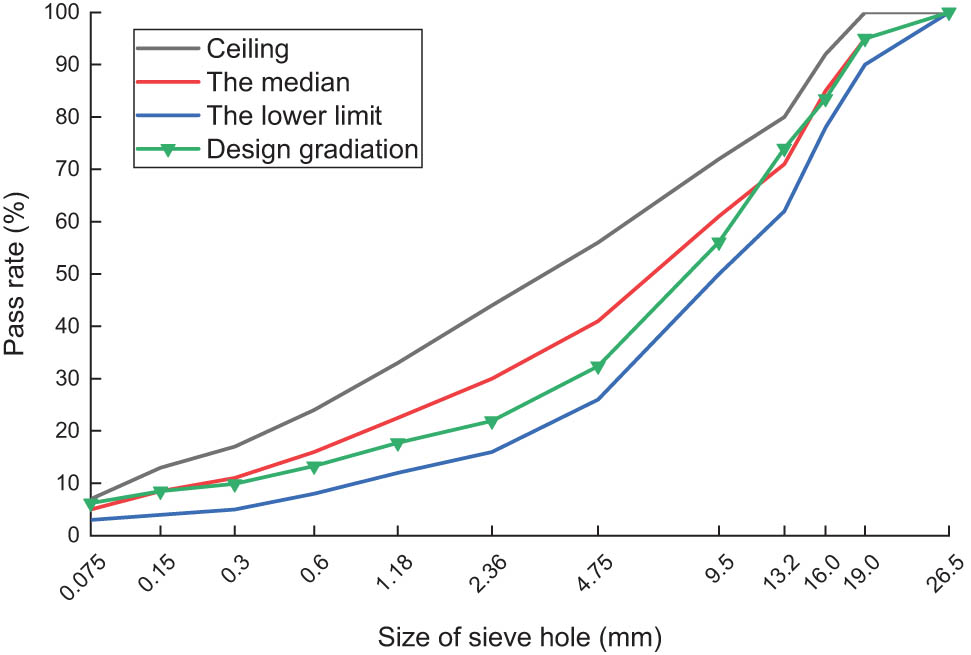
Grading curve of the AC-20C asphalt mixture.

Grading curve of the AC-25C asphalt mixture.
According to the above gradation, the Marshall test was conducted according to the test procedure [14], and the optimal oil–stone ratio of the three asphalt mixtures was determined to be 5.0, 4.5, and 3.9%. Marshall specimens were prepared according to the optimum oil–stone ratio and design grade, and the test results are shown in Table 3.
Summary of Marshall test results
| Pilot projects | AC-13C | AC-20C | AC-25C |
|---|---|---|---|
| Relative density of hair volume | 2.383 | 2.378 | 2.426 |
| Porosity (%) | 4.6 | 5.4 | 4.7 |
| Stability (kN) | 12.70 | 10.48 | 10.30 |
| Flow value (mm) | 4.05 | 4.08 | 2.93 |
| Aggregate voidage (%) | 14.3 | 14.4 | 13.0 |
| Asphalt saturation (%) | 67.7 | 62.3 | 64.3 |
3.2.2 Moisture diffusion test
Referring to the relevant literature research methods [15], the moisture diffusion test device of the asphalt mixture penetration type is designed according to the gravimetric method, as shown in Figure 9. The main part of the device includes a glass container (diameter 70 mm, height 100 mm), specimen, and distilled water. Silicone gaskets are added between the specimen and glass container and sealed with caulking wax. The device is placed in an environmental chamber so that the moisture concentration difference is formed on both sides of the specimen (relative humidity RH2 is controlled by the environmental chamber).
According to the design and grading of the asphalt mixture, the test piece is prepared by the rotating compaction method. The specific method is as follows: a cylindrical specimen with a diameter of 150 mm and a height of 170 mm is formed by a rotary compacting instrument. Then, a standard specimen with a diameter of 100 mm and a height of 150 mm is cut by a core drilling machine and cutting machine. Finally, a thin slice with a thickness of 15 mm ± 1 mm is cut from the middle of the standard specimen as the test specimen. Assemble the test device according to Figure 9. The specific assembly steps are as follows:
Mark the glass every 1 cm, and inject distilled water to a 3 cm mark;
Apply vacuum silicone grease on the upper edge of the glass container and stick the silicone gasket on the upper edge of the glass container;
Apply the melted paraffin wax evenly on the silicone gasket, and quickly cover the specimen sheet with the silicone gasket to seal the opening of the glass container. In this process, the specimen should avoid sliding;
Molten paraffin wax is used to fill the side of the specimen, the joint between the specimen and the silicone gasket, and the joint between the silicone gasket and the edge of the glass container so that only the upper surface of the specimen is in contact with the outside world;
Smooth the whole device with knives to prevent paraffin chips from falling off and affecting the test results during the later weighing process (Figure 10).

Schematic diagram of the penetrating moisture diffusion coefficient measuring device.

Assembly process of moisture diffusion device. (a) Inject distilled water into the container, (b) paste the circular silicone gasket, (c) paste the test piece, and (d) test device finished product.
In this article, five groups of specimens are set up at intervals of 5°C within 10–30°C. According to the literature, after injecting distilled water into the device, the relative humidity in the device can reach balance after 24 h, at which time the relative humidity in the device is about 100% [15]. The whole device is placed in an environment chamber with 50% relative humidity. At this time, due to the existence of the moisture concentration difference on both sides of the specimen, moisture diffuses from the side with high concentration to the side with low concentration, thus reducing the weight of the whole device. The mass reduced by the device is the moisture mass reduced by moisture diffusion.
3.2.3 Analysis of test results
Fick’s first law is often used to describe penetrating moisture diffusion, which can be expressed in the following form:
where J is the diffusion flux, g/m2 s. D is the effective diffusion coefficient, m2/s.
The relationship between moisture concentration and relative humidity is shown as follows:
where C is the moisture concentration (g/m³). P
T is the saturated vapour pressure of water at the corresponding temperature (Pa). R: 8.314 J/(K mol). RH is the relative humidity (%)
The moisture concentration at different temperatures and relative humidities can be calculated from equation (4), and the results are shown in Table 4.
Corresponding moisture concentration at different temperature and relative humidity levels
| Temperature (°C) | PT (Pa) | Moisture concentration (g/m³) | |
|---|---|---|---|
| 50% relative humidity | 100% relative humidity | ||
| 10 | 1228.1 | 4.70 | 9.40 |
| 15 | 1705.6 | 6.41 | 12.83 |
| 20 | 2338.8 | 8.64 | 17.29 |
| 25 | 3169.0 | 11.52 | 23.03 |
| 30 | 4245.5 | 15.17 | 30.35 |
The diffusion flux J is the variation in water and air per unit area in unit time, and its expression is
where A is the specimen diffusion area, and “−” indicates that the diffusion direction is the opposite direction of the concentration gradient.
The expression of the diffusion coefficient can be obtained from equations (3) and (5):
where L is the specimen thickness, mm. C i and C j are the moisture concentrations on both sides of the specimen, g/mm³.
By regularly measuring the mass loss in the device, the penetration moisture diffusion coefficient can be obtained by calculating from equations (6). The diffusion coefficients of the three asphalt mixtures at different temperatures are shown in Table 5.
Moisture diffusion coefficient of asphalt mixture specimen at different temperatures
| Temperature (°C) | Diffusion coefficient (×10−1 mm²/s) | ||
|---|---|---|---|
| AC-13C | AC-20C | AC-25C | |
| 10 | 0.262 | 0.391 | 0.5265 |
| 15 | 0.290 | 0.446 | 0.5550 |
| 20 | 0.338 | 0.472 | 0.6175 |
| 25 | 0.370 | 0.520 | 0.6308 |
| 30 | 0.439 | 0.573 | 0.7182 |
By comparing the diffusion coefficients of the three asphalt mixtures at different temperatures, it can be found that the diffusion coefficient of the AC-25C asphalt mixture is the largest, followed by the AC-20C asphalt mixture, and the AC-13C asphalt mixture is the smallest. This may be because there are more pores in the mixed material with a larger particle size, which easily forms moisture channels, which is manifested as a larger moisture diffusion coefficient. When the temperature increases from 10 to 30°C, the moisture diffusion coefficients of the AC-13C, AC-20C, and AC-25C asphalt mixtures increase by 1.676, 1.465, and 1.364, respectively. Thus, the diffusion coefficient of the AC-13C asphalt mixture is more sensitive to temperature change.
3.3 Simulation of the moisture concentration field on asphalt pavement
3.3.1 Diffusion coefficient of each structure layer of asphalt pavement
According to Section 2.3, the maximum temperature of the asphalt pavement surface is close to 60°C. According to the test results in Section 3.2.3, the moisture diffusion coefficient of the surface structure at 10–60°C is obtained, as shown in Table 6. The diffusion coefficient of the base material is referred to in the data in the literature [12].
where A 1 is the preexponential factor. R = 8.314 J/(K mol). T is the Kelvin temperature.
Diffusion coefficient of each structural layer material of asphalt pavement
| Temperature (°C) | Diffusion coefficient (×10−4 m2/h) | |||
|---|---|---|---|---|
| AC-13C | AC-20C | AC-25C | Basement layer | |
| 10 | 0.937 | 1.412 | 1.872 | 9.657 |
| 15 | 1.062 | 1.553 | 2.023 | 12.578 |
| 20 | 1.215 | 1.719 | 2.193 | 16.234 |
| 25 | 1.359 | 1.876 | 2.358 | 20.775 |
| 30 | 1.530 | 2.057 | 2.529 | 26.370 |
| 35 | 1.716 | 2.253 | 2.697 | 33.214 |
| 40 | 1.928 | 2.451 | 2.892 | 41.527 |
| 45 | 2.143 | 2.654 | 3.081 | 51.556 |
| 50 | 2.375 | 2.881 | 3.279 | 63.582 |
| 55 | 2.619 | 3.105 | 3.473 | |
| 60 | 2.889 | 3.352 | 3.694 | |
3.3.2 Model boundary condition setting
This article considers the variation of non-uniform moisture concentration field on asphalt pavement under the influence of all-weather temperature and humidity and therefore introduces ambient humidity as a boundary condition into the calculation model. It has been confirmed that the relative humidity of soil foundation is above 97% [16]. In this article, the pavement structure base is graded gravel with a large porosity, which is considered to be the same as the ambient humidity of the soil foundation. Therefore, it is assumed that the relative humidity at the boundary under the model is 100%, and the moisture concentration can be calculated as 28.33 g/m³ by using equation (4). The boundary conditions of the model are set equal to the ambient humidity. The calculated results are shown in Table 7 (the saturated vapour pressure of water at different temperatures is calculated by the linear interpolation method).
Ambient moisture concentration of asphalt pavement at different times
| Time (h) | Temperature (°C) | Relative humidity (%) | Moisture concentration (g/m³) | Time (h) | Temperature (°C) | Relative humidity (%) | Moisture concentration (g/m³) |
|---|---|---|---|---|---|---|---|
| 0 | 29.2 | 86.2 | 25.05 | 13 | 38.2 | 46.1 | 21.51 |
| 1 | 28.6 | 90.1 | 25.34 | 14 | 39.0 | 45.6 | 22.15 |
| 2 | 28.4 | 90.5 | 25.18 | 15 | 38.1 | 41.5 | 19.26 |
| 3 | 27.7 | 91.0 | 24.36 | 16 | 37.4 | 49.1 | 21.99 |
| 4 | 27.0 | 91.5 | 23.56 | 17 | 35.9 | 53.2 | 22.06 |
| 5 | 27.5 | 92.1 | 24.39 | 18 | 35.0 | 60.4 | 23.90 |
| 6 | 28.0 | 90.5 | 24.62 | 19 | 33.9 | 66.5 | 24.84 |
| 7 | 29.6 | 87.0 | 25.84 | 20 | 32.1 | 70.5 | 23.80 |
| 8 | 30.4 | 83.2 | 25.81 | 21 | 31.5 | 76.2 | 25.07 |
| 9 | 32.6 | 67.1 | 23.26 | 22 | 30.6 | 80.1 | 25.12 |
| 10 | 33.9 | 63.4 | 23.69 | 23 | 30.1 | 85.2 | 25.99 |
| 11 | 35.0 | 58.2 | 23.03 | 24 | 29.2 | 86.2 | 25.05 |
| 12 | 37.1 | 50.1 | 22.09 |
3.3.3 Temperature humidity coupling
The upper and lower moisture concentration boundary conditions of pavement structure are set into 24 analysis steps, and 24 predefined fields are created to introduce the 24 h daily temperature field simulated in Section 2.3. This part imports the all-weather temperature and humidity environment. By submitting the analysis, the non-uniform moisture concentration field of the road structure under all-weather temperature and humidity can be obtained.
3.3.4 Analysis of moisture concentration field results
Cyclic loading for 7 days under the same environmental conditions is carried out. The calculation results of the bottom of the upper layer, the bottom of the middle layer, and the bottom of the lower layer are taken to draw the curve diagram of the asphalt pavement moisture concentration field, as shown in Figure 11.
As shown in Figure 11, after the moisture concentration field inside the asphalt pavement reaches equilibrium, the moisture concentration at the bottom of the upper layer changes periodically, while the moisture concentration at the bottom of the middle and bottom layers basically remains stable. The variation range of moisture concentration inside the asphalt pavement is consistent with the ambient humidity range.

Moisture concentration curve of asphalt pavement at different times.
Seven different time points within 24 h are selected to analyse the variation rule of moisture concentration along the depth direction of the pavement structure. The variation curve is shown in Figure 12. As shown in Figure 12, after 7 days of moisture accumulation, the influence of environmental humidity on the moisture concentration of asphalt pavement is mainly concentrated in the upper layer and the middle layer. The moisture concentration of the upper layer varies greatly, while that of the lower layer is less affected.

Curve chart of moisture concentration changing with pavement structure depth at different times.
4 Establishment of the rutting calculation model for asphalt pavement
4.1 Model selection
4.1.1 Creep model
This article selects the creep model for simulating asphalt pavement rutting. There are two common ways to describe the creep characteristics of materials: the time-hardening creep model and strain-hardening creep model. The time-hardening creep model is applicable to situations where the stress state remains constant during the analysis process, while the strain-hardening creep model is applicable to situations where the stress state changes during the analysis process. Due to the fact that the occurrence of asphalt pavement rutting is always accompanied by changes in stress state, a strain hardening creep model is used for rutting analysis. The model equation can be expressed as follows:
where
4.1.2 Boundary
Academic x-direction displacement on both sides of the model. Fixed at the bottom of the model.
4.1.3 Coupled analysis
This article considers the impact of ambient temperature and humidity on asphalt pavement rutting deformation. The temperature field and moisture concentration field affect rutting by influencing pavement material parameters. Set predefined temperature and moisture concentration fields in the “load” module. First, import the temperature field calculation results at different times (select 5 h, 9 h, 11 h, and 14 h) and calculate the asphalt pavement rut depth at four different temperatures. For ambient humidity, import the calculation results of the asphalt pavement moisture concentration field at four different times and submit the analysis to obtain the asphalt pavement rut depth under different temperatures and moisture concentrations.
4.2 Finite-element analysis parameters
The creep model in the finite-element software is selected to simulate the rutting of asphalt pavement to characterize the nonlinear characteristics of the asphalt mixture. It is assumed that each structural layer is completely continuous. Based on the literature [17,18,19], the finite-element simulation parameters are determined as shown in Table 8.
Elastic parameters and creep parameters of asphalt mixtures at different temperatures
| Type of mixture | Temperature (°C) | Elastic parameter | Creep model | |||
|---|---|---|---|---|---|---|
| Modulus of resilience (MPa) | Poisson’s ratio | A | n | m | ||
| AC-13C | 20 | 1,400 | 0.3 | 6.546 × 10−11 | 0.936 | −0.591 |
| 30 | 870 | 0.3 | 3.332 × 10−9 | 0.864 | −0.584 | |
| 40 | 620 | 0.35 | 1.445 × 10−8 | 0.794 | −0.573 | |
| 50 | 554 | 0.4 | 1.391 × 10−6 | 0.414 | −0.522 | |
| 60 | 526 | 0.45 | 1.461 × 10−5 | 0.326 | −0.512 | |
| AC-20C | 20 | 1,200 | 0.3 | 4.583 × 10−11 | 0.945 | −0.594 |
| 30 | 910 | 0.3 | 2.460 × 10−9 | 0.798 | −0.587 | |
| 40 | 752 | 0.35 | 3.683 × 10−8 | 0.775 | −0.572 | |
| 50 | 540 | 0.4 | 4.812 × 10−6 | 0.589 | −0.53 | |
| 60 | 380 | 0.45 | 7.779 × 10−5 | 0.382 | −0.439 | |
| AC-25C | 20 | 1,200 | 0.3 | 4.591 × 10−11 | 0.922 | −0.581 |
| 30 | 900 | 0.3 | 3.461 × 10−9 | 0.849 | −0.575 | |
| 40 | 710 | 0.35 | 1.954 × 10−8 | 0.831 | −0.564 | |
| 50 | 500 | 0.4 | 1.207 × 10−6 | 0.322 | −0.542 | |
| 60 | 390 | 0.45 | 3.785 × 10−5 | 0.211 | −0.448 | |
4.3 Load simplification
The current “Code for Design of Highway Asphalt Pavement” (JTG D50-2006) [20] adopts a double set single axle load of 100 kN (BZZ-100) as the standard axle load. The numerical simulation computation transforms the dynamic load to the static load function based on the principle of loading time accumulation. The loading time is calculated according to the formula below. The load simplification parameters are shown in Table 9.
where t is the cumulative action time of load(s), N is the number of load actions (frequency), P is the vehicle axle load (kN), n w is the number of wheels of the shaft (number), p is the tire ground pressure (MPa), B is the tire grounding width (cm), and v is the driving speed (km/h).
Simplified load parameters of the rutting calculation model
| Tire grounding width (cm) | 21.3 |
| Tire ground pressure (MPa) | 0.7 |
| Number of wheels of shaft (number) | 4 |
| Vehicle axle load (kN) | 100 |
| Driving speed (km/h) | 80 |
| Single loading time (s) | 0.007545 |
| Number of load actions (frequency) | 500,000 |
| Load action time (s) | 3,772 |
4.4 Analysis of finite-element calculation results
4.4.1 Temperature
Considering the influence of ambient temperature, temperature fields at different times are introduced. The rutting deformation of asphalt pavement under the action of different temperature fields is shown in Figure 13 (unit: m).
Figure 13 shows the vertical deformation diagram of asphalt pavement under the action of the temperature field at different moments. Introducing 5 and 11 h temperature fields, under 500,000 axial actions, the vertical deformation of asphalt pavement is 1.082 and 1.751 mm, respectively. When 11 and 14 h temperature fields are introduced, the vertical deformation of asphalt pavement is 4.732 and 8.274 mm, respectively. The ambient temperature has a great influence on asphalt pavement rutting deformation. When the ambient temperature is low, the vertical deformation of asphalt pavement increases slightly. When the ambient temperature exceeds 30°C, the rutting deformation of asphalt pavement increases obviously. This is mainly due to the fact that the asphalt mixture is a temperature-sensitive material.

Vertical deformation diagram of asphalt pavement under different temperature fields: (a) 5 h, (b) 9 h, (c) 11 h, and (d) 14 h.
4.4.2 Ambient humidity
On the basis of Section 4.4.1, the calculation results of 5, 9, 11, and 14 h moisture concentration fields are imported. The rutting deformation of asphalt pavement under the action of different temperature and moisture concentration fields is shown in Table 10.
Calculation results of the vertical deformation of asphalt pavement
| Method | Vertical deformation (mm) | |||
|---|---|---|---|---|
| 5 h | 9 h | 11 h | 14 h | |
| Temperature field | 1.082 | 1.751 | 4.732 | 8.274 |
| Temperature field + humidity field | 1.346 | 1.820 | 4.963 | 13.8 |
According to the simulation results, it can be seen that in the low-temperature environment, the ambient humidity has less influence on the rutting deformation of asphalt pavement. When the road surface temperature reaches the maximum at 14 h, considering the influence of environmental humidity, the rutting deformation of asphalt pavement increases by 67%.
Figure 14 shows the vertical displacement curve of each structural layer of asphalt pavement under the action of a 14 h temperature field and moisture concentration field. As can be seen Figure 14, the rutting deformation of asphalt pavement mainly occurs in the upper and middle surfaces. Under the action of load, the asphalt pavement under the tire has settlement deformation. Additionally, due to the extrusion action on both sides of the tire, the pavement structure on both sides of the tire is uplifted. The rutting deformation of the upper and middle layers is a “W” shape and changes to a “V” shape with increasing structure layer depth. The ambient humidity has a great influence on the rutting deformation of the upper and middle layers of asphalt pavement.

Vertical displacement curve of each structural layer of asphalt pavement under different factors: (a) surface, (b) upper floor, (c) middle bottom, and (d) bottom layer.
5 Conclusion
The change in ambient temperature has a great influence on the generation and development of asphalt pavement rutting. When the ambient temperature exceeds 30°C, the rutting deformation of asphalt pavement develops faster with increasing temperature.
The water in the asphalt pavement migrates and diffuses in the form of gaseous water. The moisture diffusion coefficient of the AC-13C mixture specimen is more sensitive to temperature changes, while the AC-25C mixture specimen has the largest moisture diffusion coefficient.
Ambient humidity has a great influence on the moisture concentration in the upper layer of asphalt pavement. When the moisture concentration reaches a balance in asphalt pavement, the moisture concentration in the upper layer changes periodically, while the middle layer and the lower layer basically maintain stability. The change range of moisture concentration in asphalt pavement is consistent with the ambient humidity.
Ambient humidity has a great influence on the rutting deformation of the asphalt pavement surface layer and middle layer. Under the high-temperature environment, considering the influence of ambient humidity, the rutting deformation of asphalt pavement increases by 67%.
Acknowledgements
The authors acknowledge the financial support from the Science and Technology Project of the Jiangxi Provincial Department of Transportation of China (Project No. 2021C0008).
-
Funding information: This work was financially supported by the Science and Technology Project of Jiangxi Provincial Department of Transportation of China (Project No. 2021C0008).
-
Conflict of interest: Authors report no conflict of interest.
-
Data availability statement: The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
[1] Lu Y, Liu AH, Zhang WH, Zhang YC. Study on high temperature performance of asphalt pavement of existing expressway based on Hamburg rut test. J Chin Foreign Highw. 2020;40(4):68–72.Suche in Google Scholar
[2] Chen YF. Predicting rut of composite base asphalt pavement based on MEPDG. J Highw Transp Res Dev. 2020;37(12):15–23.Suche in Google Scholar
[3] Liu ZW, Guo R, Li P, Tang HB, Niu L, Xiao RK, et al. Grey theory analysis on anti-rutting property of asphalt mixture. Highway. 2020;65(3):36–42.Suche in Google Scholar
[4] Javilla B, Mo L, Hao F, Shu B, Wu S. Multi-stress loading effect on rutting performance of asphalt mixtures based on wheel tracking testing. Constr Build Mater. 2017;148:1–9.10.1016/j.conbuildmat.2017.04.182Suche in Google Scholar
[5] Pouranian MR, Imaninasab R, Shishehbor M. The effect of temperature and stress level on the rutting performance of modified stone matrix asphalt. Road Mater Pavement Des. 2018;21(5):1–13.10.1080/14680629.2018.1546221Suche in Google Scholar
[6] Liu L, Zhao Y, Han J, Cheng C, Zhang C. Coupled analysis of thermofluid-structure field for thermal properties of early-age concrete influenced by electric heating system. Geofluids. 2022;2022:1–9.10.1155/2022/3341741Suche in Google Scholar
[7] Han J, Liu L, Zuo C, Wang H, Lin F, Zhao Y, et al. Evolution and parametric analysis of concrete temperature field induced by electric heating curing in winter. Sustainability. 2023;15(10):8337.10.3390/su15108337Suche in Google Scholar
[8] Yang YH, Zhang SL, Zhang Q. Rutting depth prediction based on dynamic modulus and three-layer wheel track rutting test. J Xi’an Univ Arc Technol (Nat Sci Ed). 2019;51(5):717–23+62.Suche in Google Scholar
[9] Zhang ZQ, Shao JW, Zhao QS, Shi JR, Yang XH. Multi-factor prediction of permanent deformation of asphalt pavement at continuous variable temperature. J Jiangsu Univ (Nat Sci Ed). 2022;43(5):604–11.Suche in Google Scholar
[10] Zhang LF. Numerical simulation of rutting deformation of asphalt pavement at continuous variable temperature. J Highw Transp Res Dev. 2018;35(2):15–24.Suche in Google Scholar
[11] Behnke R, Wollny I, Hartung F, Kaliske M. Thermo-mechanical finite element prediction of the structural long-term response of asphalt pavements subjected to periodic traffic load: Tire-pavement interaction and rutting. Comput Struct. 2019;218:9–31.10.1016/j.compstruc.2019.04.003Suche in Google Scholar
[12] Yu XH, Luo R, Liu ZY, Huang TT, Shu Y. Numerical simulation of humidity field of typical cracks in asphalt pavement. J Jilin Univ (Eng Technol Ed). 2022;52(10):2343–51.Suche in Google Scholar
[13] Zhang LF. Study on the structure mechanics response of asphalt pavement based on moving load and continuous variable temperature condition. Xi’an: Chang’an University; 2018.Suche in Google Scholar
[14] JTG E20-2011. Standard test methods of bitumen and bituminous mixtures for highway engineering [S]. Beijing: Ministry of Communications of the People’s Republic of China; 2011.Suche in Google Scholar
[15] Liu ZY. Study of the influence factors of water vapor passing through asphalt mixtures [D]. Wuhan: Wuhan University of Technology; 2018.Suche in Google Scholar
[16] Yu XH, Luo R, Liu ZY, Huang TT, Shu Y. Factors of water vapor diffusion in semi-rigid base. J Harbin Inst Technol. 2022;54(9):65–71.Suche in Google Scholar
[17] Chen HC. Numerical simulation analysis of asphalt pavement rutting based on creep test [D]. Harbin: Harbin Institute of Technology; 2012.Suche in Google Scholar
[18] Feng W. Study on rutting prediction model and deformation mechanism of asphalt pavement based on full-scale test loop[D]. Changsha: Changsha University of Science & Technology; 2021.Suche in Google Scholar
[19] Cao QH. Rutting analysis of influencing factors of asphalt pavement based on temperature field [D]. Shijiazhuang: Shijiazhuang Tiedao University; 2020.Suche in Google Scholar
[20] JTG D50-2006. Design of highway asphalt pavement [S]. Beijing: Ministry of Communications of the People’s Republic of China; 2006. p. 2006.Suche in Google Scholar
© 2023 the author(s), published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Artikel in diesem Heft
- Regular Articles
- Effects of cellulose nanofibers on flexural behavior of carbon-fiber-reinforced polymer composites with delamination
- Damage mechanisms of bismaleimide matrix composites under transverse loading via quasi-static indentation
- Experimental study on hydraulic fracture behavior of concrete with wedge-splitting testing
- The assessment of color adjustment potentials for monoshade universal composites
- Metakaolin-based geopolymers filled with volcanic fly ashes: FT-IR, thermal characterization, and antibacterial property
- The effect of temperature on the tensile properties and failure mechanisms of two-dimensional braided composites
- The influence of preparation of nano-ZrO2/α-Al2O3 gradient coating on the corrosion resistance of 316L stainless steel substrate
- A numerical study on the spatial orientation of aligning fibrous particles in composites considering the wall effect
- A simulative study on the effect of friction coefficient and angle on failure behaviors of GLARE subjected to low-velocity impact
- Impact resistance capacity and degradation law of epoxy-coated steel strand under the impact load
- Analytical solutions of coupled functionally graded conical shells of revolution
- The influence of water vapor on the structural response of asphalt pavement
- A non-invasive method of glucose monitoring using FR4 material based microwave antenna sensor
- Chloride ion transport and service life prediction of aeolian sand concrete under dry–wet cycles
- Micro-damage analysis and numerical simulation of composite solid propellant based on in situ tensile test
- Experimental study on the influence of high-frequency vibratory mixing on concrete performance
- Effects of microstructure characteristics on the transverse moisture diffusivity of unidirectional composite
- Gradient-distributed ZTAp-VCp/Fe45 as new anti-wear composite material and its bonding properties during composite casting
- Experimental evaluation of velocity sensitivity for conglomerate reservoir rock in Karamay oil field
- Mechanical and tribological properties of C/C–SiC ceramic composites with different preforms
- Mechanical property improvement of oil palm empty fruit bunch composites by hybridization using ramie fibers on epoxy–CNT matrices
- Research and analysis on low-velocity impact of composite materials
- Optimizing curing agent ratios for high-performance thermosetting phthalonitrile-based glass fibers
- Method for deriving twisting process parameters of large package E-glass yarn by measuring physical properties of bobbin yarn
- A probability characteristic of crack intersecting with embedded microcapsules in capsule-based self-healing materials
- An investigation into the effect of cross-ply on energy storage and vibration characteristics of carbon fiber lattice sandwich structure bionic prosthetic foot
- Preparation and application of corona noise-suppressing anti-shedding materials for UHV transmission lines
- XRD analysis determined crystal cage occupying number n of carbon anion substituted mayenite-type cage compound C12A7: nC
- Optimizing bending strength of laminated bamboo using confined bamboo with softwoods
- Hydrogels loaded with atenolol drug metal–organic framework showing biological activity
- Creep analysis of the flax fiber-reinforced polymer composites based on the time–temperature superposition principle
- A novel 3D woven carbon fiber composite with super interlayer performance hybridized by CNT tape and copper wire simultaneously
- Effect of aggregate characteristics on properties of cemented sand and gravel
- An integrated structure of air spring for ships and its strength characteristics
- Modeling and dynamic analysis of functionally graded porous spherical shell based on Chebyshev–Ritz approach
- Failure analysis of sandwich beams under three-point bending based on theoretical and numerical models
- Study and prediction analysis on road performance of basalt fiber permeable concrete
- Prediction of the rubberized concrete behavior: A comparison of gene expression programming and response surface method
- Study on properties of recycled mixed polyester/nylon/spandex modified by hydrogenated petroleum resin
- Effect of particle size distribution on microstructure and chloride permeability of blended cement with supplementary cementitious materials
- In situ ligand synthesis affording a new Co(ii) MOF for photocatalytic application
- Fracture research of adhesive-bonded joints for GFRP laminates under mixed-mode loading condition
- Influence of temperature and humidity coupling on rutting deformation of asphalt pavement
- Review Articles
- Sustainable concrete with partial substitution of paper pulp ash: A review
- Durability and microstructure study on concrete made with sewage sludge ash: A review (Part Ⅱ)
- Mechanical performance of concrete made with sewage sludge ash: A review (Part Ⅰ)
- Durability and microstructure analysis of concrete made with volcanic ash: A review (Part II)
- Communication
- Calculation of specific surface area for tight rock characterization through high-pressure mercury intrusion
- Special Issue: MDA 2022
- Vibration response of functionally graded material sandwich plates with elliptical cutouts and geometric imperfections under the mixed boundary conditions
- Analysis of material removal process when scratching unidirectional fibers reinforced polyester composites
- Tailoring the optical and UV reflectivity of CFRP-epoxy composites: Approaches and selected results
- Fiber orientation in continuous fiber-reinforced thermoplastics/metal hybrid joining via multi-pin arrays
- Development of Mg-based metal matrix biomedical composites for acicular cruciate ligament fixation by reinforcing with rare earth oxide and hydroxyapatite – A mechanical, corrosion, and microstructural perspective
- Special Issue: CACMSE
- Preparation and application of foamed ceramic panels in interior design
Artikel in diesem Heft
- Regular Articles
- Effects of cellulose nanofibers on flexural behavior of carbon-fiber-reinforced polymer composites with delamination
- Damage mechanisms of bismaleimide matrix composites under transverse loading via quasi-static indentation
- Experimental study on hydraulic fracture behavior of concrete with wedge-splitting testing
- The assessment of color adjustment potentials for monoshade universal composites
- Metakaolin-based geopolymers filled with volcanic fly ashes: FT-IR, thermal characterization, and antibacterial property
- The effect of temperature on the tensile properties and failure mechanisms of two-dimensional braided composites
- The influence of preparation of nano-ZrO2/α-Al2O3 gradient coating on the corrosion resistance of 316L stainless steel substrate
- A numerical study on the spatial orientation of aligning fibrous particles in composites considering the wall effect
- A simulative study on the effect of friction coefficient and angle on failure behaviors of GLARE subjected to low-velocity impact
- Impact resistance capacity and degradation law of epoxy-coated steel strand under the impact load
- Analytical solutions of coupled functionally graded conical shells of revolution
- The influence of water vapor on the structural response of asphalt pavement
- A non-invasive method of glucose monitoring using FR4 material based microwave antenna sensor
- Chloride ion transport and service life prediction of aeolian sand concrete under dry–wet cycles
- Micro-damage analysis and numerical simulation of composite solid propellant based on in situ tensile test
- Experimental study on the influence of high-frequency vibratory mixing on concrete performance
- Effects of microstructure characteristics on the transverse moisture diffusivity of unidirectional composite
- Gradient-distributed ZTAp-VCp/Fe45 as new anti-wear composite material and its bonding properties during composite casting
- Experimental evaluation of velocity sensitivity for conglomerate reservoir rock in Karamay oil field
- Mechanical and tribological properties of C/C–SiC ceramic composites with different preforms
- Mechanical property improvement of oil palm empty fruit bunch composites by hybridization using ramie fibers on epoxy–CNT matrices
- Research and analysis on low-velocity impact of composite materials
- Optimizing curing agent ratios for high-performance thermosetting phthalonitrile-based glass fibers
- Method for deriving twisting process parameters of large package E-glass yarn by measuring physical properties of bobbin yarn
- A probability characteristic of crack intersecting with embedded microcapsules in capsule-based self-healing materials
- An investigation into the effect of cross-ply on energy storage and vibration characteristics of carbon fiber lattice sandwich structure bionic prosthetic foot
- Preparation and application of corona noise-suppressing anti-shedding materials for UHV transmission lines
- XRD analysis determined crystal cage occupying number n of carbon anion substituted mayenite-type cage compound C12A7: nC
- Optimizing bending strength of laminated bamboo using confined bamboo with softwoods
- Hydrogels loaded with atenolol drug metal–organic framework showing biological activity
- Creep analysis of the flax fiber-reinforced polymer composites based on the time–temperature superposition principle
- A novel 3D woven carbon fiber composite with super interlayer performance hybridized by CNT tape and copper wire simultaneously
- Effect of aggregate characteristics on properties of cemented sand and gravel
- An integrated structure of air spring for ships and its strength characteristics
- Modeling and dynamic analysis of functionally graded porous spherical shell based on Chebyshev–Ritz approach
- Failure analysis of sandwich beams under three-point bending based on theoretical and numerical models
- Study and prediction analysis on road performance of basalt fiber permeable concrete
- Prediction of the rubberized concrete behavior: A comparison of gene expression programming and response surface method
- Study on properties of recycled mixed polyester/nylon/spandex modified by hydrogenated petroleum resin
- Effect of particle size distribution on microstructure and chloride permeability of blended cement with supplementary cementitious materials
- In situ ligand synthesis affording a new Co(ii) MOF for photocatalytic application
- Fracture research of adhesive-bonded joints for GFRP laminates under mixed-mode loading condition
- Influence of temperature and humidity coupling on rutting deformation of asphalt pavement
- Review Articles
- Sustainable concrete with partial substitution of paper pulp ash: A review
- Durability and microstructure study on concrete made with sewage sludge ash: A review (Part Ⅱ)
- Mechanical performance of concrete made with sewage sludge ash: A review (Part Ⅰ)
- Durability and microstructure analysis of concrete made with volcanic ash: A review (Part II)
- Communication
- Calculation of specific surface area for tight rock characterization through high-pressure mercury intrusion
- Special Issue: MDA 2022
- Vibration response of functionally graded material sandwich plates with elliptical cutouts and geometric imperfections under the mixed boundary conditions
- Analysis of material removal process when scratching unidirectional fibers reinforced polyester composites
- Tailoring the optical and UV reflectivity of CFRP-epoxy composites: Approaches and selected results
- Fiber orientation in continuous fiber-reinforced thermoplastics/metal hybrid joining via multi-pin arrays
- Development of Mg-based metal matrix biomedical composites for acicular cruciate ligament fixation by reinforcing with rare earth oxide and hydroxyapatite – A mechanical, corrosion, and microstructural perspective
- Special Issue: CACMSE
- Preparation and application of foamed ceramic panels in interior design

