Fracture research of adhesive-bonded joints for GFRP laminates under mixed-mode loading condition

1 Introduction

The bridge deck structures composed of glass fiber-reinforced polymer (GFRP) have been widely applied in bridge structures at present. The characteristics of using GFRP bridge deck include fatigue and corrosion resistance, light weight, and high strength [1,2,3]. A GFRP bridge deck system can be integrated by adhesive-bonding several modular tube [4]. However, failure analysis showed that the weakest occurred at the adhesive bonding joints in the entire structure. The phenomenon of failure takes place owing to one or several cracks’ initiation and propagation in the joint [5,6]. For the orthotropic GFRP bridge decks, owing to the complex nature of bonded joint, an undesirable failure mode is found as the crack can extend in various paths inside the joint. This mixed failure mode is because of inappropriate bonding between the adherend and the adhesive, owing to inappropriate selection of the adhesive or poor surface preparation. To investigate this troublesome failure mode, the mixed-mode I/II fracture analysis has been widely used by the comparison between the actual energy release rate (ERR or G) and its fracture toughness G _c [7,8]. Therefore, to assess the safety and applications of the structure bonding joints, the criterion of the mixed-mode I/II fracture of adhesively bonded GFRP joints is needed.

To obtain the fracture toughness G _c and the determination of mixed-mode evaluation criterion of bonded interface, a lot of beam-type fracture specimens have been conducted. The mixed-mode bending (MMB) experiment is appropriate for the determination of mixed-mode failure criterion or failure envelops, and it has been used in American society for testing and materials (ASTM) [9]. The MMB experiment, which originally was put forward by Crews and Reeders and then improved by the same authors to guard against nonlinearities, is usually employed for the research of I/II mixed fracture conditions [10]. The interfacial fracture test for three-layer deposited metal layers and two-layer under four-point bending was conducted by Klingbeil and Beuth [11]. An explicit solution of ERR was also compared to the numerical result. The experiment of bi-layer laminates consisting of aluminum–aluminum composites under four-point bending was carried out by Zhang and Lewandoski [12]. The influence of the interfacial properties on the mechanical behavior of laminated structures is also considered. The mixed-mode I/II fracture behavior for delamination growth in multidirectional laminates considering the fiber-bridging effect was investigated by Gong et al. [13] under MMB tests. From experiments, the mixed-mode ERR Gc was measured. However, the whole strain ERR about the mixed-mode fractures is obtained in the aforementioned literature, and the mode decomposition is not derived.

To evaluate the crack behavior in bonding interface accurately, the mode components to the total fracture energy should be known clearly. A series of studies for the mode separation have been performed in the existing literature [14,15,16,17,18]. The interfacial delamination characteristics of graphite/epoxy composite materials were examined by Jurf and Pipes [14]. In this model, the critical fracture strain ERR for the opening, the shearing, and the mixed mode was determined experimentally. What is more, a quadratic fit was obtained by the experimental result. A prior knowledge about the effect of Mode I and Mode II on the cracking in GFRP–concrete bonded interface was built up by Liu and Qiao [15]. In this model, the whole ERR and the mode components with respect to Mode I and Mode II were developed. The fracture criteria for GFRP/steel joint were established by Jiang et al. [16], in which the mixed-mode relationship was investigated considering the Mode-I and Mode-II ERR. The experimental results were consistent with the finite element (FE) results. Chang et al. [17] established the linear, quadratic, and elliptical functions of Mode-I and Mode-II ERR by observing mixed failure mode of granite. The experimental failures could be suitable to some types of fitting curves. The bi-layer beam considering shear deformation was developed by Wang and Qiao [18], in which the separation of Mode-I and Mode-II ERRs was finished by the J-integral and superposition method. The interlaminar fracture toughness of thick fiber composite materials was analyzed using finite element method (FEM) by Agrawal and Jar [19]. The mode decomposition is applicable for the corrected beam with regard to different thickness specimens. Zhang et al. [20] investigated the mixed-mode fracture of adhesively bonded joints composited of pultruded composite lap by experiment. Owing to some differentia (i.e., joint geometrical configurations and failure mode) from the laminated components, they believed that the fracture behavior for the adhesively bonded pultruded laminate joints in the field of civil engineering should be studied. Shahverdi et al. [21] experimentally used asymmetric MMB specimens to investigate the mixed-mode fracture behavior of adhesively bonded pultruded GFRP joints.

From the aforementioned review, it can be concluded that GFRP laminate delamination was found in most of the literature, and the fracture toughness of determination can be obtained on the basis of available standardization. In the bridge structures, GFRP bridge deck comprising pultruded adherends connected by a moderately thick layer of adhesive (1–3 mm) is acceptable [20]. There are few studies on the analytical solutions of the fracture behavior of the GFRP bridge deck comprising a glued layer. Actually, the failure mode of the adhesive bonding joints is different from that of the GFRP laminates delamination. Therefore, it is necessary to establish the reasonableness and analytical formulas on determining the mixed-mode I/II fracture toughness of the FRP member adhesive-bonding joints. The mixed-mode fracture mechanism of adhesive-bonded composite GFRP joints adopting pultruded GFRP four-point MMB (4-MMB) specimens is studied in this article. Based on the sub-layer GFRP laminated beam theory, the deflection, ERR, and compliance of mixed-mode fracture specimens are induced later, in which the effect of moderately thick adhesive layer is considered in the model, where the continuous conditions of the displacements on the interface between the adherend and adhesive are satisfied. Combining loading conditions with continuous requirement of each sub-layer, the mathematical formula for the compliance and ERR of 4-MMB specimen is provided. In this model, the deformation of the upper and lower GFRP plates is mutually independent, and the deformable adhesive is considered to satisfy the displacement compatibility conditions on the bonding interface. The explicit theoretical solutions of the compliance and ERR using the compliance method are reduced. The comparison of the results obtained by the improved model and those by FE analysis (FEA) demonstrates the validity and accuracy of the current model. The designed 4-MMB specimens with varying the thickness of GFRP plates are used to realize various distinct fracture mode I/II mixities and to obtain the fracture toughness of GFRP adhesive-bonded composite joints based on the critical load. The fracture toughness of GFRP adhesive-bonded composite joints can be used to predict crack initiation.

2 Analysis of GFRP 4-MMB specimen within the adhesive layer

A draw of the GFRP 4-MMB specimen is seen in Figure 1. The span length of the specimen is L, the top beam and bottom beam thicknesses are h ₁ and h ₂, and the beam breadth is b. The unbonded length is a, and the adhesive layer thickness is h _a embedded in the bonding area. The forces P act on points of x = L ₀ and x = a + L ₁, where the symmetric loading is considered in 4-MMB configuration and the length a + L ₁ = L − L ₀. In this study, the left rollers can be modeled as the origin of coordinate.

Figure 1

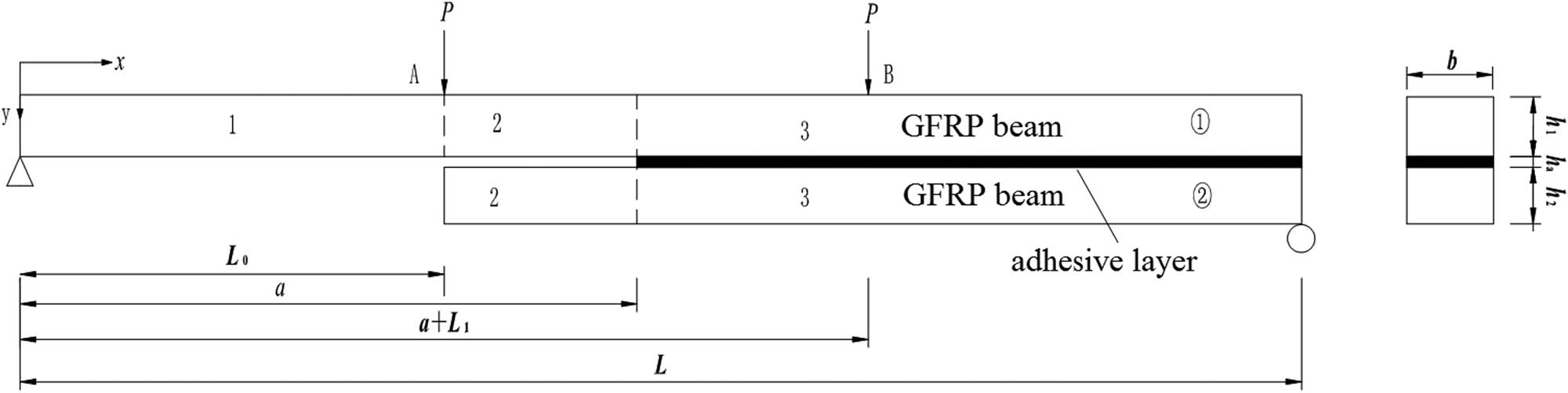
Configuration of the 4-MMB beam.

As shown in Figure 1, when the body in uncracked area (a < x < L) is isolated first, the stress resultant in cross-section is shown based on beam theory (Figure 2). Q _i , N _i , and M _i (i = 1,2) are defined as the internal transverse shear forces, axial forces and bending moments of sub-layers 1 and 2, respectively.

Figure 2

Infinitesimal isolated body configuration of sub-layers.

According to the isolated body equilibrium condition, the relationship between the stresses and internal forces are expressed by:

where σ ( x ) and τ ( x ) are the normal stress and shear stress on the bonding interface, respectively.

According to the composite material beam theory, the constitutive equations of the internal forces and displacements for each sub-layer can be described as:

where u i , ϕ i , and w i are the ith sub-layer’s axial displacement, rotation angle, and deflection, respectively; A i i , B i i , D i i , and H i i are the ith sub-layer’s axial stiffness, coupled stiffness, bending stiffness, and shear stiffness, respectively; ( A i i , B i i , D i i ) = b ∫ − h i 2 h i 2 Q i i ( 1 , z , z 2 ) d z , H i i = 5 b / 4 ∫ − h / 2 h / 2 Q i i ( 1 − 4 z 2 / h 2 ) d z , and Q i i is bias-axis stiffness coefficient, i = 1 , 2 denotes the sub-layers 1 and 2.

According to the overall equilibrium conditions:

where Q a ( x ) , N T ( x ) , Q T ( x ) , and M T ( x ) are the shear force of adhesive, total tension force, shear force, and flexural moment on the section of composite beams, respectively.

By combining equations (1)–(7), the differential equation of deflection is reduced:

where d 3 = h 1 + h 2 + 2 h a 2 .

According to the superposition principle, when the 4-MMB remains linear-elastic, the longitudinal displacement of sub-layers consists of three parts: the axial displacement of the sub-layers, the distinct rotation angle of the upper and lower plates, and the rotation angle caused by the global flexural deformation of the lower and upper adherends. Each part of the deformation can be calculated independently, and the summation is the total deformation.

Taking into account three deformation, the lower surface longitudinal displacement for the upper layers u u can be expressed as:

The upper surface displacement for lower layers u l is

where ϕ is the rotation angle resulting from the global flexural deformation of the lower and upper adherends.

Combined with equations (9) and (10), the stress and displacement of adhesive layer can be described as:

The second derivative of equation (11) yields

For the configuration of 4-MMB specimens, considering symmetric cross-ply composite triangular laminated plates, the vertical compression is neglected, i.e., w i = w , and d ϕ d x = d ϕ i d x = − d 2 w i d x 2 . By differentiating equation (12) and combining this with equation (11), the governing differential equation for deflection of the 4-MMB specimen can be given as:

where 1 E 1 A 0 = 1 E 1 A 1 + 1 E 2 A 2 .

The deflection of the uncracked region ( a ≤ x ≤ L ) is as follows:

where s = G a h a b E 1 A 0 + b d 3 h 1 + b d 3 h 2 2 ( E 1 I 1 + E 2 I 2 ) .

For the cracking region 1 ( 0 ≤ x ≤ L 0 ) , the bending moment in adherend-1 is given as:

Taking equations (14) and (15) into equation (4), the deflection is reduced to:

For the cracking region 2 ( L 0 ≤ x ≤ a ) , the flexural moment of sub-layer 1 is as follows:

Taking equations (16) and (17) into equation (4), the deflection is obtained by:

The undetermined coefficients of 4-MMB are obtained by the following boundary conditions and continuous conditions:

where α = D 1 D 1 + D 2 , D 1 and D 2 is the bending stiffness of layer 1 and layer 2, and D is the bending stiffness of bonded composite beam. In equations (16)–(19), the ten unknown constants Z 1 , … Z 6 , C 1 , … C 4 can be determined detailed in Appendix A, from which the deflection w along with the whole beam can be obtained.

Then, the deflections of the left loading point and the right loading point of 4-MMB can be established as:

Similar to the compliance method used in the literature [22,23,24], the single applied load on loading position is P, and then, the total load is 2P acting on the inner span. The load-point displacement w ¯ can be approximately regarded as the average value of the displacement w L on the left loading point and the displacement w R on the right loading point. Therefore, the compliance C is as follows:

The compliance C is then given as follows:

When the compliance of the specimen is achieved, then following [23], the ERR of the 4-MMB is calculated accurately based on the compliance method by combining with equation (23):

As displayed in equation (24), G is unrelated to the crack length, which shows that this critical value G _c can still be obtained by the critical load P _c through the experiment without measuring the crack propagation length in the fracture experiment process.

3 Mathematical model verification and discussion

To examine the reasonableness of this proposed model, the closed results for G of GFRP bonded 4-MMB specimen are checked by comparing the rigid joint model and numerical solution. As an example, the geometric dimensions of the designed GFRP bonded 4-MMB specimen Figure 1 are determined as follows: the GFRP beam’s span is L = 260 mm, and the cross-sectional size is b × h = 40 × 4 mm. The GFRP beam and GFRP beam are bonded together using the two-component epoxy adhesive and the adhesive thickness of 1 mm, where the pre-existing crack is at end of bonded beam with the crack length a = 150 mm. The material mechanical parameters of the GFRP laminate layers measured by the corresponding standards [25,26] are shown as follows: E y = 7 .29 GPa ; E x = 34 .9 GPa ; G x y = 3 .92 GPa ; and v x y = 0.258 . The mechanical properties of materials of adhesive are as follows: E a = 1 .5 GPa and v a = 0.3 . In the numerical case, the FEA is used to simulate the proposed 4-MMB fracture specimens of GFRP adhesive bonded and check the closed solution provided in Section 2. The FEA is an effective numerical analysis method that has rapidly explored with the development of electronic computers and widely used in structural mechanics analysis. It discretizes an engineering structure into a computational model composed of various elements. The mechanical relationship of the unit is analyzed. According to the variational principle, the FE equation can be obtained as KU = F, where K is the global stiffness matrix, U is the structure node displacement array, and F is the nodal load vector. The approximate solution U is computed in the whole domain. The FE modeling of 4-MMB in this study is based on commercial finite-element software ANSYS (version 12.0). The sub-layers 1 and 2 of GFRP laminate plate are modeled as the layered Plane42 element. The pre-fabricated crack surface is modeled as Targe169 and Conta172 contact element. The Combin14 spring element was selected to model the bonded region of 4-MMB specimen. The thickness of lower beam h ₂ varies to change the sub-layer 2 stiffness to realize different ratios of fracture mixed mode. The ERR G is computed by the virtual crack closure technique (VCCT) [27,28]. To reduce the influence of the FE element size on the VCCT results, the element near the crack tip with a minimum size of 0.25 mm is used to obtain precise solutions, as suggested in the previous FE studies [29]. The FE results are treated as standard results in the present research. Comparison of load-deformation relationship between the present model and the FEA results was shown in Figure 3. It can be observed that the load–deformation curves of the left loading point and the right loading point predicted by the improved model agree well with the FEM results, with maximum divergence of 3.2% and 3.5%, which is acceptable in engineering calculation. The reason might be that the FE result is not an exact solution, but a numerical solution. Besides, we found that the deflection on the left loading point is larger than that of the right loading point because of existing the left crack.

Figure 3

Typical load–deformation curves for 4-MMB specimen.

The comparison of the compliance values for the 4-MMB specimens by the present model, the FEA, and rigid joint model is displayed in Figure 4. As demonstrated in Figure 4a, all of these models demonstrate that the compliance is straightly dependent on the length of crack. However, the rigid joint model relatively underrates the compliance due to neglecting the adhesive deformation. By accounting for the distinct rotation of sub-layer and adhesive deformation, the present solution should be a better approximation to the results from FEA than the rigid joint model.

Figure 4

Typical compliance and ERR with respect to crack length for 4-MMB: (a) compliance and (b) ERR.

The ERR G of adhesive joint crack can be calculated by the VCCT in FEA. The change of ERR with respect to the cracking length using the proposed model, rigid-joint model, and FE method is displayed in Figure 4(b). As seen in Figure 4(b), when compared with the present model, the rigid-joint model undervalues the ERR due to neglect the adhesive deformation. What is more, the present calculated ERR is much closer to the result from FEA with maximum divergence of 3.8%, which reveals that the presently proposed model is useful as the determination of ERR G.

4 Experimental characterization of GFRP-bonded 4-MMB test

In this section, a series of experiments are applied to study the fracture toughness on interfacial delamination of FRP material. Scarce studies in the aforementioned investigations have been found to discuss the determination of FRP-bonded fracture toughness with a certain thickness binder. Unlike interfacial delamination in FRP material, the crack growth of the bonded joint is instable and the failure types (e.g., cohesive failure, interfacial debonding) are more complicated. In this section, an experimental program using 4-MMB specimen was conducted to portray the mixed-mode fracture behavior for GFRP-bonded joint interface. By varying the thickness of GFRP sub-layer, the mixed fracture modes can be conducted.

The 4-MMB specimens compounded from pultruded GFRP laminate and two-component epoxy binder are bonded, and a Teflon film length a was set up on the side of bonded beam to produce the pre-crack. The thin GFRP laminate plates are produced from the E-glass fiber fabric and epoxy resin by pultrusion process. Adhesive consists of two-component epoxy and curing agent. The proportioning of adhesive layer is as follows: epoxy resin:curing agent = 1:1. The material mechanical parameters of pultruded GFRP and binder listed in Table 1 are measured in accordance with ASTM. All specimens were fabricated at room temperature. To realize a standard thickness of the binder and good neatness of the GFRP laminates, the steel clamps are applied for the production of the specimens to ensure that the adhesive has a certain thickness. After fabrication, all 4-MMB specimens were solidified at room temperature for 48 h. The fracture experiments were operated on a hydraulic universal experimental machine, and a four-point flexure loading schematic diagram is shown in Figure 5, where the span of beam L = 260 mm, the length between the left supports and loading point L ₀ = 80 mm, and the width b = 40 mm. By varying the sub-layer height, a different mixed-mode fracture was characterized.

Figure 5

4-MMB experimental setup: (a) universal test machine apparatus and (b) configuration and loading for 4-MMB test.

The fracture experiments were launched adopting displacement control, and the loading rate is 0.5 mm/min. The load–displacement data and curve were continuously and automatically saved by the computer programs. In the experiment, the load acts on the specimens until the occurrence of complete bonded interfacial crack propagation for determining the critical loads for cracking and crack inhibition. A typical the load versus the deflection curve for the adhesively bonded GFRP 4-MMB specimen is displayed in Figure 6. At first, the displacement gradually linear increases with the applied load. Correspondingly, the crack tip of the bonded specimen accumulates the elastic strain energy. As the strain energy reaches to the cracking threshold value, the tiny crack propagates in the bonded joints and the elastic energy is converted into surface energy. The crack initial load P _c is characterized by a decrease in load. And then, the applied load is dropped, and the crack propagating arrests. From Figure 7, it appears that the crack propagates along the bonding interface, which shows that the bond fracture toughness of the GFRP–GFRP component is lower than the fracture toughness of interlamination of GFRP and the bonding interface is a weak link.

Figure 6

Classic load–deformation curve for 4-MMB specimen.

Figure 7

Failure modes of GFRP-bonded specimens: (a) crack propagation along the bonded interface and (b) failure of bond surface.

To obtain mode Ⅰ and mode Ⅱ ERR, the change of fracture mode ratios G _Ⅰ/G _Ⅱ with the variation of GFRP beam thicknesses is shown in Figure 8, in accordance with the global mode decomposition method [30]. As shown in Figure 8, the mode ratios of G _Ⅰ/G _Ⅱ decrease as the thickness ratios of h ₁/h ₂ increase. When h ₁/h ₂ is equal to 6, the mode ratios of G _Ⅰ/G _Ⅱ decrease slowly and then tend to be close to constant. So the maximum thickness ratio of h ₁/h ₂ is chosen 6 in the experiment. Then, according to the load–deflection curve, the total critical ERR G _c, mode Ⅰ and Ⅱ ERR of the GFRP bonded interface are determined by substituting the critical load P _c into equation (26) (Table 2). Consequently, the mixed-mode fracture ratio value G _Ⅰ/G _Ⅱ for different h ₁/h ₂ is shown in Table 2a–d, which evaluates the interfacial bonding characterization under the mixed-mode condition. The 4-MMB specimens are used to estimate the compliance and the mixed-mode ERR by changing the ratio of h ₁/h ₂ in this study. The mixed-mode fracture ratio G _Ⅰ/G _Ⅱ is determined by the h ₁/h ₂ rather than h, and the impact of h is negligible.

Figure 8

Variation of GⅠ/GⅡ for the different ratio of h ₁/h ₂.

5 Conclusions

In this study, a 4-MMB specimen of pultruded GFRP laminates is conducted for researching the interface fracture behavior of GFRP joint under mixed-mode loading condition. The comparison of classical bi-layer beam model (rigid joint model) and improved beam model including layered orthotropic adherends and an epoxy adhesive layer can provide more accurate values of compliance and ERR in the 4-MMB specimen.

Base on the model, linear correlations of the average compliance versus cracking length, as well as the constant relationship between the ERR and cracking length, are determined. The designed 4-MMB specimens by changing the thickness of GFRP plates achieve various fracture mode I/II mixities and experimentally measure the fracture threshold of GFRP adhesive-bonded composite joints based on the critical load.