Home Effects of microstructure characteristics on the transverse moisture diffusivity of unidirectional composite
Article Open Access

Effects of microstructure characteristics on the transverse moisture diffusivity of unidirectional composite

  • Meng Wang EMAIL logo and Xiaochen Hang
Published/Copyright: May 15, 2023
Download Article (PDF)
Become an author with De Gruyter Brill
Submit Manuscript Author Information
Science and Engineering of Composite Materials
From the journal Science and Engineering of Composite Materials Volume 30 Issue 1

Abstract

To reveal the effects of the microstructure characteristics including fiber shape, void, fiber distribution pattern, and interphase on the transverse moisture diffusivities of unidirectional composites, the steady analysis method based on Fick’s law is adopted. The predicted numerical results are compared with the results from the analytical models to demonstrate the accuracy. From the simulation results, it is found that the increase in the oscillation amplification of non-circular fibers contributes to the orthotropy of diffusivity properties, which attributes to different barrier effects along different directions. The consideration of interphase relieves the barrier effects and the predicted diffusivity values are increased significantly. The effects of voids increase with the void volume fraction and are dependent on the voids’ location. If the fiber random distribution pattern is considered, it is found that the average values of predicted diffusivity decrease gradually with the increase in the number of oscillations.

Keywords: diffusivity; fiber shape; void; fiber distribution pattern; interphase

1 Introduction

Due to the wide usage of polymer composites, more and more attention is paid to the environmental effects such as ultraviolet radiation, moisture, or temperature. The long-term presence of moisture could result in irreversible polymer material degradation such as plasticization, hydrolyzation, matrix cracking, and damage to the fiber/matrix interface.

To reveal the effects of moisture diffusion on the properties of composites, the first barrier is to evaluate the diffusivity of the composites [1]. Different analytical methods have been developed to predict the moisture diffusivity of the composites [2,3,4,5]. Numerical methods have also been developed to obtain the values [6,7]. The numerical diffusivity prediction methods can be divided into two groups, transient [6] and steady [7] methods. In the transient method, the full-size model based on the specimen is developed and the water uptake process is described [8]. With the curves, the diffusivity value can be obtained. For the steady method, the calculation process is based on Fick’s law and designed boundary conditions [9].

For the unidirectional composites, the microstructures are complex due to the existence of different constituents including fiber, matrix, interphase, and void. In the field of solid mechanics, the computational mechanics method has been adopted to reveal the effects of microstructure characteristics on transverse mechanical properties [10]. The microstructure characteristics of the fibers are composed of fiber distribution patterns and fiber shape. Regular fiber distribution patterns had been used to predict the mechanical properties of composites [11]. However, at the microscale of composites, the fiber distribution pattern is actually random. Thus, the random fiber distribution model is now widely used for mechanical property prediction [12,13]. The effects of the fiber arrangement on the moisture diffusion in composites along the transverse direction have been analyzed by Wang et al. [14] and it has been found that simple square or hexagonal fiber arrangements can produce similar results compared with the results of random fiber arrangement. With the development of manufacturing technology, different kinds of fiber shapes can be realized [15]. Yang et al. analyzed the effects of the triangle shaped fibers on the transverse properties of composites [16]. Besides, virtual mechanical tests with different kinds of fiber shapes have been conducted [10]. However, the effects of the fiber shape on the transverse diffusion of the composite have not been revealed.

Another microstructure characteristic of unidirectional composites is the voids that are induced by the manufacturing process [17]. The effects of voids on the elastic or inelastic mechanical properties of composites have also been evaluated [18,19,20]. The effects of voids on the diffusivity have also been revealed [21,22,23] and it can be found that the consideration of voids contributes to the increase in the diffusivity. However, the effects of certain voids’ positions have not been evaluated. Besides the fiber and void, the interphase is also an important structure characteristic in the composites [24]. The effects of interphase on the mechanical properties of composites have been revealed by Maligno et al. [25] with the assumption that the interphase is homogenized and the shape of the interphase is regular. However, Wang et al. [26,27] found that the elastic modulus in the interphase is heterogenous and the shape of the interphase is irregular. To evaluate the effects of interphase on water diffusion, both analytical [28] and numerical [29] analyses were conducted. However, the interphase was modeled without considering the heterogeneous properties and irregular microstructure.

In this study, the effects of microstructure characteristics including the fiber distribution pattern, fiber shape, void, and interphase on the transverse diffusivity of unidirectional composites will be analyzed in detail and the sensitivity of each influence factor on the diffusivity can be obtained. First, the diffusivity prediction methods including analytical and numerical methods are presented. Then, the modeling method for each microstructure characteristic is given. At last, the effects of each influence factor are analyzed, compared, and discussed.

2 Diffusivity prediction method

To predict the transverse diffusivity of unidirectional composites, both the analytical and numerical methods are adopted in this study. The analytical methods will be used to verify the numerical results predicted with numerical methods.

2.1 Analytical method

Different analytical methods have been developed to predict the transverse diffusivity of unidirectional composites. The models for the transverse diffusivity prediction are listed below including Halpin–Tsai [2] (equation (1)), Springer–Tsai [3] (equation (2)), Rayleigh [4] (equation (3)), and Woo–Piggott [5] (equation (4)), which will be adopted to demonstrate the numerical results.

(1) D t = D m 1 − V f 1 + V f ,

(2) D t = D m 1 − 2 V f / π 1 − V f ,

(3) D t = D m 1 − V f − 0.305 ⁎ V f 4 ( 1 + V f − 0.305 ⁎ V f 4 ) ( 1 − V f ) ,

(4) D t = D m 2 1 − 4 V f π tan − 1 1 + 2 V f π 1 − 2 V f π − π 2 + 1 − 2 V f π − 1 ,

where V f represents the fiber volume fraction, D m is the diffusivity of the matrix, and D t is the equivalent diffusivity along the transverse direction.

In the models listed above, only the fiber and matrix are considered. The analytical method considering interphase had been developed by Lei et al. [28] and is also adopted in this study to demonstrate the numerical results.

(5) D t D m = β V m + α ( 2 − V m ) D i / D m β ( 2 − V m ) + α V m D i / D m ,

where D i represents the diffusivity of the interphase, and V i is the interphase volume fraction, α = V i + ( V i + 2 V f ) D f / D i and β = V i + 2 V f + V i D f / D i .

2.2 Numerical method

To predict the equivalent diffusivity with the FEM, the calculation process is based on Fick’s law. The Fick’s law is composed of Fick’s first law and Fick’s second law. The Fick’s first law is used to calculate the mass diffusion flux. After considering both the influence of time and mass conservation law, the Fick’s second law can be obtained. Fick’s first law shown in equation (6) is adopted in this study for prediction of transverse diffusivity with the steady analysis method.

(6) J x = − D x ⋅ ∂ C ∂ x ,

where J x is the component of mass flux along x direction, C is the concentration of diffusion substance, x is the space coordinate, and D x is the diffusion coefficient.

To obtain the transverse diffusivity of unidirectional composite with the steady analysis method, the relative moisture concentration should be applied at the boundaries of FEM model first (Figure 1). The concentration value at x = 0 is set to be one and the concentration value at the corresponding opposite boundary with x = a is set to be zero. Then, with mass diffusion module of commercial software ABAQUS, the mass flux in each element can be obtained. At last, to obtain the average diffusivity value based on the mass flux in the FEM model, the calculation method shown in equation (7) is adopted in this study. The calculation method is similar to that used for prediction of equivalent thermal conductivity [30,31].

(7) J x ave = − D x eff ⋅ C a − C 0 a ,

where J x ave is the average mass flux on the surface of x = 0 or x = a, D x eff is the effective diffusivity along the x direction.

Figure 1 Fiber square distribution model with boundary conditions.
Figure 1

Fiber square distribution model with boundary conditions.

The diffusivity properties of the constituents are shown in the Table 1. The values are referred from previous studies [23,28]. The diffusivity of interphase is assumed to be five times larger than that of the matrix as in the study by Joliff et al. [29]. The fiber volume fraction considered in this study is chosen as 30% based on previous studies [23,28].

Table 1

Diffusivity values of the constituents [23,28]

Material Fiber Matrix Void Interphase
Diffusivity (10−6 mm2/s) 0 4.64 46.4 23.2

3 Microstructure characteristics modeling

Different kinds of microstructure characteristics have been considered in this study including fiber shape, void, fiber random distribution pattern, and interphase. The corresponding modeling methods are shown below.

3.1 Fiber shape modeling

The fiber shape is modeled with the level set function [15] as shown in equation (8). The distance between the fiber center and the boundary is defined using equation (9). With the equations, the model with different fiber shapes can be established.

(8) ϕ ( x , θ ) = ∥ x − c ∥ − R ( α ( x ) , θ ) ,

(9) R ( α ( x ) , θ ) = A + B Y 1 ( θ ) + C { Y 2 ( θ ) cos ( k 1 α ) + Y 3 ( θ ) sin ( k 1 α ) + Y 4 ( θ ) cos ( k 2 α ) + Y 5 ( θ ) sin ( k 2 α ) } ,

where α(x) is the polar angle at position x; θ is the randomness of a quantity; Y i (θ), i = 1,…,5 are the uniform random variables, with the first one controlling the variation in reference radius, while the other four control the randomness of the rough circle’s amplitude; k 1 and k 2 are deterministic constants that define the period of oscillations of the random rough circle around the shape of the reference circle; A is radius for the reference circle, with B representing its variation; and C is the mean amplitude of the random rough circle. In this study, the effects of randomness in the rough circle were ignored and only the models with the same fiber area (fiber volume fraction) were considered, so Y 1(θ) is set to be zero, Y i (θ), i = 2,…,5 are equal to 1, k 1 = 0 and k 2 is determined according to the number of oscillations. The models with different k 2, C, and fiber shape orientation ang are shown in Figure 2, which shows the capability of the modeling method.

Figure 2 Fiber square distribution model with different fiber shapes. (a) k 2 = 2, C = 0.226 μm, ang = 0°, (b) k 2 = 2, C = 0.226 μm, ang = 90°, (c) k 2 = 2, C = 0.716 μm, ang = 0°, (d) k 2 = 2, C = 0.716 μm, ang = 90°, (e) k 2 = 3, C = 0.716 μm, ang = 0°, (f) k 2 = 4, C = 0.716 μm, ang = 0°, (g) k 2 = 5, C = 0.716 μm, ang = 0°, (h) k 2 = 12, C = 0.716 μm, ang = 0°.
Figure 2

Fiber square distribution model with different fiber shapes. (a) k 2 = 2, C = 0.226 μm, ang = 0°, (b) k 2 = 2, C = 0.226 μm, ang = 90°, (c) k 2 = 2, C = 0.716 μm, ang = 0°, (d) k 2 = 2, C = 0.716 μm, ang = 90°, (e) k 2 = 3, C = 0.716 μm, ang = 0°, (f) k 2 = 4, C = 0.716 μm, ang = 0°, (g) k 2 = 5, C = 0.716 μm, ang = 0°, (h) k 2 = 12, C = 0.716 μm, ang = 0°.

3.2 Void modeling

There are different void modeling methods. One is based on the geometrical model [18] and the other one is based on the finite element model [20]. In this study, the first void modeling method is adopted. Based on the void modeling methodology by Nikopour [18], the models with different void positions are established and shown in Figure 3. The void size should be calculated based on the void volume fraction. The void volume fraction of the models shown is 5%. Besides, the shape of voids is also considered in this study and the models with elliptical voids are shown in Figure 4.

Figure 3 Circular fiber models with circular voids. (a) Void distribution pattern 1, (b) void distribution pattern 2, (c) void distribution pattern 3, and (d) void distribution pattern 4.
Figure 3

Circular fiber models with circular voids. (a) Void distribution pattern 1, (b) void distribution pattern 2, (c) void distribution pattern 3, and (d) void distribution pattern 4.

Figure 4 Models with elliptical shaped voids. (a) 0° elliptical void and (b) 90° elliptical void.
Figure 4

Models with elliptical shaped voids. (a) 0° elliptical void and (b) 90° elliptical void.

3.3 Random fiber distribution pattern

To establish the random fiber distribution model, the modified perturbation modeling process developed by Wang et al. [11] is adopted in this study. The process for the model establishment is described briefly here. First, the regular fiber distribution model is established. Then, the move limit at x and y directions are obtained under the condition that there is no fiber overlapping. Based on the move limit, a random position is selected as the new position for the fiber and each fiber is perturbated with the same process. Thereafter, a criss-crossing process is conducted, which means that the fibers in each row or column are moved to a certain distance. With the criss-crossing process, the random fiber distribution model can be generated efficiently. At last, after 100 iterations of the processes, the random fiber distribution model can be obtained and one example is shown in Figure 5(a). To establish the non-circular random fiber distribution model, the fiber orientation is also set as a random value for each fiber and it is chosen randomly within 0–360°. The random fiber distribution model with elliptical shaped fibers is shown in Figure 5(b).

Figure 5 Random fiber distribution models: (a) circular fiber and (b) elliptical fiber.
Figure 5

Random fiber distribution models: (a) circular fiber and (b) elliptical fiber.

3.4 Interphase modeling

The interphase is a very important influence factor for the moisture diffusion in the polymer composite. There are different interphase characteristics in the composites. The first one is the interphase thickness. The interphase thickness is dependent on the material systems and the manufacturing process [32]. Thus, different interphase thicknesses are considered here within 0.1–0.4 μm to reveal the effects of interphase thickness. The model with 0.4 μm interphase is shown in Figure 6(a). For the model with a non-circular fiber shape, the interphase is also considered and the model with an elliptical shaped fiber is shown in Figure 6(b). The variation in the interphase thickness around the fiber is also considered in this study and the model is shown in Figure 7. The interphase volume fraction is the same as that shown in Figure 6(a).

Figure 6 Models with interphase (a) circular fiber, (b) elliptical shaped fiber.
Figure 6

Models with interphase (a) circular fiber, (b) elliptical shaped fiber.

Figure 7 Model with interphase considering variable thickness.
Figure 7

Model with interphase considering variable thickness.

The second one is the structure characteristics [33]. The experimental results have demonstrated that the shape of the interphase is not the doughnut shape as shown in Figure 6(a) and the shape of the interphase is groove-like. The typical groove depth and width of the interphase are shown in Figure 8.

Figure 8 Groove depth and width of the interphase [31].
Figure 8

Groove depth and width of the interphase [31].

Based on the experimental results, the boundary of the interphase is described with the function equation (10) [27].

(10) y = A sin ( x ) ,

where A is 50 nm for the fiber surface roughness, x represents the circumferential position along the fiber surface. The model with groove-like interphase is shown in Figure 9 and the thickness is set to be 0.4 μm.

Figure 9 Model with groove-shaped interphase.
Figure 9

Model with groove-shaped interphase.

The third factor is the diffusivity distribution pattern within the interphase. In the study by Rocha et al. [34], the diffusivity in the interphase is assumed to decrease linearly from the fiber’s boundary to the matrix’s boundary and it is adopted in this study. Based on the assumption, D max is set to be the diffusivity of the interphase as shown in Table 1 and D m is the diffusivity of matrix (Figure 10).

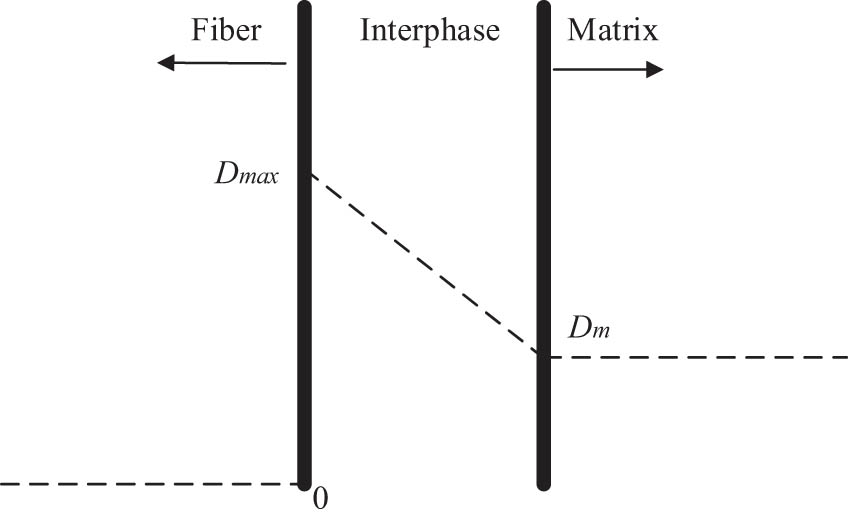
Figure 10 Heterogeneous interphase diffusivity distribution.
Figure 10

Heterogeneous interphase diffusivity distribution.

4 Results and discussion

The numerical method will be validated with the analytical method first. Then, the individual effects of each kind of microstructure characteristic will be evaluated. At last, the coupling effects of the fiber shape and interphase will be revealed.

4.1 Model validation

The fiber square distribution model is analyzed and compared with the analytical models to demonstrate the numerical results. The moisture concentration and mass flow rate (MFL) distribution patterns of the model are shown in Figure 11. Comparing the results from the numerical methods with that from the analytical methods (Table 2), the consistency between the result from the Halpin–Tsai equation and the numerical results demonstrates the effectiveness of the numerical analysis method. The values predicted from the other analytical models are larger than the results from the numerical methods. This conclusion is similar to that obtained in the study by Gao [35]. Besides, the effects of the mesh size on the transverse diffusivity are also revealed. It can be found that the increase in the mesh size from 0.1 to 0.4 μm has little influence on the predicted diffusivity. Thus, the mesh size will be chosen as 0.3 μm for the models to be analyzed next.

Figure 11 Moisture concentration and MFL distribution patterns. (a) Moisture concentration and (b) MFL.
Figure 11

Moisture concentration and MFL distribution patterns. (a) Moisture concentration and (b) MFL.

Table 2

Predicted diffusivity with analytical and numerical models

Analytical models Halpin–Tsai Springer–Tsai Rayleigh Woo–Piggott
Transverse diffusivity (×10−6 mm2/s) 2.498 2.532 3.563 4.00
Approximate mesh size (μm) 0.1 0.2 0.3 0.4
Transverse diffusivity (×10−6 mm2/s) 2.488 2.499 2.496 2.509

4.2 Effects of fiber shape

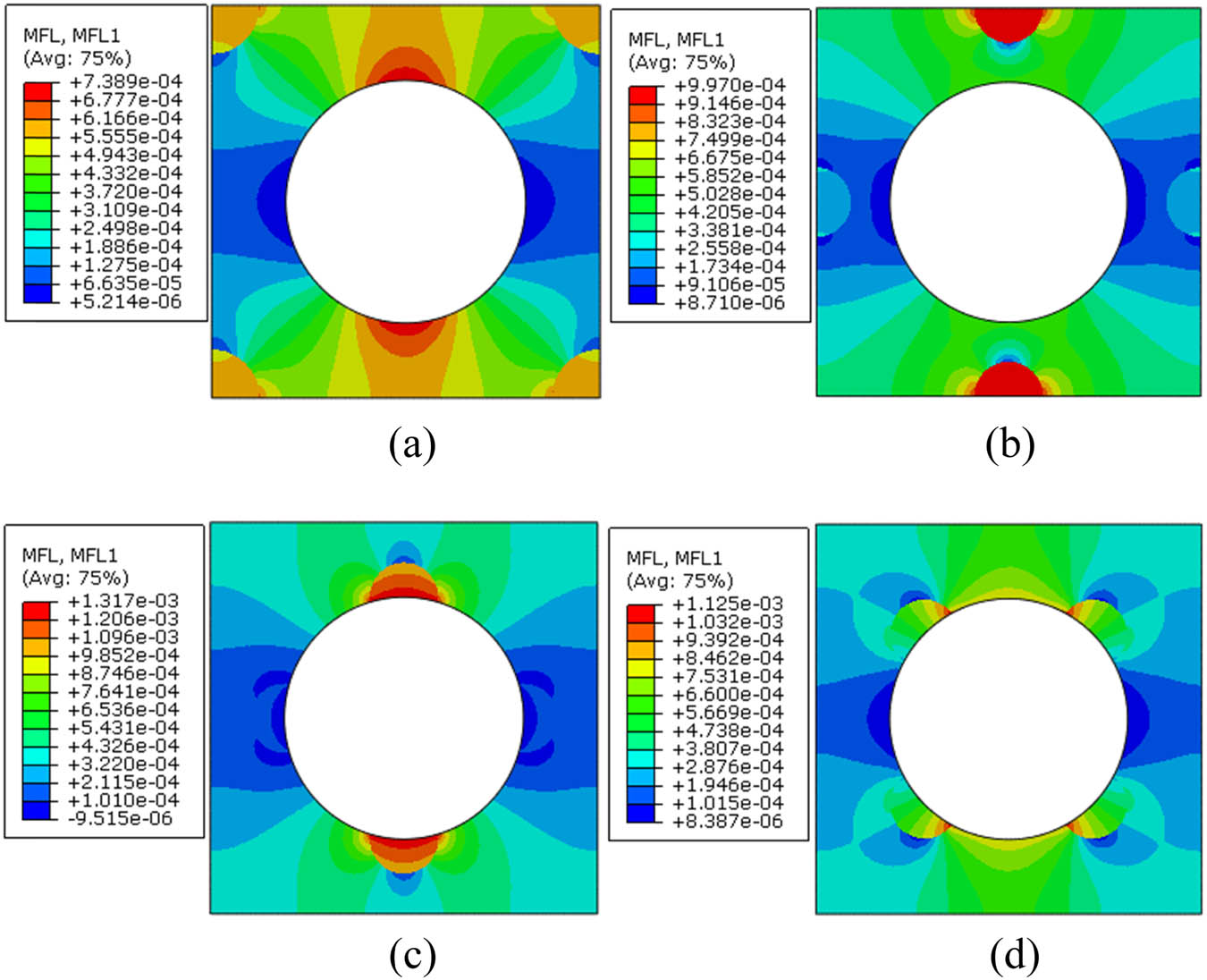
The models with different fiber shapes are analyzed here. The results of the models with elliptical-like fibers are shown in Figure 12. It can be found the orientation of the fiber shape has huge influence on the water diffusivity. Besides, with the increase in the oscillation amplification, the diffusivity is reduced dramatically when the orientation of the fiber shape is 0°, which should attribute to the barrier effect induced by the fiber shape. On the contrary, the diffusivity increases when the orientation is 90°. The moisture concentration and MFL distribution patterns are shown in Figure 13 for the models with elliptical-like fibers. Compared with the result from the circular fiber model, the max MFL value in the RVE becomes larger. However, for the model with elliptical-like fiber at 0°, the area with small MFL values is much larger than that of the model with circular fibers. For the model with elliptical-like fiber at 90°, the area with large MFL values becomes much larger, which contributes to the increase in the equivalent diffusivity.

Figure 12 Predicted diffusivity of models with circular and elliptical-like fibers.
Figure 12

Predicted diffusivity of models with circular and elliptical-like fibers.

Figure 13 Moisture concentration and MFL distribution patterns for the models with elliptical-like fibers. (a) Moisture concentration with ang = 0°, (b) Moisture concentration with ang = 90°, (c) MFL with ang = 0°, and (d) MFL with ang = 90°.
Figure 13

Moisture concentration and MFL distribution patterns for the models with elliptical-like fibers. (a) Moisture concentration with ang = 0°, (b) Moisture concentration with ang = 90°, (c) MFL with ang = 0°, and (d) MFL with ang = 90°.

The models with different fiber shapes are also analyzed and the predicted transverse diffusivity values are shown in Figure 14. It can be found that with the increase in the oscillation’s number, the difference between the models with different fiber shape orientations is decreased, which means that the effects of the fiber shape orientation are prohibited. Besides, it can be found that with the increase in the oscillation’s number, the average transverse diffusivity of the models with different fiber shapes decreases and tends to a certain value.

Figure 14 Transverse diffusivities of the models with different fiber shapes.
Figure 14

Transverse diffusivities of the models with different fiber shapes.

4.3 Effects of voids

The models with different circular void volume fractions and void distribution patterns are analyzed and the results are shown in Table 3. Compared with the model without considering voids, it can be found that the existence of voids results in the increase in the equivalent diffusivity, which is similar to the conclusion obtained in the study by Liu et al. [23]. From the models with different void distribution patterns, it can be found that when the void volume is 1%, the difference between the values of the models with different void distribution patterns is very small. When the void volume fraction is increased to 5%, the difference between the diffusivity values of the models with different void distribution patterns is increased. Besides, it can be found that the increase in the void volume fraction contributes to the increase in the water diffusivity. However, the increase percentage is relatively small compared with that induced by the fiber shapes.

Table 3

Diffusivities of the models with different void volume fraction and distribution patterns (10−6 mm2/s)

Void volume fraction Distribution pattern-1 Distribution pattern-2 Distribution pattern-3 Distribution pattern-4
1% 2.587 2.563 2.595 2.569
5% 2.771 2.853 2.966 2.870

The MFL distribution patterns of the models with 5% void volume fraction are shown in Figure 15. It can be found that the MFL distribution patterns are changed due to the voids’ positions. Especially for the model with voids located at the interface regions between the fiber and matrix, the max MFL values are much larger than the other models, which contribute to the increase in transverse diffusivity as shown in Table 3.

Figure 15 MFL distribution patterns for the models with different void distribution patterns. (a) Void distribution pattern-1, (b) void distribution pattern-2, (c) void distribution pattern-3, and (d) void distribution pattern-4.
Figure 15

MFL distribution patterns for the models with different void distribution patterns. (a) Void distribution pattern-1, (b) void distribution pattern-2, (c) void distribution pattern-3, and (d) void distribution pattern-4.

As the elliptical-like fiber has the largest impact on the moisture diffusivity, the elliptical voids are adopted to reveal the effects of the void shape on the diffusivity. The predicted diffusivity values for the elliptical void models with different void distribution patterns are shown in Table 4. The MFL distribution patterns of the model with different void orientation angles are shown in Figure 16. Compared with the circular void model with the same void distribution pattern and void volume fraction, the effects of the void shape orientation are similar with the effects of fiber shape orientation. It means that the 0° void orientation results in the decrease in the predicted diffusivity compared with the model with circular voids, under the condition that the void distribution pattern is the same. On the contrary, the 90° void orientation contributes to the increase in the predicted diffusivity. However, the differences in the moisture diffusivity values induced by the void shape orientation are much smaller than the difference induced by the fiber shape, which should attribute to the small void volume fraction. Besides, it can be found that the average value for each void distribution pattern is similar to that from the model with circular voids.

Table 4

Predicted diffusivities of the models with elliptical voids and different distribution patterns (10−6 mm2/s)

Elliptical voids orientation Distribution pattern-1 Distribution pattern-2 Distribution pattern-3 Distribution pattern-4
0° 2.655 2.781 2.821 2.756
90° 2.814 2.932 3.195 3.077
Average 2.734 2.856 3.008 2.916
Figure 16 MFL distribution patterns for the models with different void shape orientations: (a) void distribution pattern-1 and void ang = 0° and (b) void distribution pattern-1 and void ang = 90°.
Figure 16

MFL distribution patterns for the models with different void shape orientations: (a) void distribution pattern-1 and void ang = 0° and (b) void distribution pattern-1 and void ang = 90°.

4.4 Effects of random fiber distribution pattern

The models with different fiber shapes and fiber distribution patterns are analyzed and the predicted diffusivity values are shown in Figure 17. It can be found that for the circular fiber models with different random fiber distribution patterns, the diffusivity values are similar to that from the model with fiber square distribution pattern. This is similar to the conclusion obtained in the study by Wang et al. [14]. From Figure 17, it can be concluded that the average diffusivity values decrease with the increase in the number of oscillations. For the models with elliptical-like fibers, the difference between the fiber square distribution models induced by the fiber shape orientations is much larger than the difference between the random fiber distribution models. It should attribute to the consideration of the randomness of fiber shape orientation in the random fiber distribution models, which results in the prohibition of the effects of the fiber shape orientation.

Figure 17 Diffusivities of the random fiber distribution patterns.
Figure 17

Diffusivities of the random fiber distribution patterns.

4.5 Effects of interphase

Based on the analytical model developed by Lei et al. [28], the equivalent diffusivity considering interphase is 3.7086 × 10−6 mm2/s and the value is very similar to that of the result from FEM adopted here (3.709 × 10−6 mm2/s). Compared with the model without considering interphase, the 400 nm interphase contributes to a very large increase in moisture diffusivity of the model. Although the diffusivity of the void is larger than that of the interphase and the void fraction is similar to the interphase volume fraction, the increase rate of diffusivity induced by the interphase is much larger than that induced by the voids. It means that the existence of interphase provides a channel for water diffusion and bypasses the fiber barrier. The MFL distribution pattern is shown in Figure 18, which shows the channel for the water diffusion.

Figure 18 MFL distribution pattern for the model with interphase.
Figure 18

MFL distribution pattern for the model with interphase.

To reveal the effects of the interphase thickness on the equivalent diffusivity, the models with different thickness values are analyzed and the diffusivity values are shown in Table 5. It can be found that the diffusivity increases linearly with the increase in the interphase thickness. Besides, the effects of variation in the interphase thickness around the fiber are also evaluated here. The model with variable interphase thickness is analyzed and the interphase volume fraction is set to be the same as the model with 400 nm. The predicted diffusivity value (3.636 × 10−6 mm2/s) is very close to that from the model with 400 nm, which means that the variation in the thickness is not a very important influence factor.

Table 5

Predicted diffusivities of the models with different interphase thickness values

Interphase thickness 100 nm 200 nm 300 nm 400 nm
Transverse diffusivity (×10−6 mm2/s) 2.849 3.161 3.445 3.709

The model with groove interphase is analyzed here. The interphase volume fraction is also similar to that of the model with 400 nm interphase. The MFL distribution pattern is shown in Figure 19 and the predicted diffusivity value is 3.655 × 10−6 mm2/s. Compared with the diffusivity values of the circular fiber model with 400 nm interphase, it can be found that the difference between them is small and the value is close to the value from the model with variable interphase thickness, which means that the microstructure characteristics of interphase have little influences on the transverse diffusivity.

Figure 19 MFL distribution pattern for the model with groove interphase.
Figure 19

MFL distribution pattern for the model with groove interphase.

The model with heterogeneous interphase distribution pattern is analyzed and the predicted diffusivity value is 3.221 × 10−6 mm2/s. The MFL distribution pattern is shown in Figure 20(a). Compared with the predicted diffusivity value from the model with corresponding uniform interphase diffusivity (3.215 × 10−6 mm2/s), the two values are similar to each other. Thus, it can be concluded that the diffusivity of the model considering heterogeneous interphase can be predicted with the model with corresponding uniform interphase. However, the heterogeneous interphase distribution pattern results in differences in the MFL distribution patterns as shown in Figure 20.

Figure 20 MFL distribution patterns for the model with heterogeneous interphase (a) and the model with corresponding uniform interphase (b).
Figure 20

MFL distribution patterns for the model with heterogeneous interphase (a) and the model with corresponding uniform interphase (b).

4.6 Coupling effects of the fiber shape and interphase

As the fiber shape and interphase have larger impacts on the transverse diffusivity compared with the other influence factors, the coupling effects of fiber shape and interphase are evaluated here. For the non-circular fiber models with interphase, the diffusivity values are shown in Figure 21. Compared with the models without interphase, it can be found that the existence of interphase results in the increase in diffusivity. The change in diffusivities induced by the fiber shape is similar to that of the models without considering the interphase, which means that the effects of the fiber shape orientation are reserved. However, the differences in the values are smaller than those of the models without considering the interphase. This should attribute to the larger perimeter of the non-circular shape, which increases the corresponding interphase area. It is believed that it is the increase in interphase area that contributes to the decrease in the differences. The MFL distribution patterns of the models with elliptical-like fiber are shown in Figure 22. The importance of the effects of the interphase on the water diffusion is also presented.

Figure 21 Predicted diffusivities of the models with different fiber shapes considering the interphase.
Figure 21

Predicted diffusivities of the models with different fiber shapes considering the interphase.

Figure 22 MFL distribution pattern for the elliptical-like fiber models considering the interphase: (a) ang = 0° and (b) ang = 90°.
Figure 22

MFL distribution pattern for the elliptical-like fiber models considering the interphase: (a) ang = 0° and (b) ang = 90°.

5 Conclusion

The effects of microstructure characteristics including the fiber shape, void, fiber distribution pattern, and interphase on the transverse diffusivity are analyzed in this study with the FEM method. To establish the models with different fiber shapes, the modeling method based on the level set method is adopted. For the voids, different void volume fraction and void positions are considered. The modified perturbation method is adopted in this study to model the random fiber distribution pattern. For the interphase, the thickness, structure characteristics, and heterogeneous interphase diffusivity distribution patterns are all considered.

The fiber shape has great influences on the transverse diffusivity of unidirectional composites due to the different barrier effects induced by the number and amplification values of oscillations. The increase in the amplification of oscillations increases the orthotropy of transverse diffusivities. The increase in the number of oscillations contributes to the diffusivity tending to a certain value. The effects of the voids are dependent on the void volume fraction. The effects of the voids’ position become more obvious only if the void volume fraction is large. The voids located at the interphase regions contribute more to the increase in moisture diffusivity. For the random fiber distribution model, the results show that the diffusivity value decreases gradually with the increase in the oscillation number and the effects of fiber shape orientation on equivalent diffusivity are prohibited. The consideration of interphase relieves the barrier effects of the fiber. The microstructure of interphase has little influence on the equivalent diffusivity. The results of the model with heterogeneous interphase diffusivity distribution are very close to the model with corresponding uniform interphase diffusivity. When both the fiber shape and interphase are considered, the difference induced by the fiber shape is prohibited due to the increased specific surface area of non-circular fibers.

  1. Funding information: This study was funded by the Fundamental Research Funds for the Central Universities (2021QN1024) and The Natural Science Foundation of Jiangsu Province (BK20210487).

  2. Conflict of interest: The authors declare that they have no known conflict of interest or personal relationships that could have appeared to influence the work reported in this work.

Reference

[1] Almudaihesh F, Holford K, Pullin R, Eaton M. A comparison study of water diffusion in unidirectional and 2D woven carbon/epoxy composites. Polym Compos. 2022;43(1):118–29.10.1002/pc.26361Search in Google Scholar

[2] Affdl JCH, Kardos JL. The Halpin‐Tsai equations: a review. Polym Eng & Sci. 1976;16(5):344–52.10.1002/pen.760160512Search in Google Scholar

[3] Springer GS, Tsai SW. Thermal conductivities of unidirectional materials. J Compos Mater. 1967;1(2):166–73.10.1177/002199836700100206Search in Google Scholar

[4] Rayleigh JW. On the influence of obstacles arranged in rectangular order on properties of a medium. Philos Mag Ser 1. 1892;34(211):481–502.10.1080/14786449208620364Search in Google Scholar

[5] Woo M, Piggott MR. Water absorption of resins and composites. I. Epoxy homopolymers and copolymers. J Compos Technol Res. 1987;9(3):7–13.10.1520/CTR10249JSearch in Google Scholar

[6] Tang X, Whitcomb JD, Li Y, Sue HJ. Micromechanics modeling of moisture diffusion in woven composites. Compos Sci Technol. 2005;65(6):817–26.10.1016/j.compscitech.2004.01.015Search in Google Scholar

[7] Korkees F, Alston S, Arnold C. Directional diffusion of moisture into unidirectional carbon fiber/epoxy composites: experiments and modeling. Polym Compos. 2018;39(S4):E2305–15.10.1002/pc.24626Search in Google Scholar

[8] Jain D, Mukherjee A, Kwatra N. Local micromechanics of moisture diffusion in fiber reinforced polymer composites. Int J Heat Mass Transf. 2014;76:199–209.10.1016/j.ijheatmasstransfer.2014.04.031Search in Google Scholar

[9] Subramaniyan SP, Imam MA, Prabhakar P. Fiber packing and morphology driven moisture diffusion mechanics in reinforced composites. Compos Part B: Eng. 2021;226:109259.10.1016/j.compositesb.2021.109259Search in Google Scholar

[10] Herráez M, González C, Lopes CS, De Villoria RG, LLorca J, Varela T, et al. Computational micromechanics evaluation of the effect of fibre shape on the transverse strength of unidirectional composites: an approach to virtual materials design. Compos Part A: Appl Sci Manuf. 2016;91:484–92.10.1016/j.compositesa.2016.02.026Search in Google Scholar

[11] Wang M, Zhang P, Fei Q. Computational evaluation of effects of fiber shape on transverse properties of polymer composites considering voids under dynamic loading. J Aerosp Eng. 2019;32(4):04019049.10.1061/(ASCE)AS.1943-5525.0001037Search in Google Scholar

[12] Yang L, Yan Y, Liu Y, Ran Z. Microscopic failure mechanisms of fiber-reinforced polymer composites under transverse tension and compression. Compos Sci Technol. 2012;72(15):1818–25.10.1016/j.compscitech.2012.08.001Search in Google Scholar

[13] Wang M, Zhang P, Fei Q, Guo F. Computational evaluation of the effects of void on the transverse tensile strengths of unidirectional composites considering thermal residual stress. Compos Struct. 2019;227:111287.10.1016/j.compstruct.2019.111287Search in Google Scholar

[14] Wang P, Wu H, Leung CKY. Hygrothermal aging effect on the water diffusion in glass fiber reinforced polymer (GFRP) composite: Experimental study and numerical simulation. Compos Sci Technol. 2022;230:109762.10.1016/j.compscitech.2022.109762Search in Google Scholar

[15] Savvas D, Stefanou G, Papadrakakis M, Deodatis G. Homogenization of random heterogeneous media with inclusions of arbitrary shape modeled by XFEM. Computat Mech. 2014;54(5):1221–35.10.1007/s00466-014-1053-xSearch in Google Scholar

[16] Yang L, Liu X, Wu Z, Wang R. Effects of triangle-shape fiber on the transverse mechanical properties of unidirectional carbon fiber reinforced plastics. Compos Struct. 2016;152:617–25.10.1016/j.compstruct.2016.05.065Search in Google Scholar

[17] Mehdikhani M, Gorbatikh L, Verpoest I, Lomov SV. Voids in fiber-reinforced polymer composites: A review on their formation, characteristics, and effects on mechanical performance. J Compos Mater. 2019;53(12):1579–669.10.1177/0021998318772152Search in Google Scholar

[18] Nikopour H. A virtual frame work for predication of effect of voids on transverse elasticity of a unidirectionally reinforced composite. Comput Mater Sci. 2013;79:25–30.10.1016/j.commatsci.2013.05.049Search in Google Scholar

[19] Vajari DA, González C, Llorca J, Legarth BN. A numerical study of the influence of microvoids in the transverse mechanical response of unidirectional composites. Compos Sci Technol. 2014;97:46–54.10.1016/j.compscitech.2014.04.004Search in Google Scholar

[20] Wang M. Computational evaluation of the effect of defects on the tensile properties of 2D woven composite considering thermal residual stress. Compos Struct. 2022;299:116042.10.1016/j.compstruct.2022.116042Search in Google Scholar

[21] Gueribiz D, Rahmani M, Jacquemin F, Fréour S, Guillen R, Loucif K. Homogenization of moisture diffusing behavior of composite materials with impermeable or permeable fibers – application to porous composite materials. J Compos Mater. 2009;43(12):1391–408.10.1177/0021998308104229Search in Google Scholar

[22] Bourennane H, Gueribiz D, Fréour S, Fréour S, Guillen R, Loucif K. Modeling the effect of damage on diffusive behavior in a polymeric matrix composite material. J Reinf Plast Compos. 2019;38(15):717–33.10.1177/0731684419845479Search in Google Scholar

[23] Liu Z, Lei Y, Zhang X, Kang Z, Zhang J. Effect mechanism and simulation of voids on hygrothermal performances of composites. Polymers. 2022;14(5):901.10.3390/polym14050901Search in Google Scholar PubMed PubMed Central

[24] Riaño L, Belec L, Chailan JF, Joliff Y. Effect of interphase region on the elastic behavior of unidirectional glass-fiber/epoxy composites. Compos Struct. 2018;198:109–16.10.1016/j.compstruct.2018.05.039Search in Google Scholar

[25] Maligno AR, Warrior NA, Long AC. Effects of interphase material properties in unidirectional fibre reinforced composites. Compos Sci Technol. 2010;70(1):36–44.10.1016/j.compscitech.2009.09.003Search in Google Scholar

[26] Wang B, Fang G, Liu S, Liang J. Effect of heterogeneous interphase on the mechanical properties of unidirectional fiber composites studied by FFT-based method. Compos Struct. 2019;220:642–51.10.1016/j.compstruct.2019.04.049Search in Google Scholar

[27] Wang B, Wang Z, Fang G, Li M, Zhu J, Zhao Y, et al. Inverse determine the interfacial strength and surface geometry effects concerning carbon fiber reinforced epoxy composites by experiment aided FFT‐based spectral analysis. Polym Compos. 2022;43(12):9205–17.10.1002/pc.27098Search in Google Scholar

[28] Lei Y, Luo L, Kang Z, Zhang J, Zhang B. Modified Halpin–Tsai equation for predicting interfacial effect in water diffusion process. Sci Eng Compos Mater. 2021;28(1):180–9.10.1515/secm-2021-0017Search in Google Scholar

[29] Joliff Y, Rekik W, Bélec L, Chailan JF. Study of the moisture/stress effects on glass fibre/epoxy composite and the impact of the interphase area. Compos Struct. 2014;108:876–85.10.1016/j.compstruct.2013.10.001Search in Google Scholar

[30] Xu Y, Yagi K. Calculation of the thermal conductivity of randomly dispersed composites using a finite element modeling method. Mater Trans. 2004;45(8):2602–5.10.2320/matertrans.45.2602Search in Google Scholar

[31] Wang J, Chen Y, Feng Y, Zhao G, Jian X, Huang Q, et al. Influence of porosity on anisotropic thermal conductivity of SiC fiber reinforced SiC matrix composite: A microscopic modeling study. Ceram Int. 2020;46(18):28693–700.10.1016/j.ceramint.2020.08.029Search in Google Scholar

[32] Pathan MV, Tagarielli VL, Patsias S. Effect of fibre shape and interphase on the anisotropic viscoelastic response of fibre composites. Compos Struct. 2017;162:156–63.10.1016/j.compstruct.2016.11.046Search in Google Scholar

[33] Xu P, Yu Y, Guo Z, Zhang X, Li G, Yang X. Evaluation of composite interfacial properties based on carbon fiber surface chemistry and topography: Nanometer-scale wetting analysis using molecular dynamics simulation. Compos Sci Technol. 2019;171:252–60.10.1016/j.compscitech.2018.12.028Search in Google Scholar

[34] Rocha I, Raijmaekers S, Van Der Meer FP, Nijssen RP, Fischer HR, Sluys LJ. Combined experimental/numerical investigation of directional moisture diffusion in glass/epoxy composites. Compos Sci Technol. 2017;151:16–24.10.1016/j.compscitech.2017.08.002Search in Google Scholar

[35] Gao C. Research on moisture diffusion and Multiple Environment Ageing Behavior of Fiber Reinforced Polymer Composite [D]. Nanjing: Nanjing University of Aeronautics and Astronautics; 2020.Search in Google Scholar
Received: 2023-01-07
Revised: 2023-04-09
Accepted: 2023-04-20
Published Online: 2023-05-15

© 2023 the author(s), published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Regular Articles
  2. Effects of cellulose nanofibers on flexural behavior of carbon-fiber-reinforced polymer composites with delamination
  3. Damage mechanisms of bismaleimide matrix composites under transverse loading via quasi-static indentation
  4. Experimental study on hydraulic fracture behavior of concrete with wedge-splitting testing
  5. The assessment of color adjustment potentials for monoshade universal composites
  6. Metakaolin-based geopolymers filled with volcanic fly ashes: FT-IR, thermal characterization, and antibacterial property
  7. The effect of temperature on the tensile properties and failure mechanisms of two-dimensional braided composites
  8. The influence of preparation of nano-ZrO2/α-Al2O3 gradient coating on the corrosion resistance of 316L stainless steel substrate
  9. A numerical study on the spatial orientation of aligning fibrous particles in composites considering the wall effect
  10. A simulative study on the effect of friction coefficient and angle on failure behaviors of GLARE subjected to low-velocity impact
  11. Impact resistance capacity and degradation law of epoxy-coated steel strand under the impact load
  12. Analytical solutions of coupled functionally graded conical shells of revolution
  13. The influence of water vapor on the structural response of asphalt pavement
  14. A non-invasive method of glucose monitoring using FR4 material based microwave antenna sensor
  15. Chloride ion transport and service life prediction of aeolian sand concrete under dry–wet cycles
  16. Micro-damage analysis and numerical simulation of composite solid propellant based on in situ tensile test
  17. Experimental study on the influence of high-frequency vibratory mixing on concrete performance
  18. Effects of microstructure characteristics on the transverse moisture diffusivity of unidirectional composite
  19. Gradient-distributed ZTAp-VCp/Fe45 as new anti-wear composite material and its bonding properties during composite casting
  20. Experimental evaluation of velocity sensitivity for conglomerate reservoir rock in Karamay oil field
  21. Mechanical and tribological properties of C/C–SiC ceramic composites with different preforms
  22. Mechanical property improvement of oil palm empty fruit bunch composites by hybridization using ramie fibers on epoxy–CNT matrices
  23. Research and analysis on low-velocity impact of composite materials
  24. Optimizing curing agent ratios for high-performance thermosetting phthalonitrile-based glass fibers
  25. Method for deriving twisting process parameters of large package E-glass yarn by measuring physical properties of bobbin yarn
  26. A probability characteristic of crack intersecting with embedded microcapsules in capsule-based self-healing materials
  27. An investigation into the effect of cross-ply on energy storage and vibration characteristics of carbon fiber lattice sandwich structure bionic prosthetic foot
  28. Preparation and application of corona noise-suppressing anti-shedding materials for UHV transmission lines
  29. XRD analysis determined crystal cage occupying number n of carbon anion substituted mayenite-type cage compound C12A7: nC
  30. Optimizing bending strength of laminated bamboo using confined bamboo with softwoods
  31. Hydrogels loaded with atenolol drug metal–organic framework showing biological activity
  32. Creep analysis of the flax fiber-reinforced polymer composites based on the time–temperature superposition principle
  33. A novel 3D woven carbon fiber composite with super interlayer performance hybridized by CNT tape and copper wire simultaneously
  34. Effect of aggregate characteristics on properties of cemented sand and gravel
  35. An integrated structure of air spring for ships and its strength characteristics
  36. Modeling and dynamic analysis of functionally graded porous spherical shell based on Chebyshev–Ritz approach
  37. Failure analysis of sandwich beams under three-point bending based on theoretical and numerical models
  38. Study and prediction analysis on road performance of basalt fiber permeable concrete
  39. Prediction of the rubberized concrete behavior: A comparison of gene expression programming and response surface method
  40. Study on properties of recycled mixed polyester/nylon/spandex modified by hydrogenated petroleum resin
  41. Effect of particle size distribution on microstructure and chloride permeability of blended cement with supplementary cementitious materials
  42. In situ ligand synthesis affording a new Co(ii) MOF for photocatalytic application
  43. Fracture research of adhesive-bonded joints for GFRP laminates under mixed-mode loading condition
  44. Influence of temperature and humidity coupling on rutting deformation of asphalt pavement
  45. Review Articles
  46. Sustainable concrete with partial substitution of paper pulp ash: A review
  47. Durability and microstructure study on concrete made with sewage sludge ash: A review (Part Ⅱ)
  48. Mechanical performance of concrete made with sewage sludge ash: A review (Part Ⅰ)
  49. Durability and microstructure analysis of concrete made with volcanic ash: A review (Part II)
  50. Communication
  51. Calculation of specific surface area for tight rock characterization through high-pressure mercury intrusion
  52. Special Issue: MDA 2022
  53. Vibration response of functionally graded material sandwich plates with elliptical cutouts and geometric imperfections under the mixed boundary conditions
  54. Analysis of material removal process when scratching unidirectional fibers reinforced polyester composites
  55. Tailoring the optical and UV reflectivity of CFRP-epoxy composites: Approaches and selected results
  56. Fiber orientation in continuous fiber-reinforced thermoplastics/metal hybrid joining via multi-pin arrays
  57. Development of Mg-based metal matrix biomedical composites for acicular cruciate ligament fixation by reinforcing with rare earth oxide and hydroxyapatite – A mechanical, corrosion, and microstructural perspective
  58. Special Issue: CACMSE
  59. Preparation and application of foamed ceramic panels in interior design
https://doi.org/10.1515/secm-2022-0201
Keywords for this article
diffusivity; fiber shape; void; fiber distribution pattern; interphase
Creative Commons
BY 4.0

Articles in the same Issue

  1. Regular Articles
  2. Effects of cellulose nanofibers on flexural behavior of carbon-fiber-reinforced polymer composites with delamination
  3. Damage mechanisms of bismaleimide matrix composites under transverse loading via quasi-static indentation
  4. Experimental study on hydraulic fracture behavior of concrete with wedge-splitting testing
  5. The assessment of color adjustment potentials for monoshade universal composites
  6. Metakaolin-based geopolymers filled with volcanic fly ashes: FT-IR, thermal characterization, and antibacterial property
  7. The effect of temperature on the tensile properties and failure mechanisms of two-dimensional braided composites
  8. The influence of preparation of nano-ZrO2/α-Al2O3 gradient coating on the corrosion resistance of 316L stainless steel substrate
  9. A numerical study on the spatial orientation of aligning fibrous particles in composites considering the wall effect
  10. A simulative study on the effect of friction coefficient and angle on failure behaviors of GLARE subjected to low-velocity impact
  11. Impact resistance capacity and degradation law of epoxy-coated steel strand under the impact load
  12. Analytical solutions of coupled functionally graded conical shells of revolution
  13. The influence of water vapor on the structural response of asphalt pavement
  14. A non-invasive method of glucose monitoring using FR4 material based microwave antenna sensor
  15. Chloride ion transport and service life prediction of aeolian sand concrete under dry–wet cycles
  16. Micro-damage analysis and numerical simulation of composite solid propellant based on in situ tensile test
  17. Experimental study on the influence of high-frequency vibratory mixing on concrete performance
  18. Effects of microstructure characteristics on the transverse moisture diffusivity of unidirectional composite
  19. Gradient-distributed ZTAp-VCp/Fe45 as new anti-wear composite material and its bonding properties during composite casting
  20. Experimental evaluation of velocity sensitivity for conglomerate reservoir rock in Karamay oil field
  21. Mechanical and tribological properties of C/C–SiC ceramic composites with different preforms
  22. Mechanical property improvement of oil palm empty fruit bunch composites by hybridization using ramie fibers on epoxy–CNT matrices
  23. Research and analysis on low-velocity impact of composite materials
  24. Optimizing curing agent ratios for high-performance thermosetting phthalonitrile-based glass fibers
  25. Method for deriving twisting process parameters of large package E-glass yarn by measuring physical properties of bobbin yarn
  26. A probability characteristic of crack intersecting with embedded microcapsules in capsule-based self-healing materials
  27. An investigation into the effect of cross-ply on energy storage and vibration characteristics of carbon fiber lattice sandwich structure bionic prosthetic foot
  28. Preparation and application of corona noise-suppressing anti-shedding materials for UHV transmission lines
  29. XRD analysis determined crystal cage occupying number n of carbon anion substituted mayenite-type cage compound C12A7: nC
  30. Optimizing bending strength of laminated bamboo using confined bamboo with softwoods
  31. Hydrogels loaded with atenolol drug metal–organic framework showing biological activity
  32. Creep analysis of the flax fiber-reinforced polymer composites based on the time–temperature superposition principle
  33. A novel 3D woven carbon fiber composite with super interlayer performance hybridized by CNT tape and copper wire simultaneously
  34. Effect of aggregate characteristics on properties of cemented sand and gravel
  35. An integrated structure of air spring for ships and its strength characteristics
  36. Modeling and dynamic analysis of functionally graded porous spherical shell based on Chebyshev–Ritz approach
  37. Failure analysis of sandwich beams under three-point bending based on theoretical and numerical models
  38. Study and prediction analysis on road performance of basalt fiber permeable concrete
  39. Prediction of the rubberized concrete behavior: A comparison of gene expression programming and response surface method
  40. Study on properties of recycled mixed polyester/nylon/spandex modified by hydrogenated petroleum resin
  41. Effect of particle size distribution on microstructure and chloride permeability of blended cement with supplementary cementitious materials
  42. In situ ligand synthesis affording a new Co(ii) MOF for photocatalytic application
  43. Fracture research of adhesive-bonded joints for GFRP laminates under mixed-mode loading condition
  44. Influence of temperature and humidity coupling on rutting deformation of asphalt pavement
  45. Review Articles
  46. Sustainable concrete with partial substitution of paper pulp ash: A review
  47. Durability and microstructure study on concrete made with sewage sludge ash: A review (Part Ⅱ)
  48. Mechanical performance of concrete made with sewage sludge ash: A review (Part Ⅰ)
  49. Durability and microstructure analysis of concrete made with volcanic ash: A review (Part II)
  50. Communication
  51. Calculation of specific surface area for tight rock characterization through high-pressure mercury intrusion
  52. Special Issue: MDA 2022
  53. Vibration response of functionally graded material sandwich plates with elliptical cutouts and geometric imperfections under the mixed boundary conditions
  54. Analysis of material removal process when scratching unidirectional fibers reinforced polyester composites
  55. Tailoring the optical and UV reflectivity of CFRP-epoxy composites: Approaches and selected results
  56. Fiber orientation in continuous fiber-reinforced thermoplastics/metal hybrid joining via multi-pin arrays
  57. Development of Mg-based metal matrix biomedical composites for acicular cruciate ligament fixation by reinforcing with rare earth oxide and hydroxyapatite – A mechanical, corrosion, and microstructural perspective
  58. Special Issue: CACMSE
  59. Preparation and application of foamed ceramic panels in interior design
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 12.9.2025 from https://www.degruyterbrill.com/document/doi/10.1515/secm-2022-0201/html
Scroll to top button