Abstract
In order to quantitatively analyze the mesoscopic damage process of hydroxyl-terminated polybutadiene composite solid propellant under external load, periodic boundary conditions were applied to the representative volume element model based on sample composition and morphology, the mixed matrix containing aluminum powder was homogenized, and the hyperelastic matrix damage and bilinear/exponential particle–matrix interface cohesive model with initial damage were compiled through the secondary development of Abaqus. At the same time, a data interaction platform was constructed by means of Python and MATLAB, matrix and cohesion parameters were inverted according to the optimization algorithm and experimental data, and the whole process of propellant damage and fracture was simulated from the mesoscopic perspective. The results show that combining the adaptive particle swarm optimization algorithm and the Hooke–Jeeves algorithm can achieve the global optimal parameter inversion in 102 calculations, compared with the single local search algorithm, which can cut about 11% of the objective function values. Considering the matrix damage and the exponential cohesion model with initial damage, the optimal objective function value is 0.01635, which can more accurately simulate the propellant damage and fracture process compared with 0.02136 of a bilinear cohesion model.
1 Introduction
Owing to its appearance, solid propellant has been widely used as the power source of solid rocket motors in the military field because of its stable performance, simple structure, and various types. Different types of equipment formulations will also change due to different emphasis, but the requirements for maintaining stable high energy output have never changed. Therefore, solid propellants are generally composed of oxidizers, combustion agents, and auxiliary materials, which are in a multiphase state geometrically. Under long-term or excessive external load, particle dehumidification, matrix deformation damage, and even fracture will occur in the interior of this multiphase composite material, making its macroscopic mechanical properties change complex. Therefore, it is greatly significant to explore the whole process of propellant damage under load from the microscopic perspective to improve the mechanical properties and maintain the structural integrity of the propellant.
With the development of observation means and computer technology, such as scanning electron microscope and digital image processing technology, the change process of propellant micromorphology under load is established, and the mechanism of propellant micromorphology damage is further clarified. However, due to the limitations of experimental means and observation technology, it is difficult to obtain the interface parameters and damage threshold directly, and it is impossible to achieve quantitative analysis. Therefore, numerical analysis is gradually applied to the mesoscopic damage process of propellant. In order to achieve the accurate acquisition of relevant parameters, in addition to the basic experiments, the construction of geometric models, the application of boundary conditions, and the setting of material constitutive equations become the key to the analysis. Collins et al. [1] and Lee et al. [2] were the first to obtain the three-dimensional micromorphology of solid propellant by using micro-CT and reconstruct the cracks caused by the loading of the propellant. Li et al. [3] discovered the change rule of propellant micro-damage morphology under different tensile strains using high-precision micro-CT and further analyzed the impact of micro-damage on macroscopic mechanical properties. Zhang et al. [4] calculated the average stress of the mesoscopic model based on the finite-element theory and homogenization method and predicted the modulus of composite solid propellant. Tunc and Ozupek [5] and Yun et al. [6] applied the constitutive model including initial damage to the study of mechanical properties of solid propellants and further improved the simulation accuracy. Li et al. [7] proposed the superposition model of Young’s modulus of propellant, established the four-stage damage constitutive model of propellant, and verified the rationality of the model prediction. Pan and Qu [8] used a nonlinear ultrasonic method to monitor the nonlinear dynamic response of propellant in real time to determine the effect of particle dehumidification on propellant damage. Gao and Li [9] obtained the crack growth trend and stress–strain curve under different tensile rates by prefabricating different crack angles. Hou et al. [10] established a mesoscopic crack model of high-energy propellant by using the uniform displacement boundary condition and inserting the cohesive element globally. Zhou et al. [11] realized the simulation of the propellant matrix cracking process based on the secondary development of Abaqus software. Zhi et al. [12] inversely calculated the micro-particle dehumidification process by establishing the objective function of the bonding interface damage parameter and comparing the stress–strain curve of the simulation experiment. However, the aforementioned methods are limited to the optimization of a certain aspect of the numerical analysis of propellants and focus on exploring the influence of single factors such as model, constitutive, or matrix on the mechanical properties of propellants. The aforementioned main factors are not taken into account in the microscopic analysis at the same time. The use of a single inverse algorithm is also easy to make the numerical analysis fall into local optimization, and the setting of the cohesive model is mainly based on a bilinear model so as to a significant difference between the analysis result and the experiment.
In this study, on the basis of considering the cohesive model of the grain–matrix interface and the hyperelastic matrix damage, the mesoscopic particles with different grading are periodically arranged to generate representative volume element (RVE), and periodic boundary loads are applied. At the same time, zero-thickness bonding elements are inserted into the grain–matrix interface, and the matrix damage and exponential cohesion model subprograms are compiled. A data interaction platform is built through Python and MATLAB, and the global optimization and direct search algorithm are combined and compared with the in situ tensile test data to inverse the cohesion and matrix parameters, so as to realize the simulation and quantitative analysis of the whole process of mesoscopic damage of solid propellants.
2 Experimental section
Compared with the macrotensile test, the microtensile test regards the propellant sample as a mixture of microparticles and matrices. In addition to focusing on the overall mechanical properties, it focuses more on the changes of matrices, microparticles, and interface in the process of external force loading. In addition, the addition of ammonium perchlorate (AP) particles and other auxiliary agents, while strengthening the matrix, also took place a certain chemical reaction, which made the mechanical changes of the interface between the matrix and the micro-particles more complex. Therefore, the micro-dynamic tensile test was carried out using a scanning electron microscope to further analyze the micro-change of the propellant under load.
2.1 Test piece and instrument
Test piece: 20 sets of dumbbell-type test piece molds can be made according to the QJ924-85 standard [13] to ensure that the thickness of the test piece is 5 mm, the width of both sides is 12.0 mm, and the width of the central load-bearing part is 5 mm. At the same time, the raw materials purchased from the 41st Institute of the Sixth Research Academy of China Aerospace Science and Technology Corporation were pre mixed into the required slurry for casting. The formed solid propellant sample uses hydroxyl-terminated polybutadiene (HTPB) as the adhesive, AP as the oxidant, aluminum (Al) powder as the combustion aid, toluene diisocyanate (TDI) as the curing agent, and combined bonding agents (aziridine polyester [PAZ], amine polyester [PAM]) are used. The mass fractions of adhesives, oxidizers, combustion aids, and other components are 11, 18.5, 64, and 6.5%, respectively. The treatment of oxidant includes crushing, batching, drying, analysis and inspection, and other processes. For the acceptance of purity, the heating titration and decomposition absorption methods are mostly used, and for the particle size index, the mechanical vibration standard screening is used. For the determination of the properties of Al powder, the oxidation–reduction titration method and mass screening method are selected.
Instrument:
Sigma300 scanning electron microscope: Gemini, Germany;
ETD-2000 ion sputtering instrument: Rigaku, Japan;
MICROTEST200 in situ dynamic tensile test platform: Deben Company, UK;
The tensile test piece and fixture are shown in Figure 1.

In situ stretching fixture and specimen.
2.2 Meso component
The density of Al powder and AP is 2.70 and 1.95 g cm−3, respectively, and AP particle size is divided into 50–80 and 100–150 μm, which basically conforms to Gaussian distribution. Due to the small particle size of aluminum powder, most of it is embedded in the matrix, so the observed image is mostly AP particle distribution, as shown in Figure 2.

AP particle distribution.
Among them, the proportion of Al powder as auxiliary combustion agent is relatively large. However, due to its small particle size, the amount is very large. For the microparticles in the propellant, the size of the particle is proportional to the possibility of particle dehumidification, so before the aluminum powder particle dehumidification, the propellant matrix has broken [14]. Therefore, the matrix and aluminum powder mixture is homogenized according to the Mori–Tanaka model [15] to obtain the mechanical properties of the mixed matrix. According to the tensile test of the matrix film used to prepare the sample and the performance test of the filler particles conducted by the Aerospace Institute, the material parameters used in this article are shown in Table 1.
Mesoscopic material parameters
| Elastic |
|
|
Hyperelastic |
|
|
|---|---|---|---|---|---|
| AP | 32,450 | 0.14 | Substrate | 0.125 | 0.0332 |
| Al | 70,000 | 0.30 | Mixed substrate | 0.164 | 0.0273 |
Note: 1)
2.3 In situ tensile test
The prepared specimen is placed on the tensile fixture after spraying gold and the fixture is placed in the scanning electron microscope. After vacuuming, in-situ tensile tests will be conducted, and larger AP particles with significant damage will become the focus of observation. In addition, due to the slow imaging of SEM, the tensile rate of 0.05 mm/min is used to observe at 50 times magnification, and the tensile clamp is connected with the mechanical sensor, so as to transmit the tensile load data from time to time. At the mesoscopic level, the different particle distribution in the propellant makes the observed images of each specimen different, but the mechanical property curves and damage process of dozens of specimens in the in situ tensile test are basically consistent. In this article, the representative experiment with better observation effect is selected for mechanical property analysis, and the stress–strain curve and the corresponding micro-morphology changes during the in situ tensile process are shown in Figure 3.

Micro-tensile damage and fracture of propellant.
According to the figure, the change of mechanical properties of solid propellants can be divided into four stages: linear viscoelastic section, stress softening section, unloading section, and damage fracture section. At the initial stage of loading, the fine particles and the matrix are well bonded, the propellant structure is complete, and the stiffness value fluctuates within a certain range, which is in the linear viscoelastic stage. With the application of the external force load, the strain of the propellant further increases, and some micro-particles and the matrix are dehumidified, resulting in the appearance of internal pores, the reduction of homogenization modulus, the weakening of the performance of the particle reinforced matrix, and the trend of stress rise has slowed down, gradually entering the stress softening stage. Under a continuous external load, a large number of micro-particles dehumidify, which causes the pores caused by dehumidification to gather and form cracks and continue to expand. Once the strain limit of the matrix is reached, it immediately enters the damage and fracture stage from the unloading section. Compared with the standard dumbbell test piece, the volume of the loaded part of the in situ tensile test piece is smaller. Once the pores caused by particle dehumidification gather, the cracks will have a greater impact on the loaded part; at the same time, in view of the improvement of the mechanical properties of the propellant, the use of the composite bonding agent further strengthens the grain–matrix bonding interface, making the linear viscoelastic section and the stress softening section larger, and the stress unloading and damage fracture stage relatively small.
3 Model building and software development
3.1 RVE and periodic boundary conditions (PBC)
For the microscopic damage analysis, how to maximize the reflection of macroscopic phenomena with less calculation is the focus of attention. Therefore, RVE should contain enough information, including the composition, proportion, and distribution of fine particles, and not too large to cause a sudden increase in the calculation [16]. In general, the macropropellant is composed of numerous periodic arrays of mesoscopic parts, so when constructing RVE, the internal particles must be arranged periodically. In addition, because the propellant grain is cast and formed by premixed slurry, the distribution of fine particles is irregular, so with the help of the compiled Python statement, by setting the particle size, grading, spacing, and controlling the order of particle generation and the filling mass fraction, the plane space is filled with particles starting from the randomly generated initial fine particles, and the radial ratio can be set to control the particle shape. The mass fraction and particle size of AP and Al powder particles are basically consistent with the production data of samples provided by the aerospace research institute. In addition, on the premise of ensuring the accuracy of the finite-element model, the mixed phase composed of the propellant matrix and aluminum powder is homogenized and pretreated [17], and its mechanical properties are equivalent to the green area in Figure 4 to reduce the calculation cost. When the RVE size is more than three times the maximum particle size, the representative volume unit is considered to be effective [18]. Therefore, this article comprehensively considers the finite-element calculation cost and calculation accuracy, and the RVE size is set as 900 × 900 based on the particle size distribution rule. The RVE model is shown in Figure 4.

Solid propellant RVE model.
In the process of strengthening the mechanical properties of the matrix, which is closely related to the strength of the bonding interface of the matrix, once the particles are dehumidified, it tends to show an unloading phenomenon on the macrolevel. Moreover, the current research mainly focuses on how to strengthen the bonding interface [19], so that the micro-particles can avoid dehumidification as much as possible under the action of external forces. Therefore, when investigating the mechanical properties of propellants, the bonding interface becomes an inevitable factor. Dehumidification of the interface between the micro-particles and the matrix is actually the crack propagation process of the bonding interface. However, the traditional fracture mechanics research based on linear viscoelasticity not only needs to pre-crack but also often has singularity at the crack tip, which is difficult to reproduce the process of crack initiation and propagation. Compared with the traditional fracture mechanics, the cohesive zone model (CZM), as a phenomenological model, does not need to prefabricate cracks while greatly reducing the singularity of stress, and it can set different tension displacement relationships according to different materials, making it applicable and widely used. For CZM, in addition to the different constitutive design for different materials, it mainly includes two aspects, one is the initial damage criterion, and the other is the damage evolution law. The CZM element can be regarded as two faces separated by a certain thickness. These two faces share nodes with other solid elements. Once the strength limit is reached, it will immediately enter the stiffness-softening stage [20]. Therefore, when building the propellant model, it is necessary to embed the bonding element between the particles and the matrix to simulate the particle dehumidification process. Taking the bilinear cohesion model as an example, the element embedment and damage diagram is shown in Figure 5.

Schematic diagram of CZM tensile damage: (a) schematic diagram of interface CZM, (b) schematic diagram of CZM tensile damage, and (c) bilinear cohesive model of initial damage.
For bilinear cohesion model, its standard form is shown in the following equation:
where
By establishing PBC for the RVE model, that is, creating the equation relationship between the two opposite sides and the reference point, the displacement difference between the two sides of the RVE in the loaded direction is consistent with the applied load displacement, and by pre-calculating the overall Poisson’s ratio of the RVE, the shrinkage of the RVE in the direction perpendicular to the loaded direction is realized. The application of PBC ensures the continuity of stress and strain on the opposite sides of the RVE, that is, to a certain extent, the array of multiple RVEs can reflect the loading condition of the macro test piece [22]. Because the set reference point has an equation relationship with both sides of the RVE, the overall tension of the RVE can be achieved by applying displacement load to the reference point and setting the loading rate. At the same time, according to Newton’s third law, the reaction force (RF) on the reference point is the load on the RVE, and the displacement is consistent with the RVE, then the force–displacement data can be converted into the overall stress–strain data of the RVE through calculation. The schematic diagram is shown in Figure 6.

Schematic diagram of periodic boundary application.
3.2 Secondary development of ABAQUS
With the development of computer technology, finite-element analysis software is gradually applied to research various engineering problems. Because of its low resource cost and high calculation accuracy, its application scope is more and more extensive, and the problems studied are more and more complex. However, many disciplines and complex engineering problems make updating the finite-element software difficult. Therefore, many software have secondary development ports. Secondary development realized by subroutines can further expand the application field and reduce the workload [23].
Since the cohesive force model was proposed by Barenblatt and Dugdale, for many complex materials, the cohesive force model represented by bilinear, exponential, and polynomial has evolved. With the further improvement of the finite-element software, the bilinear cohesion model has been embedded in the software. However, previous studies [24] have shown that the bilinear cohesion model is applicable to brittle materials, and the exponential cohesion model is widely applied to the interface cracking of composite materials and the crack initiation process of film coating on the ductile matrix. When using the finite-element method to analyze ductile composite materials, the calculation cost is low, and the convergence is better. The fracture energy control equation is shown in the following equation:
where
The parameters
where
The normal and tangential stress equations can be obtained from the derivation of (2) as follows:
For the bonding interface of two-phase composite materials, due to the inevitable effect of external loads such as vibration, temperature or humidity during storage or transportation, the irrecoverable cumulative damage may occur, resulting in the weakening of its bearing capacity, so it is necessary to add damage factors and modify the above formula, as follows:
Since no corresponding setting of exponential cohesion model exists in the finite-element software [26], this study uses VUMAT subroutine to write tension-displacement control statements. In addition, in the finite-element software, the essence of simulating fracture is to make the damaged element stiffness zero, make it lose the ability to bear stress, and hide it to achieve the effect of fracture. Because the hyperelastic model fits the matrix constitutive model, and its damage will break when it accumulates to a certain extent. Therefore, the VUSDFLD subroutine is used for the secondary development of ABAQUS to realize the setting of fracture strain. In the explicit calculation, the DEPVAR state variable is set for the matrix material, and the field variable is customized to make the material attribute and the state variable linked, and the state variable is used to realize the deletion of the element.
4 Parameter inversion
4.1 Combinatorial optimization algorithm
Because the cohesion model parameters are difficult to measure directly and can only be optimized with the help of experimental data, the data calculated by ABAQUS under the initial parameters are imported into MATLAB, which is a data interaction platform [27], and compared with the experimental data put in advance, and the cohesion parameters and hyperelastic fracture strain data are adjusted through the optimization algorithm to achieve the optimal simulation of the real experiment. Multi-parameter optimization often involves multiple factors and the interaction between parameters. The set objective function may be multimodal, nonlinear, non-continuous, and nondifferentiable. Variables and constraint functions may also be linear, nonlinear, continuous, or discrete variable sets. In the face of these complex situations, traditional numerical optimization and direct search algorithms are difficult to find the required derivative and gradient information or often get the local optimal solution. Therefore, most scholars use the global search method to solve such complex optimization problems.
Although the global search method has strong adaptability and the ability of global search, its application is limited to a certain extent by too much computation. Therefore, the global search and numerical optimization algorithms are combined considering the advantages and disadvantages of global search and direct search algorithms. At first, the global optimization algorithm is used to locate the area where the target extreme value is located in the design space, and then the direct search algorithm is used to accurately optimize the area. This gives full play to the advantages of the global optimization algorithm in the overall design space traversal and can quickly locate the design-sensitive area, while avoiding the efficiency problem of the global algorithm in detail optimization. For the global optimization algorithm, Toushmalani [28] realized the inversion of gravity anomaly parameters generated by faults by virtue of the global optimization ability of the PSO algorithm; Zhang et al. [29] realized the inversion of the mechanical parameters of gravity dams by improving the PSO algorithm and verified it through practical engineering applications; Han et al. [30] reasonably determined the rock mass mechanical parameters of the dam foundation during construction and operation through the joint use of PSO and ABAQUS; Zeng et al. [31] used the parallel PSO algorithm to globally retrieve the optimal value in the parameter space, reducing the relative error to less than 4%. PSO algorithm is one of the heuristic search algorithms [32]. Like a swarm intelligence optimization algorithm, this algorithm starts initialization through a group of random population (particles) and adjusts the fitness of the population through an iterative update to find the global optimal solution.
The updated expression of the improved PSO can be expressed as follows:
where
At the same time, the adaptive method is used to adjust
where
For the local search algorithm, because the Hooke–Jeeves method does not need continuous objective function and line search [33] and can deal with non-continuous parameter space, the Hooke–Jeeves method is used to add a penalty term to the objective function, transform the constrained problem into an unconstrained problem for optimization, and further search the fitness interval roughly located by the PSO algorithm. The Hooke–Jeeves method mainly includes two parts, one is the detection of movement, and the other is the mode movement [34]. After the initial position and target function are determined, the detection movement is carried out along each dimension of the search space in order to determine the new base point and search direction, while the mode movement is carried out along the direction of the adjacent base point in order to make the target function meet the requirements as soon as possible. The main implementation steps are as follows:
(1) Initial base point
(2) If
(3) If
(4) If
(5) If
(6) Set
(7) If
4.2 Data interaction and inversion analysis
Although the numerical calculation and experimental results are constructed by a discrete point fitting curve, considering the calculation cost, the numerical calculation result data are relatively small, and the simulation model has no fixed length unit. Therefore, this study is based on the experimental data, smoothes the numerical calculation results with the help of the smooth function in MATLAB, and uses bilinear interpolation to supplement the missing stress values relative to the experimental data, and defines the objective function as
where
At the same time, in order to reduce the amount of calculation, on the one hand, all the calculated parameters are combined and stored to avoid repeated calculation in the process of parameter optimization. On the other hand, when the simulation process is more than halfway through, the target function value is pre-calculated. Once the result is greater than 1/2 of the previous set of data, the calculation will be stopped immediately. In addition, in addition to ABAQUS, the inverse identification of mechanical parameters also involves data interaction platform and data processing analysis, which mainly includes two parts: Python’s reading of the result data file odb and the submission of the calculation file inp; MATLAB processes the result data, calculates the objective function, and adjusts the parameters of the optimization algorithm. On the one hand, the optimization algorithm needs to preprocess the simulation data, including singular value elimination and data smoothing; on the other hand, it needs to search and judge the optimal value of the inversion parameters, so as to modify the inp file parameters. The specific implementation process is shown in Figure 7.

Data interaction process.
Inverse analysis is mainly divided into three steps: the first is to obtain the experimental stress–strain response curve, the second is the finite-element numerical analysis and result output, and the third is the optimal parameter search under the optimization algorithm. The specific analysis process is shown in Figure 8.

Parameter inversion structure diagram.
For the PSO algorithm, on the basis of comprehensive consideration of the calculation cost and accuracy, it sets the calculation parameters maximum iterations as 15, number of particles as 4, inertia as 0.9, global increment and particle increment as 0.8, maximum velocity as 0.05, and maximum failed runs as 10; for the Hooke–Jeeves algorithm, it sets the calculation parameter max evaluations to 100, relative step sizes to 0.2, and step size reduction factor to 0.5. At the same time, in order to verify the advantages of the combinatorial optimization algorithm, two modes are used for parameter inversion, one is to use only Hooke–Jeeves for local optimal search, and the other is to use the combinatorial optimization algorithm. When the Hooke–Jeeves model is used for parameter inversion alone, it is estimated to calculate 201 times, but only 101 times are actually calculated. When the combination optimization strategy is used, which is estimated that 410 times will be calculated, 61 times will be calculated in the first stage, and 41 times will be calculated in the second stage. For the three types of models, except for the numerical differences, the overall change trend of various parameters is relatively similar.
5 Results and discussion
5.1 Inversion result analysis
Although the combined optimization algorithm has more computation than the single local search algorithm in theory, it can effectively reduce the computational cost and obtain relatively superior inversion parameter values through the preprocessing of partial calculation results. Under the two inversion modes, the objective function values are shown in Figure 9.

Parameter inversion objective function value. (a) Single local search algorithm, (b) first stage of combinatorial optimization algorithm, and (c) second stage of combinatorial optimization algorithm.
Model 1 and model 2 indicate whether to consider the matrix damage and the RVE constructed by the bilinear cohesion model considering the initial damage at the bonding interface, and model 3 indicates the RVE constructed by the exponential cohesion model considering the matrix damage and the initial damage at the bonding interface. Under the single search algorithm, the minimum objective function values of model 1, model 2, and model 3 are 0.03362, 0.02364, and 0.01864, respectively. Under the combined optimization algorithm, the minimum objective function values of model 1, model 2, and model 3 are 0.03033, 0.02136, and 0.01635, respectively. The optimal values of the inversion parameters of the three models are shown in Table 2.
Inversion parameter optimal value
| Parameter |
|
|
Separation laws |
|
|
|
|---|---|---|---|---|---|---|
| Model 1 | 0.5633 | 864 | Maxs | 0.0277 | 0.9956 | |
| Model 2 | 0.5764 | 972 | Maxs | 0.0296 | 0.9964 | 1.4462 |
| Model 3 | 0.5872 | \ | Maxs | 0.0102
|
0.9982 | 1.4865 |
Note: 1)
5.2 Mesoscopic simulation analysis
With the help of parameter inversion data, the whole process of propellant tensile damage and fracture is simulated and analyzed. The damage evolution and stress distribution of each simulation model at different stages are shown in Table 3.
Stress nephogram of propellant damage evolution
| State evolution | Model 1 | Model 2 | Model 3 |
|---|---|---|---|
| Linear viscoelastic stage |

|

|

|
| Dehumidification of particles |

|

|

|
| Bearing substrate |
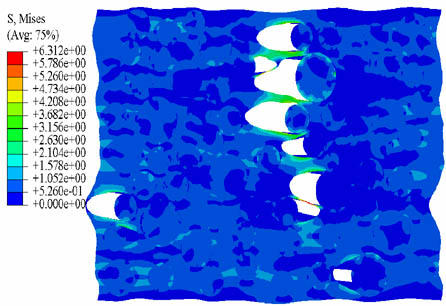
|

|

|
| Substrate damage |

|

|

|
| Tensile failure |

|

|

|
Due to the difference between the micro-particles and the matrix material, the internal stress distribution is uneven, but the stress value of the micro-particles is larger than that of the bonding interface, and the interface stress value is larger than that of the matrix part. This phenomenon reflects the strengthening effect of the micro-particles on the mechanical properties of the propellant, on the other hand, it also explains the cause of damage initiation from the interface. Without considering the matrix damage, it can be clearly seen that with the progress of the micro-particle dehumidification, the stress concentration phenomenon occurs at the matrix, which causes it to undergo large deformation. Once the matrix damage is considered, it will lead to pore expansion and tensile fracture. The three types of models can reflect the damage evolution of the propellant during the tensile process to a certain extent, but the difference of stress distribution and damage state reflects the influence of the cohesive model and the setting of matrix damage parameters on the simulation process. Through the set reference points, the stress–strain curves of three models are obtained, as shown in Figure 10.

Microscopic simulation stress–strain diagram.
By comparing Table 3 and Figure 10, it can be seen that under the action of periodic boundary load conditions, the stress of mesoscopic propellant shows nonlinear change during the tensile process. At the initial stage, the fine particles and the matrix are well bonded, showing a short linear viscoelastic stage. With the increase of tensile strain, the propellant appears to have softening phenomenon, and the slope of the curve decreases, that is, the equivalent elastic modulus begins to decline, which shows partial micro-particle dehumidification on the simulation cloud diagram. When a large number of particles are dehumidified, the stress value increased due to stretching is less than the stress value reduced due to particle dehumidification, that is, the stress reduction stage is entered. With the further intensification of the tension, the matrix reaches the strain limit, and some of the matrices appears fracture, which makes the stress drop sharply until it returns to zero.
By comparing the simulation and experimental stress–strain curves, it can be seen that the three models can reflect the stress evolution of the propellant during stretching to a certain extent in the linear viscoelastic and stress softening stages, but the linear viscoelastic stage is closer to the experimental data than the stress softening stage, and the maximum stress value is higher than the experimental results. In the stress unloading stage, the deviation of model I is larger than the actual one, and the stress will rise again with the increase of strain. Compared with model III, the transition from stress softening to stress unloading stage of model II is very rapid, and at the end of the stress softening stage, there is a sudden increase in the slope of the curve. In the stage of damage and fracture, except for model I, model II and model III reflect the process from stress unloading to tensile fracture, but the damage and fracture trend is relatively slow compared with the experimental data. In general, model III with exponential cohesion interface and considering matrix damage is close to the actual data, and its optimal objective function value is 0.01635, which is smaller than the 0.02136 deviation of model II and closer to the real value.
Although the simulated stress–strain curve of model III is close to the experimental data, there are still three problems: the curvature of the stress softening stage is too large, the maximum stress value is too high, and the damage and fracture stage is relatively flat. Compared with the experiment and simulation analysis, the error mainly comes from the following aspects: 1) After the fabrication of the microsample, some original defects or damages will inevitably occur, which are not considered in the simulation process, resulting in the high maximum stress value. 2) In the process of tensile fracture of propellant, as a ductile material, it can be considered as a layer by layer fracture. Considering the calculation cost, the simulation model is only based on the plane strain element, which makes the stress softening stage deviate from the actual data curvature. 3) At the microlevel, the simulation calculation is based on the establishment of RVE to characterize the macromodel, which results in the high proportion of the fractured matrix in the RVE. At the macrolevel, because the proportion of cracks is relatively small and the local stress concentration is more obvious, the damage and fracture stage in the simulation calculation is more gentle.
6 Conclusion
The organic combination of the global optimization of the adaptive particle swarm optimization algorithm and the local search of the Hooke–Jeeves algorithm, the optimal objective function values of model 1, model 2, and model 3 parameter inversion are 0.03033, 0.02136, and 0.01635, respectively. Compared with the single search algorithm, the objective function values are reduced by 10.85%, 10.67%, and 14.01%, respectively, and the actual calculation amount of the two inversion modes is basically the same, which shows the superiority and applicability of the combined optimization algorithm for the inversion of propellant parameters.
The optimal objective function values of the three types of RVE models decrease in turn, with model 2 reduced by 29.57% compared with model 1, and model 3 reduced by 23.46% compared with model 2, indicating that the exponential cohesive model can more accurately simulate the mechanical properties of propellants compared with bilinear, while considering the matrix damage makes the simulation data closer to the experimental data.
Comparing the simulation nephogram with the stress–strain curve, it can be seen that after the particle dehumidification, the micro-particles will no longer bear the load, the matrix between the particles will have a high-stress zone, and the overall stiffness of the RVE will be reduced, and the mechanical properties will be weakened. With the tensile fracture of the local matrix, the continuous superposition of pores caused by particle dehumidification will lead to the initiation and expansion of cracks, and the overall stress will change from slow growth to rapid decline. Therefore, the weakening of the mechanical properties of the propellant starts from the particle dehumidification and accelerates the matrix damage, and the two have a symbiotic effect.
Acknowledgments
This work is financially supported by Foundation Strengthening Area Fund (grant no. 2019061).
-
Funding information: This research was funded by Foundation Strengthening Area Fund (grant number 2019061).
-
Author contributions: Conceptualization, Y.L.; methodology, Y.L.; software, Y.L.; validation, Y.L.; formal analysis, Y.L.; investigation, Y.L.; resources, G.L.; data curation, G.L.; writing – original draft preparation, G.L.; writing – review and editing, G.L.; visualization, G.L.; supervision, G.L.; project administration, Y.L.; funding acquisition, G.L. All authors have read and agreed to the published version of the manuscript.
-
Conflict of interest: The authors declare no conflict of interest.
-
Data availability statement: The authors declare that all the data available on request from the authors.
References
[1] Collins B, Maggi F, Matous K, Jackson T. Using tomography to characterize heterogeneous propellants. 46th AIAA Aerospace Sciences Meeting and Exhibit. Reno: AIAA; 2008. p. 941–8.10.2514/6.2008-941Search in Google Scholar
[2] Lee H, Brandyberry M, Tudor A, Matous K. Three-dimensional reconstruction of statistically optimal unit cells of polydisperse particulate composite from microtomography. Phys Rev E Stat Nonlinear Soft Matter Phys. 2009;80(6):061301–13.10.1103/PhysRevE.80.061301Search in Google Scholar PubMed
[3] Li S, Qiang H, Wang G, Wang XR, Liu XG, Wang JX. Experimental study on meso-damage evolution of HTPB propellant under uniaxial tensile load. J Propuls Technol. 2022;43(9):210394-1-7.Search in Google Scholar
[4] Zhang J, Zhi S, Sun B. Estimation of relaxation modulus of composite solid propellant based on particle packing model. J Aerosp Power. 2013;28(10):2370–5.Search in Google Scholar
[5] Tunc B, Ozupek S. Implementation and validation of a three dimensional damaging finite viscoelastic model. Int J Solids Struct. 2016;102/103:275–85.10.1016/j.ijsolstr.2016.09.031Search in Google Scholar
[6] Yun KS, Park JB, Jung GD, Youn SK. Viscoelastic constitutive modeling of solid propellant with damage. Int J Solids Struct. 2016;80:118–27.10.1016/j.ijsolstr.2015.10.028Search in Google Scholar
[7] Li Z, Xu B, Guo Y, Qv S, Xue M, Wu Z, et al. Viscoelastic constitutive model of HTPB solid propellant with damage based on mesostructured. Chin J Appl Mech. 2021;38(2):490–6.Search in Google Scholar
[8] Pan Y, Qu W. A nonlinear ultrasonic method for detection and characterization of dewetting damage in solid propellant. Propellants Explos Pyrotech. 2022;47(10):1062–71.10.1002/prep.202200079Search in Google Scholar
[9] Gao B, Li Z. Study on the stress–strain relationships and deterioration modes of htpb propellant with prefabricated cracks. Adv Polym Technol. 2022;2022(1):1–9.10.1155/2022/9772946Search in Google Scholar
[10] Hou Y, Xu J, Gu Y, Zhou C. Mesoscopic model of cracking process of nepe propellant based on cohesive zone model. Acta Armamentarii. 2020;41(11):2206–15.Search in Google Scholar
[11] Zhou H, Yuan J, Lai J, Yuan S. Research on microstructural damage simulation of solid propellant at low temperature. J Solid Rocket Technol. 2017;40(6):736–40.Search in Google Scholar
[12] Zhi S, Cao F, Shen Z, Xing GQ, Cao JW. Parameters lnversion of particle dewetting damage of composite solid propellants. J Propuls Technol. 2016;37(10):1977–83.Search in Google Scholar
[13] QJ924-85. Unidirectional tensile test method of composite propellant. F. Gao, editor, Beijing: Aeronautics and Astronautics, Ministry of Industry in the People’s Republic of China; 1985.Search in Google Scholar
[14] van Ramshorst MCJ, Di Benedetto GL, Duvalois W, Hooijmeijer PA, van der Heijden A. Investigation of the failure mechanism of HTPB/AP/Al propellant by in-situ uniaxial tensile experimentation in SEM. Propellants Explos Pyrotech. 2016;41(4):700–8.10.1002/prep.201500264Search in Google Scholar
[15] Doojin L. Local anisotropy analysis based on the Mori-Tanaka model for multiphase composites with fiber length and orientation distributions. Compos Part B Eng. 2018;148(2):227–34.10.1016/j.compositesb.2018.04.050Search in Google Scholar
[16] Ganesh S. Modeling multiple damage mechanisms via a multi-fiber multi-layer representative volume element (M2RVE). Sādhanā Indian Acad Sci. 2020;45(1):31–75.10.1007/s12046-020-1299-2Search in Google Scholar
[17] Doghri L, Adam L, Bilger N. Mean-field homogenization of elasto-viscoplastic composites based on a general incrementally affine linearization method. Int J Plasticity. 2010;26:219–38.10.1016/j.ijplas.2009.06.003Search in Google Scholar
[18] Zhang H, Branko Š, Schlangen E. Towards understanding stochastic fracture performance of cement paste at micro length scale based on numerical simulation. Constr Build Mater. 2018;183:189–201.10.1016/j.conbuildmat.2018.06.167Search in Google Scholar
[19] Sungjun P. Effects of ammonium perchlorate particle size, ratio, and total contents on the properties of a composite solid propellant. Propellants Explos Pyrotech. 2020;45(9):1376–81.10.1002/prep.202000055Search in Google Scholar
[20] He Z, Deng D, Liu G, Sun A, Qian J, Li B, et al. Research on crack propagation of composite materials based on cohesive zone model. Compos Sci Eng. 2022;0(1):5–12.Search in Google Scholar
[21] Yan Y, Shang F. Cohesive zone modelling of interfacial delamination in PZT thin films. Sci Sin (Phys, Mech & Astron). 2009;39(7):1007–17.Search in Google Scholar
[22] Espadas-Escalante J, Van D, Isaksson P. A study on the influence of boundary conditions in computational homogenization of periodic structures with application to woven composites. Compos Struct. 2017;160:529–37.10.1016/j.compstruct.2016.10.082Search in Google Scholar
[23] Shi Y. A fiber model based on secondary development of abaqus for elastic–plastic analysis. Int J Steel Struct. 2018;18(5):1560–76.10.1007/s13296-018-0053-7Search in Google Scholar
[24] Hu Z. Research on interface failure mechanisms of composite adhesive joints based on the cohesive model. Hangzhou: Zhejiang University; 2018.Search in Google Scholar
[25] Huang L. The analysis of cohesive zone model and user-defined subroutine development in finite element method. Zhengzhou: Zhengzhou University; 2010.Search in Google Scholar
[26] Zhang J, Jia H, Tian Y. Development of subroutine for elastic-plastic cohesive zone model of bonded interface. J Zhengzhou Univ (Eng Sci). 2014;35(1):77–80.Search in Google Scholar
[27] Su M, He X. Parametric optimization of vortex shedder based on combination of gambit, fluent and isight. Int J Fluid Mach Syst. 2016;9(2):150–8.10.5293/IJFMS.2016.9.2.150Search in Google Scholar
[28] Toushmalani R. Gravity inversion of a fault by Particle swarm optimization (PSO). SpringerPlus. 2013;2(1):315–20.10.1186/2193-1801-2-315Search in Google Scholar PubMed PubMed Central
[29] Zhang W, Xu L, Shen Z, Ma B. A new approach for mechanical parameter inversion analysis of roller compacted concrete dams using modified PSO and RBFNN. Clust Comput. 2022;25(6):4633–52.10.1007/s10586-022-03715-ySearch in Google Scholar
[30] Han F, Xu L, Zhang T. Combined inversion of mechanical parameters of rock mass of dam foundation using particle swarm optimization method and ABAQUS. J Hohai Univ (Nat Sci). 2013;41(04):321–5.Search in Google Scholar
[31] Zeng Q, Yao J, Huo J. Inversion of rock meso-mechanical parameters based on parallel particle swarm optimization(PSO) algorithm. J Xian Shiyou Univ (Nat Sci Ed). 2015;30(4):27–32 + 5.Search in Google Scholar
[32] Li L, Zhang X. New chaos particle swarm optimization based on adaptive inertia weight. Comput Eng Appl. 2018;54(9):139–44.Search in Google Scholar
[33] Peter P, Milan S. Controlling of local search methods’ parameters in memetic algorithms using the principles of simulated annealing. Procedia Eng. 2016;136:70–6.10.1016/j.proeng.2016.01.176Search in Google Scholar
[34] Sun Y, Ding Y. An improved artificial bee colony algorithm based on Hooke-Jeeves method. Comput Sci Appl. 2017;7(2):134–45.10.12677/CSA.2017.72017Search in Google Scholar
© 2023 the author(s), published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Regular Articles
- Effects of cellulose nanofibers on flexural behavior of carbon-fiber-reinforced polymer composites with delamination
- Damage mechanisms of bismaleimide matrix composites under transverse loading via quasi-static indentation
- Experimental study on hydraulic fracture behavior of concrete with wedge-splitting testing
- The assessment of color adjustment potentials for monoshade universal composites
- Metakaolin-based geopolymers filled with volcanic fly ashes: FT-IR, thermal characterization, and antibacterial property
- The effect of temperature on the tensile properties and failure mechanisms of two-dimensional braided composites
- The influence of preparation of nano-ZrO2/α-Al2O3 gradient coating on the corrosion resistance of 316L stainless steel substrate
- A numerical study on the spatial orientation of aligning fibrous particles in composites considering the wall effect
- A simulative study on the effect of friction coefficient and angle on failure behaviors of GLARE subjected to low-velocity impact
- Impact resistance capacity and degradation law of epoxy-coated steel strand under the impact load
- Analytical solutions of coupled functionally graded conical shells of revolution
- The influence of water vapor on the structural response of asphalt pavement
- A non-invasive method of glucose monitoring using FR4 material based microwave antenna sensor
- Chloride ion transport and service life prediction of aeolian sand concrete under dry–wet cycles
- Micro-damage analysis and numerical simulation of composite solid propellant based on in situ tensile test
- Experimental study on the influence of high-frequency vibratory mixing on concrete performance
- Effects of microstructure characteristics on the transverse moisture diffusivity of unidirectional composite
- Gradient-distributed ZTAp-VCp/Fe45 as new anti-wear composite material and its bonding properties during composite casting
- Experimental evaluation of velocity sensitivity for conglomerate reservoir rock in Karamay oil field
- Mechanical and tribological properties of C/C–SiC ceramic composites with different preforms
- Mechanical property improvement of oil palm empty fruit bunch composites by hybridization using ramie fibers on epoxy–CNT matrices
- Research and analysis on low-velocity impact of composite materials
- Optimizing curing agent ratios for high-performance thermosetting phthalonitrile-based glass fibers
- Method for deriving twisting process parameters of large package E-glass yarn by measuring physical properties of bobbin yarn
- A probability characteristic of crack intersecting with embedded microcapsules in capsule-based self-healing materials
- An investigation into the effect of cross-ply on energy storage and vibration characteristics of carbon fiber lattice sandwich structure bionic prosthetic foot
- Preparation and application of corona noise-suppressing anti-shedding materials for UHV transmission lines
- XRD analysis determined crystal cage occupying number n of carbon anion substituted mayenite-type cage compound C12A7: nC
- Optimizing bending strength of laminated bamboo using confined bamboo with softwoods
- Hydrogels loaded with atenolol drug metal–organic framework showing biological activity
- Creep analysis of the flax fiber-reinforced polymer composites based on the time–temperature superposition principle
- A novel 3D woven carbon fiber composite with super interlayer performance hybridized by CNT tape and copper wire simultaneously
- Effect of aggregate characteristics on properties of cemented sand and gravel
- An integrated structure of air spring for ships and its strength characteristics
- Modeling and dynamic analysis of functionally graded porous spherical shell based on Chebyshev–Ritz approach
- Failure analysis of sandwich beams under three-point bending based on theoretical and numerical models
- Study and prediction analysis on road performance of basalt fiber permeable concrete
- Prediction of the rubberized concrete behavior: A comparison of gene expression programming and response surface method
- Study on properties of recycled mixed polyester/nylon/spandex modified by hydrogenated petroleum resin
- Effect of particle size distribution on microstructure and chloride permeability of blended cement with supplementary cementitious materials
- In situ ligand synthesis affording a new Co(ii) MOF for photocatalytic application
- Fracture research of adhesive-bonded joints for GFRP laminates under mixed-mode loading condition
- Influence of temperature and humidity coupling on rutting deformation of asphalt pavement
- Review Articles
- Sustainable concrete with partial substitution of paper pulp ash: A review
- Durability and microstructure study on concrete made with sewage sludge ash: A review (Part Ⅱ)
- Mechanical performance of concrete made with sewage sludge ash: A review (Part Ⅰ)
- Durability and microstructure analysis of concrete made with volcanic ash: A review (Part II)
- Communication
- Calculation of specific surface area for tight rock characterization through high-pressure mercury intrusion
- Special Issue: MDA 2022
- Vibration response of functionally graded material sandwich plates with elliptical cutouts and geometric imperfections under the mixed boundary conditions
- Analysis of material removal process when scratching unidirectional fibers reinforced polyester composites
- Tailoring the optical and UV reflectivity of CFRP-epoxy composites: Approaches and selected results
- Fiber orientation in continuous fiber-reinforced thermoplastics/metal hybrid joining via multi-pin arrays
- Development of Mg-based metal matrix biomedical composites for acicular cruciate ligament fixation by reinforcing with rare earth oxide and hydroxyapatite – A mechanical, corrosion, and microstructural perspective
- Special Issue: CACMSE
- Preparation and application of foamed ceramic panels in interior design
Articles in the same Issue
- Regular Articles
- Effects of cellulose nanofibers on flexural behavior of carbon-fiber-reinforced polymer composites with delamination
- Damage mechanisms of bismaleimide matrix composites under transverse loading via quasi-static indentation
- Experimental study on hydraulic fracture behavior of concrete with wedge-splitting testing
- The assessment of color adjustment potentials for monoshade universal composites
- Metakaolin-based geopolymers filled with volcanic fly ashes: FT-IR, thermal characterization, and antibacterial property
- The effect of temperature on the tensile properties and failure mechanisms of two-dimensional braided composites
- The influence of preparation of nano-ZrO2/α-Al2O3 gradient coating on the corrosion resistance of 316L stainless steel substrate
- A numerical study on the spatial orientation of aligning fibrous particles in composites considering the wall effect
- A simulative study on the effect of friction coefficient and angle on failure behaviors of GLARE subjected to low-velocity impact
- Impact resistance capacity and degradation law of epoxy-coated steel strand under the impact load
- Analytical solutions of coupled functionally graded conical shells of revolution
- The influence of water vapor on the structural response of asphalt pavement
- A non-invasive method of glucose monitoring using FR4 material based microwave antenna sensor
- Chloride ion transport and service life prediction of aeolian sand concrete under dry–wet cycles
- Micro-damage analysis and numerical simulation of composite solid propellant based on in situ tensile test
- Experimental study on the influence of high-frequency vibratory mixing on concrete performance
- Effects of microstructure characteristics on the transverse moisture diffusivity of unidirectional composite
- Gradient-distributed ZTAp-VCp/Fe45 as new anti-wear composite material and its bonding properties during composite casting
- Experimental evaluation of velocity sensitivity for conglomerate reservoir rock in Karamay oil field
- Mechanical and tribological properties of C/C–SiC ceramic composites with different preforms
- Mechanical property improvement of oil palm empty fruit bunch composites by hybridization using ramie fibers on epoxy–CNT matrices
- Research and analysis on low-velocity impact of composite materials
- Optimizing curing agent ratios for high-performance thermosetting phthalonitrile-based glass fibers
- Method for deriving twisting process parameters of large package E-glass yarn by measuring physical properties of bobbin yarn
- A probability characteristic of crack intersecting with embedded microcapsules in capsule-based self-healing materials
- An investigation into the effect of cross-ply on energy storage and vibration characteristics of carbon fiber lattice sandwich structure bionic prosthetic foot
- Preparation and application of corona noise-suppressing anti-shedding materials for UHV transmission lines
- XRD analysis determined crystal cage occupying number n of carbon anion substituted mayenite-type cage compound C12A7: nC
- Optimizing bending strength of laminated bamboo using confined bamboo with softwoods
- Hydrogels loaded with atenolol drug metal–organic framework showing biological activity
- Creep analysis of the flax fiber-reinforced polymer composites based on the time–temperature superposition principle
- A novel 3D woven carbon fiber composite with super interlayer performance hybridized by CNT tape and copper wire simultaneously
- Effect of aggregate characteristics on properties of cemented sand and gravel
- An integrated structure of air spring for ships and its strength characteristics
- Modeling and dynamic analysis of functionally graded porous spherical shell based on Chebyshev–Ritz approach
- Failure analysis of sandwich beams under three-point bending based on theoretical and numerical models
- Study and prediction analysis on road performance of basalt fiber permeable concrete
- Prediction of the rubberized concrete behavior: A comparison of gene expression programming and response surface method
- Study on properties of recycled mixed polyester/nylon/spandex modified by hydrogenated petroleum resin
- Effect of particle size distribution on microstructure and chloride permeability of blended cement with supplementary cementitious materials
- In situ ligand synthesis affording a new Co(ii) MOF for photocatalytic application
- Fracture research of adhesive-bonded joints for GFRP laminates under mixed-mode loading condition
- Influence of temperature and humidity coupling on rutting deformation of asphalt pavement
- Review Articles
- Sustainable concrete with partial substitution of paper pulp ash: A review
- Durability and microstructure study on concrete made with sewage sludge ash: A review (Part Ⅱ)
- Mechanical performance of concrete made with sewage sludge ash: A review (Part Ⅰ)
- Durability and microstructure analysis of concrete made with volcanic ash: A review (Part II)
- Communication
- Calculation of specific surface area for tight rock characterization through high-pressure mercury intrusion
- Special Issue: MDA 2022
- Vibration response of functionally graded material sandwich plates with elliptical cutouts and geometric imperfections under the mixed boundary conditions
- Analysis of material removal process when scratching unidirectional fibers reinforced polyester composites
- Tailoring the optical and UV reflectivity of CFRP-epoxy composites: Approaches and selected results
- Fiber orientation in continuous fiber-reinforced thermoplastics/metal hybrid joining via multi-pin arrays
- Development of Mg-based metal matrix biomedical composites for acicular cruciate ligament fixation by reinforcing with rare earth oxide and hydroxyapatite – A mechanical, corrosion, and microstructural perspective
- Special Issue: CACMSE
- Preparation and application of foamed ceramic panels in interior design

