Creep analysis of the flax fiber-reinforced polymer composites based on the time–temperature superposition principle

2.1 Sample preparation

FFRP plates with a 40% fiber volume fraction were manufactured using the vacuum infusion method, as illustrated in Figure 1(a). The matrix of the composites was unsaturated polyester, and the reinforcement fabrics for the 0° and 90° fiber samples were unidirectional flax fabrics with an areal density of 280 g/m². For ±45° fiber plates, ±45° flax fiber fabrics with an areal density of 300 g/m² were used. The flax fabrics were stored in a climate chamber in which the temperature was 23°C, and relative humidity was 65% before the vacuum injection. The vacuum pressure of the infusion system was kept at −1 Bar during the injection process. After the injection of resin, the samples underwent a 12-h post-curing at 120°C following the 6-h initial curing. Then, the sample plates were placed in the environment with a temperature of 23°C and relative humidity at 60% for at least 2 weeks until fully cured (Figure 1(b)). The plates were then cut into rectangular specimens with dimensions of 40 mm × 5 mm for the DMA machine and 250 mm × 15 mm for the long-term creep test equipment.

Figure 1

(a) Manufacturing configuration and (b) the manufactured sample plate.

2.2 Testing methods

2.2.1 Accelerated creep test

Accelerated tensile creep tests were performed on the DMA Q800 machine with six isothermal steps. The temperatures for the isothermal steps for 0° fiber samples are 20, 40, 60, 80, 100, and 120°C, respectively; for 90° and ±45°, fiber samples are 20, 30, 40, 50, 60, and 70°C respectively. A pre-load force (0.01 N) was applied to the specimen to keep the sample straight, and then, the specimen was subjected to constant stress for 60 min at each isothermal step. To prevent sample damage, the creep stress for 0° fiber samples was set as 5 MPa, and for samples with 90° and ±45° fibers, it was set at 2 MPa. As the glass transition temperature had been tested in the previous property test to be higher than 130°C and the creep stress was low compared to the ultimate tensile stress of the material (ultimate stress of 0° fiber samples is 300 MPa, for 90° fiber samples is 60 MPa), the samples are considered to exhibit linear viscoelastic behavior under all isothermal steps.

Because the FFRP is highly susceptible to changes in environmental humidity, it is necessary to maintain a consistent moisture content of the FFRP sample to ensure accurate mechanical testing results. Despite the availability of humidity control accessories for the testing machine, it is worth noting that FFRP samples also exhibit increased moisture absorption at elevated temperatures due to an increase in their saturated water percentage. In this regard, a Vaseline coating was directly applied to the FFRP specimens and subsequently wrapped in tinfoil to impede water evaporation, as depicted in Figure 2, and thus maintain uniform moisture content. The tinfoil was folded to reserve adequate deformation space for the tested area, ensuring that the mechanical response of the sample remained unaffected. As illustrated in Figure 3, the stress–strain test results of the pure tinfoil suit without a sample indicate an ultimate stress not exceeding 0.01 MPa and a modulus of approximately 0.5 MPa, which is negligible compared to the creep stress. Consequently, the tinfoil used for moisture protection is not expected to influence the mechanical properties of the samples.

Figure 2

Testing configuration on DMA Q800.

Figure 3

The strain–stress relationship of the outer tinfoil of the sample.

2.2.2 Long-term creep test

A self-made creep test equipment was developed for investigating the long-term tensile creep behavior of FRP samples, as depicted in Figure 4. The samples were clamped using custom-made grips, with the upper clamps supported on a steel beam, and the lower clamps connected to the loading weights. The distance between the upper and lower clamps was fixed at 100 mm. To ensure that the samples were subjected to tensile loading and not affected by shear force, they were strictly installed to be perpendicular to the clamps, and the weights were kept aligned with the sample. The fiber volume fraction of the long-term test samples was consistent with that used in the accelerated creep test. To monitor the strain change induced by creep, a strain gauge was placed on each side of the sample. The creep stress was set to 5 MPa for samples with 0° fiber and 2 MPa for samples with 0° and ±45° fiber orientations. The stress applied was calculated based on the sample size measurement. The testing system was situated in a climate room maintained at a constant relative humidity of 60% and temperature of 20°C. For each sample, long-term loading was sustained for 2,000 h.

Figure 4

Long-term creep testing equipment.

3.1 Building of the master curve based on the short-term creep

The TTSP is a widely used method for predicting the long-term creep performance of viscoelastic materials at elevated temperatures based on short-term creep responses obtained in accelerated tests. In this study, short-term creep tests were conducted on samples at six different temperatures, and the resulting individual creep strains over 60 min were plotted on a logarithmic scale (Figure 5). To apply TTSP to the short-term creep test results, samples at 0° were chosen as an example to perform the application of the superposition process. To predict the long-term creep behavior, a creep master curve was constructed by shifting the creep curves obtained at elevated temperatures using the shifting factors presented in equations (1) and (2). All short-term creep curves were horizontally shifted on a log scale using the corresponding shifting factor by determining the appropriate shifting factors for each elevated temperature.

where J is the creep compliance (GPa⁻¹) as a function of time t (s) and temperature T (°C); T _ref is the reference temperature, T _elev is the elevated temperature, α _T is the shifting factor, and t _r is the reduced time.

Figure 5

Creep compliance of 0° fiber sample in the accelerated creep test.

A practical application of TTSP can be identified by two conditions [15]: (1) the creep master curve generated is smooth enough; (2) the shifting factors can conform to the WLF Equation [29] or Arrhenius Equation [14]. However, in most cases, the WLF Equation is suggested to work in a temperature range from T _g to T _g + 100°C [15], which is not the target working temperature of FFRP studied in this study. Therefore, the Arrhenius Equation is employed here to evaluate the method for determining the shifting factors (α _{T i} ). The shifting factors can be related to temperature and time, as equation (3) shows.

where T _i is the elevated temperature (K); α _{T i} is the shifting factor corresponding to temperature T _i ; T ₀ is the reference temperature (K); E _a is the activation energy of the glass transition relaxation (kJ/mol); R is the universal gas constant (8.314 J/K/mol).

Determining shifting factors in composite materials can be achieved graphically by manually shifting curves or through computational methods using empirical equations. For the estimation of the shiftings, there are two potential computations ever successfully used for similar materials: by the frequency dependence of T _g and by the consistency of the viscoelastic properties. These potential approaches were involved in this study to determine the effective method for calculating shifting factors for the creep behavior of FFRP, and the results were evaluated based on the two necessary conditions for the application of TTSP, namely the generation of a smooth creep master curve and the determination of shifting factors that conform to the Arrhenius equation. Additionally, the predicted long-term creep behavior of the FFRP composite was validated by comparing it with the actual long-term creep test results obtained from a 2,000-h creep test conducted on a sample with the same formulation. The comparison was carried out to confirm the accuracy of the predicted long-term creep behavior of the FFRP composite.

3.1.1 Determine shifting factors by the frequency dependence of T _g

Based on the Arrhenius Equation (equation (3)), shifting factors can be determined by the material’s properly estimated activation energy E _a. In this method, the activation energy for the creep of the composites is considered to be approximately equivalent to the activation energy of glass transition [20,27]. The activation energy could be calculated and estimated by the frequency dependence of T _g (equation (4))

(4) E a = − R d ( ln ( f ) ) d ( 1 / T g ) ,

where f is the loading frequency (Hz); T _g is the glass transition temperature (K); R is the universal gas constant (8.314 J/K/mol).

Figure 6(a) illustrates the relationship between the loss factor tan δ and temperature at various loading frequencies. The glass transition temperature T _g, defined as the temperature corresponding to the peak of tan δ, is found to increase monotonically with loading frequency. Linear regression analysis results as depicted in Figure 6(b) demonstrate a good fit between ln(f) and (1/T _g). Accordingly, the activation energy (E _a) can be determined from the fitted results using equation (2), based on the calculated E _a shifting. However, it is observed that the segments of creep are shifted excessively, resulting in a non-smooth master curve. This finding is consistent with prior research on unidirectional carbon FRP composites [21]. This discrepancy could be attributed to the difference in the polymer reinforced by long-unidirectional fiber used in this study, as opposed to the polymer reinforced by short-random fiber in previous research [20,27]. Therefore, it is concluded that utilizing the frequency dependence T _g to calculate shifting factors is unsuitable for the creep of unidirectional fiber FFRP investigated in this study.

Figure 6

(a) tan δ curves for a range of frequencies at a heating rate of 1°C/min; (b) frequency in a log scale versus the inverse of T _g; (c) the superposition results of FFRP shifted with the factors calculated by the frequency dependence of T _g.

3.1.2 Determine shifting factors by the consistency of viscoelastic properties

Another potential method for calculating shifting factors is to use the consistency of viscoelastic properties, where the shifting factors for different properties are substituted for each other. This method assumes that the superposition process should be the same for all viscoelastic properties and has been previously used for storage modulus and creep development [18,30]. The applicability of this method to the FFRP is investigated in this study.

The results of storage modulus in frequency sweep tests under the same isothermal steps as the accelerated creep test are presented in Figure 7(a). The two-dimensional minimization superposition program [31], integrated with the TA Instruments Data analysis software, is utilized to horizontally and vertically shift the storage modulus curves. The generated master curve of the storage modulus is smooth and continuous, as shown in Figure 7(b). The relationship between the shifting factors and the temperature in Figure 7(c) fits well with equation (1), as determined through linear regression analysis. The activation energy (E _a) calculated from the fitted results is 144.45 kJ/mol. The applicability conditions of TTSP are satisfied by the superposition of the storage modulus. Therefore, the accelerated creep curves are shifted by the same factors used in the storage modulus superposition process. A smooth and continuous creep master curve is constructed, as shown in Figure 7(d), indicating that this method can provide suitable shifting factors for predicting long-term creep.

Figure 7

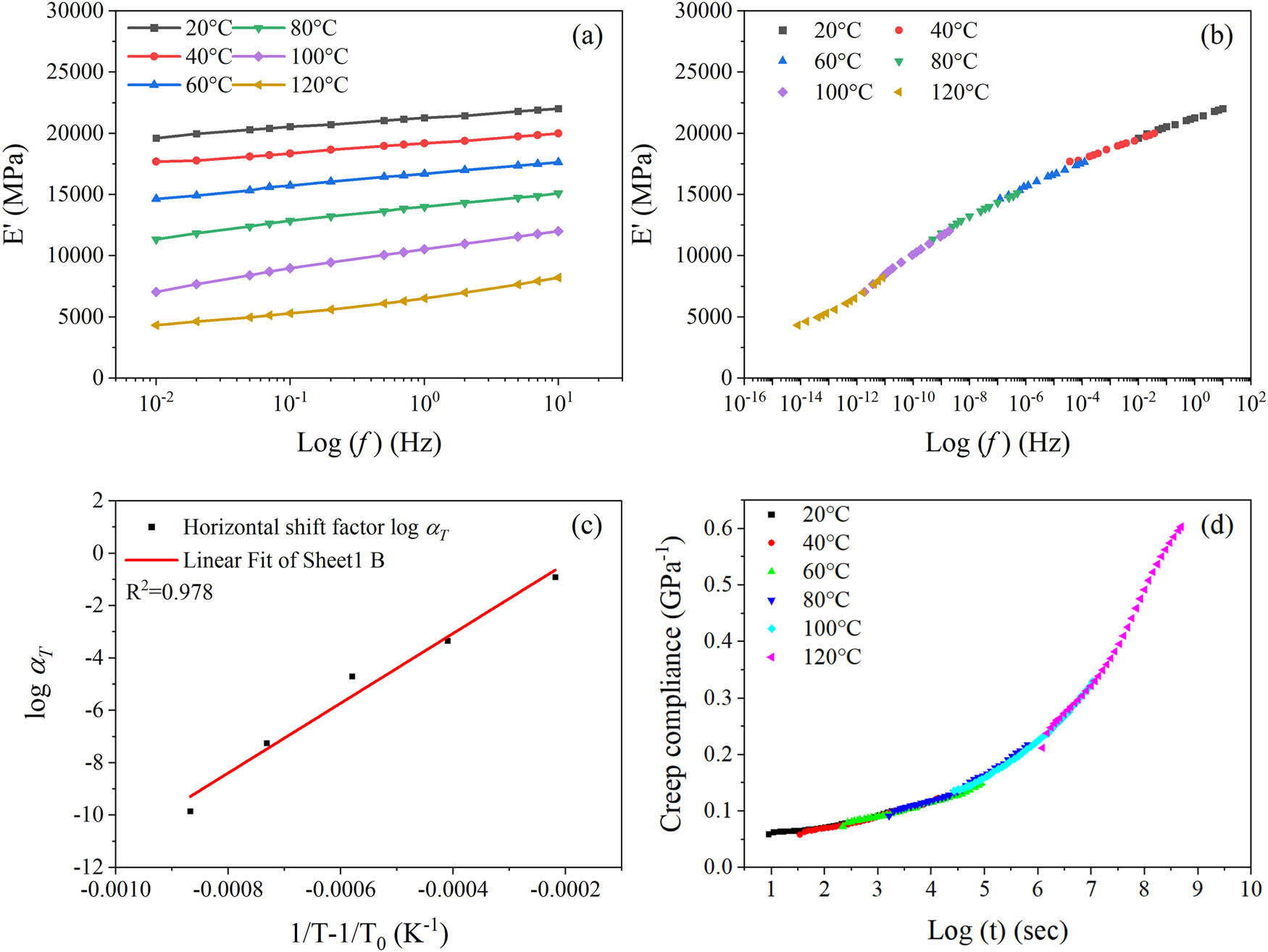
(a) Frequency sweep results of FFRP at different temperature steps. (b) The master curve of the elastic modulus. (c) Relationship between horizontal shifting factors and temperature. (d) The creep master curve constructed with shifting factors calculated by the consistency of viscoelastic properties.

3.1.3 Determine shifting factors by visual graphical method

The visual graphical method is a commonly employed approach for calculating shifting factors in TTSP applications [28,32]. This method involves manually shifting short-term creep curves to construct a continuous and smooth creep master curve. Figure 8 shows the creep master curve generated using the visual method, which is smooth and continuous. During the shifting process, the creep curves from the accelerated creep test were horizontally and vertically shifted together to make the master curve as smooth as possible.

Figure 8

Creep master curve of 0° fiber sample generated manually by the visual method.

In contrast to the mathematical methods, the visual method relies on the judgment and expertise of the researcher to manually adjust the creep curves to generate a smooth master curve. This method is particularly useful when the mathematical methods fail to produce a smooth master curve due to the complex nature of the viscoelastic behavior of the material. The visual method allows for more flexibility and control in the shifting process, as the researcher can visually assess and adjust the creep curves as needed. However, this method is subjective and may vary depending on the researcher’s experience and interpretation of the data. It is therefore important to carefully analyze and validate the results obtained using the visual method. Overall, the visual method is a valuable tool for calculating shifting factors in TTSP applications and can be used in conjunction with mathematical methods to ensure accurate and reliable results.

3.2 Comparison of the methods to generate creep master curve

Figure 6(c) shows that the shifting factors calculated by the frequency dependency of glass transition temperature result in superposition results that are too large to construct a smooth curve. This suggests that the activation energy for the creep of FFRP is much lower than the activation energy needed for the glass transition and cannot be approximated by it. Upon examining the creep master curves generated by the other two methods, it was found that both methods can help construct a smooth and continuous creep master curve. However, there were differences in the speed of creep development over a long-term period in the master curves generated by the two methods. To investigate the effectiveness of the two methods, the actual measurement results of the creep test on 0° fiber samples for 2,000 h were employed to compare with the creep master curves (Figure 9). It was found that the creep master curve generated by using the consistency of viscoelastic properties agrees better with the long-term measurement value than the visual results. The creep master curve generated by the visual method can predict the trend of creep development, but there is a non-negligible overestimation of creep. Although there is still a difference between the creep master curve generated by the consistency of viscoelastic properties and the predicted values, it is able to reflect the long-term development characteristics of creep.

Figure 9

The comparison of predicted creep results with long-term tested results.

The advantage of using the consistency of viscoelastic properties is the parameterization of the application of TTSP. Although additional frequency sweep tests are needed to use this method, it is still an efficient method to obtain the long-term creep behavior in the structural design process, when compared with traditional long-term creep measurements. The visual method provides a simpler way to know the trend of creep, but the creep master curve is influenced by subjectivity. It may be helpful in material selection before the structural design, but the error caused by the instability during the curve-shifting process should be considered in practical operation.

To further support the use of the consistency of the viscoelastic properties method, it should be noted that this approach offers several advantages beyond its efficiency. First, it allows for better control and understanding of the creep behavior of the composite material, which is essential for predicting the material’s long-term performance in structural applications. This method also provides a more accurate representation of the creep behavior by incorporating the frequency dependency of viscoelastic properties, which can improve the accuracy of the creep master curve. Additionally, using this method can aid in optimizing the composite material composition and processing parameters, as it provides a more detailed understanding of the material’s viscoelastic properties.

On the other hand, the visual method may still have applications in certain scenarios, such as when a quick assessment of creep behavior is required or when dealing with materials with relatively simple creep behavior. However, the limitations of this method should be kept in mind, as the curve-shifting process can introduce errors and inaccuracies. Therefore, it is important to carefully consider the trade-offs between the different methods when choosing an appropriate approach for generating creep master curves for composite materials. Overall, the consistency of the viscoelastic properties method is a promising approach that offers a more accurate and efficient way to obtain long-term creep behavior for composite materials.

During the creep master curve construction process, vertical shifting is required to achieve a smooth and continuous curve. This phenomenon has been observed in similar materials loaded in the direction of the fiber [32]. Vertical shifting is believed to improve the accuracy of creep analysis without affecting its accuracy. Figure 10 shows that the relationship between vertical shifting factors and testing temperature is approximately linear, indicating that the vertical shifting factors may counteract the effect of heating on properties other than creep. As shown in Figure 11, the same TTSP application process was used to generate the creep master curve of FFRP samples with fiber at 90° and ±45°. In contrast to the 0° fiber samples, there is no need for vertical shifting during the construction of creep master curves for 90° and ±45° fiber samples. The reasons for this phenomenon are complex and varied, but one important reason is the sensitivity of the initial instantaneous elastic strain to temperature. The instantaneous elastic strain of 0° fiber samples depends primarily on the stiffness of the flax fiber, resulting in a mismatch between the change in instantaneous strain and creep as the temperature increases. In contrast, the instantaneous elastic strain of the other two types of samples is determined jointly by the matrix and fiber, resulting in an initial strain increase proportional to the temperature increase and allowing for the master curve to be generated without the need for vertical shifting factors.

Figure 10

Relationship between vertical shifting factors for 0° fiber samples.

Figure 11

Creep master curve of samples made of (a) 90° fiber and (b) ±45° fiber.

This phenomenon highlights the importance of considering fiber orientation and material composition when designing experiments to obtain creep master curves. While the vertical shifting factors are necessary for 0° fiber samples, they are not required for samples with fibers oriented at 90° or ±45°. This is due to the joint contribution of the matrix and fiber in determining the instantaneous elastic strain for these samples. The temperature sensitivity of the initial strain in these samples results in an increase in strain with an increase in temperature, allowing the creep master curve to be generated without vertical shifting factors.

Understanding the factors influencing creep behavior and developing accurate predicting methods is crucial for designing composite materials structures. The TTSP method, with its efficient and parameterized approach, can be a valuable tool for determining the long-term creep behavior of these materials. The insights gained from this study can aid in developing more robust and reliable models for predicting the creep behavior of composite materials, ultimately leading to safer and more durable structures.