Abstract
In this research work, boron nitride nanosheet (BNS)-reinforced nanoplate is analyzed to evaluate its static bending performance including the effect of flexoelectricity and surface subjected to hydrostatic load, point load, and line load conditions. All edges of the nanoplate have simply supported boundary conditions, and it is transversely loaded from the top plane. The Navier method is employed to obtain the solution of the governing equation, and the static bending performance of the nanoplate is exhibited. The impact of uncertainties in the design variables and application loads have also been analyzed to evaluate the performance-based reliability of the bending response. It is noticed that both surface and flexoelectric effects are highly size-dependent and cannot be neglected at the nanoscale. Therefore, these factors are included in the model to investigate their contribution to the static bending of the BNS-reinforced nanoplate.
1 Introduction
Recently, 2D materials, such as carbon nanotubes [1,2], graphene [3], and boron nitride nanosheet (BNS) [4,5], are used in polymer matrix composites, and they exhibit excellent thermal and mechanical properties. Hexagonal BNS has attracted researchers’ attention over graphene due to its superiority in physical properties. BNS has a structure similar to the hexagonal structure of graphene, where boron and nitrogen atoms are alternatively placed in a hexagonal pattern. BNS possesses some unique properties compared to graphene, such as a wide bandgap of about 5–6 eV, which turns it into a good electrical insulator, excellent thermal conductivity of 227–280 W/mK, high stability in chemical and high-temperature environments, and high oxidation resistance [6]. Furthermore, the BNS monolayer possesses piezoelectricity as a result of a non-centrosymmetric structure. In the experimental study conducted by Ares et al. [7] using electrostatic force microscopy, it is observed that the monolayer of hexagonal boron nitride nanosheets is piezoelectric. Piezoelectric properties are greatly affected by shape and are almost independent of size [8]. In recent years, Gupta et al. [9,10,11,12] made efforts to develop micromechanical models to study the elastic and piezoelectric properties of 1–3 piezoelectric composites, with piezoelectric fibers reinforced in the thickness direction. Such composites exhibit enhanced out-of-plane piezoelectric constant, which shows better response against the transverse loading. Moreover, properties such as lightweight, high strength, and piezoelectricity make BNS an ideal candidate for nanodevices.
Over the last couple of decades, flexoelectricity effects have received enormous research attention in the development of nano-electro-mechanical-system devices. Flexoelectricity is the impulsive electric polarization generated by the non-uniform strain gradients, which is a function of flexoelectric coefficient and strain gradient magnitude. Flexoelectricity is substantiated in all dielectric materials including centrosymmetric and non-centrosymmetric crystals. Inversion symmetry of the material structure tends to locally discontinue due to non-uniform strain gradients, and as a result, a dipole moment is formed, resulting in polarization [13]. However, flexoelectric effect is extrusive at the nanoscale due to enhanced flexibility and defect-free structures [14]. Apart from the flexoelectric effect, surface phenomena originate from surface elasticity theory [15], which offers a significant contribution to the electromechanical response of the nanoscale structures [16,17]. The size-dependent properties result from the large ratio of volume and surface area of the nanostructures like nanobeams, nanoplates, and nanoshells. These nanostructures are the fundamental building blocks of nanodevices such as sensors, actuators, and energy harvesters. Hence, the combined effects of surface and flexoelectricity should be involved in evaluating the electromechanical responses of nanostructures.
Several studies, which investigate the static bending response of the nanobeams and nanoplates, including surface and flexoelectric effects, are reported in the literature. The electromechanical behavior study of curved nanobeam and nanowire [18,19], sinusoidal piezoelectric nanoplate [20], and piezoelectric nanofilms [21] are predicted using surface effects. The flexoelectric effect of the heterogenous flexoelectric membrane was studied by Mohammadi et al. [22] and predicted the electromechanical response on the membrane. Yang et al. [23] used an analytical formulation derived from the Kirchhoff plate theory to observe the static deflection of flexoelectric nanoplate and concluded that flexoelectricity affects thin composite nanoplate. The unified surface and flexoelectric effect exhibit noteworthy effects on the electromechanical performance of the nanoplates. Specifically, the effect of size is sharply noticed for the plates of smaller thickness [24,25]. Current literature also reported the analysis of bending and vibrational behavior of nanolaminates, nanosandwich structures, and nano bilayer circular plates. The bending and vibration characteristics of nanolaminates [26] are studied under surface and flexoelectric effects using the analytical models for different boundary conditions. They identified that the flexoelectric and surface effects result in stiffer nanolaminates with reduced natural frequency. Kaveh et al. [27] obtained the normalized natural frequencies of a nano sandwich structure made of functionally graded porous core and flexoelectricity-based face sheets on both sides through governing equations based on a new type of power law for porous materials, Hamilton’s principle, and modified couple stress theory. Similarly, a new flexoelectricity-based theoretical model [28] was developed for a piezoelectric layered bilayer circular nanoplate which accounted the influence of surface and flexoelectric effects on radial deflection, central deflection, polarization, and electric potential of the bilayer piezoelectric nanoplate. They noticed that flexoelectricity affects deflection when negative surface residual stress is considered while positive surface residual stress consideration influences deflection behavior controlled by surface effect. Models based on modified classical plate theory are mainly utilized to predict electromechanical response. Recently, Kundalwal and Gupta extensively studied the influence of flexoelectricity and surface on the bending rigidity of graphene/BNS-based nanostructures such as nano beams, plates, and rods. They developed various size-dependent analytical and finite element models based on theories such as Timoshenko beam theory [29], Euler Bernoulli beam theory [30,31], and Kirchhoff plate theory [32]. Yue et al. [33] investigated the static bending and free vibration properties of a variable width piezoelectric nanoplate with flexoelectricity. They derived the governing equations from the nonlinear Mindlin plate theory, flexoelectricity theory, and finite element theory. They showed that the flexoelectric effect can strongly influence the maximum deflection, the morphology of deformation, and the natural frequency of variable-width piezoelectric nanoplate. This concludes that nanostructures exhibit a significant reduction in bending deflection when surface and flexoelectric effects are simultaneously considered. Additionally, there are uncertainties and stochasticity associated with the design variables and parameters due to the inherent variability in material properties during manufacturing, structural dimensions, and applied loading conditions. The bending response of the beam under such uncertainties cannot be precisely evaluated.
Performance-based reliability analysis (PBRA) is the statistical tool employed to evaluate the reliability performance of structures and components under a specified working environment. PBRA focuses primarily on the relationship between the performance of system and the capability to achieve the predefined level of performance. Recently, the implementation of PBRA in the evaluation of fatigue life performance of complex engineering structures has been reported. Yang et al. [34] reviewed the effect of hydrogen environment on the very high cycle fatigue performance of metals. Meng et al. [35] proposed an intelligent optimization-inspired support vector regression modeling methodology to build a high-precision approximation model for fatigue life estimation of complex engineering structures like support structures of offshore wind turbines. Similarly, Liu et al. [36] employed the bootstrap error circle method of random load signals for uncertainty in the fatigue life prediction of parts. Yang et al. [37] reviewed the general formulation of the reliability-based design optimization strategy and most probable point search algorithm and proposed an RBDO strategy for various marine structures. Luo et al. [38] proposed a highly efficient structural reliability analysis method coupling the active Kriging algorithm with the conjugate first-order reliability method which offers robust and accurate performance.
In this study, BNS-reinforced nanoplate, which is simply supported on all edges, and loaded with a hydrostatic, point, and line load is considered for the study. The governing equation of the BNS nanoplate is obtained using classical plate theory, and Navier solution methodology is adopted to derive the analytical expression for the evaluation of static bending deflection of BNS nanoplate. The PBRA [39,40] of the bending response under the geometric parameters, fiber volume fraction, and applied load has been evaluated using the Monte Carlo simulation (MCS) methodology [41,42]. This technique is favored due to its ease of implementation, robustness, and capacity to provide accurate results that remain unaffected by the dimension or intricacy of the problem, although a substantial number of simulation runs are necessary to achieve a reliable estimate. To address this constraint, we employed the response surface approximation to approximate the bending response in terms of design variables to reduce the computational burden. These approximated polynomials are used to compute the bending response at each design point generated via MCS with the Latin hypercube sampling (LHS) approach [42,43] to evaluate the probability of failure from the limit state function.
Regarding the structure of this article, Section 2 presents the theoretical formulation of the modified Kirchhoff plate theory with the modification for the inclusion of the surface and flexoelectric effects. Section 3 presents the governing differential equation for the BNS-reinforced nanoplate. Section 4 presents a PBRA using the MCS approach followed by results and discussions presented in Section 5. The conclusion of this study is given in Section 6.
2 Theoretical formulation of BNS-reinforced nanoplate
In this section, the governing equation for the uniformly loaded BNS-reinforced nanoplate, which is simply supported over all edges is developed. The derivation is based on the classical plate theory and is modified to cover the surface and flexoelectric effects. The cartesian coordinate system is adopted, and the reference plate is set at the middle layer of the BNS-reinforced nanoplate.
Figure 1 displays the BNS-reinforced nanoplate with a layer of surface loaded with point load, line load, and hydrostatic load. Nanoplate has dimensions of Length a, width b, and thickness h. The thickness of the nanoplate is oriented along the z-direction. This nanoplate contains a surface layer of negligible thickness on its upper and lower surfaces.

(a) Schematic representation of the BNS reinforced nanoplate with top and bottom surface layer subjected to (b) point load, (c) line load, and (d) hydrostatic load.
As per the classical plate theory, the generalized lateral displacement of the nanoplate is given as [44]
where
Kirchhoff plate theory assumes a very small thickness as compared with its in-plane dimensions. Therefore, strain gradient components in the in-plane directions can be neglected when compared with strain gradients in the thickness direction. Past research studies [24,45] have also mentioned similar assumptions for the Euler beam model. Hence, a non-zero strain gradient in the thickness direction is written as
Some previous studies consider the surface effect on strain and stress field [15] and the effect of surface and flexoelectricity on dielectric nanomaterials [46]. Hence, to involve surface and flexoelectric effect, the electric Gibbs free energy is split into a bulk volume and a surface layer of negligible thickness. The bulk electric Gibbs free energy is given by
For the piezoelectric material, the last two terms of Eq. (6),
where
Utilizing Eqs. (7)–(9), the bulk electric Gibbs free energy may be rewritten as
and the constitutive relations can be re-written as
As strains in directions apart from thickness direction is negligible, they are not considered in the equation for simplification. The last term of Eq. (17) gives the electric field generated due to strain gradients developed in the nanoplates when no electric field is applied externally.
According to Gauss’ law of electrostatics, the electric displacement of the BNS-reinforced nanoplate without free electric charges is given by,
When the open circuit condition is considered for the nanoplate, the electric displacement on its surface is considered to be zero. Therefore, using Eq. (18), the internal electric field is derived as
where the term
When the surface effects are accounted, then the surface electric Gibbs free energy
where
wherein
Based on the surface piezoelectricity model [17], for the surface layers, the surface constitutive are given as
where
The lateral displacement after incorporation of the flexoelectric and surface effects is derived by utilizing Hamilton’s principle [48]
where
When the vibration along the horizontal plane is neglected, the kinetic energy (K) can be written as
where ρ indicates the mass density.
When the mechanical load is applied, the work done by it is defined as
Therefore, the governing equation can be expressed as
On the application of SS boundary condition on BNS reinforced nanoplate and considering the flexoelectricity and surface effects on general resultant moments and forces, the governing Eq. (31) can be reformulated and given by
with
3 Electromechanical response of the BNS-reinforced nanoplate
The governing differential equation used in the analysis of the static bending analysis of the nanoplate is written in the modified form as
As the nanoplate considered in this study is simply supported over all its edges, the solution for Eq. (34) can be obtained using Navier’s method. Utilizing the Navier’s method, the deflection of the plate in the transverse direction is expressed as
where
where
For hydrostatic loading,
For point loading,
For line loading,
Using Eqs. (32), (36)–(38), the analytical solution for lateral deflection
4 PBRA using MCS
The aim of designing a system or product is to ensure that it effectively accomplishes its intended functions while maintaining satisfactory performance criteria, where performance criteria can be expressed as a permissible degree of damage or tolerance established through an acceptable likelihood of encountering failure. The methodology proceeds with the following steps:
Step 1: Create a set of design points covering entire design space
This step generates a set of input design vectors from the design space (also referred to as the experimental region) to evaluate the limit state at each set of values. This process, commonly known as Design of Experiments in the literature, can be classified into physical experiments or computer-generated experiments depending on the type of simulation model – stochastic and/or deterministic.
For deterministic models, the response values are determined through mathematical relationships based on the input variables. As these models are devoid of random errors, they primarily exhibit system error (e.g., approximations inherent in the model that may deviate from the true response). To minimize system error, space-filling designs, such as LHS, is employed to evenly or uniformly distribute points across the design space. LHS is particularly preferred for computer experiments due to its ability to provide dense and uniform coverage of the range of each variable within the design space. Using the LHS procedure, a specified number of sampling points (64 samples in the present work) for fiber volume fraction are generated. The fiber volume fraction is utilized to predict effective elastic and piezoelectric constants using the Mori-Tanaka model. For the sake of brevity the model is not presented here, for more details regarding model, the work of Kundalwal and Gupta [32] can be referred. Using these data points, curve fitting equations are obtained for effective elastic and piezoelectric constants, and these questions are used in the classical plate theory model presented in Section 3. Each simulation of the Mori-Tanaka model takes approximately 10 CPU minutes; thus, the use of response surface using LHS significantly reduced the computational burden compared to exhaustive Monte Carlo sampling.
Step 2. Evaluate the performance-based reliabilities by employing MCS at the design points
The performance-based reliabilities can be classified according to the properties of the performance indexes into four types, i.e., bigger the better, smaller the better, nominal the best, and zero point proportional [49]. This study has been undertaken based on the “nominal the best” performance index. This type of index is shown in Figure 2, which implies that the supplied performance in terms of the bending response of nanobeams shall be closer to the target value. Then, the reliability is defined as the probability that the bending response of nanoplate is within the given target values, i.e.,
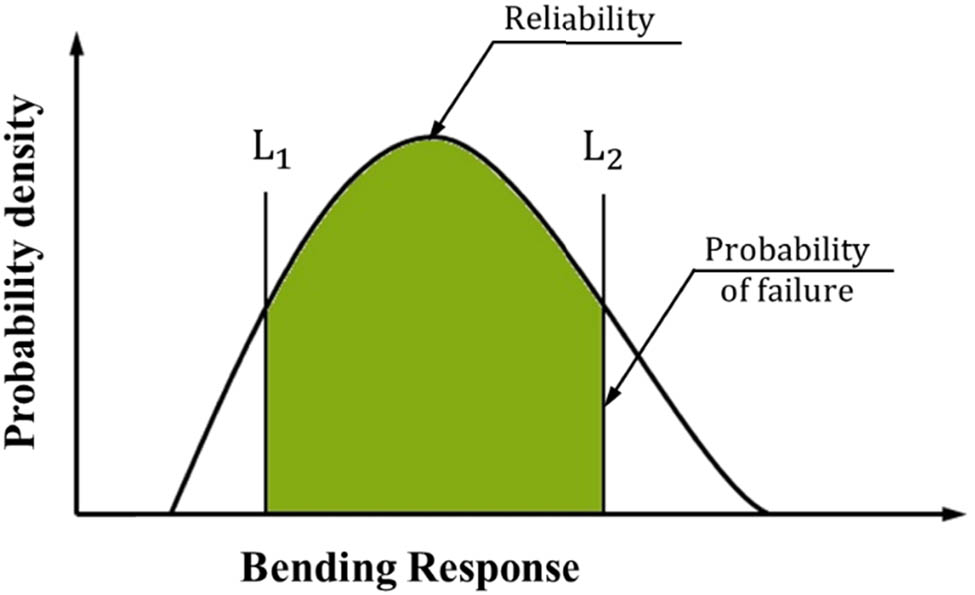
Probability density of the bending response of nanobeams.
The estimated probability of failures
where
where N is the total number of samples for MCS, and
5 Results and discussion
The BNS-reinforced nanocomposite material considered in this study consists of a polyimide matrix reinforced with piezoelectric BNNS. The mechanical and electrical properties are taken from our group’s previous study by Kundalwal and Gupta [32] and are presented in Table 1. These material properties are for 60% fiber volume fraction.
Effective material properties of BNS-reinforced nanocomposite material
| Material | Ref. |
|
|
|
|
|
|
|
|
|---|---|---|---|---|---|---|---|---|---|
| Boron nitride reinforced nanocomposite | [32] | 25.76 | 15.19 | 15.19 | 489.294 | 5.28 | −0.0090 | 0.3192 | 1.38
|
5.1 Effect of flexoelectricity and surface on the bending deflection of BNS-reinforced nanoplate
The variation in normalized bending stiffness (
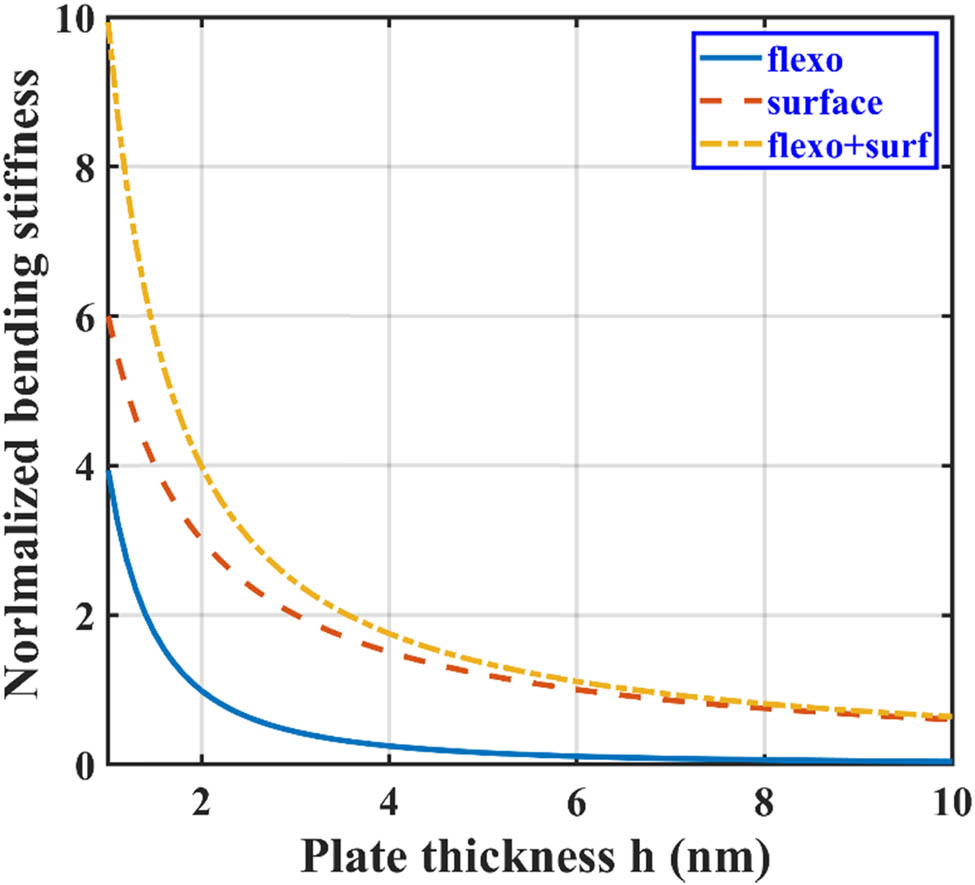
Variation in normalized bending stiffness (
To investigate the electromechanical response of the BNS-reinforced nanoplate, the results are obtained from the Kirchhoff plate theory modified to incorporate flexoelectric and surface effects. The length “a” and width “b” of the nanoplate are taken as 50 h and height h is taken as 3 nm. In this study, the aspect ratio of the plate is considered in the range of 5–80 as suggested by a previous study [51]. The load magnitude q
0 is considered to be 0.05 MPa. The flexoelectric coefficient range for the polymers is mentioned between
The effect of surface and flexoelectricity on the static bending performance of the 3 nm thick SS BNS reinforced nanoplate under point load, line load, and hydrostatic load is presented in Figures 4–6. All loads applied to the nanoplate are normal to the x-y plane. It can be seen from Figures 4–6 that the maximum deflection of the nanoplate occurs at the center of the nanoplate irrespective of the loading case. The deflection is observed to be maximum for the classical plate in all loading cases, where the effect of surface and flexoelectricity is not considered. When surface and flexoelectric effects are included in the nanoplate, there is a significant drop in maximum deflection, and it is independent of loading conditions. For example, in the point-loaded BNS reinforced nanoplate of 4 nm thickness, the reduction in maximum deflection is about 25% due to the flexoelectric effect, 75% due to the surface effect, and a significant 80% reduction can be observed when combined surface and flexoelectric effects are considered against maximum deflection of the classical plate. Size-dependent surface and flexoelectric effects are primarily responsible for this reduction in maximum deflection. The magnitude of the maximum deflection is highest in the point loading followed by line loading and lowest in the hydrostatic loading case.
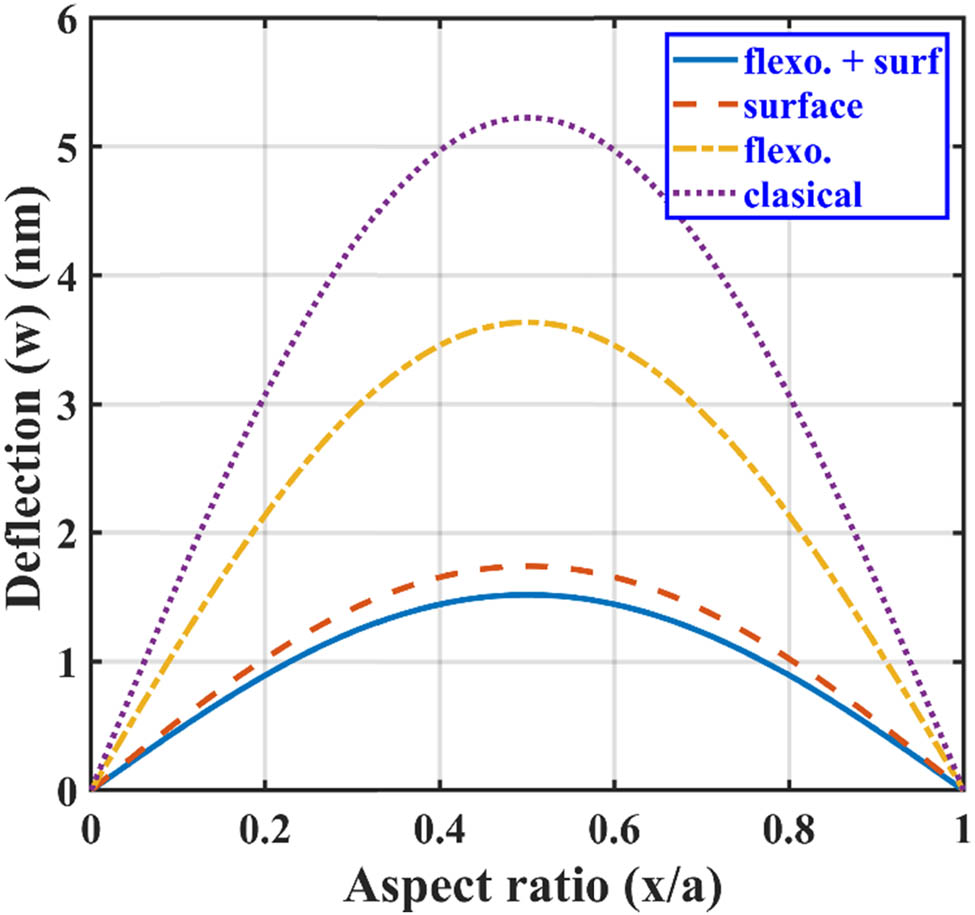
Lateral deflection of SS BN-reinforced nanoplate with aspect ratio subjected to point load.
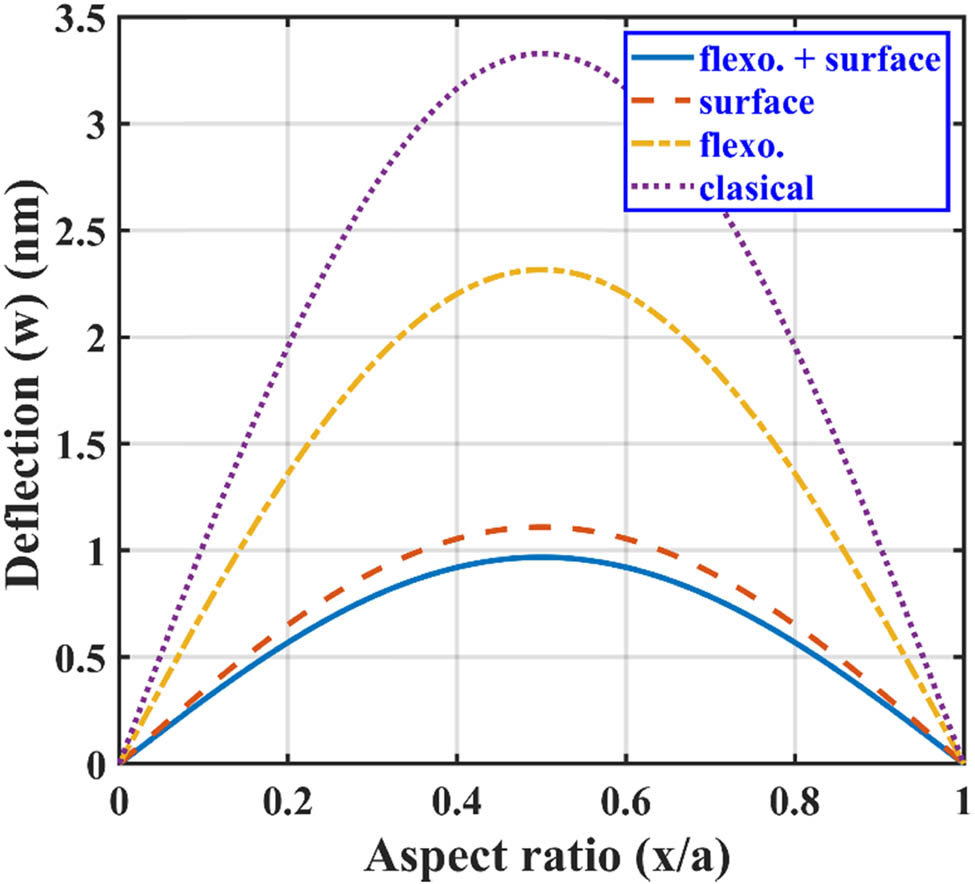
Lateral deflection of SS BNS-reinforced nanoplate with aspect ratio subjected to line load.
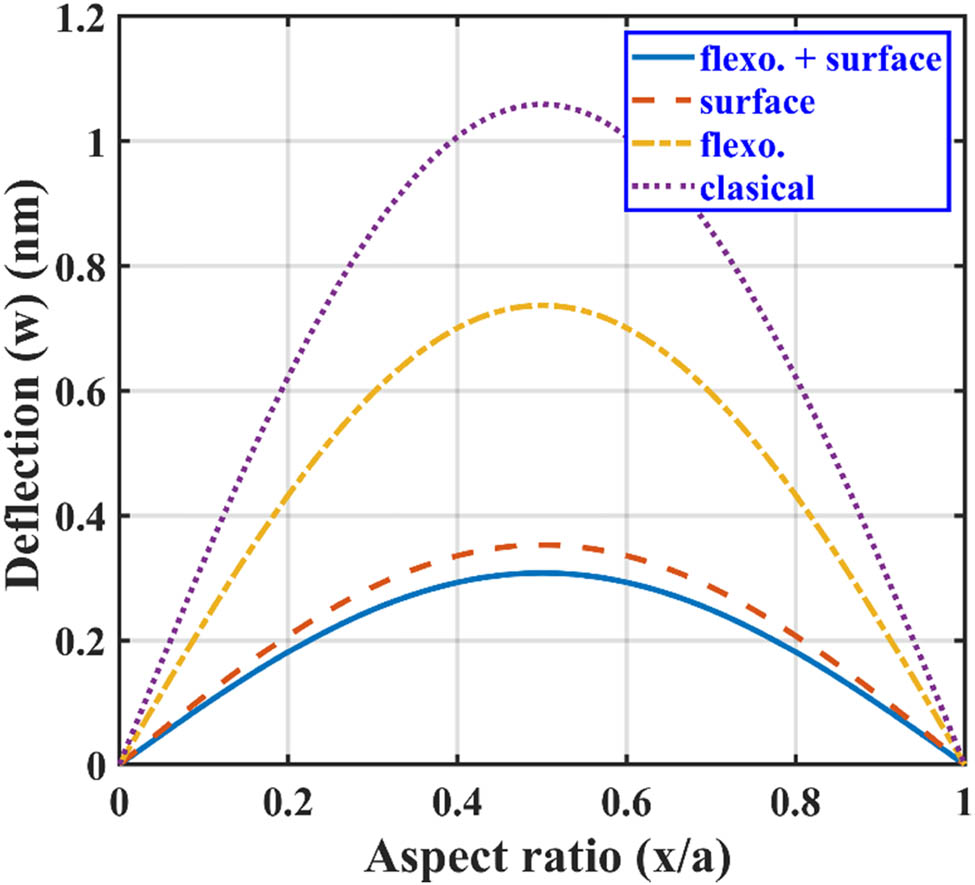
Lateral deflection of SS BNS-reinforced nanoplate with aspect ratio subjected to hydrostatic load.
Moreover, the maximum deflection is analyzed for the nanoplate thickness of 2, 4, 6, 8, and 10 nm in all three loading conditions to observe the effect of nanoplate thickness on the maximum deflection. The results are displayed in Table 2. In comparison to the classical model, for point loading with flexoelectric and surface effects, the maximum deflection is reduced by ∼80%, ∼63%, ∼53%, ∼45%, and ∼44% corresponding to 2, 4, 6, 8, and 10 nm, respectively. The maximum deflection amount reduces when the thickness of the nanoplate increases because the surface and flexoelectric effects are less prominent higher thickness. Similar observations are found for line and hydrostatic loading conditions.
Maximum lateral deflection of SS BNRC nanoplate under different loading conditions
| Thickness h (nm) | Case | Maximum deflection (nm) | |||
|---|---|---|---|---|---|
| Uniformly distributed load | Hydrostatic load | Point load | In-line load | ||
| 2 | With flexo + surf | 0.2004 | 0.1002 | 0.4944 | 0.3147 |
| With surf | 0.2497 | 0.1248 | 0.6160 | 0.3922 | |
| With flexo | 0.5034 | 0.2517 | 1.2420 | 0.7907 | |
| Classical | 0.9986 | 0.4993 | 2.4640 | 1.5690 | |
| 4 | With flexo + surf | 0.9503 | 0.4752 | 2.3450 | 1.4930 |
| With surf | 1.0440 | 0.5219 | 2.5760 | 1.6400 | |
| With flexo | 2.0940 | 1.0470 | 5.1680 | 3.2900 | |
| Classical | 2.6100 | 1.3050 | 6.439 | 4.0990 | |
| 6 | With flexo + surf | 1.42 | 0.7102 | 3.504 | 2.231 |
| With surf | 1.498 | 0.749 | 3.696 | 2.353 | |
| With flexo | 2.701 | 1.35 | 6.664 | 4.242 | |
| Classical | 2.996 | 1.498 | 7.392 | 4.706 | |
| 8 | With flexo + surf | 1.733 | 0.8663 | 4.275 | 2.721 |
| With surf | 1.793 | 0.8967 | 4.425 | 2.817 | |
| With flexo | 2.957 | 1.487 | 7.295 | 4.644 | |
| Classical | 3.138 | 1.569 | 7.744 | 4.93 | |
| 10 | With flexo + surf | 1.956 | 0.9778 | 4.485 | 3.072 |
| With surf | 2.004 | 1.002 | 4.944 | 3.147 | |
| With flexo | 3.084 | 1.542 | 7.61 | 4.845 | |
| Classical | 3.206 | 1.603 | 7.91 | 5.036 | |
We have also studied the effect of variation in the aspect ratio (x/a) on the maximum deflection of the nanoplate in all three loading conditions. For this purpose, the in-plane dimensions of the plate are kept constant as a = b = 100 nm. It can be noted from Figures 7–9 that for all loading conditions, the surface and flexoelectric effects are prominently seen for the lower nanoplate thickness, as both of these effects are size-dependent. As the thickness of the nanoplate increases, the effects of surface and flexoelectricity start diminishing and approach toward the results given for the classical plate case. It can be observed from these figures that the nanoplate subjected to point loading shows maximum defection (Figure 7), followed by line and hydrostatic loading conditions, respectively, as shown in Figures 8 and 9.
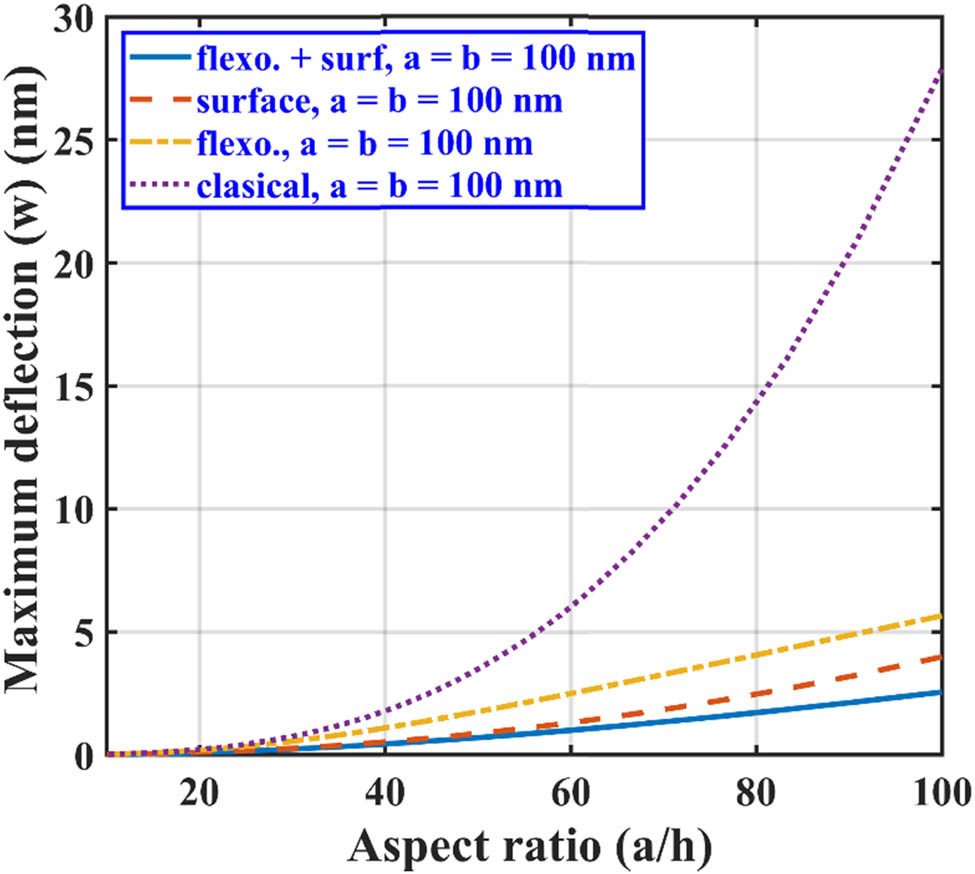
Maximum lateral deflection of SS BNS-reinforced nanoplate with aspect ratio
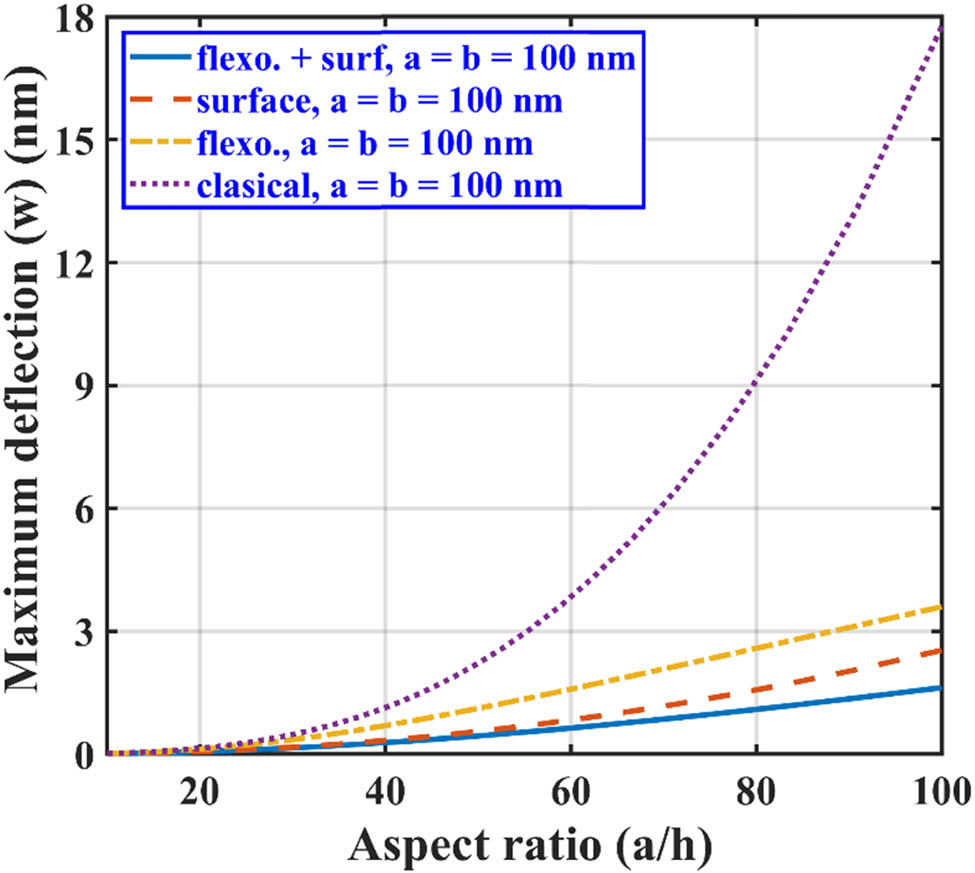
Maximum lateral deflection of SS BNS-reinforced nanoplate with aspect ratio
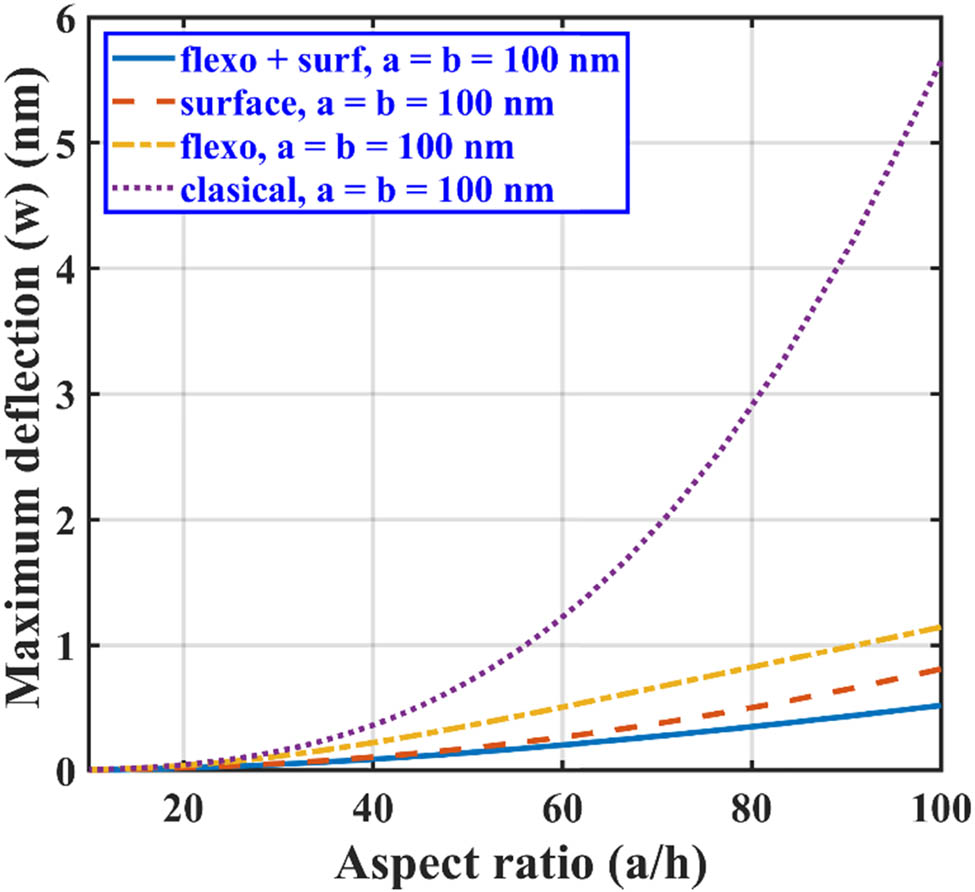
Maximum lateral deflection of SS BNS-reinforced nanoplate with aspect ratio
The maximum deflection of the 3 nm fixed thickness nanoplate is also predicted and represented in Figures 10–12. We can note that the contribution of the flexoelectric effect in maximum deflection reduction is lesser compared to the surface effect. But still, the flexoelectric effect contribution cannot be ignored. The results presented in this study highlight the significance of the size-dependent effect and aspect ratio for an accurate model of a nanostructure.
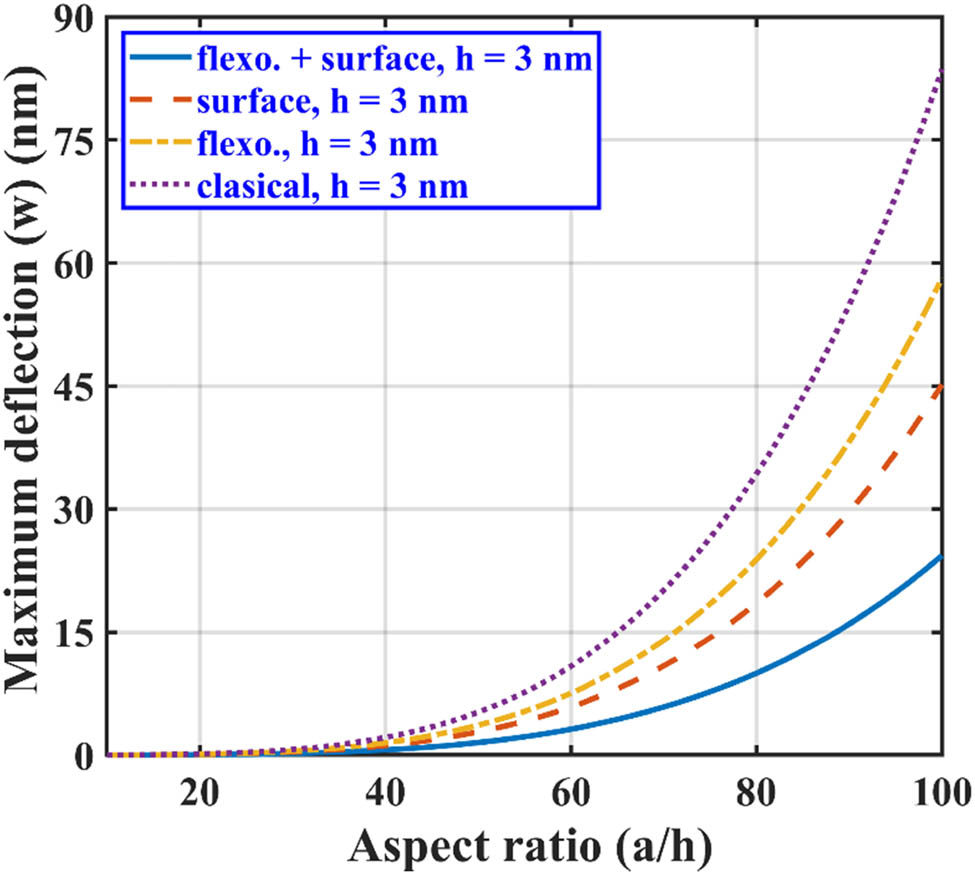
Maximum lateral deflection of SS BNS-reinforced nanoplate with aspect ratio
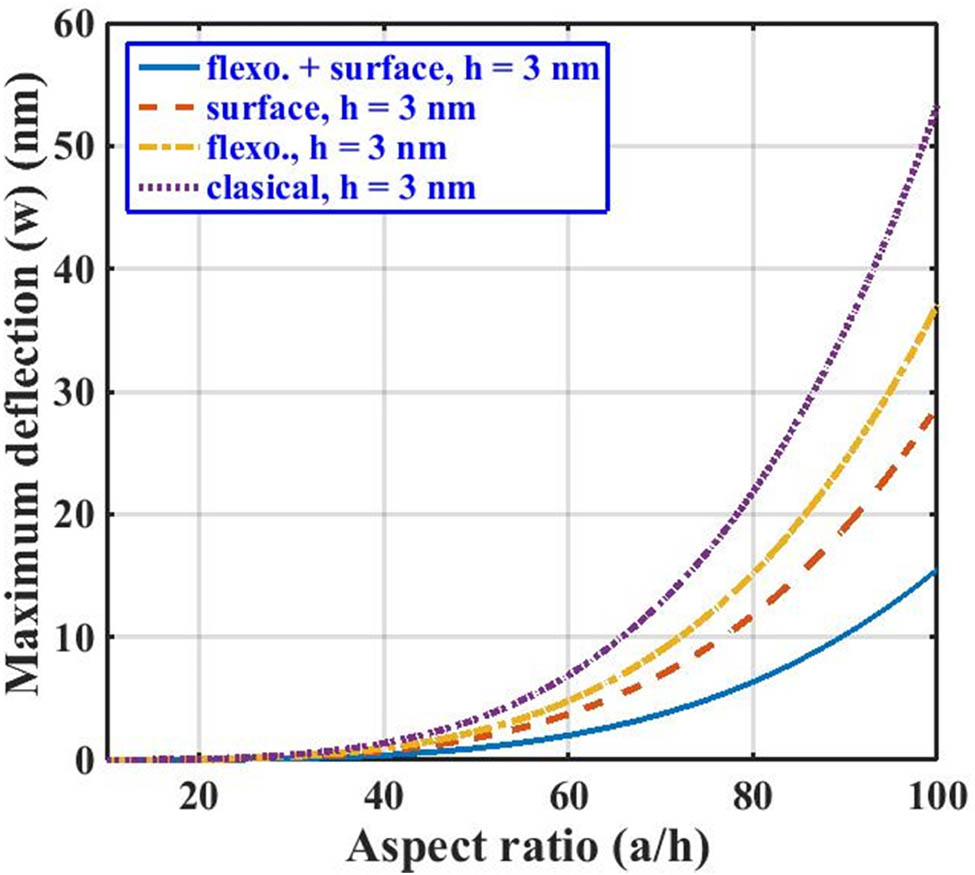
Maximum lateral deflection of SS BNS-reinforced nanoplate with aspect ratio
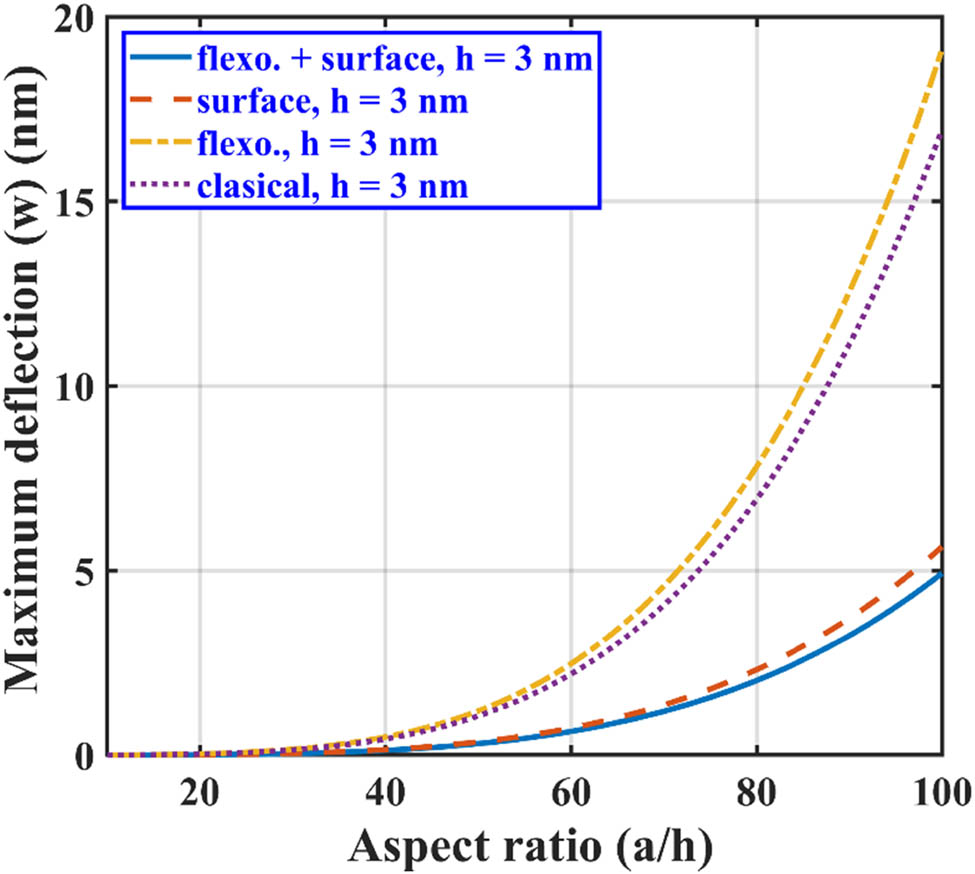
Maximum lateral deflection of SS BNS-reinforced nanoplate with aspect ratio
5.2 Influence of uncertainty parameters on the bending response of nanoplate
This section discusses the uncertainty parameters and their effects on the bending response of nanoplate for various loading conditions such as point, line, and hydrostatic loading. Table 3 tabulates the distributional properties of geometrical parameters and variables. We also considered that the volume fraction of the nanoplate is driven by uncertainty, and hence, using LHS, the random values of volume fraction were obtained following the normal distribution. Utilizing these random values of volume fraction, the elastic and piezoelectric constants are evaluated using the Mori-Tanaka approach [32]. Later, the polynomial relation is obtained using the curve fitting data as shown in Table 4.
Distributional properties of geometrical parameters and variables
| Variables/parameters | Distribution | Mean (nm) | Standard deviation (nm) |
|---|---|---|---|
| H | Normal |
|
|
| a, b | Normal |
|
|
| Q | Normal |
|
|
|
|
Normal |
|
|
| Volume fraction | Normal | 0.6 |
|
Curve fitting equations of material properties using LHS
| Material constant | Distribution | Equations | Constant | SSE | R 2 | Ad. R 2 |
|---|---|---|---|---|---|---|
|
|
Normal |
|
|
0.0025 | 1 | 1 |
|
|
Normal |
|
|
0.0011 | 1 | 1 |
|
|
Normal |
|
|
7.7 × 10−5 | 1 | 1 |
|
|
Normal |
|
|
5.0 × 10−8 | 0.998 | 0.998 |
|
|
Normal |
|
|
5.3 × 10−8 | 1 | 1 |
SSE: Sum of squared errors; R 2: Coefficient of determination; Ad. R 2: Adjusted R 2.
For this study, we used a sample size of 10,000. Since the original model is based on an exact solution, the computational cost per sample is relatively low. The computational cost of solving the bending response of a flexoelectric plate using the Kirchhoff plate theory was approximately 10–15 CPU seconds per simulation. Using MATLAB solver R2021a on a multi-core processor, the total computational cost for generating 10,000 samples was approximately 10 CPU minutes, demonstrating the efficiency of our approach. This highlights the computational efficiency of the Monte Carlo method in our study, even for a large number of simulations.
The performance of a design is usually represented with many measurable engineering specifications. These specifications are customarily marked either with a value holding tolerance or with a range having lower and upper limits. Figure 13(a) illustrates the PDF of point load with limit state function, which, in our case, is the deflection (w). The figure depicts that the performance of the piezoelectric BNRC nanocomposite is greatly affected by the uncertainty in the geometric parameters, fiber volume fraction, and applied load while designing the piezoelectric nanocomposite plate for the application of distributed sensors and actuators. The performance-related reliability of the system can be considered by choosing a zero-point proportional performance index. This type involves the output and the input being closer to a constant proportional as the better. The ideal quality may be a line across the origin. Similarly, the PDF and reliability are plotted for line and hydrostatic loading as shown in Figures 14 and 15, respectively.
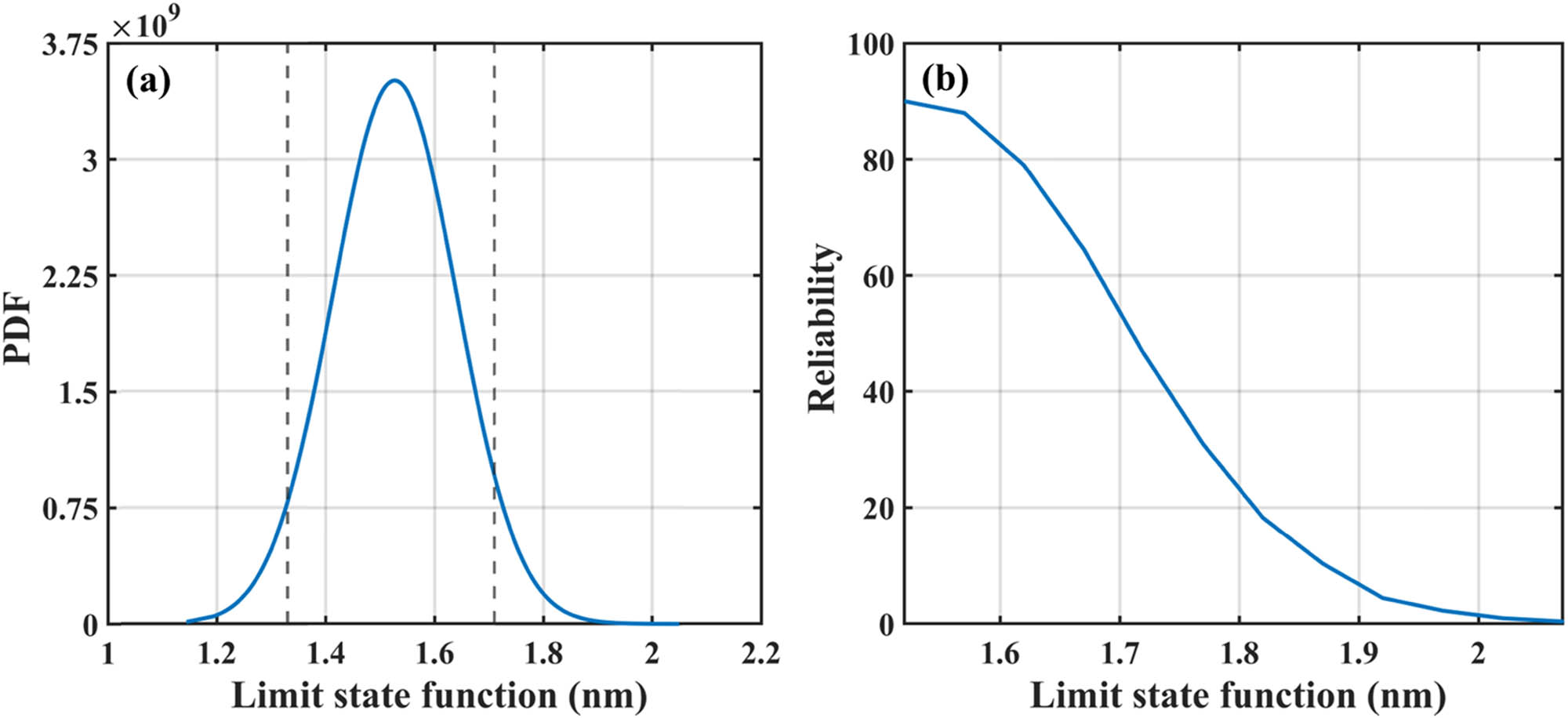
(a) PDF of limit state function and (b) variation in reliability with limit state function for point loading.
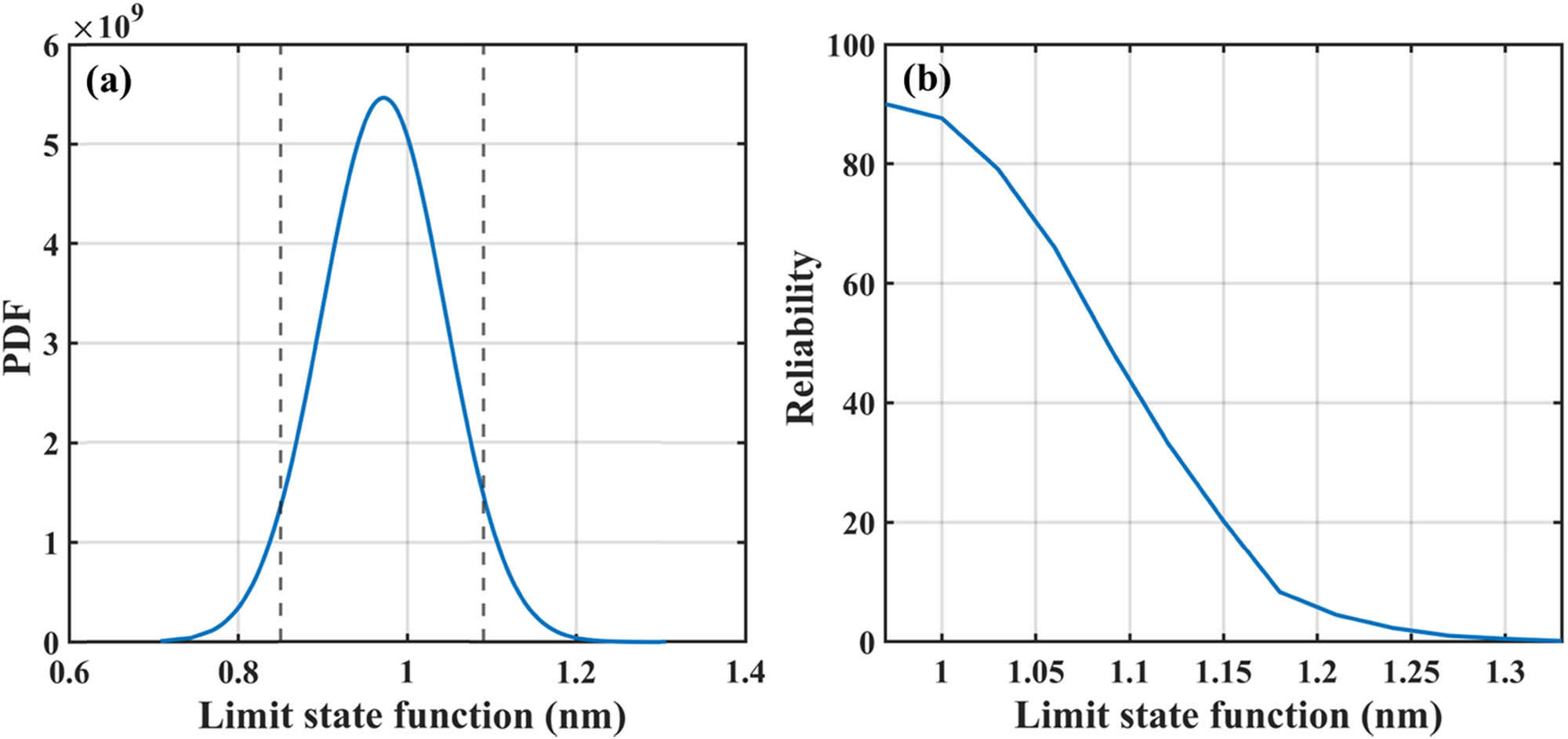
(a) PDF of limit state function and (b) variation in reliability with limit state function for line loading.
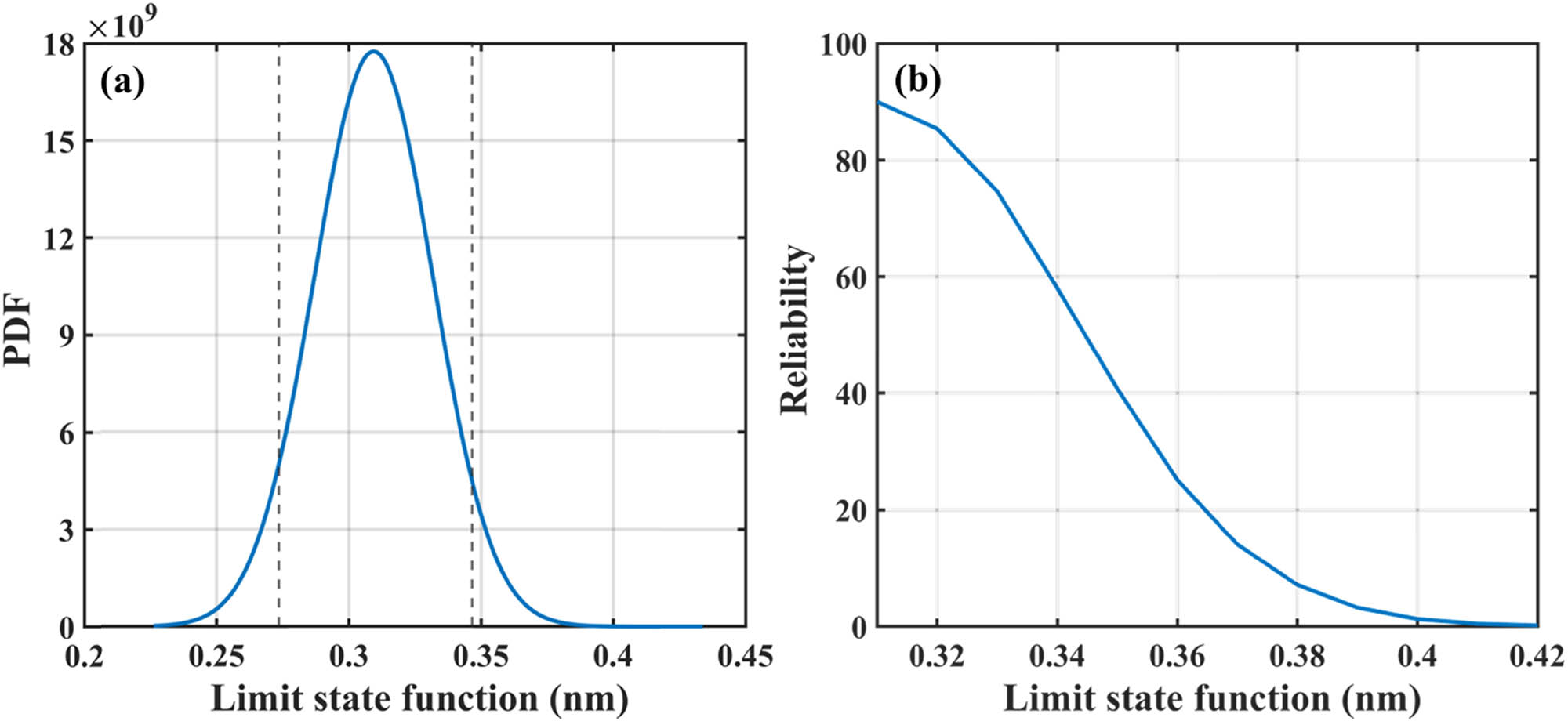
(a) PDF of limit state function and (b) variation in reliability with limit state function for hydrostatic loading.
Figure 13(b) shows the variation in the reliability with the limit state function for point loading. It can be seen that 90% reliability is obtained when deflection is
6 Conclusion
The static bending behavior of the SS BNS-reinforced nanoplate is investigated under hydrostatic load, point load, and line load case. The Navier solution method is applied to develop the closed-form solution for the governing differential equation. Surface and flexoelectric effects are incorporated in the Kirchhoff plate model, and their contribution to static bending behavior is studied. It is observed that maximum deflection occurs at the center of the nanoplate in all loading cases. The surface effect, flexoelectric effect, and integrated surface and flexoelectric effect reduce the maximum bending of the nanoplate. It is also noted that the flexoelectric and surface effects are more prominent for the smaller thickness of the nanoplate, and their effect diminishes as the plate thickness increases. Therefore, surface and flexoelectric effects are size-dependent and must be included in the model to predict the static bending response. The performance-based reliability is obtained using MCS and the results present 90% reliability for various loading conditions. The insights from this work can have practical applications in the design and optimization of advanced nanodevices. For instance, the enhanced sensitivity to flexoelectric and surface effects can be utilized to develop high-performance sensors that respond to minute mechanical stimuli. Similarly, the ability to fine-tune the electromechanical properties through material and structural parameters makes these nanoplates promising candidates for actuators, where precise control of deformation is required. Furthermore, the inclusion of flexoelectric effect can enhance the energy conversion efficiency in energy harvesting devices, enabling the development of compact and efficient systems for powering nanoscale electronics.
Acknowledgments
This work was generously supported by the Science Engineering Research Board (SERB), Department of Science and Technology, Government of India. The authors acknowledge the financial support of the SERB (grant number CRG/2022/000786, PDF/2021/000225).
-
Funding information: The authors would like to thank the Science Engineering Research Board (SERB), Department of Science and Technology, Government of India for providing financial support.
-
Author contributions: M. Gupta: data curation, formal analysis, investigation, methodology, software, validation, visualization, and writing – original draft. P.V. Bansod: formal analysis, investigation, software, validation, visualization, and writing – original draft. H. Gargama: formal analysis, investigation, software, validation, visualization, and methodology. S.I. Kundalwal: conceptualization, funding acquisition, investigation, methodology, project administration, resources, supervision, and writing – review and editing. All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
-
Conflict of interest: Authors state no conflict of interest.
-
Data availability statement: All data generated or analyzed during this study are included in this published article.
References
[1] Gupta M, Ray MC, Patil ND, Kundalwal SI. Smart damping of a simply supported laminated CNT-based hybrid composite plate using FE approach. Thin-Walled Struct. 2022;171:108782.10.1016/j.tws.2021.108782Search in Google Scholar
[2] Gupta M, Patil ND, Kundalwal SI. Active damping of multiscale composite shells using Sinus theory incorporated with Murakami’s zig-zag function. Thin-Walled Struct. 2023;191:111063.10.1016/j.tws.2023.111063Search in Google Scholar
[3] Kundalwal SI, Meguid SA, Weng GJ. Strain gradient polarization in graphene. Carbon. 2017;117:462–72.10.1016/j.carbon.2017.03.013Search in Google Scholar
[4] Chen ZG, Zou J, Liu G, Li F, Wang Y, Wang L, et al. Novel boron nitride hollow nanoribbons. ACS Nano. 2008;2(10):2183–91.10.1021/nn8004922Search in Google Scholar PubMed
[5] Nevhal SK, Gupta M, Kundalwal SI. Polarization in the van der Waals–bonded graphene/hBN heterostructures with triangular pores. Acta Mech. 2023;234(8):3469–82.10.1007/s00707-023-03568-5Search in Google Scholar
[6] Kho JG, Moon KT, Kim JH, Kim DP. Properties of boron nitride (BxNy) films produced by the spin-coating process of polyborazine. J Am Ceram Soc. 2000;83(11):2681–3.10.1111/j.1151-2916.2000.tb01615.xSearch in Google Scholar
[7] Ares P, Cea T, Holwill M, Wang YB, Roldán R, Guinea F, et al. Piezoelectricity in monolayer hexagonal boron nitride. Adv Mater. 2020;32(1):1905504.10.1002/adma.201905504Search in Google Scholar PubMed
[8] Nan Y, Tan D, Zhao J, Willatzen M, Wang ZL. Shape- and size-dependent piezoelectric properties of monolayer hexagonal boron nitride nanosheets. Nanoscale Adv. 2020;2(1):470–7.10.1039/C9NA00643ESearch in Google Scholar PubMed PubMed Central
[9] Gupta M, Ray MC, Patil ND, Kundalwal SI. Dynamic modelling and analysis of smart carbon nanotube-based hybrid composite beams: Analytical and finite element study. Proc Inst Mech Eng Part L J Mater Des Appl. 2021;235(10):2185–206.10.1177/14644207211019773Search in Google Scholar
[10] Gupta M, Ray MC, Patil ND, Kundalwal SI. Effect of orientation of CNTs and piezoelectric fibers on the damping performance of multiscale composite plate. J Intell Mater Syst Struct. 2023;34(2):194–216.10.1177/1045389X221099451Search in Google Scholar
[11] Gupta M, Patil ND, Kundalwal SI. Influence of CNT waviness on the effective young’s modulus of multiscale hybrid composite. Int. Conf. Adv. Commun. Technol. Comput. Eng. AIP Conf. Proc. 2745; 2023 Feb 24–25. Bolten, UK: AIP Publishing; 2023. p. 030006.10.1063/5.0132336Search in Google Scholar
[12] Gupta M, Kundalwal S. Active vibration control of laminated carbon nanotube-based polymer composite plates using finite element analysis. Finite element analysis of polymers and composites. United States: Woodhead Publishing; 2024. p. 237–67.10.1016/B978-0-443-14087-7.00012-4Search in Google Scholar
[13] Maranganti R, Sharma P. Atomistic determination of flexoelectric properties of crystalline dielectrics. Phys Rev B – Condens Matter Mater Phys. 2009;80(5):054109.10.1103/PhysRevB.80.054109Search in Google Scholar
[14] Wang B, Li XF. Flexoelectric effects on the natural frequencies for free vibration of piezoelectric nanoplates. J Appl Phys. 2021;129(3):034102.10.1063/5.0032343Search in Google Scholar
[15] Gurtin ME, Ian Murdoch A. A continuum theory of elastic material surfaces. Arch Ration Mech Anal. 1975;57:291–323.10.1007/BF00261375Search in Google Scholar
[16] Tagantsev AK. Piezoelectricity and flexoelectricity in crystalline dielectrics. Phys Rev B. 1986;34(8):5883–9.10.1103/PhysRevB.34.5883Search in Google Scholar
[17] Huang G-Y, Yu S-W. Effect of surface piezoelectricity on the electromechanical behaviour of a piezoelectric ring. Phys Status Solidi. 2006;243(4):R22–4.10.1002/pssb.200541521Search in Google Scholar
[18] Yan Z, Jiang L. Electromechanical response of a curved piezoelectric nanobeam with the consideration of surface effects. J Phys D Appl Phys. 2011;44(36):365301.10.1088/0022-3727/44/36/365301Search in Google Scholar
[19] Yan Z, Jiang L. Surface effects on the electromechanical coupling and bending behaviours of piezoelectric nanowires. J Phys D Appl Phys. 2011;44(7):075404.10.1088/0022-3727/44/7/075404Search in Google Scholar
[20] Li YS, Pan E. Bending of a sinusoidal piezoelectric nanoplate with surface effect. Compos Struct. 2016;136:45–55.10.1016/j.compstruct.2015.09.047Search in Google Scholar
[21] Zhang J, Wang C, Chen W. Surface and piezoelectric effects on the buckling of piezoelectric nanofilms due to mechanical loads. Meccanica. 2014;49:181–9.10.1007/s11012-013-9784-xSearch in Google Scholar
[22] Mohammadi P, Liu LP, Sharma P. A theory of flexoelectric membranes and effective properties of heterogeneous membranes. J Appl Mech Trans ASME. 2014;81(1):011007.10.1115/1.4023978Search in Google Scholar
[23] Yang W, Liang X, Shen S. Electromechanical responses of piezoelectric nanoplates with flexoelectricity. Acta Mech. 2015;226(9):3097–110.10.1007/s00707-015-1373-8Search in Google Scholar
[24] Zhang Z, Jiang L. Size effects on electromechanical coupling fields of a bending piezoelectric nanoplate due to surface effects and flexoelectricity. J Appl Phys. 2014;116(13):134308.10.1063/1.4897367Search in Google Scholar
[25] Yan Z. Size-dependent bending and vibration behaviors of piezoelectric circular nanoplates. Smart Mater Struct. 2016;25(3):035017.10.1088/0964-1726/25/3/035017Search in Google Scholar
[26] Xiao J, Lv J, Xia X, Wang J. Flexoelectric and surface effects on bending deformation and vibration of piezoelectric nanolaminates: Analytical solutions. Appl Math Model. 2024;135:541–58.10.1016/j.apm.2024.07.010Search in Google Scholar
[27] Kaveh A, Babaei H, Zavari S, Arshid E, Civalek Ö. Vibrational response of a sandwich microplate considering the impact of flexoelectricity and based on a novel porous-FGM formulation. Mech Based Des Struct Mach. 2024;52(11):9122–43.10.1080/15397734.2024.2337913Search in Google Scholar
[28] Zhou S, Li A, Zhang R, Qi L, Ren F, Zheng Z, et al. Electro-mechanical responses of flexoelectric bilayer circular nano-plate with surface effect. Int J Mech Mater Des. 2024;20(2):209–31.10.1007/s10999-023-09672-7Search in Google Scholar
[29] Nevhal SK, Gupta M, Kundalwal SI. Influence of flexoelectric effect on the bending rigidity of a Timoshenko graphene-reinforced nanorod. J Mech Behav Mater. 2023;32(1):20220295.10.1515/jmbm-2022-0295Search in Google Scholar
[30] Gupta M, Meguid SA, Kundalwal SI. Synergistic effect of surface-flexoelectricity on electromechanical response of BN-based nanobeam. Int J Mech Mater Des. 2022;18:3–19.10.1007/s10999-021-09582-6Search in Google Scholar
[31] Bansod PV, Gupta M, Gargama H, Kundalwal SI. Electromechanical response of boron nitride nanosheet reinforced nanocomposite beam: A finite element study. Proc Inst Mech Eng Part E. 2023.10.1177/09544089231192336Search in Google Scholar
[32] Kundalwal SI, Gupta M. Interdependent effects of surface and flexoelectricity on the electromechanical behavior of BNRC nanoplate. Mech Mater. 2022;175:104483.10.1016/j.mechmat.2022.104483Search in Google Scholar
[33] Yue Y, Yang X, Duan J, Liu J. Nonlinear bending and vibration analysis of a variable-width piezoelectric nanoplate with flexoelectric effects. Acta Mech. 2024;235:7641–60.10.1007/s00707-024-04112-9Search in Google Scholar
[34] Yang S, Meng D, Guo Y, Nie P, Jesus AMPde. A reliability-based design and optimization strategy using a novel MPP searching method for maritime engineering structures. Int J Struct Integr. 2023;14(5):809–26.10.1108/IJSI-06-2023-0049Search in Google Scholar
[35] Meng D, Yang S, Yang H, De Jesus AMP, Correia J, Zhu SP. Intelligent-inspired framework for fatigue reliability evaluation of offshore wind turbine support structures under hybrid uncertainty. Ocean Eng. 2024;307:118213.10.1016/j.oceaneng.2024.118213Search in Google Scholar
[36] Liu X, Wang H, Wu Q, Wang Y. Uncertainty-based analysis of random load signal and fatigue life for mechanical structures. Arch Comput Methods Eng. 2022;29:375–95.10.1007/s11831-021-09579-6Search in Google Scholar
[37] Yang S, De Jesus AMP, Meng D, Nie P, Darabi R, Azinpour E, et al. Very high-cycle fatigue behavior of steel in hydrogen environment: State of the art review and challenges. Eng Fail Anal. 2024;166:108898.10.1016/j.engfailanal.2024.108898Search in Google Scholar
[38] Luo C, Zhu SP, Keshtegar B, Macek W, Branco R, Meng D. Active Kriging-based conjugate first-order reliability method for highly efficient structural reliability analysis using resample strategy. Comput Methods Appl Mech Eng. 2024;423:116863.10.1016/j.cma.2024.116863Search in Google Scholar
[39] Foschi RO, Li H, Zhang J. Reliability and performance-based design: a computational approach and applications. Struct Saf. 2002;24(2–4):205–18.10.1016/S0167-4730(02)00025-5Search in Google Scholar
[40] Gargama H, Chaturvedi SK, Thakur AK. Experimental validation of reliability-based design optimization models for designing EMI shielding and absorbing structures. J Electromagn Waves Appl. 2018;32(2):215–28.10.1080/09205071.2017.1377120Search in Google Scholar
[41] Gargama H, Chaturvedi SK, Thakur AK. On the design and reliability analysis of electromagnetic absorbers using real-coded genetic algorithm and Monte Carlo simulation. Prog Electromagn Res B. 2012;43:169–87.10.2528/PIERB12061107Search in Google Scholar
[42] Song C, Kawai R. Monte Carlo and variance reduction methods for structural reliability analysis: A comprehensive review. Probab Eng Mech. 2023;73:103479.10.1016/j.probengmech.2023.103479Search in Google Scholar
[43] Helton JC, Davis FJ. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems. Reliab Eng Syst Saf. 2003;81(1):23–69.10.1016/S0951-8320(03)00058-9Search in Google Scholar
[44] Zhao M, Qian C, Lee SWRR, Tong P, Suemasu H, Zhang T-Y. Electro-elastic analysis of piezoelectric laminated plates. Adv Compos Mater. 2007;16(1):63–81.10.1163/156855107779755273Search in Google Scholar
[45] Yan Z, Jiang LY. Flexoelectric effect on the electroelastic responses of bending piezoelectric nanobeams. J Appl Phys. 2013;113:194102.10.1063/1.4804949Search in Google Scholar
[46] Shen S, Hu S. A theory of flexoelectricity with surface effect for elastic dielectrics. J Mech Phys Solids. 2010;58(5):665–77.10.1016/j.jmps.2010.03.001Search in Google Scholar
[47] Majdoub MS, Sharma P, Çaǧin T. Erratum: Dramatic enhancement in energy harvesting for a narrow range of dimensions in piezoelectric nanostructures (Physical Review B - Condensed Matter and Materials Physics (2008) 78 (121407)). Phys Rev B - Condens Matter Mater Phys. Vol. 79, 2009. p. 159901.10.1103/PhysRevB.79.159901Search in Google Scholar
[48] Mindlin RD. Polarization gradient in elastic dielectrics. Int J Solids Struct. 1968;4(6):637–42.10.1016/0020-7683(68)90079-6Search in Google Scholar
[49] Tsai YT, Chang HC. Reliability-based optimum design for mechanical problems using genetic algorithms. Proc Inst Mech Eng Pt C J Mech Eng Sci. 2008;222(9):1791–9.10.1243/09544062JMES157Search in Google Scholar
[50] Zhou H, Pei Y, Hong J, Fang D. Analytical method to determine flexoelectric coupling coefficient at nanoscale. Appl Phys Lett. 2016;108(10):101908.10.1063/1.4943660Search in Google Scholar
[51] Yan Z, Jiang LY. Vibration and buckling analysis of a piezoelectric nanoplate considering surface effects and in-plane constraints. Proc R Soc A Math Phys Eng Sci. 2012;468(2147):3458–75.10.1098/rspa.2012.0214Search in Google Scholar
[52] Chu B, Salem DR. Flexoelectricity in several thermoplastic and thermosetting polymers. Appl Phys Lett. 2012;101(10):103905.10.1063/1.4750064Search in Google Scholar
[53] Zhang S, Xu M, Liang X, Shen S. Shear flexoelectric coefficient μ1211 in polyvinylidene fluoride. J Appl Phys. 2015;117:204102.10.1063/1.4921444Search in Google Scholar
[54] Ru CQ. Thermoelastic dissipation of nanowire resonators with surface stress. Phys E Low Dimens Syst Nanostruct. 2009;41(7):1243–8.10.1016/j.physe.2009.02.008Search in Google Scholar
[55] Chen W. Surface effect on Bleustein-Gulyaev wave in a piezoelectric half-space. Theor Appl Mech Lett. 2011;1(4):041001.10.1063/2.1104101Search in Google Scholar
© 2025 the author(s), published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Research Articles
- Probing microstructural evolution and surface hardening of AISI D3 steel after multistage heat treatment: An experimental and numerical analysis
- Activation energy of lime cement containing pozzolanic materials
- Optimizing surface quality in PMEDM using SiC powder material by combined solution response surface methodology – Adaptive neuro fuzzy inference system
- Experimental study of the mechanical shear behaviour of steel rebar connectors in timber–concrete structure with leafy wood species
- Development of structural grade lightweight geopolymer concrete using eco-friendly materials
- An experimental approach for the determination of the physical and mechanical properties of a sustainable geopolymer mortar made with Algerian ground-granulated blast furnace slag
- Effect of using different backing plate materials in autogenous TIG welding on bead geometry, microhardness, tensile strength, and fracture of 1020 low carbon steel
- Uncertainty analysis of bending response of flexoelectric nanocomposite plate
- Leveraging normal distribution and fuzzy S-function approaches for solar cell electrical characteristic optimization
- Effect of medium-density fiberboard sawdust content on the dynamic and mechanical properties of epoxy-based composite
- Mechanical properties of high-strength cement mortar including silica fume and reinforced with single and hybrid fibers
- Study the effective factors on the industrial hardfacing for low carbon steel based on Taguchi method
- Analysis of the combined effects of preheating and welding wire feed rates on the FCAW bead geometric characteristics of 1020 steel using fuzzy logic-based prediction models
- Effect of partially replacing crushed oyster shell as fine aggregate on the shear behavior of short RC beams using GFRP rebar strengthened with TRC: Experimental and numerical studies
- Micromechanic models for manufacturing quality prediction of cantula fiber-reinforced nHA/magnesium/shellac as biomaterial composites
- Numerical simulations of the influence of thermal cycling parameters on the mechanical response of SAC305 interconnects
- Impact of nanoparticles on the performance of metakaolin-based geopolymer composites
- Enhancing mechanical and thermal properties of epoxy-based polymer matrix composites through hybrid reinforcement with carbon, glass and steel
- Prevention of crack kinetic development in a damaged rod exposed to an aggressive environment
- Ideal strain gauge location for evaluating stress intensity factor in edge-cracked aluminum plates
- Experimental and multiscale numerical analysis of elastic mechanical properties and failure in woven fabric E-glass/polyester composites
- Optimizing piezoelectric patch placement for active repair of center-cracked plates
- Experimental investigation on the transverse crushing performance of 3D printed polymer composite filled aluminium tubes
- Review Articles
- Advancing asphaltic rail tracks: Bridging knowledge gaps and challenges for sustainable railway infrastructure
- Chemical stabilization techniques for clay soil: A comprehensive review
- Development and current milestone of train braking system based on failure phenomenon and accident case
- Rapid Communication
- The role of turbulence in bottom-up nanoparticle synthesis using ultrafast laser filamentation in ethanol
- Special Issue on Deformation and Fracture of Advanced High Temperature Materials - Part II
- Effect of parameters on thermal stress in transpiration cooling of leading-edge with layered gradient
- Development of a piezo actuator-based fatigue testing machine for miniature specimens and validation of size effects on fatigue properties
- Development of a 1,000°C class creep testing machine for ultraminiature specimens and feasibility verification
- Special Issue on Advances in Processing, Characterization and Sustainability of Modern Materials - Part II
- Surface integrity studies in microhole drilling of Titanium Beta-C alloy using microEDM
- Experimental investigation on bacterial concrete by using Cantabro loss and UPV
- Influence of gas nitriding on the surface layer of M50 NiL steel for aerospace-bearing applications
- Experimental investigation on the spectral, mechanical, and thermal behaviors of thermoplastic starch and de-laminated talc-filled sustainable bio-nanocomposite of polypropylene
- Synthesis and characterization of sustainable hybrid bio-nanocomposite of starch and polypropylene for electrical engineering applications
- Microstructural and mechanical characterization of Al6061-ZrB2 nanocomposites fabricated by powder metallurgy
- Effect of edge preparation on hardness and corrosion behaviour of AA6061-T651 friction stir welds
- Mechanical improvement in acetal composites reinforced with graphene nanotubes and Teflon fibers using loss functions
- Experimental investigation on the mechanical properties of aluminum-based metal matrix composites by the squeeze casting method
- Investigation on punch force–displacement and thickness changes in the shallow drawing of AA2014 aluminium alloy sheets using finite element simulations
- Influence of liquid nitriding on the surface layer of M50 NiL steel for bearing applications
- Mechanical and tribological analyses of Al6061-GO/CNT hybrid nanocomposites by combined vacuum-assisted and ultrasonicated stir casting method
- Strengthening of structures with bacterial concrete for effective crack repair and durability enhancement
- Unique approaches in developing novel nano-composites: Evaluating their mechanical and tribological characteristics
- Load-carrying capacity of highly compact rigid deployable booms
- Investigating the influence of SiC and B4C reinforcements on the mechanical and microstructural properties of stir-casted magnesium hybrid composites
- Evaluation of mechanical and performance characteristics of bitumen mixture using waste septage ash as partial substitute
- Mechanical characterization of carbon/Kevlar hybrid woven 3D composites
- Development of a 3D-printed cervical collar using biocompatible and sustainable polylactic acid
- Mechanical characterization of walnut shell powder-reinforced neem shell liquid composite
- Special Issue on Structure-energy Collaboration towards Sustainability Societies
- Effect of tunneling conductivity of CNTs on the EMI shielding effectiveness of nanocomposite in the C-band
- Evaluation of the effect of material selection and core geometry in thin-walled sandwich structures due to compressive strength using a finite element method
- Special Issue on Sustainability and Development in Civil Engineering - Part III
- The optimum reinforcement length for ring footing resting on sandy soils resisting inclined load
- Special Issue on Advanced Materials in Industry 4.0
- Cross-dataset evaluation of deep learning models for crack classification in structural surfaces
- Mechanical and antibacterial characteristics of a 3D-printed nano-titanium dioxide–hydroxyapatite dental resin-based composite
Articles in the same Issue
- Research Articles
- Probing microstructural evolution and surface hardening of AISI D3 steel after multistage heat treatment: An experimental and numerical analysis
- Activation energy of lime cement containing pozzolanic materials
- Optimizing surface quality in PMEDM using SiC powder material by combined solution response surface methodology – Adaptive neuro fuzzy inference system
- Experimental study of the mechanical shear behaviour of steel rebar connectors in timber–concrete structure with leafy wood species
- Development of structural grade lightweight geopolymer concrete using eco-friendly materials
- An experimental approach for the determination of the physical and mechanical properties of a sustainable geopolymer mortar made with Algerian ground-granulated blast furnace slag
- Effect of using different backing plate materials in autogenous TIG welding on bead geometry, microhardness, tensile strength, and fracture of 1020 low carbon steel
- Uncertainty analysis of bending response of flexoelectric nanocomposite plate
- Leveraging normal distribution and fuzzy S-function approaches for solar cell electrical characteristic optimization
- Effect of medium-density fiberboard sawdust content on the dynamic and mechanical properties of epoxy-based composite
- Mechanical properties of high-strength cement mortar including silica fume and reinforced with single and hybrid fibers
- Study the effective factors on the industrial hardfacing for low carbon steel based on Taguchi method
- Analysis of the combined effects of preheating and welding wire feed rates on the FCAW bead geometric characteristics of 1020 steel using fuzzy logic-based prediction models
- Effect of partially replacing crushed oyster shell as fine aggregate on the shear behavior of short RC beams using GFRP rebar strengthened with TRC: Experimental and numerical studies
- Micromechanic models for manufacturing quality prediction of cantula fiber-reinforced nHA/magnesium/shellac as biomaterial composites
- Numerical simulations of the influence of thermal cycling parameters on the mechanical response of SAC305 interconnects
- Impact of nanoparticles on the performance of metakaolin-based geopolymer composites
- Enhancing mechanical and thermal properties of epoxy-based polymer matrix composites through hybrid reinforcement with carbon, glass and steel
- Prevention of crack kinetic development in a damaged rod exposed to an aggressive environment
- Ideal strain gauge location for evaluating stress intensity factor in edge-cracked aluminum plates
- Experimental and multiscale numerical analysis of elastic mechanical properties and failure in woven fabric E-glass/polyester composites
- Optimizing piezoelectric patch placement for active repair of center-cracked plates
- Experimental investigation on the transverse crushing performance of 3D printed polymer composite filled aluminium tubes
- Review Articles
- Advancing asphaltic rail tracks: Bridging knowledge gaps and challenges for sustainable railway infrastructure
- Chemical stabilization techniques for clay soil: A comprehensive review
- Development and current milestone of train braking system based on failure phenomenon and accident case
- Rapid Communication
- The role of turbulence in bottom-up nanoparticle synthesis using ultrafast laser filamentation in ethanol
- Special Issue on Deformation and Fracture of Advanced High Temperature Materials - Part II
- Effect of parameters on thermal stress in transpiration cooling of leading-edge with layered gradient
- Development of a piezo actuator-based fatigue testing machine for miniature specimens and validation of size effects on fatigue properties
- Development of a 1,000°C class creep testing machine for ultraminiature specimens and feasibility verification
- Special Issue on Advances in Processing, Characterization and Sustainability of Modern Materials - Part II
- Surface integrity studies in microhole drilling of Titanium Beta-C alloy using microEDM
- Experimental investigation on bacterial concrete by using Cantabro loss and UPV
- Influence of gas nitriding on the surface layer of M50 NiL steel for aerospace-bearing applications
- Experimental investigation on the spectral, mechanical, and thermal behaviors of thermoplastic starch and de-laminated talc-filled sustainable bio-nanocomposite of polypropylene
- Synthesis and characterization of sustainable hybrid bio-nanocomposite of starch and polypropylene for electrical engineering applications
- Microstructural and mechanical characterization of Al6061-ZrB2 nanocomposites fabricated by powder metallurgy
- Effect of edge preparation on hardness and corrosion behaviour of AA6061-T651 friction stir welds
- Mechanical improvement in acetal composites reinforced with graphene nanotubes and Teflon fibers using loss functions
- Experimental investigation on the mechanical properties of aluminum-based metal matrix composites by the squeeze casting method
- Investigation on punch force–displacement and thickness changes in the shallow drawing of AA2014 aluminium alloy sheets using finite element simulations
- Influence of liquid nitriding on the surface layer of M50 NiL steel for bearing applications
- Mechanical and tribological analyses of Al6061-GO/CNT hybrid nanocomposites by combined vacuum-assisted and ultrasonicated stir casting method
- Strengthening of structures with bacterial concrete for effective crack repair and durability enhancement
- Unique approaches in developing novel nano-composites: Evaluating their mechanical and tribological characteristics
- Load-carrying capacity of highly compact rigid deployable booms
- Investigating the influence of SiC and B4C reinforcements on the mechanical and microstructural properties of stir-casted magnesium hybrid composites
- Evaluation of mechanical and performance characteristics of bitumen mixture using waste septage ash as partial substitute
- Mechanical characterization of carbon/Kevlar hybrid woven 3D composites
- Development of a 3D-printed cervical collar using biocompatible and sustainable polylactic acid
- Mechanical characterization of walnut shell powder-reinforced neem shell liquid composite
- Special Issue on Structure-energy Collaboration towards Sustainability Societies
- Effect of tunneling conductivity of CNTs on the EMI shielding effectiveness of nanocomposite in the C-band
- Evaluation of the effect of material selection and core geometry in thin-walled sandwich structures due to compressive strength using a finite element method
- Special Issue on Sustainability and Development in Civil Engineering - Part III
- The optimum reinforcement length for ring footing resting on sandy soils resisting inclined load
- Special Issue on Advanced Materials in Industry 4.0
- Cross-dataset evaluation of deep learning models for crack classification in structural surfaces
- Mechanical and antibacterial characteristics of a 3D-printed nano-titanium dioxide–hydroxyapatite dental resin-based composite

