Assessment of ballistic impact damage on aluminum and magnesium alloys against high velocity bullets by dynamic FE simulations

2.1 Explicit dynamic simulation

Explicit dynamic simulation analysis refers to the application of explicit integration rules along with the use of the mass matrix of diagonal (“lumped”) elements. The equations of motion for the body are integrated using the explicit integration rules [20] shown in Eq. (1).

where u ̇ N is the degrees of freedom and subscript i is the number of increments in the dynamics explicit step, the center-difference integration operator explicitly uses the known values of u ̇ ( i + 1 / 2 ) N and u ̈ ̇ ( i ) N from the previous increment.

The explicit integration rule is fairly simple, but the explicit dynamics procedure does not provide good computational efficiency. The use of mass matrix of the diagonal elements can be used as a computational efficiency solution of the explicit procedure because the acceleration at the start of the increment is calculated by

where M ^NJ is the mass matrix, P ^J is the applied load vector, and I ^J is the internal force vector; the combined mass matrix is used because the inverse is simple to calculate and because the vector product of the reciprocal of mass by the inertial force requires only n operations, where n is the number of degrees of freedom in the model.

2.2 Impact ballistic limit

The ballistic impact is a study that analyzes material damage caused by the impact of projectiles/bullets. It is applied as a form of protection in military applications. The impact behavior of the sandwich depends on the size, shape, mass, speed of impact, and material of the projectile.

The speed of the bullet after hitting the plate will decrease. So, the value of residual velocity (V _r ) becomes important to evaluate and analyze the ballistic impact. In conducting ballistic impact experiments, the velocity after the projectile penetrates the target plate will be known. Some studies also use the value of the residual velocity. When analyzing the effect of the target plate on the ballistic impact, the classic Lambert–Jonas ballistic limit equation [21] is used to deal with the relationship between the initial velocity and the residual velocity of the projectile object. The Lambert–Jonas equation is given as follows:

where a and p are the appropriate cutting parameters, and V bl is the ballistic limit speeds obtained by fitting.

Plastic deformation of the projectile can be neglected because the strength of the projectile is greater than that of the target plate, and the projectile can be considered as a rigid body. Therefore, the form of deformation, damage, and destruction of the target plate is the result of the kinetic energy absorbed by the target plate

where E a means the change in kinetic energy or the amount of energy transferred. Furthermore, the energy absorption rate ( η ) of the target is defined as follows:

where E i is the kinetic energy of the projectile.

2.3 Failure mechanism

Failure of the target plate during the collision process will result in deformation that affects the ability to absorb energy. To determine the impact of the target and the cause of the failure mechanism upon impact, the determination of energy dissipation in various failure modes is very prominent. And then, the target plate will absorb the projectile’s kinetic energy; there will be stress, strain, and deformation of the projectile. In this simulation, energy absorption in the projectile was neglected due to minor deformation. At the same time, the value of the plastic strain energy on the target plate is obtained from the calculation of the stress and plastic strain during the perforation process. The value and direction of the stress–strain for each element in the normal and tangential directions (Figure 1) and the energy absorption value are obtained by adding all components of stress and strain.

Figure 1

Element deformation: (a) stress and (b) plastic strain.

Stress values are separated by direction. The resulting value of stress can use von Mises stress to compare the various models. von Mises stress is obtained from the analysis process using ABAQUS/CAE software. The plastic deformation behavior is described by a Johnson–Cook model [19]

where σ eq is the von Mises stress, ε p is the equivalent plastic strain, ε ̇ p is the testing strain rate, and T is the actual temperature.

In order to reduce the dependence of the mesh in the evolution of the damage, the deformation after failure initiation is defined as the equivalent plastic displacement, u ̄ ̇ pl , not the plastic strain. It is defined as [2]

where L is a characteristic element length calculated from the initial geometry of the element. For shell and two-dimensional elements, L is the square root of the integration point area.

2.4 Energy absorption

The energy absorption value is obtained by adding the stress and plastic strain values for all directions during the collision process. The calculation only focuses on the target plate because the projectile is considered a rigid body so that it does not deform; the projectile in the experiment experienced a deformation that was not too significant. The calculation of energy absorption value using Eqs. (9)–(13) obtained from [16]:

where W total   is the total energy absorbed, W radial is the energy absorbed in the radial stretch, W circumferential is the energy absorbed in the circumferential stretch, W axial is the energy absorbed in the axial stretch, W s h ear is the energy absorbed in shear deformations, σ and ε is the stress and plastic strains in every direction; σ 11 is the radial stress, σ 22 is the circumferential stress, σ 33 is the axial stress and σ 12 , σ 13 , σ 23 are the shear stress in the tangential direction, ( ε 11 ) plastic is the plastic strain in the radial direction, ( ε 22 ) plastic is the plastic strain in the circumferential direction, ( ε 33 ) plastic is the plastic strain in the axial direction, ( ε 12 , ε 13 , ε 23 ) plastic is the shear strain in tangential directions, and V e is the element volume.

2.5 State of the art

Research on ballistic impact has been done before. The research in Table 1 shows that many research subjects were carried out on different targets. Goda and Girardot [22] conducted research on ceramics and Kevlar-29 composites with a honeycomb core shape using a cylindrical blunt shape projectile. The numerical results reveal that the ballistic impact performance is highly dependent on the properties of the cohesive material, the stacking order, and the woven fabric material. In contrast, the smaller contribution of the supporting conditions to the characteristics of the ballistic perforation is taken into account. Rahimijonoush and Bayat [2] have researched the marine field by analyzing the performance of titanium sandwich panels against impact loads from hemispherical projectiles. The results show the impact energy is mainly absorbed by the rear face sheet in the symmetrical sandwich panels. The ballistic limit increases almost linearly with increasing thickness of the rear or front face sheet on a specimen of the same weight. Research in the field of aeronautics conducted by Chatterjee et al. [23] analyzed the performance of a composite sandwich panel against a projectile load of 9 mm bullets with an average velocity of 400 m/s. It is observed that due to the incorporation of dilatant liquid within SCP, it can absorb 20.24% of the energy incident on it. The amount of energy absorbed is 43.96% greater than that absorbed by the hollow composite, and the percentage increase in energy absorbed per unit mass increase is 22.43%. This enables the constructed SCP to be used in applications requiring enhanced energy dissipation. Yu et al. [24] conducted research in the marine field with a target Y-shaped core sandwich using a blunt shape projectile. The conclusion of this study is that the impact resistance of a composite sandwich structure with a Y-shaped core is superior to that of laminate.

Research by Khaire et al. [25] in the naval industries aims to know the performance of the honeycomb core cylindrical sandwich against the ballistic load of the conical nosed projectile. The conclusion of this study is that when the skin thickness and cell per wall thickness changed from 0.7 to 2.0 mm and 0.03 to 0.09 mm, the ballistic limit increased by 72.2 m/s and 10.9 m/s, respectively. However, when the side length changes from 3.2 to 9.2 mm, the ballistic limit decreases by 9.9 m/s. Wu et al. [26] investigated a composite armor system using aramid–carbon hybrid FRP laminated composite structures when exposed to ballistic loads from a 7.62 M61 AP projectile. The conclusion is the main failure modes of FRP laminates are fiber compression failure and tensile matrix failure, both of which can also be affected by changes in the stacking order of the FRP laminate. When the carbon fiber is stacked on the top of the FRP laminate, both the fiber compression failure area and the matrix tensile failure area are the lowest. Research on shipbuilding structure was conducted by Yang et al. [27], namely, regarding the performance of a composite double-arrow auxetic structure against ballistic loads from hemispherical shaped projectiles. The conclusion of this research is METC auxetic structure with a relative density of 16.66, which is 23.06% greater than that of the auxetic structure with a relative density of 9.08%. The ballistic limit speed increased by 35.56 and 54.89%, along with the increase in relative density from 9.08 to 16.66 and 23.06%, which has been validated by the experiment. Vescovini et al. [28] studied on composite structures using interply hybrid composites of woven Kevlar and S2-glass when ground with 0.357 Magnum FMJ. The conclusion of this study is that the deviation at the ballistic limit is always lower than 5.33% and has a maximum of 3.87% at an impact speed of 430 m/s, close to the ballistic limit. Also, although the numerical ballistic curve shows a generally smoother transition to the linear part, it fits very well with the experimental one. Mohammad et al. [16] conducted that the ballistic performance of monolithic shell targets decreased by 6.49%, whereas layered targets showed 3.88% reduction in impact resisting capacity at oblique impacts. Han et al. [29] analyzed that the deviation of the predicted ballistic limit velocities of 2-, 4-, 4.82-, 8-, and 9.94-mm-thick targets from the corresponding experimental values were, respectively, 12.3, 0.1, 0.0, 4.2, and 4.9% for simulations, while these are 9.0, 17.5, 21.5, 24.2, and 26.3%, respectively.

Research on ballistic impact has been carried out in various fields. Table 1 shows each research conducted using one type of projectile to determine the impact of damage and the amount of energy absorbed. In this case, a comparison of the engineering structures subjected to ballistic type is still scant. Therefore, in this study, four types of projectile shapes were used to determine the damage caused when struck by different projectiles. In the case of ship hijacking, it is indeed impossible to predict which form of the projectile will be used to hijack the ship.

3.1 Experiment profile

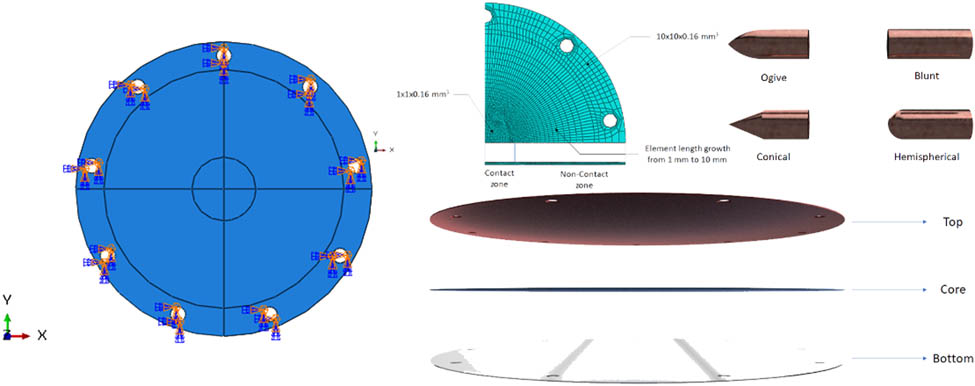
The ballistic impact experiment on a monolayered plate with a thickness of 2 mm used four projectile shapes, namely, blunt, conical, hemispherical, and ogive adapted from [16] to observe the impact on the target plate. The material of the projectile is an EN-24 steel bar. The length and diameter of the projectiles were 50.8 and 19 mm, respectively, in each uniform variation for equalizing conditions. All projectiles have the same mass, which had 52.5 g, equivalent to the projectile’s thickness, and the projectile’s density was 7,650 kg/m³ (Figure 2).

Figure 2

Dimension for (a) ogive, (b) blunt, (c) conical, and (d) hemispherical projectile shape (in mm).

All target plates were made of 1100-H12 aluminum with a plate thickness of 1 and 2 mm. The target plate was cut into circles with a total diameter of 315 mm and had nine holes with a diameter of 8 mm as plate holders during the experiment. This experiment was based on a study by Iqbal et al.; the experiment found that for ogive and blunt projectiles, the effective ratio of span diameter to projectile diameter (D/d) is between 3.6 and 10; increasing the ratio, will not increase the energy absorption. To get the maximum results by using four kinds of projectile shapes, the size of the most effective span diameter was 255 mm.

A representation of the experimental method and all components that were used is shown in Figure 3, which also has prepared by Mohammad et al. [16]. The projectile was driven using a compressed-air pneumatic gun with a maximum speed of 200 m/s. A camera was used to observe the value of the residual velocity. In the end, the projectile stops at the projectile catcher after penetrating the target plate.

Figure 3

Schematic experiment.

3.2 Mesh strategy

The target plate was divided into two zones, namely, contact and non-contact zone; all zones were meshed with three-dimensional eight-node brick elements (C3D8R) in a unit aspect ratio. In the non-contact zone ratio, the meshing size varied based on the distance from the center of the target plate. Meshing size growth from 1 mm to 10 mm was in line with the distance from the center of the target plate. In the contact zone, the mesh size was 1 mm³ × 1 mm³ × 0.16 mm³.

The contact zone was part of the target plate that was in direct contact with the bullet, so numerical analysis was focused on this part. Furthermore, the non-contact zone was part of the target plate that was not in direct contact with the projectile so that the mesh size could be larger to reduce analysis computational time (Figure 4).

Figure 4

Meshing Strategy.

Using partitions on components aims to maintain accuracy but can reduce computation time to make the simulation more efficient. If one does not use partitions, the computation time will be longer. This method is carried out on each layer of the target plate.

3.3 Benchmarking result

Experiments conducted by Mohammad et al. [16] are used as a reference in performing numerical simulations. This experiment is a ballistic impact on a monolayered plate with a thickness of 2 mm using an ogive projectile shape. Initial velocity is the velocity of the projectile just before hitting the target plate obtained from experiments with high-speed cameras.

Table 2 shows the comparison of the results between the experimental and numerical simulations. The difference between the experimental and numerical simulation results slightly indicates that the numerical simulation is appropriate.

The results of the qualitative validation are also shown in Figure 5. The failure model is obtained when an ogive projectile is hit with a speed of 107.7 m/s. Both results have an almost identical shape and radial cracks in the direction of the velocity projectile. Both target configurations show the radial cracks formation leading to the petalling of the target in the same direction as the projectile.

Figure 5

Validation results: (a) stress distribution numerical analysis (b) experimental result of monolithic target for 0° obliquity and 107.7 m/s velocity conducted by [16].

4.1 Geometrical model

The FE model consists of two parts, namely, the projectile and the target plate. There are four variations of the projectiles used, namely, blunt, conical, hemispherical, and ogive. Various projectiles are used to analyze failure mechanisms and determine the penetration phenomena caused for each projectile. The layer arrangement of the target plate is illustrated in Figure 6a. The bullet is defined as a rigid body with the discrete fixed element (R3D4) so that it will not deform. On the other side, the target plates are modeled as multilayered plates, with the thickness of each plate being 1 mm, and the diameter being 255 mm. Each plate layer has the same shape and size but with different materials, as shown in Figure 6b. The constituent materials for each layer are ZK61m magnesium alloy, 6061-T651 aluminum alloy, and 1100-H12 aluminum.

Figure 6

Numerical modeling: (a) plate target layers and (b) bullet shapes variation.

4.2 Material and failure definition

The materials used to vary the target plate are ZK61m magnesium alloy, 6061-T651 aluminum alloy, and 1100-H12 aluminum. Table 3 shows the strength comparison for each material. In this numerical analysis, the Johnson–Cook material model was applied to define the force and damage progression of the target plate when struck by a projectile.

The Johnson–Cook damage model, which integrates the effect of stress triaxiality, strain rate, and temperature on the failure strain formed in the material, was used to simulate damage initiation in the target material [31]. Johnson–Cook strength and damage model are represented by Eqs. (14)–(16)

Johnson–Cook parameters use yield stress ( A ) , strain hardening parameters ( B and n ), Young’s modulus ( E ) , and Poisson’s ratio ( v ) . Clausen et al. [32] found the values of strain rate ( C ) and thermal softening constant ( m ) . Gupta et al. [33] performed a uniaxial tensile test and obtained the values of Johnson–Cook material damage parameters, namely, D 1 , D 2 , D 3 , and D 5 for the value of D 4 obtained from [33].

where A , B , n , C , and m are material parameters, ε ̄ pl is the equation for plastic strain, ε ̄ ̇ pl is the equation for plastic strain rate, ε ̇ 0 is the reference strain rate, T ˆ is the non-dimensional temperature, T is the current temperature, T melt is the melting temperature, and T 0 is the room temperature.

where D 1 – D 5 are the material parameter σ m / σ ̄ is the stress triaxiality ratio, and σ m is the mean stress. Gupta et al. [33] stated that the material parameters A , B , and n were obtained from the uniaxial tension test on smooth cylindrical specimens, while D 1 , D 2 , and D 3 were obtained from the uniaxial tension test on notched specimens. Clausen et al. [32] did a tension test on the Hopkinson pressure bar to get the values of m and D 5 .

4.3 Boundary conditions

The circular target plate model in this numerical simulation is made of two parts: the inner and outer zones. In the inner zone, the selected element size is set to fine, while in the outer zone, it is set to be coarser, and the size will increase along with the direction and the diameter of the circle. The purpose of making these parts is to shorten the computation time in the simulation. There are nine holes in the surrounding circular plate with the same distance between them. These holes serve as a holder for the target plate to stop them from moving when the collision process occurs. The translation constraints are made in these holes in the x, y, and z directions. Between layers of the target, the plate is defined to stick completely and there are no gaps. The interaction between in-contact layered targets is developed using a tangential friction coefficient that is assigned to be 0.5 as determined by [30]. Figure 7 shows the boundary condition modeling scheme for ABAQUS/CAE.

Figure 7

Boundary conditions model in ABAQUS/CAE.

5.1 Matrix for parametric study

All simulation variations are determined from each layer’s target plate constituent material, namely aluminum 1100-H12, aluminum 6061-T651, and magnesium ZK61m. Table 4 shows the parametric study design matrix for each simulation variation. This is done to determine the largest energy absorption capacity and compare the strengths of each model. This simulation uses 12 different target plate models to be pounded with four different types of projectiles with notations V1, V2, V3, and V4.

5.2 Numerical results

5.2.1 Stress behavior

The stress value is a reaction from the collision process on the target plate. Each variation has a different energy absorption value. Figure 8 shows a comparison of the average stress values for each direction. It can be seen that model 3 has the highest average value of the other variations.

Figure 8

Average stress value every models.

The stress value used refers to the normal and tangential axes on the target plate so that there are six stress values. The graph of stress values for model 3 is relatively high, with plate layers of aluminum 1100-H12, magnesium ZK61m, and aluminum 6061-T651. Model 3 excels in the S33 value with a value of 1.085 × 10⁹ Pa. This shows that the target plate arrangement in model 3 has high stress when it gets a ballistic load. Figures 9–12 show the progressive stress distribution when the plate is struck with ogive, blunt, conical, and hemispherical projectiles, respectively. The target plate is displayed in half to show the stress distribution on the target plate that is in direct contact with the projectile and the surrounding area.

Figure 9

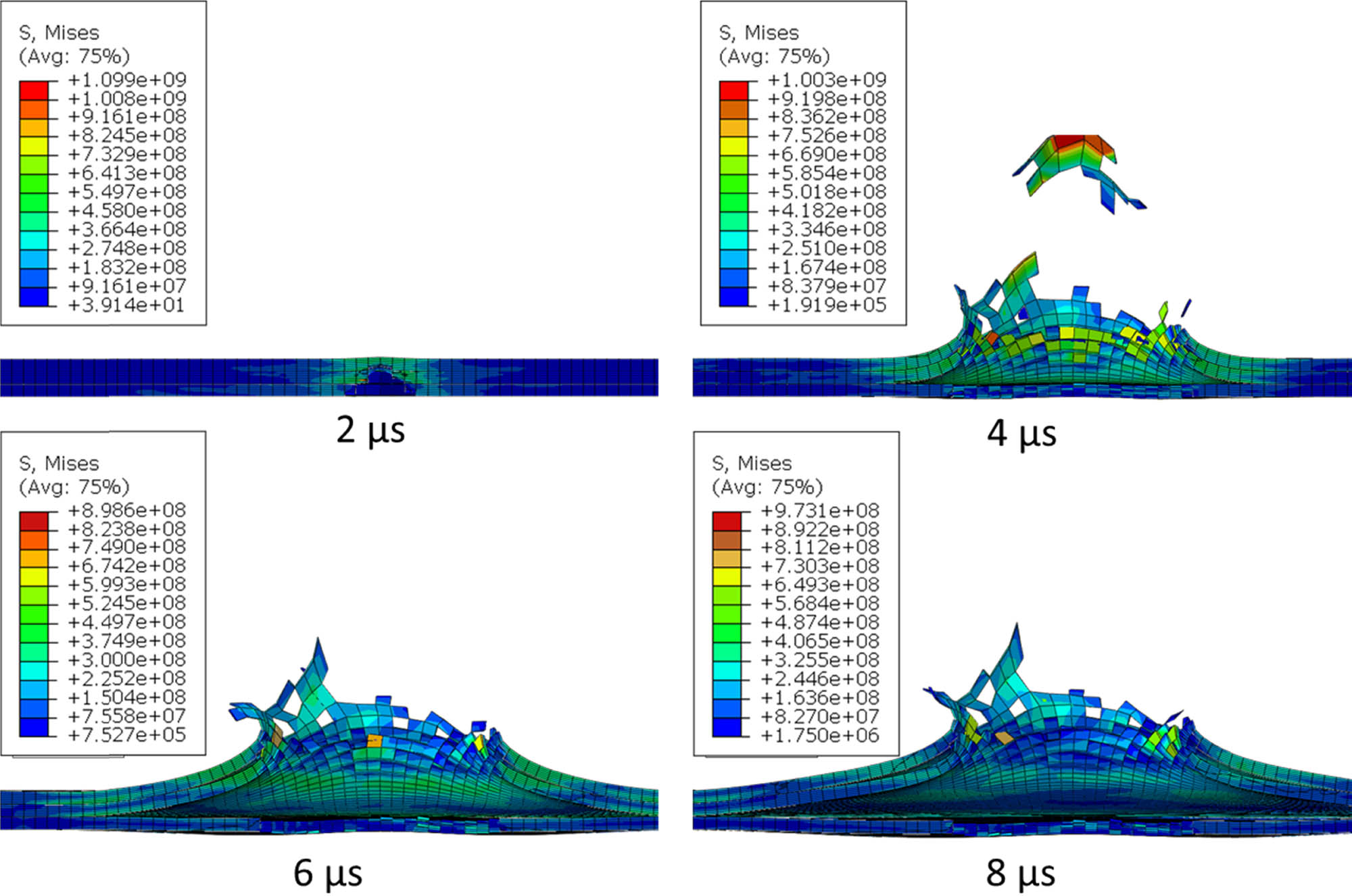
Stress distribution and deformation for model 3 against ogive projectile.

Figure 10

Stress distribution and deformation for model 3 against blunt projectile.

Figure 11

Stress distribution and deformation for model 3 against conical projectile.

Figure 12

Stress distribution and deformation for model 3 against hemispherical projectile.

The shape of the projectile seems to affect the ballistic impact mechanisms. As shown in Figure 10 for model 3, the initial impact for the blunt projectile at t = 2 μ shows a different stress distribution compared to the other proposed projectiles. It seems that the blunt projectile gives a uniform stress effect in the contact zone compared to the other projectiles, i.e., ogive, conical, and hemispherical that provides stress distribution concentrated in the center of the contact zone at time t = 2 μ , Figures 9, 11, and 12. The stress distributions at this time are at 8.090 × 10⁸, 1.099 × 10⁹, 6.734 × 10⁸, and 9.325 × 10⁸ Pa for the blunt, ogive, conical, and hemispherical projectiles, respectively. Compared to the blunt projectile, the stress distribution gives differences of −2.900 × 10⁸, 1.356 × 10⁸, and −1.235 × 10⁸ Pa for the ogive, conical, and hemispherical projectiles, respectively.

5.2.2 Strain behavior

The collision phenomenon, apart from generating stress, will also experience strain. The value of plastic strain is different for each variation. Figure 13 shows the plastic strain graph for each variation. It can be seen that model 2 has the highest average value of the other models, with a value of 9,633. In models 10–12, the plastic strain values are almost the same because the bottom layer uses magnesium ZK61m and only vary in the top and core layers.

Figure 13

Average plastic strain value for every models.

The phenomenon in variations for models 10–12 shows that magnesium ZK61m is not optimal when placed on the bottom layer because energy absorption cannot be maximized so that projectiles easily penetrate it. It will be more optimal if the magnesium ZK61m is placed on the top layer or core. The kinetic energy of the projectile can be well absorbed, thereby reducing the chance that the projectile can penetrate the target plate.

The plastic strain is the distorted body generated by force on the structure in which it does not return to its original size and shape. In this study, the effect of the projectile shape also seems to affect the plastic strain distribution of model 12. As shown in Figures 14–17, the final impact t = 8 μ for the ogive, blunt, conical, and hemispherical projectile shows a different plastic strain distribution. However, in the case of impact with ogive and blunt projectile, the strain distribution shows the same result, which is at a value of 1.177. Differences in plastic strain values occur in other projectiles, i.e., conical and hemispherical. For these projectiles, around 1.238 and 1.062 of plastic strain distribution is observed, respectively. The larger strain distribution seems to be present when the conical projectile is used to perform the ballistic impact phenomenon. Then, the following sequence is followed by an ogive and a blunt projectile in the same position. The lowest strain distribution is generated by the hemispherical projectile.

Figure 14

Plastic strain distribution and deformation for model 12 against ogive projectile.

Figure 15

Plastic strain distribution and deformation for model 12 against blunt projectile.

Figure 16

Plastic strain distribution and deformation for model 12 against conical projectile.

Figure 17

Plastic strain distribution and deformation for model 12 against hemispherical projectile.

5.2.3 Deformation modes

The efficiency of a metal plate can be estimated from its plastic deformation after impact. This is an important mechanism of kinetic energy absorption from the projectile during penetration. Figure 18 shows the displacement that occurs in each variation. Models 9–12 have the highest deformation value with a not too significant difference.

Figure 18

Average displacement value for every models.

The deformation that occurs in models 9–12 shows an impact after ballistic loading. This certainly needs to be reconsidered; in addition to the projectile that penetrates the target plate, it will be deformed so that part of the target plate may inflict additional damage to the protected component.

As shown in Figure 21, the shape of the projectile seems to affect the model deformation of ballistic impact model 7; in this case, it is the conical projectile. It also shows that the deformation seems to follow the shape of the conical projectile at time t = 4 μ . Furthermore, this phenomenon does not present in the other projectile shapes, which are ogive, blunt, and hemispherical during all the simulation time for the penetrating scheme, see Figures 19 and 20 and 22. The contact zone also appears to have the most deformations. The deformation at the final penetration is 0.006, 0.011, 0.018, and 0.003 m obtained from the ogive, blunt, conical, and hemispherical projectile after penetrating the circular target plate. These values show that the conical projectile produces a higher deformation of the circular plate. The next order of highest deformation is followed by blunt and ogive, in the second and third order, respectively, and the least deformation is produced by the hemispherical projectile.

Figure 19

Displacement for model 7 against ogive projectile.

Figure 20

Displacement for model 7 against blunt projectile.

Figure 21

Displacement for model 7 against conical projectile.

Figure 22

Displacement for model 7 against hemispherical projectile.

5.2.4 Performance of the sandwich plate target

The ability of the target plate to receive ballistic loads refers to the energy absorption results. The energy absorption value is obtained by calculating the stress and plastic strain on the normal and transverse axes. In addition, it is also necessary to pay attention to the shape of the plate deformation after the collision process because, of course, it will also affect the structure made. Figure 23 shows the energy absorption values for each variation.

Figure 23

Energy absorption for projectile shapes: (a) ogive, (b) blunt, (c) conical, and (d) hemispherical.

The highest energy absorption value obtained by model 2 when pounded using a conical projectile was 275.75 J. However, the highest average energy absorption value was obtained by model 3 because it produced 58.82 J when struck with an ogive projectile, 182.47 J with a blunt projectile, and 14.73 J with a hemispherical projectile.