Abstract
Poly(ether ketone) (PEEK) is an engineering polymer that can be used as load-bearing structures in automotive and aerospace fields, and the systematic study of its properties at different environments is crucial for the design of PEEK-based materials. In this study, a meta-model of PEEK based on molecular dynamics (MD) theory has been built, and the relevant properties (i.e., density, Young’s modulus, and Poisson’s ratio) have been carefully studied. Specifically, Young’s modulus and Poisson’s ratio values of PEEK have been obtained through tensile simulation process, and the meta-model of PEEK sample has been creatively constructed over 100–500 K and 0.5–10 atm using the Gaussian regression process algorithm. The effects of different temperatures and pressures to the sample have then been carefully investigated based on the data of meta-models. Successfully combining the MD theory with the construction of high dimensional meta-model could provide a new strategy to design and study PEEK through modeling and optimization procedures, which leads to a brand-new method to study high-performance PEEK and PEEK-based materials.
Graphical abstract

1 Introduction
Polymer materials and their based composites have shown excellent lightweight and mechanical properties compared to traditional metal and ceramic materials. Their unique advantages have attracted increasing attention from researchers in various fields, such as automotive, aerospace, and so on (1,2). For example, the applications of polymer composites have already replaced several structural components in different industrial fields, i.e., airframe structure and wind turbine blade (3,4). In recent years, the presence of thermoplastic materials has made polymer materials increasingly popular due to their high-temperature mechanical properties, high toughness, and reusability compared to traditional thermoset resin materials. Due to easier producing procedures, relatively lower expense as well as better recyclability, the thermoplastic materials have already taken the place of some traditional thermoset materials (5,6).
Among these thermoplastic materials, poly(ether ether ketone) (PEEK) is one of the most widely used high-performance thermoplastic polymers (7,8). As a semi-crystalline aromatic thermoplastic material, PEEK is one of the members of poly-aryl-ether-ketone (PAEK) family. The unique molecular structures of PAEK family result in the excellent properties, such as high strength, low density, thermal stability, and corrosion resistance, which make them potential candidates to replace aluminum alloys in the aviation field as the structural material (9–14). Verma and Sharma (15) constructed an atomic model of PAEK-based bio-composites using the molecular dynamics (MD) approach. The results show that the ultimate tensile strength and ultimate compressive strength of PAEK-based composites doped with hydroxyapatite (HAp) are significantly increased. PEEK has also been widely used in the study of low-temperature tribology due to its superior wear resistance at low temperatures (16,17). Pierik et al. (18) investigated the transient interlaminar friction response of unidirectional C/PEEK and established a PAEK shear stress model, which was able to accurately predict the measured characteristics of the transient friction response, setting the stage for future intrinsic modeling of interlaminar friction. Additionally, Bie et al. (19) studied the impact compression and spalling characteristics of PEEK through the flat plate impact experiments. The spall strength, strain rate, and fracture toughness were studied, and obtained σ H < 2.6 GPa. Therefore, it is necessary to deeply investigate the microscopic behavior and mechanical property of PEEK to make them more suitable for the application as aerospace and aviation structural components (2).
The development of computer modeling has become another method to facilitate the research of material science, which can help to study the relationship between structure and properties of PEEK. MD simulation technique has been used to study the motions and interactions of molecules and atoms. And relevant experiments have shown that MD simulations can be used to study the mechanical properties of composites with thermoplastic materials as matrix materials (2,20–26). A widely used MD force field, CHARMM, has been applied for the research of high performance polymers with high accuracy (27–29). Materials such as PEEK, which is a high-performance thermoplastic resin, can be simulated with high accuracy.
Although many studies on PEEK-based materials have been carried out, most of them are mainly based on experiment and are still limited at single-variable studies in low-dimensional space, which are complex and costly. Systematic studies are needed to comprehensively reveal the variation of various properties of PEEK under different conditions. In this study, a creative approach is proposed to construct a meta-model of pure PEEK using MD methods and Gaussian regression processes based on a large number of simulation points. Subsequently, the response surfaces of PEEK’s density, Poisson’s ratio, and Young’s modulus resulting from simulated data at different temperatures and pressures have been built, and the changing trends of these properties are carefully analyzed. To the best of our knowledge, it is rare to combine MD simulation with data optimization to study polymer materials’ properties. This study successfully combines the MD method with the meta-modeling method, which provides a brand-new way to design, simulate, analyze, and predict the PEEK-based materials.
2 Theory and methods
In this article, all the simulations are performed using the open-source MD software LAMMPS (30) and all the data analysis and workflow control are done by Python.
2.1 PEEK MD model
First, a single-molecule PEEK chain has been analyzed through Python in the CHARMM force field and the bonding relationship between PEEK units has then been saved separately, as shown in Figure 1(b). After that, the PEEK unit model and the bonding relationship obtained above can be used to construct the PEEK model of any length. Specifically, the Python codes were written to form a large molecular chain which copies the PEEK unit along the x-axis, and then copy the molecular chain along the y-axis to form a large molecular material. Finally, a three-dimensional cube was constructed with a side length equal to the length of PEEK on the x-axis, as shown in Figure 1(c), and all PEEK molecular chains could move and rotate randomly in this cube. In the whole study, there were 60 monomers on each molecular chain when the simulations were performed (model size 3.56 × 105 Å3).
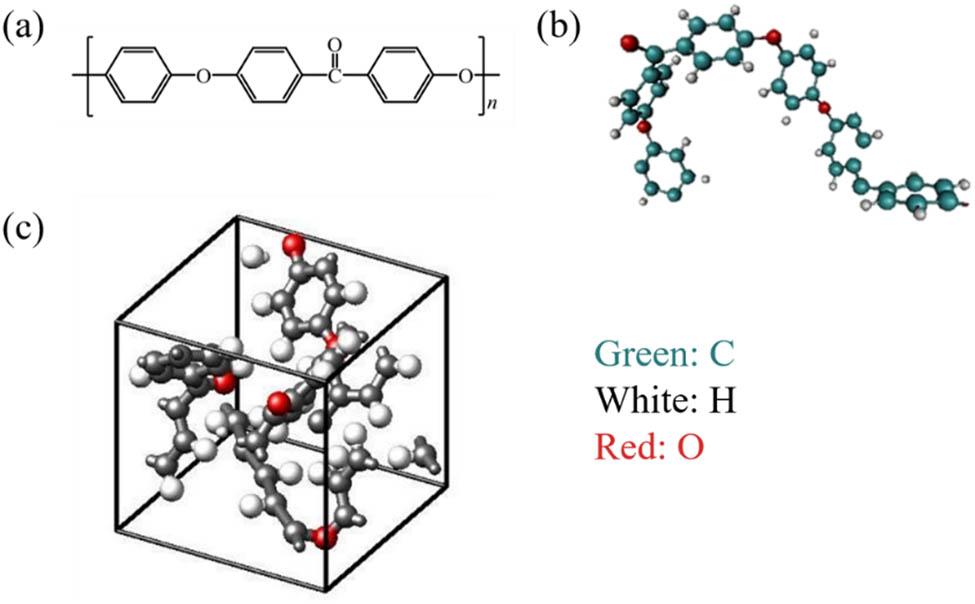
(a) Chemical structure of PEEK, (b) PEEK molecular chain of 2 units 1 molecule, and (c) unit model of pure PEEK.
After the model construction, the intermolecular interaction force in the system is at a high level due to the directly copying operations, which results in the model becoming nonphysical. Therefore, LAMMPS’s steepest descent method has been adopted to optimize the molecular configuration of the model. After the optimization, the model was relaxed using microcanonical ensemble (NVE ensemble) until it reached a stable state under constant temperature and pressure, and each atom’s moving step has been limited at less than 0.1 Å, which could make the system display better initial configuration. Meanwhile, the model temperature has been maintained at 700 K in the whole process to ensure that the molecular chain could keep fluidity. A modified relaxation procedure which is designed similar to the traditional consolidation progress has then been conducted. First, the deform command was used to quickly reduce the volume of the simulation box. After that, the density of the model is compressed to 1.29 g·cm−3 (the theoretical density of PEEK). Then, a simulation step of 1 fs has been adopted to make sure that all atoms could cross energy barriers and reach a steady state easily. Finally, the simulation step was reduced to 0.1 fs to keep the model stable under normal temperature and pressure. After compression process, the density of the model reaches theoretical level, and the compression result is shown in Figure 2(a). After the relaxation of the model, the stable model of pure PEEK under the step size of 0.1 fs can be obtained under isothermal and isobaric pressure, which is shown in Figure 2(b).
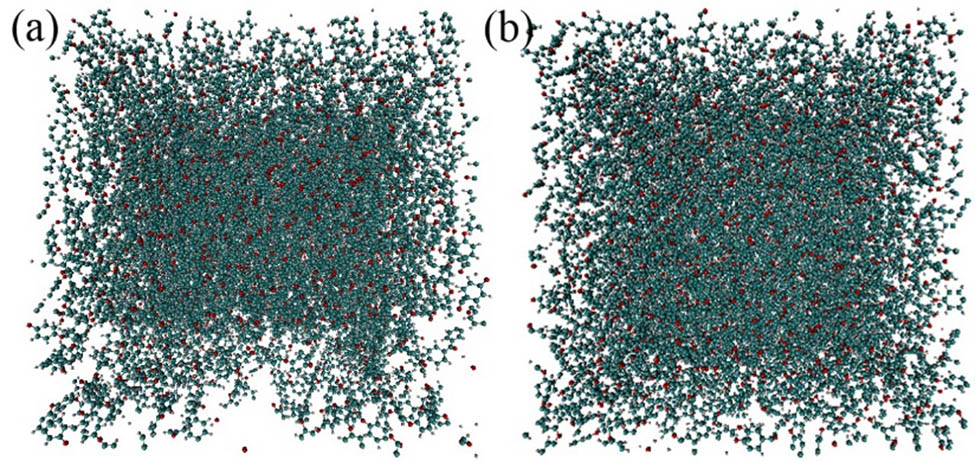
Stabilization model for pure PEEK: (a) before the isothermal isobaric relaxation and (b) after the isothermal isobaric relaxation.
2.2 PEEK stretching experiment
Based on the PEEK MD model obtained above, the PEEK stretching experiment is also controlled by a Python script, which sends commands to the LAMMPS program to perform the simulation program. The strain rate in the simulation has been controlled at 2 × 108 s−1 due to the spatiotemporal scale limitations of MD. In the stretching simulation, the simulation step of PEEK material which is located in an orthogonal simulation box was settled at 0.1 fs. LAMMPS would simulate the stretching process of PEEK along the x-axis direction at a constant rate, and then keep the pressure on both XZ and XY planes equal to one standard atmosphere. Finally, the strain of the PEEK model on the x-axis will reach 1.2 (Figure 3).
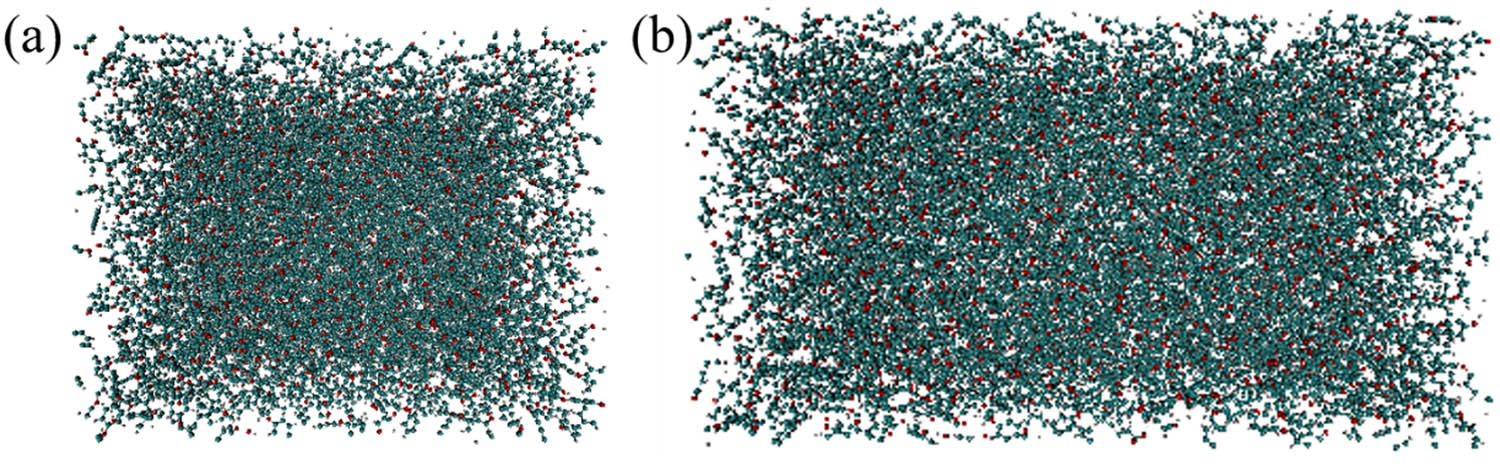
(a) Stretching processes of PEEK model and (b) maximum strain of 1.2.
2.3 Efficient simulation and meta-model construction
In order to make the model more efficient, the meta-model has been constructed using the following steps: experimental design, data collection, and data fitting. First, a sensitivity analysis has been done based on the tensile experiment simulation above and the target variables have been chosen for the meta-model construction. Afterward, the Latin hypercube sampling method has then been adopted for experimental design, and the obtained data have been inputted into the MD software for calculation and data collection. To improve the model’s running speed, some measurements including reduced cutoff distance and to run the model at a 1 fs iteration step have been adopted. The cutoff distance is 10 Å so that the atoms can properly interact with each other. Meanwhile, the iteration step in the relaxation stage of the PEEK MD model has been increased to 2 fs, while this value in the stabilization stage has returned to 0.1 fs. The 2 fs iteration step facilitated the atoms to cross the potential barrier, accelerating the relaxation speed of the model. By doing so, 200 samples have been randomly sampled in order to investigate the relevant properties at a wider range of the temperature from 100 to 500 K and the pressure range from 0.5 to 10 atm. Finally, the Gaussian process regression method has been used to fit the experimental data and construct the meta-model. By increasing the number of kernel functions and optimizing their combination forms, an efficient modeling process through a dual adaptive mechanism, which is based on the parameter space adaptive sampling and regression model intelligent selection, has been adopted. Through the deep integration of machine learning and numerical analysis, the results from 200 sampling points have been fitted through this method and a polynomial response surface meta-model is finally obtained. Therefore, the maximum pull deformation of the model is first designed to be from 1 to 1.01 under the stretching speed of 0.1 fs, and then from 1.01 to 1.1 under the stretching speed of 1 fs. And finally, Poisson’s ratio has been obtained from tensile experiment.
3 Results and discussion
First, the relaxation process of the system has been analyzed through the density variation of the PEEK model. Figure 4 shows the density profile of the PEEK model, where Figure 4(a) shows the density variation for the full step size, (b) plot shows the density profile for the stage with step size less than 24,000, and (c) plot shows the variance plot obtained from nearly 40 samples, which have been recorded by sampling every 100 steps. It can be found that the density of the model increases rapidly in the volume compression stage, and the variance of the density also increases rapidly from 0 to 10−1 orders of magnitude. From Figure 4(b), there is a significant decrease in the density of the model when the model changes from the “volume compression” phase to the “relaxation” phase. This can be ascribed to the isothermal and isobaric system of LAMMPS which controls the pressure of the system by keeping the volume scaling of the model. When the model is suddenly compressed from a very low-density state to a high-density state, the molecular configuration of the model becomes extremely unstable, the molecular chains are twisted and entangled together, and the stress cannot be effectively released, so the intermolecular forces and interatomic bonding potential of the model will be larger. In order to maintain a constant pressure, the isothermal and isobaric system of LAMMPS has been controlled to increase the volume of the simulation frame to maintain the model pressure at about 1 standard atmospheric pressure, which leads to a downward shift of the density curve. As the model relaxes, the stresses are released, and the macroscopic pressure of the model decreases, while the volume of the LAMMPS-controlled simulation box decreases, the density slowly increases.
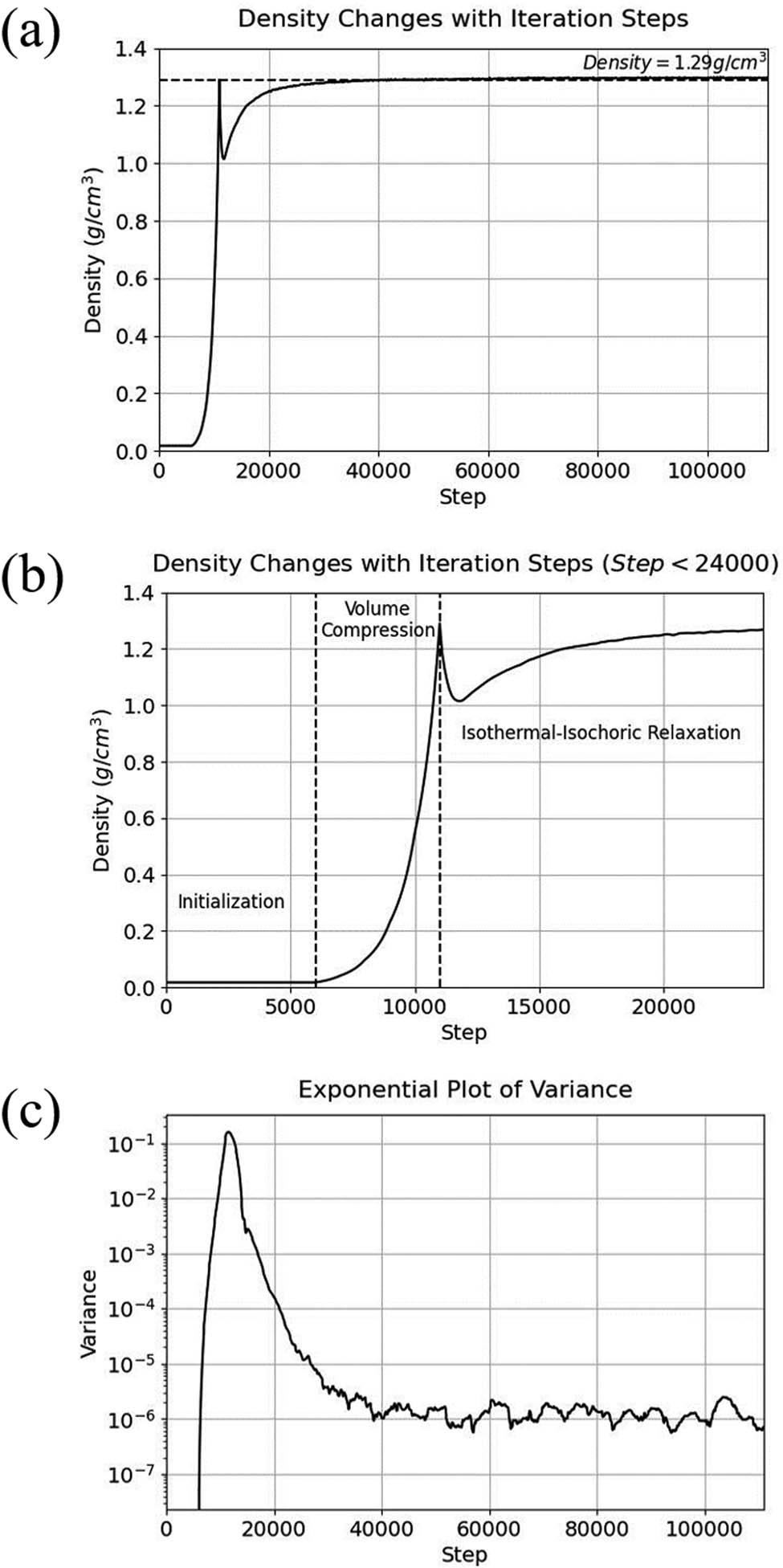
Density curve of pure PEEK: (a) full step size (0–111,000), (b) step size less than 24,000, and (c) variogram of the last 40 samples, sampled every 100 steps.
In the model construction process, the density of the model finally converges near 1.29 g·cm−3 (Figure 4), which is quite close to the theoretical value. And from the variance plot, the variance would reach 10−6 orders of magnitude when the relaxation step reaches 40,000 steps, and it can be considered that the density has converged. After extracting this model, the operation was continued for 2,000 steps and 20 PEEK models were derived, among which the model closest to ambient atmospheric pressure was selected according to the system pressure and temperature. The final data of the PEEK models are shown in Table 1. This means that the desired optimal model is found when the number of iteration steps is 113,000. The pressure of optimal model is 101,471.35 Pa and the temperature is 300.75 K, which is closest to the state of normal temperature and pressure. The simulated density of PEEK in this state is 1.2964 g·cm−3, which is also closest to the theoretical value.
Data of the model
| Iteration steps | Density (g·cm−3) | Pressure (Pa) | Temperature (K) |
|---|---|---|---|
| 113,000 | 1.2964 | 101,471.35 | 300.75 |
In order to verify the accuracy of the PEEK model, the mechanical properties of the PEEK model have been studied at room temperature and pressure, and the data results were carefully analyzed. Since the total number of atoms is relatively small and the random movement of atoms leads to random fluctuations in the stress results, several experiments were conducted to eliminate the randomness of the simulation. (during this process, the time step was always 0.1 fs.) Based on the response surface model, the fastest “ascent” method is used to iterate from a strain of 1.05 to obtain the first highest point of the model at 1.11. This value is then substituted into the response surface model and the yield limit is measured to be 225.69 MPa. According to the result of the yield limit in Figure 5(a), the stress is also obtained at 1/10 of the yield limit and Young’s modulus is measured to be 5.02 GPa. Poisson’s ratio also can be obtained from tensile experiment, whose transverse and longitudinal strains are shown in Figure 5(b). The transverse strains and longitudinal strains are then arranged into a matrix and singular value decomposition is carried out to obtain its eigenvector as (−0.93,0.34), and its slope is calculated to be −0.37, which is Poisson’s ratio. By doing so, the computational speed would be improved by 1.728 and 6.89 times, respectively. The computational acceleration at this time plus the previous computational acceleration in the tensile test can be increased by 11.9 times. Although this may somehow reduce the intermolecular forces, which would reduce the density and Young’s modulus of sample macroscopically, it can be found that the model’s Poisson’s ratio and density are less affected by the iteration step.
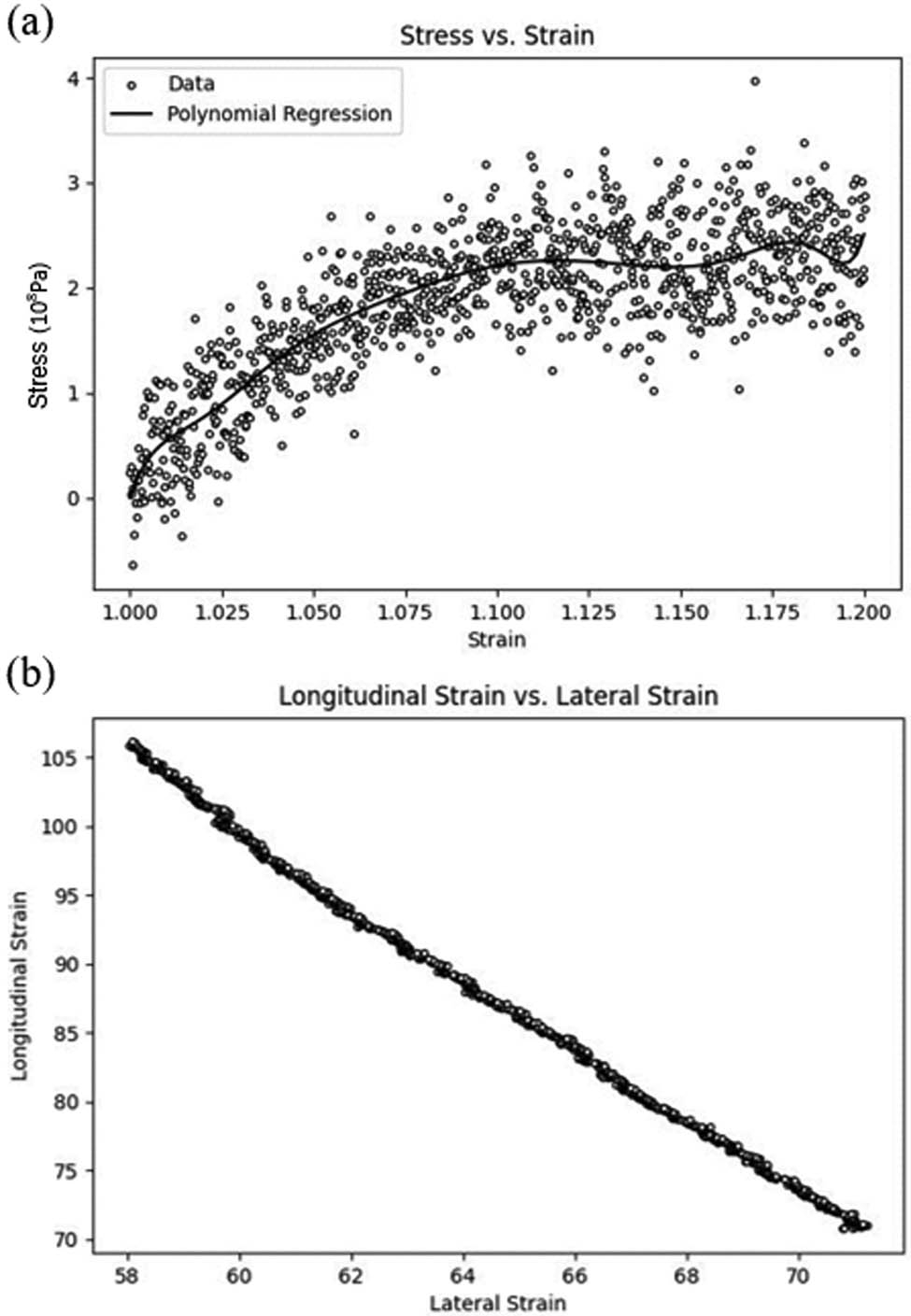
(a) Stress–strain curve for pure PEEK model and (b) transverse and longitudinal strains of pure PEEK model.
In order to verify the accuracy, the obtained data were compared to some relevant references (2,31) (Table 2). The density of PEEK in previous research is 1.30 g·cm−3 and Poisson’s ratio is 0.4. The supplier’s data given in the article are 1.30 g·cm−3 and 0.38, respectively, and the data fit well. However, the article did not give data at 10 ns−1 tensile rate, so it is not possible to compare the accuracy of the results of this study with Young’s modulus and yield limit of the article. The density of PEEK obtained by Zhang is 1.24 g·cm−3, while Young’s modulus is 5.02 GPa and the yield limit is 253 MPa, which is within the permissible error.
Data comparisons
| Physical quantity | Simulation of this study | Simulation of Ref. (2) | Experiment of Ref. (2) | Simulation of Ref. (31) |
|---|---|---|---|---|
| Young’s modulus (GPa) | 5.02 | — | — | 5.02 |
| Poisson’s ratio | 0.37 | 0.4 | 0.38 | — |
| Yield limit (MPa) | 225.69 | — | — | 253 |
| Density (g·cm−3) | 1.29 | 1.3 | 1.3 | 1.24 |
Based on the tensile experiment simulation above, 200 samples have been randomly sampled in order to investigate the relevant properties at a wider range of the temperature from 100 to 500 K and the pressure range from 0.5 to 10 atm. Afterward, the Gaussian process regression was fitted to the results from 200 sampling points and a polynomial response surface meta-model was obtained (Figure 6). It can be concluded from the theoretical study that a larger “energy fluctuation” occurs due to the smaller MD model, leading to larger fluctuations in stress, which results in the distortion of Young’s modulus. Therefore, the maximum pull deformation of the model was first designed to be from 1 to 1.01 under the stretching speed of 0.1 fs, and then from 1.01 to 1.1 under the stretching speed of 1 fs. The low step size and low deformation degree would result in more accurate Young’s modulus, while the higher step size and higher deformation degree would produce more accurate Poisson’s ratio.
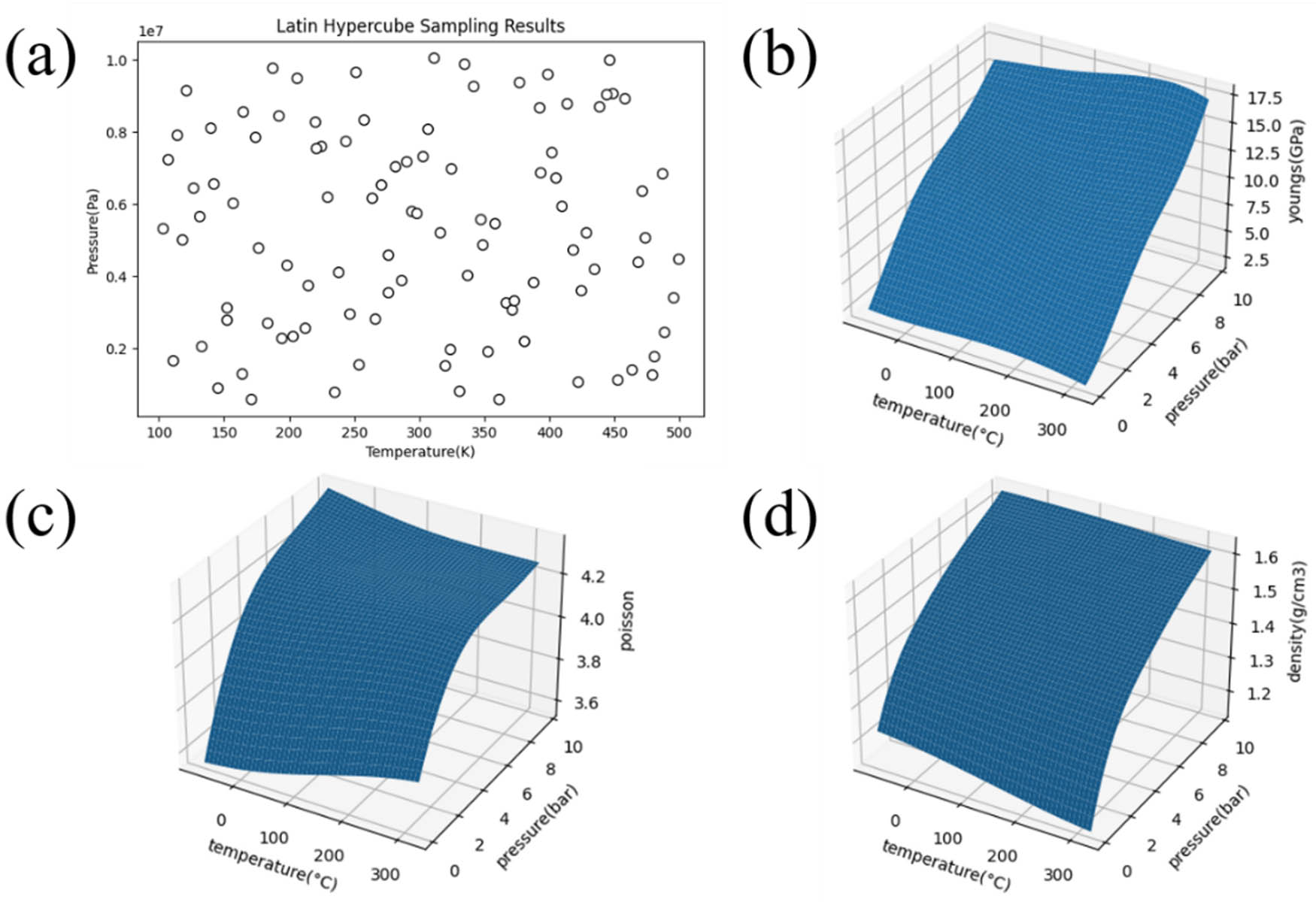
(a) Latin hypercube sampling result, (b) meta-model of Young’s modulus, (c) meta-model of Poisson’s ratio, and (d) meta-model of density.
To further study the obtained meta-model, the variation of Young’s modulus, Poisson’s ratio, and density with different temperatures at 1 atm is shown in Figure 7 in (a), (c), and (e), respectively, and the variation of Young’s modulus, Poisson’s ratio, and density with different atmospheric pressures at 300 K is shown in (b), (d), and (f), respectively. The blue curve in the figure indicates the average predicted value of the variable, while the green area indicates mean ± standard deviation. Obviously, the results show that PEEK exhibits the similar thermodynamic phase transition characteristics as traditional polymers: glassy, elastomeric, and viscous states during temperature rise. The standard deviation results of the Gaussian process regression show that the errors of both Young’s modulus and Poisson’s ratio are higher, while the fluctuations in the density output are smaller than that of Young’s modulus and Poisson’s ratio. This indicates that Young’s modulus and Poisson’s ratio are noisier at the time of sampling. The small sample size of the model produces the “energy fluctuation” that is mentioned before, which generates higher noise and leads to distortion of the data. However, the obtained density curves are accurate.
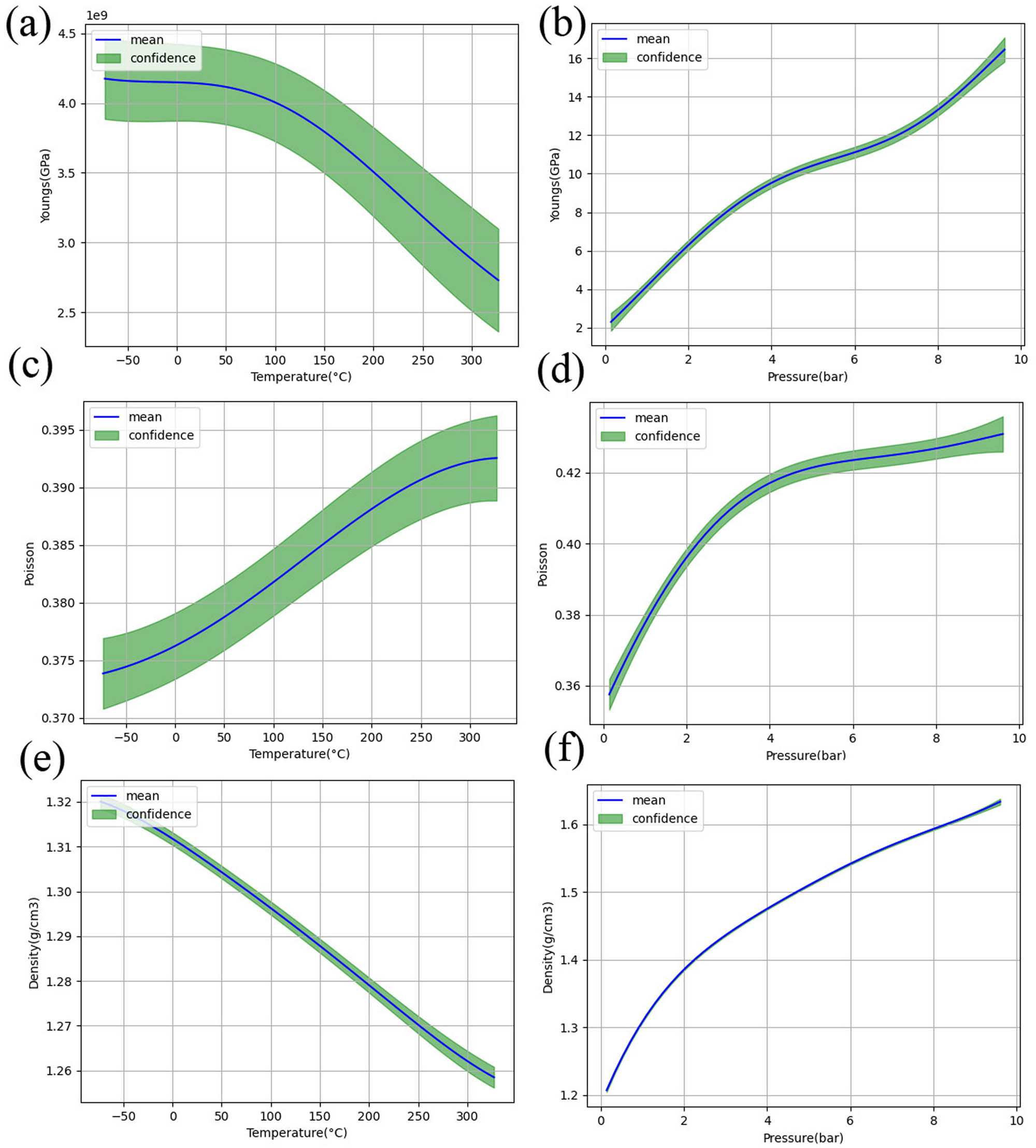
Standard deviation results from Gaussian process regression: (a) Young’s modulus versus temperature at 1 atm, (b) Young’s modulus versus pressure at 300 K, (c) Poisson’s ratio versus temperature at 1 atm, (d) Poisson’s ratio versus pressure at 300 K, (e) density versus temperature at 1 atm, and (f) density versus pressure at 300 K.
In Figure 7(a), the values of Young’s modulus decrease rapidly at high temperature and low pressure. According to the relevant properties of PEEK materials, the PEEK material will transfer into fluid state when temperature reaches the glass transition temperature at the pressure of 1 atm, Young’s modulus will accordingly decrease which indicates that the constructed meta-model can correctly reflect the trend of the glass transition. In Figure 7(b), pressure and Young’s modulus are essentially positively correlated, which can also be derived from the Pearson correlation coefficient matrix. As exception, Young’s modulus roughly increases with pressure. And in the present sampling range, the effect of temperature on Young’s modulus is small. In Figure 7(c) and (d), Poisson’s ratio increases with the increasing temperature and pressure. However, the slope of the curve becomes smaller when the temperature reaches 300 K and the pressure reaches 4 standard atmospheres. In Figure 7(e) and (f), it can be found that the effect of temperature and pressure on density is relatively large. For both curves of the density, the range of the error region becomes much smaller. Especially for (f), the error band is almost invisible, which indicates that the accuracy of the density simulation result is very high. It is worth noting that the pressure of the system has a significant regulation effect on the phase transition temperature, and the glass transition temperature (T g) and melting point (T m) both show an increasing trend with the pressure increasing.
The Pearson correlation coefficient matrices for the above physical quantities have been calculated and presented in a heat map (Figure 8). The closer the value in the matrix is to 1, the stronger the linear correlation between the two. The linear correlation coefficient between pressure and density is 0.96, while this value between pressure and Young’s modulus is 0.9, indicating that pressure has a relatively large effect on these two physical quantities and that the density or Young’s modulus can be predicted relatively accurately for a given pressure by a linear fit. Observing the effect of temperature on several output quantities, it can be found that the linear correlation coefficients of temperature with Young’s modulus, Poisson’s ratio, and density are 0.04, 0.11, and 0.03, respectively, which indicates that the linear correlation between temperature and these three physical quantities is weak, and it is difficult to predict the changes of physical quantities by linear fitting. Therefore, more attention should be paid to the changes between physical quantities with poor linear correlation in future research to find out a more reasonable and accurate simulation prediction method.
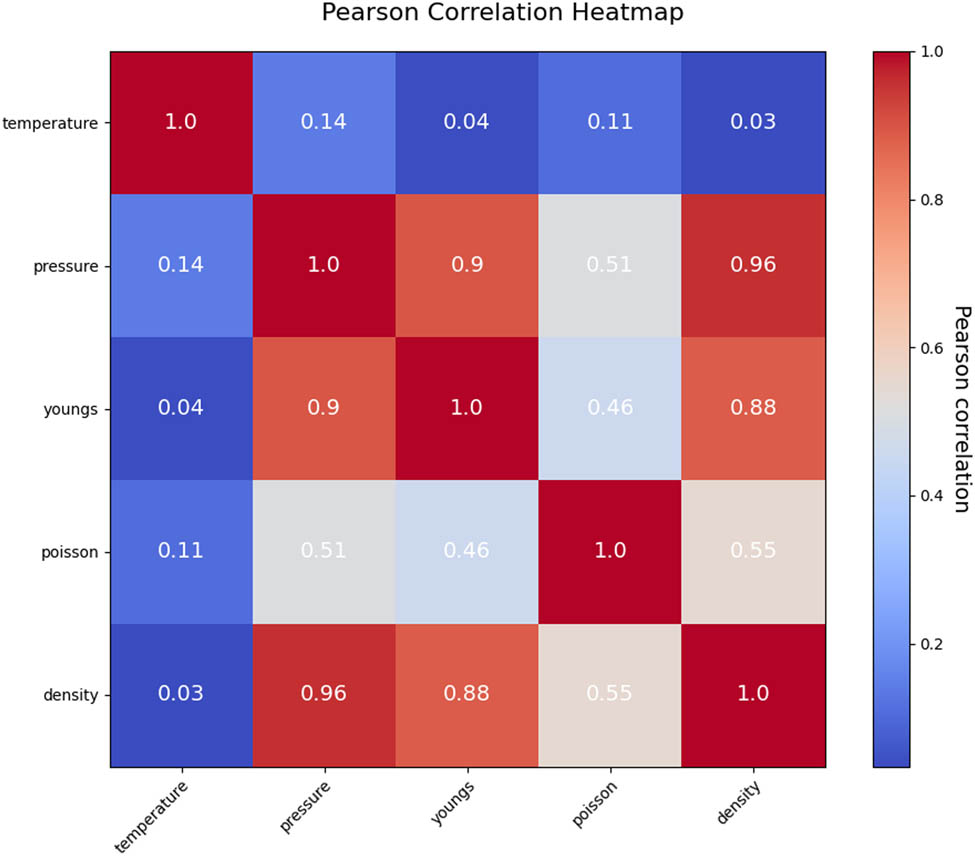
Pearson’s correlation coefficient matrix.
4 Conclusion
In this study, the model of PEEK and its relevant properties have been built and simulated through MD with the help of data optimization procedures. First, Young’s modulus, Poisson’s ratio, and density of the constructed PEEK model are simulated at a strain rate of 2 × 108 s−1, which agree with previous publications. Meanwhile, the meta-model of PEEK’s different properties over 100–500 K and 0.5–10 atm have then been obtained based on the above simulation and data analysis. In this process, the Latin hypercube sampling method has been applied to select data under different temperatures and pressures, and then analyzed their effects on the PEEK material using the response surface method. The Gaussian regression process has been used to fit the sampling points, which improved the stability and accuracy of the polynomial response surface meta-model. The accuracy of the model has been further improved by Pearson’s correlation coefficient. Therefore, a high-quality solution for the optimization design of the PEEK material under complex conditions systematic study through MD modeling and data optimization methods has been reported. The meta-model obtained can reasonably predict the performance of PEEK at various temperatures and pressures in the system. This study could not only give light on the basic research of thermoplastic polymers similar to PEEK, but also provide a strategy for PEEK based composites study with different fillers.
-
Funding information: Authors state no funding involved.
-
Author contributions: Chenxi Hu: writing – review & editing, supervision, conceptualization; Liming Chen: methodology, formal analysis, writing – original draft; Zhongqi Li: writing – original draft, investigation and validation; Yan Yu: validation, writing – review & editing, supervision.
-
Conflict of interest: Authors state no conflict of interest.
-
Data availability statement: The datasets generated and/or analyzed during the current study are available online. Data and relevant code for this research work are stored in DRYAD (http://datadryad.org/stash/share/pz5PbZ1N6XzwQjeITHjRGmnhdV1fCONUWG8jED_RS38).
References
(1) Pisani WA, Newman JK, Shukla MK. Multiscale modeling of polyamide 6 using molecular dynamics and micromechanics. Ind Eng Chem Res. 2021;60:13604–13.10.1021/acs.iecr.1c02440Search in Google Scholar
(2) Pisani WA, Radue MS, Chinkanjanarot S, Bednarcyk BA, Pineda EJ, Waters K, et al. Multiscale modeling of PEEK using reactive molecular dynamics modeling and micromechanics. Polymer. 2019;163:96–105.10.1016/j.polymer.2018.12.052Search in Google Scholar
(3) Zhang T. Applications of high performance thermoplastic composites for commercial airplane structural component. Aeronaut Manuf Technol. 2013;15:32–5.Search in Google Scholar
(4) Arwood Z, Cousins DS, Young S, Stebner AP, Penumadu D. Infusible thermoplastic composites for wind turbine blade manufacturing: static characterization of thermoplastic laminates under ambient conditions. Compos Part C: Open Access. 2023;11:100365.10.1016/j.jcomc.2023.100365Search in Google Scholar
(5) Advani SG, Hsiao KT. Introduction to composites and manufacturing processes. Manufacturing techniques for polymer matrix composites (PMCs). UK: Woodhead Publishing; 2012. p. 1–12.10.1533/9780857096258.1.1Search in Google Scholar
(6) Li C, Strachan A. Prediction of PEKK properties related to crystallization by molecular dynamics simulations with a united-atom model. Polymer. 2019;174:25–32.10.1016/j.polymer.2019.04.053Search in Google Scholar
(7) Bastan FE. Fabrication and characterization of an electrostatically bonded PEEK-hydroxyapatite composites for biomedical applications. J Biomed Mater Res Part B, Appl Biomater. 2020;108:2513–27.10.1002/jbm.b.34583Search in Google Scholar PubMed
(8) Fedel M, Micheli V, Thaler M, Awaja F. Effect of nitrogen plasma treatment on the crystallinity and self-bonding of polyetheretherketone (PEEK) for biomedical applications. Polym Adv Technol. 2020;31:240–7.10.1002/pat.4764Search in Google Scholar PubMed PubMed Central
(9) Jones DP, Leach DC, Moore DR. Mechanical properties of poly(ether-ether-ketone) for engineering applications. Polymer. 1985;26:1385–93.10.1016/0032-3861(85)90316-7Search in Google Scholar
(10) Zhang G, Li WY, Cherigui M, Zhang C, Liao H, Bordes JM, et al. Structures and tribological performances of peek(poly-ether-ether-ketone)-based coatings designed for tribological application. Prog Org Coat. 2007;60:39–44.10.1016/j.porgcoat.2007.06.004Search in Google Scholar
(11) Mbogori M, Vaish A, Vaishya R, Haleem A, Javaid M. Poly-ether-ether-ketone (PEEK) in orthopaedic practice – a current concept review. J Orthop Rep. 2022;1:3–7.10.1016/j.jorep.2022.03.013Search in Google Scholar
(12) El Magri A, Vaudreuil S. Effects of physical and chemical ageing on 3D printed poly (ether ether ketone)/poly (ether imide) [PEEK/PEI] blend for aerospace applications. J Mater Sci. 2022;58:1465–79.10.1007/s10853-022-08068-wSearch in Google Scholar
(13) Zou H, Yin W, Cai C, Wang B, Liu A, Yang Z, et al. The out-of-plane compression behavior of cross-ply AS4/PEEK thermoplastic composite laminates at high strain rates. Materials. 2018;11:2312.10.3390/ma11112312Search in Google Scholar PubMed PubMed Central
(14) Arif MF, Kumar S, Varadarajan KM, Cantwell WJ. Performance of biocompatible PEEK processed by fused deposition additive manufacturing. Mater Des. 2018;146:249–59.10.1016/j.matdes.2018.03.015Search in Google Scholar
(15) Verma S, Sharma N. Evaluating the mechanical properties of novel HAp reinforced polyaryletherketone biocomposites via molecular dynamics simulation. Mater Chem Phys. 2023;307:128106.10.1016/j.matchemphys.2023.128106Search in Google Scholar
(16) Chen D, Li J, Yuan Y, Gao C, Cui Y, Li S, et al. A review of the polymer for cryogenic application: methods, mechanisms and perspectives. Polymers. 2021;13:320.10.3390/polym13030320Search in Google Scholar PubMed PubMed Central
(17) Wang Q, Zheng F, Wang T. Tribological properties of polymers PI, PTFE and PEEK at cryogenic temperature in vacuum. Cryogenics. 2016;75:19–25.10.1016/j.cryogenics.2016.01.001Search in Google Scholar
(18) Pierik ER, Grouve WJB, Wijskamp S, Akkerman R. Prediction of the peak and steady-state ply-ply friction response for UD C/PAEK tapes. Compos Part A. 2022;163:107185.10.1016/j.compositesa.2022.107185Search in Google Scholar
(19) Bie BX, Pan RC, Xu J, Chai HW, Chen S, Du GH, et al. Dynamic compression and fracture of poly(ether-ether-ketone) under plate impact. Int J Mech Sci. 2023;246:108138.10.1016/j.ijmecsci.2023.108138Search in Google Scholar
(20) Cheng X, Liao Q, Xu J, Gu Z, He Y. Molecular dynamics simulation and experimental study on the mechanical properties of PET nanocomposites filled with CaCO3, SiO2, and POE-g-GMA. e-Polymers. 2024;24:20230144.10.1515/epoly-2023-0144Search in Google Scholar
(21) Guo L, Xu H, Wu N, Yuan S, Zhou L, Wang D, et al. Molecular dynamics simulation of the effect of the thermal and mechanical properties of addition liquid silicone rubber modified by carbon nanotubes with different radii. e-Polymers. 2023;23:20228150.10.1515/epoly-2022-8105Search in Google Scholar
(22) Radue MS, Jensen BD, Gowtham S, Klimek-McDonald DR, King JA, Odegard GM. Comparing the mechanical response of di-, tri-, and tetra-functional resin epoxies with reactive molecular dynamics. J Polym Sci Part B-Polym Phys. 2018;56:255–64.10.1002/polb.24539Search in Google Scholar PubMed PubMed Central
(23) Al Mahmud H, Radue MS, Chinkanjanarot S, Pisani WA, Gowtham S, Odegard GM. Multiscale modeling of carbon fiber-graphene nanoplatelet-epoxy hybrid composites using a reactive force field. Compos Part B-Eng. 2019;172:628–35.10.1016/j.compositesb.2019.05.035Search in Google Scholar
(24) Bao Q, Yang Z, Lu Z. Molecular dynamics simulation of amorphous polyethylene (PE) under cyclic tensile-compressive loading below the glass transition temperature. Polymer. 2020;186:121968.10.1016/j.polymer.2019.121968Search in Google Scholar
(25) Patil SU, Radue MS, Pisani WA, Deshpande P, Xu H, Al Mahmud H, et al. Interfacial characteristics between flattened CNT stacks and polyimides: a molecular dynamics study. Comput Mater Sci. 2020;185:109970.10.1016/j.commatsci.2020.109970Search in Google Scholar
(26) Pisani WA, Radue MS, Patil SU, Odegard GM. Interfacial modeling of flattened CNT composites with cyanate ester and PEEK polymers. Compos Part B-Eng. 2021;211:108672.10.1016/j.compositesb.2021.108672Search in Google Scholar
(27) Brooks BR, Bruccoleri RE, Olafson BD, States DJ, Swaminathan S, Karplus M. CHARMM: a program for macromolecular energy, minimization, and dynamics calculations. J Comput Chem. 1983;4:187–217.10.1002/jcc.540040211Search in Google Scholar
(28) MacKerell AD, Bashford D, Bellott M, Dunbrack RL, Evanseck JD, Field MJ, et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J Phys Chem B. 1998;102:3586–616.10.1021/jp973084fSearch in Google Scholar PubMed
(29) Vanommeslaeghe K, Hatcher E, Acharya C, Kundu S, Zhong S, Shim J, et al. CHARMM general force field: a force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J Comput Chem. 2010;31:671–90.10.1002/jcc.21367Search in Google Scholar PubMed PubMed Central
(30) Thompson AP, Aktulga HM, Berger R, Bolintineanu DS, Brown WM, Crozier PS, et al. LAMMPS – a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput Phys Commun. 2022;271:108171.10.1016/j.cpc.2021.108171Search in Google Scholar
(31) Zhang K. Modification design of mechanical properties for poly-ether-ether-ketone and its nanocomposites. Dalian, China: Dalian University of Technology; 2023.Search in Google Scholar
© 2025 the author(s), published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Research Articles
- Flow-induced fiber orientation in gas-powered projectile-assisted injection molded parts
- Research on thermal aging characteristics of silicone rubber composite materials for dry-type distribution transformers
- Kinetics of acryloyloxyethyl trimethyl ammonium chloride polymerization in aqueous solutions
- Influence of siloxane content on the material performance and functional properties of polydimethylsiloxane copolymers containing naphthalene moieties
- Enhancement effect of electron beam irradiation on acrylonitrile–butadiene–styrene (ABS) copolymers from waste electrical and electronic equipment by adding 1,3-PBO: A potential way for waste ABS reuse
- Model construction and property study of poly(ether-ether-ketone) by molecular dynamics simulation with meta-modeling methods
- Zinc–gallic acid–polylysine nanocomplexes with enhanced bactericidal activity for the treatment of bacterial keratitis
- Effect of pyrogallol compounds dosage on mechanical properties of epoxy coating
- Preparation of in situ polymerized polypyrrole-modified braided cord and its electrical conductivity investigation under varied mechanical conditions
- Hydrophobicity, UV resistance, and antioxidant properties of carnauba wax-reinforced CG bio-polymer film
- Janus nanofiber membrane films loading with bioactive calcium silicate for the promotion of burn wound healing
- Synthesis of migration-resistant antioxidant and its application in natural rubber composites
- Influence of the flow rate on the die swell for polymer micro coextrusion process
- Fatty acid filled polyaniline nanofibres with dual electrical conductivity and thermo-regulatory characteristics: Futuristic material for thermal energy storage
- Hydrolytic depolymerization of major fibrous wastes
- Performance of epoxy hexagonal boron nitrate underfill materials: Single and mixed systems
- Blend electrospinning of citronella or thyme oil-loaded polyurethane nanofibers and evaluating their release behaviors
- Efficiency of flexible shielding materials against gamma rays: Silicon rubber with different sizes of Bi2O3 and SnO
- A comprehensive approach for the production of carbon fibre-reinforced polylactic acid filaments with enhanced wear and mechanical behaviour
- Electret melt-blown nonwovens with charge stability for high-performance PM0.3 purification under extreme environmental conditions
- Study on the failure mechanism of suture CFRP T-joints under/after the low-velocity impact loading
- Experimental testing and finite element analysis of polyurethane adhesive joints under Mode I loading and degradation conditions
- Optimizing recycled PET 3D printing using Taguchi method for improved mechanical properties and dimensional precision
- Effect of stacking sequence of the hybrid composite armor on ballistic performance and damage mechanism
- Bending crack propagation and delamination damage behavior of orthogonal ply laminates under positive and negative loads
- Molecular dynamics simulation of thermodynamic properties of Al2O3-modified silicone rubber under silane coupling agent modification
- Precision injection molding method based on V/P switchover point optimization and pressure field balancing
- Heparin and zwitterion functionalized small-diameter vascular grafts for thrombogenesis prevention
- Metal-free N, S-co-doped carbon materials derived from calcined aromatic co-poly(urea-thiourea)s as efficient alkaline oxygen reduction catalysts
- Influence of stitching parameters on the tensile performance and failure mechanisms of CFRP T-joints
- Synthesis of PEGylated polypeptides bearing thioether pendants for injectable ROS-responsive hydrogels
- Rapid Communication
- RAFT-mediated polymerization-induced self-assembly of poly(ionic liquid) block copolymers in a green solvent
- Corrigendum
- Corrigendum to “High-strength polyvinyl alcohol-based hydrogel by vermiculite and lignocellulosic nanofibrils for electronic sensing”
Articles in the same Issue
- Research Articles
- Flow-induced fiber orientation in gas-powered projectile-assisted injection molded parts
- Research on thermal aging characteristics of silicone rubber composite materials for dry-type distribution transformers
- Kinetics of acryloyloxyethyl trimethyl ammonium chloride polymerization in aqueous solutions
- Influence of siloxane content on the material performance and functional properties of polydimethylsiloxane copolymers containing naphthalene moieties
- Enhancement effect of electron beam irradiation on acrylonitrile–butadiene–styrene (ABS) copolymers from waste electrical and electronic equipment by adding 1,3-PBO: A potential way for waste ABS reuse
- Model construction and property study of poly(ether-ether-ketone) by molecular dynamics simulation with meta-modeling methods
- Zinc–gallic acid–polylysine nanocomplexes with enhanced bactericidal activity for the treatment of bacterial keratitis
- Effect of pyrogallol compounds dosage on mechanical properties of epoxy coating
- Preparation of in situ polymerized polypyrrole-modified braided cord and its electrical conductivity investigation under varied mechanical conditions
- Hydrophobicity, UV resistance, and antioxidant properties of carnauba wax-reinforced CG bio-polymer film
- Janus nanofiber membrane films loading with bioactive calcium silicate for the promotion of burn wound healing
- Synthesis of migration-resistant antioxidant and its application in natural rubber composites
- Influence of the flow rate on the die swell for polymer micro coextrusion process
- Fatty acid filled polyaniline nanofibres with dual electrical conductivity and thermo-regulatory characteristics: Futuristic material for thermal energy storage
- Hydrolytic depolymerization of major fibrous wastes
- Performance of epoxy hexagonal boron nitrate underfill materials: Single and mixed systems
- Blend electrospinning of citronella or thyme oil-loaded polyurethane nanofibers and evaluating their release behaviors
- Efficiency of flexible shielding materials against gamma rays: Silicon rubber with different sizes of Bi2O3 and SnO
- A comprehensive approach for the production of carbon fibre-reinforced polylactic acid filaments with enhanced wear and mechanical behaviour
- Electret melt-blown nonwovens with charge stability for high-performance PM0.3 purification under extreme environmental conditions
- Study on the failure mechanism of suture CFRP T-joints under/after the low-velocity impact loading
- Experimental testing and finite element analysis of polyurethane adhesive joints under Mode I loading and degradation conditions
- Optimizing recycled PET 3D printing using Taguchi method for improved mechanical properties and dimensional precision
- Effect of stacking sequence of the hybrid composite armor on ballistic performance and damage mechanism
- Bending crack propagation and delamination damage behavior of orthogonal ply laminates under positive and negative loads
- Molecular dynamics simulation of thermodynamic properties of Al2O3-modified silicone rubber under silane coupling agent modification
- Precision injection molding method based on V/P switchover point optimization and pressure field balancing
- Heparin and zwitterion functionalized small-diameter vascular grafts for thrombogenesis prevention
- Metal-free N, S-co-doped carbon materials derived from calcined aromatic co-poly(urea-thiourea)s as efficient alkaline oxygen reduction catalysts
- Influence of stitching parameters on the tensile performance and failure mechanisms of CFRP T-joints
- Synthesis of PEGylated polypeptides bearing thioether pendants for injectable ROS-responsive hydrogels
- Rapid Communication
- RAFT-mediated polymerization-induced self-assembly of poly(ionic liquid) block copolymers in a green solvent
- Corrigendum
- Corrigendum to “High-strength polyvinyl alcohol-based hydrogel by vermiculite and lignocellulosic nanofibrils for electronic sensing”

