Abstract
To enhance the long-term operational stability of transformers, this study focuses on silicone rubber composite insulation materials for dry-type distribution transformers (D-DTs). Based on obtaining the optimal initial performance of silicone rubber composite materials through response surface model, the thermal aging characteristics and long-term stability of intrinsic silicone rubber and silicone rubber composites are compared using molecular simulations, thermogravimetric analysis, and accelerated thermal aging tests. The results indicate that the addition of a small amount of h-boron nitride (BN) and Al2O3 can improve the thermal stability of the composite materials, and the decline in elongation at break is the key factor determining the thermal lifetime of silicone rubber. The silicone rubber composite material doped with 21.42 phr h-BN, 1.58 phr carbon nanotubes, and 2.67 phr Al2O3, based on the optimal initial performance, is projected to have a lifetime of 3,128 h under accelerated thermal aging at 200°C and 27.40 years under stable operating conditions of D-DTs, making it suitable for widespread application.
1 Introduction
Transformers, as indispensable and vital equipment in power transmission and distribution systems, enable the transmission, transformation, and distribution of electrical energy, thus holding immense significance in ensuring safe and reliable operation for the normal functioning of modern economies and societies (1–3). Due to the notable advantages, including strong short-circuit resistance, high operational efficiency, compact size, and low noise levels, dry-type transformers have been widely utilized in distribution networks, in recent years (4–5). The materials used in transformers mainly include metallic materials and insulation materials. Unlike more stable metallic materials, attributing to the significant temperature variations and extremely high hot spot temperature led by prolonged operation of transformers under fluctuating loads and heavy overloads, insulation materials undergo performance degradation during prolonged thermal aging, making them susceptible to cracking under the influence of operational vibrations and electrical forces (6–9). Therefore, it is generally believed that the service lifetime of transformers primarily depends on the thermal lifetime of their insulation materials (10).
Silicone rubber, known for its high elasticity and excellent insulation properties, offers a significant advantage over traditional epoxy resin materials as it is recyclable, eliminating the need for incineration or burial and resulting in a substantial reduction in carbon emissions (11–13). This makes it an important direction for the development of insulation materials in dry-type distribution transformers (D-DTs). Current research on the application of silicone rubber composite insulation materials in electrical equipment primarily focuses on enhancing their initial performance (14–15). Among these efforts, thermal conductivity has gained significant attention from researchers as it directly impacts the heat dissipation efficiency, temperature distribution, and hot spot temperature in electrical equipment (16–19). Du and Xu achieved improved thermal conductivity and corrosion resistance in silicone rubber by incorporating boron nitride (BN) particles, and a significant effect was observed when the BN content reached 7 phr (20). There is a synergistic effect between different fillers, and the addition of fillers from various categories and particle sizes can enhance the packing density of fillers, thereby constructing a thermal conductive network within the composite material and greatly improving its heat transfer efficiency (21–22). Tang et al. combined modified silicon carbide whiskers with h-BN doping to enhance the thermal conductivity of silicone rubber, resulting in a 16.1% improvement compared to using only one type of filler (23). Kuo et al. achieved 59.6% increase in thermal conductivity in silicone rubber composites by combining Al2O3 and h-BN fillers, surpassing the improvement achieved by using a single filler (24).
The study of the thermal aging characteristics and long-term stability of insulation materials is often achieved through molecular simulation, thermogravimetric analysis (TGA), and accelerated aging methods (25–26). Tang et al. utilized molecular simulations to establish a cellulose model and evaluated the thermal stability of oil-paper insulation based on parameters such as water diffusion coefficient and cellulose chain distance, which were further validated through accelerated thermal aging tests (27). Paul et al. observed that the thermal aging rate of silicone rubber may increase when exposed to mineral oil and analyzed the thermal properties of silicone rubber aged for 200 h in mineral oil using TGA, differential thermal analysis, and infrared thermography, revealing that aging in mineral oil significantly reduces the heat dissipation efficiency of silicone rubber (28). Li et al. designed an accelerated aging test under high and low-temperature cycling conditions to predict the long-term aging performance of typical rubber materials such as ethylene-propylene diene monomer rubber, significantly reducing the required testing time (29). Zhou et al. conducted an analysis specifically targeting the unique working conditions of tropical islands with significant UV exposure, studying the aging mechanism of natural rubber under the dual effects of heat and UV radiation through combined aging tests, and the results indicated that heat promotes the UV aging process, leading to a decrease in mechanical properties and the formation of cracks in natural rubber (30).
The aforementioned research has extensively focused on enhancing the initial performance and long-term stability of polymer insulation materials, including silicone rubber. However, it is worth noting that most existing research studies on silicone rubber materials are limited to the material level, aiming to improve certain properties or characterize their long-term performance changes, while lacking consideration for the practical requirements of D-DTs (31–32). For instance, efforts to increase the thermal conductivity of silicone rubber composite materials may lead to a potential decrease in mechanical and electrical parameters, as well as thermal aging resistance, rendering them unsuitable for dry-type transformer applications. Therefore, research on the thermal aging characteristics and long-term stability of silicone rubber for D-DTs should adequately consider the specific parameter requirements and hot spot temperature in practical applications. To enhance the reliability of silicone rubber materials for D-DTs and ensure their long-term stable operation, it is necessary to consider the actual application scenarios and demands, while improving and studying the initial performance, thermal aging characteristics, and long-term stability of silicone rubber materials.
Considering the parameter requirements of practical application scenarios, this study takes the silicone rubber composite material with the optimized formulation for D-DTs obtained by response surface model as the object. For comparing the performance of intrinsic silicone rubber with modified silicone rubber, molecular simulations, TGA, and accelerated thermal aging methods were employed to analyze the thermal aging characteristics and long-term stability of silicone rubber composite materials for D-DTs. The results show that the addition of a small amount of h-BN and Al2O3 can enhance the thermal stability of the composite material. During the thermal aging process, the mass and thermal conductivity of the silicone rubber composite material exhibit minor changes. Although the insulation performance slightly decreases, it still exceeds the requirements for insulation applications. The attenuation of the elongation at break is identified as a crucial factor in determining the thermal lifetime of the silicone rubber. The silicone rubber composite material, doped with 21.42 phr h-BN, 1.58 phr carbon nanotubes (CNTs), and 2.67 phr Al2O3, is projected to have a predicted lifetime of 3,128 h under accelerated thermal aging at 200°C and 27.40 years under the stable operating conditions of D-DTs, meeting the specified standards, thus making it suitable for practical use as insulation material for D-DTs.
2 Preparation and performance analysis of silicone rubber composite materials
According to standards such as International Electro technical Commission 60310-2016, GB/T 15022.3-2011, DL/T 376-2010, and relevant research, silicone rubber materials applicating in D-DTs require the following properties: thermal conductivity greater than 0.35 W·m−1·K, volume resistivity greater than 1 × 1012 Ω·m, breakdown strength greater than 20 kV·mm−1, and tensile strength greater than 4 MPa. However, the thermal conductivity of intrinsic silicone rubber is only around 0.20–0.25 W·m−1·K, which fails to meet the application requirements. Therefore, it is common practice to enhance its properties by incorporating fillers. Multidimensional filler combinations are typically employed to achieve synergistic effects. Considering the need to increase thermal conductivity while ensuring insulation and mechanical performance in D-DTs, our research team has conducted preliminary studies on silicone rubber composite materials that meet the application requirements. The composite materials were prepared by incorporating high thermal conductivity one-dimensional filler, CNTs, insulating two-dimensional filler, h-BN, and three-dimensional filler, Al2O3.
The performance of silicone rubber composite materials is characterized by parameters such as thermal conductivity, volume resistivity, and tensile strength. The testing equipment and raw materials used are listed in Table 1. The formulation of the materials was carried out through a response surface methodology. Box Behnken central sampling experiments were conducted with h-BN ranging from 15 to 25 phr, CNTs ranging from 1 to 2 phr, and Al2O3 ranging from 2 to 4 phr. h-BN content A, CNT content B, and Al2O3 content C were selected as the dependent variables of the response surface model. The thermal conductivity λ and tensile strength σ of composite materials were selected as the response parameters of the response surface model. The intrinsic silicone rubber and the silicone rubber composite materials corresponding to the designated parameter combinations were prepared and characterized. The response values for the intrinsic silicone rubber and the specified parameter combinations are shown in Table 2. The response functions for λ and σ are defined by Eqs. 1 and 2, respectively. The variances of the response surface models were 0.92 and 0.99, respectively, indicating a good fit of the models.
Testing equipment and standards
| Type | Standard/parameter | Supplier |
|---|---|---|
| Thermal conductivity tester using heat flow method | ASTM D5470-12 | Wuhan Glamor Testing Equipment Co., Ltd |
| High impedance meter | GB/T 1410-2006 | Nichi (Shanghai) Trading Co., Ltd |
| Servo material tensile tester | GB/T 528-2009 | Dongguan Haida Instrument Co., Ltd |
| High voltage breakdown system | GB/T 1408.1-2016 | Self-built |
| h-BN | White flakes, purity > 99% | Qinhuangdao Yinuo High tech Materials Development Co., Ltd |
| CNTs | Black tubular, purity > 99% | Shenzhen Suiheng Technology Co., Ltd |
| Al2O3 | White spherical shape, purity > 99% | Qinghe Andi Metal Materials Co., Ltd |
Response values corresponding to specified combinations
| A (phr) | B (phr) | C (phr) | λ (W·m−1·K) | σ (MPa) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0.244 | 5.51 |
| 15 | 1 | 3 | 0.391 | 4.31 |
| 15 | 1.5 | 2 | 0.449 | 4.28 |
| 15 | 1.5 | 4 | 0.421 | 4.33 |
| 15 | 2 | 3 | 0.433 | 4.25 |
| 20 | 1 | 2 | 0.496 | 3.68 |
| 20 | 1 | 4 | 0.419 | 3.78 |
| 20 | 1.5 | 3 | 0.488 | 4.15 |
| 20 | 2 | 2 | 0.567 | 3.44 |
| 20 | 2 | 4 | 0.523 | 3.53 |
| 25 | 1 | 3 | 0.537 | 3.69 |
| 25 | 1.5 | 2 | 0.552 | 3.68 |
| 25 | 1.5 | 4 | 0.474 | 3.59 |
| 25 | 2 | 3 | 0.595 | 3.43 |
To optimize the formulation to achieve a tensile strength greater than 4 MPa and maximize thermal conductivity, the response functions were employed. The optimized formulation, which yielded the best performance, was found to be doped 21.42 phr of h-BN, 1.58 phr of CNTs, and 2.67 phr of Al2O3. The expected performance of this optimized formulation, as predicted by the model, and the actual performance after preparation and testing are presented in Table 3. By comparing Tables 3 and 4, it can be observed that the thermal conductivity of the optimized formulation material, which is 0.511 W·m−1·K, significantly exceeds the minimum requirement of 0.35 W·m−1·K. It exhibits an improvement of 109.4% compared to the intrinsic silicone rubber and demonstrates a small deviation of only 1.4% from the predicted value of 0.518 W·m−1·K. Additionally, the tensile strength of 4.12 MPa surpasses the standard requirement of 4.00 MPa, with a decrease of only 25.2% compared to the intrinsic silicone rubber and an error of only 3% compared to the predicted value of 4.00 MPa. Therefore, the optimized formulation meets the requirements for application in distribution transformers.
Optimized formulation performance
| Thermal conductivity (W·m−1·K) | Volume resistivity (Ω·cm) | Breakdown strength (kV·mm−1) | Tensile strength (MPa) | |
|---|---|---|---|---|
| Expected value | 0.518 | — | — | 4.00 |
| Measurement value | 0.511 | 4.11 × 1015 | 30.45 | 4.12 |
Binding energy
| Filler | E bind (kcal·mol−1) | E matrix (kcal·mol−1) | E filler (kcal·mol−1) | E total (kcal·mol−1) |
|---|---|---|---|---|
| 10 phr h-BN | 603.9 | −75,070 | −12,381.3 | −88,055.2 |
| 20 phr h-BN | 610.8 | −35,951.5 | −12,400.7 | −48,963 |
| 30 phr h-BN | 616.4 | −24,889.7 | −12,414.1 | −37,920.2 |
| 10 phr CNTs | 956.6 | −92,730.8 | 3,900.7 | −89,786.7 |
| 20 phr CNTs | 550.2 | −36,684.7 | 3,841.4 | −33,393.5 |
| 30 phr CNTs | 539.4 | −20,518.9 | 3,827.8 | −17,230.5 |
| 10 phr Al2O3 | 6,837.9 | −136,167.3 | −82,993.5 | −225,998.7 |
| 20 phr Al2O3 | 5,496.2 | −63,527.2 | −89,046.4 | −158,069.8 |
| 30 phr Al2O3 | 4,083.5 | −31,241.1 | −96,858.9 | −132,183.5 |
3 Analysis of thermal aging performance of silicone rubber composite materials based on molecular dynamics simulations
The service life of D-DTs is primarily related to the lifespan of the insulation materials. During operation, D-DTs are continuously exposed to high temperatures, which leads to thermal aging of the insulation materials and degradation in thermal, electrical, and mechanical performance. This can potentially affect the normal operation of D-DTs. Therefore, when considering the use of silicone rubber composite materials for D-DTs, it is important to not only consider their initial performance but also conduct research on their thermal aging performance and thermal lifespan through microscale methods such as molecular dynamics simulations and accelerated thermal aging tests.
3.1 Molecular dynamics model construction
By solving the Newtonian equations of motion in a molecular system, molecular dynamics simulation can simulate the dynamic processes of molecular systems containing hundreds to thousands of atoms at spatial scales ranging from angstroms to nanometers and time scales ranging from picoseconds to milliseconds. It provides thermodynamic and kinetic information about the system, including temperature, pressure, energy distribution, and molecular motion trajectories, thereby revealing its complex physical and chemical behavior. Through molecular simulations, microscopic parameters such as molecular free volume, mean square displacement (MSD), and binding energy can be obtained, which are not accessible through conventional experimental techniques.
The process of molecular dynamics simulation is as follows: first, establish a model of the research object, then, the Newtonian equations of motion are applied to solve the dynamic behaviors of individual particles in the model, obtaining the specific motion states of particles in the system. Subsequently, by incorporating principles of thermodynamics and utilizing statistical physics analysis techniques, the microscopic structural features such as particle distribution and the macroscopic performance indicators such as the glass transition temperature of the system can be derived.
The molecular dynamics model of the silicone rubber composite material was established using Material Studio (MS) software. First, the intrinsic molecular models of the silicone rubber base polymers, polydimethylsiloxane (PDMS) and polymethylhydrosiloxane (PHMS), as well as the filler molecules h-BN, CNTs, and Al2O3, were constructed as shown in Figure 1.
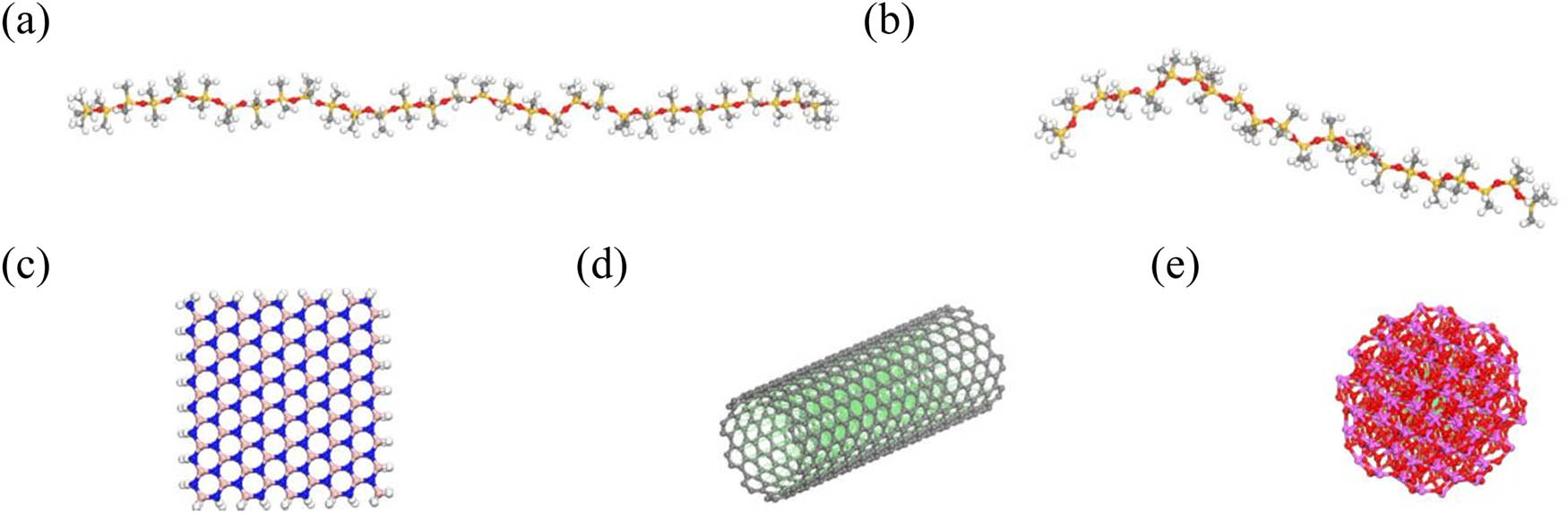
Molecular monomer models: (a) PDMS, (b) PHMS, (c) h-BN, (d) CNTs, and (e) Al2O3.
According to the ratio of broken bonds between individual PDMS and PHMS during crosslinking being 4:2, taking into account both the computational efficiency of the computer and the crosslinking density of silicone rubber, a periodic model consisting of 16 PDMS chains and 8 PHMS chains was constructed. The initial density was set to 0.6 g·cm−3 to generate the uncrosslinked intrinsic silicone rubber model. Considering that a smaller amount of filler addition leads to a larger molecular weight of the simulated molecular system, which can pose computational challenges, the modified silicone rubber models were analyzed qualitatively with filler addition amounts of 10, 20, and 30 phr.
Using the Construction function of the Amorphous Cell module in the MS software, while keeping the ratio of PDMS chains to PHMS chains at 2:1, the unit cell size of composite material model and the corresponding number of PDMS and PHMS chains were calculated for the individual h-BN, CNT, and Al2O3 models at filler addition amounts of 10, 20, and 30 phr. Subsequently, corresponding-sized unit cells were constructed, and the filler monomer models were placed at the center of the constructed unit cells. PDMS and PHMS chains were then filled into the three-dimensional periodic unit cell model, completing the construction of the uncrosslinked modified silicone rubber model. Each modified silicone rubber model contained only one filler model located at the center of the unit cell to reduce computational difficulties and simulate a well-dispersed composite material system. Partial constructed uncrosslinked models are shown in Figure 2.
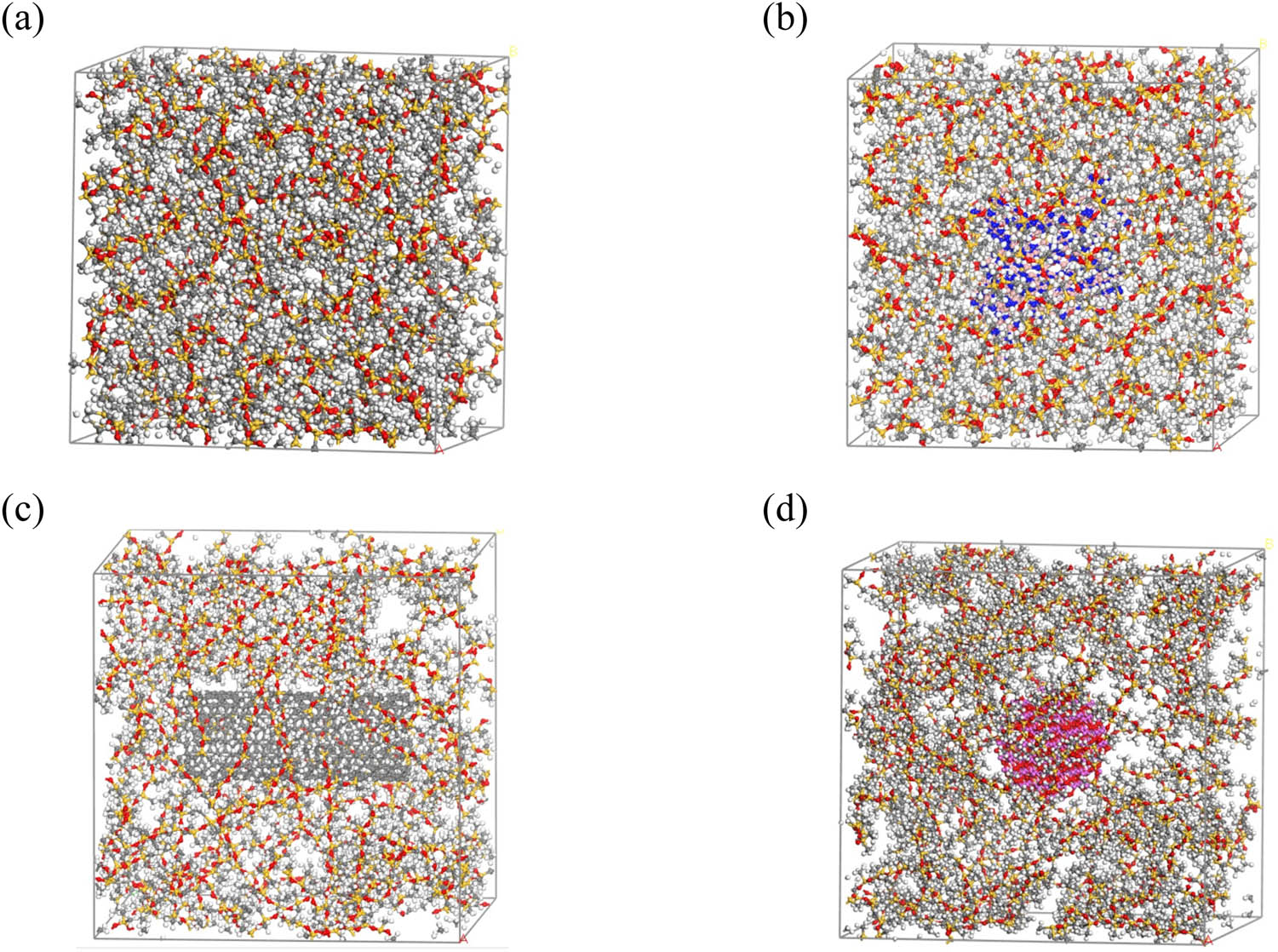
Partial uncrosslinked models: (a) Intrinsic silicone rubber, (b) 10 phr h-BN, (c) 10 phr CNTs, and (d) 10 phr Al2O3.
To prevent significant deformation of the filler models during subsequent processes, the following steps were performed sequentially on the models: (1) Fixing the structure of the filler molecules, (2) 10,000 steps of geometry optimization, and (3) constant volume and temperature (NVT) ensemble dynamics optimization at a temperature of 600 K for a duration of 100 ps.
For the models with a stable filler structure, further optimization was conducted for crosslinking and calculations, following these steps: (1) Removing the fixation on the filler molecules, (2) constant pressure and temperature (NPT) ensemble dynamics optimization at a temperature of 600 K for a duration of 100 ps, and (3) NVT ensemble dynamics optimization at a temperature of 600 K for a duration of 100 ps.
In the actual preparation process, the vinyl groups in PDMS and the polyhydrosiloxane units in PHMS undergo a hydrosilylation addition reaction, forming new Si–C bonds and resulting in the crosslinking of the polysiloxane into a network structure, as shown in Figure 3. The simulation of the crosslinking reaction was implemented using a Perl script. The crosslinking temperature was set to 438 K, with a maximum crosslinking degree of 90%. The initial reaction radius was 3.5 Å, and the maximum reaction radius was 8 Å, with a step size of 0.5 Å. The formation of crosslinking bonds is illustrated in Figure 4.
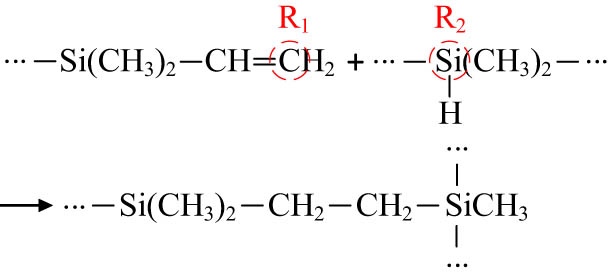
Reaction diagram.
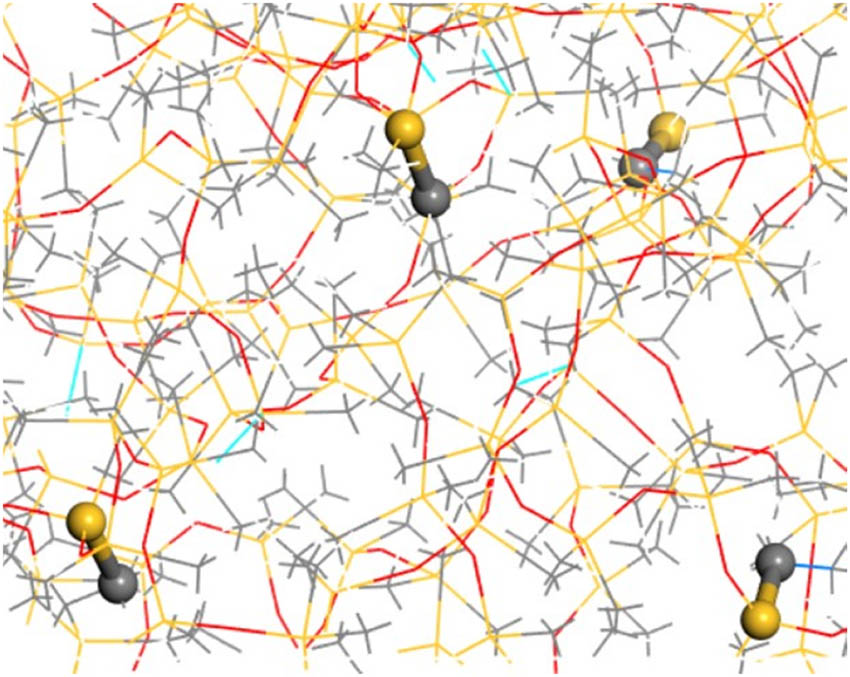
New bonds generated by crosslinking.
After the completion of crosslinking, to avoid excessively high internal stress in the system that could affect subsequent calculations, further structural optimization and dynamic relaxation of the model were performed. The following steps were executed sequentially: (1) geometry optimization for 10,000 steps, (2) five cycles of annealing in the NVT ensemble for a total duration of 100 ps, within a temperature range of 300–600 K, (3) selection of the frame with the lowest potential energy from the annealing cycles for subsequent operations, (4) NPT ensemble dynamics optimization at a temperature of 300 K for a duration of 100 ps, (5) NVT ensemble dynamics optimization at a temperature of 300 K for a duration of 200 ps, and (6) NPT ensemble dynamics optimization at a temperature of 300 K for a duration of 100 ps. The final crosslinked model for subsequent calculations is shown in Figure 5. Comparing Figures 4 and 5, it can be seen that the molecular chain distribution of the crosslinked and optimized model is more uniform.
Partial crosslinked models: (a) Intrinsic silicone rubber, (b) 10 phr h-BN, (c) 10 phr CNTs, and (d) 10 phr Al2O3.
3.2 Performance analysis of silicone rubber composite materials based on molecular simulation
3.2.1 Glass transition temperature (T g)
T g refers to the temperature at which an amorphous polymer material transitions from a glassy state to a highly elastic state. It represents the lowest temperature at which molecular segments can move and reflects the sensitivity to temperature changes.
Based on the characteristic of a significant density change of polymer materials before and after T g, a cooling experiment was conducted through molecular dynamics simulation to obtain the density–temperature curve of the silicone rubber composite material. Linear fitting was performed on the density data before and after the inflection point, and the temperature corresponding to the intersection of the two fitting curves represents the T g. To reduce the randomness in simulation calculations, three frames with the lowest energy output from the optimized models after a 100 ps simulation were selected for calculation, and the average value was taken. The simulation temperature range was from 100 to 400 K, and the results are shown in Figure 6. From Figure 6, it can be observed that the addition of h-BN and Al2O3 increases the density of the composite material, while the addition of CNTs lowers the density. This variation in density is dependent on the density of the fillers themselves. The addition of all three types of fillers leads to an increase in T g. With an increasing amount of filler addition, the T g of the composite material increases, indicating an increase in the rigidity of the molecular chains and a decrease in material elasticity. Therefore, adding excessive fillers to enhance the thermal conductivity of the material may result in the mechanical performance of the material collapsing, which is consistent with the conclusions obtained during material preparation. Furthermore, although the T g of the material increases with the addition of fillers, it remains below the actual operating temperature of transformers. This will not affect the practical application of the silicone rubber composite material. However, when transporting and using transformers in extremely cold environments, the impact of fillers on the T g of the material should be taken into consideration.
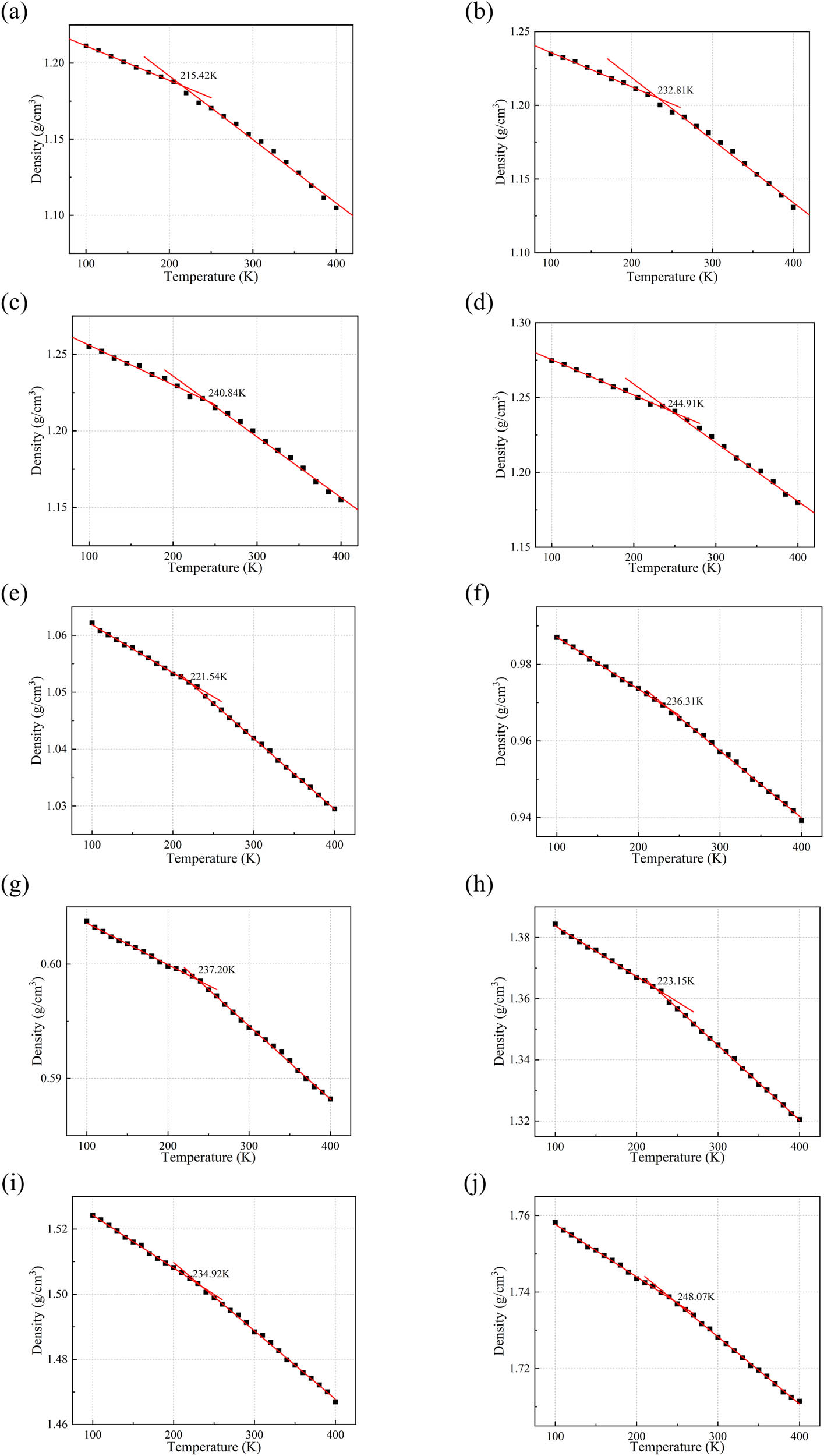
Density–temperature curve of the silicone rubber composite material: (a) intrinsic silicone rubber, (b) 10 phr h-BN, (c) 20 phr h-BN, (d) 30 phr h-BN, (e) 10 phr CNTs, (f) 20 phr CNTs, (g) 30 phr CNTs, (h) 10 phr Al2O3, (i) 20 phr Al2O3, (j) 30 phr Al2O3.
4 Binding energy
The binding energy reflects the work required to separate the components of a molecular system composed of two or more parts to “infinity” and overcome the mutual attraction between the components. It can be used to reflect the degree of tightness of the binding between the components. In molecular simulation, it can be calculated using Eq. 3, where E bind is the binding energy, E matrix is the total potential energy of the composite material model when the filler is removed and only the silicone rubber matrix remains, E filler is the total potential energy of the composite material model when the silicone rubber matrix is removed and only the filler remains, and E total is the total potential energy of the composite material model. The calculation results are shown in Table 4.
According to Table 4, the binding energy between Al2O3 and silicone rubber is much higher than the binding energy between h-BN and CNTs with silicone rubber. This is closely related to the geometric shapes of the fillers. The spherical shape of Al2O3 has a much larger contact area with the silicone rubber compared to the flake-like h-BN and the tubular CNTs. Furthermore, with an increasing amount of filler addition, the binding energy of the h-BN composite material shows an increasing trend, while the CNTs and the Al2O3 show a decreasing trend. This indicates that an excessive addition of CNTs and Al2O3 can lead to a decrease in the adhesion at the contact interface. Considering that the molecular simulation assumes the fillers to be uniformly dispersed, a decrease in binding energy makes it more likely for the fillers to aggregate. Therefore, excessive addition of CNTs and Al2O3 fillers can easily result in the collapse of the mechanical properties of the material.
5 MSD
Particles are in a state of motion in any system, and the MSD of particles is the square of the average displacement of particles per unit time, which can measure the movement ability of particles. In molecular simulation, for a system containing N atoms, the MSD is defined as Eq. 4, where R i (t) and R i (0) represent the displacement vectors of any atom i in the system at time t and the initial time. By obtaining the MSD values of composites with different filler contents through molecular simulation, the influence of fillers on the stability of composites can be obtained, and the effect of fillers on the thermal aging resistance of composites can be qualitatively analyzed.
Take the optimized model and perform dynamic optimization under the 30 ps NPT ensemble again, and perform MSD analysis to obtain the MSD curve of the composite material model. Figure 7 shows the MSD variation of the composite material with the type and content of fillers at a temperature of 300 K. From Figure 7, it can be observed that with an increase in the content of h-BN and Al2O3, the MSD of the composite material exhibits a significant decrease. This indicates a weakened mobility of the molecular chain segments within the model. The addition of highly stable h-BN and Al2O3 forms a physical barrier, limiting the rotation and sliding of silicone rubber molecular chain segments, reducing the degree of freedom of molecular chain movement, increasing the stability of the composite material, and will be beneficial for the resistance of composite material to thermal aging. On the other hand, an increase in CNT content reduces the stability of the composite material. This is because CNTs form new pathways for charge transfer within the composite material, thereby increasing the activity of the molecular chain segments.
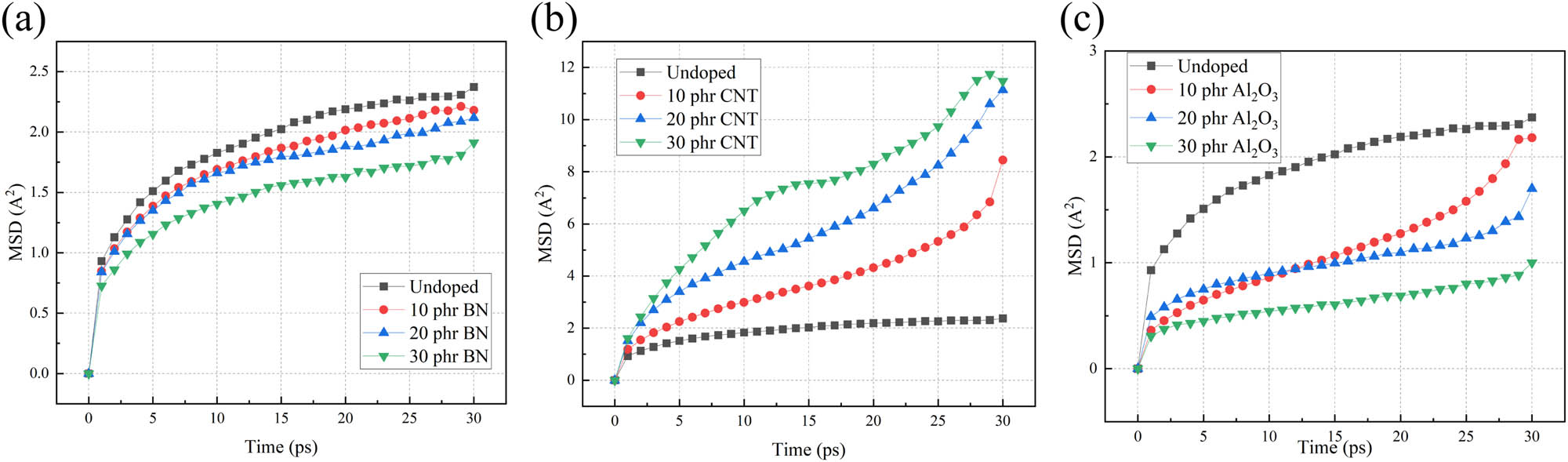
MSD variation with the fillers at 300 K, (a) h-BN, (b) CNTs, and (c) Al2O3.
6 Accelerated thermal aging test and analysis of silicone rubber composite materials
Due to the limitations of molecular simulation in simulating composite materials with low filler content and the inability to reflect the agglomeration phenomenon of fillers, it can only provide a qualitative analysis of the influence of a specific type of filler on the thermal aging performance of the composite material. To consider the intensified agglomeration effect resulting from an increased filler content, accelerated thermal aging tests need to be conducted on the silicone rubber composite material.
6.1 Selection of accelerated thermal aging samples for silicone rubber composite materials based on TGA
Activation energy is the intrinsic properties of materials, referring to the energy required for molecules to transition from a stable state to an active state where chemical reactions can easily occur. The magnitude of the activation energy can reflect the difficulty of a chemical reaction. In general, higher activation energy corresponds to a larger energy barrier that needs to be overcome, resulting in slower reaction rates. The thermal aging process of a material involves continuous physicochemical reactions occurring under the influence of heat and oxygen. Therefore, analyzing the effects of filler types and contents on the aging resistance of modified silicone rubber based on activation energy and conducting accelerated thermal aging tests on representative formulation samples is feasible.
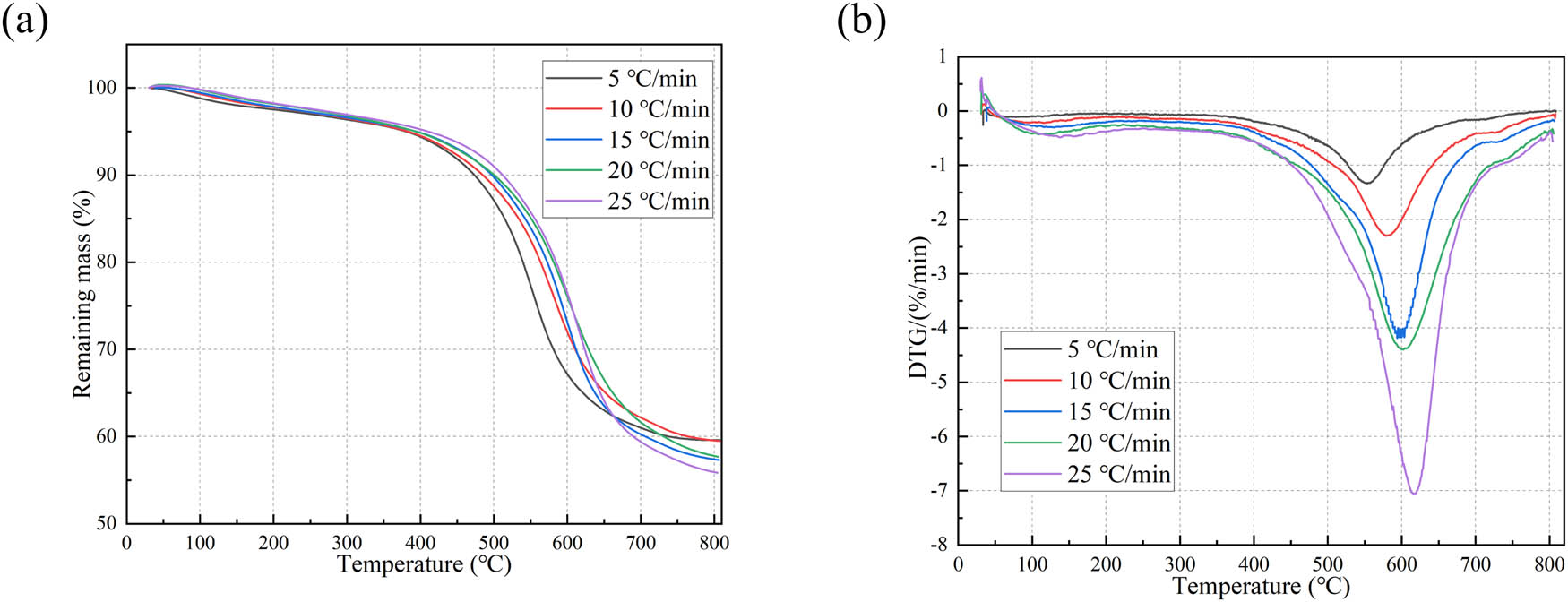
Activation energy is typically calculated through TGA. In TGA experiments, the sample is placed in a stable gas environment, and the ambient temperature is increased at a constant heating rate. As the temperature increases, the sample undergoes thermal decomposition and other reactions, resulting in changes in mass. The mass changes and their rates with respect to temperature form the thermogravimetric (TG) and derivative thermogravimetric (DTG) curves, respectively. By analyzing these curves, thermal decomposition characteristics such as activation energy can be determined. Taking the optimized formulation sample obtained from Table 3 as an example, TGA was conducted. The sample was placed under a nitrogen atmosphere, and the heating rates were set to 5, 10, 15, 20, and 25°C·min−1. The temperature range was set from 30 to 800℃. The obtained TG and DTG curves are shown in Figure 8. From Figure 9, it can be observed that the onset temperature of mass loss is consistent for different heating rates, and the peak values of the mass loss rates increase with higher heating rates. The peak values of the mass loss rates at different heating rates approximately lie in a straight line. The corresponding temperatures of the peak values at each heating rate are listed in Table 5 (convenient for subsequent calculations, values are given in units of K).

TG testing curve: (a) TG and (b) DTG.
Temperature at the peak of the mass loss rate
| Heating rate β (K·min−1) | Temperature T (K) |
|---|---|
| 5 | 553.659 |
| 10 | 578.703 |
| 15 | 593.950 |
| 20 | 602.470 |
| 25 | 616.021 |
The variation of the peak value of the mass loss rate with heating rate is directly related to the activation energy of the sample, as described by the Kissinger equation (Eq. 5). In the equation, β represents the heating rate of the sample during the test, T is the corresponding temperature at the peak of the mass loss rate, R is the molar gas constant with a value of 8.314 × 10−3 kJ·(mol·K)−1, A is the pre-exponential factor related to the nature of the reaction, and E a is the activation energy in units of kJ·mol−1. Therefore, by using 1/T as the independent variable and ln(β/T 2) as the dependent variable, a straight line can be fitted with an intercept b and a slope a. From the fitted line, the pre-exponential factor and activation energy can be determined using Eq. 6. By substituting the data from Table 6 into the equation, the activation energy of the optimized formulation sample is calculated as 67.95 kJ·mol−1, or 0.7046 eV, and the pre-exponential factor is 2.81.
Activation energy calculation results
| A (phr) | B (phr) | C (phr) | E a (kJ·mol−1) | E a (eV) | A |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0.6771 | 65.29 | 2.30 |
| 15 | 1 | 3 | 0.6787 | 65.45 | 2.38 |
| 15 | 1.5 | 2 | 0.6802 | 65.59 | 2.41 |
| 15 | 1.5 | 4 | 0.6869 | 66.24 | 2.37 |
| 15 | 2 | 3 | 0.6781 | 65.39 | 2.30 |
| 20 | 1 | 2 | 0.6852 | 66.08 | 2.62 |
| 20 | 1 | 4 | 0.6830 | 65.86 | 2.70 |
| 20 | 1.5 | 3 | 0.6928 | 66.81 | 2.80 |
| 20 | 2 | 2 | 0.6869 | 66.24 | 2.79 |
| 20 | 2 | 4 | 0.6915 | 66.68 | 2.87 |
| 25 | 1 | 3 | 0.6353 | 61.27 | 0.86 |
| 25 | 1.5 | 2 | 0.6115 | 58.97 | 0.72 |
| 25 | 1.5 | 4 | 0.5954 | 57.42 | 0.47 |
| 25 | 2 | 3 | 0.5971 | 57.58 | 0.59 |
Furthermore, the activation energy and pre-exponential factor of the intrinsic silicone rubber and the specified parameter combinations from Table 2 were calculated using the same method, as shown in Table 6. From Table 6, it can be observed that when the filler content is relatively low, the activation energy and pre-exponential factor of the composite material show little variation. The addition of h-BN and Al2O3 slightly increases the activation energy, which is consistent with the conclusions obtained from the previous molecular simulation. However, as the filler content continues to increase, the composite material experiences a significant decrease in activation energy, indicating a collapse in stability. The phenomenon was not reflected by molecular simulation, as the default fillers in molecular simulation are uniformly dispersed and well combined. However, with the increase of fillers, the agglomeration phenomenon of fillers intensifies, the compatibility between fillers and matrix interface decreases, leading to a decrease in interface energy and excessive air introduction during stirring.
Eq. 7 is the Arrhenius equation, where k represents the reaction rate and can be used to measure the speed of material aging. The pre-exponential factor A in the equation is theoretically temperature dependent, but its variation with temperature can be ignored compared to the exponential term. According to Eq. 7, as the pre-exponential factor decreases, the reaction rate decreases, and as the activation energy decreases, the reaction rate increases. Analyzing combining the data in Table 6, the influence of activation energy on the reaction rate is dominant in the index term of Eq. 7. Therefore, selecting the intrinsic silicone rubber sample as sample 1, the optimized formula sample with the highest activation energy as sample 2, and the 25 phr h-BN, 2 phr CNTs, and 3 phr Al2O3 samples with the lowest activation energy as sample 3 for accelerated thermal aging testing.
6.2 Design of thermal aging test
The accelerated thermal aging tests were conducted according to the reference standard GB/T 11026.1-2016. The aging temperature was set at a constant 200°C, and the test duration was 48 h. Material thermal aging performance tests were conducted at 14 time points: 48, 96, 144, 192, 240, 288, 336, 384, 432, 480, 528, 576, 624, and 672 h. After reaching each testing time point and waiting for the temperature of the tested material to drop to room temperature, immediately measure its mass and other parameters. The temperature control during the experiment was achieved using a 101-00A electric constant temperature drying oven, as shown in Figure 8. The specific parameters of the oven are provided in Table 7, which meet the requirements of the standard, with short-term temperature fluctuations not exceeding 3°C and a maximum allowable temperature fluctuation of 6°C.
Constant temperature drying oven.
Parameters of the oven
| Index | Parameter |
|---|---|
| Voltage | 220 V |
| Power | 800 W |
| Maximum operating temperature | 300°C |
| Temperature resolution | 1°C |
| Temperature fluctuations | ±2°C |
| Volume | 350 mm × 350 mm × 350 mm |
The constant temperature drying oven achieves temperature uniformity through forced air circulation with upper and lower airflow. It has multiple layers of internal shelves for sample placement. In order to reduce the uneven surface temperature caused by direct blowing of hot air on the samples, the samples were placed on the middle shelf and additional shelves were placed above and below, while keeping the forced air circulation continuously running. The breakdown and tensile tests in the aging performance testing were destructive tests. The sample configurations are shown in Figure 10. The sample dimensions were selected according to relevant standards such as GB/T 2941-2006. Dumbbell-shaped samples were used for tensile performance testing, small circular samples were used for thermal conductivity testing, and large circular samples were used for mass, volume resistivity, and breakdown strength testing.

Test samples.
6.3 Analysis of thermal aging test results
6.3.1 Mass loss
Figure 11 shows a visual comparison of the appearance of the silicone rubber samples before and after the aging test. There is little change in the shape of the silicone rubber samples before and after aging. The mass of each sample was measured at each time point, and the relative mass loss rate was calculated using Eq. 8. In the equation, i represents the aging time point, i = 1, 2, …, 14; η i represents the mass loss rate of the sample at the i-th aging time point; m 0 is the initial mass of the sample before aging, and m i is the mass of the sample at the i-th aging time point. The variation of the mass loss rate of the samples at each aging time point is shown in Figure 12.

Comparison before and after aging.
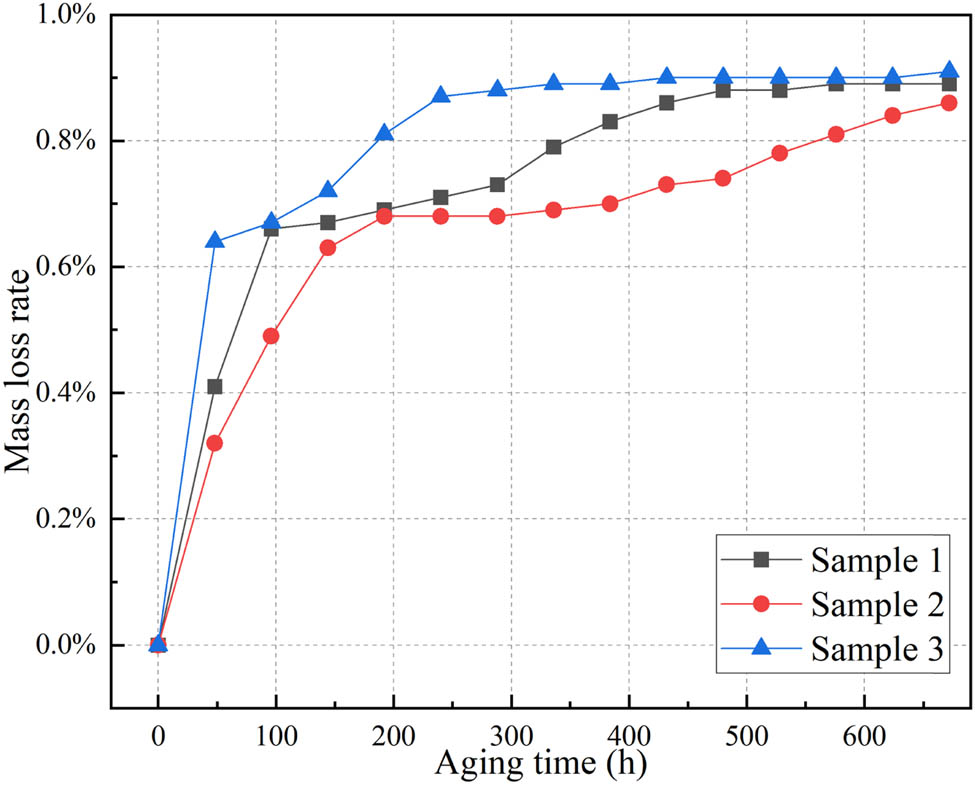
Mass loss rate during aging process.
From Figure 12, the mass loss rate of the samples initially increases rapidly and then slows down. After reaching a mass loss rate of 0.7%, the rate of increase becomes slower. This is because, at the early stage of thermal aging, the silicone rubber undergoes further cross-linking. After the mass loss rate reaches 0.85%, the rate of increase slows down further and gradually approaches stability. The mass loss rate, from fast to slow, inversely correlated with the activation energy, is sample 3, sample 1, and sample 2, respectively. Additionally, the final mass loss rate of sample 2 is 0.86%, which is significantly lower than the insulation life end-point indicators of 3% or 5% for conventional insulation materials. Therefore, from the perspective of mass loss performance, it can be concluded that silicone rubber exhibits good heat resistance and chemical stability, and the optimized formula sample shows a performance improvement compared to the intrinsic silicone rubber.
7 Thermal properties
The variation of thermal conductivity with aging time is shown in Figure 13. As observed from Figure 13, the thermal conductivity of the silicone rubber exhibits an overall stable trend with increasing aging time. During the initial stages of aging, there is a short-term increase in thermal conductivity. This can be attributed to the further cross-linking of initially insufficiently cross-linked silicone rubber chains during the vulcanization process, resulting in a denser silicone rubber structure and improved efficiency of intermolecular heat transfer. As the aging process progresses, silicone rubber undergoes decomposition or oxidation reactions in high-temperature environments. The molecular chains experience breakage or damage, leading to a loosening of the silicone rubber structure and a decrease in intermolecular heat transfer efficiency, resulting in a reduction in thermal conductivity. From the trend of thermal conductivity variation, it can be observed that the thermal conductivity of silicone rubber exhibits a relatively small change. Taking sample 2 as an example, the thermal conductivity decreases and stabilizes at 0.50 W·m−1·K, which is still at a relatively high level and far exceeds the application requirement of 0.35 W·m−1·K. Furthermore, referring to relevant simulation studies, it is known that when the thermal conductivity of an insulating material is at a high level around 0.50 W·m−1·K, a thermal conductivity variation of 0.01 W·m−1·K has minimal impact on the temperature distribution of transformers. Therefore, it can be concluded that the thermal aging process of silicone rubber insulation has a minor influence on the thermal conductivity. The aging process of sample 2 will not affect the temperature distribution of transformers.
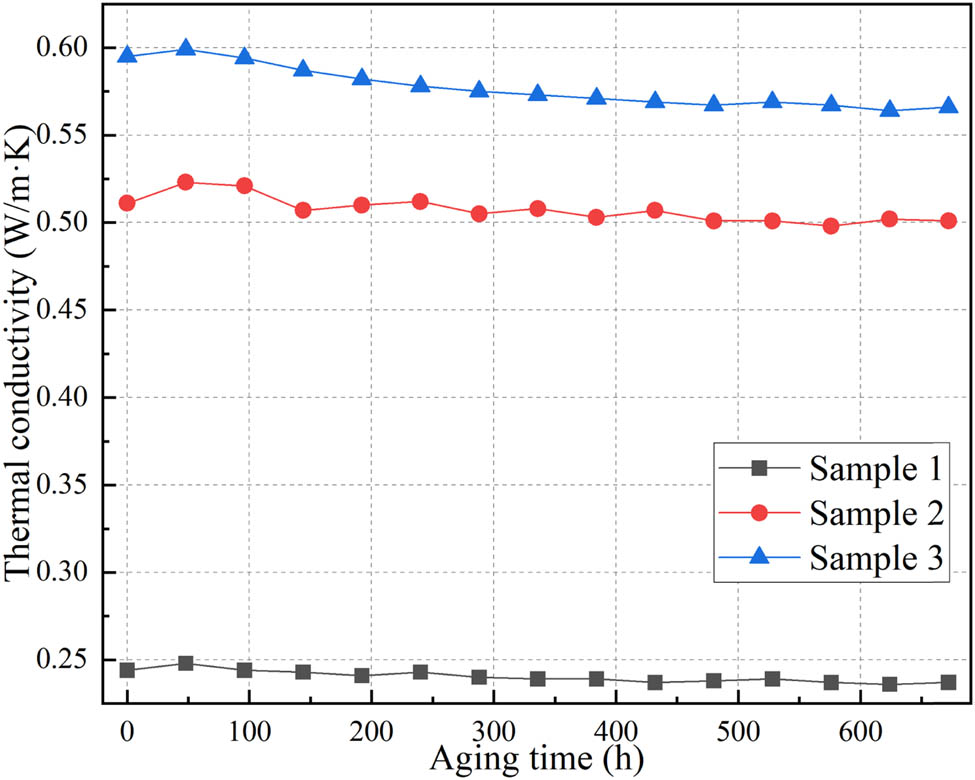
Thermal conductivity during aging process.
8 Electrical performance
The variation of breakdown field strength and volume resistivity with aging time for the samples is shown in Figure 14. The insulation performance of silicone rubber tends to decrease after thermal aging. This is mainly attributed to the breakage or damage of molecular chains within the silicone rubber, leading to the formation of localized defects. Taking sample 2 as an example, the volume resistivity decreases from 4.11 × 1015 Ω·cm before aging to 8.17 × 1014 Ω·cm, which is still significantly higher than the required insulation level of 1 × 1010 Ω·cm.
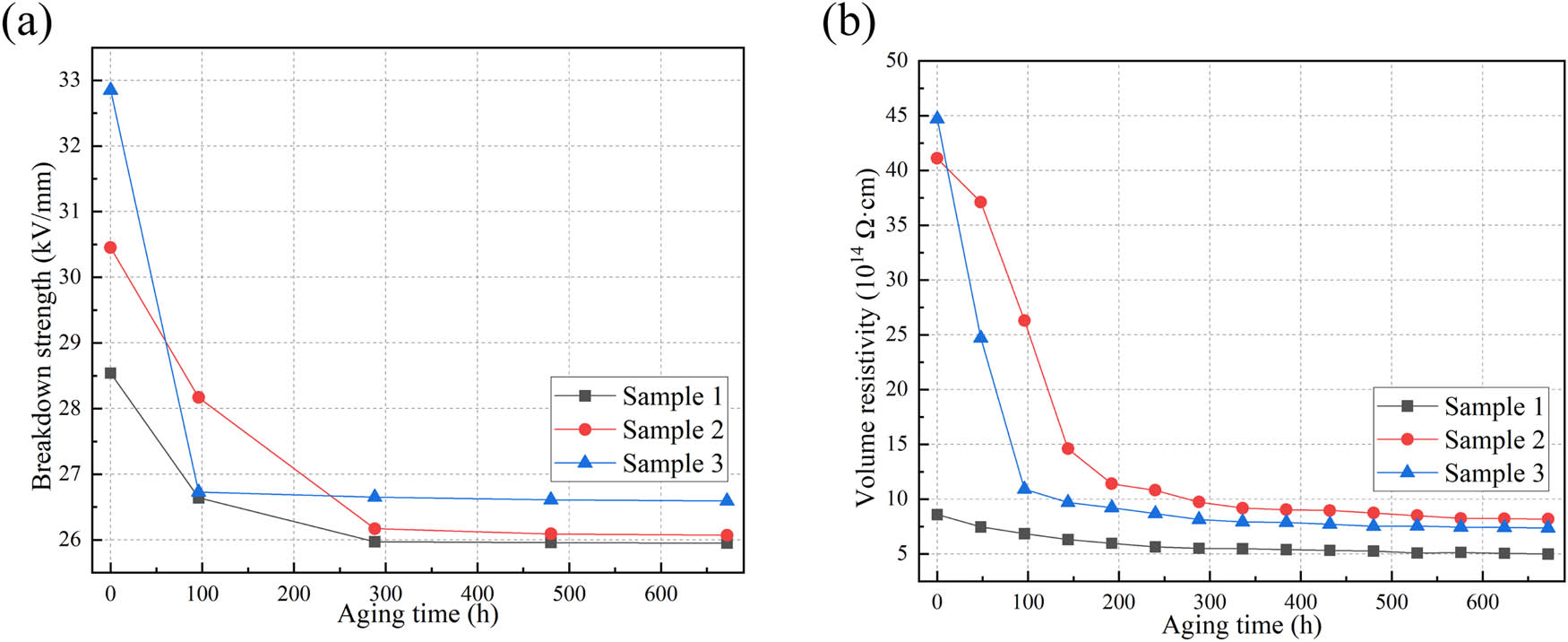
Electrical performance, (a) breakdown field strength, (b) volume resistivity.
9 Mechanical property
The variation of tensile strength with aging time for the samples is depicted in Figure 15. The overall change in tensile strength of the silicone rubber due to thermal aging is relatively small. During the initial stages of aging, there is a slight increase in tensile strength, which can be attributed to further cross-linking of initially insufficiently cross-linked silicone rubber chains during the vulcanization process. This results in a harder material and enhances the ability of the molecular chains to resist external forces.
Tensile strength.
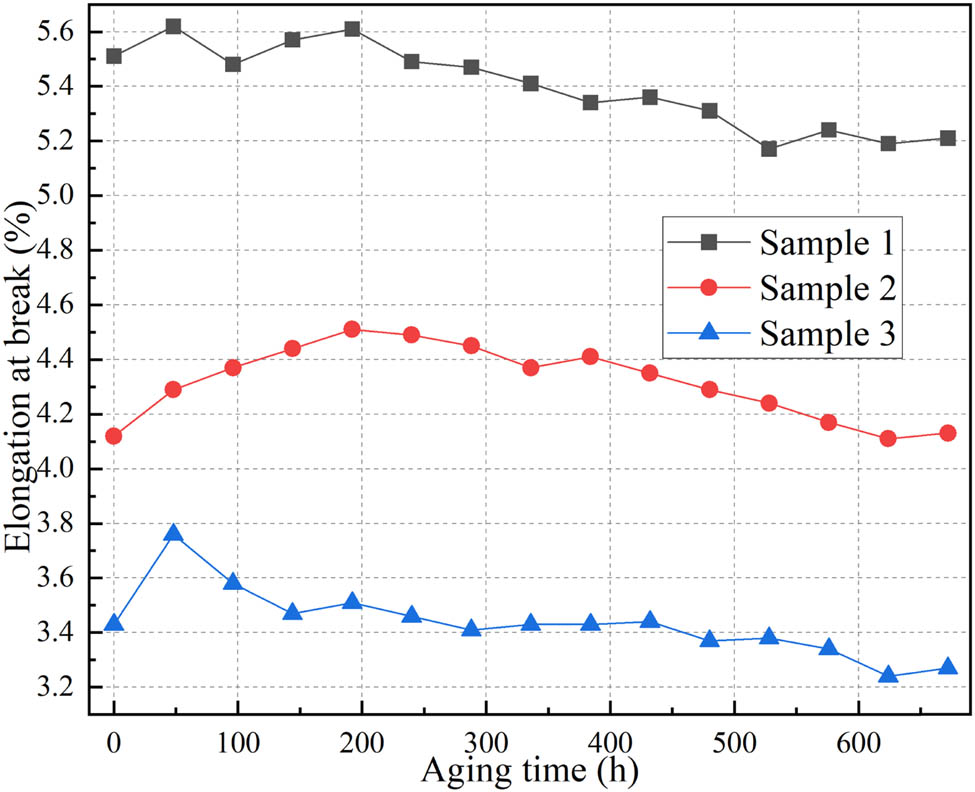
The variation of elongation at break with aging time for the samples is shown in Figure 16. The elongation at break of the silicone rubber exhibits an overall decreasing trend with thermal aging, with the rate of decrease gradually slowing down. This can be attributed to various factors. Initially, decomposition or oxidation reactions cause molecular chain scission and fracture, leading to a reduction in the length of silicone rubber chains and a decrease in its resistance to deformation. Additionally, further excessive cross-linking of the silicone rubber at high temperatures reduces its flexibility and makes the material harder. Furthermore, as the thermal aging process progresses, the free rotation of methyl groups on the silicon atoms becomes restricted. This reduces the intermolecular chain spacing and increases the intermolecular forces. Consequently, when subjected to external tensile forces, the resistance to molecular motion increases, resulting in a decrease in elongation at break. Comparing the rates of decrease in elongation at break, it can be observed that samples 1 and 3, which have lower activation energies, exhibit noticeably faster aging rates compared to sample 2, which has a higher activation energy.
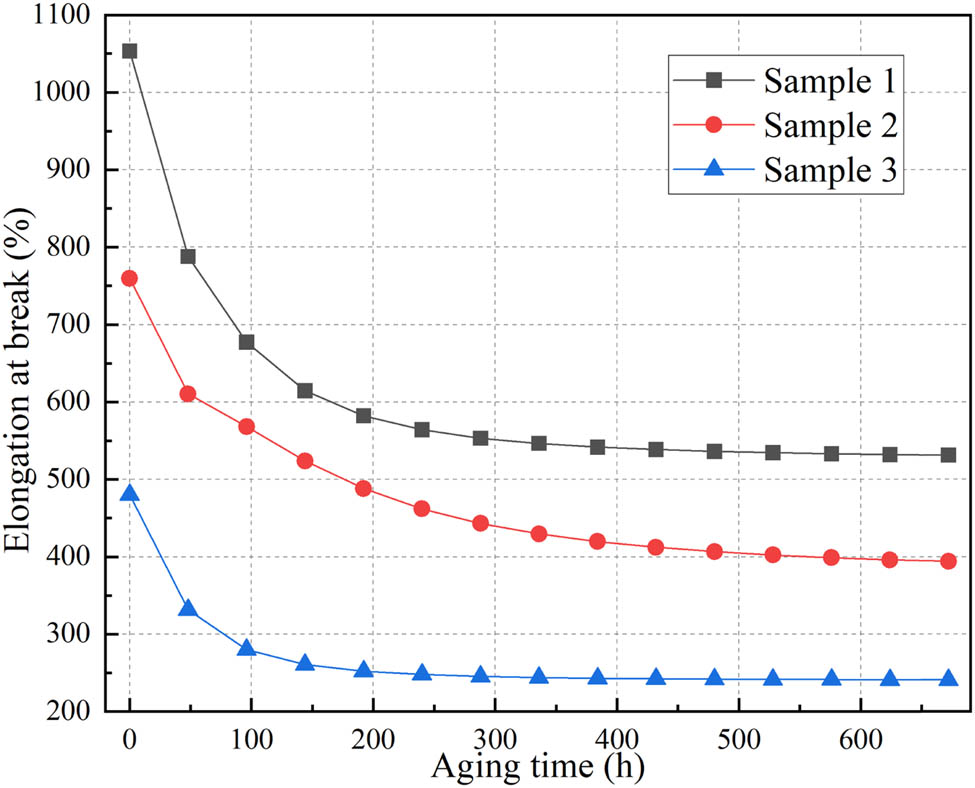
Elongation at break.
9.1 Thermal life analysis of silicone rubber composite materials
According to the standard GB/T 11026.2-2012, for elastomeric materials such as natural or synthetic vulcanized rubber, as well as silicone rubber, the recommended end-point indicators for insulation material lifetime are defined as follows: a 50% decrease in tensile stress at 100% elongation, a 50% decrease in elongation at break, or a 50% decrease in breakdown voltage compared to the initial performance. Considering the various changes in properties during thermal aging of silicone rubber, it is observed that the variation in mechanical property, specifically elongation at break, is greater than the changes in thermal and electrical properties. Therefore, disregarding the fact that the tensile strength of sample 3 does not meet the requirements for transformer applications before aging, a 50% decrease in elongation at break from the initial value is selected as the thermal end-point indicator for conducting thermal aging analysis of silicone rubber composite materials.
Since the samples did not reach the end-point of their lifetime during the thermal aging experiment, the curves in Figure 17 were fitted and extrapolated to obtain the relationship between elongation at break and aging time for the samples, as shown in Eqs. 9–11. In these equations, y 1, y 2, and y 3 represent the elongation at break for samples 1, 2, and 3, respectively, while x represents the aging time.
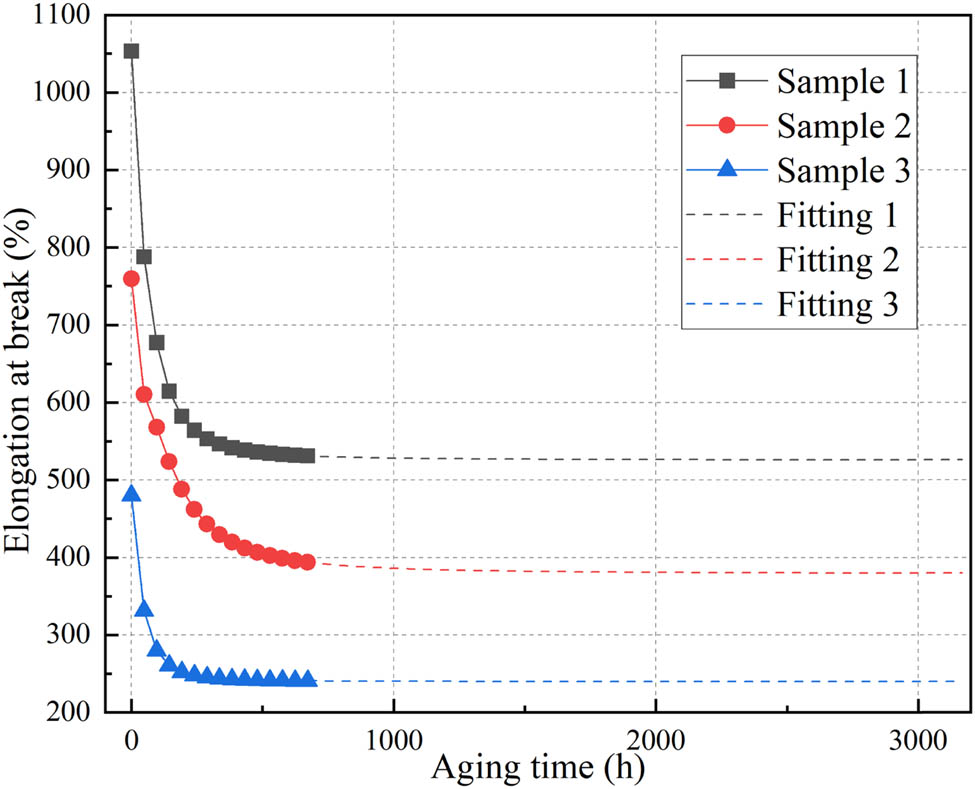
Fitting curve of elongation at break.
From the perspective of reaction rates, according to Eq. 7, the reaction rates of samples 1, 2, and 3 at 200°C can be calculated as 1.42 × 10−4, 8.87 × 10−5, and 2.57 × 10−4, respectively. These reaction rates exhibit an approximate inverse relationship with the thermal lifetime of the samples. The discrepancy is due to the occurrence of cross-linking reactions in silicone rubber during the thermal aging process. The reaction rate constants for cross-linking reactions do not align with the oxidative degradation reactions that take place during thermal aging. Additionally, the composition of silicone rubber composite materials can also influence the details of the reactions.
Taking into account that the working temperature range of silicone rubber insulation materials in transformer applications is typically from 0°C to 200°C, which is a relatively narrow temperature range, it can be assumed that the nature of the thermal aging reaction does not undergo significant changes. Therefore, the pre-exponential factor and activation energy can be considered as constants. This allows for the variation of the Arrhenius equation in Eq. 7 to perform thermal lifetime conversion for the material at different temperatures, as shown in Eq. 12. In this equation, T 1 and T 2 represent different aging temperatures (in K), while L 1 and L 2 correspond to the thermal lifetimes at the respective aging temperatures.
Considering the specifications for transformer operation, it is generally required that the maximum long-term loading rate of a transformer does not exceed 85%. Assuming a stable hot spot temperature of 105°C for a dry-type transformer operating at 85% loading rate, the thermal lifetimes of samples 1, 2, and 3 in the actual operating environment of a transformer can be calculated. The calculated lifetimes are 12.37, 27.40, and 4.70 years, respectively. Sample 2, which consists of silicone rubber composite material with the addition of 21.42 phr h-BN, 1.58 phr CNTs, and 2.67 phr Al2O3, can meet the requirement of a service life of over 20 years specified in GB/T 17468-2019 for distribution transformers.
10 Conclusions
D-DTs operate in high-temperature environments over an extended period, and their insulation materials need to consider not only basic thermal, electrical, and mechanical properties but also long-term stability under high-temperature operating conditions. This study analyzes the long-term stability of silicone rubber composite insulation materials and the insulation thermal lifetime in D-DT applications using molecular simulations, TGA, and accelerated thermal aging. The findings are summarized as follows:
The optimized formulation of silicone rubber composite material (21.42 phr h-BN, 1.58 phr CNTs, and 2.67 phr Al2O3) obtained through response surface model meets the requirements of D-DTs. The model-calculated thermal conductivity and tensile strength have errors of only 1.4% and 3%, respectively, compared to experimental measurements.
The addition of fillers increases the T g of the silicone rubber composite material. The influence of fillers on T g should be considered when transporting and using transformers in extremely cold environments. The addition of a small amount of h-BN and Al2O3 restricts the rotation and sliding of rubber molecular chains, reduces the activation energy of the composite material, and improves its thermal stability.
The mass and thermal conductivity of silicone rubber composite materials do not change much during the thermal aging process, and the insulation performance slightly decreases but still exceeds the insulation application requirements. The degradation of elongation at break is the key indicator for the end of thermal lifetime of silicone rubber.
The thermal aging rate of silicone rubber composite materials is inversely related to the activation energy. The silicone rubber composite material with the optimized formulation is expected to have a predicted lifetime of 3,128 h under accelerated thermal aging at 200°C, and 27.40 years under stable operating conditions of D-DTs, which meets the standard requirements and can be used as actual D-DTs insulation materials.
-
Funding information: This project was supported by Natural Science Foundation of Sichuan Province (Grant no. 2024NSFSC0020, 2023NSFSC0828).
-
Author contributions: Woyang Li: writing – original draft, conceptualization, formal analysis; Lijun Zhou: writing – review and editing; Yunyun Qian: methodology, resources, data curation; Qian Lei: methodology, resources, data curation; Yingyi Xia: methodology, resources, data curation; Dongyang Wang: validation, writing – review and editing.
-
Conflict of interest: Authors state no conflict of interest.
-
Data availability statement: The data presented in this study are available on request from the corresponding author.
References
(1) Li W, Zhou L, Chen J, Liu B, Gao S, Zhang C, et al. Numerical model for eddy-current loss of wound core in single-phase transformer. IEEE Trans Transp Electr. 2024;10(1):150–62.10.1109/TTE.2023.3264290Search in Google Scholar
(2) Zhou L, Li W, Xia Y, Chen J, Zhang C, Cai X, et al. Electromagnetic anisotropic homogeneous model for eddy-current field in single-phase wound core. High Voltage. 2024;9(1):172–81.10.1049/hve2.12387Search in Google Scholar
(3) Lin Z, Yang S, Zhang Y, Hao Z, Zhang B. A data-aided power transformer differential protection without inrush blocking module. IEEE Trans Power Deliv. 2023;38(3):2000–10.10.1109/TPWRD.2022.3230468Search in Google Scholar
(4) Awadallah SK, Milanović JV, Jarman PN. The influence of modeling transformer age related failures on system reliability. IEEE Trans Power Syst. 2014;30(2):970–9.10.1109/TPWRS.2014.2331103Search in Google Scholar
(5) Cremasco A, Wu W, Blaszczyk A, Cranganu-Cretu B. Network modelling on dry-type transformer cooling systems. COMPEL-Int J Comput Maths Electr Electron Eng. 2018;37(3):1039–53.10.1108/COMPEL-12-2016-0534Search in Google Scholar
(6) Wen M, Song J, Song Y, Liu Y, Li C, Wang P. Reliability assessment of insulation system for dry type transformers. IEEE Trans Dielectr Electr Insul. 2013;20(6):1998–2008.10.1109/TDEI.2013.6678847Search in Google Scholar
(7) Yuan S, Zhou L, Chen T, Wang D, Wang L. Thermally conductive h-BN/EHTPB/epoxy composites with enhanced toughness for on-board traction transformers. E-Polymers. 2022;22(1):821–33.10.1515/epoly-2022-0076Search in Google Scholar
(8) Yuan S, Zhou L, Cai F, Wang D, Wang L, Huang L. A lightweight optimization study for large capacity Dry-type on-board traction transformer of EMU based on CFD and RSM. IEEE Trans Transp Electrif. 2023;9(2):2941–54.10.1109/TTE.2022.3224503Search in Google Scholar
(9) Guo L, Xu H, Wu N, Yuan S, Zhou L, Wang D, et al. Molecular dynamics simulation of the effect of the thermal and mechanical properties of addition liquid silicone rubber modified by carbon nanotubes with different radii. E-Polymers. 2023;23(1):20228105.10.1515/epoly-2022-8105Search in Google Scholar
(10) Li G, Wang Z, Lan R, Wei Y, Nie Y, Li S, et al. The lifetime prediction and insulation failure mechanism of XLPE for high-voltage cable. IEEE Trans Dielectr Electr Insul. 2023;30(2):761–8.10.1109/TDEI.2022.3215605Search in Google Scholar
(11) Kone D, Ghunem RA, Cisse L, Hadjadj Y, El-Hag AH. Effect of residue formed during the AC and DC dry-band arcing on silicone rubber filled with natural silica. IEEE Trans Dielectr Electr Insul. 2019;26(5):1620–6.10.1109/TDEI.2019.008203Search in Google Scholar
(12) Nazir MT, Khalid A, Kabir I, Wang C, Baena JC, Akram S, et al. Flame retardancy and excellent electrical insulation performance of RTV silicone rubber. Polymers. 2021;13(17):2854.10.3390/polym13172854Search in Google Scholar PubMed PubMed Central
(13) Hamdan MA, Pilgrim JA, Lewin PL. Thermo-mechanical analysis of solid interfaces in HVAC cable joints. IEEE Trans Dielectr Electr Insul. 2019;26(6):1779–87.10.1109/TDEI.2019.008152Search in Google Scholar
(14) Guo L, Ding S, Yuan S, Gou X, Cai F, Wang D, et al. Study on the thermal properties and insulation resistance of epoxy resin modified by hexagonal boron nitride. E-Polymers. 2021;21(1):681–90.10.1515/epoly-2021-0069Search in Google Scholar
(15) Tian K, Yang S, Niu J, Wang H. Enhanced thermal conductivity and mechanical toughness of the epoxy resin by incorporation of mesogens without nanofillers. IEEE Access. 2021;9:31575–80.10.1109/ACCESS.2021.3058612Search in Google Scholar
(16) Li J, Zhao X, Ji X, Lu Y, Zhang L. Graphene/Alumina micro-nano hybrid network and thermal conductive and electrical insulating silicone rubber composites. Insul Mater. 2021;52(02):49–55.Search in Google Scholar
(17) Zhou W, Yang Z, Feng Y, Lin L. Insights into the thermophysical properties and heat conduction enhancement of NaCl-Al2O3 composite phase change material by molecular dynamics simulation. Int J Heat Mass Transf. 2022;198:123422.10.1016/j.ijheatmasstransfer.2022.123422Search in Google Scholar
(18) Dang Z, Xia Y, Zha J, Yuan J, Bai J. Preparation and dielectric properties of surface modified TiO2/silicone rubber nanocomposites. Mater Lett. 2011;65(23–24):3430–2.10.1016/j.matlet.2011.07.056Search in Google Scholar
(19) Zou Z, Wu W, Wang Y, Wang L. Enhancement of thermal conductivity and tensile strength of liquid silicone rubber by three-dimensional alumina network. Soft Mater. 2019;17(3):297–307.10.1080/1539445X.2019.1601110Search in Google Scholar
(20) Du B, Xu H. Effects of thermal conductivity on dc resistance to erosion of silicone rubber/BN nanocomposites. IEEE Trans Dielectr Electr Insul. 2014;21(2):511–8.10.1109/TDEI.2013.004139Search in Google Scholar
(21) Ou Z, Gao F, Zhao H, Dang S, Zhu L. Research on the thermal conductivity and dielectric properties of AlN and BN co-filled addition-cure liquid silicone rubber composites. RSC Adv. 2019;9(49):28851–6.10.1039/C9RA04771ASearch in Google Scholar PubMed PubMed Central
(22) Ding C, Liu L, Feng L. Effect of doped nano-SiO2, Al2O3, and polyhedral oligomeric sesquisiloxane on the thermodynamic properties of cellulose. AIP Adv. 2023;13:015104.10.1063/5.0132902Search in Google Scholar
(23) Tang X, Guo Y, Liao Z, Fan J, Zhang K, Yang Z, et al. Synergistic enhancement of thermal conductivity between SiCw and h-BN in MVQ-based composite. Fuller Nanotubes Carbon Nanostruct. 2019;27(5):434–9.10.1080/1536383X.2019.1580696Search in Google Scholar
(24) Kuo C, Chen P, Chen J. Preparation of boron nitride nanosheets using a chemical exfoliation method as a thermal conductive filler for the development of silicone thermal pads: Part II: Optimization of process parameter design on the development of a silicone thermal pad. Text Res J. 2020;90(17–18):1891–905.10.1177/0040517519900385Search in Google Scholar
(25) Wang W, He D, Yang K, Liu S, Song S, Yi D. Research of the thermal aging mechanism of polycarbonate and polyester film. E-Polymers. 2017;17(1):45–56.10.1515/epoly-2016-0179Search in Google Scholar
(26) Wu L, Zhang Y. Enhanced thermal oxidative stability of silicone rubber by using cerium-ferric complex oxide as thermal oxidative stabilizer. E-Polymers. 2019;19(1):257–67.10.1515/epoly-2019-0026Search in Google Scholar
(27) Tang C, Zhang S, Li X, Xiong B, Xie J. Experimental analyses and molecular simulation of the thermal aging of transformer insulation paper. IEEE Trans Dielectr Electr Insul. 2015;22(6):3608–16.10.1109/TDEI.2015.005003Search in Google Scholar
(28) Paul M, Mishra P, Vangapandu DN, Mondal M, Paramane A, Nazir MT. Thermal aging characteristics of silicone rubber exposed to mineral oil. IEEE Trans Dielectr Electr Insul. 2023;30(6):2828–37.10.1109/TDEI.2023.3282915Search in Google Scholar
(29) Li S, Ke Y, Xie L, Zhao Z, Huang X, Wang Y, et al. Study on the aging of three typical rubber materials under highand low-temperature cyclic environment. E-Polymers. 2022;23(1):20228089.10.1515/epoly-2022-8089Search in Google Scholar
(30) Zhou MZ, Wang HR, Guo X, Wei YC, Liao S. Synergistic effect of thermal oxygen and UV aging on natural rubber. E-Polymers. 2023;23(1):20230016.10.1515/epoly-2023-0016Search in Google Scholar
(31) Yan Z, Liang X, Gao Y, Liu Y. Aging and self-healing properties of superhydrophobic silicone rubber. IEEE Trans Dielectr Electr Insul. 2016;23(6):3531–8.10.1109/TDEI.2016.005962Search in Google Scholar
(32) Shang R, Fan H, Wang L, Yin F, Farzaneh M Analysis of high-temperature wideband dielectric properties of ATH-filled silicone rubber used for on-site insulation of bare overhead conductors. IEEE Trans Dielectr Electr Insul. 2022; 29(6): 2171–80.10.1109/TDEI.2022.3209633Search in Google Scholar
© 2025 the author(s), published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Research Articles
- Flow-induced fiber orientation in gas-powered projectile-assisted injection molded parts
- Research on thermal aging characteristics of silicone rubber composite materials for dry-type distribution transformers
- Kinetics of acryloyloxyethyl trimethyl ammonium chloride polymerization in aqueous solutions
- Influence of siloxane content on the material performance and functional properties of polydimethylsiloxane copolymers containing naphthalene moieties
- Enhancement effect of electron beam irradiation on acrylonitrile–butadiene–styrene (ABS) copolymers from waste electrical and electronic equipment by adding 1,3-PBO: A potential way for waste ABS reuse
- Model construction and property study of poly(ether-ether-ketone) by molecular dynamics simulation with meta-modeling methods
- Zinc–gallic acid–polylysine nanocomplexes with enhanced bactericidal activity for the treatment of bacterial keratitis
- Effect of pyrogallol compounds dosage on mechanical properties of epoxy coating
- Preparation of in situ polymerized polypyrrole-modified braided cord and its electrical conductivity investigation under varied mechanical conditions
- Hydrophobicity, UV resistance, and antioxidant properties of carnauba wax-reinforced CG bio-polymer film
- Janus nanofiber membrane films loading with bioactive calcium silicate for the promotion of burn wound healing
- Synthesis of migration-resistant antioxidant and its application in natural rubber composites
- Influence of the flow rate on the die swell for polymer micro coextrusion process
- Fatty acid filled polyaniline nanofibres with dual electrical conductivity and thermo-regulatory characteristics: Futuristic material for thermal energy storage
- Hydrolytic depolymerization of major fibrous wastes
- Performance of epoxy hexagonal boron nitrate underfill materials: Single and mixed systems
- Blend electrospinning of citronella or thyme oil-loaded polyurethane nanofibers and evaluating their release behaviors
- Efficiency of flexible shielding materials against gamma rays: Silicon rubber with different sizes of Bi2O3 and SnO
- A comprehensive approach for the production of carbon fibre-reinforced polylactic acid filaments with enhanced wear and mechanical behaviour
- Electret melt-blown nonwovens with charge stability for high-performance PM0.3 purification under extreme environmental conditions
- Study on the failure mechanism of suture CFRP T-joints under/after the low-velocity impact loading
- Experimental testing and finite element analysis of polyurethane adhesive joints under Mode I loading and degradation conditions
- Optimizing recycled PET 3D printing using Taguchi method for improved mechanical properties and dimensional precision
- Effect of stacking sequence of the hybrid composite armor on ballistic performance and damage mechanism
- Bending crack propagation and delamination damage behavior of orthogonal ply laminates under positive and negative loads
- Molecular dynamics simulation of thermodynamic properties of Al2O3-modified silicone rubber under silane coupling agent modification
- Precision injection molding method based on V/P switchover point optimization and pressure field balancing
- Heparin and zwitterion functionalized small-diameter vascular grafts for thrombogenesis prevention
- Metal-free N, S-co-doped carbon materials derived from calcined aromatic co-poly(urea-thiourea)s as efficient alkaline oxygen reduction catalysts
- Influence of stitching parameters on the tensile performance and failure mechanisms of CFRP T-joints
- Synthesis of PEGylated polypeptides bearing thioether pendants for injectable ROS-responsive hydrogels
- Rapid Communication
- RAFT-mediated polymerization-induced self-assembly of poly(ionic liquid) block copolymers in a green solvent
- Corrigendum
- Corrigendum to “High-strength polyvinyl alcohol-based hydrogel by vermiculite and lignocellulosic nanofibrils for electronic sensing”
Articles in the same Issue
- Research Articles
- Flow-induced fiber orientation in gas-powered projectile-assisted injection molded parts
- Research on thermal aging characteristics of silicone rubber composite materials for dry-type distribution transformers
- Kinetics of acryloyloxyethyl trimethyl ammonium chloride polymerization in aqueous solutions
- Influence of siloxane content on the material performance and functional properties of polydimethylsiloxane copolymers containing naphthalene moieties
- Enhancement effect of electron beam irradiation on acrylonitrile–butadiene–styrene (ABS) copolymers from waste electrical and electronic equipment by adding 1,3-PBO: A potential way for waste ABS reuse
- Model construction and property study of poly(ether-ether-ketone) by molecular dynamics simulation with meta-modeling methods
- Zinc–gallic acid–polylysine nanocomplexes with enhanced bactericidal activity for the treatment of bacterial keratitis
- Effect of pyrogallol compounds dosage on mechanical properties of epoxy coating
- Preparation of in situ polymerized polypyrrole-modified braided cord and its electrical conductivity investigation under varied mechanical conditions
- Hydrophobicity, UV resistance, and antioxidant properties of carnauba wax-reinforced CG bio-polymer film
- Janus nanofiber membrane films loading with bioactive calcium silicate for the promotion of burn wound healing
- Synthesis of migration-resistant antioxidant and its application in natural rubber composites
- Influence of the flow rate on the die swell for polymer micro coextrusion process
- Fatty acid filled polyaniline nanofibres with dual electrical conductivity and thermo-regulatory characteristics: Futuristic material for thermal energy storage
- Hydrolytic depolymerization of major fibrous wastes
- Performance of epoxy hexagonal boron nitrate underfill materials: Single and mixed systems
- Blend electrospinning of citronella or thyme oil-loaded polyurethane nanofibers and evaluating their release behaviors
- Efficiency of flexible shielding materials against gamma rays: Silicon rubber with different sizes of Bi2O3 and SnO
- A comprehensive approach for the production of carbon fibre-reinforced polylactic acid filaments with enhanced wear and mechanical behaviour
- Electret melt-blown nonwovens with charge stability for high-performance PM0.3 purification under extreme environmental conditions
- Study on the failure mechanism of suture CFRP T-joints under/after the low-velocity impact loading
- Experimental testing and finite element analysis of polyurethane adhesive joints under Mode I loading and degradation conditions
- Optimizing recycled PET 3D printing using Taguchi method for improved mechanical properties and dimensional precision
- Effect of stacking sequence of the hybrid composite armor on ballistic performance and damage mechanism
- Bending crack propagation and delamination damage behavior of orthogonal ply laminates under positive and negative loads
- Molecular dynamics simulation of thermodynamic properties of Al2O3-modified silicone rubber under silane coupling agent modification
- Precision injection molding method based on V/P switchover point optimization and pressure field balancing
- Heparin and zwitterion functionalized small-diameter vascular grafts for thrombogenesis prevention
- Metal-free N, S-co-doped carbon materials derived from calcined aromatic co-poly(urea-thiourea)s as efficient alkaline oxygen reduction catalysts
- Influence of stitching parameters on the tensile performance and failure mechanisms of CFRP T-joints
- Synthesis of PEGylated polypeptides bearing thioether pendants for injectable ROS-responsive hydrogels
- Rapid Communication
- RAFT-mediated polymerization-induced self-assembly of poly(ionic liquid) block copolymers in a green solvent
- Corrigendum
- Corrigendum to “High-strength polyvinyl alcohol-based hydrogel by vermiculite and lignocellulosic nanofibrils for electronic sensing”

