Abstract
Bound states in the continuum (BIC) exhibit extremely high quality factors due to the lack of radiation loss and thus are widely studied for Purcell enhancement. However, a closer examination reveals that the enhancement is absent at the BIC due to the lack of out-coupling capability, but the strong enhancement is only observed at nearby configuration, namely quasi-BIC. To study this unique behavior of the Purcell enhancement near BIC, we built an analytical model with spectral parameters to analyze the Purcell enhancement on metasurfaces supporting quasi-BIC. Our analytical model predicts the average Purcell enhancement by metasurfaces coupled to a luminescent medium, utilizing parameters that are formulated through the temporal coupled-mode theory and can be derived from measured spectra such as transmissivity and reflectivity. We analyzed several metasurfaces supporting quasi-BIC numerically and experimentally to study the behavior of the spectral parameters as well as the resultant Purcell enhancement. We formulated the interdependence between the quality factor and the out-coupling efficiency, and revealed the existence of optimal detuning from the BIC. We also discovered that our findings are general and applicable towards realistic metasurfaces that are lossy and/or asymmetric. This discovery provides an intuitive model to understand the modal qualities of quasi-BIC and will facilitate optimization of quasi-BIC for luminescence enhancement applications.
1 Introduction
Bound states in the continuum (BIC) is a concept that was first proposed in quantum mechanics, but eventually rose as a general wave phenomenon that has developed significant influence in numerous fields of physics [1], [2], [3], [4], [5]. In nanophotonics, BIC describe localized optical modes that share the same energy and momentum with planewaves (the continuum), but yet are incapable of coupling with the continuum, thus being a bound state [6], [7], [8]. There are two main types of BIC: symmetry-protected and accidental. Symmetry-protected BIC are prevented from coupling with planewaves due to symmetry mismatch between the localized optical modes and the planewave, while accidental BIC occur through Friedrich–Wintgen interference, where destructive interference between multiple leaky resonances cancels out each other and results in trapped states [2], [8], [9], [10]. Due to the bound state nature, BIC exhibit diverging radiative quality (Q) factors, which theoretically can lead to an infinite Q factor in an ideal system. In applications, BIC are often intentionally detuned to achieve weakly radiative modes with similarly high Q factors, namely quasi-BIC (q-BIC) [11], [12], [13], [14], [15], [16].
Photoluminescence on metasurfaces [17], [18], [19], nanoplasmonics [20], [21], and photonic crystals [22], [23], [24] supporting BIC have been studied extensively due to the extraordinarily high Q factor. The Purcell effect describes the enhancement in spontaneous emission rate of quantum emitters when placed in an optical cavity [25], [26], [27]. The increase in local density of optical states (LDOS) enhances the spontaneous emission rate, and the maximum enhancement is given by the Purcell factor
Recently, we derived an analytical model that uses spectral parameters to predict the average Purcell enhancement and examined the photoluminescence enhancement (PLE) in systems that support surface lattice resonance (SLR) [29]. We discovered the spectral parameter that correlates with the nearfield confinement, which enables us to predict the Purcell enhancement while circumventing the need for measuring and integrating the nearfield. This ensures that our analytical model is compatible with experimental scenarios, where spectral measurements are reasonably accessible, but the nearfield is not. We also revealed that the three contributing factors to the measurable PLE are the Q factor, the nearfield confinement, and the out-coupling efficiency, with the Q factor being the most influential factor in SLR. Here, we expand upon this analytical model to analyze the influence of the out-coupling channels on the PLE of q-BIC. We first derive the equation that predicts the PLE of q-BIC with spectral parameters, in which we highlight the importance of the out-coupling efficiency for compatibility with q-BIC. The spectral parameters are defined based on the temporal coupled-mode theory (CMT) formalism, and the values are determined through fitting with measured or simulated spectra [30], [31], [32]. We strategically examine several metasurfaces outlined in Figure 1 that support q-BIC through numerical and experimental analysis to gain a deeper understanding into the PLE. We first investigate a lossless scenario that resembles most closely an ideal symmetry-protected BIC and examine the basic spectral behaviors of q-BIC. Then, we step-by-step introduce material loss and random scattering loss into the analysis and discuss the effect of these realistic imperfections on Purcell enhancement. Finally, we also discuss the effects of asymmetry on the spectral properties and PLE of q-BIC through systems that support accidental q-BIC.
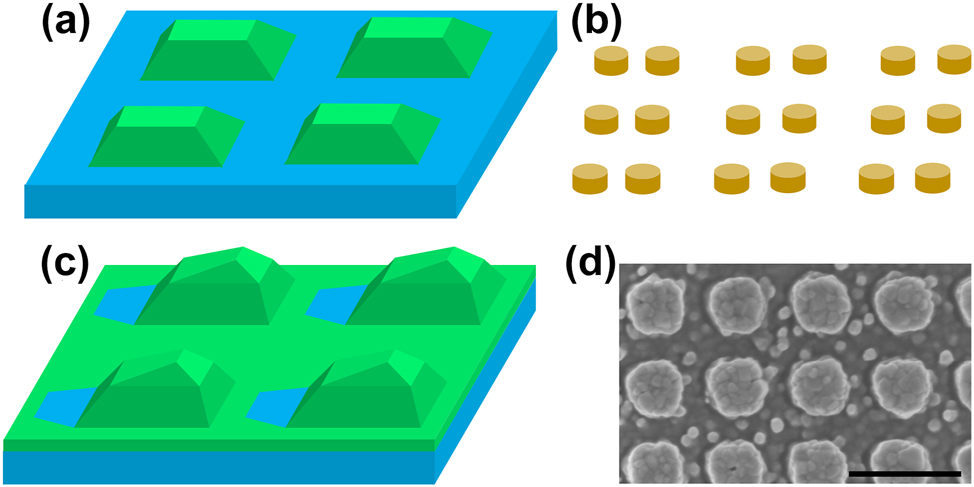
The metasurfaces that support q-BIC are illustrated. The numerically simulated (a) lossless TiO2 metasurface, (b) lossy bipartite Si metasurface, (c) asymmetric TiO2 metasurface and (d) experimental asymmetric TiO2 metasurface are investigated in Section 3.1–3.4. The colors used are: TiO2: green, SiO2 (substrate): blue, Si: orange. The scale bar in the SEM image is 500 nm.
2 Analytical modelling of Purcell enhancement of q-BIC
Numerous studies have shown that the enhancement in fractional LDOS can be predicted through the nearfield enhancement from a reciprocal source [29], [33], [34], [35], [36], [37]. If we compare the emission that leaves the metasurface and propagates away as a planewave with momentum −ℏ
k (and polarization q), the fractional LDOS enhancement is proportional to the electric field intensity
where the
In our recent work, we discovered that the nearfield confinement of a resonance can be calibrated by the absorptive decay rate contributed by dye Γabs,dye, where the nearfield region of interest is doped with a dye that absorbs at the resonant wavelength [29], [38]. The absorptive decay rate Γabs is defined through the power absorbed
where ɛ
0 is the permittivity of vacuum and ɛ″ is the imaginary part of the relative permittivity [39], [40]. Under the assumption that the dye medium is homogeneous, we can treat
which corresponds to the numerator in Eq. (1). Based on CMT, the steady-state solution gives
For simplicity, we choose a reference that is a uniform thin film of the same dye-containing homogeneous medium, placed on the same substrate without the metasurface. Thus, we get a planar structure in which determining
where
3 Results and discussion
The influence of different factors on the PLE can be dissected by re-arranging Eq. (5) into
3.1 Lossless q-BIC on TiO2 metasurface
We can first get a basic understanding of the behavior of the PLE of q-BIC by considering an ideal, lossless metasurface that supports a symmetry-protected BIC. The detailed design of the metasurface is described in the supplementary materials [41]. The angle-dependent transmissivity T and reflectivity R of the metasurface were numerically simulated and plotted in Figure 2(a) and (b). We can clearly observe the symmetry-protected BIC at incident angle θ = 0° and wavelength λ = 612.6 nm, and as detuning θ was introduced, the q-BIC emerges with a ±θ symmetry. The nearfield in the dye medium was also recorded and the numerically predicted PLE was calculated directly by Eq. (1) and plotted in Figure 2(c). The T and R of each incident angle were fitted to obtain the spectral parameters ω 0, Γtot and Γrad,in, with Eq. (S4) and (S5), respectively [41]. The extinction coefficient κ of the dye medium was modulated to calibrate the factor Γabs,dye/κ, which is the slope of Γabs against κ [41].
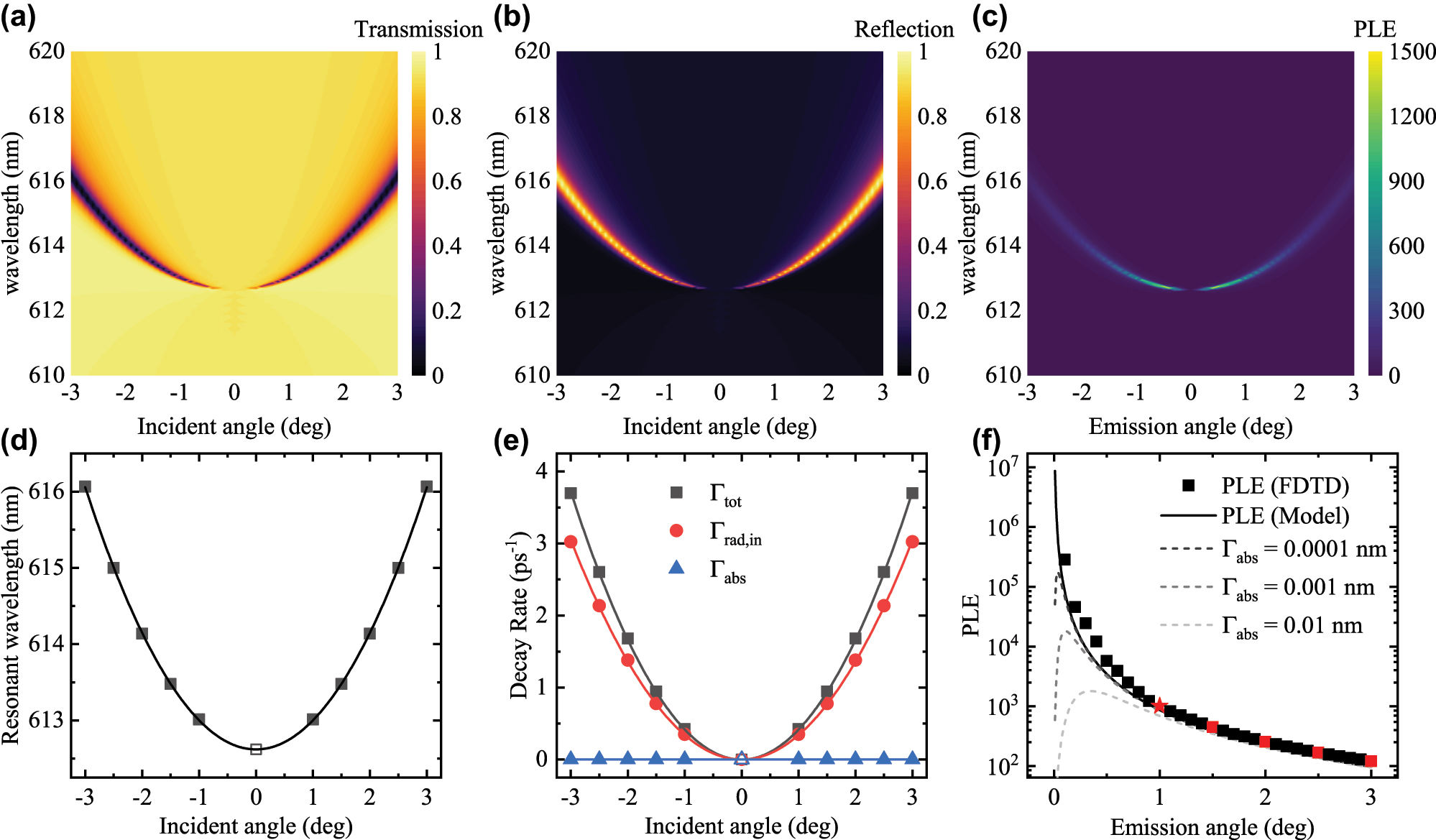
The numerically simulated (a) transmissivity, (b) reflectivity and (c) PLE of the lossless TiO2 metasurface. The (d) resonant wavelength and (e) decay rates Γtot, Γrad,in and Γabs are plotted as a function of the incident angle θ. (f) The numerical PLE and predicted PLE are plotted as a function of the emission angle θ. The PLE predicted with a small artificial Γabs are plotted as dashed lines.
Since we focus on analyzing the behavior of the metasurface within a small detuning from the BIC, we can model the change in spectral parameters by a polynomial expansion, specifically up to the quadratic term. The ω 0 and the decay rates are plotted in Figure 2(d) and (e) with their polynomial fit. As illustrated in Figure 2(e), Γabs remains zero for all incident angles while Γtot and Γrad,in increases quadratically from the BIC point. On the other hand, we can see that the factor Γabs,dye/κ remain mostly constant throughout the fitted range with a slight increase at larger θ (see Fig. S1(f)), which indicates similar nearfield confinement at different θ. As a result, the total Q factor diverges at the BIC and decreases following the inverse-squared law of the detuning (θ) [42], [43], [44]. We then predict the PLE with the best fit of the parameters and compare with the numerical PLE in Figure 2(f). The PLE increases rapidly as we approach the BIC and appears to diverge at the BIC. Since non-radiative decay rates remain zero while Γtot and Γrad,in both varies quadratically against the incident angle, the out-coupling efficiency Γrad,in/Γtot remains constant over all incident angles and did not influence (or reduce) the PLE.
However, as illustrated in Figure 2(f), the behavior is significantly different once we artificially introduce a small Γabs, which models a non-zero absorption loss and/or random scattering loss. Since the Γabs increases Γtot slightly while not affecting Γrad,in, the out-coupling efficiency Γrad,in/Γtot is no longer a constant but drops sharply around the BIC, influencing the PLE to hit a maximum and drop sharply around the BIC. We can see this effect even with very small artificial Γabs equivalent to a linewidth broadening of 0.0001 nm, which is difficult to observe with conventional spectrometers. This prompts us to explore in more detail the effect of absorption and random scattering loss.
3.2 Lossy q-BIC on Si metasurface
In the previous section, we revealed that even a very small absorption loss from the metasurface would inevitably change the characteristic behavior of PLE from BIC. However, material loss is inevitable in realistic metasurfaces [45]; nanofabrication also introduces inherent roughness into the metasurface structure, which introduces random scattering loss in application [46]. This prompts us to take a closer look into BIC supported on realistic materials with loss instead of an ideal, lossless model. Therefore, we consider a symmetry-protected BIC supported on a bipartite Si metasurface, as described in the supplementary materials [41]. The symmetry-protected BIC at λ = 704.5 nm was detuned by displacing one of the Si nanoparticles by d, and the d-dependent transmissivity T, reflectivity R, absorptivity A = 1 − T − R and PLE were numerically simulated and plotted in Figure 3(a)–(d). The T, R and A were fitted to obtain the spectral parameters ω 0, Γtot and Γrad,in, while Γabs,dye/κ was fitted by modulating κ of the dye medium [41].
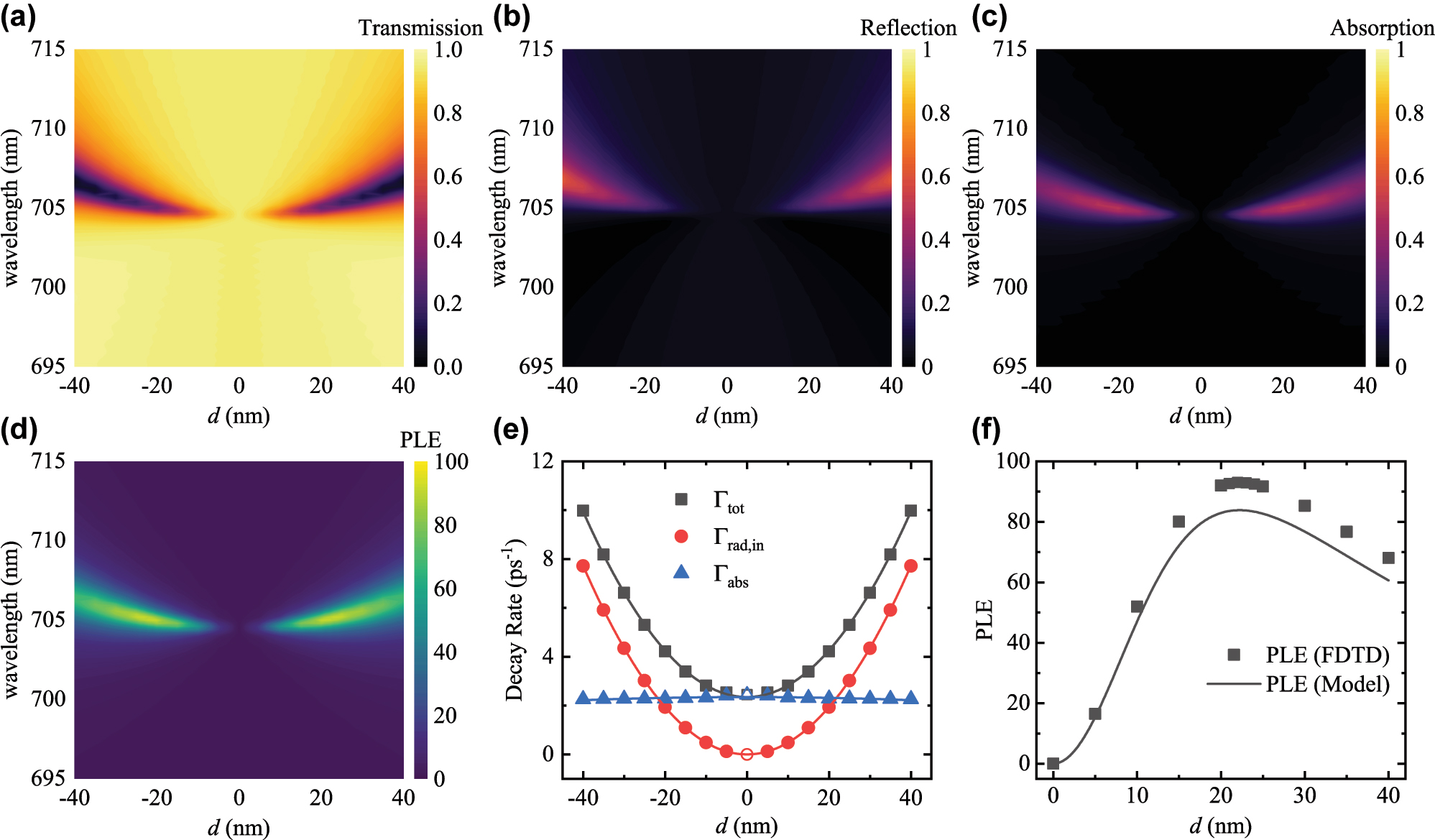
The numerically simulated (a) transmissivity, (b) reflectivity, (c) absorptivity and (d) PLE of the bipartite Si metasurface. (e) The decay rates Γtot, Γrad,in and Γabs are plotted as a function of the detuning d. (f) The numerical PLE and predicted PLE are plotted as a function of the detuning d.
As shown in Figure 3(e), Γabs remains almost constant against d with a small decrease at increasing d. This decrease is due to the gradual redshift of ω 0 as d increases and Si being less absorptive at longer wavelengths. On the other hand, Γrad,in = Γrad is zero at the BIC and increases quadratically from there. This is like what we observed in the lossless case, and we expect a quadratic dependency due to the limited range and the symmetry about ±d. Therefore, Γtot, the sum of Γabs and Γrad, roughly follows the same shape of Γrad but is displaced upwards by Γabs. Since d only shifts the position of the Si nanoparticles and does not increase or reduce the amount of dye medium, the factor Γabs,dye/κ also remains mostly constant against d, as illustrated in Fig. S2(e) [41]. This allows us to assume Γabs,dye/κ is constant and use the value at d = 20 nm for the prediction of PLE. As illustrated in Figure 3(f), the numerically simulated PLE aligned with the PLE predicted by Eq. (5). First, the PLE increases when reducing d and approaching the BIC due to the increase in Q factor. However, as we get closer to the BIC configuration, the decrease in the out-coupling efficiency overwhelms the improvement in Q factor and the PLE drops sharply near the BIC.
Interestingly, the maximum in PLE occurs very close to the point at which Γabs and Γrad intersects. This coincides with the critical coupling condition, which states that light–matter interaction is maximized when Γabs = Γrad [32]. This also presents a new perspective on how to optimize Purcell enhancement with realistic metasurfaces. First, Γabs should be as small as possible, which can be achieved by using low-loss materials for the metasurface [45], or reducing plasmonic loss with nonlocal resonances [43], [47]. The Γabs sets a lower limit to Γtot and thereby also imposes an upper bound to the Q factor. Then, Γrad should be tuned to equal Γabs to achieve the critical coupling condition and maximize light–matter interaction. If Γrad is too small, the system is dominated by the absorptive loss and most of the enhanced emission would be absorbed by the metasurface instead of out-coupled. While for large Γrad, the increase in out-coupling efficiency is not worth the decrease in Q factor and therefore the PLE is reduced.
3.3 Asymmetric TiO2 metasurface supporting accidental q-BIC
In the following sections, we explore the behavior of an off-Γ accidental q-BIC on experimental and simulated metasurfaces. We fabricated asymmetric TiO2 metasurfaces that support accidental q-BICs by glancing angle deposition of Ti followed by rapid thermal annealing (RTA) on symmetric TiO2 metasurfaces [41]. A numerical model is built to replicate the behavior of the experimental asymmetric TiO2 metasurface, which the design is described in the supplementary materials [41]. Since the TiO2 was formed through RTA of Ti, we expect some roughness in the metasurface and the random scattering loss is modelled by adding an extinction coefficient
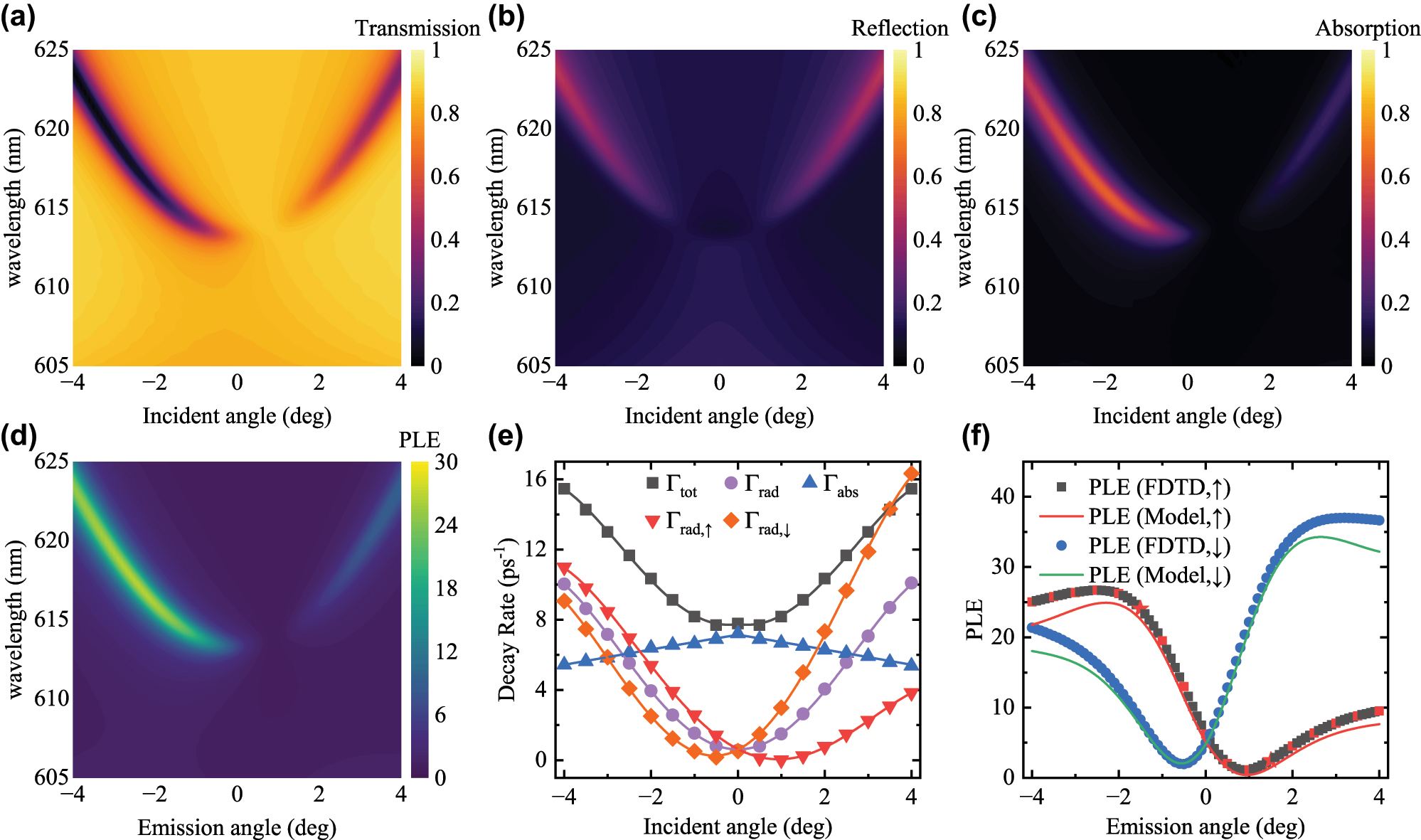
The numerically simulated (a) transmissivity, (b) reflectivity, (c) absorptivity and (d) PLE of the asymmetric TiO2 metasurface. (e) The decay rates Γtot, Γrad, Γabs, Γrad,↑ and Γrad,↓ are plotted as a function of the incident angle θ. (f) The numerical PLE and predicted PLE are plotted as a function of the incident angle θ.
The decay rates of the accidental q-BIC on the asymmetric TiO2 metasurface behave markedly differently from that of the symmetric cases. As illustrated in Figure 4(e), Γabs is largest at normal incident and decreases following a linear style when increasing |θ|. The Γrad is also symmetrical over ±θ and remains non-zero at all θ. On the other hand, the asymmetry in the metasurface splits the point where Γrad,↑ and Γrad,↓ touch zero, corresponding to the ports at the superstrate (↑) and substrate (↓) sides, towards positive and negative incident angles respectively. Γrad,↑ and Γrad,↓ now touch zero at 0.92° and −0.53° respectively. To use the parameters to predict the PLE, the decay rates were fitted with fourth-order polynomials. The polynomial fits of the parameters were then substituted into Eq. (5) to derive a prediction of the PLE. As illustrated in Figure 4(f), Eq. (5) predicted the numerical PLE with good accuracy (see Fig. S3(e) for the simulated substrate side PLE) [41]. The PLE at the superstrate side shows a minimum at 0.9° while that at the substrate side shows a minimum at −0.5°. A local maximum in PLE is observed at −2.5° at the superstrate side and the model predicted it at −2.2°. On the substrate side, a local maximum is observed at 3.2° followed by a very slow decrease in PLE, while the model predicts a local maximum at 2.5°. Overall, we see larger discrepancies between the analytical and numerical PLE near the end of the fitted range. Due to the nature of polynomial regression, the edge of the data is usually less well represented compared to the data near the center (normal incident), as the higher-order terms are truncated and they are only significant for larger |θ|. Therefore, in the trade-off between overfitting and poor fitting accuracy, we proceeded with fourth-order polynomials as they fitted the decay rates better when compared to second-order polynomials, while further increasing the polynomial order did not improve significantly upon that. While this choice is unlikely to lead us to overfitting, this also limits our accuracy, especially for the data near the edges of the fitted range.
It is worth noting that R remained symmetric over ±θ, even on an asymmetric structure. We were also able to predict the PLE at both the superstrate side and the substrate side, only with the spectra incident from the superstrate side. Both features are because Lorentz reciprocity ensures the in-coupling and out-coupling process are symmetric, which ensures a symmetric R. Also, by simultaneously fitting T and R of ±θ, we were able to determine the in-coupling constants of all ports and thus model the PLE at both the superstrate side and the substrate side.
3.4 Asymmetric TiO2 metasurface fabricated by glancing angle deposition
In this section, we experimentally investigate the behavior of accidental q-BIC on the asymmetric TiO2 metasurfaces. The asymmetric metasurface was fabricated by glancing angle deposition on a symmetric TiO2 metasurface. A Ti thin film (100 nm) was deposited on a SiO2 glass substrate by electron beam deposition, and a resist (TU7, Obducat) was spin-coated on top. A resist array with square nanoparticles of sides 160 nm arranged in a square lattice of period 370 nm was then fabricated by nanoimprinting. The pattern was transferred to the Ti thin film by O2 ashing (RIE-10NR) and etching with Cl2 and CHF3 (NLD-570). The Ti metasurface was then oxidized by RTA (900 °C, 10 min) under O2 atmosphere to fabricate a symmetric TiO2 metasurface. A 20 nm thin film of Ti was deposited onto the TiO2 metasurface from a glancing angle by tilting the substrate in an electron beam deposition apparatus. The substrate was tilted by 30° along the xz-plane. The newly deposited Ti was also oxidized with the same RTA process to create the asymmetric TiO2 metasurface. As highlighted in the SEM image of the asymmetric metasurface shown in the inset of Figure 5(d), voids formed only on the left-hand side of the TiO2 nanoparticles, at the shadow of the nanoparticles during glancing angle deposition. Finally, a PMMA layer (450 nm) was spin-coated onto the TiO2 metasurface. The PMMA is doped with an organic dye (Lumogen F 305 Red) at 1 wt% (weight percent), and the PLE on this Lumogen dye is evaluated. The T, R and PLE (I/I 0) were measured on the rotation stages illustrated in the supplementary materials [41]. The measured T, R and PLE (I/I 0) are plotted in Figure 5(a)–(c). We focus on the branch showing an accidental BIC at θ = 1.2° and λ = 710 nm. The spectral parameters ω 0, Γtot and Γrad,in were fitted from the measured spectra directly. However, to calibrate the nearfield confinement with Γabs,dye/κ, we need to use a dye that absorbs light at around λ = 700–800 nm. In place of the PMMA layer doped with Lumogen, we spin-coated a similar PMMA layer with 0.25 wt% of IR780 iodide onto the asymmetric TiO2 metasurface. The T and R of the metasurface with IR780 are then measured to fit for (mainly) Γabs and thus we derive Γabs,dye/κ [41].
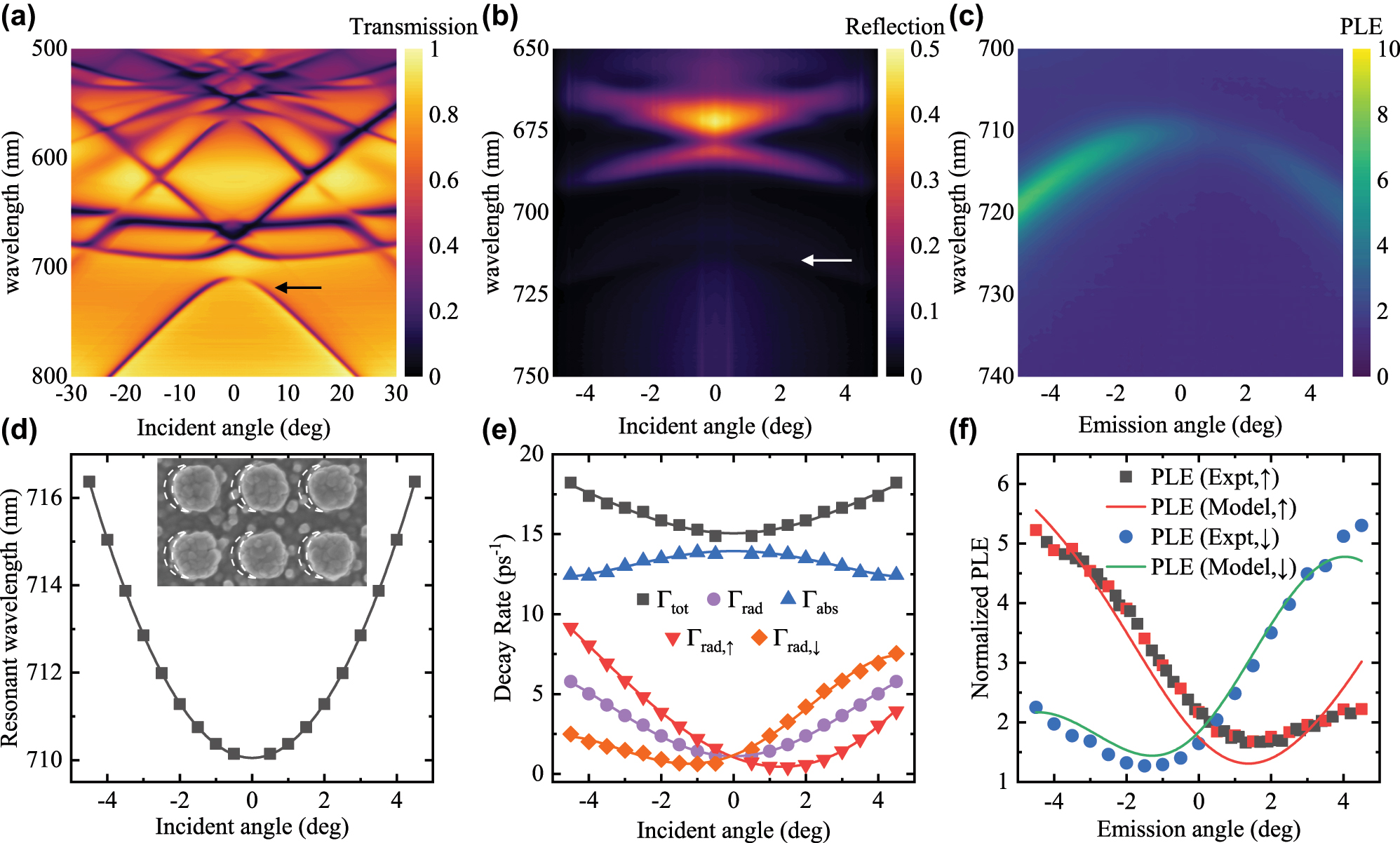
The measured (a) transmissivity, (b) reflectivity, and (c) PLE (I/I 0) of the asymmetric TiO2 metasurface fabricated by glancing angle deposition. The arrows indicate the mode of interest. The (d) resonant wavelength and (e) decay rates Γtot, Γrad, Γabs, Γrad,↑ and Γrad,↓ are plotted as a function of the incident angle θ. The inset in (d) highlights the asymmetry in the TiO2 metasurface. The void formed under the shadow of TiO2 nanoparticles during glancing angle deposition are outlined by the dashed lines. (f) The re-normalized PLE and predicted PLE are plotted as a function of the emission angle θ.
The decay rates behaved like the simulated asymmetric TiO2 metasurfaces. The Γabs is largest at normal incident and decreases slightly at larger |θ|. As illustrated in Figure 5(e), Γrad remains symmetric over ±θ, while Γrad,↑ and Γrad,↓ touches zero at 1.3° and −1.2° respectively. The parameters also show a good fit when approximated with fourth-order polynomials. We then use the polynomial fits to derive the predicted PLE through Eq. (5). While our analytical model only predicts enhancement due to the Purcell effect, enhancement in the absorption by the Lumogen dye due to the presence of the metasurface is not described, yet is included in the measured I/I 0. To minimize the influence of the absorption enhancement and the uneven excitation profile associated with higher absorption enhancement, the incident angle of the excitation laser was chosen at −31.5°, and the measured PLE was re-normalized against the baseline to isolate the Purcell effect. We can now compare the predicted PLE against the re-normalized PLE. As shown in Figure 5(f), the experimental Purcell enhancement is predicted by our analytical model. We also apply Lorentz reciprocity to predict the backside PLE, which our experimental measurements show good agreement with (see Fig. S4(c) for the measured backside PLE) [41].
4 Conclusions
In conclusion, we leveraged the proposed analytical model to analyze the influence of the changes in the out-coupling channels of q-BIC on PLE. We first derived the equation that predicts the PLE of q-BIC with spectral parameters. Then, we strategically examined several metasurfaces that support q-BIC through numerical and experimental analysis to gain a deeper understanding of the PLE. We first investigated a lossless scenario that resembles most closely to an ideal symmetry-protected BIC and examined the basic spectral behavior of q-BIC. We then introduced material loss and random scattering loss into the analysis and discussed the effect of these realistic imperfections on the Purcell enhancement. Finally, we also discussed the effects of asymmetry on the spectral properties and PLE of q-BIC through systems that support accidental q-BIC. We revealed that the interplay between the quality factor and the out-coupling efficiency is the primary contribution towards the PLE of q-BIC and maximum enhancement can be achieved by optimizing the detuning from the associated BIC. We also demonstrated the general application methodology with two different dyes for emission measurement and absorption calibration respectively. This calibration approach with two optical materials can be further generalized to analyze different types of luminescent materials, making this analytical approach compatible even with those that do not inherently absorb light. Overall, this work provides an intuitive way to understand the mechanism of photoluminescence enhancement from q-BIC, as well as a practical framework for modelling the modal behavior of experimental q-BIC directly.
Funding source: Japan Society for the Promotion of Science
Award Identifier / Grant number: 21H04619
Award Identifier / Grant number: 22H01776
Award Identifier / Grant number: 22K18884
Award Identifier / Grant number: 25K01501
Award Identifier / Grant number: 25K21709
-
Research funding: Financial support from Kakenhi (25K01501, 25K21709, 22H01776, 22K18884, 21H04619) is cordially acknowledged.
-
Author contribution: All authors have accepted responsibility for the entire content of this manuscript and consented to its submission to the journal, reviewed all the results and approved the final version of the manuscript. JTYT and SM conceived the idea. JTYT and TE designed and conducted the experiments. JTYT performed the simulations and analyzed the data. SM and KT supervised the study. JTYT prepared the manuscript with contributions from all co-authors.
-
Conflict of interest: Authors state no conflict of interest.
-
Data availability: The data that support the findings of this article are available from the corresponding author upon reasonable request.
References
[1] F. H. Stillinger and D. R. Herrick, “Bound states in the continuum,” Phys. Rev. A, vol. 11, p. 446, 1975, https://doi.org/10.1103/physreva.11.446.Search in Google Scholar
[2] C. W. Hsu, B. Zhen, A. Douglas Stone, J. D. Joannopoulos, and M. Soljačić, “Bound states in the continuum,” Nat. Rev. Mater., vol. 1, p. 16048, 2016, https://doi.org/10.1038/natrevmats.2016.48.Search in Google Scholar
[3] H. Tong, S. Liu, and K. Fang, “Merging mechanical bound states in the continuum in high-aspect-ratio phononic crystal gratings,” Commun. Phys., vol. 7, p. 197, 2024, https://doi.org/10.1038/s42005-024-01692-9.Search in Google Scholar
[4] C. M. Linton and P. McIver, “Embedded trapped modes in water waves and acoustics,” Wave Motion, vol. 45, p. 16, 2007, https://doi.org/10.1016/j.wavemoti.2007.04.009.Search in Google Scholar
[5] M. I. Molina, A. E. Miroshnichenko, and Y. S. Kivshar, “Surface bound states in the continuum,” Phys. Rev. Lett., vol. 108, p. 070401, 2012, https://doi.org/10.1103/physrevlett.108.070401.Search in Google Scholar
[6] D. C. Marinica, A. G. Borisov, and S. V. Shabanov, “Bound states in the continuum in photonics,” Phys. Rev. Lett., vol. 100, p. 183902, 2008, https://doi.org/10.1103/physrevlett.100.183902.Search in Google Scholar
[7] K. Koshelev, A. Bogdanov, and Y. Kivshar, “Meta-optics and bound states in the continuum,” Sci. Bull., vol. 64, p. 836, 2019, https://doi.org/10.1016/j.scib.2018.12.003.Search in Google Scholar PubMed
[8] S. I. Azzam and A. V. Kildishev, “Photonic bound states in the continuum: From basics to applications,” Adv. Opt. Mater., vol. 9, p. 2001469, 2021, https://doi.org/10.1002/adom.202001469.Search in Google Scholar
[9] Z. Sadrieva, K. Frizyuk, M. Petrov, Y. Kivshar, and A. Bogdanov, “Multipolar origin of bound states in the continuum,” Phys. Rev. B, vol. 100, p. 115303, 2019, https://doi.org/10.1103/physrevb.100.115303.Search in Google Scholar
[10] A. Canós Valero, Z. Sztranyovszky, E. A. Muljarov, A. Bogdanov, and T. Weiss, “Exceptional bound states in the continuum,” Phys. Rev. Lett., vol. 134, p. 103802, 2025, https://doi.org/10.1103/physrevlett.134.103802.Search in Google Scholar
[11] X. Zong, L. Li, and Y. Liu, “Bound states in the continuum enabling ultra-narrowband perfect absorption,” New J. Phys., vol. 25, p. 023020, 2023, https://doi.org/10.1088/1367-2630/acb9b3.Search in Google Scholar
[12] H. Liu, Y. Liu, H. Chen, and L. Wan, “Ultra-narrow dual-band notch filter based on merging bound states in the continuum,” Opt. Commun., vol. 569, p. 130842, 2024, https://doi.org/10.1016/j.optcom.2024.130842.Search in Google Scholar
[13] A. Kodigala, T. Lepetit, Q. Gu, B. Bahari, Y. Fainman, and B. Kanté, “Lasing action from photonic bound states in continuum,” Nature, vol. 541, p. 196, 2017, https://doi.org/10.1038/nature20799.Search in Google Scholar PubMed
[14] S. Shen et al.., “Topologically protected plasmonic bound states in the continuum,” Nano Lett., vol. 24, p. 13285, 2024, https://doi.org/10.1021/acs.nanolett.4c03636.Search in Google Scholar PubMed
[15] Z. Liu et al.., “High-Q quasibound states in the continuum for nonlinear metasurfaces,” Phys. Rev. Lett., vol. 123, p. 253901, 2019, https://doi.org/10.1103/physrevlett.123.253901.Search in Google Scholar PubMed
[16] A. M. Berghuis et al.., “Room temperature exciton−polariton condensation in silicon metasurfaces emerging from bound states in the continuum,” Nano Lett., vol. 23, p. 5603, 2023, https://doi.org/10.1021/acs.nanolett.3c01102.Search in Google Scholar PubMed PubMed Central
[17] R. Colom, F. Binkowski, F. Betz, Y. Kivshar, and S. Burger, “Enhanced Purcell factor for nanoantennas supporting interfering resonances,” Phys. Rev. Res., vol. 4, p. 023189, 2022, https://doi.org/10.1103/physrevresearch.4.023189.Search in Google Scholar
[18] B. Kalinic et al.., “Quasi-BIC modes in all-dielectric slotted nanoantennas for enhanced Er3+ emission,” ACS Photonics, vol. 10, p. 534, 2023, https://doi.org/10.1021/acsphotonics.2c01703.Search in Google Scholar PubMed PubMed Central
[19] E. Maggiolini et al.., “Strongly enhanced light–matter coupling of monolayer WS2 from a bound state in the continuum,” Nature Mater, vol. 22, p. 964, 2023, https://doi.org/10.1038/s41563-023-01562-9.Search in Google Scholar PubMed
[20] R. Heilmann, G. Salerno, J. Cuerda, T. K. Hakala, and P. Torma, “Quasi-BIC mode lasing in a quadrumer plasmonic lattice,” ACS Photonics, vol. 9, p. 224, 2022, https://doi.org/10.1021/acsphotonics.1c01416.Search in Google Scholar PubMed PubMed Central
[21] I. C. Seo, S. Kim, B. H. Woo, I. S. Chung, and Y. C. Jun, “Fourier-plane investigation of plasmonic bound states in the continuum and molecular emission coupling,” Nanophotonics, vol. 9, p. 4565, 2020, https://doi.org/10.1515/nanoph-2020-0343.Search in Google Scholar
[22] E. Forati, “Spontaneous emission rate and the density of states inside a one dimensional photonic crystal,” IEEE J. Multiscale Multiphys. Comput. Tech., vol. 7, p. 46, 2022, https://doi.org/10.1109/jmmct.2022.3153405.Search in Google Scholar
[23] B. Zhen et al.., “Enabling enhanced emission and low-threshold lasing of organic molecules using special Fano resonances of macroscopic photonic crystals,” Proc. Natl. Acad. Sci. U.S.A., vol. 110, p. 13711, 2013, https://doi.org/10.1073/pnas.1311866110.Search in Google Scholar PubMed PubMed Central
[24] A. Barreda, L. Mercadé, M. Zapata-Herrera, J. Aizpurua, and A. Martínez, “Hybrid photonic-plasmonic cavity design for very large Purcell factors at telecommunication wavelengths,” Phys. Rev. Appl., vol. 18, p. 044066, 2022. https://doi.org/10.1103/PhysRevApplied.18.044066.Search in Google Scholar
[25] E. M. Purcell, “Spontaneous emission probabilities at radio frequencies,” Phys. Rev., vol. 69, p. 681, 1946.Search in Google Scholar
[26] M. S. Tame, K. R. McEnery, Ş. K. Özdemir, J. Lee, S. A. Maier, and M. S. Kim, “Quantum plasmonics,” Nat. Phys., vol. 9, p. 329, 2013, https://doi.org/10.1038/nphys2615.Search in Google Scholar
[27] K. Liao et al.., “Photonic molecule quantum optics,” Adv. Opt. Photonics, vol. 12, p. 60, 2020, https://doi.org/10.1364/aop.376739.Search in Google Scholar
[28] Z. Zhang et al.., “High-Q collective Mie resonances in monocrystalline silicon nanoantenna arrays for the visible light,” Fundam. Res., vol. 3, p. 822, 2023, https://doi.org/10.1016/j.fmre.2022.05.020.Search in Google Scholar PubMed PubMed Central
[29] J. T. Y. Tse, S. Murai, and K. Tanaka, “Interpreting Purcell enhancement of non-Hermitian metasurfaces with spectral parameters,” Phys. Rev. A, vol. 111, p. 013511, 2025, https://doi.org/10.1103/physreva.111.013511.Search in Google Scholar
[30] H. A. Haus, Waves and Fields in Optoelectronics, New Jersey, Prentice-Hall, 1984.Search in Google Scholar
[31] S. Fan, W. Suh, and J. D. Joannopoulos, “Temporal coupled-mode theory for the Fano resonance in optical resonators,” J. Opt. Soc. Amer. A, vol. 20, p. 569, 2003, https://doi.org/10.1364/josaa.20.000569.Search in Google Scholar PubMed
[32] J. T. Y. Tse, S. Murai, and K. Tanaka, “Resonant critical coupling of surface lattice resonances with a fluorescent absorptive thin film,” J. Phys. Chem. C, vol. 127, p. 22212, 2023, https://doi.org/10.1021/acs.jpcc.3c05810.Search in Google Scholar
[33] Z. Zhang et al.., “Dual control of enhanced quasi-bound states in the continuum emission from resonant c-Si metasurfaces,” Nano Lett., vol. 23, p. 7584, 2023, https://doi.org/10.1021/acs.nanolett.3c02148.Search in Google Scholar PubMed
[34] M. Ramezani, G. Lozano, M. A. Verschuuren, and J. Gómez-Rivas, “Modified emission of extended light emitting layers by selective coupling to collective lattice resonances,” Phys. Rev. B, vol. 94, p. 125406, 2016, https://doi.org/10.1103/physrevb.94.125406.Search in Google Scholar
[35] A. Vaskin, R. Kolkowski, A. F. Koenderink, and I. Staude, “Light-emitting metasurfaces,” Nanophotonics, vol. 8, p. 1151, 2019, https://doi.org/10.1515/nanoph-2019-0110.Search in Google Scholar
[36] S. Zhang, E. R. Martins, A. G. Diyaf, J. I. Wilson, G. A. Turnbull, and I. D. Samuel, “Calculation of the emission power distribution of microstructured OLEDs using the reciprocity theorem,” Synth. Met., vol. 205, p. 127, 2015, https://doi.org/10.1016/j.synthmet.2015.03.035.Search in Google Scholar
[37] G. W. Castellanos, P. Bai, and J. Gómez Rivas, “Lattice resonances in dielectric metasurfaces,” J. Appl. Phys., vol. 125, p. 213105, 2019. https://doi.org/10.1063/1.5094122.Search in Google Scholar
[38] J. T. Y. Tse, S. Murai, and K. Tanaka, “Modified coupled-mode theory for the absorption in plasmonic lattices,” Adv. Photon. Res., vol. 5, p. 2400050, 2024, https://doi.org/10.1002/adpr.202400050.Search in Google Scholar
[39] K. J. Webb, “Shivanand, Electromagnetic field energy in dispersive materials,” J. Opt. Soc. Am. B, vol. 27, p. 1215, 2010, https://doi.org/10.1364/josab.27.001215.Search in Google Scholar
[40] F. D. Nunes, T. C. Vasconcelos, M. Bezerra, and J. Weiner, “Electromagnetic energy density in dispersive and dissipative media,” J. Opt. Soc. Am. B, vol. 28, p. 1544, 2011, https://doi.org/10.1364/josab.28.001544.Search in Google Scholar
[41] The key results of the modified temporal coupled-mode theory, the details of the numerical simulations, the nearfield confinement factor, the optical measurement setups, and the calibration for the organic dyes are presented in the supplemental material at https://doi.org/10.1515/nanoph-2025-0456.10.1515/nanoph-2025-0456Search in Google Scholar
[42] Y. Hu, S. Xie, C. Bai, W. Shen, and J. Yang, “Multiple photonic bound states in the continuum in an electromagnetically induced transparency metasurface,” IEEE Photon. J., vol. 14, p. 1, 2022, https://doi.org/10.1109/jphot.2022.3190133.Search in Google Scholar
[43] Y. Liang, D. P. Tsai, and Y. Kivshar, “From local to nonlocal high-Q plasmonic metasurface,” Phys. Rev. Lett., vol. 133, p. 053801, 2024, https://doi.org/10.1103/physrevlett.133.053801.Search in Google Scholar
[44] K. Koshelev, S. Lepeshov, M. Liu, A. Bogdanov, and Y. Kivshar, “Asymmetric metasurfaces with high-Q resonances governed by bound states in the continuum,” Phys. Rev. Lett., vol. 121, p. 193903, 2018, https://doi.org/10.1103/physrevlett.121.193903.Search in Google Scholar
[45] H. Maruyama, J. T. Y. Tse, S. Murai, and K. Tanaka, “Fabricating SiC nanovoid arrays for Mie-tronics,” Jpn. J. Appl. Phys., vol. 64, p. 03SP54, 2025, https://doi.org/10.35848/1347-4065/adaecc.Search in Google Scholar
[46] Z. F. Sadrieva et al.., “Transition from optical bound states in the continuum to leaky resonances: Role of substrate and roughness,” ACS Photonics, vol. 4, p. 723, 2017, https://doi.org/10.1021/acsphotonics.6b00860.Search in Google Scholar
[47] J. T. Y. Tse and H. C. Ong, “Quality factor of plasmonic monopartite and bipartite surface lattice resonances,” Phys. Rev. B, vol. 104, p. 125442, 2021, https://doi.org/10.1103/physrevb.104.125442.Search in Google Scholar
Supplementary Material
This article contains supplementary material (https://doi.org/10.1515/nanoph-2025-0456).
© 2025 the author(s), published by De Gruyter, Berlin/Boston
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Frontmatter
- Reviews
- Light-driven micro/nanobots
- Tunable BIC metamaterials with Dirac semimetals
- Large-scale silicon photonics switches for AI/ML interconnections based on a 300-mm CMOS pilot line
- Perspective
- Density-functional tight binding meets Maxwell: unraveling the mysteries of (strong) light–matter coupling efficiently
- Letters
- Broadband on-chip spectral sensing via directly integrated narrowband plasmonic filters for computational multispectral imaging
- Sub-100 nm manipulation of blue light over a large field of view using Si nanolens array
- Tunable bound states in the continuum through hybridization of 1D and 2D metasurfaces
- Integrated array of coupled exciton–polariton condensates
- Disentangling the absorption lineshape of methylene blue for nanocavity strong coupling
- Research Articles
- Demonstration of multiple-wavelength-band photonic integrated circuits using a silicon and silicon nitride 2.5D integration method
- Inverse-designed gyrotropic scatterers for non-reciprocal analog computing
- Highly sensitive broadband photodetector based on PtSe2 photothermal effect and fiber harmonic Vernier effect
- Online training and pruning of multi-wavelength photonic neural networks
- Robust transport of high-speed data in a topological valley Hall insulator
- Engineering super- and sub-radiant hybrid plasmons in a tunable graphene frame-heptamer metasurface
- Near-unity fueling light into a single plasmonic nanocavity
- Polarization-dependent gain characterization in x-cut LNOI erbium-doped waveguide amplifiers
- Intramodal stimulated Brillouin scattering in suspended AlN waveguides
- Single-shot Stokes polarimetry of plasmon-coupled single-molecule fluorescence
- Metastructure-enabled scalable multiple mode-order converters: conceptual design and demonstration in direct-access add/drop multiplexing systems
- High-sensitivity U-shaped biosensor for rabbit IgG detection based on PDA/AuNPs/PDA sandwich structure
- Deep-learning-based polarization-dependent switching metasurface in dual-band for optical communication
- A nonlocal metasurface for optical edge detection in the far-field
- Coexistence of weak and strong coupling in a photonic molecule through dissipative coupling to a quantum dot
- Mitigate the variation of energy band gap with electric field induced by quantum confinement Stark effect via a gradient quantum system for frequency-stable laser diodes
- Orthogonal canalized polaritons via coupling graphene plasmon and phonon polaritons of hBN metasurface
- Dual-polarization electromagnetic window simultaneously with extreme in-band angle-stability and out-of-band RCS reduction empowered by flip-coding metasurface
- Record-level, exceptionally broadband borophene-based absorber with near-perfect absorption: design and comparison with a graphene-based counterpart
- Generalized non-Hermitian Hamiltonian for guided resonances in photonic crystal slabs
- A 10× continuously zoomable metalens system with super-wide field of view and near-diffraction–limited resolution
- Continuously tunable broadband adiabatic coupler for programmable photonic processors
- Diffraction order-engineered polarization-dependent silicon nano-antennas metagrating for compact subtissue Mueller microscopy
- Lithography-free subwavelength metacoatings for high thermal radiation background camouflage empowered by deep neural network
- Multicolor nanoring arrays with uniform and decoupled scattering for augmented reality displays
- Permittivity-asymmetric qBIC metasurfaces for refractive index sensing
- Theory of dynamical superradiance in organic materials
- Second-harmonic generation in NbOI2-integrated silicon nitride microdisk resonators
- A comprehensive study of plasmonic mode hybridization in gold nanoparticle-over-mirror (NPoM) arrays
- Foundry-enabled wafer-scale characterization and modeling of silicon photonic DWDM links
- Rough Fabry–Perot cavity: a vastly multi-scale numerical problem
- Classification of quantum-spin-hall topological phase in 2D photonic continuous media using electromagnetic parameters
- Light-guided spectral sculpting in chiral azobenzene-doped cholesteric liquid crystals for reconfigurable narrowband unpolarized light sources
- Modelling Purcell enhancement of metasurfaces supporting quasi-bound states in the continuum
- Ultranarrow polaritonic cavities formed by one-dimensional junctions of two-dimensional in-plane heterostructures
- Bridging the scalability gap in van der Waals light guiding with high refractive index MoTe2
- Ultrafast optical modulation of vibrational strong coupling in ReCl(CO)3(2,2-bipyridine)
- Chirality-driven all-optical image differentiation
- Wafer-scale CMOS foundry silicon-on-insulator devices for integrated temporal pulse compression
- Monolithic temperature-insensitive high-Q Ta2O5 microdisk resonator
- Nanogap-enhanced terahertz suppression of superconductivity
- Large-gap cascaded Moiré metasurfaces enabling switchable bright-field and phase-contrast imaging compatible with coherent and incoherent light
- Synergistic enhancement of magneto-optical response in cobalt-based metasurfaces via plasmonic, lattice, and cavity modes
- Scalable unitary computing using time-parallelized photonic lattices
- Diffusion model-based inverse design of photonic crystals for customized refraction
- Wafer-scale integration of photonic integrated circuits and atomic vapor cells
- Optical see-through augmented reality via inverse-designed waveguide couplers
- One-dimensional dielectric grating structure for plasmonic coupling and routing
- MCP-enabled LLM for meta-optics inverse design: leveraging differentiable solver without LLM expertise
- Broadband variable beamsplitter made of a subwavelength-thick metamaterial
- Scaling-dependent tunability of spin-driven photocurrents in magnetic metamaterials
- AI-based analysis algorithm incorporating nanoscale structural variations and measurement-angle misalignment in spectroscopic ellipsometry
Articles in the same Issue
- Frontmatter
- Reviews
- Light-driven micro/nanobots
- Tunable BIC metamaterials with Dirac semimetals
- Large-scale silicon photonics switches for AI/ML interconnections based on a 300-mm CMOS pilot line
- Perspective
- Density-functional tight binding meets Maxwell: unraveling the mysteries of (strong) light–matter coupling efficiently
- Letters
- Broadband on-chip spectral sensing via directly integrated narrowband plasmonic filters for computational multispectral imaging
- Sub-100 nm manipulation of blue light over a large field of view using Si nanolens array
- Tunable bound states in the continuum through hybridization of 1D and 2D metasurfaces
- Integrated array of coupled exciton–polariton condensates
- Disentangling the absorption lineshape of methylene blue for nanocavity strong coupling
- Research Articles
- Demonstration of multiple-wavelength-band photonic integrated circuits using a silicon and silicon nitride 2.5D integration method
- Inverse-designed gyrotropic scatterers for non-reciprocal analog computing
- Highly sensitive broadband photodetector based on PtSe2 photothermal effect and fiber harmonic Vernier effect
- Online training and pruning of multi-wavelength photonic neural networks
- Robust transport of high-speed data in a topological valley Hall insulator
- Engineering super- and sub-radiant hybrid plasmons in a tunable graphene frame-heptamer metasurface
- Near-unity fueling light into a single plasmonic nanocavity
- Polarization-dependent gain characterization in x-cut LNOI erbium-doped waveguide amplifiers
- Intramodal stimulated Brillouin scattering in suspended AlN waveguides
- Single-shot Stokes polarimetry of plasmon-coupled single-molecule fluorescence
- Metastructure-enabled scalable multiple mode-order converters: conceptual design and demonstration in direct-access add/drop multiplexing systems
- High-sensitivity U-shaped biosensor for rabbit IgG detection based on PDA/AuNPs/PDA sandwich structure
- Deep-learning-based polarization-dependent switching metasurface in dual-band for optical communication
- A nonlocal metasurface for optical edge detection in the far-field
- Coexistence of weak and strong coupling in a photonic molecule through dissipative coupling to a quantum dot
- Mitigate the variation of energy band gap with electric field induced by quantum confinement Stark effect via a gradient quantum system for frequency-stable laser diodes
- Orthogonal canalized polaritons via coupling graphene plasmon and phonon polaritons of hBN metasurface
- Dual-polarization electromagnetic window simultaneously with extreme in-band angle-stability and out-of-band RCS reduction empowered by flip-coding metasurface
- Record-level, exceptionally broadband borophene-based absorber with near-perfect absorption: design and comparison with a graphene-based counterpart
- Generalized non-Hermitian Hamiltonian for guided resonances in photonic crystal slabs
- A 10× continuously zoomable metalens system with super-wide field of view and near-diffraction–limited resolution
- Continuously tunable broadband adiabatic coupler for programmable photonic processors
- Diffraction order-engineered polarization-dependent silicon nano-antennas metagrating for compact subtissue Mueller microscopy
- Lithography-free subwavelength metacoatings for high thermal radiation background camouflage empowered by deep neural network
- Multicolor nanoring arrays with uniform and decoupled scattering for augmented reality displays
- Permittivity-asymmetric qBIC metasurfaces for refractive index sensing
- Theory of dynamical superradiance in organic materials
- Second-harmonic generation in NbOI2-integrated silicon nitride microdisk resonators
- A comprehensive study of plasmonic mode hybridization in gold nanoparticle-over-mirror (NPoM) arrays
- Foundry-enabled wafer-scale characterization and modeling of silicon photonic DWDM links
- Rough Fabry–Perot cavity: a vastly multi-scale numerical problem
- Classification of quantum-spin-hall topological phase in 2D photonic continuous media using electromagnetic parameters
- Light-guided spectral sculpting in chiral azobenzene-doped cholesteric liquid crystals for reconfigurable narrowband unpolarized light sources
- Modelling Purcell enhancement of metasurfaces supporting quasi-bound states in the continuum
- Ultranarrow polaritonic cavities formed by one-dimensional junctions of two-dimensional in-plane heterostructures
- Bridging the scalability gap in van der Waals light guiding with high refractive index MoTe2
- Ultrafast optical modulation of vibrational strong coupling in ReCl(CO)3(2,2-bipyridine)
- Chirality-driven all-optical image differentiation
- Wafer-scale CMOS foundry silicon-on-insulator devices for integrated temporal pulse compression
- Monolithic temperature-insensitive high-Q Ta2O5 microdisk resonator
- Nanogap-enhanced terahertz suppression of superconductivity
- Large-gap cascaded Moiré metasurfaces enabling switchable bright-field and phase-contrast imaging compatible with coherent and incoherent light
- Synergistic enhancement of magneto-optical response in cobalt-based metasurfaces via plasmonic, lattice, and cavity modes
- Scalable unitary computing using time-parallelized photonic lattices
- Diffusion model-based inverse design of photonic crystals for customized refraction
- Wafer-scale integration of photonic integrated circuits and atomic vapor cells
- Optical see-through augmented reality via inverse-designed waveguide couplers
- One-dimensional dielectric grating structure for plasmonic coupling and routing
- MCP-enabled LLM for meta-optics inverse design: leveraging differentiable solver without LLM expertise
- Broadband variable beamsplitter made of a subwavelength-thick metamaterial
- Scaling-dependent tunability of spin-driven photocurrents in magnetic metamaterials
- AI-based analysis algorithm incorporating nanoscale structural variations and measurement-angle misalignment in spectroscopic ellipsometry

