Abstract
This work presents a novel approach to create and dynamically control quasi-bound states in the continuum (BIC) resonances through the hybridization of 1D and 2D metasurfaces using micro-electromechanical systems (MEMS). The quasi-BIC resonance’s central wavelength and quality factor are precisely tuned by introducing out-of-plane symmetry breaking through a silicon MEMS membrane positioned above a 1D silicon metasurface. The proposed design achieves ultranarrow resonance linewidths with the spectral tuning range exceeding 60 nm while maintaining a constant quality factor. This tuning capability, realized through both horizontal displacement within a 1D metasurface and vertical MEMS membrane movement, offers a new degree of freedom for manipulating quasi-BIC resonances. The proposed hybridization of 2D and 1D metasurfaces using a MEMS mechanism provides a practical route to dynamic modulation of transmission resonance characteristics, making it a promising candidate for tunable filters, spectroscopy, imaging, and sensing applications.
1 Introduction
The concept of bound states in the continuum (BICs) represents a remarkable phenomenon in modern physics, where certain states remain localized within a system despite existing at energies or frequencies that typically allow for radiation [1]. Originating from quantum mechanics, BICs have found significant applications in photonics and metamaterials, enabling extreme confinement of electromagnetic waves and forming extremely high-Q resonances [2], [3]. These unique properties of BICs make them invaluable for enhancing light–matter interactions, paving the way for developing advanced photonic devices [4].
Recent advancements have focused on the active control of BICs [5], where external stimuli, such as electric fields, temperature variations, or material phase transitions, are used to dynamically tune their properties [6]. This capability enables real-time reconfiguration [7], opening up opportunities for a wide range of applications, including tunable filters [8], [9], sensors [10], [11], [12], [13], [14], and modulators [15], [16], [17], which are critical components in modern communication, imaging, and sensing technologies. The precise manipulation of quasi-BIC (q-BIC) resonances in real-time could revolutionize photonic systems, enhancing device performance and functionality, and making this a rapidly growing field in applied physics and engineering [18].
Due to their compactness, precise control, and low power consumption, micro- and nano-electromechanical systems (MEMS/NEMS) have emerged as a leading technology in fields such as active nanophotonics, sensing, and telecommunications [19], [20], [21], [22]. These systems offer dynamic, strong on-demand tuning of optical properties, which has advanced many applications by enabling integration into smaller, more efficient devices. One of the most significant breakthroughs in this area is the control of high-Q resonances in metasurfaces through mechanical actuation [23], [24], [25]. This has led to significant advancements, particularly in imaging and active photonics, allowing for the real-time manipulation of optical properties with minimal energy input [26], [27].
Recently, the control of guided-mode resonances (GMR) using MEMS/NEMS has opened new avenues for dynamic manipulation of light in nanophotonic devices [28], [29], [30], [31]. By integrating MEMS/NEMS, the mechanical actuation of these structures allows for precise, real-time tuning of resonance characteristics, enabling modulation of amplitude, phase, and wavelength. Notably, NEMS technology has been employed to tune both GMR and q-BIC resonances in all-dielectric metasurfaces, enabling dynamic modulation of both amplitude and phase [32]. The interference between these two resonant modes significantly enhanced the phase response of the metasurfaces, allowing for precise control with minimal input. In particular, a phase shift of 144° was achieved experimentally with just a 4 V bias change. However, this approach exhibited non-zero reflection at the q-BIC resonance, which is less than ideal for imaging applications that require minimal reflection for optimal performance. Exploring the q-BIC resonances in transmission is critical for applications such as spectroscopy, sensing and imaging, where high transmission and precise control of resonances are essential for accurate data acquisition [21].
More recently, static and thermally tunable BIC-based metasurfaces have been proposed for use in spectrometers, achieving sub-nm resolution [33], [34]. While the proposed static designs in the optical range rely on bandstop filtering and require multiple metasurfaces to cover the desired spectral range, leading to extra computations and increased spectrometer size, respectively, the designed ultracompact tunable solutions in the infrared range face limitations, including the inability to maintain a constant bandwidth and a relatively narrow spectral tuning range of only 6 nm.
This work introduces MEMS-enabled comprehensive control over q-BIC resonances in a transmission configuration within all-silicon metasurfaces. The q-BIC resonance is achieved via breaking the out-of-plane symmetry by combining a 2D MEMS structure that moves close to a 1D metasurface without direct contact. Our modeling results show that the resonance quality factor approaches infinity as the MEMS structure moves farther from a 1D metasurface, thereby reducing the asymmetry – a defining characteristic of q-BIC resonances. The vertical movement of a MEMS structure combined with horizontal displacement within a 1D metasurface enables the central wavelength to be shifted by more than 60 nm while maintaining a consistent resonance bandwidth and Q-factor. The proposed all-silicon metasurfaces achieve an ultranarrow resonance linewidth with dynamic tunability in the infrared range, making them promising candidates for advanced tunable filtering applications and highly relevant for spectroscopy, remote sensing, and imaging.
2 Results
We start by investigating high-Q q-BIC resonances excited in all-silicon metasurfaces by a plane wave under normal incidence. Figure 1(a) presents a conceptual design of a resonant structure composed of a 1D metasurface made of silicon bars and an overlying 2D array of cuboids. The structural parameters shown in Figure 1(a) are as follows: w c = 0.8 µm, h c = 1 µm, w r = 0.8 µm, h r = 0.5 µm, d = 0.7 µm. We model the transmission in CST Studio, where we employ Floquet ports and periodic boundary conditions. The edge length of the square unit cell (p) is 1.5 µm. The polarization of the incident plane wave is shown in Figure 1(a).

Metasurfaces based on vertically adjustable cuboids. (a) Schematic of the tunable metasurface conceptual design: silicon bars and an array of cuboids, including the unit cell indicated by the dashed lines; (b) maximum electric field amplitude of the q-BIC mode within the bar for a = 1 µm (side and bottom views, the dashed lines show the position of the cube); (c) and (d) transmission and reflection coefficients for various distances between silicon bars and cuboids (a).
Figure 1(b) illustrates the electric field distribution at the q-BIC resonance when the distance between the cuboids and bars (a) is 1 µm. Transmission and reflection spectra for various distances between the bars and cuboids are depicted in Figure 1(c) and (d). This structure enables out-of-band transmission of near than or below 0.1 within the 3,100–3,300 nm range when tuning a from 0.2 to 1 µm and less than 0.04 across 2,700–3,400 nm when a is set to 1 µm. Figure 1(c) shows only a part of the wavelength range to highlight the resonance features and their shift more clearly.
In the absence of cuboids, no q-BIC resonance appears, as the non-radiating BIC mode remains confined within the bars. Nevertheless, the BIC mode was identified using the eigenmode solver. Introducing asymmetry by positioning the cuboids above the bars enables radiation leakage, leading to the appearance of high-Q resonances in transmission.
We use the Fano formula [35], [36] to fit the transmission curves shown in Figure 1(c), enabling accurate analysis of the characteristics of the excited q-BIC resonances while accounting for their asymmetry:
where
Figure 2(a) and (b) show the dependence of the q-BIC resonance wavelength and the Q-factor on the distance between the bars and the cuboids. The q-BIC resonance wavelength approaches the BIC value of approximately 3,193.2 nm as the cuboids move away from the 1D metasurface. To accurately describe the relationship between the Q-factor of the excited q-BIC resonances and the distance between the cuboids and the bars depicted in Figure 2(b), we can use the exponential growth formula:
where Q 0 is the offset parameter, Q 1 is the initial Q-factor value, k is the rate. The curve has the following parameters: Q 0 = −10.36, Q 1 = 76.38 and k = 0.008.
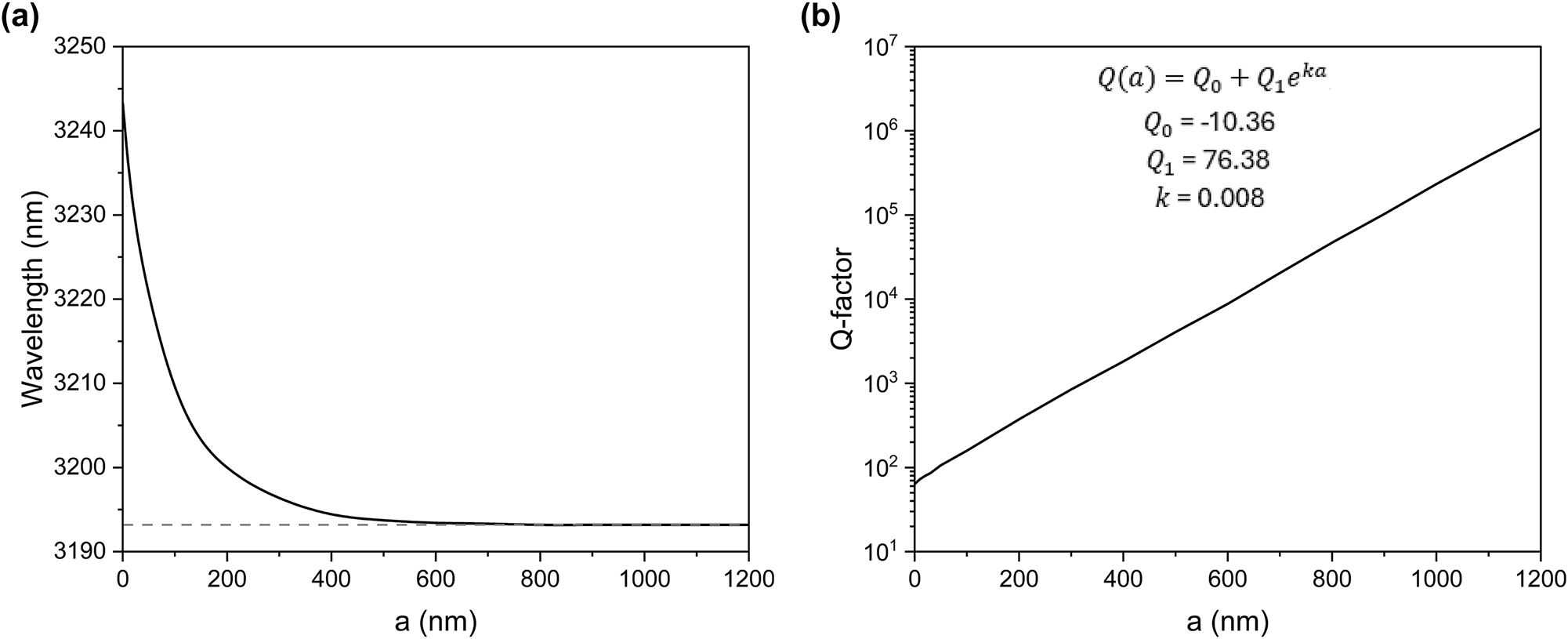
Evolution of the q-BIC resonance. (a) and (b) Dependence of the q-BIC resonance wavelength and Q-factor on the distance between the bars and cuboids.
Figure 2(b) shows that the Q-factor exponentially increases as the gap (a) widens, reaching a value of 106 when the gap is 1.2 µm. This behavior confirms the q-BIC nature of the resonance, as the quality factor of the q-BIC mode theoretically approaches infinity with decreasing asymmetry. The proximity of the cuboids to the 1D metasurface introduces asymmetry into the field distribution excited by the incident wave. Conversely, increasing the distance between the cuboids and the 1D metasurface restores the system’s symmetry, thereby reducing radiation leakage. Such control over the Q-factor of the q-BIC resonances, realized through out-of-plane symmetry breaking, offers an additional degree of freedom for tuning their characteristics. Figure 1(c) and (d) illustrate that, as the Q-factor increases, the transmission level decreases while the reflection level increases. This behavior is also accompanied by higher losses at the resonance wavelength when approaching the BIC state. Additionally, the vertical movement of the cuboids does not allow significant tuning of the central wavelength unless the separation is reduced to less than 100 nm, as shown in Figures 1(c), (d) and 2(a).
Next, we examine a more practical design featuring a 1D array of bars and a 2D MEMS membrane, as schematically shown in Figure 3(a), which enables control of the same q-BIC resonance. The MEMS membrane is flat and thin, offering a significant advantage over bulk cuboids that would require attachment to a supporting scaffolding structure for manufacturing, thereby complicating the process. Using flat membranes instead of volumetric structures greatly simplifies fabrication.

Metasurfaces based on the vertically adjustable membrane. (a) Schematic of the tunable metasurface design consisting of silicon bars and a MEMS membrane, including the unit cell indicated by the dashed lines; (b) maximum electric field amplitude of the q-BIC mode within the bar for a = 1 µm (side and bottom views, the dashed lines show the position of the MEMS membrane); (c) and (d) transmission and reflection coefficients for various distances between two layers (a).
Figure 3(a) illustrates the schematic of the proposed tunable metasurface design, comprising silicon bars and a perforated MEMS membrane, along with its transmission characteristics for varying distances between the two layers (a). The structural parameters are as follows: w m = 0.8 µm, h m = 0.3 µm, w h = 0.7 µm, l h = 1.1 µm, w c = 0.4 µm, w r = 0.8 µm, h r = 0.25 µm, d = 0.7 µm. The edge length of the square unit cell (p) is 1.5 µm. The polarization of the incident plane wave is shown using the triple of vectors in Figure 3(a). Figure 3(b) demonstrates that this design enables the excitation of the q-BIC resonance, with the electric field distribution corresponding to the loops in the bars previously depicted in Figure 1(b).
Figure 3(c) and (d) illustrate that the vertical movement of the MEMS membrane enables control over the Q-factor of the q-BIC resonances but does not provide substantial tuning of the resonance peak wavelength. The q-BIC resonance shifts by less than 20 nm when a is varied from 0.3 to 1 µm, corresponding to less than 1 % of the resonance wavelength. The Q-factor also varies with a, and the resonance exhibits an ultranarrow bandwidth of approximately 1 nm when the distance between the layers is 0.9 µm. This indicates that the MEMS-based tuning method is effective for adjusting the bandwidth but is not suitable for applications requiring significant wavelength tunability.
The height of the bars was optimized to shift the q-BIC resonance into the range of maximum reflection. This adjustment accounts for the structural differences between the cuboids and the perforated MEMS membrane, achieving out-of-band transmission below 0.1 within the 2,600–2,900 nm range when a is tuned from 0.3 µm to 1 µm. Such performance makes the proposed system suitable for spectrometers employing broadband receivers in combination with tunable filters [21].
Interestingly, the peak transmission level does not decrease with increasing the Q-factor and a, suggesting a more complex behavior of the q-BIC resonance compared to the previous case with cuboids and bars, where the peak transmission decreased as a increased. While losses remain proportional to the Q-factor, Figure 3(c) shows that the reflection at the resonance wavelength does not increase with a. This observation highlights the potential for optimizing the 2D MEMS structure to maintain high transmission values at the resonance wavelength while achieving the desired ultranarrow bandwidth.
The bars and the overlying membrane can be attached to a supporting structure (not shown in Figure 3(a)). Alternatively, the bars may be placed on a quartz substrate, which can improve the mechanical stability of the proposed metasurfaces. However, this would also increase their thickness and limit the horizontal movement of the bars. As mentioned earlier, many tunable filter applications require maintaining a constant Q-factor while significantly shifting the resonance wavelength. To meet this requirement, we further investigate the horizontal movement of the bars to gain additional control over the resonance peak wavelength.
Figure 4(a) depicts the tunable metasurface design consisting of pairs of silicon bars that can move horizontally in the direction normal to their axis, while the membrane moves vertically above the bars. The structural parameters remain consistent with those in Figure 3(a), but we alter the distance between the silicon bar pairs (d), while keeping the period p constant. The polarization of the incident plane wave is shown in Figure 4(a). Two independent orthogonal tuning mechanisms enable precise control of both the central wavelength and bandwidth (or Q-factor) of the q-BIC resonance.
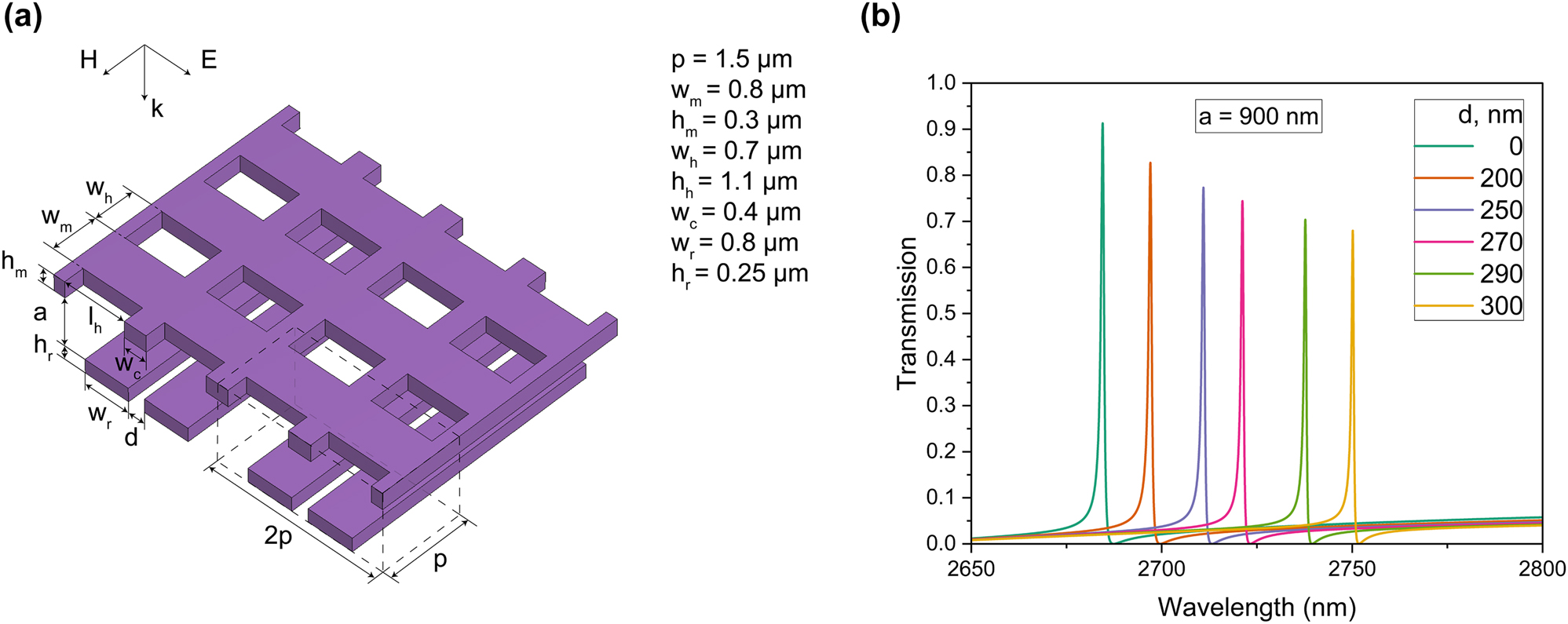
Metasurfaces based on two independent orthogonal tuning mechanisms. (a) Schematic of the tunable metasurface design consisting of pairs of silicon bars and a MEMS membrane, including the unit cell indicated by the dashed lines; (b) transmission characteristics for varying distances between the bars (d), with the distance between the two layers (a) fixed at 900 nm.
Figure 4(b) shows the transmission coefficient for various distances between the bars (d) when a = 900 nm. The horizontal movement of the bars allows for a resonance wavelength shift of approximately 65 nm. In this case, out-of-band transmission is less than 0.1 within the 2,600–3,000 nm range. The specular reflection remains almost constant as the distance between the bars increases. The reduction in transmission at the q-BIC resonance in Figure 4(b) arises from enhanced coupling of the incident wave into the first-order diffracted modes.
This approach alone does not maintain a constant bandwidth or Q-factor. As previously demonstrated, precise bandwidth control is achieved through the vertical movement of the membrane. By combining two independent orthogonal tuning mechanisms, complete control over the q-BIC resonance characteristics can be realized.
Figure 5(a) and (b) illustrate the dependence of the resonance central wavelength and Q-factor on two parameters: the distance between two layers (a) and the distance between the bars (d). By precisely adjusting both parameters, as indicated by the black lines in Figure 5(b), it is possible to maintain a constant Q-factor while tuning the central wavelength by more than 60 nm.
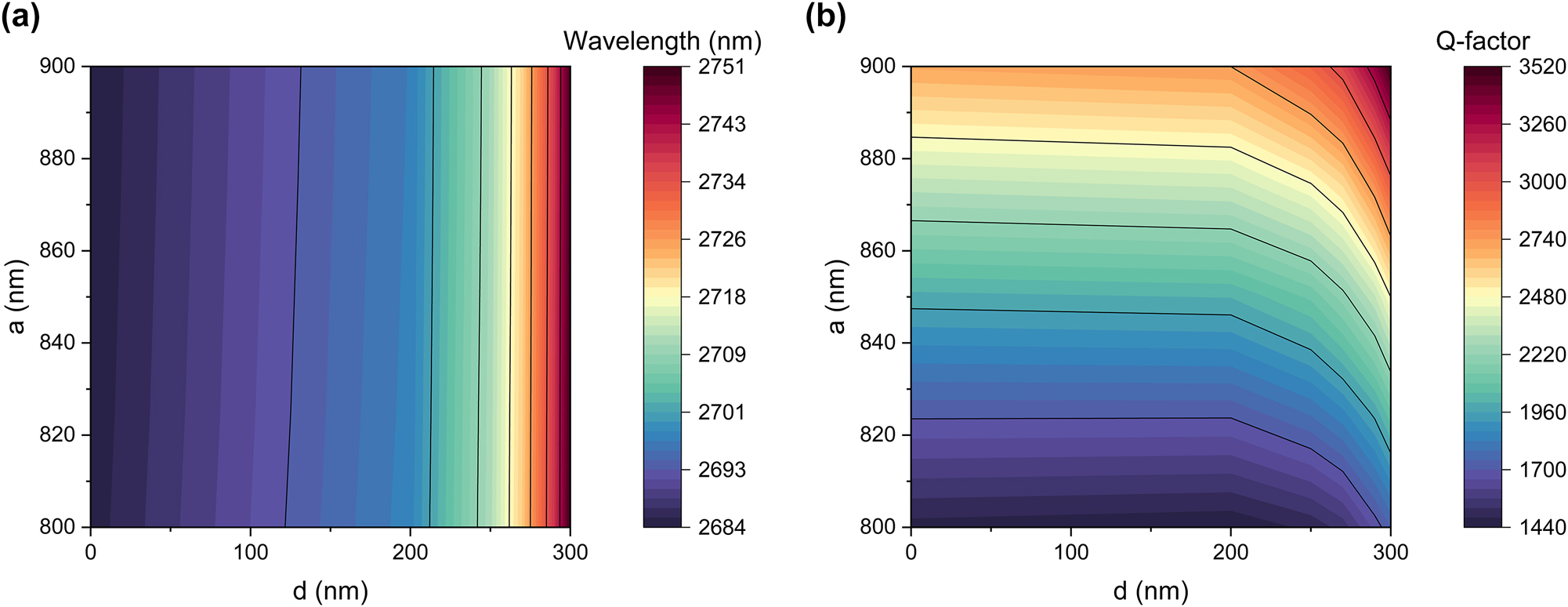
Tuning of the q-BIC resonance. (a) and (b) Dependence of the resonance central wavelength and Q-factor on two parameters: the distance between the two layers (a) and the distance between the bars (d). The black lines indicate examples of curves with constant wavelength and Q-factor, respectively.
Table 1 summarizes the characteristics of three investigated tunable metasurface designs:
Metasurface concept utilizing vertically adjustable cuboids, as shown in Figure 1(a);
Metasurface employing a single tuning mechanism based on a vertically adjustable perforated membrane, as illustrated in Figure 3(a);
Metasurfaces incorporating two independent orthogonal tuning mechanisms, as depicted in Figure 4(a).
Comparison of characteristics of the proposed tunable metasurfaces.
| Characteristic | Metasurfaces based on vertically adjustable cuboids | Metasurfaces based on the vertically adjustable membrane | Metasurfaces based on two independent orthogonal tuning mechanisms |
|---|---|---|---|
| Spectral tuning range for a > 100 nm | 15 nm | 50 nm | 65 nm |
| Constant Q factor | – | – | + |
| Range in which transmission is less than 10 % (for 1 nm resolution) | 2,700–3,500 nm | 2,600–3,000 nm | 2,600–3,000 nm |
| Flat MEMS structure | – | + | + |
Table 1 highlights the benefits of utilizing two independent orthogonal tuning mechanisms. These mechanisms enable the preservation of a consistent Q-factor of the q-BIC resonance while substantially extending the spectral tuning range. Additionally, the design ensures flat MEMS structures and achieves out-of-band transmission of less than 0.1 across a broad range near the q-BIC resonance.
3 Discussion
Our study introduces a new way to control q-BIC resonances in all-silicon metasurfaces. This is achieved by breaking out-of-plane symmetry with a supplementary 2D structure on top of a 1D metasurface where the q-BIC mode is excited. By changing the distance between the 2D MEMS structure and the 1D metasurface, we gain precise control over the Q-factor of the q-BIC resonance. Additionally, by combining two independent orthogonal tuning mechanisms within the proposed tunable metasurface designs, we demonstrated a spectral tuning range of more than 60 nm for the ultranarrow q-BIC resonance in transmission while maintaining a consistent Q-factor and out-of-band transmission below 0.1 across a broad range.
Our theoretical work outlines pathways for the experimental realization of sub-nm resolution filters combined with a wide tuning range, enabling advancements in spectroscopy and hyperspectral imaging. The proposed tunable metasurfaces can be fabricated using techniques similar to those employed for nano-electromechanical tunable suspended gratings [32]. In this approach, a buffered silicon oxide layer beneath a 1D metasurface is partially etched to achieve suspension, while the anchors remain supported by the oxide layer, ensuring structural stability.
However, we acknowledge that the experimental implementation of two independent orthogonal tuning mechanisms presents greater challenges. The bandwidth and Q-factor of the proposed metasurfaces are expected to be constrained by fabrication accuracy. Variations in the sizes of the bars, cuboids, or perforated holes in the membranes may lead to a broadening of the q-BIC resonances. Maintaining parallelism of nanostructured membranes at such small distances presents a significant practical challenge. Misalignments and membrane non-flatness are expected to broaden resonances in experiments. These detrimental effects can be mitigated by incorporating appropriate stress-compensation strategies. Counterbalancing stress-induced deformation in MEMS structures can be achieved by introducing additional layers with controlled thickness and intrinsic stress at strategic locations, thereby compensating for undesired deformations in a predictable manner [37]. Furthermore, the proposed tunable metasurface designs do not require MEMS membranes to approach the 1D metasurface closer than a few hundred nanometres, which greatly simplifies experimental realisation. Control of extraordinary optical transmission resonances through similar vertical displacement of MEMS membranes has recently been demonstrated for tunable filtering in the long-wavelength infrared range [38], showing that achieving near-zero air gaps is challenging due to fabrication non-uniformities, surface roughness, and the pull-in effect.
Our additional findings indicate that the horizontal movement of cuboids or membranes does not provide significant tunability of the q-BIC resonance wavelength while maintaining a 1 nm bandwidth. This suggests that achieving significant tunability of the q-BIC resonance wavelength within the studied metasurfaces requires modifications to the bars, where the maximum electric field is observed at resonance.
An alternative approach to realizing q-BIC resonances could be based on introduction of asymmetry within the meta-atom by positioning structures near one section of the meta-atom while leaving the other section unaffected by any additional layers. This method resembles in-plane symmetry breaking [39], [40], where geometric asymmetry enables resonance control. However, this approach will likely require MEMS structures to move close to 1D metasurfaces, which may pose challenges due to imperfections in the fabricated meta-structures.
Our work extends the exploration of additional degrees of freedom for manipulating the characteristics of q-BIC resonances and can be integrated with previously proposed permittivity-asymmetric methods [41] that rely on the electric control of silicon properties, as well as other approaches utilizing the thermal tuning of silicon [33]. MEMS structures that can be moved close to metasurfaces, particularly near high-symmetry points of undisturbed BIC modes, could act as perturbative elements and couplers to the radiation continuum [42]. The out-of-plane dimension can be leveraged to control optical chirality [43] and other key characteristics of metasurfaces, further enhancing the range of applications for mechanically tunable q-BIC resonances.
4 Conclusions
This study introduces a new method for controlling q-BIC resonances in all-silicon metasurfaces by using mechanical movements for dynamic tuning. Through breaking out-of-plane symmetry with perforated 2D MEMS membranes integrated above 1D metasurfaces, the proposed design achieves precise control over the wavelength and Q-factor of q-BIC resonances. Leveraging two independent orthogonal tuning mechanisms, the proposed method offers a spectral tuning range over 60 nm while keeping a stable Q-factor. This advancement has great potential for applications requiring tunable narrow resonances, such as imaging, sensing, and spectroscopy. Additionally, this dual MEMS tuning method can be applied to control other types of resonances.
Funding source: Australian Research Council Centre of Excellence for Transformative Meta-Optical Systems
Award Identifier / Grant number: Project ID CE200100010
Acknowledgments
The authors thank Kirill Koshelev for valuable discussions.
-
Research funding: This research was supported by the Australian Research Council Centre of Excellence for Transformative Meta-Optical Systems (Project ID CE200100010).
-
Author contributions: All authors have accepted responsibility for the entire content of this manuscript and consented to its submission to the journal, reviewed all the results and approved the final version of the manuscript. FK developed the initial idea, performed numerical modelling, and prepared the initial draft and final manuscript. IS provided funding and resources. IS, MM, and AM supervised the project. All authors analyzed the results and contributed to the discussion and manuscript writing.
-
Conflict of interest: Authors state no conflict of interest.
-
Data availability: The datasets generated and/or analysed during the current study are available from the corresponding author upon reasonable request.
References
[1] C. W. Hsu, B. Zhen, A. D. Stone, J. D. Joannopoulos, and M. Soljačić, “Bound states in the continuum,” Nat. Rev. Mater., vol. 1, no. 9, p. 16048, 2016. https://doi.org/10.1038/natrevmats.2016.48.Search in Google Scholar
[2] K. Koshelev, A. Bogdanov, and Y. Kivshar, “Meta-optics and bound states in the continuum,” Sci. Bull., vol. 64, no. 12, pp. 836–842, 2019, https://doi.org/10.1016/j.scib.2018.12.003.Search in Google Scholar PubMed
[3] S. Joseph, S. Pandey, S. Sarkar, and J. Joseph, “Bound states in the continuum in resonant nanostructures: an overview of engineered materials for tailored applications,” Nanophotonics, vol. 10, no. 17, pp. 4175–4207, 2021, https://doi.org/10.1515/nanoph-2021-0387.Search in Google Scholar
[4] S. I. Azzam and A. V. Kildishev, “Photonic bound states in the continuum: from basics to applications,” Adv. Opt. Mater., vol. 9, no. 1, p. 2001469, 2021, https://doi.org/10.1002/adom.202001469.Search in Google Scholar
[5] Y. Zeng et al.., “Manipulating light with bound states in the continuum: from passive to active systems,” Adv. Opt. Mater., vol. 12, no. 25, p. 2400296, 2024, https://doi.org/10.1002/adom.202400296.Search in Google Scholar
[6] K. Fan, I. V. Shadrivov, and W. J. Padilla, “Dynamic bound states in the continuum,” Optica, vol. 6, no. 2, p. 169, 2019, https://doi.org/10.1364/OPTICA.6.000169.Search in Google Scholar
[7] T. Gu, H. J. Kim, C. Rivero-Baleine, and J. Hu, “Reconfigurable metasurfaces towards commercial success,” Nat. Photonics, vol. 17, no. 1, pp. 48–58, 2023, https://doi.org/10.1038/s41566-022-01099-4.Search in Google Scholar
[8] T. Hu, Z. Qin, H. Chen, Z. Chen, F. Xu, and Z. Wang, “High-Q filtering and dynamic modulation in all-dielectric metasurfaces induced by quasi-BIC,” Opt. Express, vol. 30, no. 11, p. 18264, 2022, https://doi.org/10.1364/OE.457383.Search in Google Scholar PubMed
[9] F. V. Kovalev, A. E. Miroshnichenko, A. A. Basharin, H. Toepfer, and I. V. Shadrivov, “Active control of bound states in the continuum in toroidal metasurfaces,” Adv. Photonics Res., vol. 6, no. 3, p. 2400070, 2025. https://doi.org/10.1002/adpr.202400070.Search in Google Scholar
[10] X. Chen, W. Fan, and H. Yan, “Toroidal dipole bound states in the continuum metasurfaces for terahertz nanofilm sensing,” Opt. Express, vol. 28, no. 11, p. 17102, 2020, https://doi.org/10.1364/OE.394416.Search in Google Scholar PubMed
[11] W. Cen et al.., “Ultrasensitive flexible terahertz plasmonic metasurface sensor based on bound states in the continuum,” IEEE Sens. J., vol. 22, no. 13, pp. 12838–12845, 2022, https://doi.org/10.1109/JSEN.2022.3177538.Search in Google Scholar
[12] R. E. Jacobsen, A. Krasnok, S. Arslanagić, A. V. Lavrinenko, and A. Alú, “Boundary-induced embedded eigenstate in a single resonator for advanced sensing,” ACS Photonics, vol. 9, no. 6, pp. 1936–1943, 2022, https://doi.org/10.1021/acsphotonics.1c01840.Search in Google Scholar
[13] Z. Jing, W. Jiaxian, G. Lizhen, and Q. Weibin, “High-sensitivity sensing in all-dielectric metasurface driven by quasi-bound states in the continuum,” Nanomaterials, vol. 13, no. 3, p. 505, 2023, https://doi.org/10.3390/nano13030505.Search in Google Scholar PubMed PubMed Central
[14] R. Sato et al.., “Observation of edge bound states in the continuum at truncated silicon pillar photonic crystal,” Nat. Commun., vol. 15, no. 1, p. 10544, 2024, https://doi.org/10.1038/s41467-024-54929-0.Search in Google Scholar PubMed PubMed Central
[15] Y. Xu et al.., “Quasi-BIC based low-voltage phase modulation on lithium niobite metasurface,” IEEE Photon. Technol. Lett., vol. 34, no. 20, pp. 1077–1080, 2022, https://doi.org/10.1109/LPT.2022.3201268.Search in Google Scholar
[16] Z. Yang et al.., “Ultrafast Q-boosting in semiconductor metasurfaces,” Nanophotonics, vol. 13, no. 12, pp. 2173–2182, 2024, https://doi.org/10.1515/nanoph-2023-0718.Search in Google Scholar PubMed PubMed Central
[17] H. Zheng et al.., “Electromagnetically induced transparency enabled by quasi-bound states in the continuum modulated by epsilon-near-zero materials,” Opt. Express, vol. 32, no. 5, p. 7318, 2024, https://doi.org/10.1364/OE.517111.Search in Google Scholar PubMed
[18] G. Xu et al.., “Recent advances and perspective of photonic bound states in the continuum,” Ultrafast Sci., vol. 3, p. 0033, 2023, https://doi.org/10.34133/ultrafastscience.0033.Search in Google Scholar
[19] H. B. Khaniki, M. H. Ghayesh, and M. Amabili, “A review on the statics and dynamics of electrically actuated nano and micro structures,” Int. J. Non Lin. Mech., vol. 129, p. 103658, 2021, https://doi.org/10.1016/j.ijnonlinmec.2020.103658.Search in Google Scholar
[20] S. Nazir and O. S. Kwon, “Micro-electromechanical systems-based sensors and their applications,” Appl. Sci. Converg. Technol., vol. 31, no. 2, pp. 40–45, 2022, https://doi.org/10.5757/ASCT.2022.31.2.40.Search in Google Scholar
[21] M. Martyniuk et al.., “Optical microelectromechanical systems technologies for spectrally adaptive sensing and imaging,” Adv. Funct. Mater., vol. 32, no. 3, p. 2103153, 2022, https://doi.org/10.1002/adfm.202103153.Search in Google Scholar
[22] Y. Ma, W. Liu, X. Liu, N. Wang, and H. Zhang, “Review of sensing and actuation technologies – from optical MEMS and nanophotonics to photonic nanosystems,” Int. J. Optomechatron., vol. 18, no. 1, p. 2342279, 2024, https://doi.org/10.1080/15599612.2024.2342279.Search in Google Scholar
[23] A. L. Holsteen, A. F. Cihan, and M. L. Brongersma, “Temporal color mixing and dynamic beam shaping with silicon metasurfaces,” Science, vol. 365, no. 6450, pp. 257–260, 2019, https://doi.org/10.1126/science.aax5961.Search in Google Scholar PubMed
[24] Z. Ren, Y. Chang, Y. Ma, K. Shih, B. Dong, and C. Lee, “Leveraging of MEMS technologies for optical metamaterials applications,” Adv. Opt. Mater., vol. 8, no. 3, p. 1900653, 2020, https://doi.org/10.1002/adom.201900653.Search in Google Scholar
[25] Y. Chang, J. Wei, and C. Lee, “Metamaterials – from fundamentals and MEMS tuning mechanisms to applications,” Nanophotonics, vol. 9, no. 10, pp. 3049–3070, 2020, https://doi.org/10.1515/nanoph-2020-0045.Search in Google Scholar
[26] N. I. Zheludev and E. Plum, “Reconfigurable nanomechanical photonic metamaterials,” Nat. Nanotechnol., vol. 11, no. 1, pp. 16–22, 2016, https://doi.org/10.1038/nnano.2015.302.Search in Google Scholar PubMed
[27] Y. Zhao et al.., “Mechanically reconfigurable metasurfaces: fabrications and applications,” npj Nanophoton., vol. 1, no. 1, p. 16, 2024, https://doi.org/10.1038/s44310-024-00010-z.Search in Google Scholar
[28] R. Magnusson and Y. Ding, “MEMS tunable resonant leaky mode filters,” IEEE Photon. Technol. Lett., vol. 18, no. 14, pp. 1479–1481, 2006, https://doi.org/10.1109/LPT.2006.877578.Search in Google Scholar
[29] T. Sang, T. Cai, S. Cai, and Z. Wang, “Tunable transmission filters based on double-subwavelength periodic membrane structures with an air gap,” J. Opt., vol. 13, no. 12, p. 125706, 2011, https://doi.org/10.1088/2040-8978/13/12/125706.Search in Google Scholar
[30] G. Quaranta, G. Basset, O. J. F. Martin, and B. Gallinet, “Recent advances in resonant waveguide gratings,” Laser Photonics Rev., vol. 12, no. 9, p. 1800017, 2018, https://doi.org/10.1002/lpor.201800017.Search in Google Scholar
[31] Y. H. Ko, K. J. Lee, S. Das, N. Gupta, and R. Magnusson, “Micro-electromechanical-system-tuned resonant filters spanning the 8–12 µm band,” Opt. Lett., vol. 46, no. 6, p. 1329, 2021, https://doi.org/10.1364/OL.418545.Search in Google Scholar PubMed
[32] H. Kwon, T. Zheng, and A. Faraon, “Nano-electromechanical tuning of dual-mode resonant dielectric metasurfaces for dynamic amplitude and phase modulation,” Nano Lett., vol. 21, no. 7, pp. 2817–2823, 2021, https://doi.org/10.1021/acs.nanolett.0c04888.Search in Google Scholar PubMed PubMed Central
[33] X. Zhou et al.., “Ultra-compact on-chip spectrometer based on thermally tuned topological miniaturized bound states in the continuum cavity,” Opt. Lett., vol. 48, no. 19, p. 4993, 2023, https://doi.org/10.1364/OL.502507.Search in Google Scholar PubMed
[34] F. Tang et al.., “Metasurface spectrometers beyond resolution-sensitivity constraints,” Sci. Adv., vol. 10, no. 49, p. eadr7155, 2024, https://doi.org/10.1126/sciadv.adr7155.Search in Google Scholar PubMed PubMed Central
[35] M. Galli, S. L. Portalupi, M. Belotti, L. C. Andreani, L. O’Faolain, and T. F. Krauss, “Light scattering and Fano resonances in high-Q photonic crystal nanocavities,” Appl. Phys. Lett., vol. 94, no. 7, p. 071101, 2009, https://doi.org/10.1063/1.3080683.Search in Google Scholar
[36] A. E. Miroshnichenko, S. Flach, and Y. S. Kivshar, “Fano resonances in nanoscale structures,” Rev. Mod. Phys., vol. 82, no. 3, pp. 2257–2298, 2010, https://doi.org/10.1103/RevModPhys.82.2257.Search in Google Scholar
[37] M. Liu et al.., “Ultrathin tunable terahertz absorber based on MEMS-driven metamaterial,” Microsyst. Nanoeng., vol. 3, no. 1, p. 17033, 2017, https://doi.org/10.1038/micronano.2017.33.Search in Google Scholar PubMed PubMed Central
[38] O. Bannik et al.., “Micromachined double-membrane mechanically tunable metamaterial for thermal infrared filtering,” Adv. Photonics Res., vol. 6, no. 5, p. 2400185, 2025, https://doi.org/10.1002/adpr.202400185.Search in Google Scholar
[39] Z. Zheng et al.., “Planar narrow bandpass filter based on Si resonant metasurface,” J. Appl. Phys., vol. 130, no. 5, p. 053105, 2021, https://doi.org/10.1063/5.0058768.Search in Google Scholar
[40] C. Zhou et al.., “Bound states in the continuum in asymmetric dielectric metasurfaces,” Laser Photonics Rev., vol. 17, no. 3, p. 2200564, 2023, https://doi.org/10.1002/lpor.202200564.Search in Google Scholar
[41] R. Berté et al.., “Permittivity-asymmetric quasi -bound states in the continuum,” Nano Lett., vol. 23, no. 7, pp. 2651–2658, 2023, https://doi.org/10.1021/acs.nanolett.2c05021.Search in Google Scholar PubMed
[42] G. Q. Moretti, A. Tittl, E. Cortés, S. A. Maier, A. V. Bragas, and G. Grinblat, “Introducing a symmetry-breaking coupler into a dielectric metasurface enables robust high-Q quasi-BICs,” Adv. Photonics Res., vol. 3, no. 12, p. 2200111, 2022, https://doi.org/10.1002/adpr.202200111.Search in Google Scholar
[43] L. Kühner et al.., “Unlocking the out-of-plane dimension for photonic bound states in the continuum to achieve maximum optical chirality,” Light Sci. Appl., vol. 12, no. 1, p. 250, 2023, https://doi.org/10.1038/s41377-023-01295-z.Search in Google Scholar PubMed PubMed Central
© 2025 the author(s), published by De Gruyter, Berlin/Boston
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Frontmatter
- Reviews
- Light-driven micro/nanobots
- Tunable BIC metamaterials with Dirac semimetals
- Large-scale silicon photonics switches for AI/ML interconnections based on a 300-mm CMOS pilot line
- Perspective
- Density-functional tight binding meets Maxwell: unraveling the mysteries of (strong) light–matter coupling efficiently
- Letters
- Broadband on-chip spectral sensing via directly integrated narrowband plasmonic filters for computational multispectral imaging
- Sub-100 nm manipulation of blue light over a large field of view using Si nanolens array
- Tunable bound states in the continuum through hybridization of 1D and 2D metasurfaces
- Integrated array of coupled exciton–polariton condensates
- Disentangling the absorption lineshape of methylene blue for nanocavity strong coupling
- Research Articles
- Demonstration of multiple-wavelength-band photonic integrated circuits using a silicon and silicon nitride 2.5D integration method
- Inverse-designed gyrotropic scatterers for non-reciprocal analog computing
- Highly sensitive broadband photodetector based on PtSe2 photothermal effect and fiber harmonic Vernier effect
- Online training and pruning of multi-wavelength photonic neural networks
- Robust transport of high-speed data in a topological valley Hall insulator
- Engineering super- and sub-radiant hybrid plasmons in a tunable graphene frame-heptamer metasurface
- Near-unity fueling light into a single plasmonic nanocavity
- Polarization-dependent gain characterization in x-cut LNOI erbium-doped waveguide amplifiers
- Intramodal stimulated Brillouin scattering in suspended AlN waveguides
- Single-shot Stokes polarimetry of plasmon-coupled single-molecule fluorescence
- Metastructure-enabled scalable multiple mode-order converters: conceptual design and demonstration in direct-access add/drop multiplexing systems
- High-sensitivity U-shaped biosensor for rabbit IgG detection based on PDA/AuNPs/PDA sandwich structure
- Deep-learning-based polarization-dependent switching metasurface in dual-band for optical communication
- A nonlocal metasurface for optical edge detection in the far-field
- Coexistence of weak and strong coupling in a photonic molecule through dissipative coupling to a quantum dot
- Mitigate the variation of energy band gap with electric field induced by quantum confinement Stark effect via a gradient quantum system for frequency-stable laser diodes
- Orthogonal canalized polaritons via coupling graphene plasmon and phonon polaritons of hBN metasurface
- Dual-polarization electromagnetic window simultaneously with extreme in-band angle-stability and out-of-band RCS reduction empowered by flip-coding metasurface
- Record-level, exceptionally broadband borophene-based absorber with near-perfect absorption: design and comparison with a graphene-based counterpart
- Generalized non-Hermitian Hamiltonian for guided resonances in photonic crystal slabs
- A 10× continuously zoomable metalens system with super-wide field of view and near-diffraction–limited resolution
- Continuously tunable broadband adiabatic coupler for programmable photonic processors
- Diffraction order-engineered polarization-dependent silicon nano-antennas metagrating for compact subtissue Mueller microscopy
- Lithography-free subwavelength metacoatings for high thermal radiation background camouflage empowered by deep neural network
- Multicolor nanoring arrays with uniform and decoupled scattering for augmented reality displays
- Permittivity-asymmetric qBIC metasurfaces for refractive index sensing
- Theory of dynamical superradiance in organic materials
- Second-harmonic generation in NbOI2-integrated silicon nitride microdisk resonators
- A comprehensive study of plasmonic mode hybridization in gold nanoparticle-over-mirror (NPoM) arrays
- Foundry-enabled wafer-scale characterization and modeling of silicon photonic DWDM links
- Rough Fabry–Perot cavity: a vastly multi-scale numerical problem
- Classification of quantum-spin-hall topological phase in 2D photonic continuous media using electromagnetic parameters
- Light-guided spectral sculpting in chiral azobenzene-doped cholesteric liquid crystals for reconfigurable narrowband unpolarized light sources
- Modelling Purcell enhancement of metasurfaces supporting quasi-bound states in the continuum
- Ultranarrow polaritonic cavities formed by one-dimensional junctions of two-dimensional in-plane heterostructures
- Bridging the scalability gap in van der Waals light guiding with high refractive index MoTe2
- Ultrafast optical modulation of vibrational strong coupling in ReCl(CO)3(2,2-bipyridine)
- Chirality-driven all-optical image differentiation
- Wafer-scale CMOS foundry silicon-on-insulator devices for integrated temporal pulse compression
- Monolithic temperature-insensitive high-Q Ta2O5 microdisk resonator
- Nanogap-enhanced terahertz suppression of superconductivity
- Large-gap cascaded Moiré metasurfaces enabling switchable bright-field and phase-contrast imaging compatible with coherent and incoherent light
- Synergistic enhancement of magneto-optical response in cobalt-based metasurfaces via plasmonic, lattice, and cavity modes
- Scalable unitary computing using time-parallelized photonic lattices
- Diffusion model-based inverse design of photonic crystals for customized refraction
- Wafer-scale integration of photonic integrated circuits and atomic vapor cells
- Optical see-through augmented reality via inverse-designed waveguide couplers
- One-dimensional dielectric grating structure for plasmonic coupling and routing
- MCP-enabled LLM for meta-optics inverse design: leveraging differentiable solver without LLM expertise
- Broadband variable beamsplitter made of a subwavelength-thick metamaterial
- Scaling-dependent tunability of spin-driven photocurrents in magnetic metamaterials
- AI-based analysis algorithm incorporating nanoscale structural variations and measurement-angle misalignment in spectroscopic ellipsometry
Articles in the same Issue
- Frontmatter
- Reviews
- Light-driven micro/nanobots
- Tunable BIC metamaterials with Dirac semimetals
- Large-scale silicon photonics switches for AI/ML interconnections based on a 300-mm CMOS pilot line
- Perspective
- Density-functional tight binding meets Maxwell: unraveling the mysteries of (strong) light–matter coupling efficiently
- Letters
- Broadband on-chip spectral sensing via directly integrated narrowband plasmonic filters for computational multispectral imaging
- Sub-100 nm manipulation of blue light over a large field of view using Si nanolens array
- Tunable bound states in the continuum through hybridization of 1D and 2D metasurfaces
- Integrated array of coupled exciton–polariton condensates
- Disentangling the absorption lineshape of methylene blue for nanocavity strong coupling
- Research Articles
- Demonstration of multiple-wavelength-band photonic integrated circuits using a silicon and silicon nitride 2.5D integration method
- Inverse-designed gyrotropic scatterers for non-reciprocal analog computing
- Highly sensitive broadband photodetector based on PtSe2 photothermal effect and fiber harmonic Vernier effect
- Online training and pruning of multi-wavelength photonic neural networks
- Robust transport of high-speed data in a topological valley Hall insulator
- Engineering super- and sub-radiant hybrid plasmons in a tunable graphene frame-heptamer metasurface
- Near-unity fueling light into a single plasmonic nanocavity
- Polarization-dependent gain characterization in x-cut LNOI erbium-doped waveguide amplifiers
- Intramodal stimulated Brillouin scattering in suspended AlN waveguides
- Single-shot Stokes polarimetry of plasmon-coupled single-molecule fluorescence
- Metastructure-enabled scalable multiple mode-order converters: conceptual design and demonstration in direct-access add/drop multiplexing systems
- High-sensitivity U-shaped biosensor for rabbit IgG detection based on PDA/AuNPs/PDA sandwich structure
- Deep-learning-based polarization-dependent switching metasurface in dual-band for optical communication
- A nonlocal metasurface for optical edge detection in the far-field
- Coexistence of weak and strong coupling in a photonic molecule through dissipative coupling to a quantum dot
- Mitigate the variation of energy band gap with electric field induced by quantum confinement Stark effect via a gradient quantum system for frequency-stable laser diodes
- Orthogonal canalized polaritons via coupling graphene plasmon and phonon polaritons of hBN metasurface
- Dual-polarization electromagnetic window simultaneously with extreme in-band angle-stability and out-of-band RCS reduction empowered by flip-coding metasurface
- Record-level, exceptionally broadband borophene-based absorber with near-perfect absorption: design and comparison with a graphene-based counterpart
- Generalized non-Hermitian Hamiltonian for guided resonances in photonic crystal slabs
- A 10× continuously zoomable metalens system with super-wide field of view and near-diffraction–limited resolution
- Continuously tunable broadband adiabatic coupler for programmable photonic processors
- Diffraction order-engineered polarization-dependent silicon nano-antennas metagrating for compact subtissue Mueller microscopy
- Lithography-free subwavelength metacoatings for high thermal radiation background camouflage empowered by deep neural network
- Multicolor nanoring arrays with uniform and decoupled scattering for augmented reality displays
- Permittivity-asymmetric qBIC metasurfaces for refractive index sensing
- Theory of dynamical superradiance in organic materials
- Second-harmonic generation in NbOI2-integrated silicon nitride microdisk resonators
- A comprehensive study of plasmonic mode hybridization in gold nanoparticle-over-mirror (NPoM) arrays
- Foundry-enabled wafer-scale characterization and modeling of silicon photonic DWDM links
- Rough Fabry–Perot cavity: a vastly multi-scale numerical problem
- Classification of quantum-spin-hall topological phase in 2D photonic continuous media using electromagnetic parameters
- Light-guided spectral sculpting in chiral azobenzene-doped cholesteric liquid crystals for reconfigurable narrowband unpolarized light sources
- Modelling Purcell enhancement of metasurfaces supporting quasi-bound states in the continuum
- Ultranarrow polaritonic cavities formed by one-dimensional junctions of two-dimensional in-plane heterostructures
- Bridging the scalability gap in van der Waals light guiding with high refractive index MoTe2
- Ultrafast optical modulation of vibrational strong coupling in ReCl(CO)3(2,2-bipyridine)
- Chirality-driven all-optical image differentiation
- Wafer-scale CMOS foundry silicon-on-insulator devices for integrated temporal pulse compression
- Monolithic temperature-insensitive high-Q Ta2O5 microdisk resonator
- Nanogap-enhanced terahertz suppression of superconductivity
- Large-gap cascaded Moiré metasurfaces enabling switchable bright-field and phase-contrast imaging compatible with coherent and incoherent light
- Synergistic enhancement of magneto-optical response in cobalt-based metasurfaces via plasmonic, lattice, and cavity modes
- Scalable unitary computing using time-parallelized photonic lattices
- Diffusion model-based inverse design of photonic crystals for customized refraction
- Wafer-scale integration of photonic integrated circuits and atomic vapor cells
- Optical see-through augmented reality via inverse-designed waveguide couplers
- One-dimensional dielectric grating structure for plasmonic coupling and routing
- MCP-enabled LLM for meta-optics inverse design: leveraging differentiable solver without LLM expertise
- Broadband variable beamsplitter made of a subwavelength-thick metamaterial
- Scaling-dependent tunability of spin-driven photocurrents in magnetic metamaterials
- AI-based analysis algorithm incorporating nanoscale structural variations and measurement-angle misalignment in spectroscopic ellipsometry

