Integrability, exact solutions and nonlinear dynamics of a nonisospectral integral-differential system

Bo Xu; Sheng Zhang

doi:10.1515/phys-2019-0031

Artikel Open Access

Integrability, exact solutions and nonlinear dynamics of a nonisospectral integral-differential system

Bo Xu und Sheng Zhang

Veröffentlicht/Copyright: 17. Juni 2019

Veröffentlicht von

Veröffentlichen auch Sie bei De Gruyter Brill

Manuskript einreichen Informationen für Autor*innen Erkunden Sie dieses Fachgebiet

Aus der Zeitschrift Open Physics Band 17 Heft 1

Abstract

The investigations of integrability, exact solutions and dynamics of nonlinear partial differential equations (PDEs) are vital issues in nonlinear mathematical physics. In this paper, we derive and solve a new Lax integrable nonisospectral integral-differential system. To be specific, we first generalize an eigenvalue problem and its adjoint equation by equipping it with a new time-varying spectral parameter. Based on the generalized eigenvalue problem and the adjoint equation, we then derive a new Lax integrable nonisospectral integral-differential system. Furthermore, we obtain exact solutions and their reduced forms of the derived system by extending the famous non-linear Fourier analysis method–inverse scattering transform (IST). Finally, with graphical assistance we simulate a pair of reduced solutions, the dynamical evolutions of which show that the amplitudes of solutions vary with time.

Keywords: Integral-differential system; Integrability; Exact solution; Dynamical evolution; IST

PACS: 05.45.Yv; 02.30.Ik; 05.45.-a

1 Introduction

Nonlinear PDEs are important mathematical models describing some nonlinear natural phenomena like those in physics, biology, chemistry and mechanics. In the field of nonlinear science, the investigation of integrability, exact solutions and dynamics of nonlinear PDEs has attracted much attention [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]. There is no uniform definition for the integrability of PDEs. Usually, it is necessary to indicate the type of integrability [16]. In soliton theory, the non-linear PDEs are classified two types: the isospectral equations and the nonisospectral equations. Generally speaking, the spectral parameters of the eigenvalue problems associated with isospectral equations are time-independent. Otherwise when the spectral parameters are dependent of time, the associated equations are nonisospectral.

The purpose of this article is to study the integrability, exact solutions and nonlinear dynamics of the following new nonisospectral integral-differential system:

(1) q r t = − q x x + 2 q 2 r + 3 q x x + x q x x x − 2 q x ∂ − 1 ( q r ) − 4 x q r q x − 2 x q 2 r x − 8 q ∂ − 1 ( q x r ) − 2 x q r q x x + 2 x q 2 r x x − 2 q x − x q x x + 2 q ∂ − 1 ( q r ) + 2 x q 2 r + q + x q x − x q r x x − 2 q r 2 + 3 r x x + x r x x x − 2 r x ∂ − 1 ( q r ) − 4 x q r r x − 2 x r 2 q x − 8 q ∂ − 1 ( q r x ) − 2 x q r r x x + 2 x r 2 q x x + 2 r x + x r x x − 2 r ∂ − 1 ( q r ) − 2 x q r 2 + r + x r x + x r

In section 2, we derive the integral-differential system (1) and prove its Lax integrability. In section 3, we construct exact solutions and their reduced forms of system (1) by equipping the IST method [17, 18, 19] with a new time-varying spectral parameter. In section 4, a pair of reduced solutions are simulated to offer an insight into the dynamical evolutions of solutions.

2 Derivation and Lax Integrability

To derive system (1), firstly we equip the eigenvalue problem [20]:

(2) ϕ x = M ϕ , M = − i k q r i k , ϕ = ϕ 1 ϕ 2 ,

and its adjoint equation

(3) ϕ t = N ϕ , N = A B C − A ,

with a new spectral parameter k satisfying

(4) i k t = 1 2 ∑ n = 0 3 ( 2 i k ) n .

In Eqs. (2) and (3), the potential functions q = q(x, t) ^→ 0, r = r(x, t) ^→ 0 as x ^→ ±∞, all the derivatives of q and r have the same asymptotic properties, and A = A(x, t, k, q, r), B = B(x, t, k, q, r) and C = C(x, t, k, q, r) are functions of the indicated variables to be determined later.

Secondly, using the compatibility condition of Eqs. (2) and (3) we have

(5) A x = q C − r B − i k t ,

(6) q t = B x + 2 i k B + 2 q A ,

(7) r t = C x − 2 i k C − 2 r A .

In view of Eqs. (4) and (5), we suppose that

(8) A = ∂ − 1 ( r , q ) − B C − 1 2 ( 2 i k ) 2 − 1 2 ∑ n = 0 3 ( 2 i k ) n x .

Then Eqs. (5)-(7) can be simplified as

(9) q r t = L − B C − 2 i k − B C + ( 2 i k ) 2 − q r + ∑ m = 0 3 ( 2 i k ) m − x q x r ,

by the usage of the operator

(10) L = − ∂ 0 0 ∂ + 2 q − r ∂ − 1 ( r , q ) , ∂ = ∂ ∂ x , ∂ − 1 = 1 2 ∫ − ∞ x − ∫ x + ∞ d x .

Thirdly, we let

(11) − B C = ∑ m = 1 3 − b m c m ( 2 i k ) 3 − m ,

then the coefficients of 2ik in Eq. (9) give

(12) ( 2 i k ) 0 : q r t = L − b 3 c 3 + − x q x r ,

(13) ( 2 i k ) 1 : − b 3 c 3 = L − b 2 c 2 + − x q x r ,

(14) ( 2 i k ) 2 : − b 2 c 2 = L − b 1 c 1 + − q r + − x q x r ,

(15) ( 2 i k ) 3 : − b 1 c 1 = − x q x r .

Finally, substituting Eq. (12) yields system (1). This shows that system (1) is Lax integrable.

3 Exact solutions and their reductions

This section has three aspects: the first aspect is to determine the scattering data for the generalized eigenvalue problem (2); the second aspect is to construct exact solutions of system (1); and the last aspect is to reduce the obtained exact solutions.

3.1 Scattering data

Theorem 1

The generalized eigenvalue problem (2) has the following scattering data:

(16) κ j t ( t ) = − i 2 ∑ n = 0 3 2 i κ j ( t ) n c j 2 ( t ) = c j 2 ( 0 ) e ∫ 0 t ∑ s = 1 3 s ( 2 i κ j ( w ) ) s − 1 − 4 κ j 2 ( w ) d w , R ( t , k ) = R ( 0 , k ) e − 4 ∫ 0 t k 2 ( τ ) d τ

(17) κ ¯ m t ( t ) = − i 2 ∑ n = 0 3 2 i κ ¯ m ( t ) n c ¯ m 2 ( t ) = c ¯ m 2 ( 0 ) e − ∫ 0 t ∑ s = 1 3 s ( 2 i κ ¯ m ( w ) ) s − 1 − 4 κ ¯ m 2 ( w ) d w , R ¯ ( t , k ) = R ¯ ( 0 , k ) e 4 ∫ 0 t k ¯ 2 ( τ ) d τ

for j = 1 , 2 , ⋯ , n a n d m = 1 , 2 , ⋯ , n ¯ , h e r e c j ( 0 ) , c ¯ m ( 0 ) , R(0, k) and R(0, k) are the scattering data of the generalized eigenvalue problem (2) in the case of q(0, x) and r(0, x).

Proof. When ϕ(x, k) satisfies Eq. (2), ϕ_t(x, k) − Nϕ(x, k) also satisfies Eq. (2), then one has

(18) ϕ t ( x , k ) − N ϕ ( x , k ) = ρ ( t , k ) ϕ ( x , k ) + θ ( t , k ) ϕ ~ ( x , k ) .

where ϕ ( x , k ) a n d ϕ ~ ( x , k ) are a pair of fundamental solutions of Eq. (2), ρ(t, k) and θ(t, k) are undetermined coefficient functions.

Firstly, we begin with the spectral parameter k = k_j(t)(Imk_j > 0) of the discrete case. Then we must have θ(t, k) = 0 because ϕ ( x , κ j ( t ) ) and ϕ ~ ( x , k ) have opposite exponentially asymptotic properties as x ^→ +∞. Thus Eq. (18) becomes

(19) ϕ t ( x , κ j ( t ) ) − N ϕ ( x , κ j ( t ) ) = ρ ( t , κ j ( t ) ) ϕ ( x , κ j ( t ) ) ,

which can be further written as [6]

(20) d d t ϕ 1 ( x , κ j ( t ) ) ϕ 2 ( x , κ j ( t ) ) − C ϕ 1 2 ( x , κ j ( t ) ) + B ϕ 2 2 ( x , κ j ( t ) ) = 2 ρ ( t , κ j ( t ) ) ϕ 1 ( x , κ j ( t ) ) ϕ 2 ( x , κ j ( t ) )

Supposing ϕ ( x , κ j ( t ) ) and c j 2 ( t ) are the normalization eigenfunction and the normalization constant respectively, then we have [6]

(21) ρ ( t , κ j ( t ) ) = 1 2 ∑ s = 1 3 s ( 2 i κ j ( t ) ) s − 1 .

In view of Eqs. (3), (19), (21) and

(22) A → − 1 2 ∑ m = 0 3 ( 2 i κ j ( t ) ) m x − 1 2 ( 2 i κ j ( t ) ) 2 , B → 0 , C → 0 ,

(23) ϕ ( x , κ j ( t ) ) → c j ( t ) 0 1 e i κ j ( t ) x ,

as x ^→ +∞, we obtain

(24) κ j t ( t ) = − i 2 ∑ n = 0 3 ( 2 i κ j ( t ) ) n c j t ( t ) − c j ( t ) 1 2 ∑ s = 1 3 s ( 2 i κ j ( t ) ) s − 1 + 1 2 ( 2 i κ j ( t ) ) 2 = 0.

Similarly, we obtain

(25) κ ¯ m t ( t ) = − i 2 ∑ n = 0 3 ( 2 i κ ¯ m ( t ) ) n , c ¯ m t + c ¯ m 1 2 ∑ s = 1 3 s ( 2 i κ ¯ m ) s − 1 + 1 2 ( 2 i κ ¯ m ) 2 = 0.

Secondly, we consider the case when k is a real continuous spectral parameter. Since

(26) φ t ( x , k ) − N φ ( x , k ) = ε ( t , k ) φ ( x , k ) + δ ( t , k ) φ ¯ ( x , k ) ,

where φ(x, k) and φ(x, k) are another pair of fundamental solutions of Eq. (2), ε(t, k) and δ(t, k) are undetermined coefficient functions.

Letting x ^→ −∞ and using

(27) φ ( x , k ) → 1 0 e − i k x , φ ¯ ( x , k ) → 0 − 1 e i k x ,

from Eq. (26) we have

(28) ε ( t , k ) = − 4 k 2 , δ ( t , k ) = 0.

Taking the following Jost relationship with two undetermined coefficient functions λ(t, k) and μ(t, k):

(29) φ ( x , k ) = λ ( t , k ) ϕ ¯ ( x , k ) + μ ( t , k ) ϕ ( x , k ) ,

and substituting Eq. (29) into Eq. (26), we have

(30) λ ( t , k ) ϕ ¯ ( x , k ) + μ ( t , k ) ϕ ( x , k ) t − N ( λ ( t , k ) ϕ ¯ ( x , k ) + μ ( t , k ) ϕ ( x , k ) ) = − 4 k 2 ϕ ( x , k ) .

Using Eq. (30) and the asymptotical properties

(31) ϕ ( x , k ) → 0 1 e i k x , ϕ ¯ ( x , k ) → 1 0 e − i k x , x → − ∞ ,

yields

(32) d λ ( t , k ) d t = 0 , d μ ( t , k ) d t = − 4 k 2 μ ( t , k ) .

With a similar process, we obtain

(33) d λ ¯ ( t , k ) d t = 0 , d μ ¯ ( t , k ) d t = 4 k 2 μ ¯ ( t , k ) .

Directly solving Eqs. (24), (25), (32) and (33), we arrive at Eqs. (16) and (17). Thus, we finish the proof of Theorem 1.

3.2 Exact solutions

Theorem 2

With the help of scattering data k_j(t), c_j(t), R ( t , k ) , κ ¯ m ( t ) , c ¯ m ( t ) , R ¯ ( t , k ) in Eqs. (16) and (17), we can determine the following exact solutions of system (1):

(34) q ( x , t ) = − 2 K 1 ( t , x , x ) ,

(35) r ( x , t ) = K 2 x ( t , x , x ) K 1 ( t , x , x ) ,

where K₁(t, x, y) and K₂(t, x, y) satisfy:

(36) K 1 ( t , x , y ) − 1 2 π ∫ − ∞ ∞ R ¯ ( t , k ) e − i k ( x + y ) d k + ∑ j = 1 n ¯ c ¯ j 2 ( t ) e − i κ ¯ j ( t ) ( x + y ) − ∫ x ∞ K 1 ( t , x , s ) ∑ j = 1 n ∑ m = 1 n ¯ i c j 2 ( t ) c ¯ m 2 ( t ) κ j ( t ) − κ ¯ m ( t ) e i κ j ( t ) ( x + s ) − i κ ¯ m ( t ) ( x + y ) d s = 0

(37) K 2 ( t , x , y ) − ∑ j = 1 n ∑ m = 1 n ¯ i c j 2 ( t ) c ¯ m 2 ( t ) κ j ( t ) − κ ¯ m ( t ) e 2 i κ j ( t ) x − i κ ¯ m ( t ) ( x + y ) − ∫ x ∞ K 2 ( t , x , s ) ∑ j = 1 n ∑ m = 1 n ¯ i c j 2 ( t ) c ¯ m 2 ( t ) κ j ( t ) − κ ¯ m ( t ) e i κ j ( t ) ( x + s ) − i κ ¯ m ( t ) ( x + y ) d s = 0

Proof. According to Theorem 1 and the results in [6], we can easily prove Theorem 2. Here the process of the proof is omitted for simplification.

3.3 Reduction of exact solutions

Theorem 3

System (1) has the following reduced solutions:

(38) q ( x , t ) = 2 t r ( P − 1 ( x , t ) Λ ¯ Λ ¯ T ) ,

(39) r ( x , t ) = − d d x t r ( P − 1 ( x , t ) Q ( x , t ) d d x Q T ( x , t ) ) t r ( P − 1 ( x , t ) Λ ¯ Λ ¯ T ) ,

determined by

(40) P ( x , t ) = E + Q ( x , t ) Q T ( x , t ) ,

(41) Q ( x , t ) = c j ( t ) c ¯ m ( t ) κ j ( t ) − κ ¯ m ( t ) e i ( κ j ( t ) − κ ¯ m ( t ) ) x n ¯ × n ,

(42) Λ = ( c 1 ( t ) e i κ 1 ( t ) x , c 2 ( t ) e i κ 2 ( t ) x , ⋯ , c n ( t ) e i κ n ( t ) x ) T ,

(43) Λ ¯ = ( c ¯ 1 ( t ) e − i κ ¯ 1 ( t ) x , c ¯ 2 ( t ) e − i κ ¯ 2 ( t ) x , ⋯ , c ¯ n ( t ) e − i κ ¯ n ¯ ( t ) x ) T ,

where E is unit matrix, κ j ( t ) , c j ( t ) , κ ¯ m ( t ) a n d c ¯ m ( t ) are determined in Eqs. (16) and (17).

Proof. In order to reduce soliton solutions from the exact solutions (38) and (39), we set R ( t , k ) = R ¯ ( t , k ) = 0 and suppose that

(44) K 1 ( x , y , t ) = ∑ p = 1 n ¯ c ¯ p ( t ) g p ( t , x ) e − i κ ¯ p ( t ) y ,

(45) K 2 ( x , y , t ) = ∑ p = 1 n ¯ c ¯ p ( t ) h p ( t , x ) e − i κ ¯ p ( t ) y .

Substituting Eqs. (44) and (45) into Eqs. (36) and (37), we obtain

(46) K 1 ( x , y , t ) = − t r ( P − 1 ( t , x ) Λ ¯ Λ ¯ T ) ,

(47) K 2 ( x , y , t ) = i t r ( P − 1 ( t , x ) Q ( t , x ) Λ Λ ¯ T ) ,

and hence reach the reduced solutions (38) and (39), here P⁻¹(t, x) is supposed to exist. Thus, we finish the proof Theorem 3.

As a particular case, n = n ¯ = 1 , Eqs. (38) and (39) give:

(48) q = 2 c ¯ 1 2 ( 0 ) e − 2 i κ ¯ 1 ( t ) x − ∫ 0 t ∑ s = 1 3 s ( 2 i κ ¯ 1 ( w ) ) s − 1 − 4 κ ¯ 1 2 ( w ) d w 1 + c 1 2 ( 0 ) c ¯ 1 2 ( 0 ) ( κ 1 ( t ) − κ ¯ 1 ( t ) ) 2 e A

where

A = 2 i ( κ 1 ( t ) − κ ¯ 1 ( t ) ) x + ∫ 0 t ∑ s = 1 3 s ( 2 i κ 1 ( w ) ) s − 1 − ( 2 i κ ¯ 1 ( w ) ) s − 1 − κ 1 2 ( w ) + 4 κ ¯ 1 2 ( w ) } d w

(49) r = 2 c 1 2 ( 0 ) e 2 i κ 1 x + ∫ 0 t ∑ s = 1 3 s ( 2 i κ 1 ( w ) ) s − 1 − 4 κ 1 2 ( w ) d w 1 + c 1 2 ( 0 ) c ¯ 1 2 ( 0 ) ( κ 1 ( t ) − κ ¯ 1 ( t ) ) 2 e B

where

B = 2 i ( κ 1 ( t ) − κ ¯ 1 ( t ) ) x + ∫ 0 t ∑ s = 1 3 s ( 2 i κ 1 ( w ) ) s − 1 − ( 2 i κ ¯ 1 ( w ) ) s − 1 − 4 κ 1 2 ( w ) + 4 κ ¯ 1 2 ( w ) } d w

where κ 1 ( t ) and κ ¯ 1 ( t ) are respectively determined by

(50) κ 1 t ( t ) = − i 2 + κ 1 ( t ) + 2 i κ 1 2 ( t ) − 4 κ 1 3 ( t ) ,

(51) κ ¯ 1 t ( t ) = − i 2 + κ ¯ 1 ( t ) + 2 i κ ¯ 1 2 ( t ) − 4 κ ¯ 1 3 ( t ) .

4 Nonlinear dynamics

We have gained an insight into the nonlinear dynamics of system(1) by means of solutions (50) and (51). For such purpose, with the help of Mathematica 8 we determine k₁(t) and κ ¯ 1 ( t ) of Eqs. (50) and (51) as follows:

(52) κ 1 ( t ) = InverseFunction [ − i 4 ArcTan 2 # 1 + 1 16 + i 16 log ( 1 − 2 # 1 ) 2 + 1 16 − i 16 log ( 1 + 2 # 1 ) 2 − 1 8 log 1 + 4 # 1 2 & ] − t 2 + C [ 1 ] ,

(53) κ ¯ 1 ( t ) = InverseFunction [ − i 4 ArcTan 2 # 1 + 1 16 + i 16 log ( 1 − 2 # 1 ) 2 + 1 16 − i 16 log ( 1 + 2 # 1 ) 2 − 1 8 log 1 + 4 # 1 2 & ] − t 2 + C [ 2 ] ,

where InverseFunction[·] is a built-in function of Mathematica 8, and

(54) C [ 1 ] = − i 4 ArcTan [ 2 κ 1 [ 0 ] ] + 1 16 + i 16 log ⁡ [ ( 1 − 2 κ 1 [ 0 ] ) 2 ] + 1 16 − i 16 log ⁡ [ ( 1 − 2 κ 1 [ 0 ] ) 2 ] − 1 8 log ⁡ [ 1 + 4 κ 1 2 [ 0 ] ] ,

(55) C [ 2 ] = − i 4 ArcTan [ 2 κ ¯ 1 [ 0 ] ] + 1 16 + i 16 log ⁡ [ ( 1 − 2 κ ¯ 1 [ 0 ] ) 2 ] + 1 16 − i 16 log ⁡ [ ( 1 − 2 κ ¯ 1 [ 0 ] ) 2 ] − 1 8 log ⁡ [ 1 + 4 κ ¯ 1 2 [ 0 ] ] ,

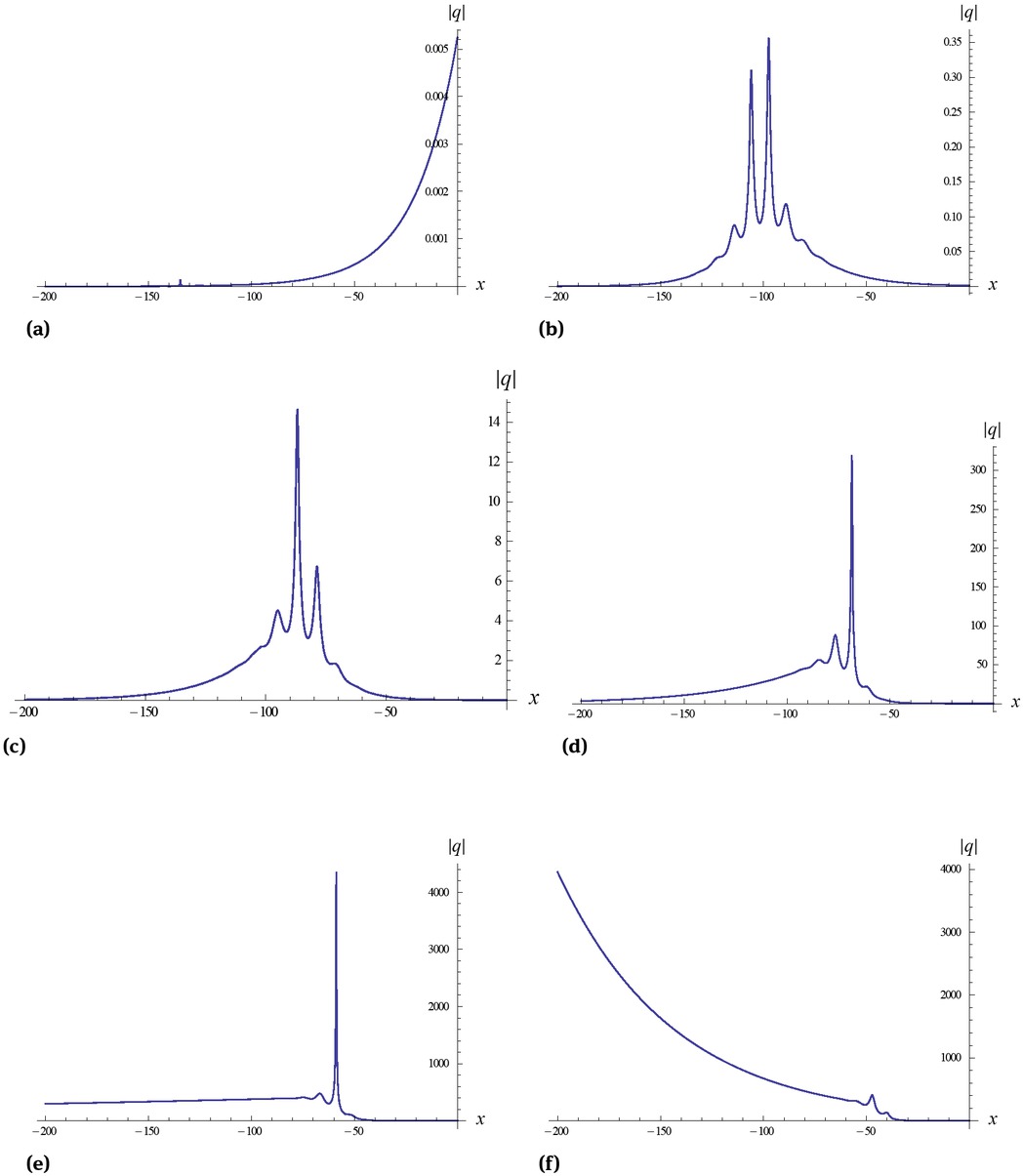
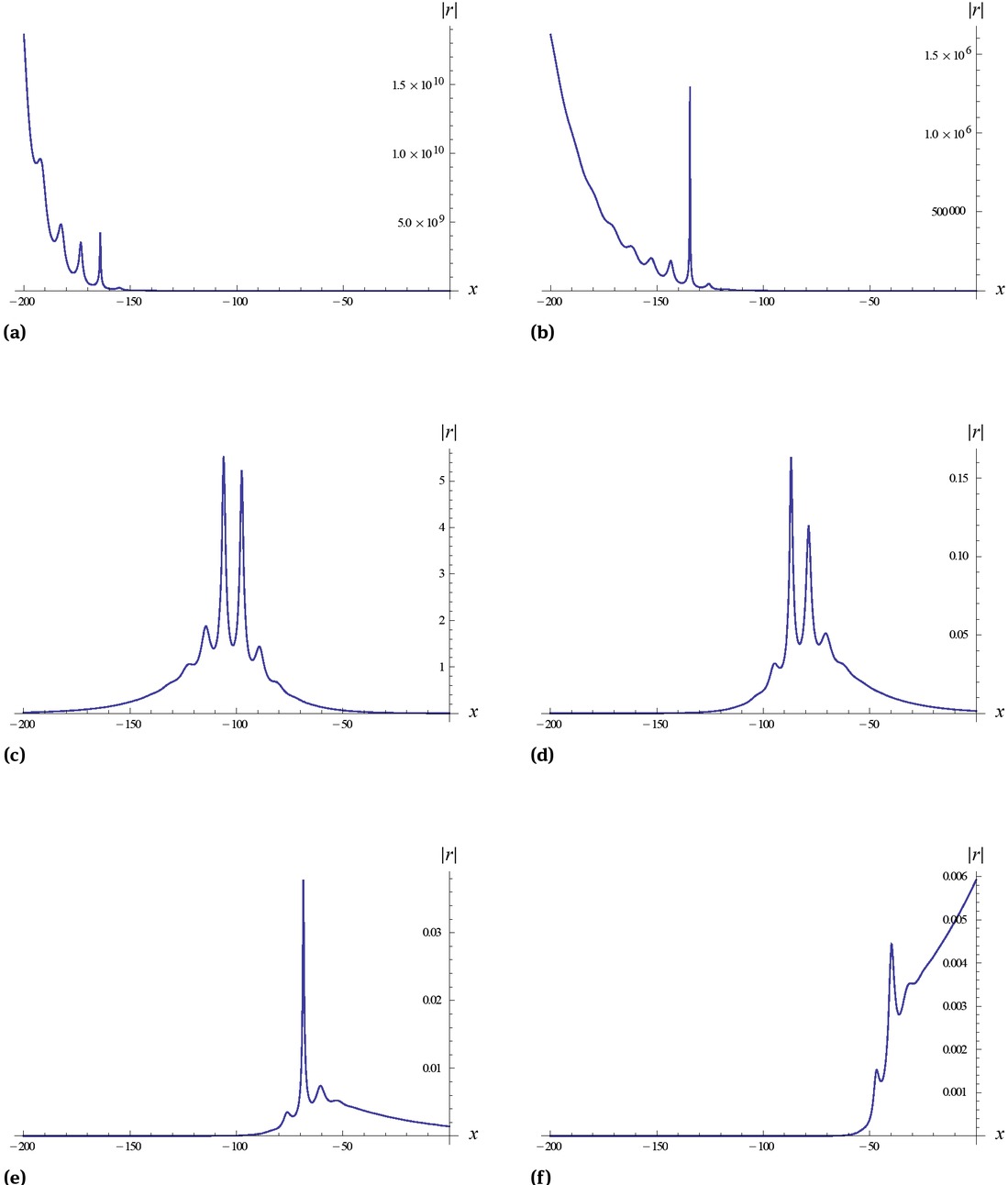
In Figures 1 and 2, the dynamical evolutions of solutions (48) and (49) determined by Eqs. (52)-(55) are shown by selecting the parameters as κ 1 ( 0 ) = 1 , κ ¯ 1 ( 0 ) = 0 , c₁(0) = −0.2 and , respectively. We can see from Figures 1

Figure 1

Dynamical evolutions of solution (48) determined by Eqs. (52)-(55) at the times: (a) t = −0.05, (b) t = 0.05, (c) t = 0.1, (d) t = 0.15, (e) t = 0.2, (f) t = 0.25

Figure 2

Dynamical evolutions of solution (49) determined by Eqs. (52)-(55) at the times: (a) t = −0.1, (b) t = −0.05, (c) t = 0.05, (d) t = 0.15, (e) t = 0.2, (f) t = 0.25

and 2 that the amplitudes of solutions (48) and (49) vary with time. In Figure 3, we simulate the graphs of the spectral parameters (52) and (53) with parameters k₁(0) = 1 and k₁(0) = 0.

Figure 3

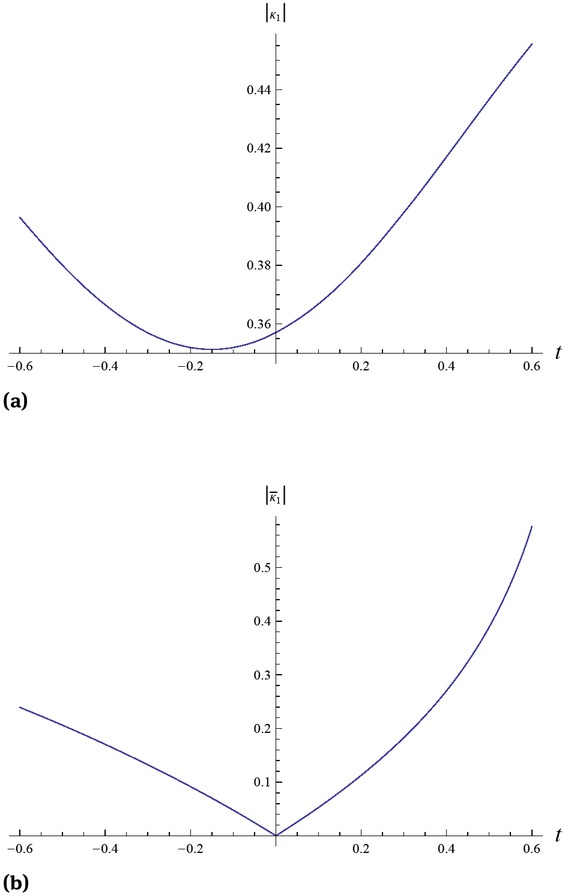
Graphs of the spectral parameters (52) and (53) with parameters: (a) k₁(0) = 1, (b) k₁(0) = 0

5 Conclusion

In summary, we have derived and solved a new nonlinear integral-differential system (1) that is nonisospectral and Lax integrable. This is due to the new spectral parameter (4) embedded into the eigenvalue problem (2) and its adjoint equation (3). By extending the IST method with the spectral parameter (4), we obtain exact solutions (38) and (39) and their reduced forms (48) and (49) of the system (1). To gain further insight into the reduced solutions (48) and (49), with the help of the dynamical evolutions we show that the amplitudes of solutions vary with time. Though there are some generalizations [21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46] of the IST method,we conclude that constructing new nonlinear systems and their exact solutions and researching the related issues [47, 48, 49, 50, 51] by analytical methods are worthy of study.

Acknowledgement

The authors B. Xu and S. Zhang are grateful to the anonymous reviewers for their helpful comments. This work was supported by the Natural Science Foundation of Liaoning Province of China (grant number 20170540007), the Natural Science Foundation of China (grant number 11547005), the Natural Science Foundation of Education Department of Liaoning Province of China (grant number LZ2017002) and Innovative Talents Support Program in Colleges and Universities of Liaoning Province of China (grant number LR2016021).

References

[1] Weiss J., Tabor M., Carnevale G., The Painlevé property for partial differential equations, J. Math. Phys., 1983, 24, 522-526.10.1063/1.525721Suche in Google Scholar

[2] Zhang S., Zhu R., KdV hierarchy with time-dependent coefficients: Lax integrability, bilinear Bäcklund transformation and soliton solutions, Optik, 2017, 142, 463-469.10.1016/j.ijleo.2017.06.018Suche in Google Scholar

[3] Zhang S., Chen M.T., Painlevé integrability and new exact solutions of the (4+1)-dimensional Fokas equation,Math. Probl. Eng., 2015, 2015, 367425.10.1155/2015/367425Suche in Google Scholar

[4] Zhang S., Chen M.T., Qian W.Y., Painleve analysis for a forced Korteveg-de Vries equation arisen in fluid dynamics of internal solitary waves, Therm. Sci., 2015, 19, 1223-1226.10.2298/TSCI1504223ZSuche in Google Scholar

[5] Ablowitz M.J., Clarkson P.A., Solitons, Nonlinear Evolution Equations and Inverse Scattering, Cambridge University Press, Cambridge, 1991.10.1017/CBO9780511623998Suche in Google Scholar

[6] Chen D.Y., Introduction of Soliton, Science Press, Beijing, 2006, (in Chinese).Suche in Google Scholar

[7] Hirota R., Exact solution of the Korteweg-de Vries equation for multiple collisions of solitons, Phys. Rev. Lett., 1971, 27, 1192-1194.10.1103/PhysRevLett.27.1192Suche in Google Scholar

[8] Fan E.G., Travelling wave solutions in terms of special functions for nonlinear coupled evolution systems, Phys. Lett. A, 2002, 300, 243-249.10.1016/S0375-9601(02)00776-4Suche in Google Scholar

[9] He J.H., Wu X.H., Exp-function method for nonlinear wave equations, Chaos Soliton. Fract., 2006, 30, 700-708.10.1016/j.chaos.2006.03.020Suche in Google Scholar

[10] Aslan I., Rational and multi-wave solutions to some nonlinear physical models, Rom. J. Phys., 2013, 58, 893-903.Suche in Google Scholar

[11] Dai C.Q., Wang Y.Y., Controllable combined Peregrine soliton and Kuznetsov-Ma soliton in PT-symmetric nonlinear couplers with gain and loss, Nonlinear Dyn., 2015, 80, 715-721.10.1007/s11071-015-1900-0Suche in Google Scholar

[12] Mirzazadeh M., Eslami M., Biswas A., 1-soliton solution to KdV6 equation, Nonlinear Dyn., 2015, 80, 387-396.10.1007/s11071-014-1876-1Suche in Google Scholar

[13] Zhang S., Tian C., QianW.Y., Bilinearization and new multi-soliton solutions for the (4+1)-dimensional Fokas equation, Pramana-J. Phys., 2016, 86, 1259-1267.10.1007/s12043-015-1173-7Suche in Google Scholar

[14] Zhang S., Liu M.Y., Xu B., New multi-soliton solutions of Whitham-Broer-Kaup shallow-water-wave equations, Therm. Sci., 2017,214, S137-S144.10.2298/TSCI17S1137ZSuche in Google Scholar

[15] Zhang S., Gao X.D., Exact N-soliton solutions and dynamics of a new AKNS equations with time-dependent coefficients, Nonlinear Dyn„ 2016, 83, 1043-1052.10.1007/s11071-015-2386-5Suche in Google Scholar

[16] Lou S.Y., Tang X.Y., Method of Nonlinear Mathematical Physics, Science Press, Beijing, 2006, (in Chinese).Suche in Google Scholar

[17] Garder C.S., Greene J.M., Kruskal M.D., Miura R.M., Method for solving the Korteweg-de Vries equation, Phys. Rev. Lett., 1967, 19, 1095-1097.10.1103/PhysRevLett.19.1095Suche in Google Scholar

[18] Chen H.H., Liu C.S., Solitons in nonuniform media, Phys. Rev. Lett., 1976, 37, 693-697.10.1103/PhysRevLett.37.693Suche in Google Scholar

[19] Hirota R., Satsuma J., N-soliton solutions of the K-dV equation with loss and nonuniformity terms, J. Phys. Soc. Jpn., 1976, 41, 2141-2142.10.1143/JPSJ.41.2141Suche in Google Scholar

[20] Ablowitz M.J., Kaup D.J., Newell A.C., Segur H., The inverse scattering transform– Fourier analysis for nonlinear problems, Stud. Appl. Math., 1974, 53, 249-315.10.1002/sapm1974534249Suche in Google Scholar

[21] Calogero F., Degasperis A., Coupled nonlinear evolution equations solvable via the inverse spectral transform, and solitons that come back: the boomeron, Lett. Nuovo Cimento, 1976, 16, 425-433.10.1007/BF02751683Suche in Google Scholar

[22] Calogreo F., Degasperis A., Exact solutions via the spectral transform method for solving nonlinear evolustions, Lett. Nuovo Cimento, 1978, 22, 131-137.10.1007/BF02804669Suche in Google Scholar

[23] Calogreo F., Degasperis A., Extension of the spectral transform method for solving nonlinear evolustions, Lett. Nuovo Cimento, 1978, 22, 263-269.10.1007/BF02820606Suche in Google Scholar

[24] Calogreo F., Degasperis A., Exact solution via the spectral transform of a generalization with linearly x-dependent coefficients of the modified Korteweg-de Vries equation, Lett. Nuovo Cimento, 1978, 22, 270-273.10.1007/BF02820607Suche in Google Scholar

[25] Nachman A.I., Ablowitz M.J., A multidimensional inverse scattering method, Stud. Appl. Math., 1984, 71, 243-250.10.1002/sapm1984713243Suche in Google Scholar

[26] Chan W.L., Li K.S., Nonpropagating solitons of the variable coefficient and nonisospectral Korteweg-de Vries equation, J. Math. Phys., 1989, 30, 2521-2526.10.1063/1.528533Suche in Google Scholar

[27] Xu B.Z., Zhao S.Q., Inverse scattering transformation for the variable coefficient sine-Gordon type equation, Appl. Math. J. Chinese Univ. B, 199, 9, 331-337, (in Chinese).10.1007/BF02665219Suche in Google Scholar

[28] Zeng Y.B., Ma W.X., Lin R.L., Integration of the soliton hierachy with selfconsistent sources, J. Math. Phys., 2000, 41, 5453-5489.10.1063/1.533420Suche in Google Scholar

[29] Serkin V.N., Hasegawa A., Novel soliton solutions of the nonlinear Schrödinger equation model, Phys. Rev. Lett., 2000, 85, 4502-4505.10.1103/PhysRevLett.85.4502Suche in Google Scholar PubMed

[30] Serkin V.N., Belyaeva T.L., The Lax representation in the problem of soliton management, Quantum Electron+,2001, 31, 1007-1015.10.1070/QE2001v031n11ABEH002093Suche in Google Scholar

[31] Ning T.K., Chen D.Y., Zhang D.J., The exact solutions for the non-isospectral AKNS hierarchy through the inverse scattering transform, Physica A, 2004, 339, 248-266.10.1016/j.physa.2004.03.021Suche in Google Scholar

[32] Serkin V.N., Hasegawa A., Belyaeva T.L., Nonautonomous solitons in external potentials, Phys. Rev. Lett., 2007, 98, 074102.10.1103/PhysRevLett.98.074102Suche in Google Scholar PubMed

[33] Serkin V.N., Hasegawa A., Belyaeva T.L., Solitary waves in nonautonomous nonlinear and dispersive systems: nonautonomous solitons, J. Mod. Optic., 2010, 57, 1456-1472.10.1080/09500341003624750Suche in Google Scholar

[34] Serkin V.N., Hasegawa A., Belyaeva T.L., Nonautonomous matter-wave solitons near the Feshbach resonance, Phys. Rev. A, 2010, 81, 023610.10.1103/PhysRevA.81.023610Suche in Google Scholar

[35] Biondini G., Kovacic G., Inverse scattering transform for the focusing nonlinear Schrödinger equation with nonzero boundary conditions, J. Math. Phys., 2014, 55, 031506.10.1063/1.4868483Suche in Google Scholar

[36] S Chakravarty., Prinari B., Ablowitz M.J., Inverse scattering transform for 3-level coupled Maxwell-Bloch equations with inhomogeneous broadening, Physica D, 2014, 278-279, 58-78.10.1016/j.physd.2014.04.003Suche in Google Scholar

[37] Zhang S., Xu B., Zhang H.Q., Exact solutions of a KdV equation hierarchy with variable coefficients, Int. J. Comput. Math., 2014, 91, 1601-1616.10.1080/00207160.2013.855730Suche in Google Scholar

[38] Zhang S., Wang D., Variable-coefficient nonisospectral Toda lattice hierarchy and its exact solutions, Pramana-J. Phys., 2015, 85, 1143-1156.10.1007/s12043-014-0918-zSuche in Google Scholar

[39] Zhang S., Gao X.D., Mixed spectral AKNS hierarchy from linear isospectral problem and its exact solutions, Open Phys., 2015, 13, 310-322.10.1515/phys-2015-0040Suche in Google Scholar

[40] Zhang S., Gao X.D., Exact solutions and dynamics of a generalized AKNS equations associated with the nonisospectral depending on exponential function, J. Nonlinear Sci. Appl., 2016, 19, 4529-4541.10.22436/jnsa.009.06.91Suche in Google Scholar

[41] Zhang S., Li J.H., On nonisospectral AKNS system with infinite number of terms and its exact solutions, IAENG Int. J. Appl.Math., 2017, 47, 89-96.Suche in Google Scholar

[42] Gao X.D., Zhang S., Time-dependent-coefficient AKNS hierarchy and its exact multi-soliton solutions, Int. J. Appl. Sci.Math., 2016, 3, 72-75.Suche in Google Scholar

[43] Zhang S., Li J.H., Soliton solutions and dynamical evolutions of a generalized AKNS system in the framework of inverse scattering transform, Optik, 2017, 137, 228-237.10.1016/j.ijleo.2017.02.104Suche in Google Scholar

[44] Zhang S., Hong S.Y., Lax integrability and soliton solutions for a nonisospectral integro-differential system, Complexity, 2017, 2017, 9457078.10.1155/2017/9457078Suche in Google Scholar

[45] Zhang S., Hong S.Y., On a generalized Ablowitz-Kaup-Newell-Segur hierarchy in inhomogeneities of media: soliton solutions and wave propagation influenced from coefficient functions and scattering data, Wave. Random Complex, 2018, 28, 435-452.10.1080/17455030.2017.1362134Suche in Google Scholar

[46] Zhang S., Hong S.Y., Lax integrability and exact solutions of a variable-coefficient and nonisospectral AKNS hierarchy, Int. J. Nonlinear Sci. Numer. Simul., 2018, 19, 251-262.10.1515/ijnsns-2016-0191Suche in Google Scholar

[47] Ding D.J., Jin D.Q., Dai C.Q., Analytical solutions of differential-difference sine-Gordon equation, Therm. Sci., 2017, 21, 1701-1705.10.2298/TSCI160809056DSuche in Google Scholar

[48] Dai C.Q., Chen R.P., Wang Y.Y., Fan Y., Dynamics of light bullets in inhomogeneous cubic-quintic-septimal nonlinear media with PT-symmetric potentials, Nonlinear Dyn., 2017, 87, 1675-1683.10.1007/s11071-016-3143-0Suche in Google Scholar

[49] Wang Y.Y., Dai C.Q., Zhou G.Q., Fan Y., Chen L., Rogue wave and combined breather with repeatedly excited behaviors in the dispersion/diffraction decreasing medium, Nonlinear Dyn., 2017, 87, 67-73.10.1007/s11071-016-3025-5Suche in Google Scholar

[50] Dai C.Q., Zhou G.Q., Chen R.P., Lai X.J., Zheng J., Vector multipole and vortex solitons in two-dimensional Kerr media, Nonlinear Dyn., 2017, 88, 2629-2635.10.1007/s11071-017-3399-zSuche in Google Scholar

[51] Wang Y.Y., Zhang Y.P., Dai C.Q., Re-study on localized structures based on variable separation solutions from the modified tanh-function method, Nonlinear Dyn., 2016, 83, 1331-1339.10.1007/s11071-015-2406-5Suche in Google Scholar

Received: 2018-04-24

Accepted: 2019-05-09

Published Online: 2019-06-17

This work is licensed under the Creative Commons Attribution 4.0 International License.

Artikel in diesem Heft

https://doi.org/10.1515/phys-2019-0031

Schlagwörter für diesen Artikel

Integral-differential system; Integrability; Exact solution; Dynamical evolution; IST

Creative Commons

BY 4.0