Bounds for partition dimension of M-wheels

Zafar Hussain; Shin Min Kang; Muqdas Rafique; Mobeen Munir; Usman Ali; Aqsa Zahid; Muhammad Shoaib Saleem

doi:10.1515/phys-2019-0037

Article Open Access

Bounds for partition dimension of M-wheels

Zafar Hussain , Shin Min Kang , Muqdas Rafique , Mobeen Munir , Usman Ali , Aqsa Zahid and Muhammad Shoaib Saleem

Published/Copyright: July 17, 2019

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information Explore this Subject

From the journal Open Physics Volume 17 Issue 1

Abstract

Resolving partition and partition dimension have multipurpose applications in computer, networking, optimization, mastermind games and modelling of chemical substances. The problem of finding exact values of partition dimension is hard so one can find bound for the partition dimension of a general family of graph. In the present article, we give the sharp upper bounds and lower bounds for the partition dimension of m-wheel, W_n,_m for all n ≥ 4 and m ≥ 1. Presented data generalise some already available results.

Keywords: Metric dimension; partition dimension; generalized Wheel

PACS: 02.10.Ox; 02.10.-v

1 Introduction

Resolving set and metric basis appeared on the scene way back in 1953 for an arbitrary metric space by Blumenthal [1]. But it did not attract much attention at that probably because of linear continuum nature of Rⁿ. Almost twenty years later, Slater pointed out a potential application of detection problem in graph theory, which brought these ideas again in the spotlight but now in the context of discrete cases like graphs and networks.

In graph and network theory, computer networks are treated as graphs with vertices as nodes and edges as communication media. One is interested to assign a unique address to each node to easily communicate and identify the failure of any device or node in this network of computers. The concept of resolving sets and metric basis are the derived to handle these situations. Slater and independently in Harary and Melter in [7] laid down the basis of these ideas in the realm of graph theory. Resolving sets play an important part in image proceeding and digital geometry [9], robot navigation and pattern recognition [11, 12], mastermind games [20], and pharmacy chemistry and drug design [6].

Let us denote by G, a simple connected graph, V be the set of vertices of graph, a metric d : V × V → W, where W is the set of non-negative integers and d(u, v) is the minimum number of edges in any path between u and v. Let W = w₁, w₂, . . . , w_k be an ordered set of vertices of G and let v be a vertex of G. The representation r(v|W) of v with respect to W is the k-tuple (dG(v, w₁), dG(v, w₂), . . . , dG(v, w_k)). If distinct vertices of G have distinct representations with respect to W, then W is called a resolving set of G, see [8, 9, 10, 11, 12]. A resolving set having minimum cardinality is called basis of G and its cardinality is the metric dimension of G, represented by β(G). This version of dimension of graph is perhaps the most famous and relatively easy to compute. It is an established fact that the problem of computing metric dimension is NP-Complete [5]. Buczkowski et al. proved that β ( W n ) = ⌊ 2 n + 2 5 ⌋ for n = 7 [18], for wheel graph W_n. Caceres et al. proved that metric dimension of fan to be ⌊ 2 n + 2 5 ⌋ for n = 7 and Tomescu et al. proved that the dimension of Jahangir graphs J_2n to be ⌊ 2 n 3 ⌋ for all n = 4. It is desirable to obtain a family of graph in which metric dimension remains independent of the particular elements of the family. Such families are called graphs of constant metric dimension. Authors in [2] proved that a graph has constant metric dimension 1 if and only if it is a path. Author computed the closed forms of metric dimension of cartesian products of graphs in [3] and metric dimension of finite connected graphs in [4]. Javaid et al. discussed some families of regular graphs having constant metric dimension, [8]. Murtaza et al. established some incomplete results about β(M_2,n) where M_2,n is a Mobius ladder with 2n number of vertices, in [14] whereas Munir et al. established complete and exact for M_2,n in [16]. Recently Zaffar et al. established bounds for the metric dimension of a kind of generalization classical Mobius Ladders in [38] which on specializing give already established results for this ladders. For other closed results about metric dimensions of families of graph, please see [12, 13, 14, 15, 16].

Slater introduced a new concept, for a connected graph [10, 20], closely related to metric dimension. It is a partition dimension which is even harder to compute. Let us take a subset S ⊆ V(G), a vertex set v, and distance d(v, S) = min{d(v, x) : x ∈ S}. If P = {S₁, . . . S_t} is considered as an ordered t-partition of V(G), then r(v|P) = {d(v, S₁), . . . , d(v, S_t)} is the t-tuple representation of v with respect to P. If this t-tuple representation of v, r(v|P) for all v ∈ V(G), are all distinct, then this P is called resolving partition. A resolving partition having minimum cardinality is often required and this minimum cardinality is partition dimension, represented as pd(G).We illustrate this with a simple example. Consider the graph G in the Figure 1 below.

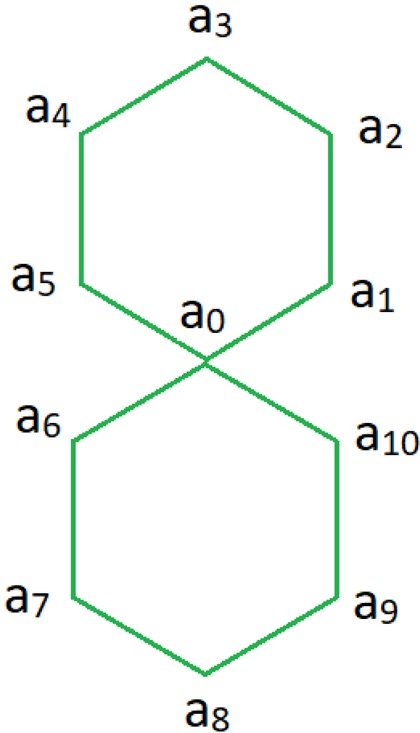
Figure 1

Let P₁ = {A₁, A₂, A₃} , where

A₁ = {a₀}, A₂ = {a₁, a₂, a₃, a₄, a₅} and A₃ = {a₆, a₇, a₈, a₉, a₁₀}.

The partition P₁ does not resolve G because r(a₁|P₁ = r(a₅|P₁ = (1, 0, 2). Now let P = {B₁, B₂, B₃} , where B₁ = {a₀, a₅}, B₂ = {a₁, a₂, a₃, a₄} and B₃ = {a₆, a₇, a₈, a₉, a₁₀}.

Next we use a_i instead of r(a_i|P), , i = 0, 1, 2, . . . , 10. The distance vectors belonging to various vertices of G relative to partition P are

a₀ = (0, 1, 1), a₁ = (1, 0, 2), a₂ = (2, 0, 3),

a₃ = (2, 0, 4), a₄ = (1, 0, 3), a₅ = (0, 1, 2),

a₆ = (1, 2, 0), a₇ = (2, 3, 0), a₈ = (2, 4, 0),

a₉ = (1, 3, 0), a₁₀ = (0, 2, 1)

Since the distance vectors belonging to various vertices of G relative to P are distinct so the partition P resolves G. Moreover any partition of G having cardinality less than 3 does not resolve G. So pd(G) = 3.

This type of dimension has been utilized in chemistry and drug design [6]. Chartrand et al. discussed partition dimension of a general graph in [25, 26]. Chappel et al. computed bounds on the metric and partition dimension of some graphs in [27]. Fernau computed partition dimension of uni-cyclic graphs in [29]. It is natural to discuss the relation of these two dimensions. In [25, 26], Chartrand et al. established that

p d ( G ) = β ( G ) + 1

for a connected graph G. Tomescu et al. in [30] established that it can be even more smaller than the metric dimension. Authors, in fact, discussed all 23 families of connected graphs having order n with partition dimensions n, n−1 or 2. Recently Hernando et al. in [28] identified the repetition in this list and proved that there are only 15 such families. In [27], authors computed some bounds for metric and partition dimension of a connected graph.

Chartrand et al. proved in [26] that if G is a connected graph of order n ≥ 2 then pd(G) = 2 if and only if G is a path, pd(G) = n if and only if G = K_n and for n = 5, pd(G) = n − 1 if and only if G is one of the graphs K_1,n−1, K_n_−e, K₁+(K₁∪K_n₊₂). In [38] Zaffar et al. computed bounds for the partition dimension of generalization of Mobius ladders and computed that these bounds depend upon the parity of mand n. Authors proved that, for m ≥ 3 and n ≥ 2, 3 ≤ pd(M_m_,n) ≤ 4 when both m and n are opposite parity and 3 ≤ pd(M_m_,n) ≤ 5 when both parameters are of same parity.

Tomescu et al. in [31] computed partition dimension and connected partition dimension of wheel graphs and showed that for n ≥ 4 , ⌈ ( 2 n ) 1 3 ⌉ = p d ( G ) = 2 ⌈ n 1 2 ⌉ + 1 . We shall generalize some results about wheel graph to generalized wheel graph. Following lemma relates bounds for the partition dimension of a graph of size n and its diameter.

Lemma: If |G| ≥ 3, then pd(G) ≤ n − diam(G) + 1. In the present article we are interested to find sharp bounds for pd(W_n_,m). The graph (W_n_,m), also called m-step or level wheel graph consisting of m number of C_n cycles and a vertex v which are connected in such a way that every vertex of each C_n is adjacent to v, as shown in Figure 1, [29]. The vertices of C_n are termed as rim vertices. The order of graph W_n_,m is nm + 1 and its diameter is 2. This graph can be taken as generalization of simple wheel graph W_n. The following Figure 2 contains an m-stepwheel with 8 rim vertices in a cycle.

Figure 2

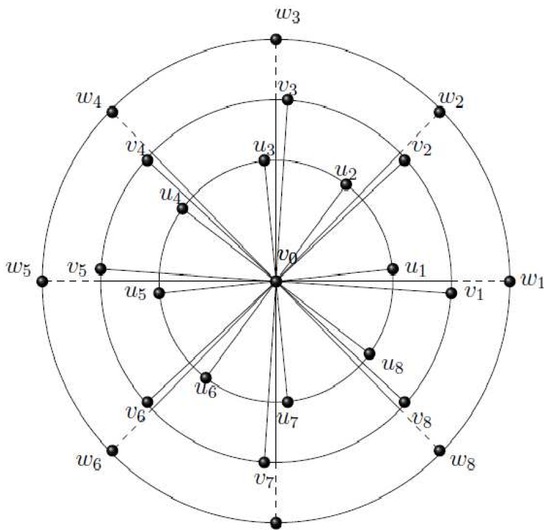
Wheel W_8,m

Wireless sensor networks and the vulnerability of networks are some of the uses of this graph [32, 34]. The wheel graph has many useful properties. From the standpoint of the hub vertex, all elements, including vertices and edges, are in its one-hop neighborhood, which indicates that the wheel structure is fully included in the neighborhood graph of the hub vertex Wheel and related graphs are extensively studied recently. In [37] authors computed metric dimension of some wheel related graphs. In [32], authors gave an algorithm to compute average lower 2-domination number and also computed this number for some wheel related graphs. Authors computed different kinds of energies associated to matrices of W_n_,m in [36], and bounds for stanley depth for W_n_,m in [35].

2 Main results

The main result of this article is given in the following theorem

Theorem 2.1. For all m ≥ 1 a n d f o r n ≥ 4 ⌈ ( 2 n m ) 1 / 3 ⌉ ⩽ p d ( W n , m ) ≤ 2 ⌈ ( n m ) 1 2 ⌉ + 1

We need following lemmas to prove our main results.

Lemma 2.2. Let Π = {S₁, S₂, . . . , S_q} be a resolving q partition of V(Wn,m).Ifc∈S1,then∣S1∣⩽1+q−12+q−11+q−10where c is the central vertex.

Proof. We analyze that r(c|Π) = (0, 1, 1, . . . , 1) and r(v|Π) = (0, . . .) for v ∈ S₁∖{c}. We also know that the diameter of W_n_,m is 2, the elements of the q vector representation r(v|Π) of each rim vertex v ∈ S₁∖{c} except the first element can be 1 or 2. But in vector representation there can be at most two elements which will be equal to 1 apart from the first position of the vector. For the rim vertices in the vector representation there are q − 1 positions which can be filled by at most two 1’s and the other can be filled by 2’s. Thus , for all vertices v ∈ S₁∖{c} there are at most q − 1 2 + q − 1 1 + q − 1 0 different vector representations. Together with these vector representations of the center, we arrive at most 1 + q − 1 2 + q − 1 1 + q − 1 0 different representations. Therefore ∣ S 1 ∣⩽ 1 + q − 1 2 + q − 1 1 + q − 1 0 .

Lemma 2.3. Let Π = {S₁, S₂, . . . , S_q} be a resolving q partition of V(W_n_,m). If c ∈ S₁, then ∣ S i ∣⩽ q − 2 2 + q − 2 1 + q − 2 0 for each 2 6 i 6 q.

Proof. We consider another class not S₁, say S₂, where c does not belong to S₂. Then for w ∈ S₂, the vector representation becomes r(w|Π) = (1, 0, . . . ). For rim vertices in the vector representation there are q − 2 which can be filled by at most two 1’s and the other can be filled by 2’s. Thus for all vertices w ∈ S₂, there are at most q − 2 2 + q − 2 1 + q − 2 0 different representations. Therefore ∣ S i ∣⩽ q − 2 2 + q − 2 1 + q − 2 0 for each 2 6 i 6 q.

With the help of above two lemmas, we can now find the lower bound for the partition dimension of W_n_,m.

Proposition 2.4. We have ⌈(2nm)^1/3⌉ 6 pd(W_n_,m), for every n > 4 and m ≥ 1.

Proof. Let us assume pd(W_n_,m) = q and Π = {S₁, S₂, . . . , S_q} be a resolving q partition of V(W_n_,m). Let c ∈ S₁ and by lemma (2.2) we have ∣ S 1 ∣⩽ 1 + q − 1 2 + q − 1 1 + q − 1 0 and by lemma (2.3) we have ∣ S i ∣⩽ q − 2 2 + q − 2 1 + q − 2 0

for 2 6 i 6 q. Using these two lemmas we get | V(W_n_,m) |= n m + 1 = ∑ 1 q ∣ S i ∣⩽ 1 + ∑ 0 2 q − 1 i + ( q − 1 ) q − 2 i . n m < ( q 3 − 3 q 2 + 6 q − 2 ) / 2 ≤ q 3 2 for every q > 2. It follows that q > ⌈(2nm)^1/3⌉.

We now move towards the upper bounds. Following two results give upper bounds for the partition dimension of W_n_,m but these bounds are not sharp enough.

Proposition 2.5. For every n > 2 we have pd(W_n_,m) ≤ ⌊ 2 n + 2 5 ⌋ + ( m − 1 ) ⌊ 2 n + 4 5 ⌋ + 1 .

Proof. We easily obtain d i m ( W n , m ) = ⌊ 2 n + 2 5 ⌋ + ( m − 1 ) ⌊ 2 n + 4 5 ⌋ , by ([29], theorem 2.2). By using elementary inequality relating metric and partition dimension we arrive at the required result.

Proposition 2.6. For every n > 2 we have pd(W_n_,m) ≤ 2 5 ( m n + 2 m − 1 ) + 1.

Proof. From above, we obtain dim ( W n , m ) = ⌊ 2 n + 2 5 ⌋ + ( m − 1 ) ⌊ 2 n + 4 5 ⌋ But using definition of floor function we have ⌊ 2 n + 2 5 ⌋ + ( m − 1 ) ⌊ 2 n + 4 5 ⌋ < 2 n + 2 5 + 2 5 ( m − 1 ) ( 2 n + 2 ) = mn + 2m − 1. Using relation between pd and dim we obtain the required result.

We now move forward to find upper bound which is sharper then the above bounds.

Proposition 2.7. We have pd(W_n_,m) ≤ p +1, For every n > 2 and p is the least prime number, such that p(p − 1) ≥ nm

Proof. Let p be a the smallest prime number in the sense that p(p − 1) > nm. Since p is the prime number, so the sequence {0, i, 2i, 3i, . . . , (p − 1)i}, where 1 6 i 6 p − 1 and all the above numbers 0, i, 2i, 3i, . . . , (p − 1)i are reduced modulo p. It is obvious that these numbers are the permutation of the set {0, 1, . . . , p − 1}. Now assume that the sequence

( x k ) k = 1 , 2 , … , p ( p − 1 ) = X 1 , X 2 , … , X ( p − 1 ) / 2

where for every 1 6 i 6 (p − 1)/2 there is a subsequence

X i = 0 , 0 , i , i , 2 i , 2 i , … ( p − 1 ) i , ( p − 1 ) i

which contains 2p terms and every pair of equal elements in above sequence different from 0, 0. And we can obtain all these numbers from the previous one by adding i module p to every component. Thus, for V(W_n_,m) the resolving partition Π = {S₁, . . . S_p₊₁} is defined as:

a) if nm = p(p−1) then S_p₊₁ = {c} and also in this case every element V_i(0 6 i 6 nm − 1) is assigned to the class S_xi₊₁₊₁;

b) if nm < p(p − 1) then S_p = {c, v_nm₋₁} and also every element v_i(0 6 i 6 nm − 2) is assigned to the class S_xi₊₁₊₁.

so,Π is a resolving connected partition of V(W_n_,m) having p + 1 classes, which implies pd(W_n , m) 6 p + 1.

Proposition 2.8. For every n ≥ 4 we have [(2nm)^1/3] ≤ p d ( W n , m ) ≤ 2 ⌈ ( n m ) 1 2 ⌉ + 1

Proof. Since p is prime then it should satisfy that p(p−1) ≥ nm so select p ≥ ⌈ ( n m ) 1 2 ⌉ + 1 . Bertrand’s postulate can be used here which states that for every n ≥ 1, there always exists a prime with

n < p ≤ 2 n .

It was proved by Chebyshev for the first time in the history, see [30]. So we can easily infer that

⌈ ( n m ) 1 2 ⌉ < p ≤ 2 ⌈ ( n m ) 1 2 ⌉ .

So it can be derived that

p d ( W n , m ) ≤ p + 1 ≤ 2 ⌈ ( n m ) 1 2 ⌉ + 1.

which is the required result.

It is clear that by putting m = 1 we obtain simple wheel W_n with the result, for 4 6 n 0 7 the pd(W_n) = 3 , and for 8 6 n 6 19 the pd(W_n) = 4 and pd(W₃) = 4 see [25]. So our results is an extension of this result.

Example. Let n = 3 and m = 10, we have ⌈(2(3)(10))^1/3⌉ 6 pd(W₃,10) 6 2⌈((3)(10))^1/2⌉ + 1 ⌈(60)_1/3 6⌉pd(W₃,10) 6 2⌈(30)^1/2⌉ + 1 3 6 pd(W₃,10) 6 11

Example. Take W_2,10 with resolving partition Π = {S₁, S₂, S₃, S₄, S₅, S₆} and S₁ = {v₂, v₇, v₈, v₁₃} , S₂ = {v₃, v₁₁, v₁₂, v₁₉},S₃ = {v₅, v₉, v₁₀, v₁₆}, S₄ = {v₆, v₁₄, v₁₅, v₁₇},S₅ = {v₀, v₁, v₄, v₁₈}

and S₆ = {c}

c | ∏ ) = ( 1 , 1 , 1 , 1 , 1 , 0 ) , ( v 0 | ∏ ) = ( 2 , 2 , 1 , 2 , 0 , 1 ) , ( v 1 | ∏ ) = ( 1 , 2 , 2 , 2 , 0 , 1 ) , ( v 2 | ∏ ) = ( 0 , 1 , 2 , 2 , 1 , 1 ) , ( v 3 | ∏ ) = ( 1 , 0 , 2 , 2 , 1 , 1 ) , ( v 4 | ∏ ) = ( 2 , 1 , 1 , 2 , 0 , 1 ) , ( v 5 | ∏ ) = ( 2 , 2 , 0 , 2 , 1 , 1 ) , ( v 6 | ∏ ) = ( 1 , 2 , 1 , 0 , 2 , 1 ) , ( v 7 | ∏ ) = ( 0 , 2 , 2 , 1 , 2 , 1 ) , ( v 8 | ∏ ) = ( 0 , 2 , 1 , 2 , 2 , 1 ) , ( v 9 | ∏ ) = ( 1 , 2 , 0 , 2 , 1 , 1 ) , ( v 10 | ∏ ) = ( 2 , 1 , 0 , 2 , 2 , 1 ) , ( v 11 | ∏ ) = ( 2 , 0 , 1 , 2 , 2 , 1 ) , ( v 12 | ∏ ) = ( 1 , 0 , 2 , 2 , 2 , 1 ) , ( v 13 | ∏ ) = ( 0 , 1 , 2 , 1 , 2 , 1 ) , ( v 14 | ∏ ) = ( 1 , 2 , 2 , 0 , 2 , 1 ) , ( v 15 | ∏ ) = ( 2 , 2 , 1 , 0 , 2 , 1 ) , ( v 16 | ∏ ) = ( 2 , 2 , 0 , 1 , 2 , 1 ) ,

v 17 | ∏ ) = ( 2 , 2 , 1 , 0 , 1 , 1 ) , ( v 18 | ∏ ) = ( 2 , 1 , 2 , 1 , 0 , 1 ) , ( v 19 | ∏ ) = ( 2 , 0 , 1 , 2 , 1 , 1 ) .

Also in the case of W_3,10 the partition dimension is 8 which is also ≤ p + 1, where p is 7.

Acknowledgement

Authors are thankful to reviewers for their comments and fruitful suggestions.

Competing interests: The authors declare that they have no competing interests.
Author’s contributions: All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.

References

[1] Blumenthal L.M., Theory and Applications of Distance Geometry Clarendon Press, Oxford (1953).Search in Google Scholar

[2] Chartrand G., Eroh L., Johnson M. A., Oellermann, O. R., Resolvibility in graphs and the metric dimension of a graph Disc. Appl. Math., 105(2000), 99-133.10.1016/S0166-218X(00)00198-0Search in Google Scholar

[3] Caceres J., Hernando C., Mora M., Pelayo I.M., Puertas M.L., Seara C., Wood D.R., On the metric dimension of cartesian product of graphs SIAM J.Disc. Math., 2(21), (2007), 423-441.10.1137/050641867Search in Google Scholar

[4] Caceres J., Hernando C., Mora M., Pelayo I.M., Puertas M.L., Seara C., Wood D.R., On the metric dimension of some families of graphs Electronic Notes in Disc. Math., 22(2005), 129-133.10.1016/j.endm.2005.06.023Search in Google Scholar

[5] Khuller S., Raghavachari B., Rosenfeld A., Landmarks in graphs Discrete Appl. Math., 70 (1996), pp. 217-229.10.1016/0166-218X(95)00106-2Search in Google Scholar

[6] Chartrand G., Erwin D., Johns G. L. , Zhang P. Boundary vertices in graphs Discrete Math. 263 (2003) 25-3410.1016/S0012-365X(02)00567-8Search in Google Scholar

[7] Harary F., Melter R. A., On the metric dimension of a graph Ars. Combinatoria 2 (1976), 191-195.Search in Google Scholar

[8] Javaid I., Rahim M.T., Ali K., Families of regular graphs with constant metric dimension Utilitas Math., 75(2008), 21-33.Search in Google Scholar

[9] Melter R.A., Tomescu I., Metric bases in digital geometry, Computer Vision, Graphics, and Image Processing 25(1984), 113-121.10.1016/0734-189X(84)90051-3Search in Google Scholar

[10] Slater P. J., Leaves of trees Congress.Number., 14(1975), 549-559.Search in Google Scholar

[11] Slater P. J., Dominating and refrences sets in graphs J. Math. Phys. sci., 22(1998), 445-455.Search in Google Scholar

[12] Rojas A., Diaz K, Distance Labellings of Möbius Ladders disertaion Worcester Polytechnic Institute 12-3-2013.Search in Google Scholar

[13] Poisson C., Zhang P., The metric dimension of unicyclic graphs J. Comb. Math Comb. Comput. 40 (2002) 17-32.Search in Google Scholar

[14] Murtaza A., Ali G., Imaran M., Baig A.Q., Kashif M., On the metric dimension of Möbius Ladder ARS Combinatoria, 105(2012), 403-410.Search in Google Scholar

[15] Shanmukha B., Sooryanarayana B., Harinath K. S., Metric dimension of wheels Far East J. Appl. Math. 8 (3) (2002) 217-229.Search in Google Scholar

[16] Munir M., Nizami A. R., Saeed H., Iqba Z., On themetric dimension of Möbius Ladder ARS Combinatoria, 135(2017), 249-256.Search in Google Scholar

[17] Sebo A., Tannier E., On metric generators of graphs Math. Oper. Res., 29(2):383-393, 2004.10.1287/moor.1030.0070Search in Google Scholar

[18] Buczkowski P.S., Chartrand G., Poisson C., Zhang, P., On k-dimensional graphs and their bases Pariodica Math. Hung, 46(1)(2003), 9-15.10.1023/A:1025745406160Search in Google Scholar

[19] Chartrand G., Poisson C., Zhang P., Resolvability and the upper dimension of graphs Comput. Math. Appl., 39(12):19-28, 2000.10.1016/S0898-1221(00)00126-7Search in Google Scholar

[20] Chvatal V., Mastermind Combinatorica, 3(3-4):325-329, 1983.10.1007/BF02579188Search in Google Scholar

[21] Hussain Z., Munir M., Chaudhary M., Kang S. M. Computing Metric Dimension and Metric Basis of 2D Lattice of Alpha-Boron Nanotubes Symmetry 2018, 10, 300.10.3390/sym10080300Search in Google Scholar

[22] Erdos P., Raenyi A., On two problems of information theory Magyar Tud. Akad. Mat. Kutatao Int. Kaozl., 8:229-243, 1963.Search in Google Scholar

[23] Frank P., Silverman R., Remarks on detection problems Amer. Math. Monthly, 74:171-173, 1967.10.2307/2315611Search in Google Scholar

[24] Hongbin M., Idrees M., Nizami A.R., Munir M., Generalized Möbius Ladder and Its Metric Dimension arXiv:1708.05199.Search in Google Scholar

[25] Chartrand G., Salehi E., Zhang P., On the partition dimension of a graph Congr. Numer., 131 (1998), pp. 55-66.10.1007/PL00000127Search in Google Scholar

[26] Chartrand G., Salehi E., Zhang P., The partition dimension of a graph Aequationes Math., 59 (2000), pp. 45-5410.1007/PL00000127Search in Google Scholar

[27] Chappell C., Glenn G., Gimbel J. Hartman C., Bounds on the metric and partition dimensions of a graph Ars Combinatoria 88, 349-366 (2008). 4.Search in Google Scholar

[28] Hernando C., Moraz M., Pelayox I. M., On the Partition Dimension and the Twin Number of a Grapharxiv.org/pdf/1602.08907v3.pdfSearch in Google Scholar

[29] Fernau H., Rodríguez-Velázquez J. A., Yero I. G., On the partition dimension of unicyclic graphs Bull. Math. Soc. Sci. Math. Roumanie, Tome 57(105) No. 4, 2014, 381-391.Search in Google Scholar

[30] Tomescu I., Imran M., On metric and partition dimensions of some infinite regular graphs Bull. Math. Soc. Sci. Math. Roumanie(100),(2009) 461-472.Search in Google Scholar

[31] Tomescu I., Imran M., Slamin M., On the partition dimension and connected partition dimension of wheels Ars Combinatoria 84 (2007) 311-317.Search in Google Scholar

[32] Turaci T., The Average Lower 2-domination Number of Wheels Related Graphs and an Algorithm Mathematical and Computational Applications, Vol. 21(3), 29, 2016.10.3390/mca21030029Search in Google Scholar

[33] Aytaç V., Turaci T.,On Aritmetic-Geometric index (GA) and edge GA index TWMS Journal of Applied and Engineering Mathematics, Vol.8, No.1, pp. 61-70, 2018.10.26837/jaem.395612Search in Google Scholar

[34] Aytaç V., Turaci T., Vertex Vulnerability Parameter of Gear Graphs International Journal of Foundations of Computer Science, Vol.22, No.5, pp. 1187-1195, 2011.10.1142/S0129054111008635Search in Google Scholar

[35] Liu J.-B., Munir M., Farooki R., Imran Q. M., Muneer Q., Stanley Depth of Edge Ideals of Some Wheel-Related Graphs Mathematics 2019, 7, 202.10.3390/math7020202Search in Google Scholar

[36] Liu J.-B., Munir M., Yousaf A., Naseem A., Ayub K. Distance and Adjacency Energies of Multi-Level Wheel Networks Mathematics 2019, 7, 43.10.3390/math7010043Search in Google Scholar

[37] Siddique H. M. A., Imran H., Computing the metric dimension of wheel related graphs Appl. Math. Comput. 2014, 242, 624-632.10.1016/j.amc.2014.06.006Search in Google Scholar

[38] Hussain Z., Khan J.A., Munir M., Saleem M.S., Iqbal Z., Sharp bounds for partition dimension of generalized Möbius ladders Open. Math. 2018, 16, 1283-1290.10.1515/math-2018-0109Search in Google Scholar

[39] Aigner M., Ziegler G. M., Proofs from THE BOOK Springer-Verlag, 1999.10.1007/978-3-662-22343-7Search in Google Scholar

[40] Tomescu I., Javaid I., On the metric dimension of the Jahangir graph Bull. Math. Soc. Sci. Math. Roumanie, 50(98), 4(2007), 371-376.Search in Google Scholar

Received: 2018-01-25

Accepted: 2019-05-21

Published Online: 2019-07-17

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/phys-2019-0037

Keywords for this article

Metric dimension; partition dimension; generalized Wheel

Creative Commons

BY 4.0