Home Physical Sciences Method for deriving twisting process parameters of large package E-glass yarn by measuring physical properties of bobbin yarn
Article Open Access

Method for deriving twisting process parameters of large package E-glass yarn by measuring physical properties of bobbin yarn

  • Xi Wang EMAIL logo , Juanfen Chen , Shuai Li , Pei Xiao , Kai Cheng , Yanhe Wang and Tianyong Zheng EMAIL logo
Published/Copyright: June 9, 2023
Download Article (PDF)
Become an author with De Gruyter Brill
Submit Manuscript Author Information
Science and Engineering of Composite Materials
From the journal Science and Engineering of Composite Materials Volume 30 Issue 1

Abstract

Twisting is an important part in the production process of large package E-glass yarn. To derive the twisting process parameters of large package E-glass yarn, a method from the physical properties of bobbin yarn is proposed based on the study of the twisting principle of E-glass yarn. After unwinding the bobbin yarn and measuring its twist, loop pitch, and corresponding diameter, the calculation is completed according to the steps of first determining the descending speed of the traveler, then fitting the spindle speed data, and finally calculating the elevating speed of the traveler. The result is that the twisting spindle speed of D450 E-glass yarn with 31.8 T/m decreases from 5,015 to 4,550 rpm, the elevating speed of the traveler is 0.91 m/min, and the descending speed of the traveler is 1.50 m/min. The accuracy of the calculation is verified by monitoring the rotating speed of the roving cake and measuring the loop pitch of bobbin yarn in the twisting experiment. The result shows that the prediction error of this method is less than 1.1%, which can effectively derive the twisting process parameters of large package E-glass yarn, and provide a reference for the twisting process design scheme of glass fiber strand manufacturers.

Keywords: continuous filament yarn; roving cake; spindle speed; traveler speed; loop pitch

1 Introduction

E-glass yarn is a kind of continuous filament yarn with fewer filaments and a small monofilament diameter [1]. The untwisted roving obtained by the drawing process usually needs a twisting process before it can be used for weaving E-glass fabric [2]. In the twisting process, the glass fiber twisting machine is used to unwind and twist the roving wound on the cake, and meanwhile, wind it on the bobbin to become a twisted bobbin yarn. In the production of continuous filament yarn, the twisting process plays an important role, especially for fine E-glass yarn. After twisting, the arrangement of filaments in the yarn changes, and the radial pressure of the yarn generates friction, which improves the clustering property of the yarn [3], so the twisted yarn is not easy to spread. However, the elongation at the break of glass fiber is low, and it is not resistant to bending and friction. Excessive yarn twist is easy to cause fiber breakage, and E-glass fabric needs to be spread in the following process [4], so the twist of E-glass yarn is usually low. In addition, the twisting process changes the package form of E-glass yarn, and the large-diameter roving cake is converted into bobbin yarn with a small diameter and long traverse, so that the yarn can be unwound at high speed along the axis of bobbin yarn in the subsequent process, and it is convenient for transportation and storage [5].

The twisting process is of great significance to E-glass yarn, and it must meet certain requirements. First, the twist of the inner and outer layers of the bobbin yarn should be consistent [6]. Second, the yarn should be tightly wound, well layered, not entangled with each other, and not cast off when unwinding. Meanwhile, the yarn winding and unwinding tension should be stable, with a low yarn breakage rate and less hairiness [7]. In addition, the package of bobbin yarn should be large to reduce the number of bobbin changes in the subsequent process and improve production efficiency.

E-glass yarn twisting and ring spinning are similar, but there are also many differences between them. Ring spinning is that the roving is drawn by the front roller, and the short fiber is converged into yarn at the outlet of the front roller by twisting [8]. However, E-glass yarn is twisted by unwinding the roving cake to output the yarn [9]. The diameter of the roving cake does not remain the same as that of the front roller of the ring spinning but gradually decreases. Ring spinning adopts short-traverse winding [10], while E-glass yarn twisting adopts long-traverse winding to realize large package and high-speed axial unwinding, which is convenient for subsequent processing. There is a step-up in the short-traverse winding of ring spinning, and the spun bobbin yarn is usually spindle-shaped [11]. However, the traverse of E-glass yarn twisting is usually set to elevate and then descend layer by layer, and the twisted bobbin yarn is bottle-shaped. Due to the influence of the long-traverse setting, there is a difference between the cylindrical loop pitch and the conical loop pitch of the bobbin yarn [12]. Therefore, it is necessary to increase the traveler speed at the cone stage to compensate for the difference caused by the change in the winding diameter of the bobbin yarn. In addition, in the short-traverse winding process of ring spinning, the half-cone angle of bobbin yarn rises from 0 degrees to the maximum and then remains unchanged [13]. While in the process of E-glass yarn twisting, the half-cone angle of bobbin yarn starts from 0 degrees and increases linearly with the twisting length, and the winding diameter also increases linearly.

Since there are some differences between E-glass yarn twisting and ring spinning, the traditional ring spinning production process cannot be copied, and the process parameters adopted by various glass fiber strand manufacturers in the twisting process are also different. Based on the study on the twisting principle of large package E-glass yarn, this article reveals the relationship between the physical properties of bobbin yarn and the twisting process parameters, proposes a method to calculate the spindle speed and the elevating and descending speed of the traveler by measuring the twist, loop pitch, and its corresponding diameter of bobbin yarn, and verifies the accuracy of the calculation by conducting experiments on a glass fiber twisting machine.

2 Twisting principle of E-glass yarn

The basic principle of E-glass yarn twisting is that twisting and winding are carried out simultaneously. The polyamide hook spins one time on the traveler, with a section of yarn from the unwinding point of the roving cake to the polyamide hook getting a twist, but the yarn is not twisted after passing through the polyamide hook [14]. When the polyamide hook spins on the traveler, the friction between the polyamide hook and the traveler produces resistance, so the polyamide hook speed lags behind the spindle speed, and the speed difference between them makes the yarn wind on the bobbin. A schematic diagram of E-glass yarn twisting is shown in Figure 1.

Figure 1 Schematic diagram of E-glass yarn twisting.
Figure 1

Schematic diagram of E-glass yarn twisting.

As shown in Figure 1, after the yarn is unwound from the roving cake, it first passes through the yarn guide, and a balloon spinning around the spindle is formed between the yarn guide and the polyamide hook, and the balloon is confined in the balloon control ring [15]. After passing through the polyamide hook on the traveler, the yarn is wound on the bobbin, which is set on the high-speed spinning spindle, and the traveler elevates and descends repeatedly to make the yarn wind all over the bobbin.

If the spindle speed is defined as N d (rpm) and the polyamide hook speed is defined as N g (rpm), and the speed difference between them results in winding, then the winding speed N j (rpm) can be expressed as follows:

(1) N j = N d − N g .

According to the relationship between linear velocity and angular velocity, if the linear velocity of yarn is defined as V s (m/min) and the winding diameter of bobbin yarn is defined as d x (m), then the winding speed can be expressed as the ratio of the linear velocity of yarn to the winding diameter of bobbin yarn. With equation (1), the winding speed equation of E-glass yarn twisting can be derived as follows:

(2) N g = N d − V s π d x .

The winding speed equation of E-glass yarn twisting is the same as that of ring spinning, but in the process of E-glass yarn twisting, the unwinding diameter of the roving cake does not remain the same as that of the front roller of ring spinning but gradually decreases. If the unwinding diameter of the roving cake is defined as D x (m) and the rotation speed of the roving cake is defined as N s (rpm), then according to the relationship between the linear velocity and angular velocity, the output yarn linear velocity can be expressed as follows:

(3) V s = π D x N s .

The length of the yarn unwound from the roving cake has a linear relationship with the diameter of the roving cake. If the rotating speed of the roving cake is constant, the linear velocity of the yarn will decrease with the decrease in the diameter of the roving cake. The twist T (T/m) of the bobbin yarn is the ratio of spindle speed to yarn linear velocity. When the linear velocity of the yarn decreases, the twist of the bobbin yarn will be changed. Therefore, the glass fiber twisting machine controls the linear velocity of yarn by adjusting the rotation speed of the roving cake to ensure the accuracy of the twist. With equation (3), the rotating speed of the roving cake can be expressed as follows:

(4) N s = N d π D x T .

During the twisting process, the rotation speed of the roving cake increases with the decrease of the diameter of the roving cake, so that the twist remains unchanged.

On bobbin yarn, the distance between adjacent loops is called loop pitch. Due to the requirement of large package and high-speed axial unwinding, bobbin yarn is wound on a slender bobbin in a bottle shape, which can be divided into cylindrical and conical parts. When the traveler elevates to the conical part and winds, the diameter of bobbin yarn gradually decreases, which also reduces the loop pitch. Therefore, by increasing the traveler speed, the loop pitch difference caused by the diameter change of the bobbin yarn can be compensated when winds are at the conical part. To ensure the accuracy of loop distance measurement, the cylindrical loop pitch of bobbin yarn is taken as the measurement basis in this article, as shown in Figure 2.

Figure 2 Schematic diagram of loop pitch and winding diameter of bobbin yarn.
Figure 2

Schematic diagram of loop pitch and winding diameter of bobbin yarn.

Within a certain traverse of the traveler, if the height of the traverse is H (m), the number of windings is S , the yarn length is L (m), the moving time is t (min), and the traveler speed is V g (m/min), then the loop pitch P (m) can be deduced from the following equation:

(5) P = H S = H L π d x = π d x H V s t = π d x H π d x N j H V g = V g N j .

Equation (5) shows that the loop pitch can be expressed as the ratio of the traveler speed to the winding speed of the yarn. With equations (2) and (5), the traveler speed equation is obtained, as shown in the following equation:

(6) V g = PV s π d x = P N d π d x T .

The elevating speed and the descending speed of the traveler are different. Generally, the elevating speed of the traveler is slow, the loop pitch is small, and the winding is tight. The yarn wound in the elevating process forms the winding layer of bobbin yarn. However, the traveler descends faster, the loop pitch is larger and the winding is sparse, and the yarn wound in the descending process forms the binding layer of bobbin yarn. If the descending speed of the traveler is defined as V gd (m/min) and the elevating speed of the traveler is defined as V gu (m/min), the coefficient between them is k , and the relationship between them can be expressed as follows:

(7) V gd = k V gu .

To prevent the yarns of the winding layer and the binding layer from overlapping, the value of the coefficient k should avoid integer and take decimal or odd number. Accordingly, the loop pitch generated when the traveler elevates is denoted as P u (mm), and the loop pitch generated when the traveler descends is denoted as P d (mm).

According to equation (6), if the twist, winding diameter, and loop pitch of bobbin yarn are known, the ratio of spindle speed to the traveler speed can be calculated. Twist, diameter, and loop pitch are the physical properties of bobbin yarn, which can be measured by unwinding bobbin yarn, while the traveler speed is a constant value on glass fiber twisting machine, so the spindle speed can be calculated by determining the traveler speed, thus obtaining the twisting process parameters of E-glass yarn.

3 Measurement of physical properties of bobbin yarn

To measure the twist, loop pitch, and corresponding diameter of bobbin yarn, it is necessary to unwind bobbin yarn in sections until the yarn is completely unwound from the bobbin. In the experiment described in this article, the commercial D450 E-glass yarn is unwound by using the YG086F electronic yarn wrap reel. The unwinding process is divided into 47 sections, with 48 sets of twist, loop pitch, and diameter data of bobbin yarn obtained.

Y331C yarn twist counter is used to test the twist of bobbin yarn. Due to the low twist of E-glass yarn, attention should be paid to prevent the yarn from unwinding in advance during sampling and test preparation. Samples are taken from the full bobbin, and then a group of samples is taken every 3,500 m of yarn unwound, and the yarn twist T is tested by the untwist–retwist method. The twist of each group is tested five times, and the average value of five times is taken as the twist test result of this group. A total of 48 sets of twist data are measured for the whole bobbin yarn. As shown in Table 1, it is known that the twist of the bobbin yarn is 31.8 T/m.

Table 1

Measurement results of physical properties of D450 E-glass yarn

No. Yarn twist T (T/m) Bobbin yarn diameter d x (mm) Elevating loop pitch P u (mm) Descending loop pitch P d (mm) No. Yarn twist T (T/m) Bobbin yarn diameter d x (mm) Elevating loop pitch P u (mm) Descending loop pitch P d (mm)
1 26.0 67.5 1.22 2.06 25 28.0 94.3 1.75 3.23
2 31.0 68.8 1.25 2.01 26 32.0 95.2 1.75 3.00
3 26.0 70.4 1.35 2.10 27 36.0 96.2 1.80 3.00
4 32.5 71.7 1.28 2.15 28 28.0 97.1 1.78 3.00
5 31.2 72.9 1.33 2.35 29 29.0 98.1 1.80 3.05
6 31.2 73.9 1.37 2.22 30 31.0 99.0 1.90 3.18
7 40.0 74.8 1.58 2.25 31 27.0 100.0 1.95 3.20
8 34.0 76.1 1.48 2.25 32 36.0 101.0 1.90 3.18
9 34.0 77.1 1.21 2.43 33 25.5 101.6 1.95 3.25
10 37.0 77.2 1.38 2.40 34 32.5 102.2 1.93 3.23
11 36.5 78.3 1.40 2.36 35 32.0 103.2 2.00 3.35
12 39.5 79.6 1.47 2.50 36 25.5 103.8 2.05 3.40
13 27.0 80.6 1.51 2.59 37 38.0 104.5 2.13 3.40
14 37.0 81.7 1.50 2.50 38 34.0 105.3 1.98 3.43
15 35.5 82.6 1.58 2.52 39 37.0 106.1 2.00 3.48
16 27.5 83.9 1.58 2.51 40 27.0 106.7 2.13 3.55
17 34.5 85.0 1.63 2.58 41 28.0 107.8 2.14 3.65
18 27.5 86.0 1.57 2.68 42 31.0 108.8 2.28 3.53
19 29.0 86.9 1.61 2.65 43 25.5 109.6 2.10 3.53
20 37.0 87.9 1.70 2.82 44 29.0 110.5 2.13 3.60
21 40.0 88.7 1.60 2.83 45 31.5 111.0 2.35 3.80
22 29.0 89.8 1.81 2.83 46 27.0 111.8 2.33 3.65
23 40.0 90.8 1.67 2.85 47 29.0 112.7 2.53 3.73
24 27.0 93.0 1.95 3.05 48 37.0 113.7 2.68 3.65

During each unwinding stage of bobbin yarn, after sampling and yarn twist test are completed, the loop pitch and diameter of bobbin yarn are measured with a steel ruler. To reduce the measurement error of the loop pitch, the sum of the loop pitch of 20 loops of yarn is measured at a time and then divided by 20, which is the measurement result of the loop pitch of this layer of yarn. The position of the yarn unwound from the first loop with a black marker is marked as the starting line; manually unwind the yarn for 20 loops, then the position of the yarn on the 20th loop is marked as the finishing line with a marker, and then the pitch between the starting line and the finishing line is measured with a steel ruler. As shown in Figure 3, 1/20 of the measured value is the loop pitch value of this group. When the yarn moves up one by one during unwinding, the measured loop pitch is the elevating loop pitch P u of bobbin yarn, and then the unwinding is continued until the yarn moves down one by one, and the above operations are repeated, and the measured loop pitch is the descending loop pitch P d of bobbin yarn, and vice versa. After testing the loop pitch at each unwinding stage, the current diameter d x of bobbin yarn is measured at once. Therefore, the measurement results of the physical properties of bobbin yarn shown in Table 1 are obtained.

Figure 3 Measurement of the loop pitch of bobbin yarn.
Figure 3

Measurement of the loop pitch of bobbin yarn.

4 Calculation of twisting process parameters

After obtaining the data of bobbin yarn twist, loop pitch, and its corresponding diameter, the twisting spindle speed can be calculated according to equation (6) only by determining the traveler speed. On the glass fiber twisting machine, the elevating speed of the traveler and the descending speed of the traveler can be input, respectively, but the two input speed values are constant and will not change during the whole twisting process [16]. In addition, due to the limitation of equipment performance and the working conditions of the traveler plate counterweight, the elevating and descending speed of the traveler should not be too high. Generally, twisting machine manufacturers will limit the elevating and descending speed of the traveler to a certain numerical range, such as Verdol twisting machine limiting the traveler speed to 2 m/min, and the Volkmann twisting machine allowing the traveler speed to be input to be less than 4 m/min. The limit of the traveler speed can limit the deriving ratio of spindle speed to the traveler speed within a reasonable range, thus making the calculation of twisting process parameters more accurate.

As the equipment used to verify the process parameters in Section 5 is Verdol twisting machine, and considering the stability of the equipment operation, it is assumed that the traveler speed is 75% of the maximum allowable value of the equipment when calculating the twisting process. As shown in Table 1, the descending loop pitch P d is greater than the elevating loop pitch P u , indicating that the descending speed of the traveler is greater than the elevating speed of the traveler, that is, V gd = 1.5 m / min . Combined with traveler speed equation shown in equation (6), the spindle speed of each testing stage can be calculated by equation (8), as shown by the blue data points in Figure 4.

(8) N d = 1 . 5 π d x T P d .

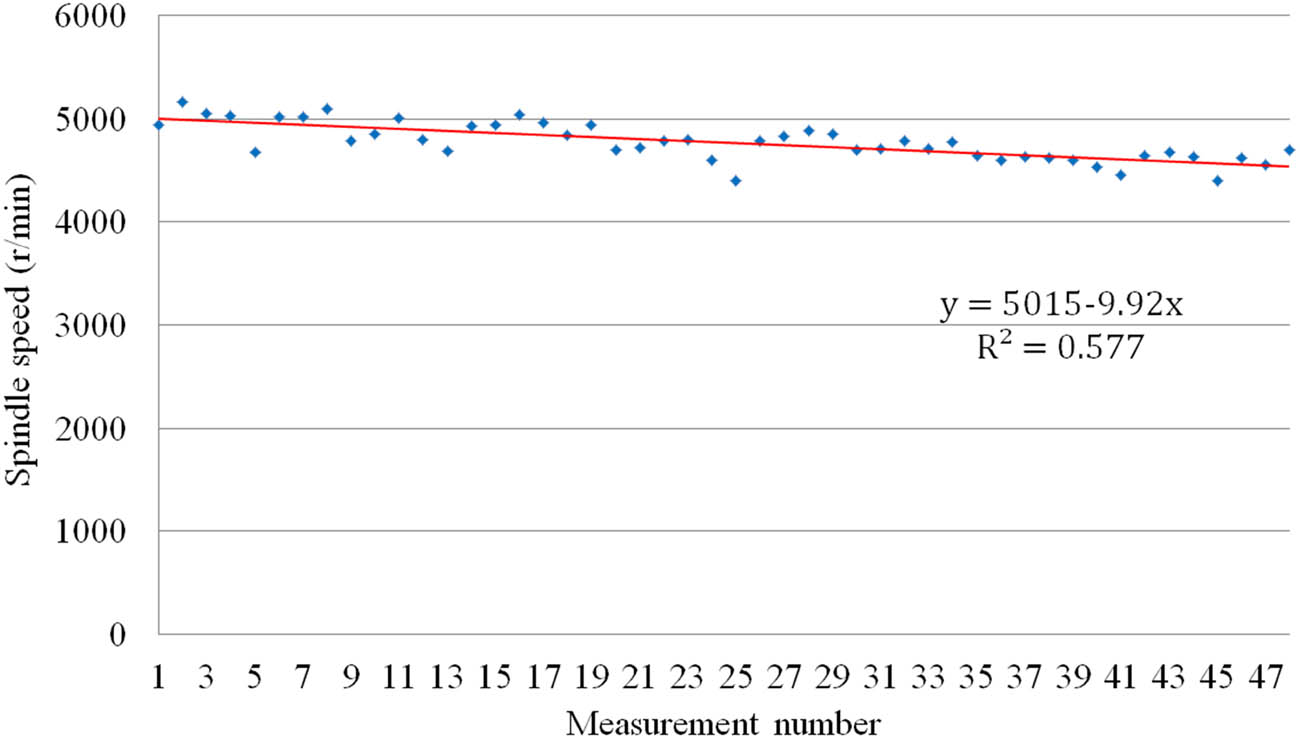
Figure 4 Data fitting of spindle speed.
Figure 4

Data fitting of spindle speed.

The calculated spindle speed data are fitted by the least square method to obtain the red straight line in Figure 4. The fitting equation is y = 5,015 − 9.92 x , and the goodness of fit is R 2 = 0.577 . Because the number of tests is 48, that is, x = 47 , it is found that the spindle speed linearly decreases from 5,015 to 4,550 rpm during twisting.

After the spindle speed is determined, the elevating speed of the traveler can be calculated by equation (6). As shown in Figure 5, the blue curve is the calculation result of the elevating traveler speed V gu , and the red curve represents the descending traveler speed V gd .

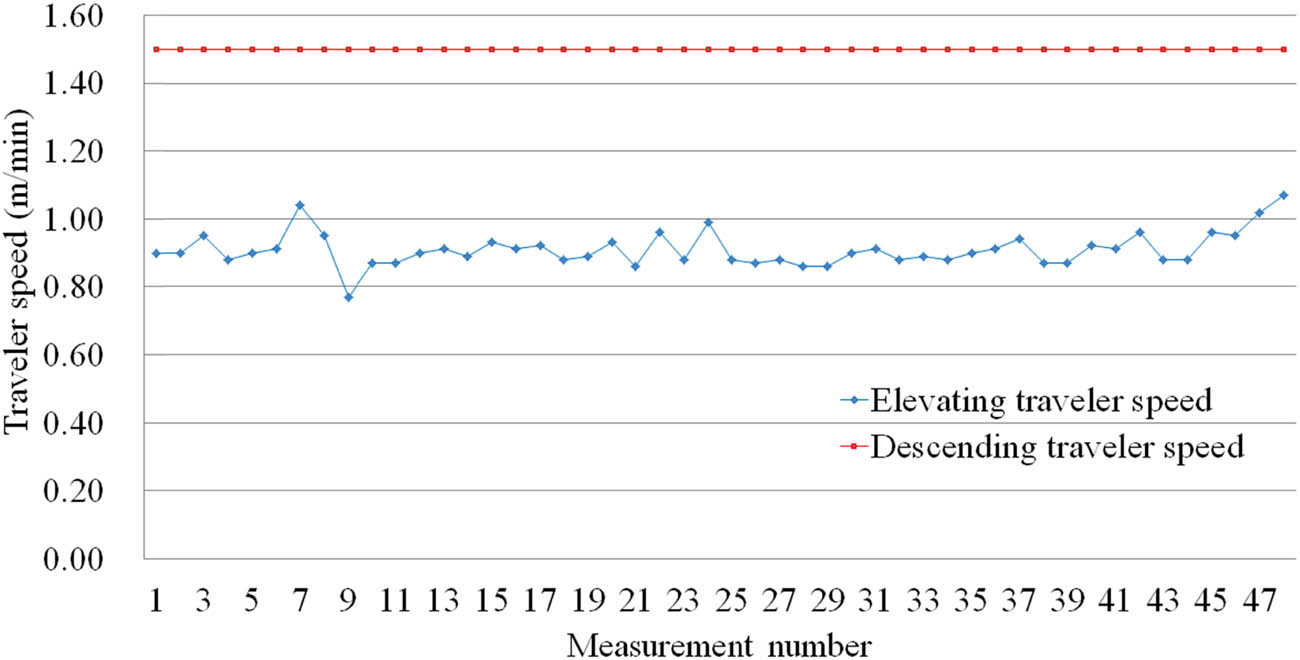
Figure 5 Calculation result of elevating traveler speed.
Figure 5

Calculation result of elevating traveler speed.

Take the average of the elevating traveler speed in Figure 5, that is, V gu = 0.91 m / min . Therefore, the twisting process parameters of D450 E-glass yarn can be calculated, as shown in Table 2.

Table 2

Twisting process parameters of D450 E-glass yarn

Process parameters Values
Yarn twist T 31.8 T/m
Initial bobbin diameter d 0 67.5 mm
Full bobbin diameter d max 113.7 mm
Bobbin yarn height H 293.0 mm
Spindle speed N d 5,015–4,550 rpm
Elevating traveler speed V gu 0.91 m/min
Descending traveler speed V gd 1.50 m/min

5 Verification of twisting process parameters

According to the process parameters calculated in Table 2, a twisting experiment is carried out on a Verdol twisting machine. The accuracy of the calculation can be verified by monitoring the real-time rotation speed of the roving cake during the twisting process, measuring the actual loop pitch of the bobbin yarn after the twisting is completed, and comparing the actual value with the predicted value.

Whether the Verdol twisting machine or Volkmann twisting machine, the control unit of the equipment can display the real-time rotating speed of the roving cake during the twisting process, and the theoretical rotating speed of the roving cake can be calculated by equation (4). In the twisting experiment, the initial diameter of the roving cake is 329 mm, which gradually decreases to 306 mm during the twisting process. Meanwhile, the twist and spindle speed data in Table 2 are substituted into equation (4), and the predicted value of the roving cake speed is calculated. By monitoring and recording the real-time rotation speed of the roving cake, it is compared with the predicted rotation speed of the roving cake, as shown in Figure 6.

Figure 6 Comparison between predicted and actual roving cake speed.
Figure 6

Comparison between predicted and actual roving cake speed.

By comparing the predicted value and the actual value of the roving cake speed in Figure 6, it is found that the theoretical rotation speed of the roving cake is very close to the actual monitoring result, and the prediction error is less than 0.4%, which indicates that the analysis and derivation of the twisting principle of E-glass yarn in Section 2 is accurate and reliable.

When the twisting experiment is finished, the elevating and descending loop pitch of the experimental bobbin yarn are measured by the same method as in Section 3. The data of twist, diameter, spindle speed, and traveler speed in Table 2 are substituted into equation (6) to calculate the theoretical loop pitch. The predicted value and the actual value of the elevating and descending loop pitch of bobbin yarn are compared, as shown in Figure 7.

Figure 7 Comparison between predicted and actual loop pitch.
Figure 7

Comparison between predicted and actual loop pitch.

By comparing the predicted value and the actual value of the elevating and descending loop pitch of bobbin yarn in Figure 7, it is found that the theoretical loop pitch of bobbin yarn is consistent with the actual measurement result, and the error between the predicted value and the actual value is less than 1.1%, which indicates that the deriving method of twisting process parameters has a precise result.

6 Discussion

In Section 4, the linear fitting method is adopted to calculate spindle speed data, and the calculated spindle speed is also in good agreement with the experimental results. However, for different types of E-glass yarn, there may be a multi-section spindle speed scheme. Verdol and Volkmann twisting machine can set the spindle speed of up to ten sections, and the spindle speed in each section can be controlled according to the yarn twisting length, but the spindle speed in each section can only change linearly or remain constant. By setting the twisting spindle speed in sections, various influencing factors such as productivity and yarn tension can be taken into account together [17], and more accurate control of the twisting process can be realized.

Besides, when setting the twisting process parameters of E-glass yarn, in addition to the main parameters such as yarn twist, spindle speed, and the elevating and descending speed of the traveler, it is also necessary to input the diameter of the roving cake at the beginning and end. Because the diameter of the roving cake gradually decreases during twisting, the glass fiber twisting machine will gradually increase the rotation speed of the roving cake according to the input diameter of the roving cake to keep the yarn twist stable. Generally, the diameter of the roving cake is input according to the actual measured value. For example, the diameter of the roving cake input in Section 5 is 329–306 mm. However, due to various process methods such as covering and stacking layer by layer during the formation of the roving cake, the diameter of the roving cake may not change linearly when it is unwound, so the actual diameter of the roving cake may not be conducive to the stability of the yarn twist. According to the roving cake forming process, it may be better to adjust the input roving cake diameter value appropriately. When the roving cake is covered layer by layer, the minimum diameter of the roving cake can be appropriately increased. When the roving cake is stacked layer by layer, the maximum diameter of the roving cake can be appropriately reduced. The study on the diameter change law of the roving cake during unwinding will help to obtain more accurate values.

7 Conclusion

Based on the research on the twisting principle of large package E-glass yarn, this article reveals the relationship between the physical properties of bobbin yarn and the twisting process parameters and proposes a method to derive the spindle speed and the traveler speed by measuring the twist, loop pitch, and its corresponding diameter of bobbin yarn. By unwinding and measuring the D450 E-glass yarn with 31.8 T/m, it is found that the twisting spindle speed linearly decreases from 5,015 to 4,550 rpm, the elevating speed of the traveler is 0.91 m/min, and the descending speed of the traveler is 1.50 m/min. And then, the twisting experiment is carried out on a Verdol twisting machine. By monitoring the real-time rotating speed of the roving cake during the twisting process and measuring the actual loop pitch of bobbin yarn after twisting, it indicates that the prediction error is less than 1.1%. By this method, the twisting process parameters of large package E-glass yarn can be derived effectively, providing a reference for the twisting process design scheme of glass fiber strand manufacturers.

Acknowledgement

This work was supported by the Science and Technology Research Project of Education Department of Jiangxi Province (grant number GJJ2202801).

  1. Conflict of interest: Authors state no conflict of interest.

References

[1] Wang X, Liao SQ, Hu LZ, Xiao P, Du PJ. A simple method for measuring the monofilament diameter of continuous filament yarn with high bending stiffness via synthetic laser imaging. Sci Eng Compos Mater. 2022;29(1):312–21.10.1515/secm-2022-0157Search in Google Scholar

[2] Bilisik K, Yolacan G. Single and multiple yarn pull-out on E-glass woven fabric structures. Text Res J. 2011;81(19):2043–55.10.1177/0040517511414976Search in Google Scholar

[3] Zheng TY, Yang KD, Wang X, Ning XC. Objective evaluation of sizing morphology of E-glass filament yarn. J Ind Text. 2022;51(4_Suppl):6563S–89S.10.1177/1528083720911218Search in Google Scholar

[4] Wang X, Zheng TY, Ning XC. Four testing and evaluation methods of the spreading effects on E-glass woven fabrics. Glass Technol-Eur J Glass Sci Technol Part A. 2021;62(6):198–204.Search in Google Scholar

[5] Wang JA, Zhou J, Wang L, Pan RR, Gao WD. Detection of residual yarn on spinning bobbins based on salient region detection. J Text Inst. 2019;110(6):838–46.10.1080/00405000.2018.1529850Search in Google Scholar

[6] Ayele M, Merga Y, Yilma A, Yilie D. Effect of yarn twist on tensile strength, abrasion and pilling resistance of plain-woven cotton fabric. Indian J Fibre Text Res. 2021;46(3):221–4.10.56042/ijftr.v46i3.31718Search in Google Scholar

[7] Celik O, Eren R. Experimental investigation of the relationship between the yarn tension and bobbin diameter in the warping process. Fibres Text East Europe. 2019;27(1):23–31.10.5604/01.3001.0012.7504Search in Google Scholar

[8] Tang HB, Xu BG, Tao XM, Feng J. Mathematical modeling and numerical simulation of yarn behavior in a modified ring spinning system. Appl Math Model. 2011;35(1):139–51.10.1016/j.apm.2010.05.013Search in Google Scholar

[9] Bobovich BB. Use of glass roving for the production of reinforced polymer composite materials by spraying. Glass Ceram. 2015;72(1–2):32–4.10.1007/s10717-015-9717-3Search in Google Scholar

[10] Koranne MV, Kanade PS, Bhagat RA, Bhavsar SD. Studies on package winding with modified traverse blades. Part I: Modification of existing system. Text Res J. 2015;85(20):2168–76.10.1177/0040517515592810Search in Google Scholar

[11] Przybyl K. Stable working conditions of the twisting-and-winding system of a ring spinning frame. Fibres Text East Europe. 2005;13(1):35–8.Search in Google Scholar

[12] Koroteeva LI, Khozina EN, Sekhin AP. Process of Creating Bobbins from Glass and Basalt Threads at High Winding Rates. Fibre Chem. 2019;50(6):584–7.10.1007/s10692-019-10035-2Search in Google Scholar

[13] Belforte G, Ivanov A, Maffiodo D, Testore F. Winding core spun elastic yarns on cone bobbins to be dyed. J Text Inst. 2009;100(5):412–9.10.1080/00405000701863319Search in Google Scholar

[14] Shim WS, Lee H, Lee DW. The interaction of moving yarns with stationary surfaces. Fibers Polym. 2013;14(1):164–71.10.1007/s12221-013-0164-xSearch in Google Scholar

[15] Hossain M, Telke C, Abdkader A, Sparing M, Espenhahn T, Huhne R, et al. Mathematical modelling of dynamic yarn path considering the balloon control ring and yarn elasticity in the ring spinning process based on the superconducting bearing twisting element. Fibres Text East Europe. 2018;26(5):32–40.10.5604/01.3001.0012.2528Search in Google Scholar

[16] Kim JS, Yoon HE, Kim DW. Design of traverse cam for yarn winding on twisting machine. Fibers Polym. 2005;6(2):151–5.10.1007/BF02875607Search in Google Scholar

[17] Hossain M, Telke C, Abdkader A, Cherif C, Beitelschmidt M. Mathematical modeling of the dynamic yarn path depending on spindle speed in a ring spinning process. Text Res J. 2016;86(11):1180–90.10.1177/0040517515606355Search in Google Scholar
Received: 2023-02-08
Revised: 2023-04-27
Accepted: 2023-05-21
Published Online: 2023-06-09

© 2023 the author(s), published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Regular Articles
  2. Effects of cellulose nanofibers on flexural behavior of carbon-fiber-reinforced polymer composites with delamination
  3. Damage mechanisms of bismaleimide matrix composites under transverse loading via quasi-static indentation
  4. Experimental study on hydraulic fracture behavior of concrete with wedge-splitting testing
  5. The assessment of color adjustment potentials for monoshade universal composites
  6. Metakaolin-based geopolymers filled with volcanic fly ashes: FT-IR, thermal characterization, and antibacterial property
  7. The effect of temperature on the tensile properties and failure mechanisms of two-dimensional braided composites
  8. The influence of preparation of nano-ZrO2/α-Al2O3 gradient coating on the corrosion resistance of 316L stainless steel substrate
  9. A numerical study on the spatial orientation of aligning fibrous particles in composites considering the wall effect
  10. A simulative study on the effect of friction coefficient and angle on failure behaviors of GLARE subjected to low-velocity impact
  11. Impact resistance capacity and degradation law of epoxy-coated steel strand under the impact load
  12. Analytical solutions of coupled functionally graded conical shells of revolution
  13. The influence of water vapor on the structural response of asphalt pavement
  14. A non-invasive method of glucose monitoring using FR4 material based microwave antenna sensor
  15. Chloride ion transport and service life prediction of aeolian sand concrete under dry–wet cycles
  16. Micro-damage analysis and numerical simulation of composite solid propellant based on in situ tensile test
  17. Experimental study on the influence of high-frequency vibratory mixing on concrete performance
  18. Effects of microstructure characteristics on the transverse moisture diffusivity of unidirectional composite
  19. Gradient-distributed ZTAp-VCp/Fe45 as new anti-wear composite material and its bonding properties during composite casting
  20. Experimental evaluation of velocity sensitivity for conglomerate reservoir rock in Karamay oil field
  21. Mechanical and tribological properties of C/C–SiC ceramic composites with different preforms
  22. Mechanical property improvement of oil palm empty fruit bunch composites by hybridization using ramie fibers on epoxy–CNT matrices
  23. Research and analysis on low-velocity impact of composite materials
  24. Optimizing curing agent ratios for high-performance thermosetting phthalonitrile-based glass fibers
  25. Method for deriving twisting process parameters of large package E-glass yarn by measuring physical properties of bobbin yarn
  26. A probability characteristic of crack intersecting with embedded microcapsules in capsule-based self-healing materials
  27. An investigation into the effect of cross-ply on energy storage and vibration characteristics of carbon fiber lattice sandwich structure bionic prosthetic foot
  28. Preparation and application of corona noise-suppressing anti-shedding materials for UHV transmission lines
  29. XRD analysis determined crystal cage occupying number n of carbon anion substituted mayenite-type cage compound C12A7: nC
  30. Optimizing bending strength of laminated bamboo using confined bamboo with softwoods
  31. Hydrogels loaded with atenolol drug metal–organic framework showing biological activity
  32. Creep analysis of the flax fiber-reinforced polymer composites based on the time–temperature superposition principle
  33. A novel 3D woven carbon fiber composite with super interlayer performance hybridized by CNT tape and copper wire simultaneously
  34. Effect of aggregate characteristics on properties of cemented sand and gravel
  35. An integrated structure of air spring for ships and its strength characteristics
  36. Modeling and dynamic analysis of functionally graded porous spherical shell based on Chebyshev–Ritz approach
  37. Failure analysis of sandwich beams under three-point bending based on theoretical and numerical models
  38. Study and prediction analysis on road performance of basalt fiber permeable concrete
  39. Prediction of the rubberized concrete behavior: A comparison of gene expression programming and response surface method
  40. Study on properties of recycled mixed polyester/nylon/spandex modified by hydrogenated petroleum resin
  41. Effect of particle size distribution on microstructure and chloride permeability of blended cement with supplementary cementitious materials
  42. In situ ligand synthesis affording a new Co(ii) MOF for photocatalytic application
  43. Fracture research of adhesive-bonded joints for GFRP laminates under mixed-mode loading condition
  44. Influence of temperature and humidity coupling on rutting deformation of asphalt pavement
  45. Review Articles
  46. Sustainable concrete with partial substitution of paper pulp ash: A review
  47. Durability and microstructure study on concrete made with sewage sludge ash: A review (Part Ⅱ)
  48. Mechanical performance of concrete made with sewage sludge ash: A review (Part Ⅰ)
  49. Durability and microstructure analysis of concrete made with volcanic ash: A review (Part II)
  50. Communication
  51. Calculation of specific surface area for tight rock characterization through high-pressure mercury intrusion
  52. Special Issue: MDA 2022
  53. Vibration response of functionally graded material sandwich plates with elliptical cutouts and geometric imperfections under the mixed boundary conditions
  54. Analysis of material removal process when scratching unidirectional fibers reinforced polyester composites
  55. Tailoring the optical and UV reflectivity of CFRP-epoxy composites: Approaches and selected results
  56. Fiber orientation in continuous fiber-reinforced thermoplastics/metal hybrid joining via multi-pin arrays
  57. Development of Mg-based metal matrix biomedical composites for acicular cruciate ligament fixation by reinforcing with rare earth oxide and hydroxyapatite – A mechanical, corrosion, and microstructural perspective
  58. Special Issue: CACMSE
  59. Preparation and application of foamed ceramic panels in interior design
https://doi.org/10.1515/secm-2022-0212
Keywords for this article
continuous filament yarn; roving cake; spindle speed; traveler speed; loop pitch
Creative Commons
BY 4.0

Articles in the same Issue

  1. Regular Articles
  2. Effects of cellulose nanofibers on flexural behavior of carbon-fiber-reinforced polymer composites with delamination
  3. Damage mechanisms of bismaleimide matrix composites under transverse loading via quasi-static indentation
  4. Experimental study on hydraulic fracture behavior of concrete with wedge-splitting testing
  5. The assessment of color adjustment potentials for monoshade universal composites
  6. Metakaolin-based geopolymers filled with volcanic fly ashes: FT-IR, thermal characterization, and antibacterial property
  7. The effect of temperature on the tensile properties and failure mechanisms of two-dimensional braided composites
  8. The influence of preparation of nano-ZrO2/α-Al2O3 gradient coating on the corrosion resistance of 316L stainless steel substrate
  9. A numerical study on the spatial orientation of aligning fibrous particles in composites considering the wall effect
  10. A simulative study on the effect of friction coefficient and angle on failure behaviors of GLARE subjected to low-velocity impact
  11. Impact resistance capacity and degradation law of epoxy-coated steel strand under the impact load
  12. Analytical solutions of coupled functionally graded conical shells of revolution
  13. The influence of water vapor on the structural response of asphalt pavement
  14. A non-invasive method of glucose monitoring using FR4 material based microwave antenna sensor
  15. Chloride ion transport and service life prediction of aeolian sand concrete under dry–wet cycles
  16. Micro-damage analysis and numerical simulation of composite solid propellant based on in situ tensile test
  17. Experimental study on the influence of high-frequency vibratory mixing on concrete performance
  18. Effects of microstructure characteristics on the transverse moisture diffusivity of unidirectional composite
  19. Gradient-distributed ZTAp-VCp/Fe45 as new anti-wear composite material and its bonding properties during composite casting
  20. Experimental evaluation of velocity sensitivity for conglomerate reservoir rock in Karamay oil field
  21. Mechanical and tribological properties of C/C–SiC ceramic composites with different preforms
  22. Mechanical property improvement of oil palm empty fruit bunch composites by hybridization using ramie fibers on epoxy–CNT matrices
  23. Research and analysis on low-velocity impact of composite materials
  24. Optimizing curing agent ratios for high-performance thermosetting phthalonitrile-based glass fibers
  25. Method for deriving twisting process parameters of large package E-glass yarn by measuring physical properties of bobbin yarn
  26. A probability characteristic of crack intersecting with embedded microcapsules in capsule-based self-healing materials
  27. An investigation into the effect of cross-ply on energy storage and vibration characteristics of carbon fiber lattice sandwich structure bionic prosthetic foot
  28. Preparation and application of corona noise-suppressing anti-shedding materials for UHV transmission lines
  29. XRD analysis determined crystal cage occupying number n of carbon anion substituted mayenite-type cage compound C12A7: nC
  30. Optimizing bending strength of laminated bamboo using confined bamboo with softwoods
  31. Hydrogels loaded with atenolol drug metal–organic framework showing biological activity
  32. Creep analysis of the flax fiber-reinforced polymer composites based on the time–temperature superposition principle
  33. A novel 3D woven carbon fiber composite with super interlayer performance hybridized by CNT tape and copper wire simultaneously
  34. Effect of aggregate characteristics on properties of cemented sand and gravel
  35. An integrated structure of air spring for ships and its strength characteristics
  36. Modeling and dynamic analysis of functionally graded porous spherical shell based on Chebyshev–Ritz approach
  37. Failure analysis of sandwich beams under three-point bending based on theoretical and numerical models
  38. Study and prediction analysis on road performance of basalt fiber permeable concrete
  39. Prediction of the rubberized concrete behavior: A comparison of gene expression programming and response surface method
  40. Study on properties of recycled mixed polyester/nylon/spandex modified by hydrogenated petroleum resin
  41. Effect of particle size distribution on microstructure and chloride permeability of blended cement with supplementary cementitious materials
  42. In situ ligand synthesis affording a new Co(ii) MOF for photocatalytic application
  43. Fracture research of adhesive-bonded joints for GFRP laminates under mixed-mode loading condition
  44. Influence of temperature and humidity coupling on rutting deformation of asphalt pavement
  45. Review Articles
  46. Sustainable concrete with partial substitution of paper pulp ash: A review
  47. Durability and microstructure study on concrete made with sewage sludge ash: A review (Part Ⅱ)
  48. Mechanical performance of concrete made with sewage sludge ash: A review (Part Ⅰ)
  49. Durability and microstructure analysis of concrete made with volcanic ash: A review (Part II)
  50. Communication
  51. Calculation of specific surface area for tight rock characterization through high-pressure mercury intrusion
  52. Special Issue: MDA 2022
  53. Vibration response of functionally graded material sandwich plates with elliptical cutouts and geometric imperfections under the mixed boundary conditions
  54. Analysis of material removal process when scratching unidirectional fibers reinforced polyester composites
  55. Tailoring the optical and UV reflectivity of CFRP-epoxy composites: Approaches and selected results
  56. Fiber orientation in continuous fiber-reinforced thermoplastics/metal hybrid joining via multi-pin arrays
  57. Development of Mg-based metal matrix biomedical composites for acicular cruciate ligament fixation by reinforcing with rare earth oxide and hydroxyapatite – A mechanical, corrosion, and microstructural perspective
  58. Special Issue: CACMSE
  59. Preparation and application of foamed ceramic panels in interior design
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 14.12.2025 from https://www.degruyterbrill.com/document/doi/10.1515/secm-2022-0212/html?lang=en
Scroll to top button