Abstract
Recent astrophysical observations hint toward the need for an extended theory of gravity to explain puzzles presented by the standard cosmological model such as the need for dark matter and dark energy to understand the dynamics of the cosmos. This paper investigates the effect of a repulsive central universal force field on the behavior of celestial objects. Negative tidal effect on the solar and galactic orbits, like that experienced by Pioneer spacecrafts, was derived from the central force and was shown to manifest itself as dark matter and dark energy. Vertical oscillation of the sun about the galactic plane was modeled as simple harmonic motion driven by the repulsive force. The proposed universal field was used to infer the shape of dark matter halos as generated from a planar component of the universal force and to explain galactic warp, galactic halo density, and galactic rotation curves. It was found that the repulsive field addition to Newton’s gravity mimics the Yukawa potential correction employed by many current gravitational theories that modify gravity.
1 Introduction
The success of the standard cosmological model (𝛬CDM) [1, 2] has been marred by a number of puzzling large scale cosmological observations [3, 4] which hint toward the need for modifications of the model. Therefore, extended theory of gravity may be needed since it is clear from recent astrophysical observations that Einstein equations are no longer good enough to test gravitation in the solar system and at the galactic scale, unless we admit some kind of exotic matter-energy to the matter side of Einstein field equations, dubbed “dark matter” and “dark energy”; see [5] and references therein.
The existence of dark matter is mostly inferred from gravitational effects on visible matter and is thought to account for approximately 85% of the matter in the universe while dark energy is inferred from the accelerated expansion of the universe and along with dark matter constitutes about 95% of the total mass-energy content in the universe. The origin of dark matter is a mystery and a wide range of theories speculate its type, its particle’s mass, its self-interaction and its interaction with normal matter. Also, experiments to directly detect dark matter particles in the lab have failed to produce positive results which presents a serious challenge to its existence; see [6, 7] and references therein. Nevertheless the hunt for a dark particle continues; such as the new approach to directly detect dark matter particles by observing them interacting with electrons from nuclear scattering [8]. Other problems that face the existence of dark matter is that simulations of dark matter according to current models that best describe it relevant to corresponding theories present further challenges when compared with observation; such as producing more steeply rising rotation curves than we see in many low surface brightness galaxies, suggesting that simulations produce an overabundance of dark matter [9] and when explaining the average velocity dispersions for the Milky Way and Andromeda, there should be five times more dark matter satellite galaxies according to theory [10]. For all of these challenges that face the proof of the existence of dark matter one may have to consider looking forward for alternate theories.
We propose that such as there has been equal amounts of normal baryonic matter and antimatter in the early universe with baryonic matter prevailing over antimatter due to matter-antimatter asymmetry, there has also been equal amounts of dark matter and anti-dark matter with dark matter prevailing and escaping complete destruction due to asymmetric anti-dark matter [11]. If that was the case, dark matter then might have separated and formed their own pockets in the universe. This scenario prompts the consideration of a long range gravitational interaction by dark matter “worlds” and our baryonic matter worlds. It is suggested here that this interaction might be negative and we can build on that to explain cosmological behavior of our baryonic worlds.
Attempts to explain various cosmological anomalies have not been very promising so far. To name few, attempts have been made to explain the Pioneer anomaly, ranging from systematic effects to new theoretical approaches [12, 13, 14, 15, 16, 17, 18, 19, 20], and to explain galactic rotation curves by invoking the existence of the perplexing dark matter [21, 22, 23] or by modifying the law of gravity [24, 25].
The concept of antimass was invoked by Albert Einstein himself. The newest in the literature in that regard is a “dark” fluid theory with repulsive behavior and constant creation of matter that help understand dark matter and dark energy at cosmological scales [26].
Classical theories of repulsive gravity have been published as extensions of general relativity where antiparticles “live” in an inverted spacetime [27, 28, 29]. Non-classical theories of repulsive gravity have also been published [30]. Against general consensus in the field, the notion of anti-gravity that is based on the assumption that antimatter gravitationally repels matter drives scientists to test this possibility. Theories of that notion, if successful, must await confirmation by experiment, probably by ALPHA-g and GBAR experiments at CERN,which are yet to bear fruit as of current time.
In the weak-field limit of most of the current gravitational theories present today that try to explain the perplexing cosmological gravitational deviation from GR/Newtonian mechanics, such as nonsymmetric, scalar-tensor-vector (MOG), quantum gravitational theories of gravity. . .etc., result in a Yukawa-like type of gravitational potential [31, 32, 33]. For example, MOG is a covariant, relativistic, alternative gravitational theory whose field equations are derived from an action that supplements the spacetime metric tensor with vector and scalar fields.MOG predicts that far from the source of gravity, i.e., the core of a galaxy, the force field is stronger than the normal inverse-square Newtonian one, but at shorter distances, it is counteracted by a repulsive “fifth force” due to a vector field [34, 35].MOGhas been successfully applied to explain the rotation curves of the Milky Way galaxy [36] and the dynamics of galaxy clusters without dark matter. It has also been shown in a recent study that the theory satisfies the weak equivalence principle and is consistent with observations of the neutron star merger and gamma ray burster event GW170817/GRB170817A [37].
In a recent research, it was suggested that observational evidence for the existence of cold dark matter particles in the cores of dwarf galaxies could be explained through the interaction of a Yukawa potential [38]. Therefore it has been suggested that the experimental and observational search for an explanation of gravitational deviation from GR/Newton gravity might result in new type of physics [39]. Here, it is suggested that in a mass-antimass universe, the result of the existence of nearby aggregates of antimass could be a repulsive gravitational force field and would materialize as acceleration in the radial direction from theantimass aggregates, which presents a strong candidate to dark matter and dark energy, assuming antimass and normal mass gravitationally repel each other. In this scenario, the repulsive universal field serves as the source to the Yukawa field, or fifth force, that acts as a correction to the Newtonian classical potential in the mentioned gravitational theories.
In this paper, it is shown that galactic dynamics can be, in principle, achieved through extended theories of gravity. The existence of a force field originating from the center of the universe (assuming a spherical universe), possibly local universe, is proposed to drive much of the dynamics of the cosmos and explains many cosmic anomalies. This vector field could be the work of a constant repulsive force that could be the one responsible for the initiation of the Big Bang event and situated at the center of the universe or it could be the result of a nearby repulsive antimass aggregate. Here, the possibility of the existence of a universal repulsive force field is explored, and its effect on solar and galactic dynamics is studied since a model of extended gravity is pursued. To achieve that, a model of the universe with equal amounts of mass and antimass repelling each other and preserving a universal radial gravitational field is presented. Influenced by the repulsive universal force field, our Milky Way galaxy and its components feel the outward radial acceleration. A negative-tidal force resulting from a component of the repulsive central force acting on the solar system results in a sunward acceleration felt by the sun’s orbiters. This is simply the opposite process of the tidal force that causes tides on earth. Here, Pioneer anomaly is explained mainly by considering the action of the negative central force field. It is demonstrated that the success of Newtonian mechanics in explaining the dynamics of the solar system can be extended to explain the rotational speed of stars in galaxies (galactic rotation curves) when corrected by the proposed repulsive universal force based on the assumption that Newtonian gravity is a good approximation without the need for large amounts of dark matter in galaxies.
2 Effect of a repulsive universal force on the solar system and galactic dynamics
Consider a situation where the radial direction of the universe lies in the orbital plane of a planet in the solar system so the planet would be between the center of the universe and the sun at one point and on the opposite side after half orbital period. The proposed universal repulsive force will have a negative tidal effect on the solar system and can cause inward bulge (toward the sun) of the planet’s orbit as acceleration of the sun in the upward direction is larger than that of the planet when the planet is situated above the sun relative to the center of the universe while the acceleration of the planet is larger than that of the sun when it is situated below the sun (or component of the repulsive force toward the sun when the orbital plane is tilted relative to the radial direction). Figure 1 shows the force acting on a celestial system, like our solar system, with an orbital plane perpendicular to the universal radial direction (tangential to a spherical shell concentric with the center of the universe).
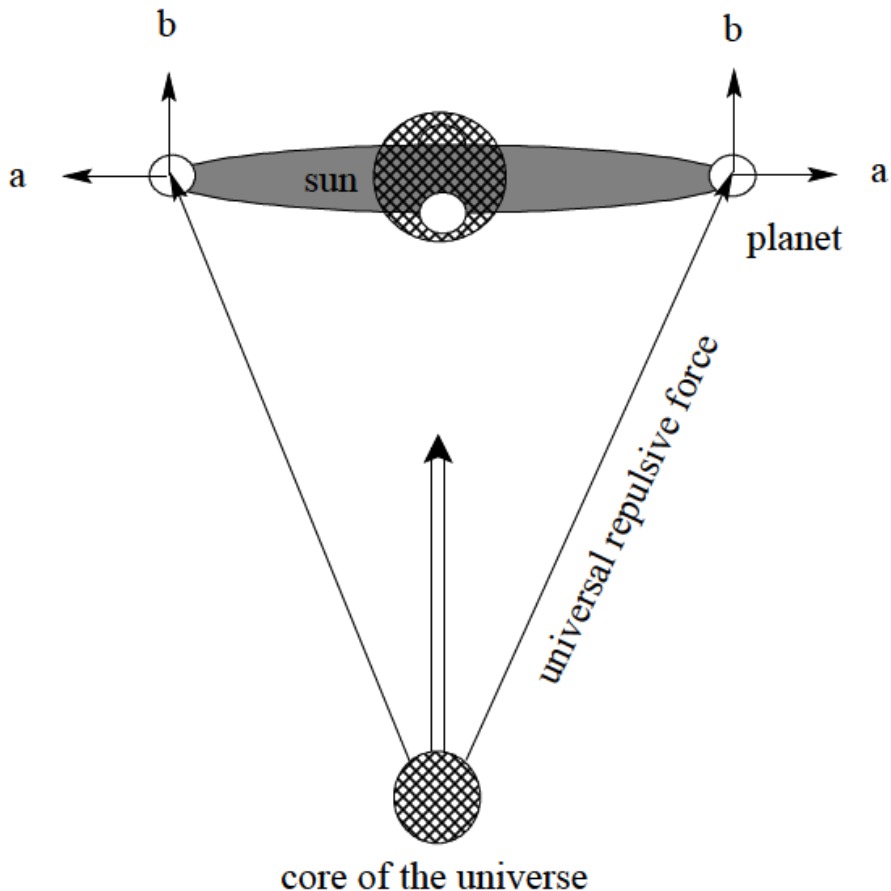
Universal repulsive force produces circular orbital shape of the planetary orbit in the absence of other effects when the orbit is perpendicular to the radial direction of the universal force
Similarly, the repulsive force affects the dynamics of galaxies. The unequal forces of b1 and b2 in an orbital plane of a star orbiting the galactic center that is not perpendicular to the universal radial direction as might be the case of the Milky Way imparts unequal accelerations relative to the position of the star with respect to the core of the universe. Repulsive tidal force also produces oscillation of the stars about their galactic plane as will be discussed in detail. While perpendicular components of the repulsive forces (b-forces in Figure 1) produce bulges of the orbital stars, the in-plane forces (a-forces in Figure 1) act as the restoring forces that produce oscillations of the stars about their galactic plane. Celestial systems then are oscillators oriented at random relative to each other due to the universal repulsive force acting on them.
The sun-orbiting objects, as in the case of the Pioneer spacecraft, feel negative tidal forces in all directions due to their orbital plane tilting relative to the tangential plane of the universal concentric shell at the location of the sun with varying magnitudes producing a bulge toward the sun as opposed to that of the normal positive tidal effect on earth by the sun and the moon.
3 Pioneer anomaly
Pioneer anomaly is a constant acceleration directed towards the Sun of
a = (8.74 ± 1.33) × 10−10m/s2, registered by Pioneer spacecraft [40]. It is commonly believed that attempts to explain this anomaly gravitationally have failed so far.
Following the previous argument in section 2, the Pioneer Effect can be explained that due to the external universal repulsive force acting on the Pioneer spacecraft which produces negative tidal force that results in a constant sun-ward acceleration.
4 Modeling the sun’s dynamics as simple harmonic motion
The sun oscillation about the galactic plane can be treated as simple harmonic motion modeled by a simple pendulum that extends from the center of the galaxy to the sun with the sun acting as the bob and a component of the repulsive central universal force (a-forces in Figure 1) as the restoring force. Using the period of the simple pendulum as the oscillation period of the sun to compute the gravitational field strength at the sun’s location with the restoring forces pronounced when the galactic plane is perpendicular to the universal radial direction, the equation
5 Maximum height of stars from the galactic plane
Models of gravitational force law perpendicular to the galactic plane allow the determination of the galactic velocity-distance relation with close fit to the velocity distance observations. Those models mainly assume an in-plane galactic potential as entirely made by baryonic matter with observational confirmation of star counts, which increases the enigma of how a dark matter galactic halo is distributed in galaxies with the inner part of the galactic disk assumed to be mainly free of dark matter to explain perpendicular motion of stars about the galactic plane with unexplained in-plane dark matter-baryonic matter gravitational relationship. The perpendicular to the galactic plane velocity-distance relationship of stars obtained from the simple harmonic model of the sun agrees with observation and assumes the whole galaxy is free of dark matter as described in the introduction. Figure 2 illustrates the mechanism of the sun vertical oscillation about the galactic plane as modeled by simple harmonic motion.
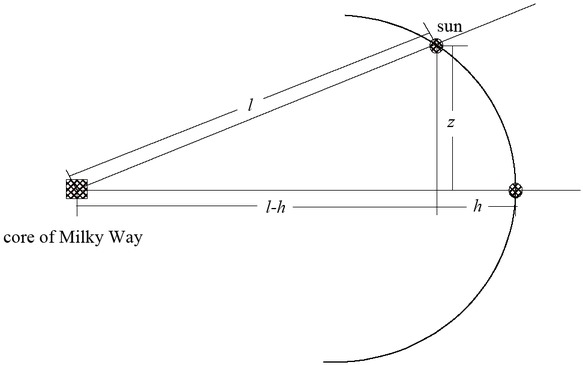
Vertical oscillation of the sun about galactic plane modeled as simple harmonic motion
As clear in Table 1, the sun galactic velocity-distance computed from the simple harmonic model is in close agreement with that from reference [41] computed from distribution function modeling technique.
Sun galactic velocity-distance
| Velocity m/s at z=0 | Zmaximum (Pc), simple harmonic model | Zmaximum (Pc), Kuikken & Gilmore paper |
|---|---|---|
| 0 | 0 | 0 |
| 8400 | 149 | 100 |
| 15700 | 279 | 200 |
| 21900 | 390 | 300 |
| 27300 | 486 | 400 |
| 32100 | 571 | 500 |
| 36500 | 650 | 600 |
| 40600 | 722 | 700 |
| 44500 | 792 | 800 |
| 48300 | 859 | 900 |
| 51800 | 921 | 1000 |
| 58600 | 1042 | 1200 |
| 68300 | 1214 | 1500 |
| 83200 | 1477 | 2000 |
To compute the velocity-distance of the sun in Table 1, the following governing equations have been used following the illustration in Figure 2.
where g is the gravitational field strength at the sun vicinity, taken as a = 8.74 × 10−10m s−2, as that registered by Pioneer spacecraft, and l is the distance of the sun-galaxy center taken as 27700 ly. Equation (1) is derived from conservation of mechanical energy with v is the sun’s velocity at z = 0 and h is the pendulum maximum height obtained from equation (1), obeying the equation
5.1 Galactic disk warp
Galactic disk warps can be explained in terms of the central universal repulsive force. At least half of all galaxies are warped and are long-lived or continuously generated. Galaxies with small dark halo core radii are less likely to be warped which indicates a direct relationship between galactic warp and dark matter halo. Also, it is thought that galactic warp is environmentally driven as galactic disks embedded in rotating halos experience a dynamical friction force which causes it to warp when the angular momentum axes of the disk and halo are misaligned [42].
Most of the galaxies with both sides warped are anti-symmetric with S-shape warps. The warp of galaxies is normally explained in literature in terms of contained dark matter [43, 44]. In this paper dark matter is explained in terms of the central universal repulsive force and so is the galactic warp. Figure 3 shows the repulsive force acting on a proposed galaxy. If the galactic plane is not tangential to a spherical shell with its center as that of the universe, the central repulsive force will act with different magnitudes of perpendicular force components along the galactic plane. The longest arm of the force provides the smallest force component while the shortest provides the largest component because the whole galaxy is accelerated in the radial direction due to the central repulsive force but one end of the galaxy is accelerated faster than the opposite one, with perpendicular force distribution as shown in Figure 3. This produces warp of the galactic disk most pronounced away from the central bulge i.e. in a spiral galaxy. The warping mechanism made by the universal repulsive force clearly explains why the warps are S-shaped.
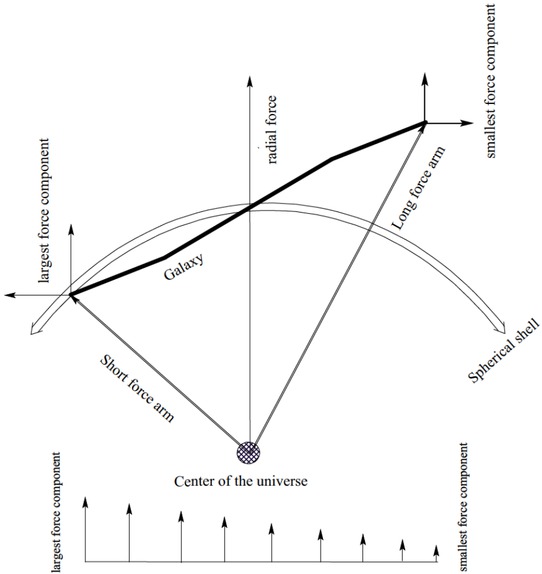
Galactic warp (not to scale)
6 Effect of repulsive force on the Milky Way galaxy at the sun vicinity (dark matter halo)
We can approximate the “virtual” amount of DM at the sun’s location due to the action of the proposed universal repulsive force. Since rotation curves of our galaxy show that the sun is moving about 60 km s−1 faster than what is contributed by visible matter, as the actual sun’s velocity measures about 220 km s−1 while that contributed by visible matter is about 160 km s−1, the centripetal acceleration of a negative tidal force component on the sun can account for the difference with magnitude 0.24×10−10 ms−2 (computed from the pendulum model); where
7 Dark matter cosmic distribution
It is easy to infer that the distribution of dark matter follows the distribution of baryonic matter by considering an external repulsive gravitational field as the cause of baryonic material behavior as discussed above to produce larger orbital velocities of galactic components than obtained by normal matter alone. This may account for what astrophysicists interpret as the work of an existing dark matter in the cosmos which only exists where baryonic matter exists.
8 Halo density of galaxies
It is known that LSB galaxies, mostly dwarf galaxies, have low luminosity and low baryonic mass and are much more dominated by dark matter than large galaxies [45]. As an example, our Milky Way is a large galaxy with about 50% dark matter. Galaxies with 1/100 of the luminosity of the Milky Way galaxy are about 90% dark. The smallest dwarf galaxies known are almost completely made of dark matter. In light of the universal repulsive force, this can be explained by that galactic dark matter content is a manifestation of the proposed universal repulsive force. Since dark matter halo is approximated by the formula
9 Modeling repulsive mass-antimass universe and dark energy
The universe can be modeled as one made with equal amounts of mass and antimass and of consecutive normal mass and antimass spherical shells of specified thickness with the outermost made from one kind considering that the repelling entity to normal mass is the antimass. The mechanism of the acceleration of the universe arises from the fact that matter of the outermost shell of the universe feels a net repulsive force due to the existence of net opposite mass bounded by the shell. This results in acceleration of the outer shell in the outward radial direction. The next inner shell (the second outermost shell) faces the same scenario and so on. An observer in any galaxy sees galaxies of his own shell accelerate away from each other with relative magnitudes since the whole shell increases in size by time except those galaxies that are aligned in the radial universal direction, which leads to that shells become thinner over time. This mechanism would be pronounced if our observable universe was only a patch of space in one shell. This accelerated movement of galaxies away from opposite kind galaxies and the self-aggregation of own kind galaxies leaves voids [46] among them which in principle accounts for the overall sponge-like structure of the universe. This is the same anywhere in the universe due to its spherical symmetry. The accelerated movement of galaxies in the context of the universal repulsive force presents strong candidate to “Dark Energy”. Unlike matter creation theories, such as the “dark” fluid theory mentioned in the introduction, here, dark energy can be seen as the work of the universal repulsive force, hence there is no need for constant creation of matter in the cosmos as proposed by the dark fluid theory; see reference [26].
10 Rotation curves and the shape of dark matter halo
Observations of orbital velocities in spiral galaxies suggest a mass structure according to
where the second term serves as a correction to the Newtonian classical term and M* is the “effective mass” due to menclosed, r is the star-galactic center distance and the rotational speed component in the second term is a function of θ. Note that the second term in equation (3) accounts for the negative tidal force acting on the star due to the existence of the universal repulsive force as explained earlier.
Rotation curves of galaxies (RCs) precisely describe their dynamics [47]. Since the distribution of stars in galaxies doesn’t match observations of their rotation as expected from application of Kepler’s laws, luminous matter alone does not account for the total mass of galaxies [48], prompting the existence of hidden dark matter.
RCs are used to describe dark matter distribution in halos [49]. It is well known that rotation curves of spiral galaxies are flat. This is usually attributed to the existence of halos surrounding galaxies that contain unseen dark matter, which should in theory constitute the missing mass.
Employing the proposed repulsive universal force field we can see in Figure 4 the universal force lines acting on a star with their relative angles.
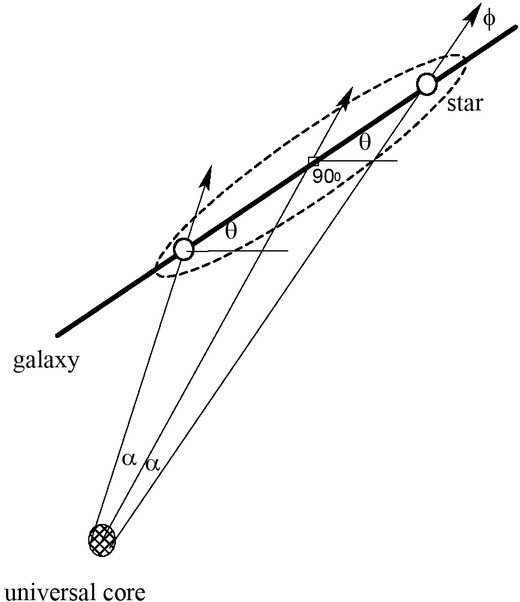
Universal repulsive force field lines on a star with their relative angles (not to scale)
We can see now how the universal repulsive force may account for the shape of the galactic rotation curves supposedly due to hypothetical dark matter: restricting the halo within the volume of the galaxy, we can infer from Figure 4 that the shape of the component of the galactic rotational speed of an edge star that lies on the galactic diameter of highest tilt (solid line in Figure 4), derived from the repulsive universal force, is governed by,
To descriptively represent the shape of a galactic halo from the galactic center to the edge, equation (4) may be employed to approximate the rotational speed component of a star due to the repulsive universal force along the galactic diameter with maximum tilt. The formula was derived from the component of the centripetal acceleration due to the universal repulsive force of v2/d = Φcos φ, where d is replaced by sin α, φ = 90− θ − α, θ is the inclination angle of the galactic plane and Φ is the gravitational field due to the universal repulsive force and approximated to have the same value everywhere at the location of the galaxy with a value of unity. In Figure 5, the shape of the halo is inferred by plotting the rotational speed of the star against the angle α representing the galactic radius.
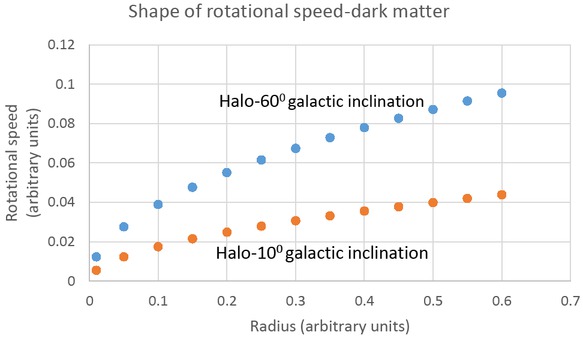
The shape of dark matter halo generated from galactic planar component of the universal repulsive force
As expected, the increase of the inclination angle increases dark matter halo density as shown in Figure 5. Also, the halo density increases with radius which produces flattening of the RCs as opposed to Keplerian rotation.
11 Repulsive universal force as the source of a Yukawa-like field
Current research on gravitational theories explores non-Newtonian component of the gravitational field and presents it as a Yukawa-type correction to the classical gravitational potential and successfully describes various observational astrophysical and cosmological phenomena without resorting to dark matter; see references [31, 32, 33]. For a two-body system of a secondary body of mass m under the gravitational influence of a primary body of massMp, the secondary body’s potential energy can be described by additional modified term [50] as follows,
where G is the gravitation constant, α is the strength of the Yukawa interaction relative to gravity, λ is its range, and r is the separation distance between the two bodies. The Yukawa modified Newtonian potential is used to study a wide range of cosmological gravitational phenomena that pertain to deviation from normal celestial kinematics and even to estimate the mass of the graviton mediating the interaction in celestial bodies; see reference [32]. Similarly, the modified gravity (MOG) theory introduces a Yukawa-like modification term to Newton’s gravity; see reference [37] and references therein. Among extra dimension theories, models with large extra dimensions propose that the interaction between massive objects by exchanging light KK graviton successfully modify Newton’s law of universal gravitation at small distances by adding a Yukawa potential to the ordinary Newtonian potential in the static limit [51].
The gravitational correction to Newton’s law on a two-body satellite system as described by equation (3) mimics the Yukawa potential correction. The second term in the equation replaces the Yukawa correction term and introduces a source of the potential as originating from the proposed negative central mass in a mass-antimass universe that produces a tidal force on celestial objects as described in this paper, where the effective mass “M*” is interpreted as the mass contribution by the source that produces the Yukawa-like field. Since M* depends on the location of the two-body system relative to the repulsive source (center of the universe), and thereby the value of the potentialΦin the equation v2/d = Φcos φ, we conclude that the rest of the parameters involved in equations (3) and (4) must be observation-dependent. Observational verification to the gravitational correction by the universal gravitational field is presented through studying the kinematics of the sun insections 4, 5 and 7. A quantitative assessment of a universal repulsive field acting on a celestial object, perhaps a two-body celestial system, is intended for future work by parameterizing equations (3) and (4) and fitting available cosmological data.
12 Conclusion
As an extended gravity model, it was shown that by accounting for repulsive component of a universal force field in Newtonian mechanics we can provide reasonable explanation to several cosmic puzzles such as dark matter, dark energy, rotation curves, Pioneer anomaly, and galactic disk warp. Importantly, it was shown that negative tidal effect on solar orbits may explain the extra sunward acceleration experienced by Pioneer spacecrafts. The negative tidal force was used to show similar inward acceleration experienced by stars in their galactic orbits and descriptively was used to show how it manifests itself to produce non-Keplerian rotation curves. Similarly, the shape of dark matter halo was inferred by employing the negative tidal force. Vertical oscillation of the sun about the galactic plane was modeled as simple harmonic motion driven by a component of the universal repulsive field and was compared with another model computed from distribution function modeling technique. Accordingly, it was found that the repulsive component of the proposed universal field mimics a Yukawa potential correction to the normal Newtonian field which recently has attracted much attention in the current gravitational theories that modify gravity.
Acknowledgement
I would like to acknowledge the encouragement and support by Prince Mohammad Bin Fahd University. I also would like to express my appreciation to the reviewers whose inputs were invaluable addition to the manuscript.
References
[1] Perivolaropoulos L., Large scale cosmological anomalies and inhomogeneous dark energy, Galaxies, 2014, 2(1), 22-61.10.3390/galaxies2010022Suche in Google Scholar
[2] Hamilton J.-C., What have we learned from observational cosmology? 2013, arXiv:1304.4446.10.1016/j.shpsb.2013.02.002Suche in Google Scholar
[3] Perivolaropoulos, L., Six puzzles for LCDM cosmology, ArXiv E-Prints, 2008, arXiv:0811.4684.Suche in Google Scholar
[4] Yang, R.J., and Zhang, S.N., The age problem in 𝛬CDM model, Mon. Not. R. Astron. Soc., 2010, 407, 1835–1841.10.1111/j.1365-2966.2010.17020.xSuche in Google Scholar
[5] Corda, C., Interferometric Detection of Gravitational Waves: The Definitive Test for General Relativity. International Journal of Modern Physics D, 2009, 18, 2275-2282.10.1142/S0218271809015904Suche in Google Scholar
[6] Arun K., Gudennavar S. B., and Sivaram C., Dark matter, dark energy, and alternate models: A review, ArXiv E-Prints, 2017, arXiv: 1704.06155.10.1016/j.asr.2017.03.043Suche in Google Scholar
[7] Garrett K., and Duda G., Dark matter: A primer, Advances in Astronomy, 2010, 2011(6), 968283.10.1155/2011/968283Suche in Google Scholar
[8] Dolan M. J., Kahlhoefer F., and McCabe C., Directly detecting sub-GeV dark matter with electrons from nuclear scattering, Phys. Rev. Lett., 2018, 121, 101801.10.1103/PhysRevLett.121.101801Suche in Google Scholar PubMed
[9] Klypin A., Kravtsov A. V., Valenzuela O., and Prada F., Where are the missing galactic satellites? Astrophysical Journal, 1999, 522(1), 82–92.10.1086/307643Suche in Google Scholar
[10] Moore B., Quinn T., Governato F., Stadel J., and Lake G., Cold collapse and the core catastrophe, Monthly Notices of the Royal Astronomical Society, 1999, 310(4), 1147–1152.10.1046/j.1365-8711.1999.03039.xSuche in Google Scholar
[11] Frandsen M. T., and Sarkar S., Asymmetric dark matter and the Sun, Phys. Rev. Lett., 2010, 105, 011301.10.1103/PhysRevLett.105.011301Suche in Google Scholar PubMed
[12] Anderson J. D., Laing P. A., Lau E. L., Liu A. S., Nieto M. M., and Turyshev S. G., Indication, from Pioneer 10/11, Galileo, and Ulysses data, of an apparent anomalous, weal, long-range acceleration, Phys. Rev. Lett., 1998, 81, 2858.10.1103/PhysRevLett.81.2858Suche in Google Scholar
[13] Turyshev S. G., Toth V. T., Kellogg L.R., Lau E. L., and Lee K. J., A study of the Pioneer anamoly: new data and objectives for new investigation, International Journal of Modern Physics, 2006, 15, 01, 1-55.10.1142/S0218271806008218Suche in Google Scholar
[14] Bertolami O., and Paramos J., The Pioneer anomaly in the context of the braneworld scenario, Class. Quantum Grav., 2004, 21 3309.10.1088/0264-9381/21/13/013Suche in Google Scholar
[15] Turyshev S. G., Toth V. T., Kinsella G., Lee S.-C., Lok S. M., Ellis J., Support for the thermal origin of Pioneer anomaly, Physical Review Letters, 2012, 108 (24).10.1103/PhysRevLett.108.241101Suche in Google Scholar
[16] Anderson J.D., Lau E. L., Turyshev S.G., Laing P.A., and Nieto M.M., Search for the standard explanation of Pioneer anomaly, Mod. Phys. Lett., 2002, A17, 875.10.1142/S0217732302007107Suche in Google Scholar
[17] Jaekel M.T., and Reynaud S., Gravity tests in the solar system and Pioneer anomaly, Mod. Phys. Lett., 2005, A20 1047.10.1142/S0217732305017275Suche in Google Scholar
[18] Ranada A.F., The Pioneer anomaly as acceleration of the clocks, Found. Phys., 2005, 341955.Suche in Google Scholar
[19] Nottale L., The Pioneer anomalous acceleration: a measurement of the cosmological constant at the scale of the solar system, ArXiv E-Prints, 2011, arXiv: gr-qc/0307042.Suche in Google Scholar
[20] Foot R., and Volkas R.R., A mirror world explanation for the Pioneer spacecraft anomalies? Phys. Lett., 2001, B 517 13.10.1016/S0370-2693(01)01011-5Suche in Google Scholar
[21] Weinberg D. H., Colombi S., Dave R., and Katz N., Baryon dynamics, dark matter substructure, and galaxies, The Astrophysical Journal, 2008, 678 (1): 6–21.10.1086/524646Suche in Google Scholar
[22] Duffy A. R., Schaye J., Kay S. T., Vecchia C. D., Battye R. A., and Booth C. M., Impact of Baryon physics on dark matter structure: a detailed simulation study of halo density profiles, Monthly Notices of the Royal Astronomical Society, 2010, 405(4):2161–2178.10.1111/j.1365-2966.2010.16613.xSuche in Google Scholar
[23] De Blok W. J. G., and McGaugh S., The dark and visible matter content of low surface brightness disc galaxies, Monthly Notices of the Royal Astronomical Society, 1997, 290 (3): 533–552.10.1093/mnras/290.3.533Suche in Google Scholar
[24] Milgrom M., A modification of the Newtonian dynamics as a possible alternative to hidden mass hypothesis, Astrophysical Journal, 1983, 270: 365–370.10.1086/161130Suche in Google Scholar
[25] Milgrom M.,MONDLaws of Galaxy Dynamics, ArXiv E-Prints, 2013, arXiv: 1212.2568.Suche in Google Scholar
[26] Farnes J.S., A unifying energy of dark energy and dark matter: negative matter and mass creation within a modified 𝛬CDM framework, Astronomy & Astrophysics, 2018, 620: A92.10.1051/0004-6361/201832898Suche in Google Scholar
[27] Santilli R.M., A classical isodual theory of antimatter and its prediction of antigravity, International Journal of Modern Physics A, 1999, 14 (14): 2205–2238.10.1142/S0217751X99001111Suche in Google Scholar
[28] Villata M., CPT symmetry and antimatter gravity in general relativity, EPL., 2011, 94 (2): 20001.10.1209/0295-5075/94/20001Suche in Google Scholar
[29] Villata M., On the nature of dark energy: the lattice universe, Astrophysics and Space Science, 2013, 345 (1): 1–9.10.1007/s10509-013-1388-3Suche in Google Scholar
[30] Cabbolet M. J. T. F., Addendum to the elementary process theory, Annalen der Physik, 2011, 523 (12): 990–994.10.1002/andp.201100194Suche in Google Scholar
[31] Piazza F., and Marinoni C., Models for Gravitational Interaction between Dark Matter and Baryons, Phys Rev Lett., 2003, 91, 14.10.1103/PhysRevLett.91.141301Suche in Google Scholar PubMed
[32] Martz C., Middelkoop S. V., Gkigkitzis I., Haranas I., and Kotsireas I., Yukawa potential orbital energy: it relation to orbital mean motion as well to graviton mediating the interaction in celestial bodies, Advances in Mathematical Physics, 2019, 2019, 6765827.10.1155/2019/6765827Suche in Google Scholar
[33] Mukherjee R., and Sounda S., Single particle closed orbits in Yukawa potential, Indian Journal of Physics, 2018, 92 (2), 197–203.10.1007/s12648-017-1100-5Suche in Google Scholar
[34] Moffat J. W., Scalar tensor vector gravity theory, Journal of Cosmology and Astroparticle Physics, 2006, 3 (3): 4.10.1088/1475-7516/2006/03/004Suche in Google Scholar
[35] Moffat J.W., and Toth V. T., Testing modified gravity with globular cluster velocity dispersions, Astrophysical Journal, 2008, 680 (2): 1158–1161.10.1086/587926Suche in Google Scholar
[36] Negrelli S. C., Benito M., Landau S., Iocco F., and Kraiselburd L., Testing modified gravity theory in the Milky Way, Phys. Rev. 2018, D 98, 104061.10.1103/PhysRevD.98.104061Suche in Google Scholar
[37] Green M. A., Moffat J. W., and Toth V. T., Modified gravity (MOG), the speed of gravitational radiation and the event GW170817/GRB170817A, Physics Letters B, 2017, 780, 300-302.10.1016/j.physletb.2018.03.015Suche in Google Scholar
[38] Chan H. M., Observational evidence of the Yukawa potential interacting dark matter, The Astrophysical Journal Letters, 2013, 91, 14, 2003 2.10.1088/2041-8205/769/1/L2Suche in Google Scholar
[39] Adelberger E. G., Heckel B. R., and Nelson A. E., Test of the gravitational inverse square law, Annual Review of Nuclear and Particle Science, 2003, 53, 77-121.10.1146/annurev.nucl.53.041002.110503Suche in Google Scholar
[40] Anderson J. D., Laing P. A., Lau E.L., Liu A. S., Nieto M. M., and Turyshev S. G., Indication from Pioneer 10 /11 Galileo, and Ulysses data, of an apparent anomalous, weak, long-range, acceleration, Phys. Rev. Lett., 1998, 81, 2858.10.1103/PhysRevLett.81.2858Suche in Google Scholar
[41] Kuiken K., and Gilmore G. F., The mass distribution in galactic disc -II- determination of the surface massdensity of the galactic disc near the sun, MNRAS, 1989, 239, 605.10.1093/mnras/239.2.605Suche in Google Scholar
[42] Debattista V.P., and Sellwood J.A., Warped galaxies from misaligned angular momenta, The Astrophysical Journal, 1999, 513:L107 – L110.10.1086/311913Suche in Google Scholar
[43] Sparke L.S., and Casertano S., A model for persistent galactic warps, MNRAS, 1988, 234, 873.10.1093/mnras/234.4.873Suche in Google Scholar
[44] Binney J., Warps, ARA&A, 1992, 30, 51.10.1146/annurev.aa.30.090192.000411Suche in Google Scholar
[45] Se-Heon O., Deidre A. H., Elias B., Bruce G. E., Andreas S., Fabian W., et al., High-resolutions mass models of dwarf galaxies from LITTLE THINGS, The Astronomical Journal, 2015, 149, 6.10.1088/0004-6256/149/6/180Suche in Google Scholar
[46] Nella H. Di, Couch W., Parker Q., and Paturel G., Unveiling a connection between large-scale structures behind the southern Milky Way, MNRAS, 1997, 287, 472.10.1093/mnras/287.2.472Suche in Google Scholar
[47] Sofue Y., and Rubin V. C., Rotation curves of spiral galaxies, ARAA, 2001, 39, 137.10.1146/annurev.astro.39.1.137Suche in Google Scholar
[48] Rubin V., Thonnard N., Ford W. K. Jr., Rotational properties of 21 SC galaxieswith a large range of luminosities and radii, from NGC 4605/R = 4kpc/ to UGC 2885 /R = 122 kpc/, The Astrophysical Journal, 1980, 238: 471.10.1086/158003Suche in Google Scholar
[49] Honma M., and Sofue Y., Rotation curve of the galaxy, PASJ, 1997, 49, 453.10.1093/pasj/49.4.453Suche in Google Scholar
[50] Fischbach E., Talmadge C., and Krause D.E., Exponential models of non-Newtonian gravity, Phys. Rev. D, 1991, 43, 460.10.1103/PhysRevD.43.460Suche in Google Scholar
[51] Schmitz K., Experimental Tests of the Gravity Sector, DESY Werk-statt seminar, Physics of Extra Dimensions, 2011, Summer Term.Suche in Google Scholar
© 2019 K. Barghout, published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Artikel in diesem Heft
- Regular Articles
- Non-equilibrium Phase Transitions in 2D Small-World Networks: Competing Dynamics
- Harmonic waves solution in dual-phase-lag magneto-thermoelasticity
- Multiplicative topological indices of honeycomb derived networks
- Zagreb Polynomials and redefined Zagreb indices of nanostar dendrimers
- Solar concentrators manufacture and automation
- Idea of multi cohesive areas - foundation, current status and perspective
- Derivation method of numerous dynamics in the Special Theory of Relativity
- An application of Nwogu’s Boussinesq model to analyze the head-on collision process between hydroelastic solitary waves
- Competing Risks Model with Partially Step-Stress Accelerate Life Tests in Analyses Lifetime Chen Data under Type-II Censoring Scheme
- Group velocity mismatch at ultrashort electromagnetic pulse propagation in nonlinear metamaterials
- Investigating the impact of dissolved natural gas on the flow characteristics of multicomponent fluid in pipelines
- Analysis of impact load on tubing and shock absorption during perforating
- Energy characteristics of a nonlinear layer at resonant frequencies of wave scattering and generation
- Ion charge separation with new generation of nuclear emulsion films
- On the influence of water on fragmentation of the amino acid L-threonine
- Formulation of heat conduction and thermal conductivity of metals
- Displacement Reliability Analysis of Submerged Multi-body Structure’s Floating Body for Connection Gaps
- Deposits of iron oxides in the human globus pallidus
- Integrability, exact solutions and nonlinear dynamics of a nonisospectral integral-differential system
- Bounds for partition dimension of M-wheels
- Visual Analysis of Cylindrically Polarized Light Beams’ Focal Characteristics by Path Integral
- Analysis of repulsive central universal force field on solar and galactic dynamics
- Solitary Wave Solution of Nonlinear PDEs Arising in Mathematical Physics
- Understanding quantum mechanics: a review and synthesis in precise language
- Plane Wave Reflection in a Compressible Half Space with Initial Stress
- Evaluation of the realism of a full-color reflection H2 analog hologram recorded on ultra-fine-grain silver-halide material
- Graph cutting and its application to biological data
- Time fractional modified KdV-type equations: Lie symmetries, exact solutions and conservation laws
- Exact solutions of equal-width equation and its conservation laws
- MHD and Slip Effect on Two-immiscible Third Grade Fluid on Thin Film Flow over a Vertical Moving Belt
- Vibration Analysis of a Three-Layered FGM Cylindrical Shell Including the Effect Of Ring Support
- Hybrid censoring samples in assessment the lifetime performance index of Chen distributed products
- Study on the law of coal resistivity variation in the process of gas adsorption/desorption
- Mapping of Lineament Structures from Aeromagnetic and Landsat Data Over Ankpa Area of Lower Benue Trough, Nigeria
- Beta Generalized Exponentiated Frechet Distribution with Applications
- INS/gravity gradient aided navigation based on gravitation field particle filter
- Electrodynamics in Euclidean Space Time Geometries
- Dynamics and Wear Analysis of Hydraulic Turbines in Solid-liquid Two-phase Flow
- On Numerical Solution Of The Time Fractional Advection-Diffusion Equation Involving Atangana-Baleanu-Caputo Derivative
- New Complex Solutions to the Nonlinear Electrical Transmission Line Model
- The effects of quantum spectrum of 4 + n-dimensional water around a DNA on pure water in four dimensional universe
- Quantum Phase Estimation Algorithm for Finding Polynomial Roots
- Vibration Equation of Fractional Order Describing Viscoelasticity and Viscous Inertia
- The Errors Recognition and Compensation for the Numerical Control Machine Tools Based on Laser Testing Technology
- Evaluation and Decision Making of Organization Quality Specific Immunity Based on MGDM-IPLAO Method
- Key Frame Extraction of Multi-Resolution Remote Sensing Images Under Quality Constraint
- Influences of Contact Force towards Dressing Contiguous Sense of Linen Clothing
- Modeling and optimization of urban rail transit scheduling with adaptive fruit fly optimization algorithm
- The pseudo-limit problem existing in electromagnetic radiation transmission and its mathematical physics principle analysis
- Chaos synchronization of fractional–order discrete–time systems with different dimensions using two scaling matrices
- Stress Characteristics and Overload Failure Analysis of Cemented Sand and Gravel Dam in Naheng Reservoir
- A Big Data Analysis Method Based on Modified Collaborative Filtering Recommendation Algorithms
- Semi-supervised Classification Based Mixed Sampling for Imbalanced Data
- The Influence of Trading Volume, Market Trend, and Monetary Policy on Characteristics of the Chinese Stock Exchange: An Econophysics Perspective
- Estimation of sand water content using GPR combined time-frequency analysis in the Ordos Basin, China
- Special Issue Applications of Nonlinear Dynamics
- Discrete approximate iterative method for fuzzy investment portfolio based on transaction cost threshold constraint
- Multi-objective performance optimization of ORC cycle based on improved ant colony algorithm
- Information retrieval algorithm of industrial cluster based on vector space
- Parametric model updating with frequency and MAC combined objective function of port crane structure based on operational modal analysis
- Evacuation simulation of different flow ratios in low-density state
- A pointer location algorithm for computer visionbased automatic reading recognition of pointer gauges
- A cloud computing separation model based on information flow
- Optimizing model and algorithm for railway freight loading problem
- Denoising data acquisition algorithm for array pixelated CdZnTe nuclear detector
- Radiation effects of nuclear physics rays on hepatoma cells
- Special issue: XXVth Symposium on Electromagnetic Phenomena in Nonlinear Circuits (EPNC2018)
- A study on numerical integration methods for rendering atmospheric scattering phenomenon
- Wave propagation time optimization for geodesic distances calculation using the Heat Method
- Analysis of electricity generation efficiency in photovoltaic building systems made of HIT-IBC cells for multi-family residential buildings
- A structural quality evaluation model for three-dimensional simulations
- WiFi Electromagnetic Field Modelling for Indoor Localization
- Modeling Human Pupil Dilation to Decouple the Pupillary Light Reflex
- Principal Component Analysis based on data characteristics for dimensionality reduction of ECG recordings in arrhythmia classification
- Blinking Extraction in Eye gaze System for Stereoscopy Movies
- Optimization of screen-space directional occlusion algorithms
- Heuristic based real-time hybrid rendering with the use of rasterization and ray tracing method
- Review of muscle modelling methods from the point of view of motion biomechanics with particular emphasis on the shoulder
- The use of segmented-shifted grain-oriented sheets in magnetic circuits of small AC motors
- High Temperature Permanent Magnet Synchronous Machine Analysis of Thermal Field
- Inverse approach for concentrated winding surface permanent magnet synchronous machines noiseless design
- An enameled wire with a semi-conductive layer: A solution for a better distibution of the voltage stresses in motor windings
- High temperature machines: topologies and preliminary design
- Aging monitoring of electrical machines using winding high frequency equivalent circuits
- Design of inorganic coils for high temperature electrical machines
- A New Concept for Deeper Integration of Converters and Drives in Electrical Machines: Simulation and Experimental Investigations
- Special Issue on Energetic Materials and Processes
- Investigations into the mechanisms of electrohydrodynamic instability in free surface electrospinning
- Effect of Pressure Distribution on the Energy Dissipation of Lap Joints under Equal Pre-tension Force
- Research on microstructure and forming mechanism of TiC/1Cr12Ni3Mo2V composite based on laser solid forming
- Crystallization of Nano-TiO2 Films based on Glass Fiber Fabric Substrate and Its Impact on Catalytic Performance
- Effect of Adding Rare Earth Elements Er and Gd on the Corrosion Residual Strength of Magnesium Alloy
- Closed-die Forging Technology and Numerical Simulation of Aluminum Alloy Connecting Rod
- Numerical Simulation and Experimental Research on Material Parameters Solution and Shape Control of Sandwich Panels with Aluminum Honeycomb
- Research and Analysis of the Effect of Heat Treatment on Damping Properties of Ductile Iron
- Effect of austenitising heat treatment on microstructure and properties of a nitrogen bearing martensitic stainless steel
- Special Issue on Fundamental Physics of Thermal Transports and Energy Conversions
- Numerical simulation of welding distortions in large structures with a simplified engineering approach
- Investigation on the effect of electrode tip on formation of metal droplets and temperature profile in a vibrating electrode electroslag remelting process
- Effect of North Wall Materials on the Thermal Environment in Chinese Solar Greenhouse (Part A: Experimental Researches)
- Three-dimensional optimal design of a cooled turbine considering the coolant-requirement change
- Theoretical analysis of particle size re-distribution due to Ostwald ripening in the fuel cell catalyst layer
- Effect of phase change materials on heat dissipation of a multiple heat source system
- Wetting properties and performance of modified composite collectors in a membrane-based wet electrostatic precipitator
- Implementation of the Semi Empirical Kinetic Soot Model Within Chemistry Tabulation Framework for Efficient Emissions Predictions in Diesel Engines
- Comparison and analyses of two thermal performance evaluation models for a public building
- A Novel Evaluation Method For Particle Deposition Measurement
- Effect of the two-phase hybrid mode of effervescent atomizer on the atomization characteristics
- Erratum
- Integrability analysis of the partial differential equation describing the classical bond-pricing model of mathematical finance
- Erratum to: Energy converting layers for thin-film flexible photovoltaic structures
Artikel in diesem Heft
- Regular Articles
- Non-equilibrium Phase Transitions in 2D Small-World Networks: Competing Dynamics
- Harmonic waves solution in dual-phase-lag magneto-thermoelasticity
- Multiplicative topological indices of honeycomb derived networks
- Zagreb Polynomials and redefined Zagreb indices of nanostar dendrimers
- Solar concentrators manufacture and automation
- Idea of multi cohesive areas - foundation, current status and perspective
- Derivation method of numerous dynamics in the Special Theory of Relativity
- An application of Nwogu’s Boussinesq model to analyze the head-on collision process between hydroelastic solitary waves
- Competing Risks Model with Partially Step-Stress Accelerate Life Tests in Analyses Lifetime Chen Data under Type-II Censoring Scheme
- Group velocity mismatch at ultrashort electromagnetic pulse propagation in nonlinear metamaterials
- Investigating the impact of dissolved natural gas on the flow characteristics of multicomponent fluid in pipelines
- Analysis of impact load on tubing and shock absorption during perforating
- Energy characteristics of a nonlinear layer at resonant frequencies of wave scattering and generation
- Ion charge separation with new generation of nuclear emulsion films
- On the influence of water on fragmentation of the amino acid L-threonine
- Formulation of heat conduction and thermal conductivity of metals
- Displacement Reliability Analysis of Submerged Multi-body Structure’s Floating Body for Connection Gaps
- Deposits of iron oxides in the human globus pallidus
- Integrability, exact solutions and nonlinear dynamics of a nonisospectral integral-differential system
- Bounds for partition dimension of M-wheels
- Visual Analysis of Cylindrically Polarized Light Beams’ Focal Characteristics by Path Integral
- Analysis of repulsive central universal force field on solar and galactic dynamics
- Solitary Wave Solution of Nonlinear PDEs Arising in Mathematical Physics
- Understanding quantum mechanics: a review and synthesis in precise language
- Plane Wave Reflection in a Compressible Half Space with Initial Stress
- Evaluation of the realism of a full-color reflection H2 analog hologram recorded on ultra-fine-grain silver-halide material
- Graph cutting and its application to biological data
- Time fractional modified KdV-type equations: Lie symmetries, exact solutions and conservation laws
- Exact solutions of equal-width equation and its conservation laws
- MHD and Slip Effect on Two-immiscible Third Grade Fluid on Thin Film Flow over a Vertical Moving Belt
- Vibration Analysis of a Three-Layered FGM Cylindrical Shell Including the Effect Of Ring Support
- Hybrid censoring samples in assessment the lifetime performance index of Chen distributed products
- Study on the law of coal resistivity variation in the process of gas adsorption/desorption
- Mapping of Lineament Structures from Aeromagnetic and Landsat Data Over Ankpa Area of Lower Benue Trough, Nigeria
- Beta Generalized Exponentiated Frechet Distribution with Applications
- INS/gravity gradient aided navigation based on gravitation field particle filter
- Electrodynamics in Euclidean Space Time Geometries
- Dynamics and Wear Analysis of Hydraulic Turbines in Solid-liquid Two-phase Flow
- On Numerical Solution Of The Time Fractional Advection-Diffusion Equation Involving Atangana-Baleanu-Caputo Derivative
- New Complex Solutions to the Nonlinear Electrical Transmission Line Model
- The effects of quantum spectrum of 4 + n-dimensional water around a DNA on pure water in four dimensional universe
- Quantum Phase Estimation Algorithm for Finding Polynomial Roots
- Vibration Equation of Fractional Order Describing Viscoelasticity and Viscous Inertia
- The Errors Recognition and Compensation for the Numerical Control Machine Tools Based on Laser Testing Technology
- Evaluation and Decision Making of Organization Quality Specific Immunity Based on MGDM-IPLAO Method
- Key Frame Extraction of Multi-Resolution Remote Sensing Images Under Quality Constraint
- Influences of Contact Force towards Dressing Contiguous Sense of Linen Clothing
- Modeling and optimization of urban rail transit scheduling with adaptive fruit fly optimization algorithm
- The pseudo-limit problem existing in electromagnetic radiation transmission and its mathematical physics principle analysis
- Chaos synchronization of fractional–order discrete–time systems with different dimensions using two scaling matrices
- Stress Characteristics and Overload Failure Analysis of Cemented Sand and Gravel Dam in Naheng Reservoir
- A Big Data Analysis Method Based on Modified Collaborative Filtering Recommendation Algorithms
- Semi-supervised Classification Based Mixed Sampling for Imbalanced Data
- The Influence of Trading Volume, Market Trend, and Monetary Policy on Characteristics of the Chinese Stock Exchange: An Econophysics Perspective
- Estimation of sand water content using GPR combined time-frequency analysis in the Ordos Basin, China
- Special Issue Applications of Nonlinear Dynamics
- Discrete approximate iterative method for fuzzy investment portfolio based on transaction cost threshold constraint
- Multi-objective performance optimization of ORC cycle based on improved ant colony algorithm
- Information retrieval algorithm of industrial cluster based on vector space
- Parametric model updating with frequency and MAC combined objective function of port crane structure based on operational modal analysis
- Evacuation simulation of different flow ratios in low-density state
- A pointer location algorithm for computer visionbased automatic reading recognition of pointer gauges
- A cloud computing separation model based on information flow
- Optimizing model and algorithm for railway freight loading problem
- Denoising data acquisition algorithm for array pixelated CdZnTe nuclear detector
- Radiation effects of nuclear physics rays on hepatoma cells
- Special issue: XXVth Symposium on Electromagnetic Phenomena in Nonlinear Circuits (EPNC2018)
- A study on numerical integration methods for rendering atmospheric scattering phenomenon
- Wave propagation time optimization for geodesic distances calculation using the Heat Method
- Analysis of electricity generation efficiency in photovoltaic building systems made of HIT-IBC cells for multi-family residential buildings
- A structural quality evaluation model for three-dimensional simulations
- WiFi Electromagnetic Field Modelling for Indoor Localization
- Modeling Human Pupil Dilation to Decouple the Pupillary Light Reflex
- Principal Component Analysis based on data characteristics for dimensionality reduction of ECG recordings in arrhythmia classification
- Blinking Extraction in Eye gaze System for Stereoscopy Movies
- Optimization of screen-space directional occlusion algorithms
- Heuristic based real-time hybrid rendering with the use of rasterization and ray tracing method
- Review of muscle modelling methods from the point of view of motion biomechanics with particular emphasis on the shoulder
- The use of segmented-shifted grain-oriented sheets in magnetic circuits of small AC motors
- High Temperature Permanent Magnet Synchronous Machine Analysis of Thermal Field
- Inverse approach for concentrated winding surface permanent magnet synchronous machines noiseless design
- An enameled wire with a semi-conductive layer: A solution for a better distibution of the voltage stresses in motor windings
- High temperature machines: topologies and preliminary design
- Aging monitoring of electrical machines using winding high frequency equivalent circuits
- Design of inorganic coils for high temperature electrical machines
- A New Concept for Deeper Integration of Converters and Drives in Electrical Machines: Simulation and Experimental Investigations
- Special Issue on Energetic Materials and Processes
- Investigations into the mechanisms of electrohydrodynamic instability in free surface electrospinning
- Effect of Pressure Distribution on the Energy Dissipation of Lap Joints under Equal Pre-tension Force
- Research on microstructure and forming mechanism of TiC/1Cr12Ni3Mo2V composite based on laser solid forming
- Crystallization of Nano-TiO2 Films based on Glass Fiber Fabric Substrate and Its Impact on Catalytic Performance
- Effect of Adding Rare Earth Elements Er and Gd on the Corrosion Residual Strength of Magnesium Alloy
- Closed-die Forging Technology and Numerical Simulation of Aluminum Alloy Connecting Rod
- Numerical Simulation and Experimental Research on Material Parameters Solution and Shape Control of Sandwich Panels with Aluminum Honeycomb
- Research and Analysis of the Effect of Heat Treatment on Damping Properties of Ductile Iron
- Effect of austenitising heat treatment on microstructure and properties of a nitrogen bearing martensitic stainless steel
- Special Issue on Fundamental Physics of Thermal Transports and Energy Conversions
- Numerical simulation of welding distortions in large structures with a simplified engineering approach
- Investigation on the effect of electrode tip on formation of metal droplets and temperature profile in a vibrating electrode electroslag remelting process
- Effect of North Wall Materials on the Thermal Environment in Chinese Solar Greenhouse (Part A: Experimental Researches)
- Three-dimensional optimal design of a cooled turbine considering the coolant-requirement change
- Theoretical analysis of particle size re-distribution due to Ostwald ripening in the fuel cell catalyst layer
- Effect of phase change materials on heat dissipation of a multiple heat source system
- Wetting properties and performance of modified composite collectors in a membrane-based wet electrostatic precipitator
- Implementation of the Semi Empirical Kinetic Soot Model Within Chemistry Tabulation Framework for Efficient Emissions Predictions in Diesel Engines
- Comparison and analyses of two thermal performance evaluation models for a public building
- A Novel Evaluation Method For Particle Deposition Measurement
- Effect of the two-phase hybrid mode of effervescent atomizer on the atomization characteristics
- Erratum
- Integrability analysis of the partial differential equation describing the classical bond-pricing model of mathematical finance
- Erratum to: Energy converting layers for thin-film flexible photovoltaic structures

