Combined Multi-Agent Method to Control Inter-Department Common Events Collision for University Courses Timetabling

Jalil Nourmohammadi-Khiarak; Yashar Zamani-Harghalani; Mohammad-Reza Feizi-Derakhshi

doi:10.1515/jisys-2017-0249

Artikel Open Access

Combined Multi-Agent Method to Control Inter-Department Common Events Collision for University Courses Timetabling

Jalil Nourmohammadi-Khiarak , Yashar Zamani-Harghalani und Mohammad-Reza Feizi-Derakhshi

Veröffentlicht/Copyright: 21. Dezember 2017

Veröffentlicht von

Veröffentlichen auch Sie bei De Gruyter Brill

Manuskript einreichen Informationen für Autor*innen

Aus der Zeitschrift Journal of Intelligent Systems Band 29 Heft 1

Abstract

University course timetabling is the scheduling of courses at different time slots in a university. The two important issues in this process are (i) the allocation of all events (professors, courses, and students) to resources (time slots daily/weekly and theory/practical classes) in a semester, and (ii) maximizing the satisfaction of common events (professors, courses, and students) among multiple departments. Accumulating evidences in university course timetabling problems suggest dividing the problem into several sub-problems. This study attempted to investigate the appropriateness of using the genetic algorithm (GA) and the imperialist competitive algorithm (ICA). The proposed technique consists of two steps: (i) using the proposed manipulated GA for solving the timetabling problem of each department, and (ii) eliminating the interference of common events among multiple departments and satisfying the hard and soft constraints by using ICA. Finally, a report on the efficiency of the methodology used in this study was obtained from the University of Tabriz in Iran and University of Udine in Italy. In this paper, the results are revealed in two ways: (i) reduction in the problems due to shrinking of the database and solving of the problems in parallel and (ii) solving the different parts of the problem by using various criterion results, increasing the common events satisfaction in that sub-problem. Eventually, the proposed model provided successful satisfaction of the hard constraints in <700 iterations with GA and elimination of interference in 40 iterations with ICA in most of the cases.

Keywords: University course timetabling; imperialist competitive algorithm; genetic algorithm

1 Introduction

University course timetabling problems and common events solving among multiple departments are considered among the major challenges in a university. The timetabling problem for universities concerns professors, students, courses, classrooms, and time slots/class schedules, such that professors and students meet during one or more time slots during the week in certain classrooms for their courses [23]. In this work, we tried to resolve these issues based on the priorities and demands of common events with respect to the allocation of free resources among multiple departments. Common events among multiple departments are a problem that needs to be resolved. Therefore, there needs to exist a solution to make smooth timetabling of university courses and common events in order to avoid collision of common events among multiple departments and also to maintain the non-collision of events associated with allocations with maximum satisfaction. This satisfaction in the allocation of common resources to common events should be maintained. However, resolving the timetabling of common events among multiple departments gives rise to a developed and scalable timetabling process that increases either the magnitude of the problem or the volume of data.

The problem of university course timetabling in all states belongs to the NP-complete class in terms of complex computation, as was completely proved in Refs. [7, 8]; thus, there is no algorithm with time complexity of polynomial order to solve this problem. Precision algorithms and approximation algorithms can be used to solve scheduling problems. Precision algorithms are unessential for solving such problems, as the execution time of this set of algorithms exponentially increases with the size of the problem [20]; therefore, approximation algorithms are used, such as heuristic and meta-heuristic algorithms. Among these algorithms are the genetic algorithm (GA) [39], tabu search [25], and honey bee algorithm [33].

In this research, the approach considered was a “divide and conquer method,” in which dividing problems into sub-problems can reduce the amount of data descriptors. Every department independently and in parallel manner resolves the problems with other departments. Every department, after resolving its own timetabling problems according to its criteria, sends some typical possible timetables to an interface agent. Agents of each department do not need to send extra information to the interface agent to allocate common resources to common events. An interface agent tries to maintain each department’s offers, extracts free resources from possible timetables, and allocates common events using the imperialist competitive algorithm (ICA). Each department is assumed as an agent. These agents try to produce typical possible timetabling by using GA. The proposed GA has been designed for maximum satisfaction in the output of timetabling.

Several studies have attempted to solve university course timetabling problems [3, 14, 19, 26, 29, 37, 39]. For solving the problem, we need a distributed environment and interface agent for accommodating various timetabling agents that cooperate to improve a common comprehensive solution [14]. The primary solution for a multi-agent system is earned based on usage of a marketplace and an artificial currency. Nandhini and Kanmani [26] implemented a class timetabling approach with multi-agents by the steepest ascent as proposed for the hill climbing algorithm. The agents they used included (i) a combination generator, which generates the maximum possible combinations for inputting in the timetable, and (ii) a minimum finder, which finds a combination with minimum evaluation function value for successive examinations. Obit et al. [29] proposed a multi-agent approach using a distributed solution environment in which a mediator agent coordinates various timetabling agents that cooperate to improve a common global solution.

Many multi-agent methods have been proposed for solving the problem of university course timetabling. Babkin et al. [4] presented a multi-agent method that uses a mathematical model to solve this problem, and the basis of the proposed algorithm is the famous multi-agent algorithm MSRAC for scheduling meetings. In another paper [21], a multi-agent method based on an interface agent that performs coordination among other agents was designed. Also, a multi-agent system consisting of a combined heuristic that includes graph coloring heuristics and local search was proposed [29]. In Ref. [27], a multi-agent model named multi-factor model for university courses timetabling (MATP) was presented. This model was based on agents that compete together and can process parallel and distributed problems. Nouri and Driss [28] presented this problem and attempted to examine the diversity of the number of messages in terms of priority of allocation privilege and the effect of the number of messages per CPU time.

In recent years, hybridization of meta-heuristic approaches has been proven to be effective in solving university timetabling problems. According to comprehensive surveys on timetabling problems [2, 15, 22, 31, 34], “There are many research directions generated by considering the hybridization of meta-heuristic methods particularly between population-based methods and other approaches.” Blum and Roli [6] summarized that “population-based methods are better in identifying promising areas in the search space, whereas trajectory methods excel in exploring promising areas in the search space. Thus, meta-heuristic hybrids in some way manage to combine the advantages of population-based methods with the strength of trajectory methods.” As an example, Eley [16] proposed two different versions of ant colony algorithms (MMAS-ET and ANTCOL-ET) in solving examination timetabling problems. Both approaches involved the hybridization of an ant algorithm and a hill climbing approach. The experimental results demonstrated that ANTCOL-ET outperformed MMAS-ET. This approach is better in exploring promising search regions and is able to escape from local optima; however, it is poor in fine-tuning the final solution search region. Wangmaeteekul [37] narrowed the gap between the theoretical and practical aspects of university timetabling. The author used four different principles for organizing the interaction between the agents: sequential FIFO, interleaved FIFO, round-robin and sequential, and round-robin and interleaved.

2 Proposed Method

The issue of research involves several different departments. Each department is associated with one agent and the research approach will be based on a participatory procedure [30]. Every department accomplishes timetabling separately and plans the procedure as an autonomous agent. GAs have been used for this work and have achieved better results compared to others. In this regard, every department satisfies its own hardness and softness constraints. A “surveyor agent” extracts common events among multiple departments associated with respective constraints and additional available resources. This is done by searching in the provided timetables by departments. Then, “the interface agent,” which is the imperialist, receives the extracted information by “the surveyor agent” and uses ICA to move toward the elimination of interferences, and the common events satisfaction increases [19]. During the ICA process, mapping priorities, constraints, and common events demand free resources among multiple departments.

The proposed algorithm is shown in Figure 1 and consists of the following four factors:

Figure 1:

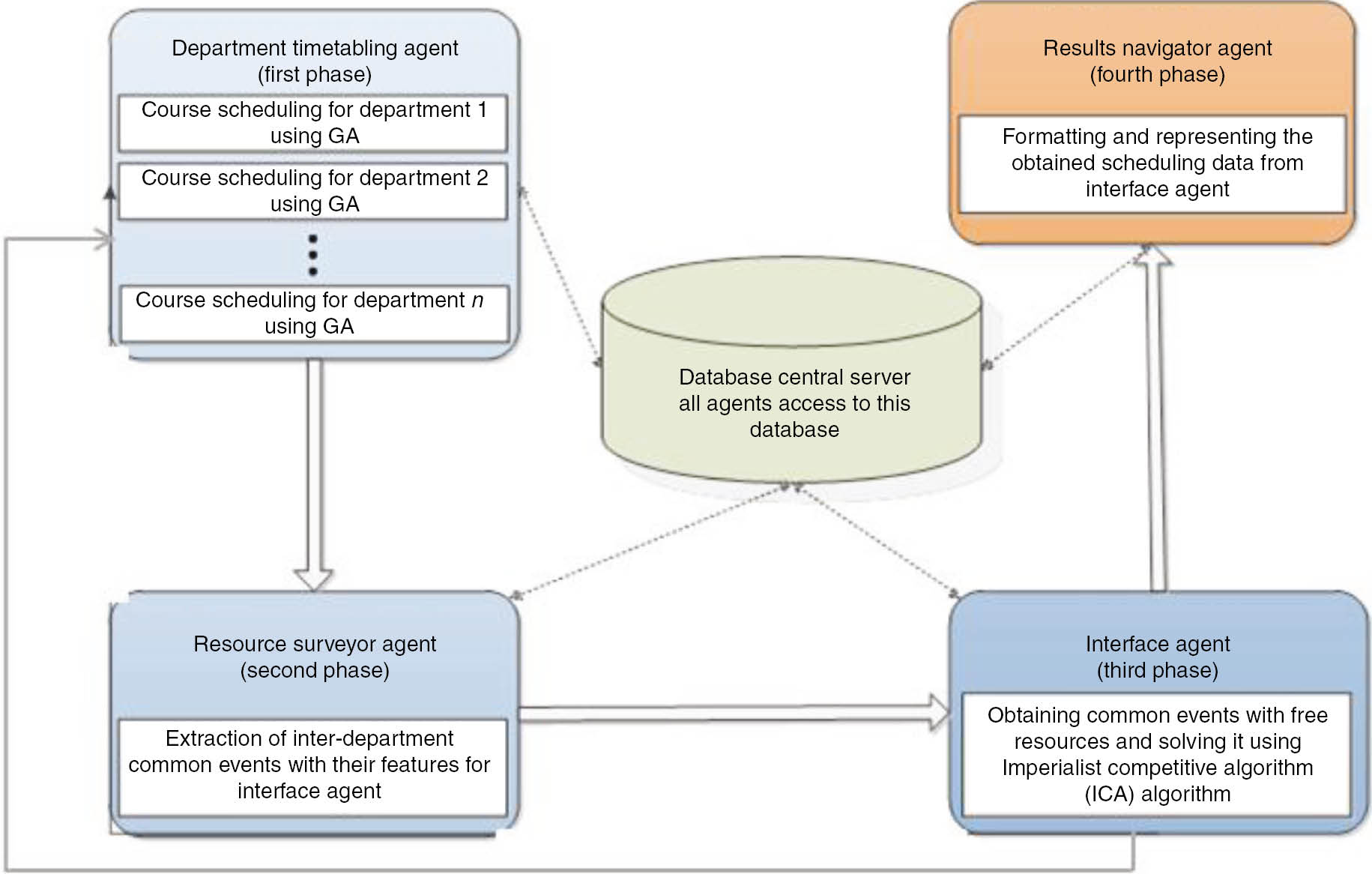
Detailed Steps of the Proposed Algorithm.

n factors for department timetabling;
Resources surveyor agent;
Interface agent;
Results surveyor agent.

2.1 Constraints

Hard constraints:

Different courses taught by the same teacher should not be scheduled at the same time.
There should be no missing class in the final result.
When two courses require the same classroom, those two courses cannot be scheduled at the same time, such as laboratory classes.
Courses that have been scheduled for the same time cannot be assigned to the same classroom.
Each teacher must be accessible at all times when the course is scheduled for them.
Each course must be exactly scheduled for one time and one classroom.
Some courses cannot be repeated more than a limited number of weeks.
The teacher with a common event should not have the same course to teach at two separate departments at the same time.

Soft constraints:

The teacher may have a priority for daily/weekly time for class attendance, so satisfaction of this priority is considered.
Teachers can request a special classroom for teaching.
Each course should be assigned to a classroom that is near the building of one department or is near the teacher’s office or location.
Events should be uniformly distributed (courses, teachers, etc.) among resources. This will facilitate the allocation of resources (time and classrooms). Moreover, this distribution maximizes productivity while reducing waste of resources.
Start of classes can be from 8:00 to 16:00 or from 9:00 to 17:00 (this constraint is optional).

Additional optional costs (fines):

MINWorkingDay: setting the bottom limit for each teacher.
IsolatedLecture: classes that cannot be changed for any condition, such as laboratory classes.
RoomStability: all sessions of a course are held in a constant classroom.
TravelDistance: if the students are going to attend two courses in two distinct buildings, then this distance between the buildings should be at a minimum.
RoomSuitability: suitability of the room for the course (e.g. some courses require a projector, amplifier, etc.) should be maximized.
DoubleLectures: it may sometimes be necessary to conduct two courses in one class session.

2.2 n Agents for Department Timetabling

In this section, it is attempted to extract and deliver to the next agent a separate scheduling for each department using the GA. We will take the input data for each department at this stage, and we will only send an optimum output obtained with GA to the resource surveyor agent in order to eliminate inter-department common events collision.

In a GA [1, 11, 39], the genetic population (community) or the same set of chromosomes, the genetic operators or the same coupling through integration and mutation, and quantitative parameters such as population size and mutation rate are considered. In this section, assuming the benefits of a standard GA in designing timetables, the hypothesis of timetabling is shown in Table 1. The boundary parameters in Table 1 are obtained through trial and error. In this paper, a permutation approach is used for chromosome encoding in which integer numbers represent genes in the chromosomes [39]. For the number of genes, there are integer numbers in the chromosome. The integration must be such that after combining two chromosomes, a repeated gene is not produced in offspring. Each gene has been used in a limited range of integer numbers. For example, the number range of 1 to 5 is utilized to represent the days of the week from Saturday to Wednesday. The pseudo-code used for the GA in the university schedule is as follows.

Table 1:

Values of Selected Parameters of the Proposed GA for Scheduling Courses in Each Department.

Parameter name	Comment
Population size	100
Chromosome length	Number of required courses
Crossover operator probability	0.85%
Mutation operator probability	0.05%
Termination conditions	Number of iterations=2000 or number of hard constraint=0

Algorithm:

GA(NumTi, NumRep, μ).

//Initialize generation 0:

k:=0;

Pk:=a population of n randomly generated individuals;

//Evaluate Pk:

Compute fitness(i) for each i∈Pk;

{//Create generation k+1:

//1. Copy:

Select (1−NumRep)×NumTi members of Pk and insert into Pk+1;

//2. Crossover:

Select NumRep×NumTi members of Pk; pair them up; produce offspring; insert the offspring into Pk+1;

//3. Mutate:

Select μ×NumTi members of Pk+1; invert a randomly

selected bit in each;

//Evaluate Pk+1:

Compute fitness(i) for each i ∈ Pk;

//Increment:

k:=k+1;

}

when fitness of the fittest individual in Pk is not high enough;

return the fittest individual from Pk;

NumTi is the number of schedules per department that is considered as the primary population in the genetics; NumRep is the fraction of the population that is replaced in each repetition; and μ is the mutation rate.

In many previous works [18, 36], the idea of adapting mutation and crossover was applied for the improvement of GA production. Schaffer and Morishima [35] proposed a crossover mechanism where the crossover points were chosen depending on the performance of the generated offspring. Davis [9] proposed a mechanism of adapting probabilities based on the performance of the operators. To select the parameters of the proposed GA for scheduling courses in each department, we obtained some experience. Crossover and mutation are important parameters in GA. For choosing the best values, we repeat the algorithm and set the best values, as shown in Figure 2.

Figure 2:

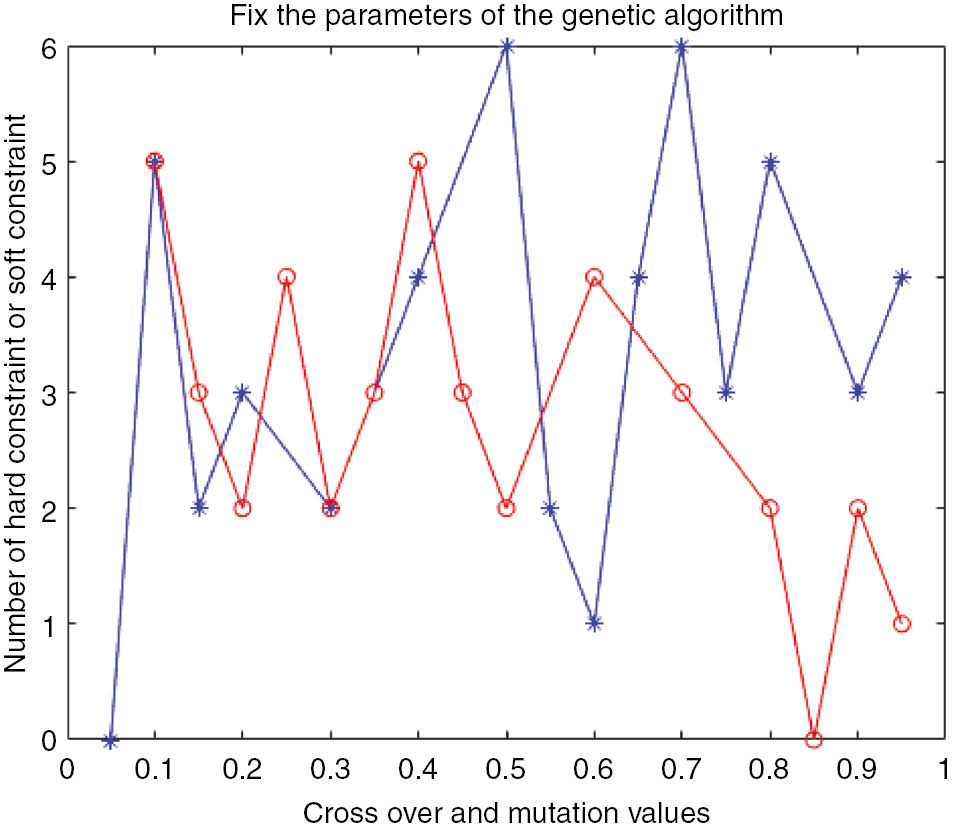
Fixing the Parameters of GA (Crossover and Mutation).

Crossover operator type: In the proposed crossover, parents for the crossover operation are first selected. Roulette wheels are used and the chromosomes that had better expenses will have more chances of being a parent. After the parents have been chosen, 20% of the first parent’s chromosomes are displaced by another parent’s chromosome regarding the course number gene. This means that copies of both parents are first produced. Twenty percent of the first chromosome’s courses are randomly chosen (every time the database is randomly filtered by one of the courses) and then another chromosome associated with this course code is filtered. These courses are displaced between the two chromosomes without changing any other fields. This kind of crossover does not give rise to any repetitive courses or professors at all, which means that it is regarded as a permutation of the problem.

Mutation operator type: The integer number of the gene is randomly exchanged with the allowed value of the gene in two or more positions in the table (chromosome). For example, if a gene represents random changes of a day, the integer number of 1 to 5 is given. In the mutation operation, random changes are different for different chromosomes and each chromosome changes according to its own law. As we are taking into account some soft constraints in the crossover and mutation operations, any random change should be checked with regard to whether it violates the restrictions or not. For example, one of the limitations is that there should not be more than 2 h for a course every day (soft constraint). If the gene associated with information about the day of the course is selected for a mutation, the chosen day should be different from the second day of holding the course, if possible. These kinds of rules in many cases avoid the existence of chromosomes that violate the soft constraints.

Equation (1) represents the utilized fitness function in this paper:

(1) Fitness(x)=∑i=1numclass∗5∗12c∗NumSCi+NumHci,

where Fitness(x) is the fitting function for calculating the value of each chromosome, c is a constant factor for soft constraints, NumSC is the number of violated soft constraints, NumHc is the number of hard violated constraints, numclass is the number of classes, the number 5 represents the number of days, and the number 12 represents the number of time periods. Our aims are to minimize the amount of the cost function.

The algorithm termination conditions are as follows:

There are no violated hard constraints, and violated soft constraints are minimized.
A certain number of iterations are done (in our experiments, the repeated time is considered 100).
The population converges (in the designed algorithm, the occurrence probability of this condition is close to zero in large populations). GA is an efficient method in which the positive characteristics of the random and greedy approaches are embedded.

2.3 Resource Surveyor Agent

When using several agents with the genetic optimization algorithm, the scheduling of each department is conducted and the resource surveyor agent collects all the results, which are delivered in the form of a general timetable, i.e. interface agent. We have used this agent because the interface agent only has the role of solving the inter-department common events collision and only reports constraints, and in fact extracts or scans the scheduling by the resources surveyor agent.

2.4 Implementation of the Interface Agent (ICA)

The task of the interface agent is resolving the conflicts between the open source and command events. Open sources are extracted by a scanner and will be available for the interface agent. This agent will try to complete the resulting timetabling of the department’s agents with command events. In the case of conflict in timetabling, the conflict is resolved and again will return to autonomous agents of departments. The ICA, like other evolutionary optimization methods, starts with an initial population. In this algorithm, each element of the population is called the country. Countries are divided into two categories: colony and colonizer. Each colonizer dominates some colonial countries depending on its strength.

As the ICA is inherently a continuous algorithm, it must be discrete to allow its use in this article. This was done by Lotfi [17] in his paper, and it is used in this paper for implementation of scheduled common events. This converted algorithm is shown in Figure 3.

Figure 3:

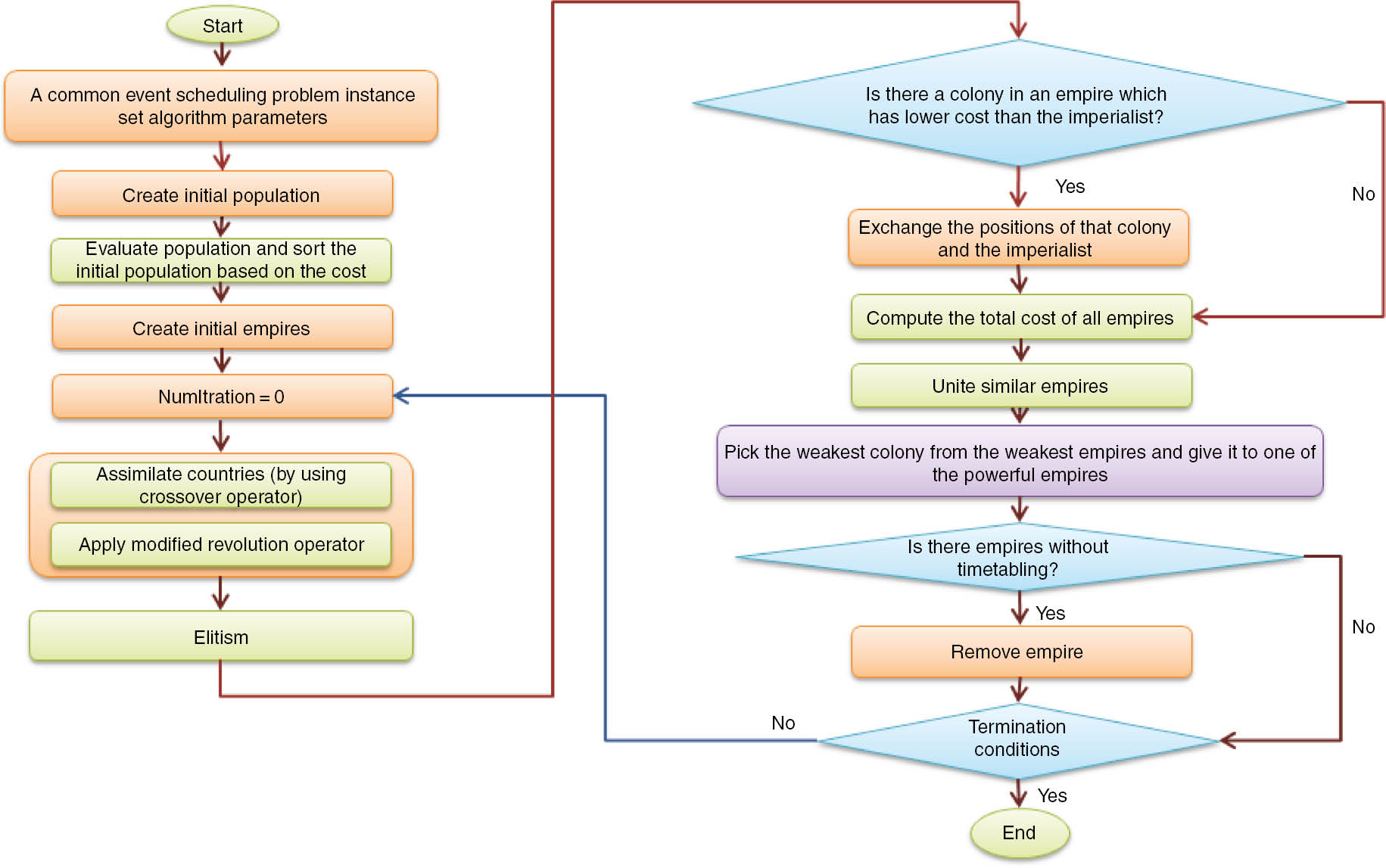
Flowchart of the Process of Applying Discrete ICA on Common Events Solving Among Multiple Departments.

The pseudo-code used for the ICA to resolve inter-department common events collision is as follows:

Step 1. Select some random timetable on the function and initialize the empires

Fit=F(Xcountry)=F(f1, f2,…, fn).

Step 2. Move the timetables (colonies) toward their relevant imperialist (assimilation).

Step 3. If there is a timetable (colony) in an empire that has a lower cost than that of the imperialist, exchange the positions of the imperialist and the colony:

Fitm=max{costi}−costm.

Step 4. Compute the total cost of an empire (related to the power of both imperialist and its timetables):

T⋅Cn=cost(imperialistn)+mean{Cost(colonies of empiren)}.

Step 5. Pick the weakest colony from the weakest empire and give it to the empire that has the most likelihood to possess it (imperialist competition):

Pn=|Cn∑i=1NimpCi|.

Step 6. Eliminate the powerless empires.

Step 7. If there is just one empire, stop; else, go to step 2.

In this pseudo-code of X_country, there is a scheduler (country) or solution. The cost of each colony is in the empire, and Cost_m is the cost of the empire itself. C_n is the total cost of n^th empire.

In this paper, the discrete ICA is used to solve scheduling of command events among departments, and assessing this algorithm will show its efficiency to solve this problem. In the discrete ICA, the assimilation operator causes colonies to move toward their respective empires. The assimilation process indicates that colonies are similar to their empires. Empires try to improve their colonies and use the policy of assimilation to raise their colonies for more colonies in their empire. This operator is in continuity mode in the ICA, and as our problem is resolving common events among departments and is considered as a discrete problem, this part of the ICA should be converted to a discrete problem.

The two-point crossover is used to model the policy of assimilation in discrete mode for scheduling of common courses. By using crossover, some parts of the colonies of the empires are changed between their colonies. It should be noted that the colonies of the empires are changed together. In the two-point crossover, both schedulers (colony) will be cut at two arbitrary points and then the values of cut parts will be changed together to make two new schedulers. In this section, the ICA will be used to resolve the problem of scheduling of common events among departments, and the used parameters and the assigned values are clearly shown in Table 2.

Table 2:

Values of Selected Parameters of the Proposed GA for the Common Events Solving Among Multiple Departments.

Parameter name	Value
Population size	300
Number of initial imperialists	30
Number of all colonies	270
Number of decades/iteration count	50
Revolution rate	0.3
Uniting threshold	0.05
Assimilation coefficient	1.25
Assimilation angle coefficient	0.7
Damp ratio	0.80

The advantages of the ICA can be summarized as follows:

The basic idea of the algorithm is novel.
It is the first optimization algorithm based on a social-political process.
Its optimization capabilities are on par or even higher in comparison with various optimization algorithms according to variety of optimization problems.
It has appropriate speed to find the optimal solution.

2.5 Result Surveyor Agent

This agent, in fact, is similar to the resource surveyor agent, with the difference that we have overall outcomes and timing in the output, and also the output will be our final outcome. However, in the resource surveyor agent, several departments were the scheduling inputs and the output was an incomplete scheduling, i.e. interfering. In this agent, when a scheduler is received from the interface agent, it checks whether the possible interactions have been resolved or not. If all the interactions are resolved, the outcome will be displayed as a complete scheduler at the outlet and sent to all departments.

3 Data Sets

To test the proposed algorithm, the dataset consists of faculties, departments, time slots weekly/daily, and classrooms. In this dataset for each course, several professors (up to five), three departments (literature, humanities, and mathematics), 5 weekly time slots (Saturday, Sunday, Monday, Tuesday, and Wednesday), 12 time slots (four 2-h slots and eight 1-h slots for every day), and 17 classrooms for each department (3 practical classrooms and 14 theoretical classrooms) are considered.

4 Experimental Results and Comparison with Other Papers

Now, we pay attention to the operation of the proposed algorithm on the dataset. First, the number of common events among three departments associated with their features and constraints are extracted by the surveyor resource (see Figure 4). Later, the ICA will be applied on common events based on their constraints due to interface agents. Surveyor operations and gathering of excess resources from each of the three departments by resource surveyor agents is done while the interface agent operates the ICA. In the end, process mapping and common events among the three departments in excess resources are fulfilled.

Figure 4:

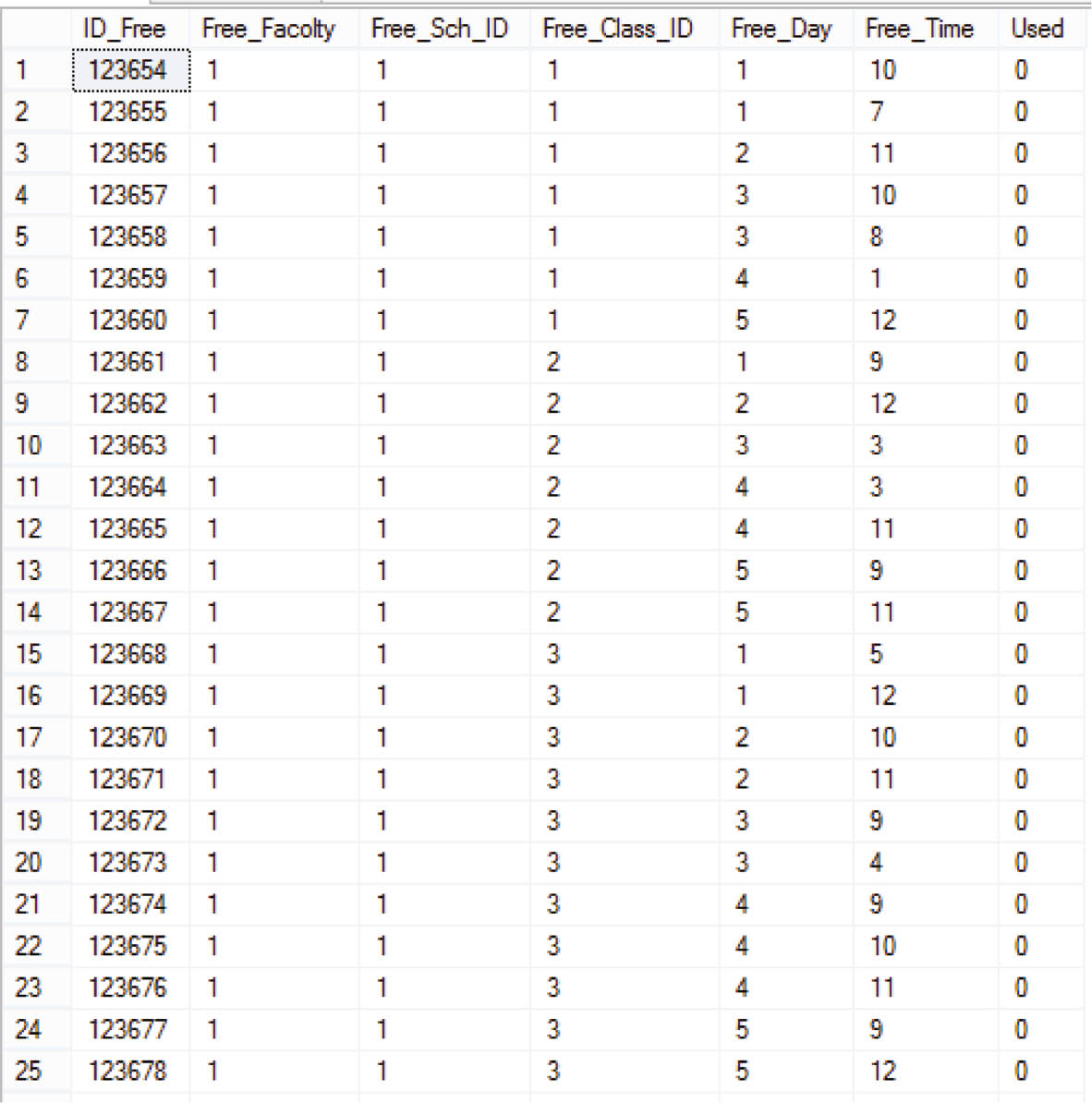
Free Resources for Each Department in Timetabling.

The ultimate goals of the interface agent are as follows:

Satisfying all the hard constraints;
Respecting the priorities and aspirations of the common events;
Minimizing the waste of surplus resources among departments;
Equitably distributing the common events among free resources.

In the following, we consider the timetabling of each department. Each of the department agents finds several responses for the departments and sends these responses to the ICA. The goal is that the produced populations should have many features to achieve satisfaction of the common events. If we use just one timetable, we would be confined to one response, and in extracting the optimum response, we would be limited to a certain band of response. However, by using several responses, we consider an exploration problem, which means that this leads to concentrating on a response band [38]. The response obtained from GA leads to extraction of several timetables that satisfy either hard constraints or soft constraints associated with the departments. Figure 5 represents the portion of the timetable associated with department 1, class 1, and timetable 1. In Figure 4, everything is almost specified clearly and the only things that may bring questions to mind are time 1 and time 2. This innovation is utilized as online in order to satisfy some of the constraints. We have known that courses can be in the state of 4. In courses of unit one and four, one of the soft constraints is that a course must not be held more than one time in a day.

Figure 5:

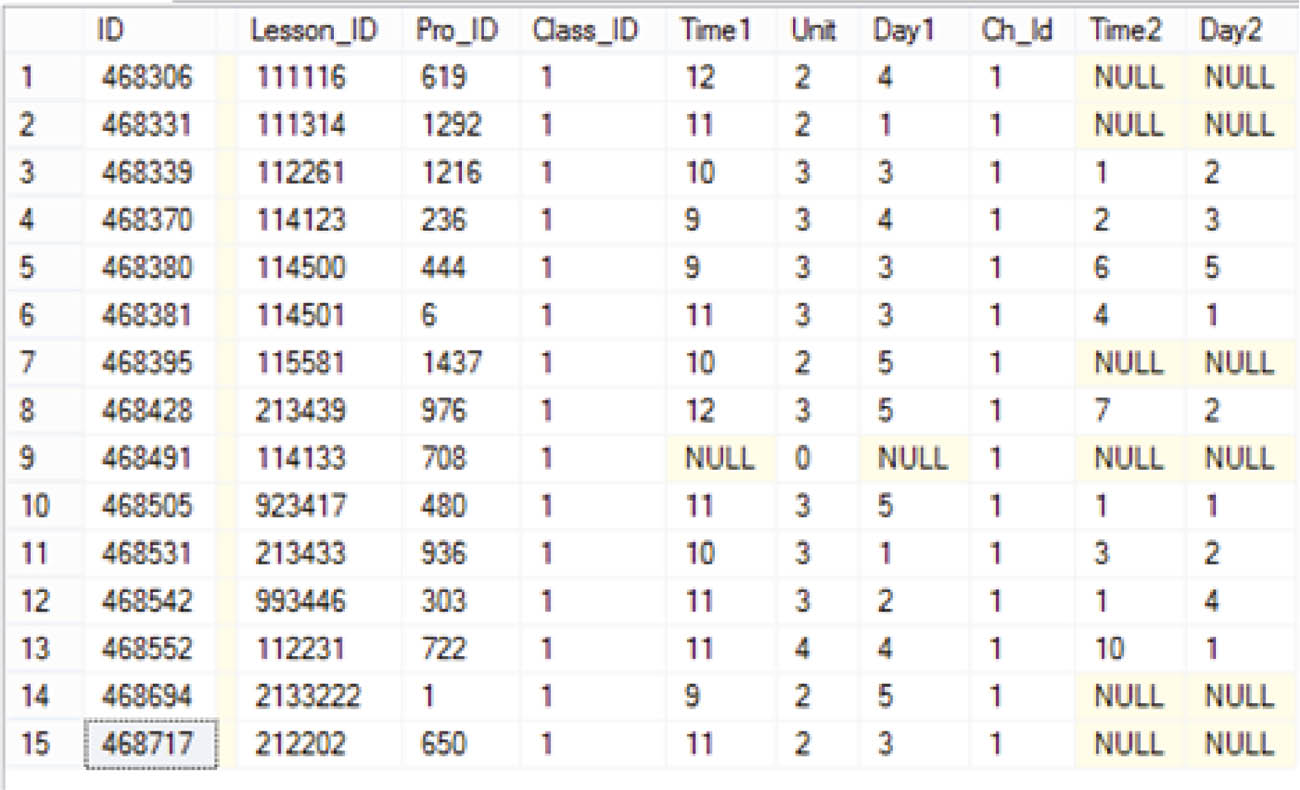
Obtained Results from the Proposed GA in a Department.

Now, with this approach, we are readily able to satisfy the random initialization of these constraints and other constraints. Assume that we want to initialize a three-unit course. We allocate a random number between 1 and 5 to “day1” and for the course, we put a random number between 1 and 4 to the field “time1.” As a short note, 1 to 4 means a 2-h class. Then, we should determine the remaining 1-h status, so we allocate a random number to the field “day2”; however, if the random number would be equal to the field “day1,” we produce another random number. We continue this operation unless these two numbers are equal. For the time interval of the unit, we produce a random number between 5 and 12 (1-h class) and put it in the field “time2.” Using this solution, we regard the random initialization and avoid the occurrence of some states that are opposite to the hard or soft constraints.

Keep in mind that in this article, we satisfied restrictions more than did the rest of the other articles. The GA that we have used in this paper has exclusive features such as crossover and mutation approaches. The crossover and mutation that are used here are completely based on an innovation, and a logical answer is produced differently from the rest of the works. A comparison of the algorithm criteria with other papers is shown in Table 3.

Table 3:

Parameters of the Proposed Algorithm.

Parameter name	Alsmadi et al. [1]	Proposed algorithm
Input	Courses list	Courses list
Output	Optimum timetabling	Optimum timetabling
Population size	100	100
Chromosome length	Number of courses	Number of courses
Crossover rate	0.6	0.85
Mutation rate	0.07	0.05–0.15
Termination conditions	Number of iterations=2000 and achieve zero hard constraint	Number of iterations=2000 and achieve zero hard constraint

The number of repetitions associated with the obtained responses used by Alsmadi et al. [1] is shown in Figure 6. Figure 7 represents the results of the proposed algorithm in which the repetition number is much less than those used by Alsmadi et al. [1].

Figure 6:

Results Using GA with Various Populations [1].

Figure 7:

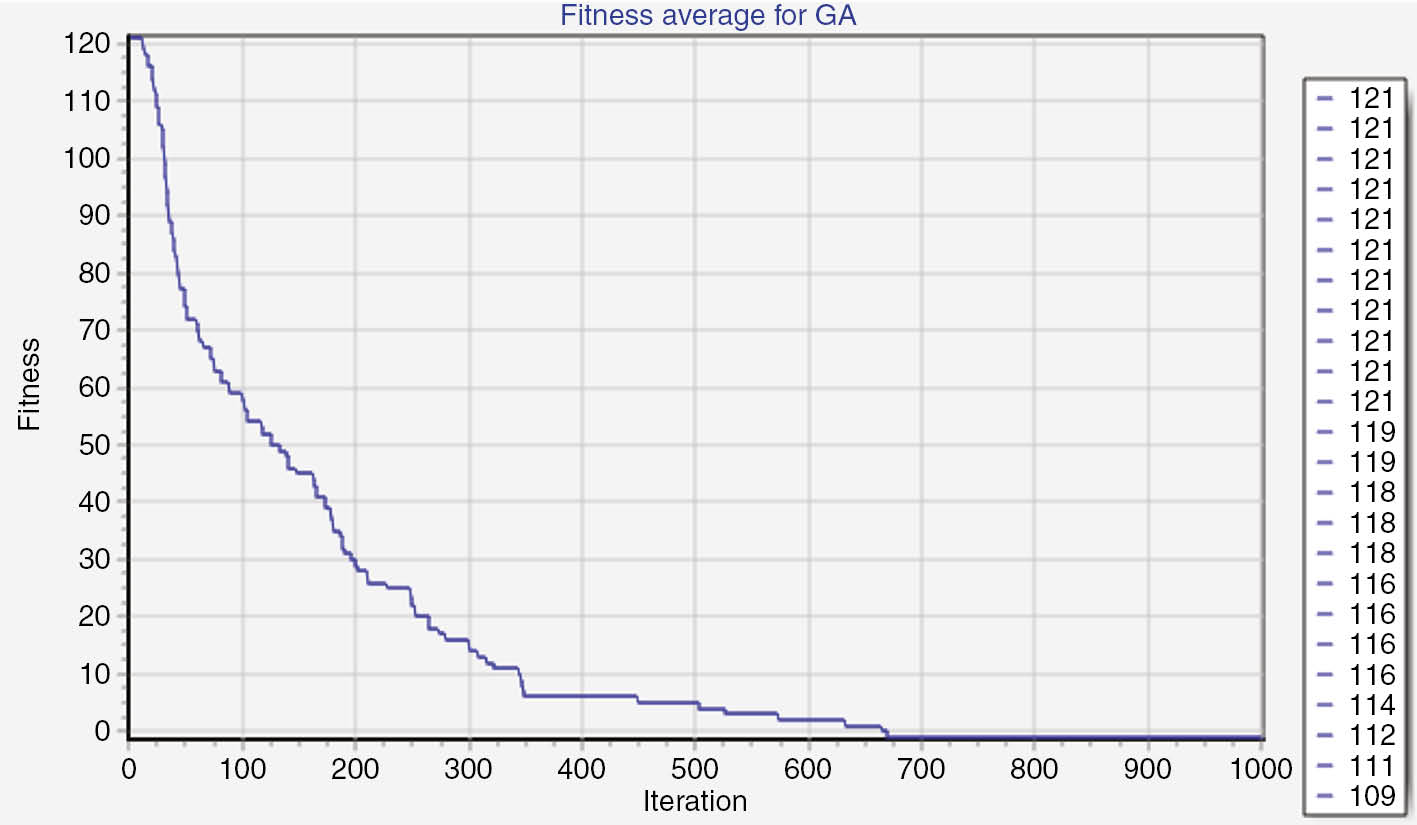
Results Using the Proposed GA with 100 Populations.

We consider the results of common events timetabling in the departments. We have used ICA to solve the common events timetabling problem, which was described in details in a previous section. The ICA used in this paper is the discrete version of ICA [17]. The results of this algorithm represent its high efficiency in optimization. We employed this algorithm in the third part as an interface agent, and Figure 8 shows the algorithm efficiency. During different experiments, we obtained good results and the fastest convergence was achieved.

Figure 8:

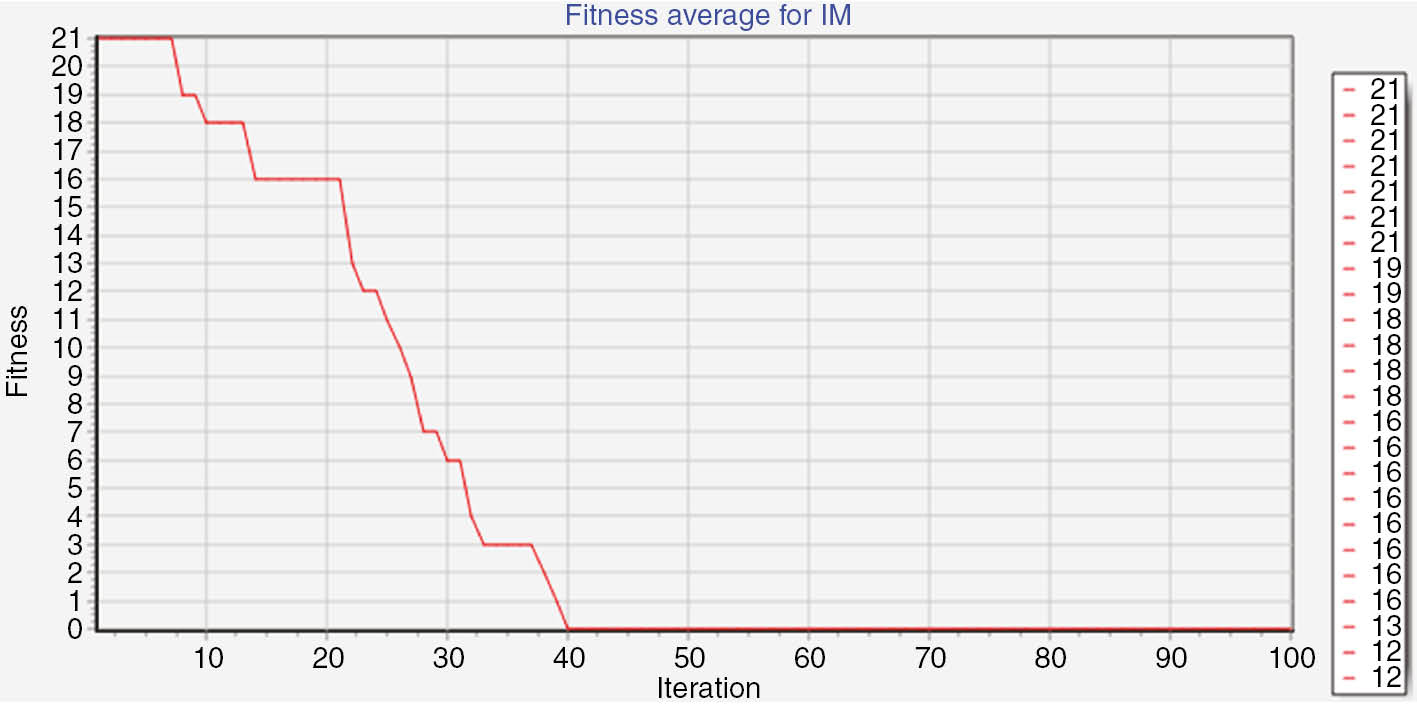
Using ICA to Solve Common Events Timetabling among Departments.

A typical response that has been obtained is shown in Figure 9.

Figure 9:

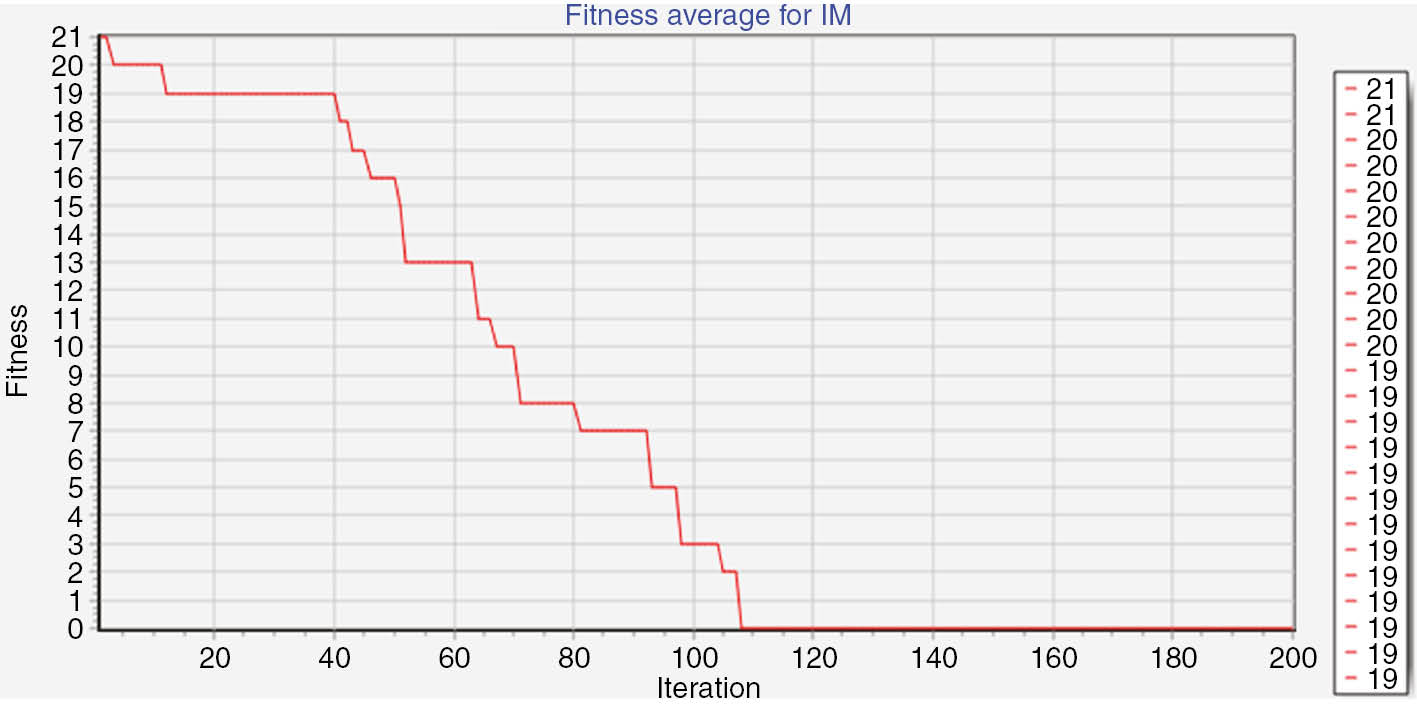
Other Solution for Common Events Timetabling among Departments Using ICA.

4.1 Formulation

The means of formulation is to consider different weights for different constraints. For this purpose, we considered the formulas used in Refs. [12, 13], and also the three formulas presented in Ref. [10] so that we can evaluate our proposed method. The UD6 of our formula is in line with the wishes of Tabriz University in Table 4. We downloaded the dataset of from a web site (http://tabu.diegm.uniud.it/ctt) related to Ref. [10].

Table 4:

Problem Formulation Descriptions.

Problem formulation: cost component	UD1	UD2	UD3	UD4	UD5	UD6
Lectures	H	H	H	H	H	H
Conflicts	H	H	H	H	H	H
RoomOccupancy	H	H	H	H	H	H
Availability	H	H	H	H	H	H
RoomCapacity	1	1	1	1	1	1

MinWorkingDays	5	5	–	1	5	1
IsolatedLectures	1	2	–	–	1	1
Windows	–	–	4	1	2	–
RoomStability	–	1	–	–	–	1
StudentMinMaxLoad	–	–	2	1	2	1
TravelDistance	–	–	–	–	2	–
RoomSuitability	–	–	3	H	–	3
DoubleLectures	–	–	–	1	–	–

Table 4 shows the values for each formula that have been considered. If H is written, this means that this limitation is strict. If it is “–,” then this means that the restriction is not considered in the particular formula. All information needed to benchmark the proposed algorithm and for comparing it with other research is presented.

In Table 5, the set of cases cited from Comp01 to Comp21 are the states proposed in Ref. [10], and the Test1 to Test4 modes are those presented in Ref. [12]. De Cesco et al. [10] added seven other modes that they claim to have come from the real world, which are aggregated from different institutions. They are referred to as DDS1 to DDS7 modes. Another case called Toy is presented in Ref. [10], which was extensively used by the authors for testing and troubleshooting.

Table 5:

Description of the Samples.

Instance	C	L	R	PpD	D	Cu	MML	Co	TA	CL	RO
Comp01	30	160	6	6	5	14	2–5	13.2	93.1	3.24	88.9
Comp02	82	283	16	5	5	70	2–4	7.97	76.9	2.62	70.8
Comp03	72	251	16	5	5	68	2–4	8.17	78.4	2.36	62.8
Comp04	79	286	18	5	5	57	2–4	5.42	81.9	2.05	63.6
Comp05	54	152	9	6	6	139	2–4	21.7	59.6	1.8	46.9
Comp06	108	361	18	5	5	70	2–4	5.24	78.3	2.42	80.2
Comp07	131	434	20	5	5	77	2–4	4.48	80.8	2.51	86.8
Comp09	86	324	18	5	5	61	2–4	4.52	81.7	2	72
Comp09	76	279	18	5	5	75	2–4	6.64	81	2.11	62
Comp10	115	370	18	5	5	67	2–4	5.3	77.4	2.54	82.2
Comp11	30	162	5	9	5	13	2–6	13.8	94.2	3.94	72
Comp12	88	218	11	6	6	150	2–4	13.9	57	1.74	55.1
Comp13	82	308	19	5	5	66	2–3	5.16	79.6	2.01	64.8
Comp14	85	275	17	5	5	60	2–4	6.87	75	2.34	64.7
Comp15	72	251	16	5	5	68	2–4	8.17	78.4	2.36	82.8
Comp16	108	366	20	5	5	71	2–4	5.12	81.5	2.39	73.2
Comp17	99	339	17	5	5	70	2–4	5.49	79.2	2.33	79.8
Comp18	47	138	9	6	6	52	2–3	13.3	64.6	1.53	42.6
Comp19	74	277	16	5	5	66	2–4	7.45	76.4	2.42	69.2
Comp20	121	390	19	5	5	78	2–4	5.06	78.7	2.5	82.1
Comp21	94	327	18	5	5	78	2–4	6.09	82.4	2.25	72.7
Test1	46	207	12	4	5	26	2–4	5.25	97.6	1.97	86.2
Test2	52	223	12	4	5	30	2–4	5.57	86.1	2.11	92.9
Test3	56	252	13	4	5	55	2–4	5.89	78.1	2	96.9
Test4	55	250	10	5	5	55	2–4	5.98	76.8	2	100
DDS1	201	900	21	15	5	99	3–7	4.58	21.3	5.18	57.1
DDS2	82	146	11	11	6	11	3–6	23.2	34.8	4.06	20.1
DDS3	50	206	8	11	5	9	3–6	12.4	58.8	4.76	46.8
DDS4	217	972	31	10	5	105	3–6	2.85	91.4	3.78	62.7
DDS5	109	560	18	12	6	44	3–6	2.19	66	1.89	43.2
DDS6	107	324	17	5	5	62	2–4	5.79	77.8	2.38	76.2
DDS7	49	254	9	10	6	37	3–6	14	89	3.01	47
Toy	4	16	3	4	5	2	2–3	75	90	2.1	26.7
TU-DS1	94	215	15	5	5	55	2–4	6.01	71.1	2.2	60.2
TU-DS2	52	233	12	4	5	41	2–4	4.6	89.2	2.9	45.7
TU-DS3	116	480	16	10	5	52	3–6	8.1	74.1	4.5	41.2

In Table 5, the important features of each mode are shown with similar statistical values. In the headers, C, L, R, PpD, D, Cu, MML, Co, TA, CL, and RO represent the course, sum of the courses, rooms, repetition per day, days, curriculum, minimum and maximum session for one course, mean of collisions, average teacher’s availability, average of the courses in each curriculum per day, and average occupancy of the room, respectively. Co is a feature that counts each couple of courses that cannot be scheduled at the same time (for a similar teacher and curriculum).

It should be explained that Co and TA are computed for a single lecture toward the course level; this means that the courses are with different lectures.

According to De Cesco et al. [10] and Di Gaspero and Schaerf [12, 13], we considered the values necessary for our variables close to the models of those authors that could satisfy the demands of Tabriz University as much as possible. Therefore, the test with the formula given in Table 1 with the title DU6 was implemented with the modes we created, including TUDS1 to TUDS3, and the results were compared with the results of the references. For this, we have added to this system the various constraints that we have implemented based on referenced data (Tables 6–10 ).

Table 6:

Results of References Part 1.

Form/instance	Comp01	Comp02	Comp03	Comp04	Comp05	Comp06	Comp07
UD1	4	35	52	21	244	27	13
UD2	5	75	93	45	326	62	38
UD3	8	34	45	2	434	14	12
UD4	6	49	371	20	408	28	35
UD5	11	270	206	92	1269	202	213
UD6	2	18	29	9	123	13	7

Table 7:

Results of References Part 2.

Form/instance	Comp08	Comp09	Comp10	Comp12	Comp13	Comp14
UD1	24	61	10	268	38	30
UD2	50	119	27	358	77	59
UD3	8	18	2	140	32	2
UD4	20	47	18	147	51	21
UD5	102	208	190	665	195	138
UD6	8	17	4	121	20	5

Table 8:

Results of References Part 3.

Form/instance	Comp15	Comp16	Comp17	Comp18	Comp19	Comp20	Comp21
UD1	46	28	44	41	36	25	69
UD2	87	47	86	71	74	54	117
UD3	30	12	14	10	34	24	30
UD4	42	23	38	32	39	39	60
UD5	259	182	216	150	224	309	247
UD6	21	11	14	9	19	14	28

Table 9:

Results of References Part 5.

Form/instance	Test1	Test2	Test3	Test4
UD1	214	8	36	43
UD2	234	17	86	132
UD3	200	0	18	24
UD4	213	4	22	37
UD5	245	24	108	173
UD6	111	0	10	21

Table 10:

Results of References Part 6.

Form/instance	DDS1	DDS2	DDS3	DDS4	DDS5	DDS6	DDS7
UD1	238	0	0	233	0	5	0
UD2	1024	0	0	261	0	11	0
UD3	5944	128	22	3988	56	2	40
UD4	2593	78	11	6735	165	10	29
UD5	9677	93	22	13,064	128	185	97
UD6	115	0	0	111	0	2	0

5 Comparison of the Proposed ICA with the IP/LP Approach

The purpose of this comparison is to survey the objective function related to each approach that has solved the university timetabling problems. In this research, the proposed algorithm is cooperative and we have used the ICA approach in order to achieve the objective of the research. The IP/LP approach, by formulizing hard and soft constraints of university timetabling, has done events for the resources by using the branch and threat algorithm. The LP approach in formulizing and solving problems is related to limited resource performance and ability of initialization [32]. The IP/LP approach is completely a mathematical method that is based on the structure and type of the departments and interviews from deans, heads of groups, etc.

In solving the timetabling problem of university courses [1, 5, 24, 38], the solutions are different from institute to institute and are affected by the size of the institutes. It is rather difficult to obtain an optimum solution for the timetabling of university courses at the end of the IP/LP method, so these kinds of approaches are utilized separately. A comparison of the objective function associated with its parameters in the proposed approach with the IP/LP method is shown in Table 11.

Table 11:

Parametric Comparison between the IP/LP and ICA Methods to Solve the Timetabling Problem.

Method comparison parameters	IP/LP for solving university timetabling	ICA method for solving common event problems (proposed)
Reducing event dissatisfactions in a department based on the objective function	✓
Reducing common events dissatisfactions among departments based on the objective function		✓
Minimizing excess resource dissipation in more than one department		✓
For common events, if two or more courses are offered to a professor, those courses must not overlap with each other	✓	✓
For classrooms, one classroom must not be dedicated to more than one course at the same time	✓	✓
Compatibility of classrooms: all periods of a specific course must be held in a room at a certain time	✓	✓
If a course has theoretical and practical prerequisites, the practical classes must be held before the theoretical classes	✓
Common event time slots are expressed optionally and are expressed by themselves	✓
Priorities of common event time slots of inter-departments are optionally expressed by themselves		✓
Compatibilities of classrooms: all periods of a course must be held in the same classroom in a day	✓	✓
The time complexity for obtaining timetabling corresponds to desirable objective of solutions		✓
Reducing dissatisfactions of non-department events at a department based on the objective function	✓	✓

6 Conclusion and Future Work

We have obtained desirable results by implementing the proposed algorithm. The results include the performance of the GA for every department timetabling and the ICA for solving the common events problem among departments, in order to meet the research objectives within a collaborative search solution. The results of the proposed solution can be expressed as follows: (i) dissipation of excess resources (unused) in each department has been minimized so that it represents an allocation improvement of common events to resources, and (ii) the proposed approach creates descending satisfactions of common event priorities among departments for allocation of excess resources.

It should be mentioned that using the methods based on multi-agent systems leads to increase in the timetabling independence of each of department. This prevents autonomy, scalability of collisions, and unplanned allocations due to negotiating between agents in a distributed environment. Using methods like colonialism for common events will lead to uniform distribution and allocation of excess resources in the timetabling process. Because of varying constraints and priorities of the common events among departments, all demands cannot be satisfied to a desirable level in reality. Future work should be conducted to solve this problem.

Bibliography

[1] O. M. Alsmadi, Z. S. Abo-Hammour, D. Abu-Al-Nadi and A. Algsoon, A novel genetic algorithm technique for solving university course timetabling problems, in: 7th International Workshop on Systems, Signal Processing and their Applications (WOSSPA 2011), Ecole Nationale Polytechnique, Algeria Tipaza, Algeria, 2011.10.1109/WOSSPA.2011.5931449Suche in Google Scholar

[2] M. G. Asham, M. M. Soliman and R. A. Ramadan, Trans genetic coloring approach for timetabling problem, Int. J. Comput. Appl. (2011), 17–25. Doi: 10.5120/2824-205.10.5120/2824-205Suche in Google Scholar

[3] H. Babaei and A. Hadidi, A review of distributed multi-agent systems approach to solve university course timetabling problem, Adv. Comput. Sci. 3 (2014), 19–28.Suche in Google Scholar

[4] E. Babkin, H. Abdulrab and T. Babkina, AgentTime: a distributed multi-agent software system for university’s timetabling, in: M. Aziz-Alaoui, C. Bertelle, eds., From System Complexity to Emergent Properties, pp. 341–354, Springer, Berlin, 2009.10.1007/978-3-642-02199-2_17Suche in Google Scholar

[5] M. A. Bakir and C. Aksop, A 0-1 integer programming approach to a university timetabling problem, Hacettepe J. Math. Stat. 37 (2008), 1–15.Suche in Google Scholar

[6] C. Blum and A. Roli, Metaheuristics in combinatorial optimization: overview and conceptual comparison, ACM Comput. Surv. (CSUR) 35 (2003), 268–308.10.1145/937503.937505Suche in Google Scholar

[7] E. Burke and P. Ross, Practice and Theory of Automated Timetabling: First International Conference, Edinburgh, UK, August 29–September 1, 1995, Selected Papers, vol. 1153, Springer Science & Business Media, New York, 1996.10.1007/3-540-61794-9_63Suche in Google Scholar

[8] T. B. Cooper and J. H. Kingston, The complexity of timetable construction problems, in: International Conference on the Practice and Theory of Automated Timetabling, Edinburgh, UK, 1995.10.1007/3-540-61794-9_66Suche in Google Scholar

[9] L. Davis, Adapting operator probabilities in genetic algorithms, in: Proceedings of the 3rd International Conference on Genetic Algorithms, San Francisco, CA, USA, 1989.Suche in Google Scholar

[10] F. De Cesco, L. Di Gaspero and A. Schaerf, Benchmarking curriculum-based course timetabling: formulations, data formats, instances, validation, and results, in: Proceedings of the 7th PATAT Conference, Montréal, Canada, 2008.Suche in Google Scholar

[11] P. Demeester, B. Bilgin, P. De Causmaecker and G. Vanden Berghe, A hyperheuristic approach to examination timetabling problems: benchmarks and a new problem from practice, J. Schedul. 15 (2012), 83–103.10.1007/s10951-011-0258-5Suche in Google Scholar

[12] L. Di Gaspero and A. Schaerf, Multi-neighbourhood local search with application to course timetabling, in: International Conference on the Practice and Theory of Automated Timetabling, Pittsburgh, PA, USA, 2002.10.1007/978-3-540-45157-0_17Suche in Google Scholar

[13] L. Di Gaspero and A. Schaerf, Neighborhood portfolio approach for local search applied to timetabling problems, J. Math. Model. Algorithms 5 (2006), 65–89.10.1007/s10852-005-9032-zSuche in Google Scholar

[14] L. Di Gaspero, S. Mizzaro and A. Schaerf, A multiagent architecture for distributed course timetabling, in: Proceedings of the 5th International Conference on the Practice and Theory of Automated Timetabling (PATAT-2004), Pittsburgh, PA, USA, 2004.Suche in Google Scholar

[15] M. Dimopoulou and P. Miliotis, Implementation of a university course and examination timetabling system, Eur. J. Oper. Res. 130 (2001), 202–213.10.1016/S0377-2217(00)00052-7Suche in Google Scholar

[16] M. Eley, Ant algorithms for the exam timetabling problem, in: Practice and Theory of Automated Timetabling VI, pp. 364–382, Springer, Berlin, 2007.10.1007/978-3-540-77345-0_23Suche in Google Scholar

[17] H. Emami and S. Lotfi, Graph colouring problem based on discrete imperialist competitive algorithm, (IJFCST), Vol. 3, July 2013, pp. 1–12. arXiv preprint arXiv:1308.3784.Suche in Google Scholar

[18] T. Fogarty, Varying the probability of mutation in the genetic algorithm, in: Proceedings of the 3rd International Conference on Genetic Algorithms, Virginia, USA, 1989.Suche in Google Scholar

[19] C. W. Fong, H. Asmuni and B. McCollum, A hybrid swarm based approach to university timetabling, IEEE Trans. Evol. Comput. 19 (2015), 870–884.10.1109/TEVC.2015.2411741Suche in Google Scholar

[20] M. R. Garey and D. S. Johnson, Computers and Intractability: A Guide to the Theory of NP-Completeness, W. H. Freeman & Co., New York, 1979.Suche in Google Scholar

[21] A. B. Hassine, X. Defago and T. B. Ho, Agent-based approach to dynamic meeting scheduling problems, in: Third International Joint Conference on Autonomous Agents and Multiagent Systems, vol. 3, New York, NY, USA, 2004.Suche in Google Scholar

[22] J. Henry Obit, Developing Novel Meta-heuristic, Hyper-heuristic and Cooperative Search for Course Timetabling Problems. University of Nottingham, Nottingham, England, 2010.Suche in Google Scholar

[23] L. Kang, G. H. von Schoenberg and G. M. White, Complete university timetabling using logic, Comput. Educ. 17 (1991), 145–153.10.1016/0360-1315(91)90092-6Suche in Google Scholar

[24] A. H. Karami and M. Hasanzadeh, University course timetabling using a new hybrid genetic algorithm, in: 2nd International eConference on Computer and Knowledge Engineering (ICCKE), Ferdowsi University of Mashhad, Mashhad, Iran, 2012.10.1109/ICCKE.2012.6395368Suche in Google Scholar

[25] Z. Lü and J. K. Hao, Adaptive tabu search for course timetabling, Eur. J. Oper. Res. 200 (2010), 235–244.10.1016/j.ejor.2008.12.007Suche in Google Scholar

[26] M. Nandhini and S. Kanmani, Implementation of class timetabling using multi agents, in: International Conference on Intelligent Agent & Multi-Agent Systems, 2009, IAMA, Chennai, India, 2009.10.1109/IAMA.2009.5228065Suche in Google Scholar

[27] H. E. Nouri and O. B. Driss, Distributed model for university course timetabling problem, in: International Conference on Computer Applications Technology (ICCAT), Zone Touristique El Kantaoui Sousse, Tunisia, 2013.10.1109/ICCAT.2013.6521990Suche in Google Scholar

[28] H. E. Nouri and O. B. Driss, MATP: a multi-agent model for the university timetabling problem, in: Software Engineering Perspectives and Application in Intelligent Systems, pp. 11–22, Springer, Berlin, 2016.10.1007/978-3-319-33622-0_2Suche in Google Scholar

[29] J. H. Obit, D. Landa-Silva, D. Ouelhadj, T. K. Vun and R. Alfred, Designing a multi-agent approach system for distributed course timetabling, in: 11th International Conference on Hybrid Intelligent Systems (HIS), Melacca, Malaysia, 2011.10.1109/HIS.2011.6122088Suche in Google Scholar

[30] M. Oprea, MAS_UP-UCT: a multi-agent system for university course timetable scheduling, Int. J. Comput. Commun. Control 2 (2007), 94–102.10.15837/ijccc.2007.1.2341Suche in Google Scholar

[31] R. Qu, E. K. Burke, B. McCollum, L. T. Merlot and S. Y. Lee, A survey of search methodologies and automated system development for examination timetabling, J. Schedul. 12 (2009), 55–89.10.1007/s10951-008-0077-5Suche in Google Scholar

[32] T. A. Redl, A Study of University Timetabling That Blends Graph Coloring with the Satisfaction of Various Essential and Preferential Conditions, Texas Southern University, Houston, TX, 2004.Suche in Google Scholar

[33] N. R. Sabar, M. Ayob, G. Kendall and R. Qu, A honey-bee mating optimization algorithm for educational timetabling problems, Eur. J. Oper. Res. 216 (2012), 533–543.10.1016/j.ejor.2011.08.006Suche in Google Scholar

[34] S. C. Sarin, Y. Wang and A. Varadarajan, A university-timetabling problem and its solution using Benders’ partitioning – a case study, J. Schedul. 13 (2010), 131–141.10.1007/s10951-009-0157-1Suche in Google Scholar

[35] J. D. Schaffer and A. Morishima, An adaptive crossover distribution mechanism for genetic algorithms, in: Genetic Algorithms and their Applications: Proceedings of the Second International Conference on Genetic Algorithms, Massachusetts, USA, 1987.Suche in Google Scholar

[36] T. Starkweather, D. Whitley and K. Mathias, Optimization using distributed genetic algorithms, in: International Conference on Parallel Problem Solving from Nature, Dortmund, Germany, 1990.Suche in Google Scholar

[37] P. Wangmaeteekul, Using Distributed Agents to Create University Course Timetables Addressing Essential & Desirable Constraints and Fair Allocation of Resources, Durham University, Durham, 2011.Suche in Google Scholar

[38] Y. Yang, R. Paranjape, L. Benedicenti and N. Reed, A system model for university course timetabling using mobile agents, Multiagent Grid Syst. 2 (2006), 267–275.10.3233/MGS-2006-2305Suche in Google Scholar

[39] E. Yu and K. S. Sung, A genetic algorithm for a university weekly courses timetabling problem, Int. Trans. Oper. Res. 9 (2002), 703–717.10.1111/1475-3995.00383Suche in Google Scholar

Received: 2017-05-26

Published Online: 2017-12-21

This work is licensed under the Creative Commons Attribution 4.0 Public License.

Artikel in diesem Heft

https://doi.org/10.1515/jisys-2017-0249

Schlagwörter für diesen Artikel

University course timetabling; imperialist competitive algorithm; genetic algorithm

Creative Commons

BY 4.0

Form/instance	Comp08	Comp09	Comp10	Comp12	Comp13	Comp14
UD1	24	61	10	268	38	30
UD2	50	119	27	358	77	59
UD3	8	18	2	140	32	2
UD4	20	47	18	147	51	21
UD5	102	208	190	665	195	138
UD6	8	17	4	121	20	5

Form/instance	Comp15	Comp16	Comp17	Comp18	Comp19	Comp20	Comp21
UD1	46	28	44	41	36	25	69
UD2	87	47	86	71	74	54	117
UD3	30	12	14	10	34	24	30
UD4	42	23	38	32	39	39	60
UD5	259	182	216	150	224	309	247
UD6	21	11	14	9	19	14	28

Form/instance	Test1	Test2	Test3	Test4
UD1	214	8	36	43
UD2	234	17	86	132
UD3	200	0	18	24
UD4	213	4	22	37
UD5	245	24	108	173
UD6	111	0	10	21

Form/instance	Comp08	Comp09	Comp10	Comp12	Comp13	Comp14
UD1	24	61	10	268	38	30
UD2	50	119	27	358	77	59
UD3	8	18	2	140	32	2
UD4	20	47	18	147	51	21
UD5	102	208	190	665	195	138
UD6	8	17	4	121	20	5

Form/instance	Comp15	Comp16	Comp17	Comp18	Comp19	Comp20	Comp21
UD1	46	28	44	41	36	25	69
UD2	87	47	86	71	74	54	117
UD3	30	12	14	10	34	24	30
UD4	42	23	38	32	39	39	60
UD5	259	182	216	150	224	309	247
UD6	21	11	14	9	19	14	28

Form/instance	Test1	Test2	Test3	Test4
UD1	214	8	36	43
UD2	234	17	86	132
UD3	200	0	18	24
UD4	213	4	22	37
UD5	245	24	108	173
UD6	111	0	10	21

Form/instance	Comp08	Comp09	Comp10	Comp12	Comp13	Comp14
UD1	24	61	10	268	38	30
UD2	50	119	27	358	77	59
UD3	8	18	2	140	32	2
UD4	20	47	18	147	51	21
UD5	102	208	190	665	195	138
UD6	8	17	4	121	20	5

Form/instance	Comp15	Comp16	Comp17	Comp18	Comp19	Comp20	Comp21
UD1	46	28	44	41	36	25	69
UD2	87	47	86	71	74	54	117
UD3	30	12	14	10	34	24	30
UD4	42	23	38	32	39	39	60
UD5	259	182	216	150	224	309	247
UD6	21	11	14	9	19	14	28

Form/instance	Test1	Test2	Test3	Test4
UD1	214	8	36	43
UD2	234	17	86	132
UD3	200	0	18	24
UD4	213	4	22	37
UD5	245	24	108	173
UD6	111	0	10	21