Home Texture Feature Extraction Using Intuitionistic Fuzzy Local Binary Pattern
Article Open Access

Texture Feature Extraction Using Intuitionistic Fuzzy Local Binary Pattern

  • Mohd Dilshad Ansari EMAIL logo , Satya Prakash Ghrera and Arunodaya Raj Mishra
Published/Copyright: December 8, 2016
Download Article (PDF)
Become an author with De Gruyter Brill
Submit Manuscript Author Information
Journal of Intelligent Systems
From the journal Journal of Intelligent Systems Volume 29 Issue 1

Abstract

In this paper, intuitionistic fuzzy local binary for texture feature extraction (IFLBP) has been proposed to encode local texture from the input image. The proposed method extends the fuzzy local binary pattern approach by incorporating intuitionistic fuzzy sets in the representation of local patterns of texture in images. Intuitionistic fuzzy local binary pattern also contributes to more than one bin in the distribution of IFLBP values, which can further be used as a feature vector in the various fields of image processing. The performance of the proposed method has been demonstrated on various medical images and processing images of size 256×256. The obtained results validated the effectiveness and usefulness of our proposed method over the other reported methods, and new improvements are suggested.

Keywords: Fuzzy local binary pattern; intuitionistic fuzzy sets; intuitionistic fuzzy local binary pattern; entropy

1 Introduction

Feature extraction is a process to extract the compact and essential information from an image. The major objective of feature extraction is to find the most significant information from original or raw data. When the input image or data to an algorithm is excessively bulky to be processed, it is supposed to be redundant (a large amount of data but a little information). Afterwards, the input data will be transformed into a highly reduced dimension representation or a set of features (also known as features vector). These extracted feature vectors represent the whole image. If extracted features are carefully selected, it is expected that the feature set will extract significant information in order to carry out the preferred task using this reduced representation instead of input image or full data. Extracted features have been used in various fields of image processing and signal processing, such as image forensics, remote sensing, pattern recognition, visual inspection, object discrimination, biomedical image processing, character recognition, terrain delimitation, image classification, document verification, reading bank deposit slips, applications for credit cards, and script recognition [3, 4, 8, 10, 28, 45, 46, 48].

The most common features available in an image include color, texture, and shape. Feature extraction is mainly dependent on these three types of features, and the performance of any desired task is also dependent on these extracted features. Generally, feature representation methods are divided in three categories: global, block-based, and region-based features [10, 45]. Less concentration has been given to image feature extraction compared to a significant amount of research on the construction of annotation/retrieval model itself. Therefore, in this paper, our attention is only on texture-based feature extraction. We have tested our algorithm on various medical images, i.e. X-ray, thyroid and brain computed tomography (CT) scan, and image processing images, i.e. Lena image and JUIT logo.

A number of textural feature extraction methods have been proposed [36, 47]. The local binary pattern (LBP) method [34], which is based on the concept of binary patterns (BPs) for representation of texture, has been broadly adopted because it is simple yet effective in describing the local spatial structure of an image. The LBP approach has been extended and combined with other approaches, resulting in a wide range of texture representation schemes suitable for different image analysis tasks. Typical examples include LBP extensions featuring scale invariance [9], rotation invariance [12, 38], combination of inter- and intra-spatial structure of the LBP patterns [49], and fusion of micro-LBP and macro-Gabor features [30].

2 Related Work

One of the first studies on visual inspection [22] has shown that LBP features can be successfully used for surface defect detection. Later, in Ref. [42], BP-based features have been used for wood quality discrimination, and more recently such features have also been applied on automatic defect detection [16, 44] as well as in remote sensing [14]. A variety of studies have shown that the BP-based feature extraction approaches are suitable for content-based image retrieval [23, 29], whereas recently the LBP approach has been adopted in a discriminative model for image ranking from text queries [15]. Moreover, in the area of face recognition, the LBP is recognized as a highly efficient texture representation approach. For example, it has been used for invariant face recognition [43, 52], face authentication [11], and the recognition of facial expressions [40]. Excellent results have also been obtained from its application on biomedical domain, including video endoscopy [20], the classification of protein images [33], and computer-aided neuroblastoma prognosis system [39]. In the area of motion analysis, the application of BP-based approaches has been investigated for underwater image matching [13], modeling and detection of moving objects [19], and object tracking [37].

The research community has a lot of interest on LBP texture representation, and various approaches have been proposed based on the BP model. An approach has been proposed for the estimation of a local contrast measure [34]. The LBP/C approach, which is based on the joint distribution of LBP codes and local contrast measures, has shown resistance to variations of the illumination. It has been used to enhance the discrimination ability of the original LBP approach [34]. Another variation of LBP is the local edge patterns approach, which has been proposed for image segmentation [50]. It describes the spatial structure of local texture according to the spatial arrangement of edge pixels. In the same spirit, Hafiane et al. [17] proposed median BP (MBP), which is intensity-shift invariant. According to this approach, the texture primitives are determined by localized thresholding against the local median. In a subsequent study, a hashed version of MBP to a binary chain or equivalence class has been evaluated, resulting in a resolution- and rotation-invariant MBP texture descriptor [18].

Fuzzy sets provide a flexible framework for handling the indeterminacy characterizing real-world systems, arising mainly from the imprecise and/or imperfect nature of information. However, fuzzy sets do not cope with the hesitancy (intuitionistic index) in images that originate from various factors, which in their majority are caused by inherent weaknesses of the acquisition and imaging mechanisms. Distortions that occur as a result of the limitations of acquisition chain, such as quantization noise, the suppression of dynamic range, or the non-linear behavior of the mapping system, affect our certainty regarding the “brightness” or “edginess” of a pixel, and therefore introduce a degree of hesitancy associated with the corresponding pixel. The fuzzy sets theory was introduced by Zadeh [51] on the extraction of texture spectrum features [7] and their efficient successors. The LBP features could possibly enhance their robustness to noise [21, 24, 25, 26, 27]. However, these studies can only be considered as preliminary as they include only a limited experimental evaluation. Iakovidis et al. [21] and Keramidas et al. [27] proposed a generic, uncertainty-aware methodology for the derivation of fuzzy LBP (FLBP) texture models. Additionally, the intuitionistic fuzzy set theory proposed by Atanassov [5] and Atanassov and Gargov [6] provides a flexible mathematical framework to cope with uncertainty with the hesitancy originating from imperfect or imprecise information [31, 32]. A prominent characteristic of IFS is that it assigns to each element a membership degree and a non-membership degree with a certain amount of hesitation degree. In this paper, we propose intuitionistic FLBP (IFLBP) for texture representation using Atanassov’s intuitionistic fuzzy sets.

2.1 Local Binary Pattern

LBP is a kind of gray-scale texture operator that is used for describing the spatial structure of an image texture [34]. The LBP texture model is based on the comparison of pixel values of a pixel neighborhood. A binary value is assigned to each pixel px, belonging to a local neighborhood. This value is calculated by comparing the value of a pixel intensity gx with a center pixel intensity gc, which is the same for all pixels in the neighborhood. Therefore, two crisp sets of pixels can be defined for each pixel neighborhood, as follows:

Let U={0, 1,…, n−1} be the universal set of all pixels in the n×n pixel neighborhood. Let A={px∈U:ℓA(x)}, where ℓA(x) is a predicate defined as gx≥gc, be the set of all pixels px and B be the set of all neighborhood pixels px with gray value gx≤gc under the universal set U, respectively. Hence, set B is the complement of set A relative to the universal set U.

Logically, for crisp set A, the characteristic functions are χ(x)=0, px∉A and χ(x)=1, px∈A. Similarly, the respective characteristic functions for set B are χ(x)=0, px∈B and χ(x)=1, px∉B.

Based on these binary values of the characteristic function χ(x) for a neighborhood of n pixels, a unique LBP code can be calculated as follows:

(1) LBPcode=∑x = 0k − 1dx⋅wx,

where dx=χ(x), k∈(0, n] being the number of pixels in the neighborhood that were considered for the creation of BP and wx=2x, x∈{0, 1, …, k} is a weight function that assigns a weight value at each pixel of the neighborhood. Each pixel of the local neighborhood is characterized by a single LBP code out of 2k possible codes.

2.2 Fuzzy LBP

A drawback of the LBP method as well as all local descriptors that apply vector quantization is that they are not robust in the sense that a small change in the input image would always cause only a small change in the output. To increase the robustness of the operator, the thresholding function is replaced by two fuzzy membership functions [1]. In order to enhance the LBP approach so that it can handle the uncertainty introduced by the speckle noise, Keramidas et al. [25, 26] incorporated fuzzy logic to the computation of the BPs to cope with inexactness and improve the discrimination power of the LBP approach in noise-degraded images. In this section, we have presented FLBP for texture representation proposed by Iakovidis et al. [21] and Keramidas et al. [27].

The fuzzy logic, as a multi-valued logic, allows intermediate values between the typical values 0/1 or true/false. Fuzzy logic permits the replacement of crisp sets A and B by two fuzzy sets à and B˜. Members of these fuzzy sets are pixels of the neighborhood that may belong simultaneously to the fuzzy set à (to one degree) and the fuzzy set B˜ (to a different degree). More specifically, pixels with intensity values that are inside the interval [gc+T, gmax] belong to set Ã, while those with intensity values that are inside the interval [0, gc−T] belong to set B˜. Pixels with intensity values that are inside the interval [gc−T, gc+T] belong partially to set à and partially to set B˜. The value of gmax is the maximum intensity value that can be given to a pixel, while T is a parameter that controls the degree of fuzziness of sets à and B˜. The fuzzy set à under the universal set U can be expressed as a set of ordered pairs:

(2) A˜={〈px, μA˜(x)〉|x∈U},

where μA:U→[0, 1] is the degree of the membership to which pixel px with gray value gx is greater than or equal to the gray value of the center pixel gc, and can be defined as follows:

(3) μA˜(x)={1if gx≥gc+T,0.5(1+(gx−gc)T)if gc−T<gx<gc+T, T≠0,0if gx≤gc−T, T≠0,0if gx<gc+T, T=0.

Similarly, the complement of fuzzy set à can be expressed as

(4) B˜={〈px, μB˜(x)〉|px∈U},

where μB˜:U→[0, 1] is the degree of membership to which a pixel px with gray value gx is less than the gray value of the center pixel gc and can be defined as follows:

(5) μB˜(x)=1−μA˜(x).

Both μA˜(x) and μB˜(x) for T∈[0, gmax] represent parameter that controls the degree of fuzziness.

It may be noted that for the original LBP operator, a single LBP code characterizes an n×n pixel neighborhood. However, in the FLBP approach, an n×n pixel neighborhood can be characterized by more than one LBP code and contribution CFLBP values. The degree to which each LBP code characterizes a neighborhood depends on the membership and non-membership functions μA˜ and μB˜. When the local neighborhood consists of k sampling points, the resulting histogram has bins numbered 0, 1, …, 2k.

For an n×n pixel neighborhood, the contribution CFLBP of each LBP code in a single bin i of FLBP histogram is estimated by

(6) CFLBP(x, y, i)=∏r = 0k − 1[br(i)μA˜(x)+(1−br(i))μB˜(x)],

where k∈(0, n] is the number of neighboring pixels participating in the FLBP code computation, (x, y) denotes the coordinates of a pixel, and br(i)∈{0, 1} denotes the numerical value of the rth bit of binary representation of bin i, i=0, 1, …, 2k. The complete FLBP histogram is computed by summing the contributions of all the pixels in the input image:

(7) HFLBP(i)=∑x,yCFLBP(x, y, i), i=0, 1, …, 2k−1,

under the condition

(8) ∑i = 02k − 1CFLBP(x, y, i)=1.

3 Proposed Method

In order to generalize the FLBP approach so that it can handle the uncertainty with hesitancy originating from imperfect or imprecise information, we propose IFLBP for texture representation using the intuitionistic fuzzy sets as follows.

Let U={0, 1…,n−1} be the universal set for n pixel neighborhood. Then, an intuitionistic fuzzy set à under the universal set U is given by

(9) A˜={〈px, μA˜(x), νA˜(x)〉|px∈U},

where μA˜:U→[0, 1] and νA˜:U→[0, 1] denote the degree of membership and non-membership to which an element px has either greater or less gray value than gc in Ã, respectively, with the condition 0≤μA˜(x)+νA˜(x)≤1. The amount πA˜(x)=1−μA˜(x)−νA˜(x), ∀px∈U is called the degree of indeterminacy (hesitation part). It is the degree of uncertainty whether px belongs to à or not.

The membership and non-membership functions of IFS Ã can be defined as follows:

(10) μA˜(x)={0if gx<gc−T,0.5(1+h)(1+gx−gc)T)if gx∈[gc−T, gc], T≠0,0.5[(1+gx−gc)T)+h(gx−gc)T−1)]if gx∈(gc, gc+T], T≠0,1if gx≥gc+T.

and

(11) νA˜(x)={1if gx<gc−T,0.5[(1−(gx−gc)T)−h(1+(gx−gc)T)]if gx∈[gc−T, gc], T≠0,0.5(1+h)(1−(gx−gc)T)if gx∈(gc, gc+T], T≠0,0if gx≥gc+T.

For an n×n pixel neighborhood, the contribution CIFLBP of each IFLBP code in a single bin of IFLBP histogram is estimated as follows:

(12) CIFLBP(x, y, i)=∏r = 0k − 1[br(i)μA˜(x)+(1−br(i))νA˜(x)],

where k∈(0, n], (x, y) and br(i)∈{0, 1} represent the number of neighboring pixels, the coordinates of a pixel and numerical value of the rth bit of binary representation of bin i, respectively. The complete IFLBP histogram is given by

(13) HIFLBP(i)=∑x,yCIFLBP(x, y, i), i=0, 1, …, 2k−1.

It may be noted that using the crisp LBP operator, each n×n pixel neighborhood always contributes to one bin of the histogram; however, in case of both FLBP and IFLBP histograms, each n×n pixel neighborhood typically contributes to more than one bin of the histogram. The sum of the contribution of an each n×n pixel neighborhood (IFLBP code) to the bins of the IFLBP histogram is equal to 1, that is

(14) ∑i = 02k − 1CIFLBP(x, y, i)=1.

An example of IFLBP computation scheme for a 3×3 pixel neighborhood is shown in Figure 1.

Figure 1: IFLBP Computation Scheme for a 3×3 Pixel Neighborhood. (A) Gray levels of a 3×3 pixel neighborhood. (B) Intuitionistic fuzzy threshold values along with membership and non-membership values. (C) Binomial weights matrix. (D) IFLBP codes and CIFLBP.
Figure 1:

IFLBP Computation Scheme for a 3×3 Pixel Neighborhood.

(A) Gray levels of a 3×3 pixel neighborhood. (B) Intuitionistic fuzzy threshold values along with membership and non-membership values. (C) Binomial weights matrix. (D) IFLBP codes and CIFLBP.

Remark 3.1: When T≠0, h=0, the resulting intuitionistic fuzzy membership and non-membership functions given by Eqs. (10) and (11) are almost equivalent to the fuzzy membership function μA(x) given by Eq. (3), the difference being that μA˜(x)=νA˜(x)=0.5 whereas μA(x)=1 when gi=gc.

Remark 3.2: When T=0, the resulting intuitionistic fuzzy membership and non-membership functions are equivalent to the crisp thresholding function χA(x).

4 Performance Metrics: Entropy of IFLBP Features

The information content of an image is often measured by calculating the uncertainty or entropy of an image. As the magnitude of entropy increases, more information is associated with the image. The entropy measures the average, global information content of an image in terms of average bits per pixel.

Shannon entropy [41] is defined as

(15) H=−∑i = 0255pilogpi

where pi is the probability of the ith pattern.

It is worth mentioning that in the logarithmic entropic measure [Eq. (15)], as pi→0, its corresponding self-information of this event, I(pi)=−log pi→∞ but I(pi=1)=log pi→0. Thus, we see that information gain from an event is neither bounded at both ends nor defined at all points. In practice, the gain in information from an event, whether highly probable or highly unlikely, is expected to lie between two finite limits. For example, as more and more pixels in an image are analyzed, the gain in information increases, and when all the pixels are inspected, the gain attains its maximum value irrespective of the content of an image.

In Shannon’s entropy, which is highly praised, we find that the measure of self-information of an event with probability pi is taken as log pi, a decreasing function of pi. The same decreasing character alternatively may be maintained by considering it as a function of (1−pi) rather than of 1/pi. The additive property, which is considered crucial in Shannon’s approach, of the self-information function for independent events may not have a strong relevance (impact) in practice as well as in some situations. Alternatively, as in the case of probability law, the joint self-information may be the product rather than the sum of the self-information in two independent cases. The above considerations suggest the self-information as an exponential function of (1−pi) instead of logarithmic behavior. This is also appropriate while considering the concept of information gain in an image. Pal and Pal entropy [35] is defined by

(16) H=∑i = 0255pie1 − pi.

5 Experimental Results and Analysis

It can be observed that the Keramidas et al. method [27] and the Ansari and Ghrera method [2] have zero values for some bins out of 255 bins. However, the proposed method histograms do not have bins with zero values and there are more spikes, though limited in magnitude. This indicates that the Ansari and Ghrera method [2] is more informative than the Keramidas method [27], and the proposed method is more informative than existing methods. Entropy is a measure of uncertainty associated with random occurrences, normally considered as the measure of “disorder”. Pal and Pal entropy [35] is a statistical measure of randomness that can be used to characterize the texture of an input image (Figure 2).

Figure 2: Proposed Model.
Figure 2:

Proposed Model.

The more diversified signal implies higher entropy and more actual information gain. If all the bins of the histogram have equal probability, then the maximum entropy will be reached. Apparently, for the fixed threshold T, the histograms of the proposed method always give greater entropy than the histograms of the existing method. However, the histograms of the Ansari method [2] for the same threshold and using hesitation threshold values h∈[0, 1] give greater entropy than the histograms of the Keramidas method [27]. Therefore, the IFLBP histogram gains more information than the histograms of other reported methods.

Additionally, we apply the proposed IFLBP approach on various images as shown in Figures 3–7 of size 256×256 to calculate the histogram feature vectors for different threshold values and varying hesitation (h∈[0, 1]), as well as computed entropies from these histograms; finally, the results are shown in Tables 1–5. We can examine from these tables that the maximum entropies obtained in Table 1 for T=6 and T=10 are at h=0.3, and those for T=2, T=14, T=20, and T=12 are at h=0.1. We follow the same procedure for the remaining images; the results are shown in Tables 2–5 and Figures 4–7. Therefore, the entropies obtained by the proposed method are always greater than the entropies obtained by existing methods. We plot the histograms of IFLBP codes of every image where we have found the maximum entropy, as shown in Figures 3–7. From these histograms, we can observe that the IFLBP histograms do not have bins with zero values. In addition, the IFLBP features of all images are more informative than existing features.

Figure 3: Histogram Plot of IFLBP Codes for X-ray Image.
Figure 3:

Histogram Plot of IFLBP Codes for X-ray Image.

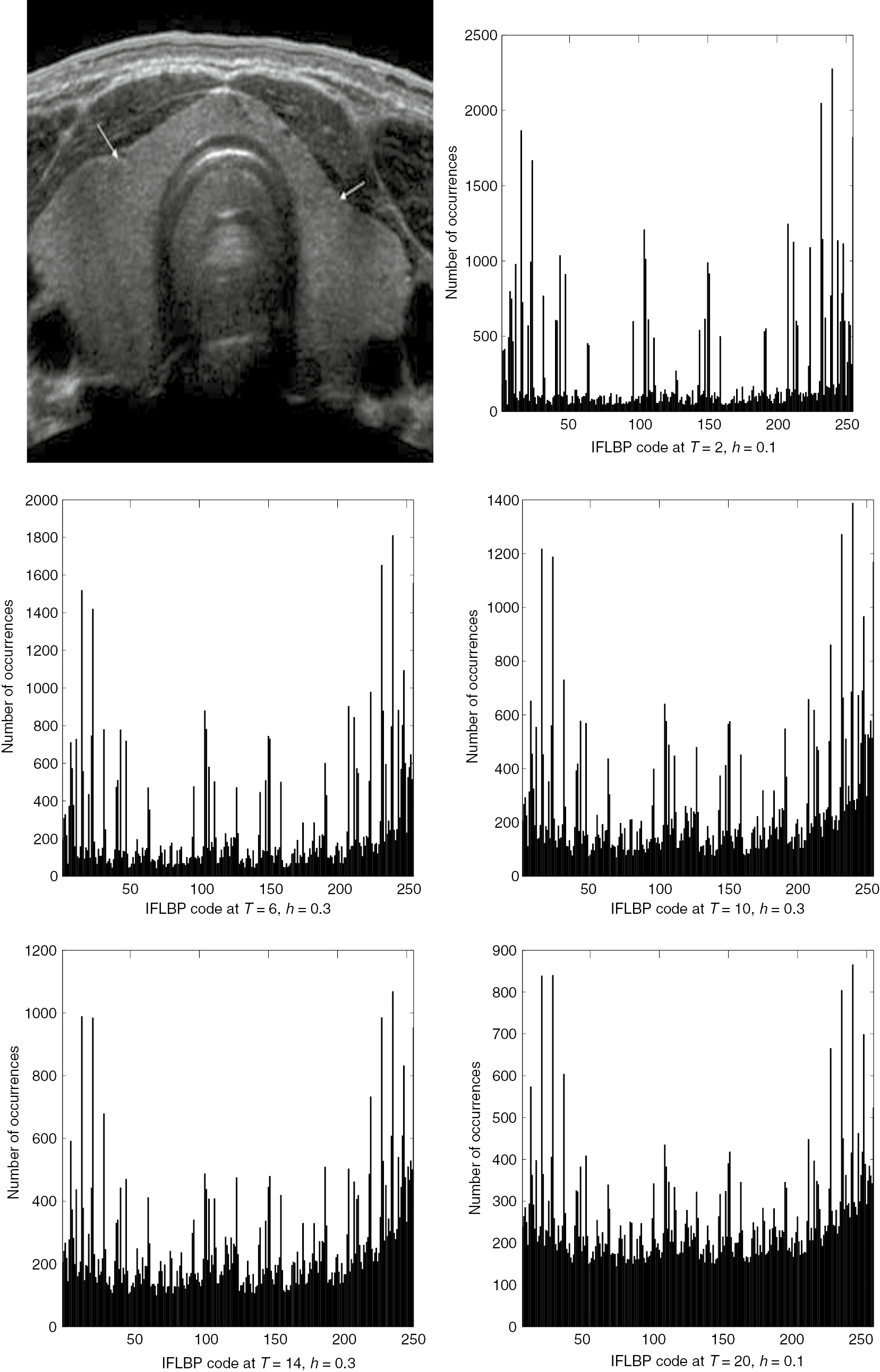
Figure 4: Histogram Plot of IFLBP Codes for Thyroid Image.
Figure 4:

Histogram Plot of IFLBP Codes for Thyroid Image.

Figure 5: Histogram Plot of IFLBP Codes for Brain CT Scan Image.
Figure 5:

Histogram Plot of IFLBP Codes for Brain CT Scan Image.

Figure 6: Histogram Plot of IFLBP Codes for Lena Image.
Figure 6:

Histogram Plot of IFLBP Codes for Lena Image.

Figure 7: Histogram Plot of IFLBP Codes for JUIT Logo.
Figure 7:

Histogram Plot of IFLBP Codes for JUIT Logo.

Table 1:

Entropy Values at Different Thresholds and Hesitation for X-ray Image.

Methods Hesitation (h)↓ Thresholds (T)→
2 6 10 14 20
Keramidas et al. [27] 0.0 1.9016 1.68193 0.8708 0.5800 0.3889
Ansari et al. [2] 0.1 1.8530 1.6693 0.8570 0.5997 0.3815
0.3 1.7715 1.6195 1.0229 0.5905 0.4978
0.5 1.7941 1.6513 1.2770 0.8684 0.5713
0.7 1.7825 1.8069 1.7239 1.5165 1.1406
1.0 1.6766 1.6686 1.4254 1.3292 1.3247
Proposed method 0.1 2.6884 2.6999 2.6999 2.7058 2.7068
0.3 2.6877 2.7001 2.7040 2.7056 2.7065
0.5 2.6844 2.6983 2.7024 2.7040 2.7048
0.7 2.6751 2.6923 2.6970 2.6987 2.6995
1.0 2.6167 2.6474 2.6538 2.6549 2.6540

Bold value indicates maximum entropy in a bin.

Table 2:

Entropy Values at Different Thresholds and Hesitation for Thyroid Image.

Methods Hesitation (h)↓ Thresholds (T)→
2 6 10 14 20
Keramidas et al. [27] 0.0 1.6859 1.9053 1.6529 0.8107 0.5882
Ansari et al. [2] 0.1 1.7407 1.8767 1.6371 1.0325 0.5531
0.3 1.8344 1.8491 1.6540 1.1170 0.5800
0.5 1.7409 1.8557 1.6227 1.4990 0.6631
0.7 1.6966 1.8292 1.7060 1.4552 0.8107
1.0 1.3570 1.6481 1.6132 1.3624 0.8700
Proposed method 0.1 2.6854 2.6938 2.6997 2.7031 2.7055
0.3 2.6842 2.6938 2.7000 2.7033 2.7054
0.5 2.6800 2.6914 2.6982 2.7016 2.7037
0.7 2.6669 2.6822 2.6902 2.6940 2.6961
1.0 2.5672 2.5988 2.6106 2.6152 2.6169

Bold value indicates maximum entropy in a bin.

Table 3:

Entropy Values at Different Thresholds and Hesitation for Brain CT Scan Image.

Methods Hesitation (h)↓ Thresholds (T)→
2 6 10 14 20
Keramidas et al. [27] 0.0 1.6118 1.4533 0.8742 0.7741 0.5749
Ansari et al. [2] 0.1 1.6143 1.5051 1.1713 1.0018 0.6372
0.3 1.7682 1.7247 1.7263 1.5873 1.2027
0.5 1.7776 1.8007 1.7948 1.7139 1.6238
0.7 1.4923 1.4875 1.5137 1.5539 1.6139
1.0 1.1053 1.1505 1.1139 1.1621 1.1341
Proposed method 0.1 2.6978 2.6998 2.7020 2.7038 2.7055
0.3 2.6933 2.6958 2.6987 2.7009 2.7131
0.5 2.6784 2.6822 2.6865 2.6901 2.6935
0.7 2.6290 2.6362 2.6441 2.6505 2.6567
1.0 2.2237 2.2478 2.6888 2.2903 2.2979

Bold value indicates maximum entropy in a bin.

Table 4:

Entropy Values at Different Thresholds and Hesitation for Lena Image.

Methods Hesitation (h)↓ Thresholds (T)→
2 6 10 14 20
Keramidas et al. [27] 0.0 1.7785 1.6843 1.1374 0.6021 0.4921
Ansari et al. [2] 0.1 1.7785 1.6843 0.9180 0.5782 0.4859
0.3 1.7718 1.6040 0.7613 0.5782 0.4589
0.5 1.7921 1.5580 0.9119 0.6599 0.5320
0.7 1.7935 1.5909 1.2017 0.8528 0.7343
1.0 1.8024 1.5971 1.4603 1.4030 1.4637
Proposed method 0.1 2.6764 2.6936 2.6998 2.7029 2.7051
0.3 2.6676 2.6959 2.7016 2.7041 2.7059
0.5 2.6776 2.6959 2.7016 2.7041 2.7059
0.7 2.6678 2.6970 2.7017 2.7036 2.7048
1.0 2.6769 2.6965 2.7000 2.7008 2.7007

Bold value indicates maximum entropy in a bin.

Table 5:

Entropy Values at Different Thresholds and Hesitation for JUIT Logo.

Methods Hesitation (h)↓ Thresholds (T)→
2 6 10 16 20
Keramidas et al. [27] 0.0 0.7454 0.7087 0.6803 0.6768 0.6258
Ansari et al. [2] 0.1 0.9311 0.6210 0.6033 0.5662 0.5249
0.3 1.7927 1.7443 1.7103 1.6453 1.5690
0.5 1.8470 1.8102 1.7920 1.7842 1.7757
0.7 1.5003 1.5689 1.5803 1.5624 1.6087
1.0 1.1239 1.0441 1.0343 1.0431 1.0514
Proposed method 0.1 2.7010 2.7032 2.7040 2.7046 2.7051
0.3 2.6969 2.6996 2.7005 2.7010 2.7016
0.5 2.6822 2.6858 2.6867 2.6871 2.6876
0.7 2.6302 2.6341 2.6340 2.6337 2.6333
1.0 2.1837 2.1643 2.1480 2.1369 2.1266

Bold value indicates maximum entropy in a bin.

6 Conclusions and Future Work

We have proposed a novel IFLBP for texture feature extraction to encode local texture from an image by incorporating the intuitionistic fuzzy set theory in the representation of local patterns of texture in the images. The proposed method is an extension of the FLBP approach. IFLBP also contributes to more than one bin in the distribution of the IFLBP values. Further, it can be used as a feature vector in various tasks. The proposed IFLBP approach is experimentally evaluated for various medical and image processing images of size 256×256. It can be observed from Tables 1–5 that the entropy values of the proposed method are always greater than those of the existing approaches. The obtained results validate the effectiveness and usefulness of our proposed method over the existing feature extraction methods. The proposed IFLBP approach can be applied for feature extraction in the various fields of image processing and biomedical image processing, i.e. image forgery detection, image segmentation, image de-noising problems, pattern classification and recognition, etc.

Acknowledgments

The authors are sincerely thankful to the editor and anonymous reviewers for their critical comments and suggestions to improve the quality of this work.

Bibliography

[1] T. Ahonen and M. Pietikäinen, Soft histograms for local binary patterns, in: Proceedings of the Finnish Signal Processing Symposium, FINSIG, vol. 5, p. 1, 2007.Search in Google Scholar

[2] M. D. Ansari and S. P. Ghrera, Intuitionistic fuzzy local binary pattern for features extraction, Int. J. Inf. Commun. Technol., in press.10.1504/IJICT.2018.090435Search in Google Scholar

[3] M. D. Ansari, S. P. Ghrera and V. Tyagi, Pixel-based image forgery detection: a review, IETE J. Educ. 55.1 (2014), 40–46.10.1080/09747338.2014.921415Search in Google Scholar

[4] M. D. Ansari, S. P. Ghrera and M. Wajid, An approach for identification of copy-move image forgery based on projection profiling, Pertan. J. Sci. Technol., in press.Search in Google Scholar

[5] K. T. Atanassov, Intuitionistic fuzzy sets, Fuzzy Sets Syst. 20 (1986), 87–96.10.1016/S0165-0114(86)80034-3Search in Google Scholar

[6] K. T. Atanassov and G. Gargov, Interval-valued intuitionistic fuzzy sets, Fuzzy Sets Syst. 31 (1989), 343–349.10.1016/0165-0114(89)90205-4Search in Google Scholar

[7] A. Barcelo, E. Montseny and P. Sobrevilla, Fuzzy texture unit and fuzzy texture spectrum for texture characterization, Fuzzy Sets Syst. 158 (2007), 239–252.10.1016/j.fss.2006.10.008Search in Google Scholar

[8] G. Castellano, L. Bonilha, L. M. Li and F. Cendes, Texture analysis of medical images, Clin. Radiol. 59 (2004), 1061–1069.10.1016/j.crad.2004.07.008Search in Google Scholar PubMed

[9] C. Chan, J. Kittler and K. Messer, Multi-scale local binary pattern histograms for face recognition, in: ICB 2007, Seoul, Korea, LNCS 4642, pp. 809–818, Springer, 2007.10.1007/978-3-540-74549-5_85Search in Google Scholar

[10] T. W. S. Chow and M. K. M. Rahman, A new image classification technique using tree-structured regional features, Neurocomputing 70 (2007), 1040–1050.10.1016/j.neucom.2006.01.033Search in Google Scholar

[11] A. Destrero, C. De Mol, F. Odone and A. Verri, A regularized framework for feature selection in face detection and authentication, Int. J Comput. Vis. 83 (2009), 164–177.10.1007/s11263-008-0180-2Search in Google Scholar

[12] J. Fehr, Rotational invariant uniform local binary patterns for full 3D volume texture analysis, in: FINSIG 2007, Oulu, Finland, 2007.10.1109/ICPR.2008.4761098Search in Google Scholar

[13] R. Garcia, X. Cufi and J. Batlle, Detection of matchings in a sequence of underwater images through texture analysis, in: Proc. IEEE International Conference on Image Processing, vol. 1, pp. 361–364, 2001.10.1109/ICIP.2001.959028Search in Google Scholar

[14] H. Grabner, T. T. Nguyen, B. Gruber and H. Bischof, On-line boosting-based car detection from aerial images, ISPRS J. Photogramm. Remote Sens. 63 (2008), 382–396.10.1016/j.isprsjprs.2007.10.005Search in Google Scholar

[15] D. Grangier and S. Bengio, A discriminative kernel-based approach to rank images from text queries, IEEE Trans. Pattern Anal. Mach. Intell. 30 (2008), 1371–1384.10.1109/TPAMI.2007.70791Search in Google Scholar PubMed

[16] H. Hadizadeh and S. Baradaran Shokouhi, Random texture defect detection using 1-D hidden Markov models based on local binary patterns, IEICE Trans. Inform. Syst. 91 (2008), 1937–1945.10.1093/ietisy/e91-d.7.1937Search in Google Scholar

[17] A. Hafiane, G. Seetharaman and B. Zavidovique, Median binary pattern for textures classification, ICIAR 4633 (2007), 387–398.10.1007/978-3-540-74260-9_35Search in Google Scholar

[18] A. Hafiane, G. Seetharaman, K. Palaniappan and B. Zavidovique, Rotationally invariant hashing of median binary patterns for texture classification, Proc. Image Anal. Recognit. LNCS (2008), 619–629.10.1007/978-3-540-69812-8_61Search in Google Scholar

[19] M. Heikkila and M. Pietikainen, A texture-based method for modeling the background and detecting moving objects, IEEE Trans. Pattern Anal. Mach. Intell. 28 (2006), 657–662.10.1109/TPAMI.2006.68Search in Google Scholar PubMed

[20] D. K. Iakovidis, D. Maroulis and S. Karkanis, An intelligent system for automatic detection of gastrointestinal adenomas in video endoscopy, Comput. Biol. Med. 36 (2006), 1084–1103.10.1016/j.compbiomed.2005.09.008Search in Google Scholar PubMed

[21] D. K. Iakovidis, E. G. Keramidas and D. Maroulis, Fuzzy local binary patterns for ultrasound texture characterization, in: Image Analysis and Recognition, pp. 750–759, Springer, Berlin, 2008.10.1007/978-3-540-69812-8_74Search in Google Scholar

[22] J. Iivarinen, Surface defect detection with histogram-based texture features, in: Intelligent Robots and Computer Vision XIX: Algorithms, Techniques, and Active Vision, vol. 4197, pp. 140−145, 2000.10.1117/12.403757Search in Google Scholar

[23] J. Jiang, A. Armstrong and G. C. Feng, Web-based image indexing and retrieval in JPEG compressed domain, Multimed. Syst. 9 (2004), 424–432.10.1007/s00530-003-0115-2Search in Google Scholar

[24] E. G. Keramidas, Ultrasound image processing and analysis framework, MSc thesis, University of Athens, Greece, 2007.Search in Google Scholar

[25] E. G. Keramidas, D. K. Iakovidis and D. Maroulis, Noise-robust statistical feature distributions for texture analysis, in: Signal Processing Conference, 2008 16th European, pp. 1–5, IEEE, 2008.Search in Google Scholar

[26] E. G. Keramidas, D. K. Iakovidis, D. Maroulis and N. Dimitropoulos, Thyroid texture representation via noise resistant image features, IEEE Int. Symp. Comput. Based Med. Syst. (2008), 560–565.10.1109/CBMS.2008.108Search in Google Scholar

[27] E. G. Keramidas, D. K. Iakovidis and D. Maroulis, Fuzzy binary patterns for uncertainty-aware texture representation, Electron. Lett. Comput. Vis. Image Anal. 10 (2011), 63–78.10.5565/rev/elcvia.408Search in Google Scholar

[28] Y. Li and J. X. Peng, Remote sensing texture analysis using multi-parameter and multi-scale features, Photogramm. Eng. Remote Sens. 69 (2003), 351–356.10.14358/PERS.69.4.351Search in Google Scholar

[29] C. J. Liao and S. Y. Chen, Complementary retrieval for distorted images, Pattern Recognit. 35 (2002), 1705–1722.10.1016/S0031-3203(01)00164-9Search in Google Scholar

[30] L. Ma and R. C. Staunton, Optimum Gabor filter design and local binary patterns for texture segmentation, Pattern Recognit. Lett. 29 (2008), 664–672.10.1016/j.patrec.2007.12.001Search in Google Scholar

[31] A. R. Mishra, D. Jain and D. S. Hooda, On logarithmic fuzzy measures of information and discrimination, J. Inform. Optim. Sci. 37 (2016), 213–231.10.1080/02522667.2015.1103041Search in Google Scholar

[32] A. R. Mishra, Intuitionistic fuzzy information with application in rating of township development, Iran. J. Fuzzy Syst. 13 (2016), 49–70.Search in Google Scholar

[33] L. Nanni and A. Lumini, A reliable method for cell phenotype image classification, Artif. Intell. Med. 43 (2008), 87–97.10.1016/j.artmed.2008.03.005Search in Google Scholar

[34] T. Ojala, M. Pietikinen and D. Harwood, A comparative study of texture measures with classification based on featured distribution, Pattern Recognit. 29 (1996), 51–59.10.1016/0031-3203(95)00067-4Search in Google Scholar

[35] N. R. Pal and S. K. Pal, Object-background segmentation using new definitions of entropy, IEE Proc. E Comput. Digit. Techn. 136 (1989), 284–295.10.1049/ip-e.1989.0039Search in Google Scholar

[36] M. Petrou and P. G. Sevilla, Image Processing: Dealing with Texture, Wiley, New York, 2006.10.1002/047003534XSearch in Google Scholar

[37] N. Petrović, L. Jovanov, A. Pižurica and W. Philips, Object tracking using naive Bayesian classifiers, in: International Conference on Advanced Concepts for Intelligent Vision Systems, pp. 775–784, Springer, Berlin Heidelberg, 2008.10.1007/978-3-540-88458-3_70Search in Google Scholar

[38] G. Pok, K. H. Ryu and J. Lyu, Rotation and gray-scale invariant classification of textures improved by spatial distribution of features, in: International Conference on Database and Expert Systems Applications, pp. 250–259, Springer, Berlin Heidelberg, 2005.10.1007/11546924_25Search in Google Scholar

[39] O. Sertel, J. Kong, H. Shimada, U. V. Catalyurek, J. H. Saltz and M. N. Gurcan, Computer-aided prognosis of neuroblastoma on whole-slide images: classification of stromal development, Pattern Recognit. 42 (2009), 1093–1103.10.1117/12.770666Search in Google Scholar

[40] C. Shan, S. Gong and P. W. McOwan, Facial expression recognition based on local binary patterns: a comprehensive study, Image Vis. Comput. 27 (2009), 803–816.10.1016/j.imavis.2008.08.005Search in Google Scholar

[41] C. E. Shannon, A mathematical theory of communication, Bell Syst. Techn. J. 27 (1948), 623–656.10.1002/j.1538-7305.1948.tb00917.xSearch in Google Scholar

[42] O. Silven, M. Niskanen and H. Kauppinen, Wood inspection with non-supervised clustering, Mach. Vision Appl. 13 (2003), 275–285.10.1007/s00138-002-0084-zSearch in Google Scholar

[43] Z. Stan, C. RuFeng, L. ShengCai and Z. Lun, Illumination invariant face recognition using near-infrared images, IEEE Trans. Pattern Anal. Mach. Intell. 29 (2007), 627–639.10.1109/TPAMI.2007.1014Search in Google Scholar

[44] F. Tajeripour, E. Kabir and A. Sheikhi, Fabric defect detection using modified local binary patterns, EURASIP J. Adv. Signal Process. 2008 (2008), 783–898.10.1109/ICCIMA.2007.50Search in Google Scholar

[45] D. P. Tian, A review on image feature extraction and representation techniques, Int. J. Multimed. Ubiq. Eng. 8.4 (2013), 385–396.Search in Google Scholar

[46] O. Tsymbal, V. Lukin, N. Ponomarenko, A. Zelensky, K. Egiazarian and J. Astola, Three-state locally adaptive texture preserving filter for radar and optical image processing, EURASIP J. Adv. Signal Process. 8 (2005) 1185–1204.10.1155/ASP.2005.1185Search in Google Scholar

[47] T. Wagner, Texture analysis, in: Handbook of Computer Vision and Application, Academic Press, Orlando, FL, 1999.Search in Google Scholar

[48] Z. Wang and J. H. Yong, Texture analysis and classification with linear regression model based on wavelet transform, IEEE Trans. Image Process. 17 (2008), 1421–1430.10.1109/TIP.2008.926150Search in Google Scholar

[49] W. Wu, J. Li, T. Wang and Y. Zhang, Markov chain local binary pattern and its application to video concept detection, in: 15th IEEE International Conference on Image Processing, pp. 2524–2527, IEEE, 2008.Search in Google Scholar

[50] C. H. Yao and S. Y. Chen, Retrieval of translated, rotated and scaled color textures, Pattern Recognit. 36 (2003), 913–929.10.1016/S0031-3203(02)00124-3Search in Google Scholar

[51] L. Zadeh, Fuzzy sets, J. Inform. Control 8 (1965), 338−353.10.21236/AD0608981Search in Google Scholar

[52] X. Zhang, Y. Gao and M. Leung, Recognizing rotated faces from frontal and side views: an approach toward effective use of mugshot databases, IEEE Trans. Inform. Forens. Secur. 3 (2008), 684–697.10.1109/TIFS.2008.2004286Search in Google Scholar
Received: 2016-08-24
Published Online: 2016-12-08

©2020 Walter de Gruyter GmbH, Berlin/Boston

This work is licensed under the Creative Commons Attribution 4.0 Public License.

Articles in the same Issue

  1. An Optimized K-Harmonic Means Algorithm Combined with Modified Particle Swarm Optimization and Cuckoo Search Algorithm
  2. Texture Feature Extraction Using Intuitionistic Fuzzy Local Binary Pattern
  3. Leaf Disease Segmentation From Agricultural Images via Hybridization of Active Contour Model and OFA
  4. Deadline Constrained Task Scheduling Method Using a Combination of Center-Based Genetic Algorithm and Group Search Optimization
  5. Efficient Classification of DDoS Attacks Using an Ensemble Feature Selection Algorithm
  6. Distributed Multi-agent Bidding-Based Approach for the Collaborative Mapping of Unknown Indoor Environments by a Homogeneous Mobile Robot Team
  7. An Efficient Technique for Three-Dimensional Image Visualization Through Two-Dimensional Images for Medical Data
  8. Combined Multi-Agent Method to Control Inter-Department Common Events Collision for University Courses Timetabling
  9. An Improved Particle Swarm Optimization Algorithm for Global Multidimensional Optimization
  10. A Kernel Probabilistic Model for Semi-supervised Co-clustering Ensemble
  11. Pythagorean Hesitant Fuzzy Information Aggregation and Their Application to Multi-Attribute Group Decision-Making Problems
  12. Using an Efficient Optimal Classifier for Soil Classification in Spatial Data Mining Over Big Data
  13. A Bayesian Multiresolution Approach for Noise Removal in Medical Magnetic Resonance Images
  14. Gbest-Guided Artificial Bee Colony Optimization Algorithm-Based Optimal Incorporation of Shunt Capacitors in Distribution Networks under Load Growth
  15. Graded Soft Expert Set as a Generalization of Hesitant Fuzzy Set
  16. Universal Liver Extraction Algorithm: An Improved Chan–Vese Model
  17. Software Effort Estimation Using Modified Fuzzy C Means Clustering and Hybrid ABC-MCS Optimization in Neural Network
  18. Handwritten Indic Script Recognition Based on the Dempster–Shafer Theory of Evidence
  19. An Integrated Intuitionistic Fuzzy AHP and TOPSIS Approach to Evaluation of Outsource Manufacturers
  20. Automatically Assess Day Similarity Using Visual Lifelogs
  21. A Novel Bio-Inspired Algorithm Based on Social Spiders for Improving Performance and Efficiency of Data Clustering
  22. Discriminative Training Using Noise Robust Integrated Features and Refined HMM Modeling
  23. Self-Adaptive Mussels Wandering Optimization Algorithm with Application for Artificial Neural Network Training
  24. A Framework for Image Alignment of TerraSAR-X Images Using Fractional Derivatives and View Synthesis Approach
  25. Intelligent Systems for Structural Damage Assessment
  26. Some Interval-Valued Pythagorean Fuzzy Einstein Weighted Averaging Aggregation Operators and Their Application to Group Decision Making
  27. Fuzzy Adaptive Genetic Algorithm for Improving the Solution of Industrial Optimization Problems
  28. Approach to Multiple Attribute Group Decision Making Based on Hesitant Fuzzy Linguistic Aggregation Operators
  29. Cubic Ordered Weighted Distance Operator and Application in Group Decision-Making
  30. Fault Signal Recognition in Power Distribution System using Deep Belief Network
  31. Selector: PSO as Model Selector for Dual-Stage Diabetes Network
  32. Oppositional Gravitational Search Algorithm and Artificial Neural Network-based Classification of Kidney Images
  33. Improving Image Search through MKFCM Clustering Strategy-Based Re-ranking Measure
  34. Sparse Decomposition Technique for Segmentation and Compression of Compound Images
  35. Automatic Genetic Fuzzy c-Means
  36. Harmony Search Algorithm for Patient Admission Scheduling Problem
  37. Speech Signal Compression Algorithm Based on the JPEG Technique
  38. i-Vector-Based Speaker Verification on Limited Data Using Fusion Techniques
  39. Prediction of User Future Request Utilizing the Combination of Both ANN and FCM in Web Page Recommendation
  40. Presentation of ACT/R-RBF Hybrid Architecture to Develop Decision Making in Continuous and Non-continuous Data
  41. An Overview of Segmentation Algorithms for the Analysis of Anomalies on Medical Images
  42. Blind Restoration Algorithm Using Residual Measures for Motion-Blurred Noisy Images
  43. Extreme Learning Machine for Credit Risk Analysis
  44. A Genetic Algorithm Approach for Group Recommender System Based on Partial Rankings
  45. Improvements in Spoken Query System to Access the Agricultural Commodity Prices and Weather Information in Kannada Language/Dialects
  46. A One-Pass Approach for Slope and Slant Estimation of Tri-Script Handwritten Words
  47. Secure Communication through MultiAgent System-Based Diabetes Diagnosing and Classification
  48. Development of a Two-Stage Segmentation-Based Word Searching Method for Handwritten Document Images
  49. Pythagorean Fuzzy Einstein Hybrid Averaging Aggregation Operator and its Application to Multiple-Attribute Group Decision Making
  50. Ensembles of Text and Time-Series Models for Automatic Generation of Financial Trading Signals from Social Media Content
  51. A Flame Detection Method Based on Novel Gradient Features
  52. Modeling and Optimization of a Liquid Flow Process using an Artificial Neural Network-Based Flower Pollination Algorithm
  53. Spectral Graph-based Features for Recognition of Handwritten Characters: A Case Study on Handwritten Devanagari Numerals
  54. A Grey Wolf Optimizer for Text Document Clustering
  55. Classification of Masses in Digital Mammograms Using the Genetic Ensemble Method
  56. A Hybrid Grey Wolf Optimiser Algorithm for Solving Time Series Classification Problems
  57. Gray Method for Multiple Attribute Decision Making with Incomplete Weight Information under the Pythagorean Fuzzy Setting
  58. Multi-Agent System Based on the Extreme Learning Machine and Fuzzy Control for Intelligent Energy Management in Microgrid
  59. Deep CNN Combined With Relevance Feedback for Trademark Image Retrieval
  60. Cognitively Motivated Query Abstraction Model Based on Associative Root-Pattern Networks
  61. Improved Adaptive Neuro-Fuzzy Inference System Using Gray Wolf Optimization: A Case Study in Predicting Biochar Yield
  62. Predict Forex Trend via Convolutional Neural Networks
  63. Optimizing Integrated Features for Hindi Automatic Speech Recognition System
  64. A Novel Weakest t-norm based Fuzzy Fault Tree Analysis Through Qualitative Data Processing and Its Application in System Reliability Evaluation
  65. FCNB: Fuzzy Correlative Naive Bayes Classifier with MapReduce Framework for Big Data Classification
  66. A Modified Jaya Algorithm for Mixed-Variable Optimization Problems
  67. An Improved Robust Fuzzy Algorithm for Unsupervised Learning
  68. Hybridizing the Cuckoo Search Algorithm with Different Mutation Operators for Numerical Optimization Problems
  69. An Efficient Lossless ROI Image Compression Using Wavelet-Based Modified Region Growing Algorithm
  70. Predicting Automatic Trigger Speed for Vehicle-Activated Signs
  71. Group Recommender Systems – An Evolutionary Approach Based on Multi-expert System for Consensus
  72. Enriching Documents by Linking Salient Entities and Lexical-Semantic Expansion
  73. A New Feature Selection Method for Sentiment Analysis in Short Text
  74. Optimizing Software Modularity with Minimum Possible Variations
  75. Optimizing the Self-Organizing Team Size Using a Genetic Algorithm in Agile Practices
  76. Aspect-Oriented Sentiment Analysis: A Topic Modeling-Powered Approach
  77. Feature Pair Index Graph for Clustering
  78. Tangramob: An Agent-Based Simulation Framework for Validating Urban Smart Mobility Solutions
  79. A New Algorithm Based on Magic Square and a Novel Chaotic System for Image Encryption
  80. Video Steganography Using Knight Tour Algorithm and LSB Method for Encrypted Data
  81. Clay-Based Brick Porosity Estimation Using Image Processing Techniques
  82. AGCS Technique to Improve the Performance of Neural Networks
  83. A Color Image Encryption Technique Based on Bit-Level Permutation and Alternate Logistic Maps
  84. A Hybrid of Deep CNN and Bidirectional LSTM for Automatic Speech Recognition
  85. Database Creation and Dialect-Wise Comparative Analysis of Prosodic Features for Punjabi Language
  86. Trapezoidal Linguistic Cubic Fuzzy TOPSIS Method and Application in a Group Decision Making Program
  87. Histopathological Image Segmentation Using Modified Kernel-Based Fuzzy C-Means and Edge Bridge and Fill Technique
  88. Proximal Support Vector Machine-Based Hybrid Approach for Edge Detection in Noisy Images
  89. Early Detection of Parkinson’s Disease by Using SPECT Imaging and Biomarkers
  90. Image Compression Based on Block SVD Power Method
  91. Noise Reduction Using Modified Wiener Filter in Digital Hearing Aid for Speech Signal Enhancement
  92. Secure Fingerprint Authentication Using Deep Learning and Minutiae Verification
  93. The Use of Natural Language Processing Approach for Converting Pseudo Code to C# Code
  94. Non-word Attributes’ Efficiency in Text Mining Authorship Prediction
  95. Design and Evaluation of Outlier Detection Based on Semantic Condensed Nearest Neighbor
  96. An Efficient Quality Inspection of Food Products Using Neural Network Classification
  97. Opposition Intensity-Based Cuckoo Search Algorithm for Data Privacy Preservation
  98. M-HMOGA: A New Multi-Objective Feature Selection Algorithm for Handwritten Numeral Classification
  99. Analogy-Based Approaches to Improve Software Project Effort Estimation Accuracy
  100. Linear Regression Supporting Vector Machine and Hybrid LOG Filter-Based Image Restoration
  101. Fractional Fuzzy Clustering and Particle Whale Optimization-Based MapReduce Framework for Big Data Clustering
  102. Implementation of Improved Ship-Iceberg Classifier Using Deep Learning
  103. Hybrid Approach for Face Recognition from a Single Sample per Person by Combining VLC and GOM
  104. Polarity Analysis of Customer Reviews Based on Part-of-Speech Subcategory
  105. A 4D Trajectory Prediction Model Based on the BP Neural Network
  106. A Blind Medical Image Watermarking for Secure E-Healthcare Application Using Crypto-Watermarking System
  107. Discriminating Healthy Wheat Grains from Grains Infected with Fusarium graminearum Using Texture Characteristics of Image-Processing Technique, Discriminant Analysis, and Support Vector Machine Methods
  108. License Plate Recognition in Urban Road Based on Vehicle Tracking and Result Integration
  109. Binary Genetic Swarm Optimization: A Combination of GA and PSO for Feature Selection
  110. Enhanced Twitter Sentiment Analysis Using Hybrid Approach and by Accounting Local Contextual Semantic
  111. Cloud Security: LKM and Optimal Fuzzy System for Intrusion Detection in Cloud Environment
  112. Power Average Operators of Trapezoidal Cubic Fuzzy Numbers and Application to Multi-attribute Group Decision Making
https://doi.org/10.1515/jisys-2016-0155
Keywords for this article
Fuzzy local binary pattern; intuitionistic fuzzy sets; intuitionistic fuzzy local binary pattern; entropy
Creative Commons
BY 4.0

Articles in the same Issue

  1. An Optimized K-Harmonic Means Algorithm Combined with Modified Particle Swarm Optimization and Cuckoo Search Algorithm
  2. Texture Feature Extraction Using Intuitionistic Fuzzy Local Binary Pattern
  3. Leaf Disease Segmentation From Agricultural Images via Hybridization of Active Contour Model and OFA
  4. Deadline Constrained Task Scheduling Method Using a Combination of Center-Based Genetic Algorithm and Group Search Optimization
  5. Efficient Classification of DDoS Attacks Using an Ensemble Feature Selection Algorithm
  6. Distributed Multi-agent Bidding-Based Approach for the Collaborative Mapping of Unknown Indoor Environments by a Homogeneous Mobile Robot Team
  7. An Efficient Technique for Three-Dimensional Image Visualization Through Two-Dimensional Images for Medical Data
  8. Combined Multi-Agent Method to Control Inter-Department Common Events Collision for University Courses Timetabling
  9. An Improved Particle Swarm Optimization Algorithm for Global Multidimensional Optimization
  10. A Kernel Probabilistic Model for Semi-supervised Co-clustering Ensemble
  11. Pythagorean Hesitant Fuzzy Information Aggregation and Their Application to Multi-Attribute Group Decision-Making Problems
  12. Using an Efficient Optimal Classifier for Soil Classification in Spatial Data Mining Over Big Data
  13. A Bayesian Multiresolution Approach for Noise Removal in Medical Magnetic Resonance Images
  14. Gbest-Guided Artificial Bee Colony Optimization Algorithm-Based Optimal Incorporation of Shunt Capacitors in Distribution Networks under Load Growth
  15. Graded Soft Expert Set as a Generalization of Hesitant Fuzzy Set
  16. Universal Liver Extraction Algorithm: An Improved Chan–Vese Model
  17. Software Effort Estimation Using Modified Fuzzy C Means Clustering and Hybrid ABC-MCS Optimization in Neural Network
  18. Handwritten Indic Script Recognition Based on the Dempster–Shafer Theory of Evidence
  19. An Integrated Intuitionistic Fuzzy AHP and TOPSIS Approach to Evaluation of Outsource Manufacturers
  20. Automatically Assess Day Similarity Using Visual Lifelogs
  21. A Novel Bio-Inspired Algorithm Based on Social Spiders for Improving Performance and Efficiency of Data Clustering
  22. Discriminative Training Using Noise Robust Integrated Features and Refined HMM Modeling
  23. Self-Adaptive Mussels Wandering Optimization Algorithm with Application for Artificial Neural Network Training
  24. A Framework for Image Alignment of TerraSAR-X Images Using Fractional Derivatives and View Synthesis Approach
  25. Intelligent Systems for Structural Damage Assessment
  26. Some Interval-Valued Pythagorean Fuzzy Einstein Weighted Averaging Aggregation Operators and Their Application to Group Decision Making
  27. Fuzzy Adaptive Genetic Algorithm for Improving the Solution of Industrial Optimization Problems
  28. Approach to Multiple Attribute Group Decision Making Based on Hesitant Fuzzy Linguistic Aggregation Operators
  29. Cubic Ordered Weighted Distance Operator and Application in Group Decision-Making
  30. Fault Signal Recognition in Power Distribution System using Deep Belief Network
  31. Selector: PSO as Model Selector for Dual-Stage Diabetes Network
  32. Oppositional Gravitational Search Algorithm and Artificial Neural Network-based Classification of Kidney Images
  33. Improving Image Search through MKFCM Clustering Strategy-Based Re-ranking Measure
  34. Sparse Decomposition Technique for Segmentation and Compression of Compound Images
  35. Automatic Genetic Fuzzy c-Means
  36. Harmony Search Algorithm for Patient Admission Scheduling Problem
  37. Speech Signal Compression Algorithm Based on the JPEG Technique
  38. i-Vector-Based Speaker Verification on Limited Data Using Fusion Techniques
  39. Prediction of User Future Request Utilizing the Combination of Both ANN and FCM in Web Page Recommendation
  40. Presentation of ACT/R-RBF Hybrid Architecture to Develop Decision Making in Continuous and Non-continuous Data
  41. An Overview of Segmentation Algorithms for the Analysis of Anomalies on Medical Images
  42. Blind Restoration Algorithm Using Residual Measures for Motion-Blurred Noisy Images
  43. Extreme Learning Machine for Credit Risk Analysis
  44. A Genetic Algorithm Approach for Group Recommender System Based on Partial Rankings
  45. Improvements in Spoken Query System to Access the Agricultural Commodity Prices and Weather Information in Kannada Language/Dialects
  46. A One-Pass Approach for Slope and Slant Estimation of Tri-Script Handwritten Words
  47. Secure Communication through MultiAgent System-Based Diabetes Diagnosing and Classification
  48. Development of a Two-Stage Segmentation-Based Word Searching Method for Handwritten Document Images
  49. Pythagorean Fuzzy Einstein Hybrid Averaging Aggregation Operator and its Application to Multiple-Attribute Group Decision Making
  50. Ensembles of Text and Time-Series Models for Automatic Generation of Financial Trading Signals from Social Media Content
  51. A Flame Detection Method Based on Novel Gradient Features
  52. Modeling and Optimization of a Liquid Flow Process using an Artificial Neural Network-Based Flower Pollination Algorithm
  53. Spectral Graph-based Features for Recognition of Handwritten Characters: A Case Study on Handwritten Devanagari Numerals
  54. A Grey Wolf Optimizer for Text Document Clustering
  55. Classification of Masses in Digital Mammograms Using the Genetic Ensemble Method
  56. A Hybrid Grey Wolf Optimiser Algorithm for Solving Time Series Classification Problems
  57. Gray Method for Multiple Attribute Decision Making with Incomplete Weight Information under the Pythagorean Fuzzy Setting
  58. Multi-Agent System Based on the Extreme Learning Machine and Fuzzy Control for Intelligent Energy Management in Microgrid
  59. Deep CNN Combined With Relevance Feedback for Trademark Image Retrieval
  60. Cognitively Motivated Query Abstraction Model Based on Associative Root-Pattern Networks
  61. Improved Adaptive Neuro-Fuzzy Inference System Using Gray Wolf Optimization: A Case Study in Predicting Biochar Yield
  62. Predict Forex Trend via Convolutional Neural Networks
  63. Optimizing Integrated Features for Hindi Automatic Speech Recognition System
  64. A Novel Weakest t-norm based Fuzzy Fault Tree Analysis Through Qualitative Data Processing and Its Application in System Reliability Evaluation
  65. FCNB: Fuzzy Correlative Naive Bayes Classifier with MapReduce Framework for Big Data Classification
  66. A Modified Jaya Algorithm for Mixed-Variable Optimization Problems
  67. An Improved Robust Fuzzy Algorithm for Unsupervised Learning
  68. Hybridizing the Cuckoo Search Algorithm with Different Mutation Operators for Numerical Optimization Problems
  69. An Efficient Lossless ROI Image Compression Using Wavelet-Based Modified Region Growing Algorithm
  70. Predicting Automatic Trigger Speed for Vehicle-Activated Signs
  71. Group Recommender Systems – An Evolutionary Approach Based on Multi-expert System for Consensus
  72. Enriching Documents by Linking Salient Entities and Lexical-Semantic Expansion
  73. A New Feature Selection Method for Sentiment Analysis in Short Text
  74. Optimizing Software Modularity with Minimum Possible Variations
  75. Optimizing the Self-Organizing Team Size Using a Genetic Algorithm in Agile Practices
  76. Aspect-Oriented Sentiment Analysis: A Topic Modeling-Powered Approach
  77. Feature Pair Index Graph for Clustering
  78. Tangramob: An Agent-Based Simulation Framework for Validating Urban Smart Mobility Solutions
  79. A New Algorithm Based on Magic Square and a Novel Chaotic System for Image Encryption
  80. Video Steganography Using Knight Tour Algorithm and LSB Method for Encrypted Data
  81. Clay-Based Brick Porosity Estimation Using Image Processing Techniques
  82. AGCS Technique to Improve the Performance of Neural Networks
  83. A Color Image Encryption Technique Based on Bit-Level Permutation and Alternate Logistic Maps
  84. A Hybrid of Deep CNN and Bidirectional LSTM for Automatic Speech Recognition
  85. Database Creation and Dialect-Wise Comparative Analysis of Prosodic Features for Punjabi Language
  86. Trapezoidal Linguistic Cubic Fuzzy TOPSIS Method and Application in a Group Decision Making Program
  87. Histopathological Image Segmentation Using Modified Kernel-Based Fuzzy C-Means and Edge Bridge and Fill Technique
  88. Proximal Support Vector Machine-Based Hybrid Approach for Edge Detection in Noisy Images
  89. Early Detection of Parkinson’s Disease by Using SPECT Imaging and Biomarkers
  90. Image Compression Based on Block SVD Power Method
  91. Noise Reduction Using Modified Wiener Filter in Digital Hearing Aid for Speech Signal Enhancement
  92. Secure Fingerprint Authentication Using Deep Learning and Minutiae Verification
  93. The Use of Natural Language Processing Approach for Converting Pseudo Code to C# Code
  94. Non-word Attributes’ Efficiency in Text Mining Authorship Prediction
  95. Design and Evaluation of Outlier Detection Based on Semantic Condensed Nearest Neighbor
  96. An Efficient Quality Inspection of Food Products Using Neural Network Classification
  97. Opposition Intensity-Based Cuckoo Search Algorithm for Data Privacy Preservation
  98. M-HMOGA: A New Multi-Objective Feature Selection Algorithm for Handwritten Numeral Classification
  99. Analogy-Based Approaches to Improve Software Project Effort Estimation Accuracy
  100. Linear Regression Supporting Vector Machine and Hybrid LOG Filter-Based Image Restoration
  101. Fractional Fuzzy Clustering and Particle Whale Optimization-Based MapReduce Framework for Big Data Clustering
  102. Implementation of Improved Ship-Iceberg Classifier Using Deep Learning
  103. Hybrid Approach for Face Recognition from a Single Sample per Person by Combining VLC and GOM
  104. Polarity Analysis of Customer Reviews Based on Part-of-Speech Subcategory
  105. A 4D Trajectory Prediction Model Based on the BP Neural Network
  106. A Blind Medical Image Watermarking for Secure E-Healthcare Application Using Crypto-Watermarking System
  107. Discriminating Healthy Wheat Grains from Grains Infected with Fusarium graminearum Using Texture Characteristics of Image-Processing Technique, Discriminant Analysis, and Support Vector Machine Methods
  108. License Plate Recognition in Urban Road Based on Vehicle Tracking and Result Integration
  109. Binary Genetic Swarm Optimization: A Combination of GA and PSO for Feature Selection
  110. Enhanced Twitter Sentiment Analysis Using Hybrid Approach and by Accounting Local Contextual Semantic
  111. Cloud Security: LKM and Optimal Fuzzy System for Intrusion Detection in Cloud Environment
  112. Power Average Operators of Trapezoidal Cubic Fuzzy Numbers and Application to Multi-attribute Group Decision Making
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 15.9.2025 from https://www.degruyterbrill.com/document/doi/10.1515/jisys-2016-0155/html
Scroll to top button