Abstract
This paper presents an efficient thermo-elastoplastic method for the prediction of welding-induced distortions in a large panel structure. It is based on a shell/3D modeling technique which was proposed and experimentally validated in the authors’ previous study. Two numerical examples are analyzed to evaluate the accuracy and efficiency of the present method. In the first example, the recommendations for the estimation of the minimum 3D zone size in the shell/3D model reported in the authors’ previous work are verified, in comparison with the full 3D model, on a T-joint model consisting of plates with different thicknesses. It is shown that the shell/3D modeling technique provides a significant reduction in the computational time needed for the simulation of the welding process and thus enables efficient thermo-elastoplastic analyses on large structures. In the second example, the proposed model is validated on a large panel structure by corresponding the experimental data and inherent strain solutions from the literature.
1 Introduction
Welding is one of the main joining technologies for assembling various parts in many industrial fields such as ship-building, bridge-building, petrol industry, automobile manufactory, etc., due to its low price, reliability and simplicity of performance. The welding process is characterized by a large local heat input that leads to the melting of the filler material and its adjacent area. The fast cooling after the welding results in permanent plastic deformations that exist in the fusion zone vicinity and cause residual stresses and dimensional imperfections in the welded structure. Residual stresses combined with workload can significantly contribute to the reduction of structure life-time and accelerate the formation of fatigue cracks, brittle fractures or stress corrosion cracking [1, 2]. Moreover, the dimensional inaccuracies can cause problems during the assembly of the structure. The elimination of residual stresses and dimensional imperfections using the post-weld thermal [3, 4] or mechanical [5, 6] procedures requires additional financial costs, increases production time and is often unsuitable because of the weldedstructure size and the assembly place. In order to reduce the above-mentioned post-welding consequences, it is necessary to know the magnitude of residual stresses and deformations as early as the structure design phase for which numerical methods have successfully been used in recent decades [7, 8, 9, 10].
For the accurate prediction of residual stresses and deformations, the numerical simulations of the welding process should be carried out with the use of a nonlinear thermo-elastoplastic (TEP) method within the solid three-dimensional (3D) finite elements (FEs). Because of its highly nonlinear and transient behavior, the thermo-mechanical welding analysis requires considerable computer power and disk storage, especially in the case of models with a large number of finite elements. It makes such simulations impractical or even impossible. Therefore, the TEP method employing a full 3D FE mesh is limited to small or medium structures. There are only a limited number of papers in the literature that deals with the TEP method for cases of large-scale structural components. Chen et al. [11] investigated the residual stresses and post-weld deformations on a large panel structure using a mixture of shell elements with section integration and solid three-dimensional finite elements to speed-up the calculation process. Here, the whole model was essentially created with shell elements while only the weld bead was created with solid ones. Applying the same modeling method Chen and Li [12] investigated the influence of the mechanical restraints on the residual stresses and deflections of the large panel structures. Huang et al. [13] presented a transient thermo-mechanical analysis for large welded structures based on a dual mesh scheme that significantly cuts down the computation time. Li et al. [14] simulated the welding of a large panel and proposed the use of interface elements between the skin plate and stiffener to improve computational accuracy. Although many accurate and reliable results were obtained, which can be generally found in the literature, the high computational costs of the TEP methods hamper their wider application.
Nowadays, the most frequently used method in engineering practices for calculating residual strains and deformations in large welded structures is the inherent strain method (ISM). In this method, the residual plastic strains, also named inherent strains, are considered to be a source of residual stress and welding distortion. The ISM neglects the whole welding process, and estimates the welding induced deformations via an elastic FE analysis using the inherent strains as initial strains. Thus, there is no need for temperature dependent material properties and elastoplastic behavior of materials. However, the fundamental problem of the ISM is how to identify the inherent strain region and estimate its values. Two methods are usually used to predict the inherent deformations: experimental and TEP. In doing so, Deng et al. [15] have employed the ISM method to investigate the influence of the initial gap between the plates on the plate deflections on a large panel structure sample. Wang et al. [16] applied the ISM method to predict the out-the-plane welding deformations in a large welded panel of a car carrier ship. Here, the ISM method was verified with a small scale TEP model. Similarly, Murakawa et al. [17] employed an iterative substructure method to predict the numerical residual stresses and deflections in large panel structures. Furthermore, Ma et al. [18] investigated out-of-plane deformations on both parallel and cross stiffened welded panels using the ISM method. In general, there is a lot of valuable research based on the elastic ISM method primarily due to its short simulation time. However, it is necessary to know the exact amount of inherent strains in advance as it does not describe the whole welding process and is therefore less accurate than the TEP method. As proposed by Deng et al. [19], inherent strains should be determined through a TEP analysis of a characteristic smaller-scale welded model and then the whole structure could be analyzed by the elastic FE analysis. Therefore, to increase the numerical accuracy of the ISM method, the efficiency of the TEP method should be improved to enable an accurate estimation of inherent deformation values in every welded joint of large-scale structures as well as to enable the verification of the ISM method on large-scale models.
The focus of the present paper is to develop a TEP method with a higher computational accuracy and shorter computing time in order to perform the welding process numerical simulations of large-scale structural components. In that regard, the shell/3D modeling technique proposed and experimentally validated in the authors’ previous study [10] is applied. Here, in contrast to the widely used full 3D FE model, 3D continuum elements are only used in the weld region where the temperature, strain and stress gradients are high, while the zones away from the weld bead are discretized with shell elements to reduce the overall model size. To verify the temperature and distortion solutions obtained by the shell/3D modeling technique, two numerical examples are analyzed. The first example is a small-scale T-joint fillet welding of two plates, while the second is a large welded panel. The recommendations for the estimation of the minimum 3D zone size in the shell/3D model set out in the authors’ previous work [10] are verified here on T-joint models consisting of plates with different thicknesses. It is shown that when compared to the full 3D model, the computational time and computer resources needed to simulate the welding process can be considerably reduced. Additionally, the accuracy of the proposed model is validated by comparing the simulation results with the published experimental results for a large panel with two longitudinal stiffeners.
The paper is structured as follows. Section 2 provides a brief review of the used FE analysis procedures. A full 3D numerical model and a combined shell/3D finite element model of a small-scale T-joint fillet welding as well as a combined shell/3D finite element model of a large panel are described in Section 3. Next, in Section 4, detailed quantitative comparisons of the results obtained by the full 3D numerical model, the shell/3D model and experimental results from the literature are shown. Finally, concluding remarks are drawn in Section 5.
2 Finite element formulation
In this work, a sequentially coupled numerical simulation of a welding process is applied [20, 21, 22]. The complete numerical analysis therefore consists of a thermal analysis which is independent, i.e. standalone, and a mechanical analysis which uses the temperature field result of the thermal analysis as input.
2.1 Thermal FE analysis
The thermal analysis of the welding process is based on a transient nonlinear heat transfer differential equation:
that incorporates the thermal material properties which are strongly temperature dependent. Here, kx, ky, and kz are the thermal conductivities in the x, y and z directions, respectively; T denotes the temperature; Q is the heat input; ρ stands for the material density; C represents the specific heat capacity of the material; and t is the time. In order to solve Eq. (1) the following initial and boundary conditions are introduced
where N x, Ny, and Nz are the direction cosine of the normal to the boundary; hc and h r are the convection and radiation heat transfer coefficients, respectively; qs represents the heat flux over the body boundaries; Tr denotes the temperature of radiation; and T∞ represents the ambient temperature. Radiation heat loses are expressed by the relation
where σ denotes the Stefan–Boltzmann constant, ϵ is the surface emissivity factor, and F is the configuration factor. The total heat input applied to the weld can be expressed with the following equation:
where η is the efficiency of the welding process, I is welding current, U is the arc voltage, and VH is the volume of heat source, i.e. the volume of filler material.
According to the governing Eq. (1), the thermal FE equations for an element can be obtained by using the Galerkin method, as follows:
where c is the specific heat matrix, T represents the nodal temperature vector, kT is the thermal conductivity matrix, while f is the nodal load vector in terms of internal heat source and boundary conditions. Matrices c, k and f are defined in terms of element shape functions matrix.
2.2 Mechanical FE analysis
Mechanical analyses in this work are conducted through standard elastoplastic procedure employing the implicit return mapping algorithm. Herein, it is assumed that both base and weld materials are homogeneous, isotropic, elastic-perfectly plastic solid that yields according to the von Mises criterion with the associated flow rule. The nonlinear material behavior is thus modeled via incremental plasticity while also assuming the geometrically nonlinear behavior of the welded plates. Furthermore, in the mechanical analysis of the present study, the influence of the steel phase transformation is not considered because its influence on the residual stress field and deformations is small in low-carbon steel [23].Additionally, the creep material behavior is neglected as the duration of the thermal cycles during the welding process is short. Accordingly, the total strain increment can then be additively decomposed into three components:
where the subscripts “e”, “p” and “th” denote reversible elastic, irreversible plastic and thermal strain increments, respectively. The governing equations used to carry out the mechanical FE analysis of the welding process are the well- known equilibrium equation (8), strain–displacement relationship (9) and constitutive equation for thermal elastoplastic material (10):
where L is the Cartesian coordinates partial derivatives matrix, σ is the stress tensor, b represents the body force vector, ϵ is the strain vector, u represents the displacement vector and C is the elastic constitutive material matrix. Using the virtual work principle and standard finite element method manipulations, the finite element equation can be derived in an incremental form as
where k1 is the element stiffness matrix, k2 is the element thermal stiffness matrix, v represents the vector of nodal degrees of freedom (DOF) and r is the nodal force vector. To solve the nonlinear equations (11), the iterative Newton-Raphson method is employed within the FE solver. Here, the updated values of the state variables at the end of the time step (n−1t, n t) have to be calculated for the given values of the incremental strain tensor components Δε and the state variables at time n−1t. More details about an algorithm for solving non-isothermal elastoplastic problems with the finite element method can be found in the authors’ earlier paper [24].
3 Numerical models
With the goal of increasing the efficiency and accuracy of the welding simulation of large-scale structural components, in the first phase of the authors’ study [10], the numerical analysis was carried out by applying the shell/3D coupling model, which is based on the transition from the shell model to the 3D model discretizing the weld and its vicinity. The method combines the accuracy of the full 3D model while taking advantage of the shell finite element’s computational efficiency in the regions away from weld vicinity, as they are not prone to locking problems and are thus accurate on relatively coarser meshes compared to full 3D model. The technique was verified on a T-joint fillet welding example with 10 mm thick plates and weld leg lengths of 7 mm, where a parametric study was performed to identify the influence of the local 3D model size (i.e. the distance from the weld zone to the shell-to-solid interface) on the temperature, displacement and residual stress distributions. The conclusions extracted from that work based on the experimental data and numerical results compared to the reference full 3D model showed that the necessary size of the 3D zone on a flange and web to obtain satisfactory accuracy in terms of studied output was at least 3 times the plate thickness. The present paper is a continuation of that work where the shell/3D coupling model is applied to simulate and predict welding distortions and residual stresses of large-scale structural components such as a large stiffened panel. The main aim is to investigate if the conclusions of the above-mentioned work can be generalized to other T-joint fillet models with different thicknesses of flange and web plates and corresponding weld sizes. In this way, two different models are analyzed in the present study. In the first example, the accuracy of the shell-to-solid modeling technique is verified on a small-scale T-joint model in comparison with the full 3D model. Here, the T-joint model with different thicknesses of flange and web plates is considered corresponding to a large panel model dimensions. Then, the large panel model with two longitudinal stiffeners is analyzed using the verified shell/3D modeling technique in the second example.
3.1 Small-scale T-joint model
The geometry of the small-scale T-joint model, including the welding sequence and direction, is presented in Figure 1a. The size of the horizontal base plate (flange) is 500 × 500 mm and the height of the stiffener (web) is 140 mm. The thickness of the base plate and the stiffener are 9 mm and 12 mm, respectively. It is assumed that two steel plates are welded by fillet welds with 6 mm leg lengths in two single passes with no time in between the passes using the metal active gas (MAG) welding procedure. Since the initial gap between the plates was very small and the plates were tack-welded prior to the start of welding process, the influence of the small gap on the final residual stress and deflection field can be neglected [20]. Therefore, both the horizontal and vertical plates were modeled as a single unit. Moreover, due to the negligible heat input to the work piece, the tack welds’ heat influence has not been taken into the account in the numerical analyses conducted in this study. Furthermore, the small initial gap between the horizontal and the vertical plate is not taken into account. The welding parameters are provided in Table 1. The plates are free welded, without any restraints, but in the mechanical analysis the boundary conditions are imposed to the horizontal plate to prevent its rigid body motion as it is schematically shown in Figure 1. The material of the plates is a low-carbon shipbuilding steel SM400A whose chemical composition is given in Table 2. Its thermo-mechanical temperature dependent properties are given in Figures 2 and 3. Due to the lack of thermo-mechanical data for the weld filler material, the material properties were assumed to be the same as the base metal. The dimensions of the solid and shell parts for the shell/3D small-scale T-joint model are given in Figure 1b. Since the small-scale T-joint model is geometrically very similar to the model analyzed in [10] and is subjected to the same heat input, the size of the 3D zone in the shell/3D model is estimated in accordance with the recommendations set out in that authors’ previous study. Therefore, to obtain a continued stress transfer across the shell-to-solid interface, the size of the 3D zone is set to approximately 3 wall thicknesses of the thicker plate.
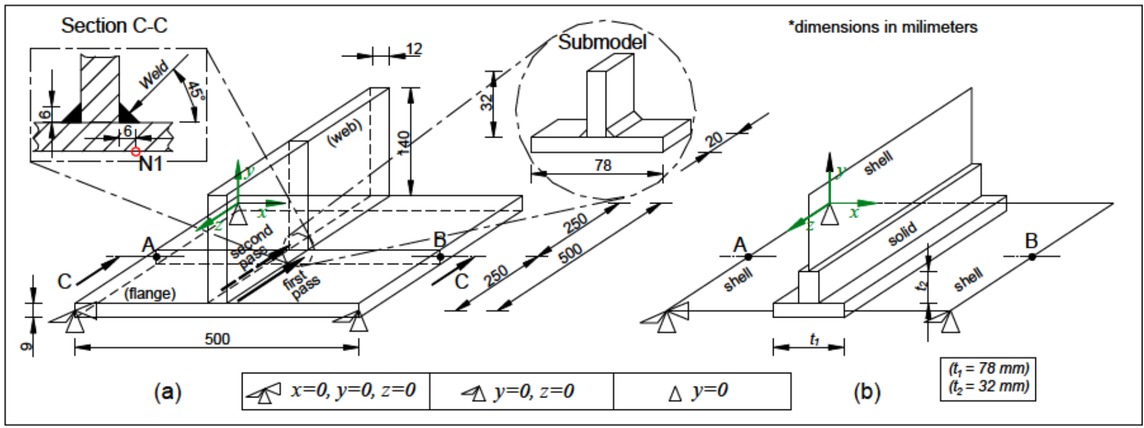
Geometry of small-scale T-joint model: (a) full 3D model and (b) shell/3D model
![Figure 2 Thermal properties of SM400A steel [26]](/document/doi/10.1515/phys-2019-0076/asset/graphic/j_phys-2019-0076_fig_002.jpg)
Thermal properties of SM400A steel [26]
![Figure 3 Mechanical properties of SM400A steel [26]](/document/doi/10.1515/phys-2019-0076/asset/graphic/j_phys-2019-0076_fig_003.jpg)
Mechanical properties of SM400A steel [26]
Welding parameters [25]
| Welding current (A) | Welding voltage (V) | Welding speed (mm/min) | Angle of torch (∘) |
|---|---|---|---|
| 270 | 29 | 400 | 45 |
The heat generation rate approach based on the heat flux prescribed on a weld element volume is employed for modeling the welding heat input in the thermal analyses. The uniformly distributed heat flux per weld volume Q = 5.22 × 1010 Jm−3s−1 is applied [27, 28] according to Eq. (5) and Table 1, where the weld volume VH is determined by the weld cross-sectional area and the welding speed. On the outer body surfaces, the following boundary conditions are assumed: convective heat transfer coefficient k = 10 Wm−2K−1 and emissivity ϵ = 0.9. The welding process efficiency η = 80% is taken in accordance with the EN ISO 1011-1 norm.
Finite element meshes for the small-scale T-joint model are shown in Figure 4. To discretize the full 3D model (Figure 4a), 3D linear hexahedral elements with 8 nodes and full integration scheme are used: DC3D8 elements for the thermal analysis and corresponding C3D8R elements with reduced integration scheme for the mechanical analysis. As may be seen from Figure 4a, a fine mesh is used in the fillet weld region for both longitudinal and transverse directions to capture very high gradients of temperatures, strains and stresses caused by the heat, while the regions far away from the welding zone are discretized with a relatively coarse mesh to reduce the overall model size. The finite element mesh of the full 3D model consists of 16,068 elements. For the discretization of the shell/3D model (Figure 4b), DC3D8 elements and DS4 shell elements are applied for the thermal analysis and corresponding C3D8R and S4 shell elements are applied during the mechanical analysis to improve computational efficiency and reduce storage space. Here, the solid part of the shell/3D model is discretized with 3D continuum elements using the same mesh density as in the full 3D model (Figure 4a). The shell/3D FE mesh (Figure 4b) consists of 7,332 solid and 2,184 shell elements. The solid to shell transition is easily achieved by constraining the interface nodes to couple the motion/ temperature of a shell edge to the motion/ temperature of an adjacent solid face. The Abaqus “tie” constraint in the thermal analysis and the “shell to solid coupling” option in the mechanical analysis are used for this purpose. To check the mesh sensitivity for the convergence of solutions, the submodeling technique [29] is employed on a small volume of the full 3D small-scale T-joint model (Figure 1a). Its ability to implement it on a small part of the model containing a much finer finite element mesh, without the need of remeshing the whole model, is what makes it more efficient than the conventional method, and is the reason why it used in this work. As presented in the authors’ former work [30], the submodel boundary must lie far enough from the high temperature and stress gradients where nodal temperature and displacement solutions for the driven nodes of the submodel will be correctly interpolated from the results of the global model. Accordingly, the dimensions of the submodel volume were 78 × 32 × 20 mm3 (Figure 1a). The submodel consisted of about 6,120 solid finite elements while the same volume of the global model had only 564 ones.
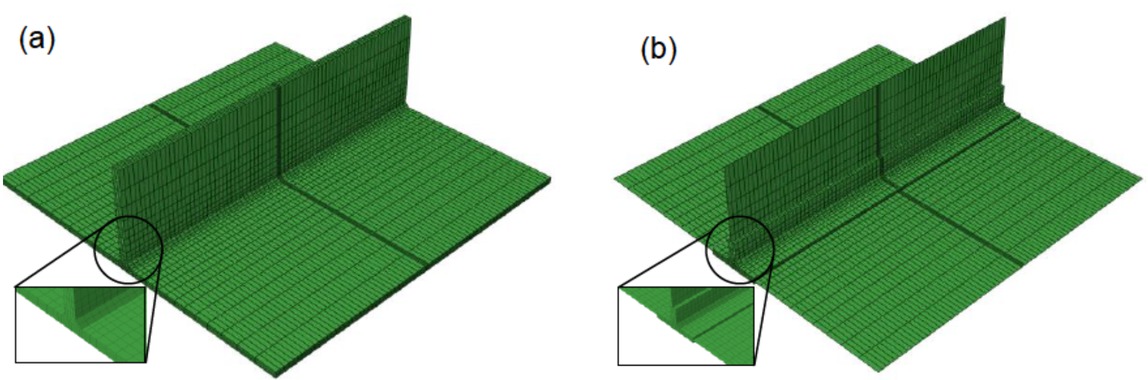
Finite element for small-scale T-joint model: (a) full 3D model and (b) shell/3D model
Thus, the submodel mesh had more than ten times greater density than the equivalent part of the global model. The same element types are used for both global and submodel. In the thermal analysis, the addition of weld filler is simulated by the element birth and death technique [31, 32] available in the finite element software package Abaqus. The subsequent mechanical analysis is then done without applying the element birth and death technique [33] to further accelerate the calculation speed.
3.2 Large panel model
To investigate the deformations in the large welded panel using the shell/3D modeling technique, an experimentally tested model taken from the literature [34] is considered. Figure 5 shows the geometry of the large panel model with restraint conditions and the weld leg dimension of the fillet weld. As can be seen from Figures 1 and 5, the large panel model size is six times greater than that of the small-scale T-joint model. On a horizontal plate of dimensions 1000 mm × 1500 mm, two vertical plates of dimensions 140 × 1500 mm are MAG welded without any gap between the plates in four single weld passes. Since the welding sequences are not given in [34], they are assumed as shown in Figure 5. The welding conditions, material properties and boundary conditions are the same as in the small-scale T-joint model. Additionally, the same finite element types and mesh densities are used to discretize the shell/3D model geometry of the large panel in thermal and mechanical analysis, according to the shell/3D small-scale T-joint model. The finite element mesh consisting of 48,336 solid and 12,312 shell elements of the large panel model is shown in Figure 6. All the numerical simulations in this study are performed using the Abaqus/Standard software.
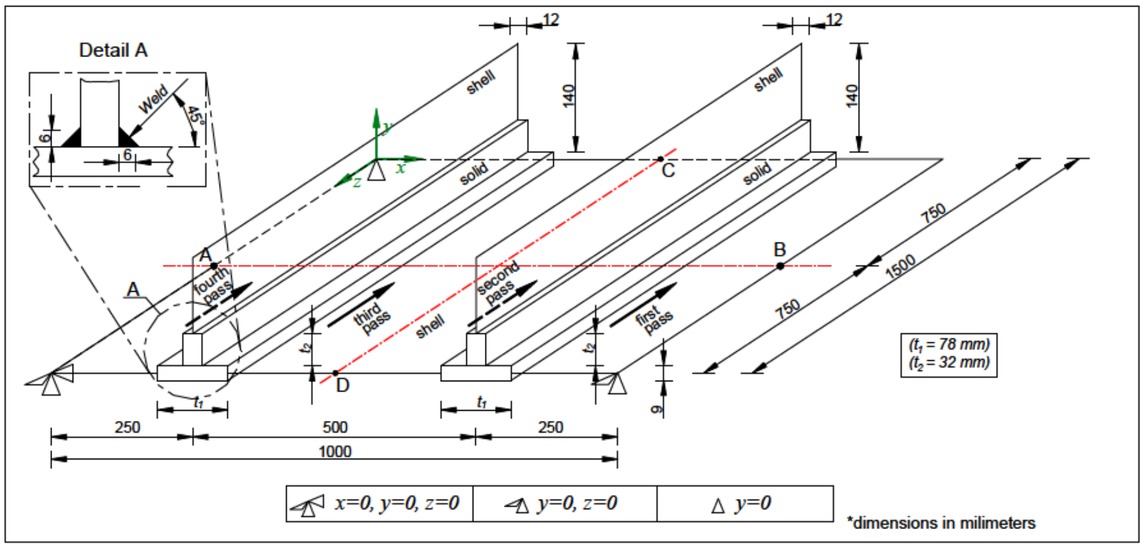
Large panel model geometry
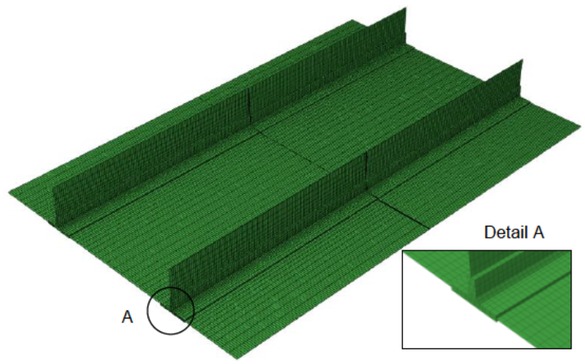
Finite element mesh of large panel model
4 Results and discussion
This section contains detailed quantitative comparisons of the results obtained with the full 3D and shell/3D numerical models as well as with the experimental results and ISM method from the literature. To verify the temperature and dispacement calculations performed by the shell/3D modeling technique, the results are firstly compared with those obtained from the full 3D model for the small-scale T-joint model. Herein, the full 3D model is used as a reference solution. The shell/3D modeling technique is then applied to simulate the welding process of the large panel with two longitudinal stiffeners. The numerical results are validated by corresponding the experimental data and compared with the inherent strain solutions from the literature.
4.1 Small-scale T-joint model
Figure 7 shows a comparison of results for the temperature profiles predicted by the full 3D and shell/3D models at the middle surface of the horizontal plate along line A-B shown in Figure 1, 150 s after the beginning of the welding process. It is obvious that the temperature profiles are almost the same along the observed path. The peak temperature reaches about 350∘C for the full 3D model and the deviation from the shell/3D model is negligible. The temperature history of the arbitrarily selected point N1 located at the bottom surface of the horizontal plate (Figure 1a) near the weld bead for the first 300 s after the beginning of the welding process is given in Figure 8. Again, the temperatures of both models during the welding process and cooling stage to ambient temperature are almost the same with negligible deviations. Finally, it can be concluded that the use of a shell/3D technique gives almost identical spatial-temporal temperature distribution during the welding and cooling process as with the application of a full 3D model.
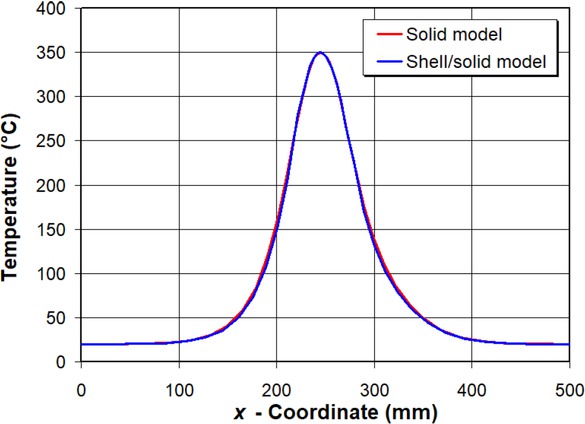
Temperature profiles for full 3D and shell/3D models 150 s after beginning of welding process at middle surface of horizontal plate along line A-B in Figure 1
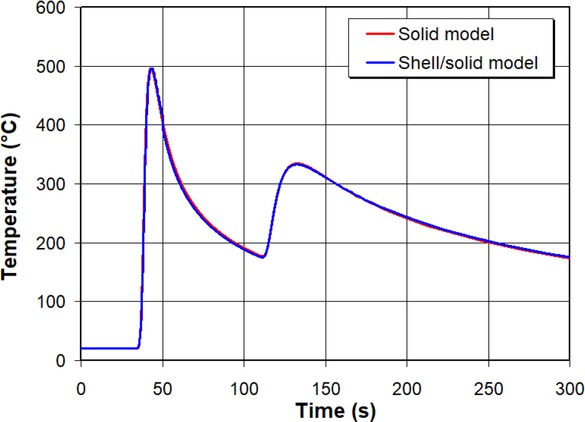
Temperature-time history of node N1 (Figure 1a) for full 3D and shell/3D models for first 300 s after beginning of welding process
Figure 9 shows the horizontal plate deflections in y-direction at middle surface along line A-B (Figure 1) after the cooling of the welded T-joint to ambient temperature (20∘C). The maximum deflection in y-direction (vertical deflection) of the full 3D small-scale T-joint model is about 5.4 mm for both full 3D and shell/3D models. The full field vertical deflection distributions after the cooling process to ambient temperature obtained by the full 3D model and shell/3D modeling techniques are provided in Figures 10a and 10b.
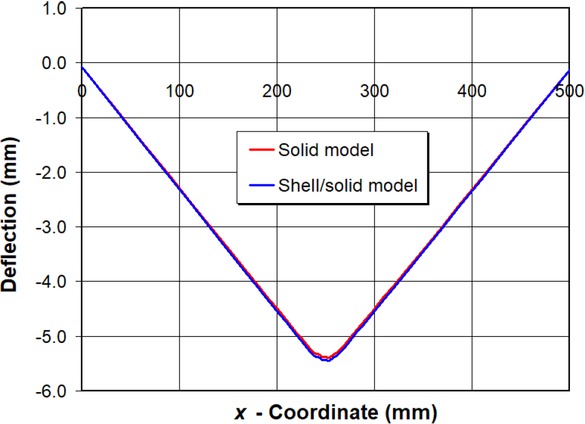
Horizontal plate deflection in y-direction at middle surface after welding process along line A–B in Figure 1
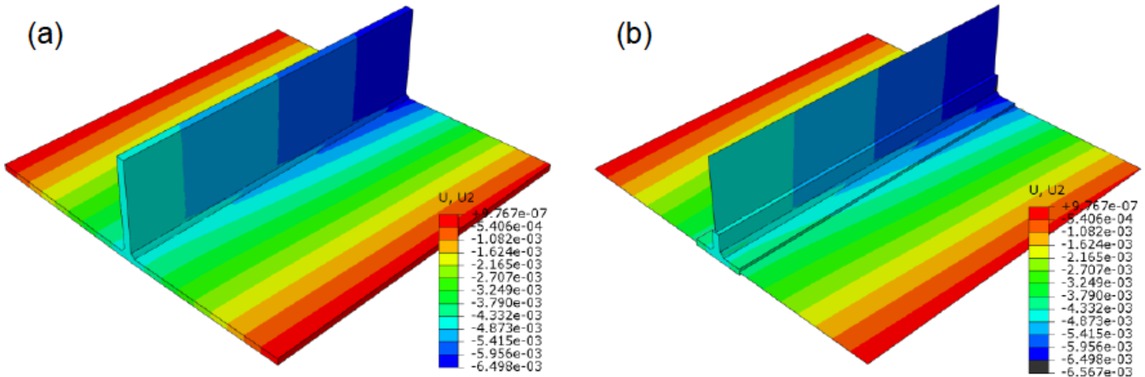
Full field vertical deflection distributions after cooling process: (a) full 3D model and (b) shell/3D model
These results are in agreement with the previous literature reports and with the experimental results obtained by the authors in [10]. As seen in the figures, almost the same results are obtained with both the shell/3D and full 3D models. Thus, it is shown that the recommendations set out by the authors of this contribution in [10] for the estimation of the minimum 3D zone size in the shell/3D model can be applied not only to the T-joint models with the same thicknesses of flange and web plates but also to the T-joint models consisting of plates with different thicknesses. This is very useful in engineering practice because the fillet welded stiffened panel structures are generally composed of longitudinal stiffeners with attached plates of different thicknesses.
The main advantage of the shell/3D model can be clearly seen in Table 3, which shows that the shell/3D model shortens the simulation time by 52% compared with the full 3D model. Additional savings in computing time for the shell/3D model can be achieved by parametrically varying the sizes of the 3D zone on the flange and web as well as the weld leg dimensions for each specific geometry of the T-joint model. However, the time required to perform the parametric analyses and define the optimal 3D zone size could be greater than the savings in CPU time in that case. The numerical simulations of the small scale T-joint are performed on a PC with an Intel® Core™i3 processor with 8 GB of RAM memory.
CPU time comparison of full 3D and shell/3D models
| Model | CPU time in thermal analysis (s) | CPU time in mechanical analysis (s) | Total CPU time (s) |
|---|---|---|---|
| Full 3D | 82,724 | 19,575 | 102,299 |
| Shell/3D | 38,637 | 10,363 | 49,000 |
Furthermore, the results of the mesh sensitivity study are presented here. Figure 11 shows a temperature profile comparison of the global model and submodel along line A-B (Figure 1) 150 s after the beginning of the welding process. As already mentioned, the submodel has the mesh of extreme density, i.e. more than ten times denser than the global mesh, so it can be concluded that the global mesh of the T-joint small-scale joint is properly designed. The same conclusion can be drawn from Figure 12,where it can be seen that the vertical deflection of the horizontal plate of the global model converges to the submodel values. A slight deviation of the results is observed only in the weld region where the large stress gradients occur.
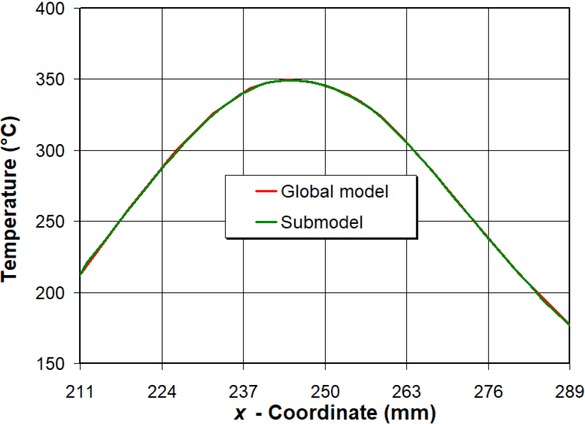
Temperature profiles of global model and submodel 150 s after beginning of welding process at middle surface of horizontal plate along line A-B in Figure 1
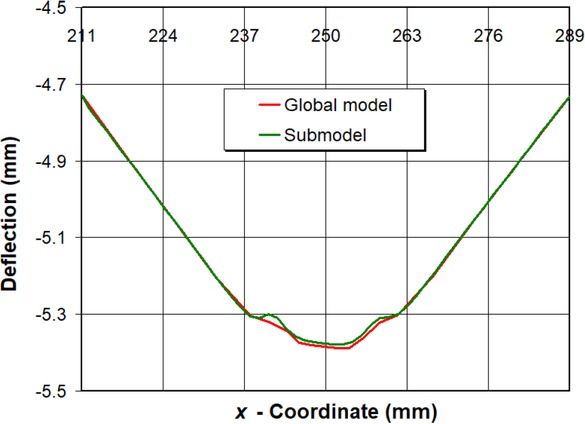
Horizontal plate deflection of global model and submodel in y-direction at middle surface after welding process along line A–B in Figure 1
Finally, it can be concluded that the use of a shell/3D model has negligible influence on the temperature and deformation distribution in comparison with the full 3D model. Moreover, the mesh sensitivity analysis verified that the finite element mesh of the small-scale model is sufficiently dense and thus the mesh density can be successfully expanded on a larger-size model, i.e. a large panel model.
4.2 Large panel model
The next step is to test the shell/3D modeling technique to predict the out-of-plane deformations and residual stresses in a large panel model with two longitudinal stiffeners. The results of the mechanical analysis are presented in comparison with the experimental results from the literature [34]. Figure 13 shows the deflection profile of the base plate along line A-B shown in Figure 5. The maximum deflection computed by the shell/3D model reaches 12.6 mm which is very close to the experimental measurement and by using the ISM method. Furthermore, it is apparent that a nearly full numerically obtained curve matches well with the experimental measurements. A similar conclusion can be drawn for the vertical deflections along line C-D (Figure 5) shown in Figure 14, where the ISM method misses the experimental curve trend completely as it is not able to take the welding process history into the account, while the proposed method shows a very good matching with the experimental data on the right half of the figure. On the other hand, the partial deviation of the numerical results from the experimental measurements could be attributed to the welding parameters used in this work, mainly the order of welding passes, time between the passes and mechanical boundary conditions, which were not provided in the literature [34] where the model was taken from. Further investigation into the welding conditions is needed to address these discrepancies, which is out of the scope of this paper. Additionally, from Figures 13 and 14, it can be seen that the panel deflection profiles obtained by the ISM are strongly dependent on the input data. As they are obviously applied symmetrically, the calculated deflections are symmetric along paths A-B and C-D. This is sometimes very far from reality so that more realistic solutions can be obtained using the presented shell/3D TEP model. Generally, the peak deflections for both shell/3D and ISM methods agree well, but the trend of the shell/3D model is more realistic compared with the experimental measurements. A full field of vertical deflections can be seen in Figure 15. The numerical simulations of the welding process for a large panel model are performed on a Sun three-node cluster with 48 cores in total, 32 GB of RAM, and 500 GB of storage each.
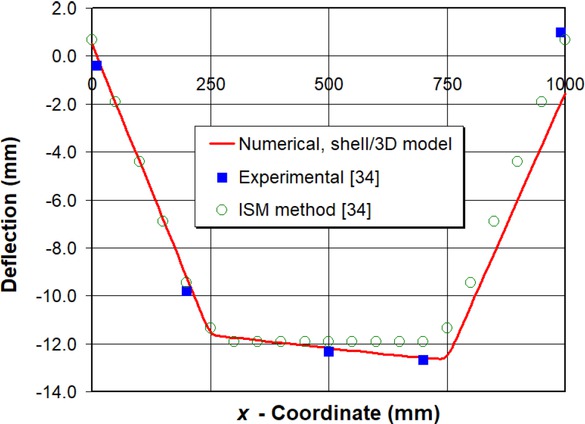
Horizontal plate deflection in y-direction at middle surface after welding process along line A–B in Figure 5
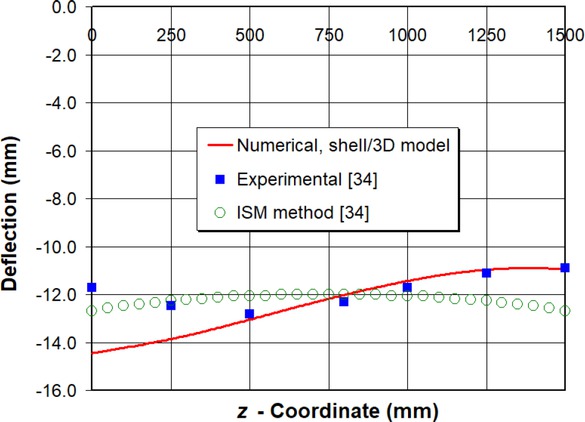
Horizontal plate deflection in y-direction at middle surface after welding process along line C–D in Figure 5
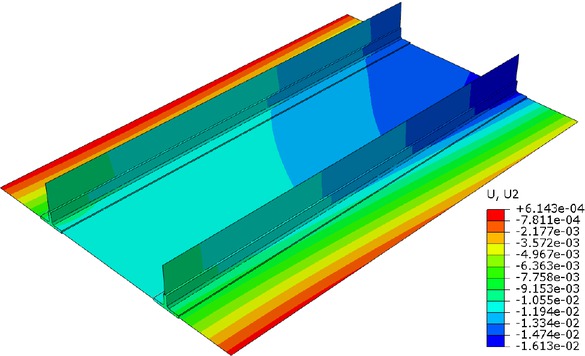
Full field deflection distribution of large panel model
5 Conclusions
In the presented research, an efficient thermo-elastoplastic finite element procedure is developed for a welding process simulation of large-scale structural components. This is achieved through a shell/3D modeling technique which was proposed and experimentally validated on a T-joint welding of two plates with the same thicknesses in the authors’ earlier work. Here, the 3D solid elements are used only in the weld and its vicinity, where the thermal gradients are high, while in the rest of the model shell elements are used. Accordingly, this shell/3D technique combines the accuracy of the full 3D model and computational efficiency of a shell FE solution reducing the model size and computation cost. The main goal of the present study was to investigate if the recommendations for the estimation of the minimum 3D zone size in the shell/3D model reported in the authors’ previous work can be generalized to other T-joint fillet models with different thicknesses of flange and web plates and corresponding weld sizes.
To verify the accuracy and efficiency of the present technique, two numerical examples are analyzed. In the first example, the temperature and displacement calculations performed by the shell/3D coupling technique are evaluated on a small-scale T-joint model with different thicknesses of plates corresponding to the large panel model dimensions. Herein, the size of the 3D zone in the shell/3D model (approximately 3 wall thicknesses of the thicker plate) is estimated in accordance with the recommendations set out in the authors’ previous study and a full 3D model is used as a reference solution. In order to check finite element mesh sensitivity, a submodeling technique is applied. Nearly the same results are obtained with both the shell/3D and full 3D models which confirms that the recommendations set out by the authors for the estimation of the minimum 3D zone size in the shell/3D model can be applied not only to T-joint models with the same thicknesses of plates but also to T-joint models consisting of plates with different thicknesses. Thus, the present numerical model is highly applicable in a practical engineering analysis since the panel structures are generally composed of stiffeners with attached plates of different thicknesses. It is shown that the main advantage of the model is that it provides a significant reduction in the computational time needed for the simulation of the welding process and thus enables efficient nonlinear transient analyses on large structures. The advantage of using the shell/3D model can be better seen in cases of numerical simulations of extremely large structures, where it is possible to create much larger areas with shell elements than in the analyzed case, so that the percentage savings on time could be significantly higher.
In the second example, the proposed model is validated on a large panel structure with two longitudinal stiffeners by corresponding the experimental data and inherent strain solutions from the literature. It is shown that the simulated results obtained by the shell/3D modeling technique are in good agreement with the results observed experimentally. Furthermore, it could be concluded that when compared to the ISM method, more realistic solutions for a large panel structure can be obtained by using the presented shell/3D technique.
As a general conclusion, it can be noted that the proposed combined shell/3D modeling technique can serve as an effective tool for the estimation of inherent deformation values in every welded joint of large-scale panel structures as well as for the verification of the inherent strain method on large-scale models.
References
[1] Chen Z., Xiong Y., Qiu H., Lin G. and Li Z. Stress intensity factor-based prediction of solidification crack growth during welding of high strength steel. J. Mater. Process. Tech., 2018, 252, 270-278. https://doi.org/10.1016/j.jmatprotec.2017.09.03110.1016/j.jmatprotec.2017.09.031Search in Google Scholar
[2] Oh S. H., Ryu T. Y., Park H. S., Won M. G., Kang S. J., Lee K. S. et al. Evaluation of J-groove weld residual stress and crack growth rate of PWSCC in reactor pressure vessel closure head. J. Mech. Sci. Technol., 2015, 29, 1225-1230. https://doi.org/10.1007/s12206-015-0236-510.1007/s12206-015-0236-5Search in Google Scholar
[3] Dong P., Song S. and Zhang J. Analysis of residual stress relief mechanisms in post-weld heat treatment. Int. J. Pres. Ves. Pip., 2014, 122, 6-14. https://doi.org/10.1016/j.ijpvp.2014.06.00210.1016/j.ijpvp.2014.06.002Search in Google Scholar
[4] Perić M., Garašić I., Nižetić S. and Dedić-Jandrek H. Numerical analysis of longitudinal residual stresses and deflections in a T-joint welded structure using a local preheating technique. Energies, 2018, 11, 3487. https://doi.org/10.3390/en1112348710.3390/en11123487Search in Google Scholar
[5] Cozzolino L. D., Coules E, Colegrove A. P. and Wen S. Investigation of post-weld rolling methods to reduce residual stress and distortion. J. Mater. Process. Tech., 2017, 247, 243-256. https://doi.org/10.1016/j.jmatprotec.2017.04.01810.1016/j.jmatprotec.2017.04.018Search in Google Scholar
[6] Yang Y. P. Understanding of vibration stress relief with computation modeling. J. Mater. Eng. Perform., 2009, 18, 856-862. https://doi.org/10.1007/s11665-008-9310-910.1007/s11665-008-9310-9Search in Google Scholar
[7] Huang H., Tsutsumi S., Wang J., Li L. and Murakawa, H. High performance computation of residual stress and distortion in laser welded 301L stainless sheets. Finite Elem. Anal. Des., 2017, 135, 1-10. https://doi.org/10.1016/j.finel.2017.07.00410.1016/j.finel.2017.07.004Search in Google Scholar
[8] Rong Y., Zhang G. and Huang Y. Study of welding distortion and residual stress considering nonlinear yield stress curves and multi-constraint equations. J. Mater. Eng. Perform., 2016, 10, 4484-4494. https://doi.org/10.1007/s11665-016-2259-110.1007/s11665-016-2259-1Search in Google Scholar
[9] Shen J. and Chen Z. Welding simulation of fillet welded joint using shell elements with section integration. J. Mater. Process. Tech., 2014, 214, 2529-2536. https://doi.org/10.1016/j.jmatprotec.2014.04.03410.1016/j.jmatprotec.2014.04.034Search in Google Scholar
[10] Perić M., Tonković Z., Rodić A., Surjak M., Garašić I., Boras I. and Švaić, S. Numerical analysis and experimental investigation of welding residual stresses and distortions in a T-joint fillet weld. Mater. Design, 2014, 53, 1052-1063. http://dx.doi.org/10.1016/j.matdes.2013.08.01110.1016/j.matdes.2013.08.011Search in Google Scholar
[11] Chen Z., Yu Q., Luo Y. and Shenoi R. A. Comparative study of welding deformation of a stiffened panel under various welding procedures. P. I. Mech. Eng. B-J. Eng., 2019, 233, 182-191. https://doi.org/10.1177/095440541771255010.1177/0954405417712550Search in Google Scholar
[12] Chen Z.and Li G. A study on the spring-back deflections and constraint forces of a bottom grillage cling welding. Ships Offshore Struc., 2017, 12, 1077-1085. https://doi.org/10.1080/17445302.2017.131318610.1080/17445302.2017.1313186Search in Google Scholar
[13] Huang H., Ma N., Murakawa H. and Feng, Z. A dual-mesh method for efficient thermal stress analysis of large-scale welded structures. Int. J. Adv. Manuf. Tech., 2019, 103, 769-780. https://doi.org/10.1007/s00170-019-03606-410.1007/s00170-019-03606-4Search in Google Scholar
[14] Li Y., Wang K., Jin Y., Xu,M. and Lu H. Prediction of welding deformation in stiffened structure by introducing thermo-mechanical interface element. J. Mater. Process. Tech., 2015, 216, 440-446. http://dx.doi.org/10.1016/j.jmatprotec.2014.10.01210.1016/j.jmatprotec.2014.10.012Search in Google Scholar
[15] Deng D., Murakawa H. and Liang W. Numerical simulation of welding distortion in large structures. Comput. Method. Appl. M., 2007, 196, 4613-4627. https://doi.org/10.1016/j.cma.2007.05.02310.1016/j.cma.2007.05.023Search in Google Scholar
[16] Wang J., Rashed S.,Murakawa H. and Luo, Y. Numerical prediction and mitigation of out-of-plane welding distortion in ship panel structure by elastic FE analysis. Mar. Struct., 2013, 34, 135-155. http://dx.doi.org/10.1016/j.marstruc.2013.09.00310.1016/j.marstruc.2013.09.003Search in Google Scholar
[17] Murakawa H.,Ma N. and Huang, H. Iterative substructure method employing concept of inherent strain for large-scale welding problems. Weld. World, 2015, 59, 53-63. https://doi.org/10.1007/s40194-014-0178-rez10.1007/s40194-014-0178-zSearch in Google Scholar
[18] Ma N., Wang J. and Okumoto Y. Out-of-plane welding distortion prediction and mitigation in stiffened welded structures. Int. J. Adv. Manuf. Tech., 2016, 84, 1371-1389. https://doi.org/10.1007/s00170-015-7810-y10.1007/s00170-015-7810-ySearch in Google Scholar
[19] Deng D., Murakawa H. and Shibahara M. Investigations on welding distortion in an asymmetrical curved block by means of numerical simulation technology and experimental method. Comp. Mater. Sci., 2010, 48, 187-194. https://doi.org/10.1016/j.commatsci.2009.12.02710.1016/j.commatsci.2009.12.027Search in Google Scholar
[20] Perić M., Tonković Z., Garašić I. and Vuherer T. An engineering approach for a T-joint fillet welding simulation using simplified material properties. Ocean Eng. 2016, 128, 13-21. https://doi.org/10.1016/j.oceaneng.2016.10.00610.1016/j.oceaneng.2016.10.006Search in Google Scholar
[21] Seleš K., Perić M. and Tonković Z. Numerical simulation of a welding process using a prescribed temperature approach. J. Constr. Steel Res., 2018, 145, 49-57. https://doi.org/10.1016/j.jcsr.2018.02.01210.1016/j.jcsr.2018.02.012Search in Google Scholar
[22] Lostado R. L., Garcia R. E., Martinez R. F. and Martinez Calvo M. A. Using genetic algorithms with multi-objective optimization to adjust finite element models of welded joints. Metals, 2018, 230. https://doi.org/10.3390/met804023010.3390/met8040230Search in Google Scholar
[23] Deng D. FEM prediction of welding residual stress and distortion in carbon steel considering phase transformation effects. Mater. Design, 2009, 30, 359-366. https://doi.org/10.1016/j.matdes.2008.04.05210.1016/j.matdes.2008.04.052Search in Google Scholar
[24] Tonković Z., Sorić J. and Krätzig W. B. On nonisothermal elastoplastic analysis of shell-components employing realistic hardening responses. Int. J . Solids Struct., 2001, 38, 5019-5039. https://doi.org/10.1016/S0020-7683(00)00336-X10.1016/S0020-7683(00)00336-XSearch in Google Scholar
[25] Deng D., Liang, W. and Murakawa, H. Determination of welding deformation in fillet-welded joint by means of numerical simulation and comparison with experimental measurements. J. Mater. Process. Tech., 2007, 183, 219–225. https://doi.org/10.1016/j.jmatprotec.2006.10.01310.1016/j.jmatprotec.2006.10.013Search in Google Scholar
[26] Gannon, L., Liu Y., Pegg N. and Smith, M. Effect of welding sequence on residual stress and distortion in flat-bar stiffened plates. Mar. Struct., 2010, 23, 385-404. https://doi.org/10.1016/j.marstruc.2010.05.00210.1016/j.marstruc.2010.05.002Search in Google Scholar
[27] Perić M., Tonković Z., Karšaj I. and Stamenković D. A simplified engineering method for a T-joint welding simulation. Therm. Sci., 2018, 22, 867-873. https://doi.org/10.2298/TSCI171108020P10.2298/TSCI171108020PSearch in Google Scholar
[28] Perić M., Stamenković D. and Milković V. Comparison of residual stresses in butt-welded plates using software packages Abaqus and Ansys. Sci. Tec. Rev., 2010, 60, 22-26.Search in Google Scholar
[29] Perić M., Tonković Z., Maksimović S. K. and Stamenković D. Numerical analysis of residual stresses in a T-joint fillet weld using a submodeling technique. FME Transactions, 2019, 47, 183-189. https://doi.org/10.5937/fmet1901183P10.5937/fmet1901183PSearch in Google Scholar
[30] Marenić E., Skozrit I. and Tonković, Z. On the calculation of stress intensity factors and J-integrals using the submodeling technique. J. Press. Vess-T. ASME, 2010, 132, 041203. https://doi.org/10.1115/1.400126710.1115/1.4001267Search in Google Scholar
[31] Yue J., Dong X., Guo R., Liu W. and Li, L. Numerical simulation of equivalent heat source temperature field of asymmetrical fillet root welds. Int. J. Heat Mass Tran., 2019, 130, 42-49. https://doi.org/10.1016/j.ijheatmasstransfer.2018.10.07510.1016/j.ijheatmasstransfer.2018.10.075Search in Google Scholar
[32] Mondal, A. K., Biswas, P., and Bag, S. Prediction of welding sequence induced thermal history and residual stresses and their effect on welding distortion, Weld. World, 2017, 61, 711-721. https://doi.org/10.1007/s40194-017-0468-310.1007/s40194-017-0468-3Search in Google Scholar
[33] Perić M, Garašić I., Tonković Z., Vuherer T., Nižetić S. and Dedić-Jandrek H. Numerical prediction and experimental validation of temperature and residual stress distributions in buried-arc welded thick plates. Int. J. Energ. Res., 2019, 43, 3590-3600. https://doi.org/10.1002/er.450610.1002/er.4506Search in Google Scholar
[34] Deng D., Murakawa H. and Liang W. Prediction of welding distortion in a curved plate structure by means of elastic finite element method. J. Mater. Process. Tech., 2008, 203, 252–266. https://doi.org/10.1016/j.jmatprotec.2007.10.00910.1016/j.jmatprotec.2007.10.009Search in Google Scholar
© 2019 M. Perić et al., published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Regular Articles
- Non-equilibrium Phase Transitions in 2D Small-World Networks: Competing Dynamics
- Harmonic waves solution in dual-phase-lag magneto-thermoelasticity
- Multiplicative topological indices of honeycomb derived networks
- Zagreb Polynomials and redefined Zagreb indices of nanostar dendrimers
- Solar concentrators manufacture and automation
- Idea of multi cohesive areas - foundation, current status and perspective
- Derivation method of numerous dynamics in the Special Theory of Relativity
- An application of Nwogu’s Boussinesq model to analyze the head-on collision process between hydroelastic solitary waves
- Competing Risks Model with Partially Step-Stress Accelerate Life Tests in Analyses Lifetime Chen Data under Type-II Censoring Scheme
- Group velocity mismatch at ultrashort electromagnetic pulse propagation in nonlinear metamaterials
- Investigating the impact of dissolved natural gas on the flow characteristics of multicomponent fluid in pipelines
- Analysis of impact load on tubing and shock absorption during perforating
- Energy characteristics of a nonlinear layer at resonant frequencies of wave scattering and generation
- Ion charge separation with new generation of nuclear emulsion films
- On the influence of water on fragmentation of the amino acid L-threonine
- Formulation of heat conduction and thermal conductivity of metals
- Displacement Reliability Analysis of Submerged Multi-body Structure’s Floating Body for Connection Gaps
- Deposits of iron oxides in the human globus pallidus
- Integrability, exact solutions and nonlinear dynamics of a nonisospectral integral-differential system
- Bounds for partition dimension of M-wheels
- Visual Analysis of Cylindrically Polarized Light Beams’ Focal Characteristics by Path Integral
- Analysis of repulsive central universal force field on solar and galactic dynamics
- Solitary Wave Solution of Nonlinear PDEs Arising in Mathematical Physics
- Understanding quantum mechanics: a review and synthesis in precise language
- Plane Wave Reflection in a Compressible Half Space with Initial Stress
- Evaluation of the realism of a full-color reflection H2 analog hologram recorded on ultra-fine-grain silver-halide material
- Graph cutting and its application to biological data
- Time fractional modified KdV-type equations: Lie symmetries, exact solutions and conservation laws
- Exact solutions of equal-width equation and its conservation laws
- MHD and Slip Effect on Two-immiscible Third Grade Fluid on Thin Film Flow over a Vertical Moving Belt
- Vibration Analysis of a Three-Layered FGM Cylindrical Shell Including the Effect Of Ring Support
- Hybrid censoring samples in assessment the lifetime performance index of Chen distributed products
- Study on the law of coal resistivity variation in the process of gas adsorption/desorption
- Mapping of Lineament Structures from Aeromagnetic and Landsat Data Over Ankpa Area of Lower Benue Trough, Nigeria
- Beta Generalized Exponentiated Frechet Distribution with Applications
- INS/gravity gradient aided navigation based on gravitation field particle filter
- Electrodynamics in Euclidean Space Time Geometries
- Dynamics and Wear Analysis of Hydraulic Turbines in Solid-liquid Two-phase Flow
- On Numerical Solution Of The Time Fractional Advection-Diffusion Equation Involving Atangana-Baleanu-Caputo Derivative
- New Complex Solutions to the Nonlinear Electrical Transmission Line Model
- The effects of quantum spectrum of 4 + n-dimensional water around a DNA on pure water in four dimensional universe
- Quantum Phase Estimation Algorithm for Finding Polynomial Roots
- Vibration Equation of Fractional Order Describing Viscoelasticity and Viscous Inertia
- The Errors Recognition and Compensation for the Numerical Control Machine Tools Based on Laser Testing Technology
- Evaluation and Decision Making of Organization Quality Specific Immunity Based on MGDM-IPLAO Method
- Key Frame Extraction of Multi-Resolution Remote Sensing Images Under Quality Constraint
- Influences of Contact Force towards Dressing Contiguous Sense of Linen Clothing
- Modeling and optimization of urban rail transit scheduling with adaptive fruit fly optimization algorithm
- The pseudo-limit problem existing in electromagnetic radiation transmission and its mathematical physics principle analysis
- Chaos synchronization of fractional–order discrete–time systems with different dimensions using two scaling matrices
- Stress Characteristics and Overload Failure Analysis of Cemented Sand and Gravel Dam in Naheng Reservoir
- A Big Data Analysis Method Based on Modified Collaborative Filtering Recommendation Algorithms
- Semi-supervised Classification Based Mixed Sampling for Imbalanced Data
- The Influence of Trading Volume, Market Trend, and Monetary Policy on Characteristics of the Chinese Stock Exchange: An Econophysics Perspective
- Estimation of sand water content using GPR combined time-frequency analysis in the Ordos Basin, China
- Special Issue Applications of Nonlinear Dynamics
- Discrete approximate iterative method for fuzzy investment portfolio based on transaction cost threshold constraint
- Multi-objective performance optimization of ORC cycle based on improved ant colony algorithm
- Information retrieval algorithm of industrial cluster based on vector space
- Parametric model updating with frequency and MAC combined objective function of port crane structure based on operational modal analysis
- Evacuation simulation of different flow ratios in low-density state
- A pointer location algorithm for computer visionbased automatic reading recognition of pointer gauges
- A cloud computing separation model based on information flow
- Optimizing model and algorithm for railway freight loading problem
- Denoising data acquisition algorithm for array pixelated CdZnTe nuclear detector
- Radiation effects of nuclear physics rays on hepatoma cells
- Special issue: XXVth Symposium on Electromagnetic Phenomena in Nonlinear Circuits (EPNC2018)
- A study on numerical integration methods for rendering atmospheric scattering phenomenon
- Wave propagation time optimization for geodesic distances calculation using the Heat Method
- Analysis of electricity generation efficiency in photovoltaic building systems made of HIT-IBC cells for multi-family residential buildings
- A structural quality evaluation model for three-dimensional simulations
- WiFi Electromagnetic Field Modelling for Indoor Localization
- Modeling Human Pupil Dilation to Decouple the Pupillary Light Reflex
- Principal Component Analysis based on data characteristics for dimensionality reduction of ECG recordings in arrhythmia classification
- Blinking Extraction in Eye gaze System for Stereoscopy Movies
- Optimization of screen-space directional occlusion algorithms
- Heuristic based real-time hybrid rendering with the use of rasterization and ray tracing method
- Review of muscle modelling methods from the point of view of motion biomechanics with particular emphasis on the shoulder
- The use of segmented-shifted grain-oriented sheets in magnetic circuits of small AC motors
- High Temperature Permanent Magnet Synchronous Machine Analysis of Thermal Field
- Inverse approach for concentrated winding surface permanent magnet synchronous machines noiseless design
- An enameled wire with a semi-conductive layer: A solution for a better distibution of the voltage stresses in motor windings
- High temperature machines: topologies and preliminary design
- Aging monitoring of electrical machines using winding high frequency equivalent circuits
- Design of inorganic coils for high temperature electrical machines
- A New Concept for Deeper Integration of Converters and Drives in Electrical Machines: Simulation and Experimental Investigations
- Special Issue on Energetic Materials and Processes
- Investigations into the mechanisms of electrohydrodynamic instability in free surface electrospinning
- Effect of Pressure Distribution on the Energy Dissipation of Lap Joints under Equal Pre-tension Force
- Research on microstructure and forming mechanism of TiC/1Cr12Ni3Mo2V composite based on laser solid forming
- Crystallization of Nano-TiO2 Films based on Glass Fiber Fabric Substrate and Its Impact on Catalytic Performance
- Effect of Adding Rare Earth Elements Er and Gd on the Corrosion Residual Strength of Magnesium Alloy
- Closed-die Forging Technology and Numerical Simulation of Aluminum Alloy Connecting Rod
- Numerical Simulation and Experimental Research on Material Parameters Solution and Shape Control of Sandwich Panels with Aluminum Honeycomb
- Research and Analysis of the Effect of Heat Treatment on Damping Properties of Ductile Iron
- Effect of austenitising heat treatment on microstructure and properties of a nitrogen bearing martensitic stainless steel
- Special Issue on Fundamental Physics of Thermal Transports and Energy Conversions
- Numerical simulation of welding distortions in large structures with a simplified engineering approach
- Investigation on the effect of electrode tip on formation of metal droplets and temperature profile in a vibrating electrode electroslag remelting process
- Effect of North Wall Materials on the Thermal Environment in Chinese Solar Greenhouse (Part A: Experimental Researches)
- Three-dimensional optimal design of a cooled turbine considering the coolant-requirement change
- Theoretical analysis of particle size re-distribution due to Ostwald ripening in the fuel cell catalyst layer
- Effect of phase change materials on heat dissipation of a multiple heat source system
- Wetting properties and performance of modified composite collectors in a membrane-based wet electrostatic precipitator
- Implementation of the Semi Empirical Kinetic Soot Model Within Chemistry Tabulation Framework for Efficient Emissions Predictions in Diesel Engines
- Comparison and analyses of two thermal performance evaluation models for a public building
- A Novel Evaluation Method For Particle Deposition Measurement
- Effect of the two-phase hybrid mode of effervescent atomizer on the atomization characteristics
- Erratum
- Integrability analysis of the partial differential equation describing the classical bond-pricing model of mathematical finance
- Erratum to: Energy converting layers for thin-film flexible photovoltaic structures
Articles in the same Issue
- Regular Articles
- Non-equilibrium Phase Transitions in 2D Small-World Networks: Competing Dynamics
- Harmonic waves solution in dual-phase-lag magneto-thermoelasticity
- Multiplicative topological indices of honeycomb derived networks
- Zagreb Polynomials and redefined Zagreb indices of nanostar dendrimers
- Solar concentrators manufacture and automation
- Idea of multi cohesive areas - foundation, current status and perspective
- Derivation method of numerous dynamics in the Special Theory of Relativity
- An application of Nwogu’s Boussinesq model to analyze the head-on collision process between hydroelastic solitary waves
- Competing Risks Model with Partially Step-Stress Accelerate Life Tests in Analyses Lifetime Chen Data under Type-II Censoring Scheme
- Group velocity mismatch at ultrashort electromagnetic pulse propagation in nonlinear metamaterials
- Investigating the impact of dissolved natural gas on the flow characteristics of multicomponent fluid in pipelines
- Analysis of impact load on tubing and shock absorption during perforating
- Energy characteristics of a nonlinear layer at resonant frequencies of wave scattering and generation
- Ion charge separation with new generation of nuclear emulsion films
- On the influence of water on fragmentation of the amino acid L-threonine
- Formulation of heat conduction and thermal conductivity of metals
- Displacement Reliability Analysis of Submerged Multi-body Structure’s Floating Body for Connection Gaps
- Deposits of iron oxides in the human globus pallidus
- Integrability, exact solutions and nonlinear dynamics of a nonisospectral integral-differential system
- Bounds for partition dimension of M-wheels
- Visual Analysis of Cylindrically Polarized Light Beams’ Focal Characteristics by Path Integral
- Analysis of repulsive central universal force field on solar and galactic dynamics
- Solitary Wave Solution of Nonlinear PDEs Arising in Mathematical Physics
- Understanding quantum mechanics: a review and synthesis in precise language
- Plane Wave Reflection in a Compressible Half Space with Initial Stress
- Evaluation of the realism of a full-color reflection H2 analog hologram recorded on ultra-fine-grain silver-halide material
- Graph cutting and its application to biological data
- Time fractional modified KdV-type equations: Lie symmetries, exact solutions and conservation laws
- Exact solutions of equal-width equation and its conservation laws
- MHD and Slip Effect on Two-immiscible Third Grade Fluid on Thin Film Flow over a Vertical Moving Belt
- Vibration Analysis of a Three-Layered FGM Cylindrical Shell Including the Effect Of Ring Support
- Hybrid censoring samples in assessment the lifetime performance index of Chen distributed products
- Study on the law of coal resistivity variation in the process of gas adsorption/desorption
- Mapping of Lineament Structures from Aeromagnetic and Landsat Data Over Ankpa Area of Lower Benue Trough, Nigeria
- Beta Generalized Exponentiated Frechet Distribution with Applications
- INS/gravity gradient aided navigation based on gravitation field particle filter
- Electrodynamics in Euclidean Space Time Geometries
- Dynamics and Wear Analysis of Hydraulic Turbines in Solid-liquid Two-phase Flow
- On Numerical Solution Of The Time Fractional Advection-Diffusion Equation Involving Atangana-Baleanu-Caputo Derivative
- New Complex Solutions to the Nonlinear Electrical Transmission Line Model
- The effects of quantum spectrum of 4 + n-dimensional water around a DNA on pure water in four dimensional universe
- Quantum Phase Estimation Algorithm for Finding Polynomial Roots
- Vibration Equation of Fractional Order Describing Viscoelasticity and Viscous Inertia
- The Errors Recognition and Compensation for the Numerical Control Machine Tools Based on Laser Testing Technology
- Evaluation and Decision Making of Organization Quality Specific Immunity Based on MGDM-IPLAO Method
- Key Frame Extraction of Multi-Resolution Remote Sensing Images Under Quality Constraint
- Influences of Contact Force towards Dressing Contiguous Sense of Linen Clothing
- Modeling and optimization of urban rail transit scheduling with adaptive fruit fly optimization algorithm
- The pseudo-limit problem existing in electromagnetic radiation transmission and its mathematical physics principle analysis
- Chaos synchronization of fractional–order discrete–time systems with different dimensions using two scaling matrices
- Stress Characteristics and Overload Failure Analysis of Cemented Sand and Gravel Dam in Naheng Reservoir
- A Big Data Analysis Method Based on Modified Collaborative Filtering Recommendation Algorithms
- Semi-supervised Classification Based Mixed Sampling for Imbalanced Data
- The Influence of Trading Volume, Market Trend, and Monetary Policy on Characteristics of the Chinese Stock Exchange: An Econophysics Perspective
- Estimation of sand water content using GPR combined time-frequency analysis in the Ordos Basin, China
- Special Issue Applications of Nonlinear Dynamics
- Discrete approximate iterative method for fuzzy investment portfolio based on transaction cost threshold constraint
- Multi-objective performance optimization of ORC cycle based on improved ant colony algorithm
- Information retrieval algorithm of industrial cluster based on vector space
- Parametric model updating with frequency and MAC combined objective function of port crane structure based on operational modal analysis
- Evacuation simulation of different flow ratios in low-density state
- A pointer location algorithm for computer visionbased automatic reading recognition of pointer gauges
- A cloud computing separation model based on information flow
- Optimizing model and algorithm for railway freight loading problem
- Denoising data acquisition algorithm for array pixelated CdZnTe nuclear detector
- Radiation effects of nuclear physics rays on hepatoma cells
- Special issue: XXVth Symposium on Electromagnetic Phenomena in Nonlinear Circuits (EPNC2018)
- A study on numerical integration methods for rendering atmospheric scattering phenomenon
- Wave propagation time optimization for geodesic distances calculation using the Heat Method
- Analysis of electricity generation efficiency in photovoltaic building systems made of HIT-IBC cells for multi-family residential buildings
- A structural quality evaluation model for three-dimensional simulations
- WiFi Electromagnetic Field Modelling for Indoor Localization
- Modeling Human Pupil Dilation to Decouple the Pupillary Light Reflex
- Principal Component Analysis based on data characteristics for dimensionality reduction of ECG recordings in arrhythmia classification
- Blinking Extraction in Eye gaze System for Stereoscopy Movies
- Optimization of screen-space directional occlusion algorithms
- Heuristic based real-time hybrid rendering with the use of rasterization and ray tracing method
- Review of muscle modelling methods from the point of view of motion biomechanics with particular emphasis on the shoulder
- The use of segmented-shifted grain-oriented sheets in magnetic circuits of small AC motors
- High Temperature Permanent Magnet Synchronous Machine Analysis of Thermal Field
- Inverse approach for concentrated winding surface permanent magnet synchronous machines noiseless design
- An enameled wire with a semi-conductive layer: A solution for a better distibution of the voltage stresses in motor windings
- High temperature machines: topologies and preliminary design
- Aging monitoring of electrical machines using winding high frequency equivalent circuits
- Design of inorganic coils for high temperature electrical machines
- A New Concept for Deeper Integration of Converters and Drives in Electrical Machines: Simulation and Experimental Investigations
- Special Issue on Energetic Materials and Processes
- Investigations into the mechanisms of electrohydrodynamic instability in free surface electrospinning
- Effect of Pressure Distribution on the Energy Dissipation of Lap Joints under Equal Pre-tension Force
- Research on microstructure and forming mechanism of TiC/1Cr12Ni3Mo2V composite based on laser solid forming
- Crystallization of Nano-TiO2 Films based on Glass Fiber Fabric Substrate and Its Impact on Catalytic Performance
- Effect of Adding Rare Earth Elements Er and Gd on the Corrosion Residual Strength of Magnesium Alloy
- Closed-die Forging Technology and Numerical Simulation of Aluminum Alloy Connecting Rod
- Numerical Simulation and Experimental Research on Material Parameters Solution and Shape Control of Sandwich Panels with Aluminum Honeycomb
- Research and Analysis of the Effect of Heat Treatment on Damping Properties of Ductile Iron
- Effect of austenitising heat treatment on microstructure and properties of a nitrogen bearing martensitic stainless steel
- Special Issue on Fundamental Physics of Thermal Transports and Energy Conversions
- Numerical simulation of welding distortions in large structures with a simplified engineering approach
- Investigation on the effect of electrode tip on formation of metal droplets and temperature profile in a vibrating electrode electroslag remelting process
- Effect of North Wall Materials on the Thermal Environment in Chinese Solar Greenhouse (Part A: Experimental Researches)
- Three-dimensional optimal design of a cooled turbine considering the coolant-requirement change
- Theoretical analysis of particle size re-distribution due to Ostwald ripening in the fuel cell catalyst layer
- Effect of phase change materials on heat dissipation of a multiple heat source system
- Wetting properties and performance of modified composite collectors in a membrane-based wet electrostatic precipitator
- Implementation of the Semi Empirical Kinetic Soot Model Within Chemistry Tabulation Framework for Efficient Emissions Predictions in Diesel Engines
- Comparison and analyses of two thermal performance evaluation models for a public building
- A Novel Evaluation Method For Particle Deposition Measurement
- Effect of the two-phase hybrid mode of effervescent atomizer on the atomization characteristics
- Erratum
- Integrability analysis of the partial differential equation describing the classical bond-pricing model of mathematical finance
- Erratum to: Energy converting layers for thin-film flexible photovoltaic structures

