Review of muscle modelling methods from the point of view of motion biomechanics with particular emphasis on the shoulder

Radosław Bednarski; Adrianna Bielak; Adam Wojciechowski

doi:10.1515/phys-2019-0056

Article Open Access

Review of muscle modelling methods from the point of view of motion biomechanics with particular emphasis on the shoulder

Radosław Bednarski , Adrianna Bielak and Adam Wojciechowski

Published/Copyright: October 4, 2019

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information Explore this Subject

From the journal Open Physics Volume 17 Issue 1

Abstract

Correct modelling of human muscle is very difficult issue. The digital model can be used for understandig, how the muscle works, what kinds of processes take places during their work. It can be also used for check correctness of animation synteze. Researchers have developed many methods for creating shoulder models. They differ not only in the approach to creating models, but also in applications. In this article, the authors reviewed the methods of modelling muscles and applied these models for possible application in biomechanics.

Keywords: deltoid; muscle modelling; biomechanics; shoulder

PACS: 87.85.gj; 87.19.Ff; 87.19.rs

1 Introduction

Modelling human muscles, is a difficult but important issue to help in getting to know: their structure, processes taking place during muscle work, and biomechanics of movement. Various methods for modelling muscles can be found in the literature. They differ not only in the approach to creating models, but also in their application. One of the most difficult muscles to model is the shoulder muscle model. Due to its complexity, the shoulder joint is perceived as one of the most difficult to reproduce. The main emphasis in creating the model of this pond is located on

the deltoid, as it has the greatest impact on movement in all planes. There are several methods to create a deltoid, among them we can distinguish: the use of lines, the use of a set of lines, 3D modelling, a model taking into account the thermochemical reaction and a model based on physical dependencies

2 Construction of human shoulder

The shoulder joint despite its simple anatomical structure is one of the more difficult modelling joints. The difficulty is caused by the mutual surrounding and interaction between the muscles that make up the shoulder joint. Numerous muscles and ligaments make the shoulder the most mobile structure in the human body. To describe the structure of the shoulder should begin with bone parts that include: humerus, humerus head, spatula, acetabulum, acromion, clavicle, clavivular joint, coracoid process. Equally extensive are the muscles affecting the shoulder movement, including: deltoid muscle, supraspinatus, infraspinatus muscle, teres minor, teres major, subscapularis (Figure 1).

Figure 1

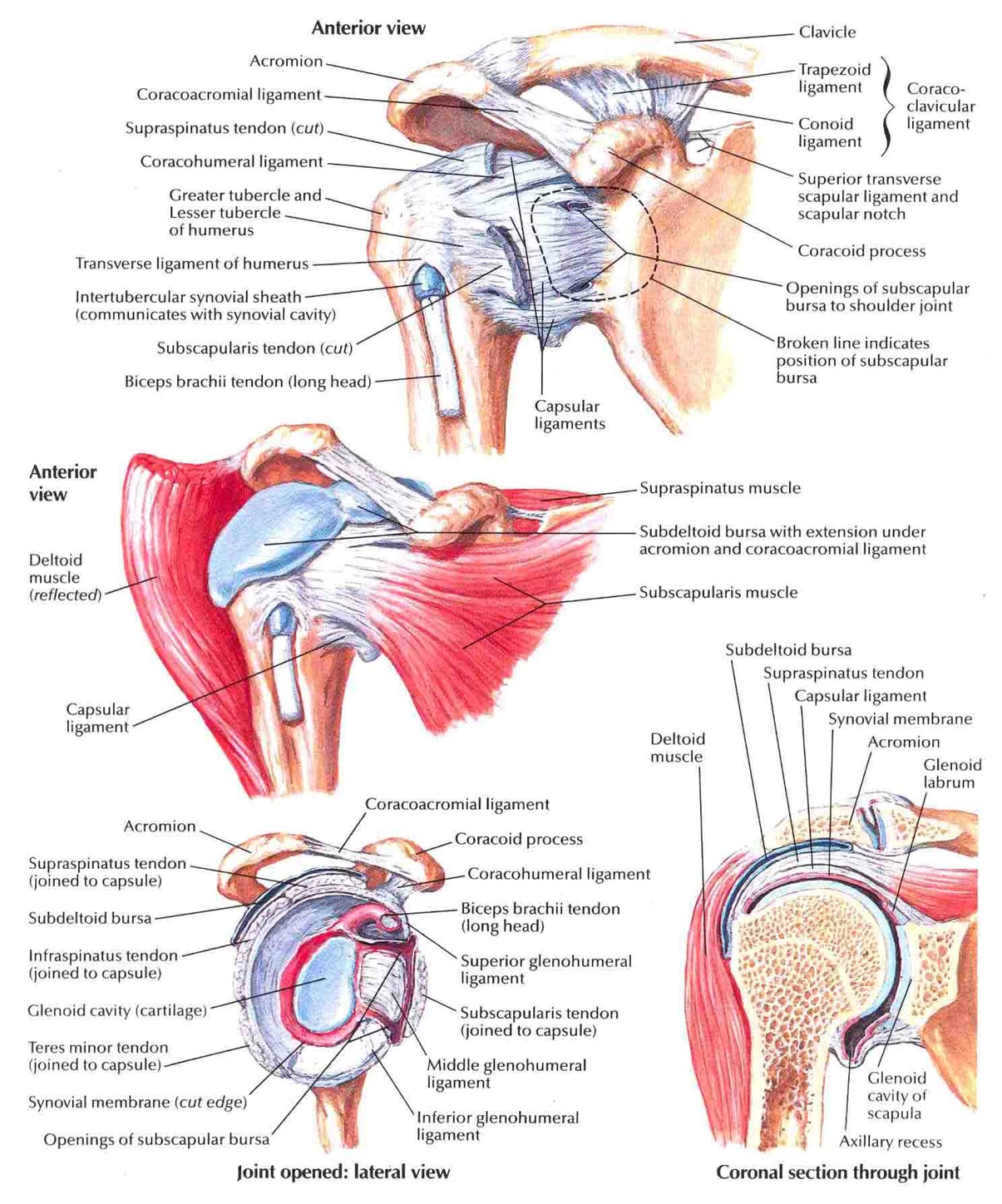
Shoulder joint anatomy

2.1 Structure and function of the deltoid muscle

The deltoid muscle is located on the outside of the shoulder, has three initial trailers, which are divided into parts (Figure 1):

The anterior clavicular part, attached to the end of the clavicle (The anterior or clavicular fibers)
The middle part - the shoulder part, attached to the shoulder process (Lateral or acromial fibers)
Back part - comb, attached to the comb (Posterior or spinal fibers)

The common end-trailer of all parts of the deltoid muscle is located in the humeral deltoid (delta tuberosity) of the humerus (Figure 1) From the point of view of the range of motion, the most commonly used muscle is the deltoid muscle. Contraction of all parts of the deltoid muscle causes the shoulder joint to move to the level. The tension of the deltoid muscle stabilizes the shoulder joint. Contraction of the anterior (clavicular) part is bent forward and the arm recurs. The back (comb) part bends backwards and inverts the arm. The middle part (shoulder) moves the arm to the level.

2.2 Movement in the shoulder joint

The correct movement of the shoulder joint depends on the bone, muscle and ligament components. Bone components alone can not guarantee the stability of the shoulder joint. To analyze the movement in the shoulder joint, the local coordinate system should be defined for the kinematic analysis. The following input parameters should be considered for the biomechanical model of the shoulder joint: rotations and chest positions, degrees of freedom of the shoulder strap, radial bone rotation, elbow and forearm movements, and wrist rotation. The following equations of the shoulder joint describe the rotation around the z (1a, 2a), y (1b, 2b), x (1c,2c) axes respectively:

left hand (Figure 2)

Figure 2

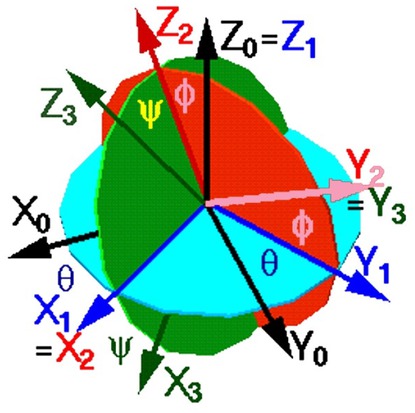
Movement for left hand

(1a) M z ( θ ) = cos ⁡ ( θ ) − sin ⁡ ( θ ) 0 sin ⁡ ( θ ) cos ⁡ ( θ ) 0 0 0 1

(1b) M y ( ϕ ) = cos ⁡ ( ϕ ) 0 sin ⁡ ( ϕ ) 0 1 0 − sin ⁡ ( ϕ ) 0 cos ⁡ ( ϕ )

(1c) M x ( ψ ) = 1 0 0 0 ] c o s ( ψ ) − sin ⁡ ( ψ ) 0 sin ⁡ ( ψ ) cos ⁡ ( ψ )

right hand (Figure 3)

Figure 3

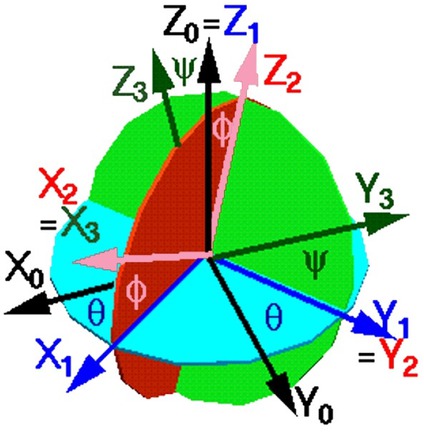
Movement for right hand

(2a) M z ( θ ) = cos ⁡ ( θ ) − sin ⁡ ( θ ) 0 sin ⁡ ( θ ) cos ⁡ ( θ ) 0 0 0 1

(2b) M y ( ψ ) = cos ⁡ ( ψ ) 0 sin ⁡ ( ψ ) 0 1 0 − sin ⁡ ( ψ ) 0 cos ⁡ ( ψ )

(2c) M x ( ϕ ) = 1 0 0 0 cos ⁡ ( ϕ ) − sin ⁡ ( ϕ ) 0 sin ⁡ ( ϕ ) cos ⁡ ( ϕ )

Considering the construction of the joint for individual movements, we can determine their ranges in accordance with the ISOM standard (Table 1)

Table 1

The joint ranges for individual movements in accordance with the ISOM standard.

Joint name	The plane of movement	Kind of movement
Hoop of upper limbs	Sagital	extension - 0 - flexion
	Frontial	abduction - 0 - addiction
	Transverse	extension - 0 flexion
	Rotation	external rotation - 0 - internal rotation
	Rotation	external rotation - 0 -internal rotation

Joint name	Plane symbol	Standard according to ISOM in deegres
Hoop of upper limbs	S	50 - 0 - 170
	F	170 - 0 - 0
	T	30 - 0 - 135
	R(F0)*	60 - 0 - 70
	R(F90)**	90 - 0 - 80

R (F0) * - external and internal rotation in the shoulder joint are examined in the frontal plane when the arm is in the attachment> F0

R (F90) ** - external and internal rotation in the shoulder joint are examined in the frontal plane when the arm is in the advent 90> F90

3 Review of muscle modelling methods

In the current research, the approach to shoulder muscle modelling differed not only in the different methods of model creation, but also in its subsequent use. In the papers analyzed by us, the authors proposed methods based on: the 3D finite elements methode (FEM), numerical methods, B-spline methods, imaging methods of rope muscles (single lines), muscle simulations using biomechanical equations. The first significant work on muscle modelling took place in 1996. In the article [1] the authors presented the calf muscle model, modeled using the finite volume method. The purpose of the 3D model was to enable the simulation of operations. The model focuses on: deformation calculation speed, optimization (regardless of the time costs before calculation), visual correctness of the model, the possibility of making cuts in the model. The proposed system for simulating the operation was based on the method of elastic deformation. The authors showed that the simulation of operations for the proposed model took place in real time.

In 1998, in the article [2], the authors proposed a method with the use of a solid B-spline to make a model of soleus being a part of the calf, with the assumption that it can be used to create a library that will allow multiple use of it to creating deformable models of the human body. In their work, the authors used algorithms to minimize muscle distortion that may arise during the fit of the B-spline shape to the shape of the muscle.

The authors divided the creation of the model’s into the following stages:

Acquiring data from the Visible Human Male set and calf muscle images (cross-sections)
Building a volume sampling function CVSF (continuous volume sampling function)
Matching selected data to B-spline (using the CVSF function)
Volume visualization of the muscle (after obtaining accurate data approximating the muscle using B-spline)

The authors compared the results of their work with data recorded in the Visible Human Data Set database. It was found that the proposed method is useful in modelling deformable skeletal muscles, because of its structure (control points and vectors) it is more optimal (contains less data) than polygons. The authors also stated that a properly designed CVFS function provides information on the orientation of human muscle fibers. The authors also see the imperfections of the applied method, want to refine the B-spline body model to prepare the ground for further research on its application for invasive surgical simulation using functional, deformable tissue models, especially with skeletal muscles.

In the article [3] the author presented a new approach to muscle modelling. He used the Usik model developed in 1973 [4] taking into account the thermomechanics of continuous media. This enabled the coupling of mechanical, electrical, chemical and thermal phenomena in muscle tissue. The author described the model in the article but did not implement it. From the point of view of muscle modelling, it was an innovative approach, which according to the author had limited usefulness with quite significant scientific and didactic values. The limited practical utility of the model resulted from the number of scalar equations (46 + 4n + 2r, where n - the number of components, r - the number of reactions), which with the power of contemporary computers was a rather complex problem. The implementation of the Usik model is described in the article [5]. The authors described in it the calf muscle model, made with regard to thermomechanical parameters and B-splines. The model made by the authors was compared with real calf muscle models. The authors showed that using the Usik model can be obtained in a complete muscle model, which can be used in further studies on both simu lations, e.g. surgery and research on the correctness of motion biomechanics in computer animation.

A different method of modelling the behavior of the upper limb is presented in the doctoral dissertation by D. Ziemiański [6]. The author presented the physical model of the kinematic chain of the upper limb obtained by parametric synthesis. Parameters were obtained as a result of numerical analysis of data obtained from real measurements made on a specially constructed test bench and selected to minimize the difference between the output signals recorded on the real object and signals registered at the model output. The work uses a flat biomechanical model (Figure 4) and an original model modelling moments in the joints. According to the author of the dissertation, the proposed mathematical model of the upper limb was undefined. The only way to find unknown parameters is to introduce additional dependencies describing the activity of human muscles. The results obtained may be helpful in diagnosing the disease of the overload syndrome. They can also be used to assess the frequency and location of expected damage to the musculoskeletal system.

Figure 4

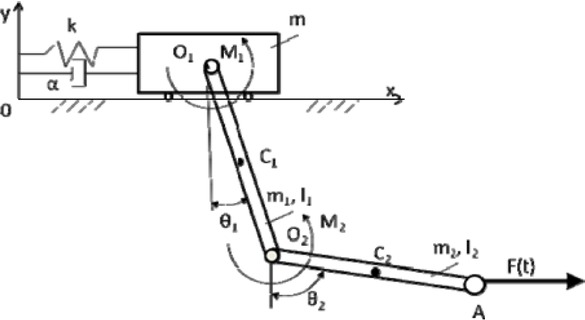
Biomechanical model of upper limb

In 2011 L.A.Spyrou together with N. Aravase developed a fourth generation 3D model for the muscles and tissue of the tendon [7]. The nonlinear model was velocity dependent and had anisotropy due to the local arrangement of muscle fibers. It allowed for the implementation of active and passive muscle behavior. The tension of the muscle fibers depended on the load (length), strain rate (speed) and muscle activation level, while the tendon fiber showed only passive behavior, and stress depended only on deformation. The model was used to simulate parallel muscles (biceps) and oblique muscles, semi-sinew muscle. Although both models were created on the basis of real data obtained during the patient’s examination by means of tomography (CT) and resonance (MRI), it did not include thermomechanical reactions in the muscle, which were proposed in the Usik model.

In 2014 J.Webb, S.Blemker and S.Depl create an 3d model of based on developed 3D finite element models of the deltoid and rotator cuff muscles and used the models to examine muscle function shoulder [8]. The image obtained with the help of an MRI of a single healthy object, 26 years without injuries. (human) has been divided into segments in order to obtain individual anatomical structures to which the finite element mesh was matched. The bones were presented as rigid bodies. The proposed method allowed to create a 3D model of the arm muscle considering the diversity of the length of muscle fibers. The model allows you to study muscle reactions during movements (trailers, contacts between particular structures). The authors describe that in some places inaccurate results were obtained in the coupling between individual muscles groups. There were significant differences between the models composed of the line,which was used in earlier works, and the model presented in the article. Linear models are not adapted to muscle building, therefore there are differences in model change in the case of rotational motion compared to the model 3D. 3D models predicted significant muscle variability during arm movement which was not included in the linear model. In the rope model, there are no movement restrictions for individual muscles, which meant that individual parties could move freely in relation to each other. The 3D model allows you to introduce movement restrictions of individual structures in relation to each other.

In the same year K.Ch. Edward, B. Dimitra, F.K. Robert and A.J. van den Bogert published the model originally built in SIMM (MusculoGraphics, Inc.) using anatomical data from corpses [9]. These data are available on SimTK.org Later the model was imported into Opensim, where the functions of the arm and the length of the muscles were generated. Simulation of the model was performed by using Matlab and C language. It consisted of seven body segments (chest, collar bone, shoulder blade, humerus, ulna, radius and arm) and eleven degrees of freedom (three perpendicular hinges in sternoclavicular joints, clavicular - clavicular and brachiocephalic as well as elbow-prolonged flexion and forearm supination). It contained 138 muscle elements. The goal was to check the dynamic performance and mechanical behavior of the arm and shoulder girdle in real time. The flexion of the arm turned out faster the real time and modelled maximum isometric torque values were correct in comparison to literature values. The authors pointed out the problem that in the case of muscle stretching the model values were lower than in the literature, while in the case of the adduction movement they were higher.

Table 2

The summary of the described models.

Publication number in references	Modeled muscle	Modeling method	Conclusion
1	Calf muscle	The method (elements) of 3D finite volumes. Four methods of elastic deformation in real time	System for simulating operations using the applied elastic deformation methods. The authors showed that real-time simulation of the proposed muscle models is possible
2	Soleus - a part of calf muscle	Solid B-splajn method with CVSF function for match B-splajn to muscle shape. Data obtained from Visible Human Data Set	The usefulness of using B-splajn for modeling deformable skeletal muscle models has been demonstrated. B-splajn defined with control points and vectors contain less data that sets of polygons. The proposed method allows volumetric analysis of shapes. The proposed solution was compared with the data from the Visible Humans data set
3	The work presents a little-known Usik model which through the use of thermo-mechanics of continuous media, allows the coupling of mechanical, electrical, chemical and thermal phenomena in muscle tissue. The model was compared with classic muscle models	Balance equations describing the causes of phenomena were used: mass balance, mass balance of the k-th component, balance of momentum, entropy balance, free energy balance	General results, total number of equations scalar is 46 + 4n + 2r (n - number of components, r- number of reactions), according to the authors of the model too complex for engineering applications, however interesting from the point of view of knowledge due to a comprehensive description of reactions and their connections. No model implementation
5	Gastrocnemius	Solid B-splajn with implementation of the continuum Usik model. The system describing motion of the continuous medium under consideration, possessing mechanochemical reactions, contains the following equations: equation of continuity having displacement vector, equation of conservation of momentum which takes into account stress tensor, chemical potential, the second rank tensor, mass density, the affinity of the chemical reaction, deviator of the stress tensor, time, equation of conservation of mass of the components with deviator of the stress tensor, velocity of the influx, scalar of the rate formation, chemical potential, time, equation of heat influx containing tensor parameter (biofactor), a one control point form the B-spline v solid, mass density, thermodynamic free energy, scalars of the rate formation, absolute temperature, deformation, source density, deviator of the stress tensor, mass concentration, mass, time	The 3D gastrocnemius model was created as a combination of 3D representation through B-spline solids and the continuum Usik's model and was successful. It is close to the actual muscle structure, which affects the better relevance of results in the case of the Usik's model which although focusing on mechanical and chemical phenomena occurring in the muscle takes into account the actual muscle structure, i.e. it does not interpret it as blocks and springs and as a continuum material composed of several layer with specific properties
6	The physical model of the kinematic chain of the upper limb obtained by parametric synthesis. A flat biomechanical model was used in the work and an original model was used in the work and an original model modeling the moments in the joints of the upper limb	The parameters were obtained as a result of numerical data analysis obtained from real measurements made on a special basis constructed test bench and selected so as to minimize the difference between the output signals recorded on the real object and signals registered at the model output	The obtained results may be helpful in explaining the diseases of the overload syndrome. They can also be used to assess the frequency and location of expected damage to the musculoskeletal system
7	A 3D constitutive model for muscle and tendon tissue was developed. A non-linear speed-dependent and anisotropic model due to the local arrangement of muscle fibers	Active and passive muscle behavior was taken into account. The tension of muscle fibers depends on the load (length), the rate of deformation (speed) and the level of muscle activation, while the tendinous fiber has only passive behavior, and the stress depends only on the deformation	The behavior of parallel-fibered and pennate muscles, as well as the human semitendinosus muscle, is studied
8	Shoulder muscle	The finite elements methode (FEM). Presentation of the muscle by means of a solids (not a line - fibers)	The proposed method allowed to create a 3D model of the arm muscle considering the diversity of the length of muscle fibers
9	The 3D Shoulder Girdle and Arm Dynamics model	The model consisted of seven body segments and elecen degrees of freedom and contained 138 muscle elements The method of finite 3D elements. Presentation of the muscle by means of a solids (not a line - fibers)	The flexion of the arm turned out faster the real time and modelled maximum isometric torque values were correct in comparison to literature values. Muscle stretching values of the model were lower that in the literature, while in the case of the adduction movement they were higher
10	A musculoskeletal model of the human shoulder	The synovial articulations were ideal ball, the bones were rigid bodies and that the muscles are frictionless, massless cables wrapping over the skeletal structure. The relationship between muscle strength and motion was defined by the arm moment of muscles. Muscles were geometrically modeled by defining the arm cables around each joint	The purpose was to estimating forces in the glenohumeral joint and in the muscles. The model was similar with many models of cable-driven robots and corresponded to the requirements of the dynamic shoulder model. The model does not activate the forechest and suggested that the cables of the model could be wrongly spread around the bones in 3D space by incorrectly attaching the muscle to the bone
11	A numerical 3D model of the muscoloskeletal shoulder	The input data to the kinematic model was used to isolate the performance of this part of the model. The optimized angles between the clavicle relative to the thorax and the shoulder in relation to the chest were compared to the input angles, calculating the peak differences between the rotations and the square root (RMS) of the rotation difference. Changing the input angles of the axial rotation of the clavicle and the rotation of the forward blade were used to test their effect on the angles being processed	The model grave valuable information on the pitching motion of sports and get more insight into the biomechanical aspects of pitching motion to help e.g. in reducing the injury risk. There were several problems: that maximum force of the model could be too limited, there was the lack of proper kinematic recordings and the extreme character of the motion was occured

In the article [10] D. Ingram presented a musculoskeletal model of the human shoulder as a part of the PhD thesis. The main assumptions of the model was that the synovial articulations were ideal ball, the bones were rigid bodies and that the muscles are frictionless, massless cables wrapping over the skeletal structure. The relationship between muscle strength and motion was defined by the arm moment of muscles. Muscles were geometrically modeled by defining the arm cables around each joint. The author adopted the term cable as simply flexible tubes similar in shape to the muscle fibers. A torque on each joint that contributes to movement was constructed by multiplying of the strength of the cable by its arm of the muscle. The model also included an ellipsoid model of the scapulothoracic contact. It was created by the author for the purpose of estimating forces in the glenohumeral joint and in the muscles. The model was similar with many models of cable-driven robots and corresponded to the requirements of the dynamic shoulder model. However the author [10] pointed out that the model does not activate the forechest and suggested that the cables of the model could be wrongly spread around the bones in 3D space by incorrectly attaching the muscle to the bone.

Another approach in the master’s thesis was presented by the P.Hordijk in 2017 [11]. The author created a numerical model without graphical representation. First, the input data to the kinematic model was used to isolate the performance of this part of the model. The optimized angles between the clavicle relative to the thorax and the shoulder in relation to the chest were compared to the input angles, calculating the peak differences between the rotations and the square root (RMS) of the rotation difference. The relative length of the muscle was compared to the active force and length relationship. Changing the input angles of the axial rotation of the clavicle and the rotation of the forward blade were used to test their effect on the angles being processed. Here the movement was determined by a selected group of athletes. The model gave valuable information on the pitching motion of sports and get more insight into the biomechanical aspects of pitching motion to help e.g. in reducing the injury risk. The author pointed out several problems: that maximum force of the model could be too limited, there was the lack of proper kinematic recordings and the extreme character of the motion was occured.

4 Summary

The most important justification for creating reviews of the musculoskeletal models is the high demand for such models, which allow the study of the behavior of the musculoskeletal structures in a dynamic state. The arm, which has the ability to generate a wide variation of motion, thus being a contraction pond, requires special interest in this aspect. This kind of simulation is needed in the context of validate a new movement in sport to check potentially injured movements (e.g. swimming with a crawl, hitting the ball, American football kicks, etc.) to determine what kind of force can cause injury and in which phase of movement [10]. On the other hand, such models are needed in medicine in a situation in which the patient suffered a serious injury (e.g. breaking/tearing of soft structures) and there is a need to check whether the current state of soft structures is functioning properly after rehabilitation. If it can be examined in a static state with the help of RM/MRI, then in the dynamic state is is impossible [5].

As a summary, a table collecting models described by the authors is presented below (Table 2).

References

[1] Bro-Nielsen M., Cotin S.,Real-time Volumetric Deformable Models for Surgery Simulation using Finite Elements and Condensation, Dept. of Mathematical Modelling, Technical University of Denmark, In: Computer Graphics Forum, 1996,vol. 15(3), p. 57-6610.1111/1467-8659.1530057Search in Google Scholar

[2] Ng-Thow-Hing V., Agur A., Ball K.A., Fiume E., McKee N., Shape reconstruction and subsequent deformation of soleus muscle models using B-spline solid primitives, Proc. SPIE 3254, Laser-Tissue Interaction IX, 199810.1117/12.308192Search in Google Scholar

[3] Oracz M., Usik model and classical models of muscular tissue, Zakład Mechaniki, Instytut Techniki Lotniczej i Mechaniki Stosowanej, Politechnika Warszawska, Warszawa. In: Current Problems of Biomechanics,2007, vol. 7(1), p. 159–164Search in Google Scholar

[4] Usik P.I., Continual mechanochemical model of muscular tissue, In: PMM Vol.37, Np3, 1973, pp. 448-458, Moscow10.1016/0021-8928(73)90086-5Search in Google Scholar

[5] Bielak A., Bednarski R., Wojciechowski A., 3D Modeling of Leg Muscle Using Mechanochemical Representations ofMuscular Tissue and Solid Fibers. In: Pietka E., Badura P., Kawa J., Wieclawek W. (eds) Information Technology in Biomedicine. ITIB 2018. Advances in Intelligent Systems and Computing,2019, vol 762. Springer, Cham10.1007/978-3-319-91211-0_39Search in Google Scholar

[6] Ziemiański D., Identyfikacja i modelowanie wybranych zachowań dynamicznych układu człowiek – otoczenie, PhD thesis , Cracow University of Technology, 2011(in Polish)Search in Google Scholar

[7] Spyrou L.A., Aravas N., Muscle and Tendon Tissues: Constitutive Modeling and Computational Issues, Department of Mechanical Engineering, University of Thessaly, The Mechatronics Institute, Center for Research and Technology Thessaly Volos, Greece. In: Journal of Applied Mechanics, 2011, vol. 78(4)Search in Google Scholar

[8] Webb J.D., Blemker S.S., Delp S.L., 3D finite element models of shoulder muscles for computing lines of actions and moment arms, Computer Methods in Biomechanics and Biomedical Engineering 201410.1080/10255842.2012.719605Search in Google Scholar PubMed PubMed Central

[9] Chadwik E.K.,Blana D., Kirsch R.F., van den Bogert A.J., Real-Time Simulation of Three-Dimensional Shoulder Girdle and Arm-Dynamics, IEEE Transactions on Biomedical Engineering,2014, 61(7),p. 1947–195610.1109/TBME.2014.2309727Search in Google Scholar PubMed PubMed Central

[10] Ingram D., Musculoskeletal Model of the Human Shoulder for Joint Force Estimation, PhD thesis in Systeme de Production Et Robotique, École polytechnique fédérale de Lausanne, 2015Search in Google Scholar

[11] Hordijk P., Musculoskeletal modelling of the shoulder during baseball pitching: A research combining 3D kinematic measurements with musculoskeletal modelling, master thesis, Delft University of Technology, 2017Search in Google Scholar

Received: 2019-05-31

Accepted: 2019-07-13

Published Online: 2019-10-04

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/phys-2019-0056

Keywords for this article

deltoid; muscle modelling; biomechanics; shoulder

Creative Commons

BY 4.0