Abstract
Polarization is a fundamental property of light that can be engineered and controlled efficiently with optical metasurfaces. Here, we employ chiral metasurfaces with monoclinic lattice geometry and achiral meta-atoms for resonant engineering of polarization states of light. We demonstrate, both theoretically and experimentally, that a monoclinic metasurface can convert linearly polarized light into elliptically polarized light not only in the linear regime but also in the nonlinear regime with the resonant generation of the third-harmonic field. We reveal that the ellipticity of the fundamental and higher-harmonic fields depends critically on the angle of the input linear polarization, and the effective chiral response of a monoclinic lattice plays a significant role in the polarization conversion.
1 Introduction
Among many remarkable achievements associated with the name Federico Capasso, metasurfaces play an important role as efficient planar components of future photonic devices [1], [2], [3]. One of the fundamental functionalities of metasurfaces is the control of polarization of light, which is a versatile degree of freedom that can be manipulated or engineered for numerous applications [4], [5]. Conventional approaches to manipulating polarization often rely on bulk components such as wave plates. Although effective, these components are constrained by their size.
Metasurfaces, composed of subwavelength structures, that is, meta-atoms, are powerful tools for overcoming size and weight limitations, allowing ultra-thin and multifunctional optical devices [6], [7], [8]. The operational principle for using metasurfaces in the control of polarization relies on transforming an incident waveform into an ensemble of individual beams generated by meta-atoms with different polarization states that beat along the optical axis, thereby changing the resulting polarization at will. Many recent papers have been devoted to the study of linear polarization conversion with single metasurfaces (see, e.g. Refs. [9], [10], [11], [12], [13]), as well as multiple metasurfaces with stacking and twisted configurations [14], [15]. Polarization transformations with metasurfaces have been extensively explored by the Federico Capasso group [16], [17], [18]. In particular, the designer-specified polarization response was shown to be employed for computer-generated holograms whose far-fields implement parallel polarization analysis and customized waveplates [18]. Additionally, full-stokes polarization encoding in metasurfaces has been demonstrated in both the near [19], [20] and far-field regimes [21], [22].
Chiral metasurfaces are particularly suitable for polarization engineering because of their inherit ability to mix polarization states, e.g. to convert directly linearly polarized light into elliptically or circularly polarized states [23]. The use of resonant effects in metasurfaces has been demonstrated to enhance polarization conversion efficiencies and enable functionalities such as circularly polarized lasing and high-contrast polarization detection [24], [25], [26] as well as achieving huge imbalance in the third harmonic intensity depending on the helicity of the input field [27].
In this work, we uncover the hidden potential of resonant chiral monoclinic metasurfaces, recently introduced and characterized in Ref. [28], for polarization conversion. While the previous study focused on circularly polarized input, this work explores the metasurfaces’ response from linearly polarized input, and expands this concept to the nonlinear polarization conversion for the generation of third-harmonic chiral fields (Figure 1). Using both computational and experimental approaches, we demonstrate their ability to convert linearly polarized light into elliptically polarized light in both the linear and nonlinear regimes. Specifically, we explore the third harmonic generation (THG) process and show that the ellipticity of the generated light is strongly dependent on the input polarization angle. By analyzing the role of chiral resonances, we underpin the underlying mechanisms that govern these effects, highlighting the versatility of monoclinic metasurfaces as compact polarization engineering platforms. This builds on previous work exploring multifunctional metasurfaces for polarization conversion and control [29], [30].

Concept of monoclinic chiral metasurfaces. (a) Design principle of the chiral metasurfaces utilizing monoclinic meta-atom lattices. (b) Schematic of a chiral metasurface which transforms incident linearly polarized plane wave into elliptically polarized light. (c) Scanning electron microscope (SEM) image of the fabricated metasurface.
2 Results
The object of our research is a chiral resonant dielectric metasurface, which consists of Si cylinders in a monoclinic arrangement on a SiO2 substrate. Such a metasurface is geometrically chiral, i.e. it does not possess any mirror symmetry: the up-down mirror symmetry is broken by the substrate, and all in-plane mirror symmetries are broken by the monoclinic arrangement itself. Circular dichroism studies of this metasurface can be found in Ref. [28].
Realization of a polarization transformation can be conveniently visualized on the unit Poincaré sphere [5], [31] via the following three parameters:
These parameters show the degrees of the vertical/horizontal (τ), diagonal/anti-diagonal (χ), and right-hand/left-hand circular polarizations (σ), see Figure 2. Here, the complex components of the electric field e
x
and e
y
are normalized so that |e
x
|2 + |e
y
|2 = 1. In the far-field plane the field is transverse, i.e. e
z
= 0. Experimentally, Stokes parameters are calculated by performing six different intensity measurements: vertical and horizontal I
V/H, diagonal and anti-diagonal I
D/A, polarized on the right and left circular I
R/L. The normalized Stokes parameters satisfy τ
2 + χ
2 + σ
2 ≤ 1, where “

Poincarè sphere and illustration of the polarization states.
The metasurface exhibits resonant behavior. The design parameters are as follows: the meta-atoms are cylinders with a height of 400 nm and a radius of 430 nm, composed of silicon (Si); the monoclinic arrangement is defined by two lattice vectors with lengths a = 1,100 nm and b = 1,000 nm, and a lattice angle of 105° (Figure 1a); the substrate is made of SiO2. We find several eigenmodes of the systems in the vicinity of the wavelength telecommunication range. In particular, there is an eigenmode with a resonant wavelength of 1,553 nm and Q-factor of Q ≈ 100. We show its electric field distribution in Figure 3a. Geometrically chiral metasurface supports chiral eigenmodes, however, their high level of chirality – selective interaction with right and left circularly polarized output channels – is not guaranteed, and has to be engineered [28], [32], [33], [34]. It was shown in Ref. [28] that the eigenmode in Figure 3a exhibits strong chiral properties, which manifests in a strong circular dichroism.
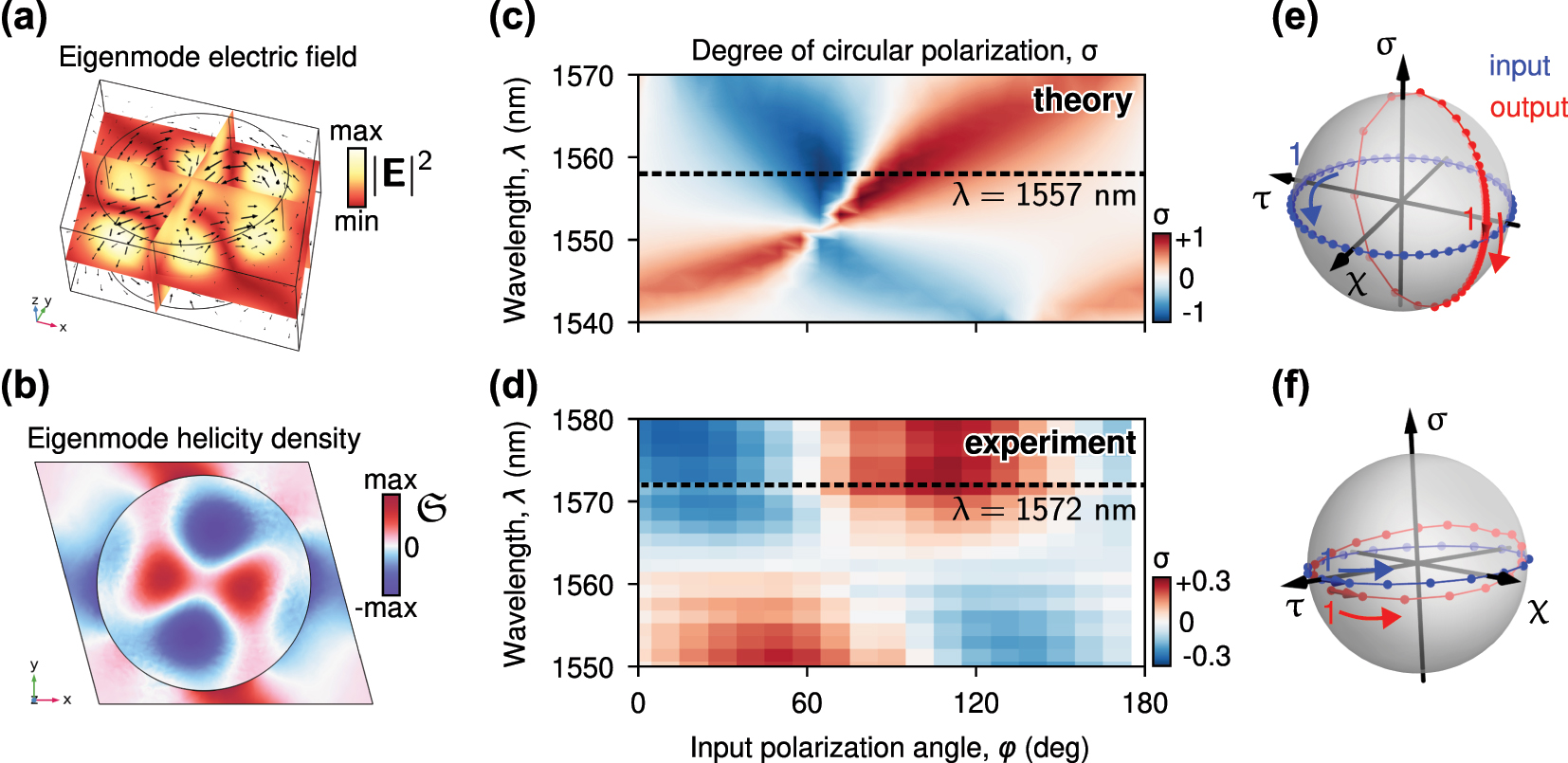
Linear chiral optical properties. Theoretical electric field (a) and helicity density (b) of the excited eigenmode at 1,557 nm. Theoretical (c) and experimental (d) degree of circular polarization σ dependence on input polarization angle and wavelength. Output theoretical (e) and experimental (f) polarization state (red dots) for various input linear polarization angles (blue dots) plotted on the Poincare sphere.
Additionally to the transmission properties of the resonant chiral metasruface with monoclinic lattice arrangement, we also shed the light on its local properties. Helicity density is a local property of the electromagnetic field distribution. In particular it has direct application in chiral sensing [35], [36], which is often referred as one of the promising applications of the chiral metasurfaces. For monochromatic field at frequency ω it is written as [37], [38], [39].
where E and H are the electric and magnetic fields, c is the speed of light. The quantity (2) characterizes the difference between the numbers of right-hand and left-hand circularly polarized photons. We plot the distribution of helicity density of the eigenmode in Figure 3b.
Next, we study the polarization transformation of such metasurface for the linearly polarized input light in the linear and nonlinear regime, i.e. polarization state of the third harmonic generation signal.
2.1 Polarization transformation in linear transmission
Here we examine the manifestation of the chiral mode of choice in the context of polarization transformation for the linearly polarized input. We set the input field to be a monochromatic linearly polarized plane wave at frequency ω and wave vector k = −
where angle φ shows linear polarization orientation with respect to the x-axis,
We incrementally change polarization angle φ in the range [0, π] with a constant step Δφ, as the results are π-periodic.
Adjusting the polarization angle φ and the wavelength λ of the incident wave, we examine the polarization of the outgoing signal (Figure 3c). Near the chiral resonance, the circular polarization degree σ is strongly dependent on λ and φ. At certain λ and φ, the transmitted field approaches circular polarization, |σ| ≈ 1. Although the input polarization states (4) are evenly spaced, the output states are not. This is illustrated on the Poincarè sphere in Figure 3e. In particular, the output states form a circle on the sphere, indicated by red dots.
To validate our theoretical prediction regarding the polarization change, we measure all Stokes parameters of light transmitted through the metasurface taking into account Eq. (1) (see Supplemental Material for experimental details). The experimentally determined values of σ, as a function of the wavelength and the input polarization angle, are presented in Figure 3d. The output light exhibits elliptical polarization around the optical resonance. The behavior observed qualitatively agrees with the theoretical protection. However, the degree of circular polarization varies from −0.18 to 0.26 at 1,572 nm. The output polarization state is illustrated in Figure 3f by red dots, while the input polarization state is also depicted by blue dots. The experimental pattern is similar to the theoretical prediction. The difference between theoretical and experimental results is primarily attributed to fabrication imperfections and the broad range of incident light wave vectors in the experiment, which result in different mode excitations to the theoretical prediction. We provide theoretical and experimental results for wider range in Supplementary Materials.
2.2 Polarization engineering of the third harmonic generation
At higher intensities, the electron oscillations within a dielectric structure become anharmonic, which can be effectively described using the extended Lorentz model [40]. In its bulk crystalline form, silicon is a centrosymmetric material, making second harmonic generation (SHG) symmetry-forbidden (except surface effects [41]). Therefore, the third harmonic generation (THG) was examined to demonstrate the nonlinear behavior of the metasurface. The nonlinear polarization current responsible for THG can be expressed as
The coupling strength of the incident field to the resonant mode strongly depends on the overlap integral between the two [28], [32], [34], [44]. This coupling shows a strong polarization dependence, providing different field distribution at the fundamental frequency E (ω) for different input polarizations, and hence different P (3ω) and third harmonic response.
We evaluate the nonlinear numerical results by calculating the THG emitted along the zeroth order for a linearly polarized pump and decomposing THG transmission signal into the right- and left-circular polarized components,

Nonlinear theory. (a) Third harmonic intensity output from a linearly polarized beam along x-axis. (b) Poincarè spheres which show simulated polarization states of the third harmonic output taken at different wavelengths for linear polarization input at different angles on the fundamental frequency. (c) The green and magenta lines are the intensity of the right and left circular polarization intensities of the third harmonic signal, respectively.
To test the theoretical predictions, we measure the THG from the metasurface (see Supplemental Material for more details). The laser wavelength was tuned from 1,500 to 1,730 nm at 5 nm intervals, while the polarization angle was varied from 0° to 180° with 10°. For each combination of these parameters, we record the THG spectra and extract the maximum values. Figure 5a shows the maximum THG value as a function of the pump wavelength and input polarization angle. We observe THG enhancement in both expected and unexpected spectral regions. The exact reason of such discrepancy between numerical simulations and experimental observation is rather unknown. However we speculate here on possible reasons:
imperfections in fabrications are much more noticeable on the scale of λ (3ω)/n ≃ 125 nm (the typical wavelength of the TH signal inside metasurface material with refractive index n), specifically at the cylinders edges where the high-harmonic modes are mostly localized as they resemble whispery gallery modes;
difference in the refractive index dispersion used in simulations and dispersion of the real sample, as the change of the refractive index tend to shift the position of the resonances;
deviation of excitation shape from a plane wave, which was used in the theoretical calculations.

Experimental nonlinear polarization properties. THG intensity (a) and degree of circular polarization (b) from the metasurface as a function of the pump wavelength and polarization angle. (c) Poincarè spheres illustrating polarization states of the output THG at 1,510 nm, 1,590 nm and 1,635 nm wavelengths for linear polarized input, varying linear polarization angle at the fundamental harmonic.
Numerical simulations of the THG intensity signal of the range shown in Figure 5a and typical mode profiles at 3ω frequencies are shown in Supplementary Materials.
To investigate the degree of circular polarization σ we extract this parameter from the THG data taking into account Eq. (1) – the dependence on the pump wavelength and input polarization angle is shown in Figure 5b. The results reveal complex dependencies with significant changes in the polarization state as the pump polarization angle. We provide a possible justification in the Supplementary Material. We further extract the polarization parameters for the resonant wavelengths 1,510 nm and 1,635 nm. These values are plotted on Poincarè spheres, showing σ ranges of −0.73 to 0.71 at the wavelength of 1,635 nm and −0.74 to 0.70 at 1,510 nm (Figure 5c). Like the theoretical results, these points do not lie in a single plane as we would expect from the experimental results, and reach higher values for circular polarization than those in the linear regime. In the non-resonant regime at 1,590 nm, while σ values are non-zero (−0.39 to 0.58), the low output intensity means other fabrication errors were likely to play a large role. The deviation between the experimental and theoretical results is attributed to the same factors as in the linear case. Additionally, the THG exhibits greater sensitivity to all possible imperfections and pump parameters compared to the linear regime. Considering the impact of the modes at the THG wavelength, it is challenging to fully replicate the simulated result in a real finite sample.
3 Conclusions
We have studied the effect of resonances on the polarization conversion in chiral dielectric metasurfaces, for both linear and nonlinear regimes. We have demonstrated that metasurfaces composed of a monoclinic lattice of achiral meta-atoms possess a chiral response that can be employed for active polarization engineering. We have verified that such an intrinsic chirality of the metasurface can transform input linearly polarized light into elliptically polarized light, and we have demonstrated that this effect can be used to control the polarization of the generated third harmonic field. We believe that our results provide the first step in exploring polarization transformations in the nonlinear regime for resonant chiral metasurfaces, and they lay the foundation for future work to optimize such phenomena for applications in chiral sensing, chirality encoding, and chiral imaging.
Funding source: Australian Research Council
Award Identifier / Grant number: DP210101292
Funding source: National Natural Science Foundation of China
Award Identifier / Grant number: 12261131500, 12025402,12334016
Acknowledgments
YK thanks M. Gorkunov, K. Konishi, and O. Martin for useful discussions of monoclinic metasurfaces and nonlinear chiral effects. The authors thank S. Xiao for valuable suggestions on the fabrication.
-
Research funding: Australian Research Council (Grant No. DP210101292), International Technology Center Indo-Pacific (ITC IPAC) via Army Research Office (Contract FA520923C0023), National Natural Science Foundation of China (Grants No. 12261131500, No. 12025402, and No. 12334016), Shenzhen Fundamental Research Projects (Grant No. JCYJ20241202123719025).
-
Author contributions: YK and QS conceived the idea and supervised the research. DH and IT developed the theoretical model and performed numerical simulations. FL fabricated the samples. DH and PT designed and carried out the experiments. IT and PT drafted the initial version of the manuscript. All authors have accepted responsibility for the entire content of this manuscript and consented to its submission to the journal, reviewed all the results and approved the final version of the manuscript.
-
Conflict of interest: Authors state no conflict of interest.
-
Data availability: The datasets generated during and/or analyzed during the current study are available from the corresponding authors on reasonable request.
References
[1] A. Kuznetsov, et al.., “Roadmap for optical metasurfaces,” ACS Photonics, vol. 11, no. 3, pp. 816–865, 2024, https://doi.org/10.1021/acsphotonics.3c00457.Suche in Google Scholar PubMed PubMed Central
[2] S. Schulz, et al.., “Roadmap on photonic metasurfaces,” Appl. Phys. Lett., vol. 124, no. 26, p. 260701, 2024. https://doi.org/10.1063/5.0204694.Suche in Google Scholar
[3] T. Cui, et al.., “Roadmap on electromagnetic metamaterials and metasurfaces,” J. Phys. Photonics, vol. 6, no. 3, pp. 032–502, 2024, https://doi.org/10.1088/2515-7647/ad1a3b.Suche in Google Scholar
[4] D. H. Goldstein and D. Goldstein, Polarized Light (Optical Engineering 83), 2nd ed., rev. and expanded, New York Basel, Marcel Dekker, 2003.Suche in Google Scholar
[5] E. Collett, Field Guide to Polarization, vol. 1, Bellingham, Washington, SPIE, 2005.10.1117/3.626141Suche in Google Scholar
[6] C. Jung, et al.., “Metasurface-driven optically variable devices,” Chem. Rev., vol. 121, no. 21, pp. 13013–13050, 2021. https://doi.org/10.1021/acs.chemrev.1c00294.Suche in Google Scholar PubMed
[7] S. Chen, W. Liu, Z. Li, H. Cheng, and J. Tian, “Metasurface-empowered optical multiplexing and multifunction,” Adv. Mater., vol. 32, no. 3, p. 1805912, 2020. https://doi.org/10.1002/adma.201805912.Suche in Google Scholar PubMed
[8] D. Wen, F. Yue, W. Liu, S. Chen, and X. Chen, “Geometric metasurfaces for ultrathin optical devices,” Adv. Opt. Mater., vol. 6, no. 17, p. 1800348, 2018. https://doi.org/10.1002/adom.201800348.Suche in Google Scholar
[9] F. Ding, S. Tang, and S. I. Bozhevolnyi, “Recent advances in polarization-encoded optical metasurfaces,” Adv. Photonics Res., vol. 2, no. 6, p. 2000173, 2021, https://doi.org/10.1002/adpr.202000173.Suche in Google Scholar
[10] B. Lin, W. Huang, J. Guo, X. Ji, Y. Wang, and R. Zhu, “Design of polarization conversion metasurface for arbitrary polarized wave,” Opt. Commun., vol. 540, p. 129529, 2023, https://doi.org/10.1016/j.optcom.2023.129529.Suche in Google Scholar
[11] Z. Shen and X. Lin, “A review of metasurface polarization devices,” Opt. Mater., vol. 146, p. 114567, 2023, https://doi.org/10.1016/j.optmat.2023.114567.Suche in Google Scholar
[12] F. Li, H. Chen, J.-Y. Yin, and J.-Y. Deng, “A polarization conversion metasurface for broadband and high efficiency bidirectional filtering,” Phys. Scr., vol. 99, no. 10, p. 105525, 2024, https://doi.org/10.1088/1402-4896/ad7416.Suche in Google Scholar
[13] F.-J. Li, et al.., “Metasurface polarization optics: from classical to quantum,” Appl. Phys. Rev., vol. 11, no. 4, pp. 041–332, 2024, https://doi.org/10.1063/5.0226286.Suche in Google Scholar
[14] F. Mei, et al.., “Cascaded metasurfaces for high-purity vortex generation,” Nat. Commun., vol. 14, no. 1, p. 6410, 2023, https://doi.org/10.1038/s41467-023-42137-1.Suche in Google Scholar PubMed PubMed Central
[15] Y. Yuan, K. Zhang, Q. Wu, S. N. Burokur, and P. Genevet, “Reaching the efficiency limit of arbitrary polarization transformation with nonorthogonal metasurfaces,” Nat. Commun., vol. 15, no. 1, p. 6682, 2024, https://doi.org/10.1016/j.optcom.2023.129529.Suche in Google Scholar
[16] A. Zaidi, N. Rubin, A. Dorrah, J.-S. Park, and F. Capasso, “Generalized polarization transformations with metasurfaces,” Opt. Express, vol. 29, no. 24, pp. 39065–39078, 2021, https://doi.org/10.1364/OE.442844.Suche in Google Scholar PubMed
[17] A. H. Dorrah, N. A. Rubin, A. Zaidi, M. Tamagnone, and F. Capasso, “Metasurface optics for on-demand polarization transformations along the optical path,” Nat. Photonics, vol. 15, no. 4, pp. 287–296, 2021, https://doi.org/10.1038/s41566-020-00750-2.Suche in Google Scholar
[18] N. A. Rubin, A. Zaidi, A. H. Dorrah, Z. Zhujun Shi, and F. Capasso, “Jones matrix holography with metasurfaces,” Sci. Adv., vol. 7, no. 33, p. eabg7488, 2021, https://doi.org/10.1126/sciadv.abg7488.Suche in Google Scholar PubMed PubMed Central
[19] S. Asadulina, A. Bogdanov, and O. Yermakov, “All-dielectric meta-waveguides for flexible polarization control of guided light,” Laser Photonics Rev., vol. 18, no. 12, p. 2300544, 2024. https://doi.org/10.1002/lpor.202300544.Suche in Google Scholar
[20] S. Polevoy and O. Yermakov, “Excitation of surface waves with on-demand polarization at self-complementary metasurface,” IEEE Antenn. Wireless Propag. Lett., vol. 22, no. 8, pp. 1962–1966, 2023. https://doi.org/10.1109/lawp.2023.3270456.Suche in Google Scholar
[21] J. Zuo, et al.., “Chip-integrated metasurface full-Stokes polarimetric imaging sensor,” Light: Sci. Appl., vol. 12, no. 1, p. 218, 2023. https://doi.org/10.1038/s41377-023-01260-w.Suche in Google Scholar PubMed PubMed Central
[22] Z.-L. Deng, et al.., “Poincare sphere trajectory encoding metasurfaces based on generalized malus’ law,” Nat. Commun., vol. 15, no. 1, p. 2380, 2024. https://doi.org/10.1038/s41467-024-46758-y.Suche in Google Scholar PubMed PubMed Central
[23] A. Overvig, N. Yu, and A. Alù, “Chiral quasi-bound states in the continuum,” Phys. Rev. Lett., vol. 126, no. 7, p. 073001, 2021, https://doi.org/10.1103/PhysRevLett.126.073001.Suche in Google Scholar PubMed
[24] I. Katsantonis, A. C. Tasolamprou, E. N. Economou, T. Koschny, and M. Kafesaki, “Ultrathin, dynamically controllable circularly polarized emission laser enabled by resonant chiral metasurfaces,” ACS Photonics, vol. 2024, no. 2024, 2024, https://doi.org/10.1021/acsphotonics.4c01005.Suche in Google Scholar PubMed PubMed Central
[25] J. Bai and Y. Yao, “Highly efficient anisotropic chiral plasmonic metamaterials for polarization conversion and detection,” ACS Nano, vol. 15, no. 9, pp. 14263–14274, 2021. https://doi.org/10.1021/acsnano.1c02278.Suche in Google Scholar PubMed
[26] X. Zhang, Y. Liu, J. Han, Y. Kivshar, and Q. Song, “Chiral emission from resonant metasurfaces,” Science, vol. 377, no. 6611, pp. 1215–1218, 2022. https://doi.org/10.1126/science.abq7870.Suche in Google Scholar PubMed
[27] M. Gandolfi, A. Tognazzi, D. Rocco, C. De Angelis, and L. Carletti, “Near-unity third-harmonic circular dichroism driven by a quasibound state in the continuum in asymmetric silicon metasurfaces,” Phys. Rev. A, vol. 104, no. 2, p. 023524, 2021. https://doi.org/10.1103/PhysRevA.104.023524.Suche in Google Scholar
[28] I. Toftul, et al.., “Chiral dichroism in resonant metasurfaces with monoclinic lattices,” Phys. Rev. Lett., vol. 133, no. 21, p. 216901, 2024. https://doi.org/10.1103/PhysRevLett.133.216901.Suche in Google Scholar PubMed
[29] Y. Deng, C. Wu, C. Meng, S. I. Bozhevolnyi, and F. Ding, “Functional metasurface quarter-wave plates for simultaneous polarization conversion and beam steering,” ACS Nano, vol. 15, no. 11, pp. 18532–18540, 2021. https://doi.org/10.1021/acsnano.1c08597.Suche in Google Scholar PubMed
[30] M.-E. Mustafa, M. Amin, O. Siddiqui, and F. A. Tahir, “Quasi-crystal metasurface for simultaneous half- and quarter-wave plate operation,” Sci. Rep., vol. 8, no. 15743, pp. 1–10, 2018. https://doi.org/10.1038/s41598-018-34142-y.Suche in Google Scholar PubMed PubMed Central
[31] C. Cisowski, J. B. Götte, and S. Franke-Arnold, “Colloquium: geometric phases of light: insights from fiber bundle theory,” Rev. Mod. Phys., vol. 94, no. 3, p. 031001, 2022. https://doi.org/10.1103/RevModPhys.94.031001.Suche in Google Scholar
[32] M. V. Gorkunov, A. A. Antonov, and Y. S. Kivshar, “Metasurfaces with maximum chirality empowered by bound states in the continuum,” Phys. Rev. Lett., vol. 125, no. 9, p. 093903, 2020. https://doi.org/10.1103/PhysRevLett.125.093903.Suche in Google Scholar PubMed
[33] A. S. Shalin, A. C. Valero, and A. Miroshnichenko, All-Dielectric Nanophotonics, San Diego, Elsevier, 2023.Suche in Google Scholar
[34] M. V. Gorkunov, A. A. Antonov, A. V. Mamonova, E. A. Muljarov, and Y. Kivshar, “Substrate-induced maximum optical chirality of planar dielectric structures,” Adv. Opt. Mater., no. 3, p. 2402133, 2024, https://doi.org/10.1002/adom.202402133.Suche in Google Scholar
[35] M. L. Solomon, A. A. E. Saleh, L. V. Poulikakos, J. M. Abendroth, L. F. Tadesse, and J. A. Dionne, “Nanophotonic platforms for chiral sensing and separation,” Acc. Chem. Res., vol. 53, no. 3, pp. 588–598, 2020. https://doi.org/10.1021/acs.accounts.9b00460.Suche in Google Scholar PubMed
[36] I. Toftul, S. Golat, F. J. Rodríguez-Fortuño, F. Nori, Y. Kivshar, and K. Y. Bliokh, “Radiation forces and torques in optics and acoustics,” arXiv, 2024, https://doi.org/10.48550/arXiv.2410.23670.Suche in Google Scholar
[37] K. Y. Bliokh and F. Nori, “Characterizing optical chirality,” Phys. Rev. A, vol. 83, no. 2, p. 021803, 2011, https://doi.org/10.1103/PhysRevA.83.021803.Suche in Google Scholar
[38] K. Y. Bliokh, Y. S. Kivshar, and F. Nori, “Magnetoelectric effects in local light-matter interactions,” Phys. Rev. Lett., vol. 113, no. 3, p. 033601, 2014, https://doi.org/10.1103/PhysRevLett.113.033601.Suche in Google Scholar PubMed
[39] R. P. Cameron, S. M. Barnett, and A. M. Yao, “Optical helicity, optical spin and related quantities in electromagnetic theory,” New J. Phys., vol. 14, no. 14, p. 053050, 2012. https://doi.org/10.1088/1367-2630/14/5/053050.Suche in Google Scholar
[40] R. W. Boyd, Nonlinear Optics, 3rd ed. Amsterdam; Boston, Academic Press, 2008.Suche in Google Scholar
[41] P. Tonkaev, et al.., “Even-order optical harmonics generated from centrosymmetric-material metasurfaces,” Phys. Rev. Res., vol. 6, no. 3, p. 033073, 2024. https://doi.org/10.1103/PhysRevResearch.6.033073.Suche in Google Scholar
[42] Y.-H. Zhang, H. Liu, Z.-G. Chen, G. Jia, and C. Ren, “Research on third-order susceptibility tensor of silicon at telecom wavelength,” in Proceedings Volume 7656, 5th International Symposium on Advanced Optical Manufacturing and Testing Technologies: Optical Test and Measurement Technology and Equipment, vol. 7656, SPIE, 2010, pp. 1673–1677.10.1117/12.865458Suche in Google Scholar
[43] D. J. Moss, H. M. van Driel, and J. E. Sipe, “Dispersion in the anisotropy of optical third-harmonic generation in silicon,” Opt. Lett., vol. 14, no. 1, pp. 57–59, 1989. https://doi.org/10.1364/OL.14.000057.Suche in Google Scholar PubMed
[44] K. Koshelev, Y. Tang, Z. Hu, I. I. Kravchenko, G. Li, and Y. Kivshar, “Resonant chiral effects in nonlinear dielectric metasurfaces,” ACS Photonics, vol. 10, no. 1, pp. 298–306, 2023. https://doi.org/10.1021/acsphotonics.2c01926.Suche in Google Scholar
Supplementary Material
This article contains supplementary material (https://doi.org/10.1515/nanoph-2025-0019).
© 2025 the author(s), published by De Gruyter, Berlin/Boston
This work is licensed under the Creative Commons Attribution 4.0 International License.
Artikel in diesem Heft
- Frontmatter
- Editorial
- In honor of Federico Capasso, a visionary in nanophotonics, on the occasion of his 75th birthday
- Reviews
- Flat nonlinear optics with intersubband polaritonic metasurfaces
- Polaritonic quantum matter
- Machine-learning-assisted photonic device development: a multiscale approach from theory to characterization
- Perspectives
- Towards field-resolved visible microscopy of 2D materials
- Perspective on tailoring longitudinal structured beam and its applications
- Tunable holographic metasurfaces for augmented and virtual reality
- Polarization-sensitive diffractive optics and metasurfaces: “Past is Prologue”
- Compound meta-optics: there is plenty of room at the top
- Nonlocal metasurfaces: universal modal maps governed by a nonlocal generalized Snell’s law
- Resonant metasurface-enabled quantum light sources for single-photon emission and entangled photon-pair generation
- Active metasurface designs for lensless and detector-limited imaging
- Letter
- Real-time tuning of plasmonic nanogap cavity resonances through solvent environments
- Research Articles
- On the generalized Snell–Descartes laws, shock waves, water wakes, and Cherenkov radiation
- Silicon rich nitride: a platform for controllable structural colors
- Overcoming stress limitations in SiN nonlinear photonics via a bilayer waveguide
- High-harmonic generation from subwavelength silicon films
- Space-time wedges
- XUV yield optimization of two-color high-order harmonic generation in gases
- Skyrmion bag robustness in plasmonic bilayer and trilayer moiré superlattices
- Quantum-enhanced detection of viral cDNA via luminescence resonance energy transfer using upconversion and gold nanoparticles
- Deep neural networks for inverse design of multimode integrated gratings with simultaneous amplitude and phase control
- Topological chiral-gain in a Berry dipole material
- Diagnostic oriented discrimination of different Shiga toxins via PCA-assisted SERS-based plasmonic metasurface
- Quantum emitter interacting with a dispersive dielectric object: a model based on the modified Langevin noise formalism
- 3D-printed mirror-less helicity preserving metasurface “mirror” for THz applications
- Supershift properties for nonanalytic signals
- Enhancing radiative heat transfer with meta-atomic displacement
- Quasi-bound states in the continuum in finite waveguide grating couplers
- Long lived surface plasmons on the interface of a metal and a photonic time-crystal
- Tailoring propagation-invariant topology of optical skyrmions with dielectric metasurfaces
- Experimental generation of optimally chiral azimuthally-radially polarized beams
- Tailoring optical response of MXene thin films
- Nonlinear analog processing with anisotropic nonlinear films
- Optical levitation of Janus particles within focused cylindrical vector beams
- Large tuning of the optical properties of nanoscale NdNiO3 via electron doping
- Combining quantum cascade lasers and plasmonic metasurfaces to monitor de novo lipogenesis with vibrational contrast microscopy
- Monoclinic nonlinear metasurfaces for resonant engineering of polarization states
- Non-linear bistability in pulsed optical traps
- Tutorial: Hong–Ou–Mandel interference with structured photons
- Inhomogeneous broadening in the time domain
- MoS2 based 2D material photodetector array with high pixel density
- Temporal interface in dispersive hyperbolic media
- Measurement of the cavity dispersion in quantum cascade lasers using subthreshold luminescence
- Designing the response-spectra of microwave metasurfaces: theory and experiments
- Exciton–polariton condensation in MAPbI3 films from bound states in the continuum metasurfaces
- Experimental analysis of the thermal management and internal quantum efficiency of terahertz quantum cascade laser harmonic frequency combs
- Energy-efficient thermally smart windows with tunable properties across the near- and mid-infrared ranges
Artikel in diesem Heft
- Frontmatter
- Editorial
- In honor of Federico Capasso, a visionary in nanophotonics, on the occasion of his 75th birthday
- Reviews
- Flat nonlinear optics with intersubband polaritonic metasurfaces
- Polaritonic quantum matter
- Machine-learning-assisted photonic device development: a multiscale approach from theory to characterization
- Perspectives
- Towards field-resolved visible microscopy of 2D materials
- Perspective on tailoring longitudinal structured beam and its applications
- Tunable holographic metasurfaces for augmented and virtual reality
- Polarization-sensitive diffractive optics and metasurfaces: “Past is Prologue”
- Compound meta-optics: there is plenty of room at the top
- Nonlocal metasurfaces: universal modal maps governed by a nonlocal generalized Snell’s law
- Resonant metasurface-enabled quantum light sources for single-photon emission and entangled photon-pair generation
- Active metasurface designs for lensless and detector-limited imaging
- Letter
- Real-time tuning of plasmonic nanogap cavity resonances through solvent environments
- Research Articles
- On the generalized Snell–Descartes laws, shock waves, water wakes, and Cherenkov radiation
- Silicon rich nitride: a platform for controllable structural colors
- Overcoming stress limitations in SiN nonlinear photonics via a bilayer waveguide
- High-harmonic generation from subwavelength silicon films
- Space-time wedges
- XUV yield optimization of two-color high-order harmonic generation in gases
- Skyrmion bag robustness in plasmonic bilayer and trilayer moiré superlattices
- Quantum-enhanced detection of viral cDNA via luminescence resonance energy transfer using upconversion and gold nanoparticles
- Deep neural networks for inverse design of multimode integrated gratings with simultaneous amplitude and phase control
- Topological chiral-gain in a Berry dipole material
- Diagnostic oriented discrimination of different Shiga toxins via PCA-assisted SERS-based plasmonic metasurface
- Quantum emitter interacting with a dispersive dielectric object: a model based on the modified Langevin noise formalism
- 3D-printed mirror-less helicity preserving metasurface “mirror” for THz applications
- Supershift properties for nonanalytic signals
- Enhancing radiative heat transfer with meta-atomic displacement
- Quasi-bound states in the continuum in finite waveguide grating couplers
- Long lived surface plasmons on the interface of a metal and a photonic time-crystal
- Tailoring propagation-invariant topology of optical skyrmions with dielectric metasurfaces
- Experimental generation of optimally chiral azimuthally-radially polarized beams
- Tailoring optical response of MXene thin films
- Nonlinear analog processing with anisotropic nonlinear films
- Optical levitation of Janus particles within focused cylindrical vector beams
- Large tuning of the optical properties of nanoscale NdNiO3 via electron doping
- Combining quantum cascade lasers and plasmonic metasurfaces to monitor de novo lipogenesis with vibrational contrast microscopy
- Monoclinic nonlinear metasurfaces for resonant engineering of polarization states
- Non-linear bistability in pulsed optical traps
- Tutorial: Hong–Ou–Mandel interference with structured photons
- Inhomogeneous broadening in the time domain
- MoS2 based 2D material photodetector array with high pixel density
- Temporal interface in dispersive hyperbolic media
- Measurement of the cavity dispersion in quantum cascade lasers using subthreshold luminescence
- Designing the response-spectra of microwave metasurfaces: theory and experiments
- Exciton–polariton condensation in MAPbI3 films from bound states in the continuum metasurfaces
- Experimental analysis of the thermal management and internal quantum efficiency of terahertz quantum cascade laser harmonic frequency combs
- Energy-efficient thermally smart windows with tunable properties across the near- and mid-infrared ranges

