Real-time tuning of plasmonic nanogap cavity resonances through solvent environments

2.1 Solvent environments to tune metasurface resonance

Metasurfaces consisting of arrays of nanoscale patch antennas were constructed from square gold nanoparticles separated from a flat gold film by a thin dielectric spacer. The gold nanoparticles were square blocks with a height of 35 nm and side lengths (L) ranging from 120 to 1,100 nm, and nanoparticle arrays had a pitch of twice the side length. The dielectric spacer consisted of a SiO₂ layer with thickness of 10, 20, or 40 nm deposited using plasma-enhanced chemical vapor deposition (PECVD) (Figure 1). As reported previously, the antenna array formed a metasurface which exhibited a highly efficient absorptive mode corresponding to the coupled plasmonic oscillations of the nanostructure and gold film. This results in significant light absorption at the resonance wavelength, where the resonance was determined by the side length of the gold nanoparticles and the SiO₂ layer thickness. Metasurfaces with nanoparticle side lengths of 120–1,100 nm studied herein exhibited narrow resonances, with typical full width half max (FWHM) values ∼10–15 % of the resonance wavelength, across a broad spectral range from 1 µm to 5 μm (Fig. S1).

Figure 1:

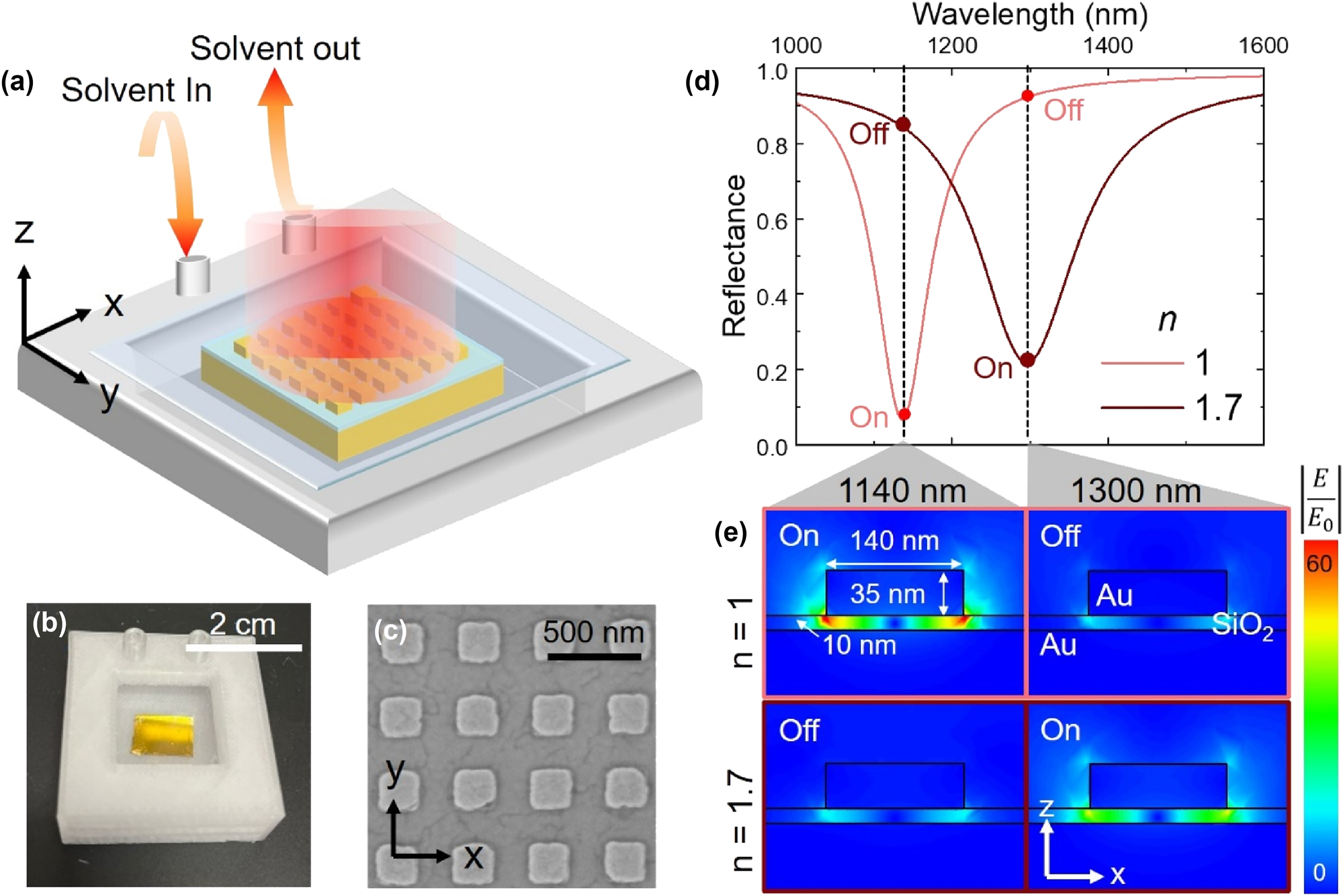
Geometric and dielectric control of resonant absorption in nano-gap metasurfaces. (a) Schematic representation of the metasurface sample in the flow cell. (b) Photographic image of the device flow cell. (c) SEM image of the metasurface elements. (d) COMSOL simulation of reflectance spectrum of the metasurface and (e) electric field at 1,140 and 1,300 nm for two refractive indexes (1 and 1.7) of surrounding medium. “On” and “off” refer to on- and off-resonance wavelengths.

Each metasurface was fully immersed in a solvent environment established within a flow cell (1.5 cm × 1.5 cm × 1 cm) made from polypropylene using a 3D printer (Bambu lab x1-carbon). The solvent flow cell included two channels to facilitate solvent exchange, and a cover glass formed a window to ensure a uniform solvent thickness of 1 mm. The first channel was used to introduce solvents into the flow cell. After reflectance measurements, the second channel was used to remove the solvent. To wash away residue of the previous solvent, the subsequent solvent was flowed through the cell for 30 s before refilling the cell with fresh solvent. This cell enabled precise, real-time modulation of the refractive index surrounding the metasurface through exchange of commercial solvents (Cargille-Sacher) which act as refractive index standards (Figure 1a, Fig. S2).

Finite element simulations were used to predict the influence of the solvent refractive index (n, measured at 589 nm) on the metasurface absorption resonance (Figure 1d). The simulated absorbance of a metasurface with nanoparticle side lengths of 140 nm in air (n = 1) showed a maximum absorption (∼93 %) at 1,140 nm, while the same structure in a simulated solvent environment of n = 1.7 exhibited a maximum absorption at 1,300 nm (Figure 1d). As the refractive index near the nanostructure changed, it effectively changed the optical path length and the coupling conditions of the incident light. This caused the metasurface resonance frequency to decrease with higher n solvents according to:

Here, ω_res is the effective resonance frequency, ω_p is the free electron plasma frequency of the metasurface, and ɛ _m is the permittivity of the surrounding medium. The resonance wavelength was inversely related to the resonance frequency, λ_res = 2πc/ω_res [1], [2], [3], [4]. Simulations further showed that absorption of resonant light generated extreme, heterogeneous electric fields within the dielectric layer (Figure 1e), while non-resonant light resulted in little to no cavity field.

Within the flow cell, the solvent environment was used to actively control the refractive index surrounding the metasurface, here consisting of square gold nanoparticles with 500 nm side lengths and a 40 nm thick SiO₂ dielectric spacer. We utilized five different commercially available refractive index standards consisting of chlorofluorocarbon mixtures with refractive indexes between 1.3 and 1.7 measured at 589 nm (Fig. S2). The solvent was exchanged using the flow cell, and the reflectance spectrum was collected by a Fourier-transform infrared (FTIR) spectrometer (Bruker Invenio R). As shown in Figure 2a, the metasurface exhibited a resonance wavelength at 2,430 nm with 245 nm FWHM in air (n = 1). This FWHM was notably broader than predicted in simulations (150 nm), which likely results from small inhomogeneities in the electron beam lithography (EBL)-patterned metasurface. The side lengths of individual EBL-generated nanostructures exhibited a standard deviation of 4–7 nm, as quantified through scanning electron microscopy (SEM) images. As the refractive index increased, the resonance wavelength red-shifted linearly at a rate of 40–60 nm per 0.1 refractive index increment for a total shift of 280 nm from air to n = 1.7. This red-shifted tuning was accompanied by an increase in FWHM, though it should be noted that this increased FWHM becomes negligible when the spectra are plotted in wavenumber rather than wavelength (Fig. S3). Throughout the tuning, metasurface absorption remains consistently high (>95 %) (Figure 2).

Figure 2:

Resonance wavelength tuning via surrounding refractive index. (a) Experimental reflectance spectra of a metasurface (500 nm nanoparticle side length and 40 nm SiO₂ thickness) showing the effect of increasing the refractive index of the surrounding medium, where higher indexes are represented by darker red colors. (b) Wavelength shift (black) and FWHM (red) of reflectance spectra with varying solvent refractive indexes.

2.2 Broadband wavelength tuning

Similar real-time resonance tuning through solvent exchange was observed over a wide range of nanoparticle side lengths and dielectric layer thicknesses, which resulted in real-time tuning over a broad spectral range. Spectra in Figure 3a correspond to metasurfaces of 300, 500, 700, 900 and 1,100 nm side lengths with a 40 nm SiO₂ thickness. Increased nanostructure side lengths resulted in dramatic red shifts in peak absorption wavelength from 1 µm to 5 µm. Red shifts in the resonance were accompanied by a systematic decrease in absorption efficiency, which has previously been demonstrated to result in decreased electric field intensities within the larger mode volumes underneath nanoparticles with larger side lengths [34]. Nanostructures with 300 nm side lengths absorbed 98 % of incident light at the peak resonance wavelength (1,560 nm), while nanostructures with 1,100 nm side lengths absorbed 65 % incident light at the peak resonance wavelength (5,000 nm).

Figure 3:

Real-time tuning across a broad spectral range. (a) Reflectance spectra of the metasurfaces of different side lengths (300–1,100 nm) with 40 nm SiO₂ with longer lengths indicated by a darker color. (b) Red bars indicate resonance wavelength (λ_res) tuning as a function of metasurface absorber size with refractive index change. Darker red colors represent higher refractive indexes. (c) Reflectance spectra of the metasurfaces of three side lengths (300, 500, 900 nm) with 40 nm SiO₂ thickness indicated with solid, dash-dotted, and dashed lines, showing the resonance wavelength shifting with changing solvent refractive index. Darker red lines represent higher refractive indexes. Inset is a schematic of the metasurface structure where L is as indicated. (d) Change in resonance wavelength as the refractive index increases from 1 to the indicated refractive indexes. Darker dots indicate a larger nanoparticle side length (L).

Exchange of the solvent environment resulted in similar resonance tuning across metasurfaces with all side lengths studied herein. Metasurfaces with resonances in air of 1.56, 2.42, and 4.11 μm each exhibited significant red-shifts in solvent environments with refractive indexes 1.0 to 1.7 as predicted in Eq. 1 (Figure 3c). Metasurfaces exhibited resonance tuning ranges up to 300 nm from air to n = 1.7, which corresponded to ∼ 17 meV resonance shift per 0.1 refractive index increment (Fig. S3). This demonstrated how tailoring the absorber size and adjusting the refractive index of the medium actively tuned the resonance wavelength across a broad wavelength range. Despite this broadband tunability, solvent tuning was limited in spectral regions where the solvent itself demonstrated optical activity. Specifically, the commercial solvent standards utilized in this study absorbed significant light at wavelengths 3,300–3,600 nm and > 5,000 nm (Fig. S4). In these spectral ranges, competitive solvent absorption masked the metasurface absorption and either prevented or obscured measurable resonance tuning (Fig. S1). This limit suggests that alternative solvent mixtures with higher IR transparency might allow for resonance tuning over a truly arbitrary spectral range well into the mid- and long wave-infrared portions of the electromagnetic spectrum.

The metasurface resonance shifts due to changed solvent environment was reversible, exhibiting little or no hysteresis upon two solvent exchange cycles (Figure 4). Metasurface absorption spectra of a single sample were measured first upon solvent exchange from low to high refractive indexes and then from high to low refractive indexes. The resonance wavelength was observed to vary < 7 nm for a given refractive index between forward and reverse cycles, and spectra measured before and after the solvent exchange exhibited a minimal change in FWHM < 12 nm. A slight shift was detected at n=1 in the forward and backward sequences; we attribute this to small residual amounts of solvent trapped within the metasurface by capillary forces. However, by flushing the cell with additional solvent between measurements, the overall hysteresis remained below 7 nm. These results demonstrate the robustness and reliability of this tuning method, suggesting that the resonance wavelength can be consistently controlled with a high degree of precision.

Figure 4:

Reversibility of spectral shifts upon solvent exchange. (a) Hysteresis plot of absorption spectra showing the changes during a forward and backward sequence of solvent exchange. (b) Resonance wavelength shift as a function of refractive index, comparing the forward and backward sequence.

2.3 Applications of nano-gap cavity microfluidics

The integration of microfluidic systems with nanophotonic devices and metasurfaces has been proposed as a promising tool for sensing, imaging, lasers, and more [32], [29]. A distinct advantage of integrating nano-gap cavity metasurfaces with microfluidics, however, is that cavity fields, which are localized within the gap layer, are spatially distinct from the solvent environment (Figure 1e). Though the environment surrounding the metal nanoparticle changes, the gap cavity itself, i.e. the dielectric material between the nanoparticle and metal film, does not come into direct contact with the solvent. This confers a distinct advantage to nano-gap cavities within microfluidic systems in contrast to more standard metasurfaces such as plasmonic lattice arrays, waveguides, gratings, and dielectric metasurfaces. Namely, the location of the field is protected from the potentially harsh and reactive solvents within the microfluidic device. As such, nano-gap cavity metasurfaces are uniquely well-suited to the integration of delicate materials such as quantum dots, transition metal dichalcogenides, small molecules, and polymer thin films into these fields. The broad microfluidic resonance tuning demonstrated herein could allow for the dynamic control of light–matter coupling, the Purcell effect, photothermal effects, or allowing otherwise forbidden of optical transitions while protecting the materials from potentially deleterious or complicating solvent interactions.