Startseite Technik Geometry and surface state effects on the mechanical response of Au nanostructures
Artikel
Lizenziert
Nicht lizenziert Erfordert eine Authentifizierung

Geometry and surface state effects on the mechanical response of Au nanostructures

  • William M. Mook , John M. Jungk , Megan J. Cordill , Neville R. Moody , Yugang Sun , Younan Xia und William W. Gerberich EMAIL logo
Veröffentlicht/Copyright: 14. Februar 2022
Veröffentlichen auch Sie bei De Gruyter Brill
Manuskript einreichen Informationen für Autor*innen
International Journal of Materials Research
Aus der Zeitschrift International Journal of Materials Research Band 95 Heft 6

Abstract

A study of ultra-thin gold films and thin-walled nanoboxes has confirmed that length scales in terms of dislocation spacing can predict flow stress. Initial stages of deformation conform to linear hardening with average dislocation spacing controlled by the number of geometrically necessary dislocations in a pile-up. Later stages of deformation exhibit parabolic behavior with Taylor hardening interpreted in terms of a dislocation density described by the total line length of prismatic loops per unit volume. Comparisons of 20 and 40 nm thick planar films could be made to 205 nm high hollow gold nanoboxes with a wall thickness of 24 nm. These highly constrained, ultra-thin planar films demonstrated increased hardness from about 2 to 10 GPa with strains of 20 percent while less constrained nanoboxes increased from 0.8 to 4 GPa for the same strain magnitude.

Keywords: Nanostructure; Hardness; Dislocation; Length scale

Dedicated to Professor Dr. Peter Neumann on the occasion of his 65th birthday

William Gerberich University of Minnesota Department of Chemical Engineering and Materials Science 151 Amundson Hall 421 Washington Ave. S.E. Minneapolis, MN 55455 Tel.: +1 612 625 8548 Fax: +1 612 626 7246

  1. The authors would like to acknowledge David P. Adams of Sandia National Laboratories for supplying the gold films and Joel W. Hoehn and Dick Greenlee of Seagate Technology Corp. for deposition of ALD films. Additionally, the authors would like to acknowledge support through Seagate Technology and the Center for Micromagnetics and Information Technology (MINT), NSF-IGERT through grant DGE-0114372 and a current NSF grant CMS-0322436 funded with Brown U.

References

[1] D.A. Hughes, N. Hansen: Phys. Rev. Lett. 87 (2001) 135503-1.10.1103/PhysRevLett.87.135503Suche in Google Scholar

[2] W.W. Gerberich, W.M. Mook, C.R. Perrey, C.B. Carter, M.I. Baskes, R. McKherjee, A. Gidwani, J. Heberlein, P.H. McMurry, S.L. Girshick: J. Mech. Phys. Sol. 51 (2003) 979.10.1016/S0022-5096(03)00018-8Suche in Google Scholar

[3] P. Neumann: Acta Metallurgica 17 (1969) 1219.10.1016/0001-6160(69)90099-6Suche in Google Scholar

[4] J.J. Vlassak, W.D. Nix: J. Mater. Res. 7 (1992) 3242.10.1557/JMR.1992.3242Suche in Google Scholar

[5] W. Sharpe, Jr., K. Turner, R. Edwards: Experimental Mech. 39 (1999) 162.10.1007/BF02323548Suche in Google Scholar

[6] H. Huang, F. Spaepen: Acta Mater. 48 (2000) 3261.10.1016/S1359-6454(00)00128-2Suche in Google Scholar

[7] T.F. Page, W.C. Oliver, C.J. McHargue: J. Mater. Res. 7 (1992) 450.10.1557/JMR.1992.0450Suche in Google Scholar

[8] D.F. Bahr, D.E. Kramer, W.W. Gerberich: Acta Mater. 46 (1998) 3605.10.1016/S1359-6454(98)00024-XSuche in Google Scholar

[9] T.R. Page, S.V. Hainsworth: Surf. Coat. Technol. 61 (1993) 201.10.1016/0257-8972(93)90226-ESuche in Google Scholar

[10] J. Greer, F. Gang, W.D. Nix: Mat. Res. Soc. Fall Meeting, Presentation U9.11, Boston, MA, Dec. 1–5, 2003, unpublished results.Suche in Google Scholar

[11] Y. Sun, Y. Xia: Science 298 (2002) 2176.10.1126/science.1077229Suche in Google Scholar PubMed

[12] W.D. Nix, H. Gao: J. Mech. Phys. Sol. 46 (1998) 411.10.1016/S0022-5096(97)00086-0Suche in Google Scholar

[13] W.W. Gerberich, J.M. Jungk, M. Li, A.A. Volinsky, J.W. Hoehn, K. Yoder: Intern. J. Fracture 119/120 (2003) 387.10.1023/A:1024927812734Suche in Google Scholar

[14] M.F. Horstemeyer, M.I. Baskes, S.J. Plimpton: Acta. Mater. 49 (2001) 4363.10.1016/S1359-6454(01)00149-5Suche in Google Scholar

[15] V. Yamakov, D. Wolf, M. Salazar, S.R. Phillpot, H. Gleiter: Acta Mater. 49 (2001) 2713.10.1016/S1359-6454(01)00167-7Suche in Google Scholar

[16] E. Van der Giessen, A. Needleman: Model. Simul. Mater. Sci. Engng. 3 (1995) 689.10.1088/0965-0393/3/5/008Suche in Google Scholar

[17] H. Zbib, E. Aifantis: Res. Mech. (1989) 261.Suche in Google Scholar

[18] G.S. Was, T. Foecke: Thin Solid Films 286 (1996) 1.10.1016/S0040-6090(96)08905-5Suche in Google Scholar

[19] J.M. Jungk, W.M. Mook, M. Cordill, D.F. Bahr, N. Moody, J. Hoehn, M. Chambers, W.W. Gerberich: accepted by J. Mater Res. (2004).Suche in Google Scholar

[20] S.M. George, A.W. Ott, J.W. Klaus: J. Phys. Chem. 100 (1996) 13121–13131.10.1021/jp9536763Suche in Google Scholar

[21] N. Moody, D. Adams, M. Cordill, D. Bahr, A. Volinsky: Plasticity Effects on Interfacial Fracture of Thin Gold Films, SAND2003– 8146C, Sandia National Laboratories (2003); also in the Proceedings of the 9th International Conference on the Mechanical Behavior of Materials, Geneva Switzerland, May 25–29, 2003.Suche in Google Scholar

[22] W.W. Gerberich, N.I. Tymiak, J.C. Grunlan, M.F. Horstemeyer, M.I. Baskes: J. Appl. Mech. 69 (2002) 433.10.1115/1.1469004Suche in Google Scholar

[23] D.E. Kramer, K.B. Yoder, W.W. Gerberich: Philos. Mag. A 81 (2001) 2033.10.1080/01418610108216651Suche in Google Scholar

[24] A.W. Ott, J.W. Klaus, J.M. Johnson, S.M. George: Thin Solid Films 292 (1997) 135.10.1016/S0040-6090(96)08934-1Suche in Google Scholar

[25] T.M. Mayer, J.W. Elam, S.M. George, P.G. Kotula, R.S. Goeke: Appl. Phys. Lett. 82 (2003) 2883.10.1063/1.1570926Suche in Google Scholar

[26] W.C. Oliver, G.M. Pharr: J. Mater. Res. 7 (1992) 1564.10.1557/JMR.1992.1564Suche in Google Scholar

[27] W.W. Gerberich, W.M. Mook, M. Cordill, C.B. Carter, C. Perrey, J. Heberlein, S. Girshick: accepted by Intern. J. Plasticity (2004).Suche in Google Scholar

[28] R.E. Miller, L.E. Shilkrot, W.A. Curtin: Acta Mater. 52 (2004) 271.10.1016/j.actamat.2003.09.011Suche in Google Scholar

6 Appendix

Dislocation density in the gold nanoboxes is interpreted in terms of prismatic loops being punched out along the side-walls.With the interpretation in terms of line length per unit volume we first calculate the line length based on the following assumptions. We assume circular loops along glide cylinders with the diameter of the loops restricted to the wall thickness. The depiction is schematically shown in Fig. A-1. Here the top and bottom of the enclosed box are not shown for clarity and it is assumed that the resistance to deformation is controlled by the dislocation density in the sidewalls only. For the number of dislocations along the glide cylinder, we assume a geometrically necessary number based upon the displacement as given by Eq. (10). The number of these glide cylinders along each wall is approximated as h/t. Since there are four vertical sidewalls,

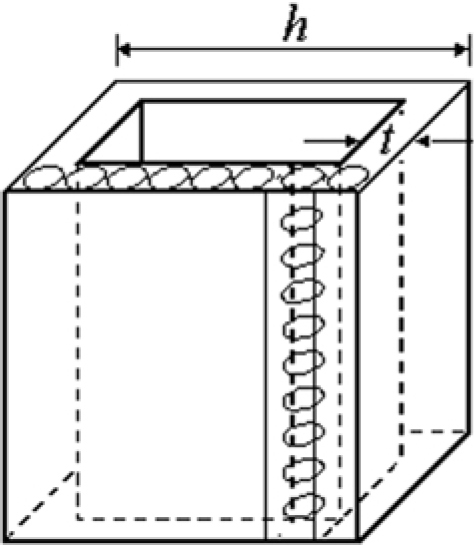
Fig. A-1 Schematic depiction of simplified cubic Au nanobox with the top and bottom not shown for clarity. Dislocation density in the gold nanoboxes is interpreted in terms of circular prismatic loops being punched out along glide cylinders with the diameter of the loops restricted to the wall thickness. One glide cylinder is shown.
Fig. A-1

Schematic depiction of simplified cubic Au nanobox with the top and bottom not shown for clarity. Dislocation density in the gold nanoboxes is interpreted in terms of circular prismatic loops being punched out along glide cylinders with the diameter of the loops restricted to the wall thickness. One glide cylinder is shown.

(A-1) ρ=N⋅ loop length  unit volume =δ2b⋅4ht⋅πt⋅1V

For the volume we once again only consider the sidewalls and consider a plane strain assumption with the box retaining its exterior dimensions and the cavity closing during compression by wall thickening. Based on ɛ1 = –ɛ3 with ɛ1 = δ/h we find the bearing area increases during thickening giving

(A-2) A=h2−[ h−2t(1+δh) ]2=4ht−4t2+4tδ

For the present study, with h = 205 nm and t = 24 nm, one can show that for the vast majority of the deformation range from 2 to 60 nm, elimination of the last two terms only changes the result by ± 4%. To first order then we use 4ht as the bearing area and with the height changing by h – δ, the volume becomes

(A-3) V≅4ht(h−δ)

It is noted that this is not constancy of volume but we propose this is appropriate because of some of the deformed volume going into the top and bottom of the box which is not participating in the side wall strengthening. With Eqs. (A-1) and (A-2) the dislocation density is approximated by

(A-4) ρ≅πδ2bt(h−δ)

used as Eq. (6) in the main text.
Received: 2004-01-08
Accepted: 2004-03-03
Published Online: 2022-02-14

© 2004 Carl Hanser Verlag, München

Artikel in diesem Heft

  1. Frontmatter
  2. Editorial
  3. Editorial
  4. Articles Basic
  5. Thermally assisted motion of dislocations in solid solution-strengthened fcc alloys and the concept of “stress equivalence”
  6. From single to collective dislocation glide instabilities: A hierarchy of scales, embracing the Neumann strain bursts
  7. Geometry and surface state effects on the mechanical response of Au nanostructures
  8. Microstructural evolution and its effect on the mechanical properties of Cu–Ag microcomposites
  9. Deformation behaviour of strontium titanate between room temperature and 1800 K under ambient pressure
  10. The deformation response of ultra-thin polymer films on steel sheet in a tensile straining test: the role of slip bands emerging at the polymer/metal interface
  11. Influence of dissolved gas molecules on the size recovery kinetics of cold-rolled BPA-PC
  12. Comparison between Monte Carlo and Cluster Variation method calculations in the BCC Fe–Al system including tetrahedron interactions
  13. Experimental study and Cluster Variation modelling of the A2/B2 equilibria at the titanium-rich side of the Ti–Fe system
  14. Phases and phase equilibria in the Fe–Al–Zr system
  15. On the plate-like τ-phase formation in MnAl–C alloys
  16. Articles Applied
  17. The grain boundary hardness in austenitic stainless steels studied by nanoindentations
  18. The effect of grain size on the mechanical properties of nanonickel examined by nanoindentation
  19. Microstructures and mechanical properties of V–V3Si eutectic composites
  20. Grain boundary characterization and grain size measurement in an ultrafine-grained steel
  21. On the determination of the volume fraction of Ni4Ti3 precipitates in binary Ni-rich NiTi shape memory alloys
  22. Mechanical properties of NiAl–Cr alloys in relation to microstructure and atomic defects
  23. Characterization of the cyclic deformation behaviour and fatigue crack initiation on titanium in physiological media by electrochemical techniques
  24. Effect of prestraining on high-temperature fatigue behaviour of two Ni-base superalloys
  25. Influence of surface defects and edge geometry on the bending strength of slip-cast ZrO2 micro-specimens
  26. Tensile failure in a superplastic alumina
  27. Notifications/Mitteilungen
  28. Personal/Personelles
  29. Conferences/Konferenzen
https://doi.org/10.1515/ijmr-2004-0089
Schlagwörter für diesen Artikel
Nanostructure; Hardness; Dislocation; Length scale

Artikel in diesem Heft

  1. Frontmatter
  2. Editorial
  3. Editorial
  4. Articles Basic
  5. Thermally assisted motion of dislocations in solid solution-strengthened fcc alloys and the concept of “stress equivalence”
  6. From single to collective dislocation glide instabilities: A hierarchy of scales, embracing the Neumann strain bursts
  7. Geometry and surface state effects on the mechanical response of Au nanostructures
  8. Microstructural evolution and its effect on the mechanical properties of Cu–Ag microcomposites
  9. Deformation behaviour of strontium titanate between room temperature and 1800 K under ambient pressure
  10. The deformation response of ultra-thin polymer films on steel sheet in a tensile straining test: the role of slip bands emerging at the polymer/metal interface
  11. Influence of dissolved gas molecules on the size recovery kinetics of cold-rolled BPA-PC
  12. Comparison between Monte Carlo and Cluster Variation method calculations in the BCC Fe–Al system including tetrahedron interactions
  13. Experimental study and Cluster Variation modelling of the A2/B2 equilibria at the titanium-rich side of the Ti–Fe system
  14. Phases and phase equilibria in the Fe–Al–Zr system
  15. On the plate-like τ-phase formation in MnAl–C alloys
  16. Articles Applied
  17. The grain boundary hardness in austenitic stainless steels studied by nanoindentations
  18. The effect of grain size on the mechanical properties of nanonickel examined by nanoindentation
  19. Microstructures and mechanical properties of V–V3Si eutectic composites
  20. Grain boundary characterization and grain size measurement in an ultrafine-grained steel
  21. On the determination of the volume fraction of Ni4Ti3 precipitates in binary Ni-rich NiTi shape memory alloys
  22. Mechanical properties of NiAl–Cr alloys in relation to microstructure and atomic defects
  23. Characterization of the cyclic deformation behaviour and fatigue crack initiation on titanium in physiological media by electrochemical techniques
  24. Effect of prestraining on high-temperature fatigue behaviour of two Ni-base superalloys
  25. Influence of surface defects and edge geometry on the bending strength of slip-cast ZrO2 micro-specimens
  26. Tensile failure in a superplastic alumina
  27. Notifications/Mitteilungen
  28. Personal/Personelles
  29. Conferences/Konferenzen
Jetzt anmelden und 20% sparen
Institutioneller Zugang
Wie funktioniert Authentifizierung?
Haben Sie eine Idee, wie wir unsere Website verbessern können?
Bitte schreiben Sie uns.
© 2025 De Gruyter Brill
Heruntergeladen am 30.12.2025 von https://www.degruyterbrill.com/document/doi/10.1515/ijmr-2004-0089/html
Button zum nach oben scrollen