Defect tolerance under environmentally assisted cracking conditions

1 Introduction

Various mechanisms may cause environmentally assisted cracking (EAC) problems induced by joint chemical-mechanical damage, among them stress corrosion cracking (SCC), due to stress-enhanced chemical reactions at crack tips; hydrogen embrittlement (HE), due to high hydrostatic stresses induced by the penetration of small H atoms inside the gaps of crystalline lattices and/or grain boundaries; liquid metal embrittlement (LME), due to the interaction of liquid metals like Hg, Pb, Ga, Cd, or Zn with tensioned surfaces of sensitive structural alloys; solid metal embrittlement, caused by tensioned inclusions or coatings below their melting points, as observed, e.g. in cadmium or lead-plated high-strength steels; and corrosion-fatigue, due to a synergic interaction between cyclic loads and electrochemical reactions at crack tips. No matter their differences, all such EAC mechanisms have a common feature: unlike in other corrosion problems, they depend both on the environment/material pair and on the stress state, since cracks cannot grow unless loaded by tensile stresses. Hence, they all require a sensitive material, a suitable aggressive environment, and tensile stresses at the critical point of the component (Cramer & Covino, 2003; Dietzel, 2001; Fontana, 1986; Korb & Olson, 1992; Leis & Eiber, 1997; Lisagor, 2005; Lynch, 2003; McEvily & Wei, 1972; Vasudevan & Sadananda, 2009, 2011a,b,c). As the terminology SCC enhances this mutual dependence, it probably might be profitably used to generically name all EAC mechanisms when there is no need separate them, but to avoid doubts, this practice will not be followed here.

If the tensile stresses are high enough, and if the material is sensitive to the environment it is immersed in, then EAC damage can initiate cracks in undamaged or virgin surfaces and eventually propagate them up to the fracture of the structural component. In such cases, EAC-induced damage includes a time-dependent crack nucleation period, followed by a steady crack growth phase, and eventually by the final fracture, which occurs when the stress intensity factor (SIF) of the dominant crack K_I reaches the toughness of the material K_C inside the aggressive medium. EAC damage can occur even under constant tensile loads, but its kinetics depend on the material-environment pair and on the stress state: it is affected by the material, including its alloy composition, its microstructural characteristics, and its thermo-mechanical history; by the chemistry of the environment; by the electrochemical state of the system relative to its surroundings; and by the stress gradients near the structural component surface. However, although the stress alone can cause failures even in inert media, it must be emphasized that EAC failures do not occur in aggressive environments without the stress contribution (Vasudevan & Sadananda, 2009).

Many aggressive environments can induce localized chemical reactions that decrease cohesive forces or surface energies in sensitive material regions, reducing the local stresses required to break their atomic bonds. EAC failures can occur even under nominally elastic stresses if the environment effect is high enough, and for some materials, they may happen in common media like water vapor or salt water. Alloy additions can significantly affect the formation of protective films and/or local electrochemical states. Microstructural features (e.g. grain size, segregation, precipitates, second phase particles, and inclusions) and/or mechanical and heat treatments (which affect the microstructure, mechanical properties, and/or the resident or residual stress state) may play an important role in EAC as well. Electrochemical factors may contribute in different ways; e.g. the applied potential has been reported to have little effect on EAC thresholds in low-alloy high-strength 4340 steels but a high effect on high-strength high-toughness maraging steels (Lisagor, 2005).

From the electrochemical point of view, EAC damage may be separated into anodic (when it involves dissolution and material at loss the crack tip) and cathodic (when the corrosive process forces embrittlement agents to penetrate inside the material microstructure without material removal from the crack tip) (Cramer & Covino, 2003). Cracks induced by EAC frequently start at small superficial defects such as corrosion pits, notches, or scratches, simply because the stresses there are increased by their stress concentration effect, or at microstructural features such as inclusions or grain boundaries, which can be more sensitive to the chemical environment. However, purely chemical models cannot describe the entire EAC process because they do not include its equally important mechanical driving force.

EAC failures can be intergranular, transgranular, or mixed, and contaminants or minor changes in the concentration level of the environment can strongly affect EAC rates as well. EAC failures are particularly dangerous because they can occur without overall corrosion evidence under low linear elastic (LE) static tensile loads, well below the material yield strength S_Y. Like fatigue cracks, the cracks induced by the joint effect of stress and chemical driving forces can initiate, grow, and eventually cause sudden failures without evident warning. However, unlike fatigue cracks, they can do so under constant loads. Moreover, such cracks are as difficult to detect as fatigue cracks, and they also tend to initiate at notch tips or at small surface flaws in unnotched surfaces.

In fact, if the aggressive medium is unavoidable, there are so many chemical and metallurgical details involved in practical EAC problems that they are usually solved by using a material immune to it, even if much more expensive than the original one. However, as such radical solutions ignore the stress role in EAC, they may be wasteful, to say the least. Besides, they may be useless if such problems appear only after the sensitive equipment has been operating for a while. For instance, an unexpected case of a formerly benign environment becoming propitious to sulfate-reducing bacteria proliferation and then producing unforeseen amounts of H₂S occurred in the Wilmington oil field in California, USA, which originally had only trace amounts of H₂S, but after a period of sea water reinjection into the well, its H₂S content increased to about 1000 ppm (Bertness, Chilingarian, & Al-Bassam, 1989). The H₂S gas is commonly associated with sulfide stress corrosion (SSC) and can cause serious catastrophic failures in components and equipment. Since bacteria can grow in the presence of sulfate ions and soluble organics, care to maintain the water quality must be taken by the use of bactericides or detergents and by keeping it clean enough to avoid the spread of bacteria into the well. In anaerobic conditions; e.g. inside steel pipelines, sulfate-reducing bacteria utilize the hydrogen atoms formed at cathodic sites of the metal to reduce sulfate to sulfides bring forth corroded iron and more bacteria, following reactions like

For structural integrity evaluations in such cases, and even for general structural engineering applications, it would be better to include all such complex chemical details in environmentally dependent mechanical properties, which should reflect their effects on the mechanical strength of the structural component when it is loaded inside the aggressive environment. Note, however, that the mechanical driving force for crack initiation and/or propagation under EAC conditions includes both (i) the stresses induced by externally applied loads and (ii) the internal residual stresses caused by any means. Indeed, although they may be difficult to evaluate, residual stresses can contribute to both the maximum value of the local stress σ_max in uncracked components and the maximum value of the SIF, K_max, after the crack is induced; thus, they cannot be neglected in EAC applications. If high enough for a given material-environment pair, such combined (service+residual) stresses can initiate a crack by EAC after some incubation time and then can propagate the crack under EAC rates da/dt that depend on the SIF induced by them.

Like typical fatigue crack growth (FCG) curves, such da/dt×K_I curves also have three phases, as schematized in Figure 1. Phase I has a propagation threshold (true or practical) called K_IEAC, below which the crack does not grow by EAC alone, and a rate very sensitive to its SIF. EAC rates in phase II, on the other hand, may present a plateau-like behavior almost independent (case A) or weakly dependent on the SIF value (case B) (Vasudevan & Sadananda, 2011a,b,c), whereas in phase III, the da/dt rates induced by EAC are again very sensitive to the SIF value, increasing quickly as it approaches the material toughness K_C, which usually depends on the environment as well. Such three-phase EAC vs. SIF or da/dt×K_I curves are observed in both gaseous and aqueous environments, as well as in liquid metal and in HE problems.

Figure 1:

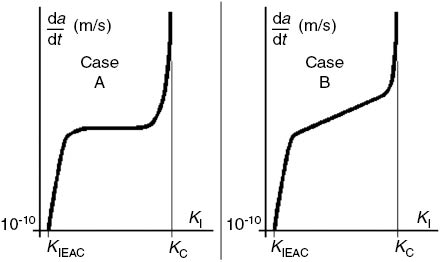
Typical da/dt×K_I crack growth under EAC curves is similar to fatigue crack propagation da/dN×ΔK curves, a motivation to explore the analogy used in this work.

The similarity with the fatigue case is still more pronounced. Indeed, like in fatigue problems, it is usually accepted that there is also a strength limit S_EAC below which a crack does not initiate by EAC at the surface of smooth components for a given material-environment pair. Even though the time for crack nucleation may be dependent on the load type, such S_EAC limits can be measured by testing suitable smooth tensile or bending specimens immersed during sufficient time in the desired environment under various constant loads or fixed displacements, using Dixon’s (1965) staircase or up-and-down techniques, or else using very slowly increasing strain rates until a crack appears at their surfaces, following Prot’s approach (Lin, Lee, & Lu, 2011). Threshold stress intensity values, K_IEAC, below which cracks do not grow under EAC conditions, can be measured as well by testing precracked standard specimens under similar procedures. Although the results of different test methods may be not identical, S_EAC and K_IEAC are usually accepted as mechanical properties of the material-environment pair. In fact, there are many standards that specify acceptable experimental practices to properly measure them (see, e.g. Cramer & Covino, 2003; and Korb & Olson, 1992, for a comprehensive review of such standard test methods). Figure 2 schematizes the results of an S_EAC test. Note how similar this S×t curve is to traditional SN curves, which depict the material resistance to fatigue crack initiation.

Figure 2:

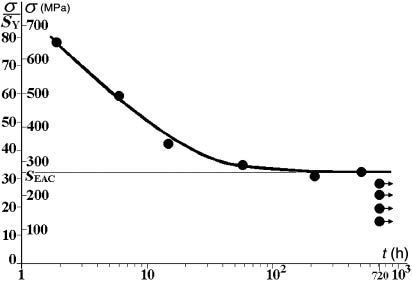
Typical S×t curve obtained by testing smooth specimen inside a given medium to identify the material resistance to crack initiation by EAC, S_EAC (720 h≅1 month), which is similar to SN fatigue curves, another indication of their analogous behavior.

Due to the similitudes between the basic EAC and fatigue cracking behavior, the methodology proposed in Meggiolaro, Miranda, and Castro (2007), Wu, Imad, Nouredine, Castro, and Meggiolaro (2010), and Castro et al. (2012) to analyze tolerance to small fatigue cracks that start from notch tips has been recently extended to the EAC case (Castro & Leite, 2013; Castro, Landim, Leite, & Meggiolaro, 2015; Castro & Meggiolaro, 2013, 2014). Such an attempt is a small step toward the desired development of stress analysis procedures for dealing with EAC problems, and it is pursued in this work by investigating its applicability to other EAC mechanisms.

Fatigue damage is associated to two driving forces, one that activates cyclic and the other that activates static damage mechanisms. In this way, FCG rates on any given environment depend on ΔK and K_max, the SIF range and maximum, or on any other equivalent pair of parameters related to them, like ΔK and R=K_min/K_max, the most used pair to present fatigue data (even though R is not a crack driving force). Recall that the loading includes externally applied efforts and also internal self-equilibrating residual stresses. However, as residual stresses are static load components (if not altered in service by elastoplastic loads or thermally activated mechanisms), they affect K_max and R, but not ΔK, so they may play a relatively smaller role in fatigue than in EAC.

To propagate long cracks by fatigue under fixed {ΔK, K_max} or {ΔK, R} loading conditions, the applied SIF range ΔK must be higher than the FCG threshold at the given R ratio, ΔK_th(R)=ΔK_thR. Cracks may be considered short while their FCG thresholds are smaller than the long crack FCG threshold; thus, such cracks can grow under ΔK<ΔK_thR. This apparently odd behavior is, on the contrary, natural, since otherwise the stress ranges, Δσ, required to propagate short cracks at a given R would be higher than their fatigue limits, ΔS_L(R)=ΔS_LR, the stress range needed to initiate and propagate cracks in smooth specimens at that R ratio, a nonsense. Indeed, assuming as usual that at any given fixed R ratio the FCG process is driven by the SIF range ΔK∝Δσ√(πa), if very short cracks with size a→0 had the same ΔK_thR threshold the long cracks have, they would need Δσ→∞ to grow by fatigue, a meaningless requirement (El Haddad, Smith, & Topper, 1979; El Haddad, Topper & Smith, 1979; Kitagawa & Takahashi, 1976; Lawson, Chen, & Meshii, 1999; McEvily, 1988; Sadananda & Vasudevan, 1997; Yu, DuQuesnay & Topper, 1988). Such statements assume that the stresses are induced by external loads only, but if the cracks start from notch tips or from smooth surfaces also loaded by residual stress fields caused by plastic strain gradients or by any other mechanism, such resident stresses must be added to the externally applied stresses as static loading components (which affect R but not ΔK, as mentioned above).

Microstructurally, short cracks, those small compared to the grain size gr, are much affected by microstructural barriers like grain boundaries (see, e.g. Chapetti, 2003, 2008; Krupp et al., 2004; Lorenzino & Navarro, 2013; Navarro & de los Rios, 1988; Verreman, 2008). Their study may be academically important, but as they cannot be well modeled for structural design purposes using macroscopic stress analysis techniques and isotropic properties, they are considered beyond the scope of this paper. Mechanically short cracks, on the other hand, say with sizes a>gr, may be modeled by LE fracture mechanics (LEFM) concepts if the stress field that surrounds them is predominantly LE and if the material can be treated as isotropic and homogeneous in such a scale. Since near-threshold FCG is always associated with small-scale yielding conditions, it is reasonable to expect that the classical LEFM concepts can be useful to model short cracks as well (Atzori, Lazzarin, & Filippi, 2001; Atzori, Lazzarin, & Meneghetti, 2003, 2005; Atzori, Meneghetti, & Susmel, 2005; Castro & Meggiolaro, 2015; Ciavarella & Meneghetti, 2004; Du Quesnay, Yu, & Topper, 1988; Livieri & Tovo, 2004; Vallellano, Navarro, & Dominguez, 2000). Therefore, to check if short cracks can really be modeled in such a way, the idea is to follow Irwin’s steps by first assuming that such concepts are valid and then verifying if their predictions are validated by proper tests. Hence, in the sequence, first, LEFM techniques are used to develop a model for the FCG behavior of mechanically short cracks, in particular those that depart from notches, then these concepts are extended for the analogous EAC problem, and finally, predictions of short crack tolerance under EAC conditions based on it are corroborated by proper experiments.

2 The behavior of mechanically short cracks

As discussed in Castro et al. (2015) and Castro and Meggiolaro (2015), to reconcile the fatigue (crack initiation) limit, ΔS_L0=2S_L(R=0), with the FCG threshold of long cracks under pulsating loads, ΔK_th0=ΔK_th(R=0), El Haddad et al. (1979) added to the physical crack size a hypothetical short crack characteristic size, a₀, a wise stratagem that forces the SIF of all cracks, short or long, to obey the correct FCG limits:

So, long cracks with a>>a₀ do not grow by fatigue if ΔK_I=Δσ√(πa)<ΔK_th0, while very small cracks with a→0 do not grow if Δσ<S_L0, since ΔK_I=Δσ√(πa₀)<ΔS_L0√(πa₀)=ΔK_th0 in this case. Moreover, this idea reproduces the tendency of typical Δσ_j×a_j data points in Kitagawa-Takahashi diagrams, where Δσ_j is the stress range needed to propagate a fatigue crack with size a_j (see Figure 3), where the fatigue limit ΔS_L0 and the stress range associated to the long crack threshold Δσ(a)=ΔK_th0/√(πa) limit the region that may contain nonpropagating cracks. The El Haddad-Topper-Smith (ETS) curve predicts that cracks of any size should stop when

Figure 3:

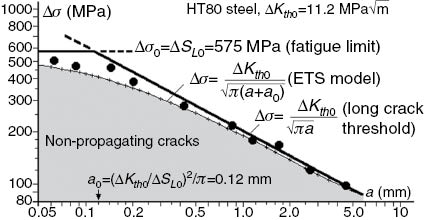
Kitagawa-Takahashi diagram showing the stress ranges Δσ(a) required to propagate fatigue short and long cracks of size a under R=0 in a large HT80 steel plate with ΔK_th0=11.2 MPa√m and ΔS_L0=575 MPa.

As the generic SIF of cracked structural components is given by K_I=σ√(πa)g(a/w), Yu et al. (1988) used the geometry factor g(a/w) to generalize Eq. (2) and redefined the short crack characteristic size by

The largest stress range, Δσ, that does not propagate microcracks in this case is also the fatigue limit, as it should: if a<<a₀, ΔK_I=ΔK_th0⇒Δσ→ΔS_L0. However, when the crack starts from a notch, as usual, its driving force is the stress range Δσ at the notch tip, not the nominal stress range Δσ_n normally used in SIF expressions. Hence, as in such cases the g(a/w) factor includes the stress concentration effect of the notch K_t=σ_max/σ_n, it is better to split it into two parts: g(a/w)=ηφ(a), where φ(a) quantifies the effect of the stress gradient near the notch tip, which for microcracks tends toward K_t, i.e. φ(a→0)→K_t, while the constant η quantifies the effect of the other parameters that affect K_I, such as the free surface. In this way, it is better to redefine a₀ by:

The stress gradient effect quantified by φ(a) does not affect a₀, since the stress ranges at notch tips must be smaller than the fatigue limit to avoid cracking, Δσ(a→0)=K_t Δσ_n=φ(0)Δσ_n<ΔS_L0. However, since SIFs are crack driving forces, they should be material-independent. Hence, the a₀ effect on the short crack behavior should be used to modify FCG thresholds instead of SIFs, making them a function of the crack size, a trick that is quite convenient for operational reasons. In this way, the a₀-dependent FCG threshold for pulsating loads ΔK_th(a, R=0)=ΔK_th0(a) becomes

Note that for large cracks with a>>a₀, this short crack FCG threshold tends to ΔK_th0, the long crack FCG threshold, and becomes independent of the crack size, as it should. Since Eq. (6) is just one of the models that obey the long and short crack limit behaviors, a data fitting parameter γ proposed by Bazant (1997) may be introduced in it to obtain the minimum stress ranges Δσ₀ needed to propagate short or long cracks under pulsating loads as a function of the crack size a:

This γ may allow a better fitting of experimental data, like those collected by Tanaka, Nakai, and Yamashita (1981) and by Livieri and Tovo (2004). Eq. (7) reproduces the original ETS model when γ=2, and the bilinear limits Δσ=ΔS_L0 and Δσ=ΔK_th0/√(πa), when γ→∞. The curves shown in Figure 4 illustrate the influence of γ on these model predictions.

Figure 4:

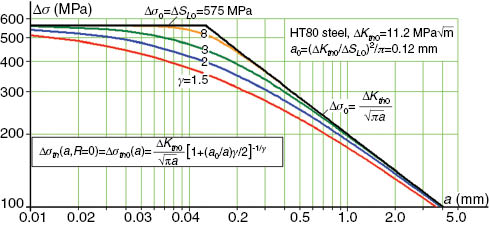
Influence of γ in the fatigue limit curves Δσ₀(a) predicted by Eq. (7).

However, as fatigue damage depends on two driving forces, ΔK and K_max, Eq. (7) should be extended to consider the σ_max effect (indirectly modeled by the R ratio) on the short crack behavior. Hence, if ΔK_thR=ΔK_thR(a>>a_R, R) is the FCG threshold for long cracks, ΔS_LR=ΔS_L(R) is the fatigue limit at the desired R ratio, and a_R is the characteristic short crack size at that R, then:

Moreover, unavoidable small defects like inclusions, voids, or scratches may be modeled as mechanically short cracks using LEFM concepts when they are not much smaller than a₀. In fact, all structural components should be designed to tolerate such and any other undetectable short cracks. Despite self-evident, this prudent requirement is still not included in most fatigue (let alone in EAC) design routines, which just intend to maintain the service stresses at critical points below their fatigue limits, Δσ<ΔS_LR/φ_F, where φ_F is a suitable safety factor. Nevertheless, since most long-life designs work well in practice, they certainly are somehow tolerant to undetectable or to functionally admissible short cracks. However, the question “how much tolerant” cannot be answered by the classical SN or εN procedures alone. Such problem can be avoided by adding a tolerance to short crack requirement to their “infinite” life design criteria, which, in its simplest version (the one that deals with constant amplitude loads, those with fixed {Δσ, σ_max}), may be given by

Since the fatigue limit ΔS_LR already reflects the effect of microstructural defects that are inherent to the material, Eq. (9) complements it by describing the tolerance to cracks of size a (small or not) that may pass unnoticed in actual service conditions. Such estimates can be very useful for designers and quality control engineers. They can be used, e.g. as a quantitative tool to evaluate the effect of an accidental damage on the surface of otherwise well-behaved components.

3 Short crack tolerance under EAC conditions

EAC involves the nucleation and/or the growth of cracks in susceptible materials inside aggressive media under tensile loads. This time-dependent chemical-mechanical damage process may be caused by different mechanisms, but all with a common feature: unlike other corrosion problems, they depend both on the environment-material pair and on the stress state, since cracks cannot grow unless loaded by tensile stresses. So, it can be useful to think that the environment contribution is to decrease the material resistance to the cracking process.

However, for structural design and analysis purposes, most EAC problems have been treated so far by a simplistic overconservative policy on susceptible material-environment pairs: if aggressive media are unavoidable during the service lives, the standard design practice is to choose a material resistant to EAC in such media to build the structural components. A less expensive alternative solution may be to recover the structural component surface with a suitable nobler coating, if such a coating is available. Such overconservative design criteria may be safe, but they can also be too expensive if an otherwise attractive material is summarily disqualified in the design stage when it may suffer EAC in the service environment, without properly considering any stress analysis issues. In fact, the EAC behavior cannot be properly evaluated neglecting the influence of the stress fields that drive them. Decisions based on such an inflexible pass/fail approach may cause severe cost penalties, since no crack can grow unless driven by tensile stresses caused by the service loads and by the residual stresses eventually induced by previous loads and overloads.

In other words, although EAC conditions may be difficult to define in practice due to the number of metallurgical, chemical, and mechanical variables that may affect them, sound structural integrity assessment procedures must include proper stress analysis techniques for calculating maximum tolerable flaw sizes. Such techniques are important in the design stage, but they are even more useful to evaluate operating structural components not originally designed for EAC service, when by any reason they must begin to work under such conditions due to some unavoidable operational change (e.g. a pipeline that must transport originally unforeseen amounts of H₂S due to changes in oil well conditions while a new one specifically designed for such service is built and commissioned). Economical pressures to take such a structural risk may be inescapable, since loss of profits associated with the very long time required for replacing the structural component can be huge, especially in offshore applications. Such risky decisions can, in principle, be controlled by the methodology proposed as follows, which extends to EAC problems the analysis developed to mechanically quantify the behavior of short fatigue cracks. Indeed, if cracks behave well under EAC conditions, i.e. if LEFM concepts can be used to properly describe them, then a “short crack characteristic size under EAC conditions” can be defined by (Castro et al., 2015):

So, assuming (as usual) that all chemical effects involved in EAC problems can be appositely described and quantified by the traditional material resistances to crack initiation and propagation under fixed environmental and stress conditions, S_EAC and K_IEAC, the “short crack characteristic size” a₀ concept in EAC follows exactly the same idea of its analogous size so useful for fatigue purposes: it uses the otherwise separated material resistances K_IEAC and S_EAC to model and predict the behavior of mechanically short cracks and as such can be equally useful in EAC problems. Such resistances are well-defined material properties for a given environment-material pair and can be measured by standard procedures. Moreover, although EAC problems are time dependent, S_EAC and K_IEAC are not, since they quantify the limit stresses required for starting or for growing cracks under EAC conditions. Hence, supposing that the mechanical parameters that limit EAC damage behave analogously to the equivalent parameters ΔK_thR and ΔS_LR that limit fatigue damage, a Kitagawa-like diagram can be used as well to quantify the crack sizes a tolerable by any given component that works under fixed EAC and (tensile) stress conditions (see Figure 5).

Figure 5:

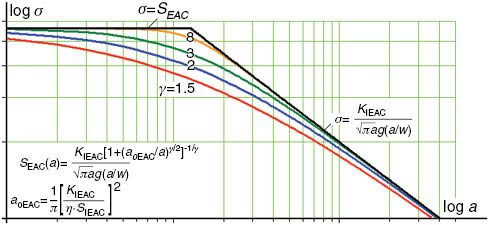
A Kitagawa-Takahashi-like diagram proposed to describe the behavior of short and long cracks under EAC conditions for structural design purposes, using the similitude between the fatigue and EAC problems, assuming that K_IEAC is analogous to ΔK_thR and that S_EAC is analogous to ΔS_LR.

This idea can be further expanded. For example, Figure 6 presents an extended Kitagawa-Takahashi diagram that shows four regions that may contain nonpropagating cracks. First, starting from the bottom, the region bounded by the material resistances to crack initiation and large crack growth by fatigue in a given aggressive medium ΔS_LR and ΔK_thR/√(πa), which limits the tolerance zone that may contain non propagating fatigue cracks in that environment under fixed stress ranges at a given R ratio; second, the region limited by S_EAC and K_IEAC/√(πa) that may contain nonpropagating cracks by EAC in that medium; third, the crack tolerance region limited by ΔS_Lvac and ΔK_thvac, the R-independent fatigue limit and FCG threshold of the given material in vacuum; and fourth, the region limited by the intrinsic material properties S_Uvac and K_ICvac/√(πa), which can be measured only in vacuum or in truly inert environments. The main advantage of looking at this problem in such an integrated way is that it naturally accepts the attempts to treat mechanical and chemical damage under a unified analysis procedure, following, e.g. Vasudevan and Sadananda’s Unified Approach methodologies (Sadananda, 2013; Sadananda & Vasudevan, 2011).

Figure 6:

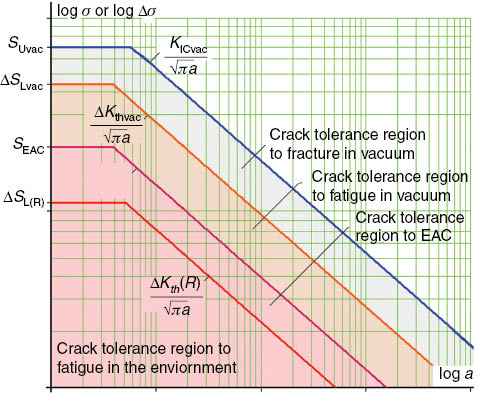
Extended Kitagawa diagram including fatigue and EAC limiting conditions for crack growth.

In other words, if cracks loaded under EAC conditions behave as they should, i.e. if their mechanical driving force is indeed the SIF applied on them; and if the chemical effects that influence their behavior can be described by the material resistance to crack initiation from smooth surfaces quantified by S_EAC and by its resistance to crack propagation measured by K_IEAC, then it can be expected that cracks induced by EAC may depart from sharp notches and then stop, due to the stress gradient ahead of the notch tips, eventually becoming nonpropagating cracks, exactly as in the fatigue case. In such cases, the size of nonpropagating short cracks can be calculated using the same procedures used for fatigue, and the tolerance to such defects can be properly quantified using a “short crack characteristic size under EAC conditions” in structural integrity assessments. Hence, a criterion for the maximum tolerable stress under EAC conditions can be proposed as

Such equations can be used for stress analyses of notched components under EAC conditions. So, they are potentially useful for structural design purposes when overconservative pass/nonpass criteria used to “solve” most practical SCC problems nowadays are not affordable or cannot be used for any other reason. In fact, they can form the basis for a mechanical criterion for SCC that can be applied even by structural engineers, since it does not require much expertise in chemistry to be useful. Moreover, they can be properly tested, as follows.

4 Verification of the crack-tolerance predictions under LME conditions

To test short crack tolerance predicted by the model proposed here, tests were made first in the Al 2024-liquid gallium pair (Ga is liquid above 30°C), whose main advantage is its very quick LME reactions, in the order of minutes. In comparison, EAC-sensitive Al alloys may take weeks to crack in NaCl-water solutions. Moreover, contrary to other liquid metals that may cause LME, like mercury, Ga is a safe, nontoxic material. LME may occur in solid metal-liquid metal couples that form simple eutectic phase diagrams without any intermetallics (Glickman, 2011; Robertson, 1966). LME leads to low levels of crack nucleation and propagation thresholds, with reported values of K_IEAC as low as 0.1 MPa√m and propagation velocity as fast as 0.1 m/s. Whereas EAC in aqueous environment involves metal oxidation at anodic sites and an electrical current flow between anodic and cathodic sites that causes loss of metal and local dissolution at the crack tip, LME does not involve oxidation reactions because the very high electrical conductivity of liquid metals do not allow for separation between locally anodic and cathodic sites.

This 2024 Al alloy was obtained in a T351 temper as a 12.7-mm-thick plate, with analyzed composition Al+4.44Cu-1.35Mg-0.54Mn-0.18Zn-0.16Fe-0.12Si-0.02Cr-0.01Zr in weight percent. However, it had first to be annealed to remove its residual stresses, since in the original as-received plate condition, the Ga environment would induce the test specimens to break during manipulation, spoiling all attempts to properly measure the EAC properties of this pair. All test specimens were cut on the TL direction of the plate, identified by standard metallographic procedures. The basic mechanical properties of the annealed 2024 Al alloy were measured by ASTM E8M procedures at 35°C, resulting in E=70 GPa, S_Y=113 MPa, S_U=240 MPa, and ultimate strain ε_U=16%.

EAC sensibility and reaction rates of the Al-Ga pair were qualitatively evaluated also at 35°C in very slow dε/dt=4.5×10^-8/s strain rate tension tests made in a servo-controlled electromechanical testing machine, following ASTM G129 and NACE recommendations. The liquefied Ga was applied on the test specimen surfaces with a brush, and light bulbs were used to maintain the warm 35°C temperature during the tests. To guarantee that the exposure time was long enough to ensure the full LME reactions, the time necessary to propagate a crack in the annealed Al 2024-liquid Ga pair was double checked by testing precracked C(T) specimens like those used to measure K_IEAC. To do so, two precracked specimens were tested under 12 MPa√m and failed in <3 h. Then, two other similar specimens were tested under 7.5 MPa√m and did not fail after 2 days. So, following standard procedures and assuming that the incubation time should be a value close to 3 h, a preload of 7.5 MPa√m was applied for 1 day on the test specimens used to measure K_IEAC. Similarly, a preload of 30 MPa was applied for 1 day on the test specimens used to measure S_EAC. Then the basic EAC resistances were measured using small incremental load steps induced by calibrated load rings following ASTM E1681, ASTM F1624, and ISO 7539 standard procedures: S_EAC tests started at 30 MPa and used 2.5-MPa steps and K_IEAC tests initiated at 7.5 MPa√m and used 0.25-MPa√m steps. The time between successive load steps was at least 1 h. The EAC resistances measured by such standard procedures were S_EAC=43.6±4.2 MPa (average of nine samples, with 95% reliability) and K_IEAC=8.8±0.3 MPa√m (eight samples, 95% reliability).

Finally, using these standard EAC properties, four pairs of C(T)-like notched test specimens were designed to support a maximum local stress σ≅90 MPa>2S_EAC at their notch tips. The dimensions chosen for such notches were {b, ρ, b/w}={20 mm, 0.5 mm, 0.33}, {12 mm, 0.5 mm, 0.2}, {20 mm, 0.2 mm, 0.33}, and {40 mm, 4.5 mm, 0.67}, respectively, for specimens called TS1-TS2, TS3-TS4, TS5-TS6, and TS7-TS8, where b and ρ are the notch depth and tip radius and w is the specimen width, with both b and w measured from the load line. The idea was, of course, to study the effect of different combinations of their stress concentration factor K_t and stress gradient ahead of the notch tip in order to ensure tolerance to the short cracks that should start at the tips of their notches, since they all were loaded well above S_EAC. The (different) loads applied on each one of such notched test specimens were maintained for at least 48 h, a time much longer than the time required to measure the material resistances to EAC; see Castro et al. (2015) for further details.

Despite being submitted to a much longer exposure than that required to measure S_EAC and K_IEAC according to standard procedures, none of the designed notched C(T)-like specimens failed during the tests, exactly as predicted (beforehand, during their design stage). Figure 7 shows some of the unbroken notched test specimens after being loaded for a time period 50 times longer than the one required for the standard S_EAC measurements by a maximum local stress at the notch tip higher than twice the material resistance to crack initiation under EAC conditions, σ_max>2S_EAC.

Figure 7:

Notched C(T)-like specimens of an annealed Al 2024 alloy after being immersed in liquid Ga for 48 h, a time much longer than the time required to measure the material resistances to EAC, all with width w=60 mm and, from top to bottom, with {b, ρ, b/w}={20 mm, 0.5 mm, 0.33}, {12 mm, 0.5 mm, 0.2}, {20 mm, 0.2 mm, 0.33}, and {40 mm, 4.5 mm, 0.67} after being tested under a peak stress σ_max≅90 MPa>2·S_SCC at the notch tip, or twice the stress that would lead unnotched specimens to fail by EAC.

Needless to say, since the chance of eight specimens tolerating stresses twice higher than the stress needed to start and propagate cracks in unnotched specimens is very low, this can be seen as a strong experimental evidence that the method proposed here can indeed be useful to evaluate the tolerance to short cracks that depart from notch tips under EAC conditions. However, to double check such predictions, a set of similar tests was made in another material-environment pair, one where the EAC mechanism is completely different, as explained in the sequence.

5 Verification of the crack-tolerance predictions under SSC conditions

SSC was the second EAC mechanism chosen to verify the notch sensitivity effects and the tolerance to short crack predictions made by the model proposed here. SSC is usually accepted to be a form of HE, where the cracking process can be induced by tensile stresses in a susceptible material immersed in an aggressive media containing sufficient amounts of free atomic hydrogen. In the oil and gas industry, in marine applications, and in other organically enriched sediments where the reduction of sulfate ions caused by sulfate-reducing bacteria can produce sufficient H₂S, this gas is commonly associated with HE in high-strength low-alloy (HSLA) steels. Known as an acidic gas, the H₂S at low pH is stable and can form some acidic solutions after being dissolved in aqueous environments. In particular, the anaerobic corrosion processes typically found in oilfield production occurs as follows:

Anodic reaction:

H₂S dissociation reaction:

Cathodic reaction:

Overall reaction:

In this corrosion process, atomic hydrogen (H⁰) production at local cathodic sites can be seen where it is adsorbed onto the metal surface and forms iron-sulfur compounds with various phases as corrosion products. Different stoichiometric ratios of iron and sulfur produce many solids, including cubic iron sulfide, mackinawite, and troilite (all FeS), pyrite (cubic FeS₂), marcasite (FeS₂), greigite (Fe₃S₄), pyrrhotite (Fe_1-xS or Fe₇S₈), and smythite (Fe₉S₁₁) (Bai et al., 2014). The atomic hydrogen commonly recombines on the metal surface with another H⁰ to form hydrogen gas (H₂), but the presence of H₂S or other sulfur species as dissolved HS^- and S^-2 can significantly delay that process and increases the atomic hydrogen absorption by the material. This recombination behavior is similar to what happens with other species, such as Sn, Pb, Sb, and P. The main environmental variables associated to SSC in HSLA steels are temperature, pH, and partial pressure of H₂S. Low pH normally is more severe than high pH, probably because low pH indicates more hydrogen into the solution. Tests at room temperature are more susceptible to SSC than are tests at relatively high temperature like 200°C, since high partial pressures of H₂S increase the susceptibility to SSC (Kane, 1998).

Standard laboratory tests were made with a material previously known to be SSC susceptible, the AISI 4140 steel, to verify whether its crack initiation threshold under SSC conditions was as low enough as in the LME tests made before, say S_EAC<S_Y/2, in order to validate the proposed model predictions by applying a local tensile stress at notch tips about twice as high as S_EAC, like in the Al-Ga pair tested before, but maintaining LEFM conditions without failure. The aggressive environment was an aqueous solution containing 5 wt% sodium chloride, 2.5 wt% of glacial acetic acid (CH₃COOH), and 0.41 wt% sodium acetate (CH₃COONa), referenced as solution B in the NACE TM0177 standard (2005), with pH range 3.4–3.6 at 1 bar total pressure and with a H₂S partial pressure of 125 mbar and 875 mbar of CO₂ at room temperature. The AISI 4140 steel was received as a round bar, with nominal chemical composition Fe plus 0.8–1.1 Cr, 0.75–1.0 mn, 0.38–0.43 C, 0.15–0.35 Si, 0.15–0.25 mo, 0.04 S max, 0.03 P max in weight percentage. The basic material tensile properties, measured following ASTM E8M standard procedures at 25°C±1°C, were S_Y=670 MPa and S_U=976 MPa.

First, the crack initiation threshold, S_EAC, that characterizes the basic resistance of this material-environment pair to SSC or HE conditions was prospected by using small incremental load steps, following ASTM F1624 standard procedures. The test was performed in a servo electromechanical machine following a 10/10/2,4 load profile, with 10 initial load steps of 2 h holding time, followed by 10 load steps of 4 h holding time. The threshold measured with this method was S_EAC=332±11.3 MPa. To ensure that the test condition reproduced the same anodic and cathodic reactions described previously, the dissolved oxygen was removed by purging the solution and the test vessel for 2 h per liter with 99,999% pure nitrogen gas before the specimen was immersed into the aggressive solution. As the test vessels must be made from materials that are inert to the test environment, they were manufactured in glass and PTFE (see Figure 8). After the purge, the anaerobic solution was transferred to the test vessel, and the saturation with the test gas was performed for 2 h. After this process, a film developed at the specimen surface and the cathodic reaction could be visualized by the H₂ bubbles it produces on the specimen surface (see Figure 9).

Figure 8:

Servo electro-mechanic machine used for the incremental 10/10/2,4 tensile tests; test vessel with a smooth 6.35-mm diameter 4140 steel test specimen used to measure its basic resistance to crack initiation under EAC, S_EAC; and the vessels containing the aqueous solution of 5 wt% NaCl, 2.5 wt% CH₃COOH, and 0.41 wt% CH₃COONa used the aggressive environment for the SCC tests.

Figure 9:

4140 steel specimen immersed into the anaerobic solution after the purge (left) and the same specimen after saturation, showing the cathodic reaction generating H₂ bubbles on the specimen surface (right).

The fractographic analyses of the EAC-induced failures in those unnotched tensile specimens in a scanning electron microscope showed a characteristic transgranular cracking behavior, as illustrated in Figure 10.

Figure 10:

SEM cross-section fractography of the 4140 steel tensile specimen used to measure its S_EAC resistance after it was loaded by the 10/10/2,4 profile.

The crack propagation threshold for those SSC conditions was measured using standard NACE TM0177 method D procedures, by testing four side-grooved Double Cantilever Beam specimens machined by wire electrical discharge to avoid residual stresses (see Figure 11). These specimens were immersed in the anaerobic test solution for 14 days and loaded by double tapered wedges in order to provide a crack mouth displacement, δ=0.63 mm, using all precautions adopted in the step loading tests to avoid oxygen contamination. After the test, the specimens were loaded in a servo electro-mechanical machine to obtain the equilibrium wedge-load (P). Finally, the specimens were broken in liquid nitrogen to measure the crack, resulting in K_IEAC=34.2 MPa√m (see Figure 12).

Figure 11:

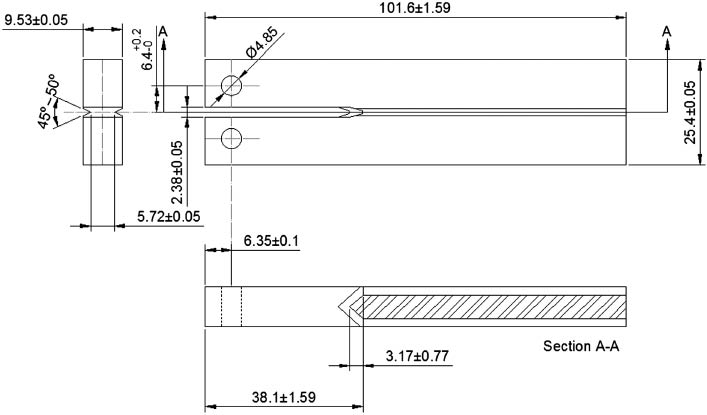
DCB specimens used to measure the basic 4140 resistance to crack propagation under EAC conditions inside the aggressive solution, K_IEAC (dimensions in mm).

Figure 12:

DCB specimen loaded by an imposed displacement in a servo electromechanical testing machine at equilibrium wedge-load (left), before it was immersed in the aggressive solution, and its fracture surface after it was broken in liquid nitrogen (right).

Using the model proposed here and the measured S_EAC and K_IEAC properties, two notched DC(T)-like specimens were designed and machined with two different notch sizes, to reach at the notch tip a maximum stress near twice the crack initiation threshold S_EAC, without exceeding the material yielding strength S_Y to maintain LE conditions all over the tested specimens. These notched specimen dimensions were width w=60 mm, initial notch size b/w=0.3, and two different notch tip radii, one ρ=0.5 mm and the other ρ=1.5 mm (see Figure 13). Such notched specimens were loaded in proof rings to obtain a maximum stress σ_max=610 MPa=1.84·S_EAC=0.91·S_Y at the notch tip. The loads applied by the proof rings were monitored in real time using strain gages (see Figure 14). As shown in Figure 15, exactly as predicted beforehand, these specimens did not broke under such high loads after 30 days of immersion, more than twice the time needed to measure K_IEAC.

Figure 13:

Notched DC(T)-like specimens of 4140 steel before their EAC tests. Note the two different tip radii.

Figure 14:

EAC tests of the notched 4140 steel DC(T)-like specimens used to verify the tolerance to short cracks under HE conditions predicted by the model proposed here (right), immersed in the aggressive solution and assembled in proof rings (left), and a front view of one of them.

Figure 15:

Notched 4140 steel DC(T)-like specimens after their SSC exposition.

Figure 15 shows the two notched DC(T)-like specimens after being exposed during 30 days to the aggressive environment that causes HE in its material. Note once again that although such 4140 steel specimens were loaded to induce a maximum stress at their notch tips σ_max=1.84·S_EAC, a value much higher than material resistance to start and propagate a crack by EAC in unnotched specimens, they did not break after 30 days immersed in that aggressive environment. Nevertheless, this high stress level did start nonpropagating short cracks at the notch, exactly as predicted by the model proposed here (see Figure 16). This experimental result confirms once again that this mechanical model has the potential to be useful to consider stress analysis issues when analyzing and designing structural components for EAC applications.

Figure 16:

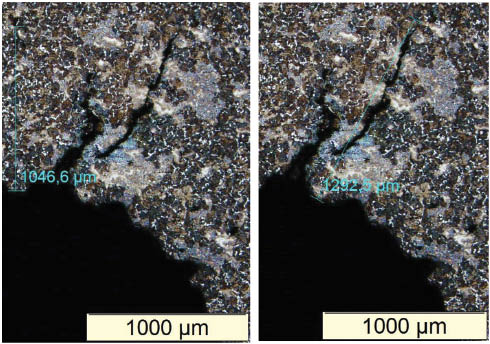
Tip of one of the notched DC(T)-like specimen after the corrosive exposition showing the short cracks that started there but did not propagate even when exposed to a stress σ_max=1.84·S_EAC during a time more than twice longer than the one needed to measure the EAC crack propagation threshold by standard procedures, exactly as predicted by the model proposed here.

6 Additional comments

Before closing this work, it must be emphasized that the predictions made here complement the most important contributions of previous pioneer research on crack tolerance under EAC conditions, e.g. those presented in the classic work of Parkins (1979) on the effect of slow strain-rate tests on the EAC behavior. These early works clearly identified the existence of a crack propagation threshold under EAC conditions, so in a sense, they can be used to evaluate the stresses tolerable by cracked components.

However, this classic concept is directly applicable only to long cracks, those that are not affected by stress gradients induced by notches. Moreover, if the crack itself is induced by EAC mechanisms, it is sensitive to the maximum tensile stress at its initiation point, which of course must be higher than the minimum stress level required to start it, σ>S_EAC. If the SIF K_I of such a crack increases with its size a, the usual case if it departs from a smooth surface and if the cracked component is loaded by an imposed (constant) load, then the initiated crack can propagate until the final fracture of the component. Note that under imposed displacements, like in the DCD specimens used to measure the 4140 steel K_IEAC value under SCC conditions as described above, the crack can stop (and thus become a nonpropagating crack) because its SIF decreases as it grows until reaching the arrest condition K_I(a)<K_IEAC. But since many, if not most, components work under fixed loads, thus having K_I(a) values that increase with a, the only safe procedure recognized so far to avoid their failures under EAC conditions is to limit their maximum stresses to values below their crack initiation threshold, σ_max<S_EAC.

If the resistance to crack initiation under EAC conditions, S_EAC, is relatively low, say smaller than the material yield limit, then the only choice to avoid such failures indeed seems to be to change the material for a more resistant one. However, from the point of view of a structural engineer, this criterion has a major setback: the stress concentration effects induced by operational or accidental notches, which are unavoidable in practice. As the maximum stress at those notch tips can be much higher than the nominal stresses that act elsewhere in the component, they control the EAC failures, and if its material is sensible to EAC inside its working environment, the need to change it seems inevitable.

This problem can lead to expensive solutions in the design stage (e.g. the use of super duplex stainless steel for sensitive pipelines in the oil industry), but it is not a major barrier in such cases. The real trouble is with unforeseen problems as mentioned before: how to decide what to do with an already built and operating structure in such cases. If the problem is discovered before the structure fails and obviously is still safe, how much safe is it? For how long can it continue operating under the service loads within an acceptable risk level? There is simply no way to answer such and similar questions without a proper stress analysis procedure, one that properly considers the unavoidable notch effects. That is the main contribution of Eq. (11), which properly considers the notch sensitivity under EAC conditions. Note that although its deduction has been purely mechanical, and because of that it may seem a little bit strange to those more trained in chemical than in mechanical techniques, its predictions that notch tips could tolerate stresses much higher than S_EAC have been confirmed by two sets of discriminating tests made inside aggressive media that induced different EAC mechanisms. Besides, the model considers the chemical contribution to the EAC problems by using the resistances to crack initiation and growth inside the aggressive environment, properties traditionally recognized to properly quantify these chemical effects. So, albeit the tests presented here are certainly not enough to claim that this model should be included in structural evaluations routines, the authors believe that it has potential to be really useful in such situations, and thus deserve to be further studied.

Finally, some words of caution. Microstructurally short cracks, those small compared to the grain size gr, are much affected by microstructural barriers like grain boundaries or 2nd phase particles, so they cannot be well modeled by macroscopic stress analysis techniques. Their behavior can be academically important, but as such microscopic cracks cannot be mapped in most practical applications, they are not part of this work scope. On the other hand, mechanically short cracks, which have sizes that are not small compared to the grain size and, as depicted in the Kitagawa-like diagram, have thresholds smaller than ΔK_IEAC, can be properly modeled by LEFM concepts (i) if the stress field that surrounds them is predominantly LE and (ii) if the material can be treated as isotropic and homogeneous in this scale, both qualitative conditions. Hence, the idea here was to follow Irwin’s steps by first assuming that these concepts are valid and then by verifying whether their predictions are validated by proper tests. The several tests made under LE peak stresses at the notch tips inside the two environments that induced totally different EAC mechanisms supported the model predictions, but their limitations have not been checked yet. Indeed, the model developed and used in this work assumes that the crack effects can be properly quantified by their SIFs, a hypothesis that must be reviewed if they grow through predominantly plastic stress fields, those associated to plastic zones that are not much smaller than the residual uncracked ligament. The model also assumes that the short cracks grow unidimensionally, so they can be properly characterized by its size, a, only. However, when the surface flaws are much smaller than the piece dimensions, they probably look like small surface or corner cracks and should be treated as so, recognizing that they are 2D cracks that grow in two directions, usually changing their shape as they propagate, although maintaining their original plane under mode I loads. Anyway, even though these model limitations must be explored in complementary works, they do not invalidate the main contribution proposed in this work: the existence of a clearly definable notch sensitivity factor that can be used to introduce proper stress analysis tools for EAC structural integrity evaluation and design purposes.

7 Conclusions

A generalized ETS parameter was used to model the dependence of the threshold stress intensity range for short fatigue cracks on the crack size, as well as the behavior of nonpropagating cracks induced by tensile stresses under EAC conditions. This dependence was used to estimate the notch sensitivity factor of shallow and elongated notches both for fatigue and for EAC conditions, from the propagation behavior of short nonpropagating cracks that might initiate from their tips, and then stopped due to the high-stress gradients that may act ahead of the notch tips. As made for the fatigue case before, these predictions were verified by proper experiments for two different EAC mechanisms, LME and HE. Based on this promising performance, the criterion proposed to evaluate the influence of small or large surface flaws in fatigue and in EAC problems may be useful for practical applications and deserves further attention.