Abstract
In this paper, we introduce a new way-below relation in T0 topological spaces based on cuts and give the concepts of SI2-continuous spaces and weakly irreducible topologies. It is proved that a space is SI2-continuous if and only if its weakly irreducible topology is completely distributive under inclusion order. Finally, we introduce the concept of 𝓓-convergence and show that a space is SI2-continuous if and only if its 𝓓-convergence with respect to the topology τSI2(X) is topological. In general, a space is SI-continuous if and only if its 𝓓-convergence with respect to the topology τSI(X) is topological.
1 Introduction
Domain theory which arose from computer science and logic, started as an outgrowth of theories of order. Rapidly progress in this domain required many materials on topologies (see [1, 2, 3]). Conversely, it is well known that given a topological space one can also define order structures (see [3, 4, 5, 6]). At the 6th International Symposium in Domain Theory, J.D. Lawson emphasized the need to develop the core of domain theory directly in T0 topological spaces instead of posets. Moreover, it was pointed out that several results in domain theory can be lifted from the context of posets to T0 topological spaces (see [5, 6]). In the absence of enough joins, Erné introduced the concept of s2-continuous posets and the weak Scott topology by means of the cuts instead of joins (see [7]). The notion of s2-continuity admits to generalize most important characterizations of continuity from dcpos to general posets and has the advantage that not even the existence of directed joins has to be required. In [6], Erné further proved that the weak Scott topology is the weakest monotone determined topology with a given specialization order. In [5], Zhao and Ho defined a new way-below relation and a new topology constructed from any given topology on a set using irreducible sets in a T0 topological space replacing directed subsets and investigated the properties of this derived topology and k-bounded spaces. It was proved that a space X is SI-continuous if and only if SI(X) is a C-space.
Many convergent classes in posets were studied in [3, 8, 9, 10, 11, 12]. By different convergences, not only many notions of continuity are characterized, but also they make order and topology across each other. In [3], the concept of 𝓢-convergence for dcpos was introduced by Scott to characterize continuous domains. It was proved that for a dcpo, the 𝓢-convergence is topological if and only if it is a continuous domain. The main purpose of this paper is to lift the notion of s2-continuous posets to topology context. By the manner of Erné we introduce a new way-below relation in T0 topological spaces based on cuts and give the concepts of SI2-continuous spaces and weakly irreducible topologies. It is proved that a space is SI2-continuous if and only if its weakly irreducible topology is completely distributive under inclusion order. Finally, we introduce the concept of 𝓓-convergence and show that a space is SI2-continuous if and only if its 𝓓-convergence with respect to the topology τSI2(X) in a topological space is topological. Furthermore, a space is SI-continuous if and only if its 𝓓-convergence with respect to the topology τSI(X) is topological. The work carry out here is another response to the call by J. D. Lawson to develop domain theory in the wider context of T0 topological spaces instead of restricting to posets.
2 Preliminaries
Let P be a partially ordered set (poset, for short). A nonempty set D ⊆ P is directed if for any d1, d2 in D there exists d in D above d1 and d2. The principal ideal generated by x ∈ P is ↓ x = {y ∈ P : y ≤ x}. ↓ A = ⋃a∈A ↓ a is the lower set or downset generalized by A ⊆ P; The principal filter ↑ x and upper set ↑ A are defined dually. A↑ and A↓ denote the sets of all upper and lower bounds of A, respectively. A cut δ of A in P is defined by Aδ = (A↑)↓ for every A ⊆ P. Notice that x ∈ Aδ means x ≤ ⋁ A whenever A has a join (supremum).
On the one hand, given a poset P, we can generate some intrinsic topologies. The upper sets form the Alexandroff upper topology α(P). The weak Scott topology σ2(P) consists of all upper sets U such that Dδ ∩ U ≠ ∅ implies D ∩ U ≠ ∅ for all directed sets D of P. In case P is a dcpo, the weak Scott topology coincides with the usual Scott topology σ(P), which consists of all upper sets U such that ⋁ D ∈ U implies D ∩ U ≠ ∅ for all directed sets D in P. The upper topology generating by the complements of the principal ideals is denoted by υ(P). Clearly, υ(P) ⊆ σ2(P) ⊆ σ(P) ⊆ α(P).
On the other hand, for a topological space (X, τ), the specialization order ≤ on X is defined by y ≤ x if and only if y ∈ cl{x}. It is antisymmetric, hence a partial order, if and only if (X, τ) is T0. The specialization order on X is denoted by ≤τ if there is need to emphasize the topology τ. Note that the specialization order of the Alexandroff upper topology on a poset coincides with the underlying order and ↓ x = cl{x}.
If not otherwise stated, in topological contexts, lower sets, upper sets and related notions refer to the specialization order.
Remark 2.1
Let (X, τ) be a T0 space.
If D ⊆ X is a directed set with respect to the specialization order, then D is irreducible;
If U ⊆ X is an open set, then U is an upper set; Similarly, if F ⊆ X is a closed set, then F is a lower set.
Definition 2.1
[7] Let P be a poset.
For any x, y ∈ P, we say that x is way below y, written x ≪ y if for all directed sets D ⊆ P with y ∈ Dδ, there exists d ∈ D such that x ≤ d. The set {y ∈ P : y ≪ x} will be denoted by ⇓ x and {y ∈ P : x ≪ y} denoted by ⇑ x;
P is called s2-continuous if for all x ∈ P, x ∈ (⇓ x)δ and ⇓ x is directed.
Indeed, since ⇓ x ⊆ ↓ x we have x = ⋁ ⇓ x if and only if x ∈ (⇓ x)δ.
Definition 2.2
[5] Let (X, τ) be a T0 space. For x, y ∈ X, define x ≪SI y if for all irreducible sets F, y ≤ ⋁ F implies there exists e ∈ F such that x ≤ e whenever ⋁ F exists. The set {y ∈ X : y ≪SI x} is denoted by ↡SI x and the set {y ∈ X : x ≪SI y} by ↟SI x.
Definition 2.3
[5] Let (X, τ) be a T0 space. X is called SI-continuous if the following conditions are satisfied:
↡SI x is directed for all x ∈ X;
x = ⋁ ↡SI x for all x ∈ X;
↟SI x ∈ τ for all x ∈ X.
Definition 2.4
[5] Let (X, τ) be a T0 space. A subset U ⊆ X is called SI-open if the following conditions are satisfied:
U ∈ τ;
For all F ∈ Irrτ(X), ⋁ F ⋂ U ≠ ∅ implies F ⋂ U ≠ ∅ whenever ⋁ F exists.
The set of all SI-open sets of (X, τ) is denoted by τSI(X).
3 SI2-continuous spaces
In this section, we define a SI2-continuous space derived by the irreducible set of a topological space. Some properties of this derived SI2-continity are investigated.
Let (X, τ) be a topological space. A nonempty subset F ⊆ X is called irreducible if for every closed sets B and C, whenever F ⊆ B ⋃ C, one has either F ⊆ B or F ⊆ C. The set of all irreducible sets of the topological space (X, τ) will be denoted by Irrτ(X) or Irr(X).
Definition 3.1
Let (X, τ) be a T0 space and x, y ∈ X. Define x ≪r y if for ervery irreducible set E, y ∈ Eδ implies there exists e ∈ E such that x ≤ e. We denote the set {y ∈ X : y ≪r x} by ↡r x and the set {y ∈ X : x ≪r y} by ↟r x.
Remark 3.1
Let (X, τ) be a T0 space and x, y, u, v ∈ X.
x ≪r y implies x ≤ y;
u ≤ x ≪r y ≤ v implies u ≪r v.
Definition 3.2
Let (X, τ) be a T0 space. A subset U ⊆ X is called weakly irreducibly open if the following conditions are satisfied:
U ∈ τ;
Fδ ⋂ U ≠ ∅ implies F ⋂ U ≠ ∅ for all F ∈ Irrτ(X).
The set of all weakly irreducibly open sets of (X, τ) is denoted by τSI2(X). Complements of all weakly irreducibly open sets are called weakly irreducibly closed sets.
Lemma 3.1
Let (X, τ) be a T0 space. Then τSI2(X) is a topology on X.
Proof
Clearly ∅, X ∈ τSI2(X);
It claims that U ⋂ V ∈ τSI2(X) for any U, V ∈ τSI2(X). Indeed, for any F ∈ Irrτ(X), if Fδ ⋂ (U ⋂ V) ≠ ∅, then Fδ ⋂ U ≠ ∅ and Fδ ⋂ V ≠ ∅. Note U, V ∈ τSI2(X), we have F ⋂ U ≠ ∅ and F ⋂ V ≠ ∅. Since F ∈ Irrτ(X), we have F ⋂ (U ⋂ V) ≠ ∅. Clearly U ∩ V ∈ τ, so U ⋂ V ∈ τSI2(X).
Assume that {Ui : i ∈ I} ⊆ τSI2(X). Firstly, ⋃i∈I Ui ∈ τ. Secondly, for any F ∈ Irrτ(X), if Fδ ⋂ (⋃i∈I Ui) = ⋃i∈I(Fδ ⋂ Ui) ≠ ∅, then there exists some i ∈ I such that Fδ ⋂ Ui) ≠ ∅. Note that F ∈ Irrτ(X) and U ∈ τSI2(X), then F ⋂ Ui ≠ ∅. Thus we have F ⋂ (⋃i∈I Ui) ≠ ∅. Therefore ⋃i∈I Ui ∈ τSI2(X). □
Remark 3.2
Let (X, τ) be a T0 space. Then τSI2(X) is always coarser than τSI(X), and if any irreducible set in X has a supremum, then both topologies coincide. In the following, the space (X, τSI2(X)) is also simply denoted by SI2(X).
The following example is due to Erné (see [7, Example 2.5]).
Example 3.1
Let P be poset delineated by Figure 1 and B = {bn: n = 0, 1, 2, …}, C = {ck : k = 1, 2, …}. The order ≤ on P = B ∪ C is defined as follows:
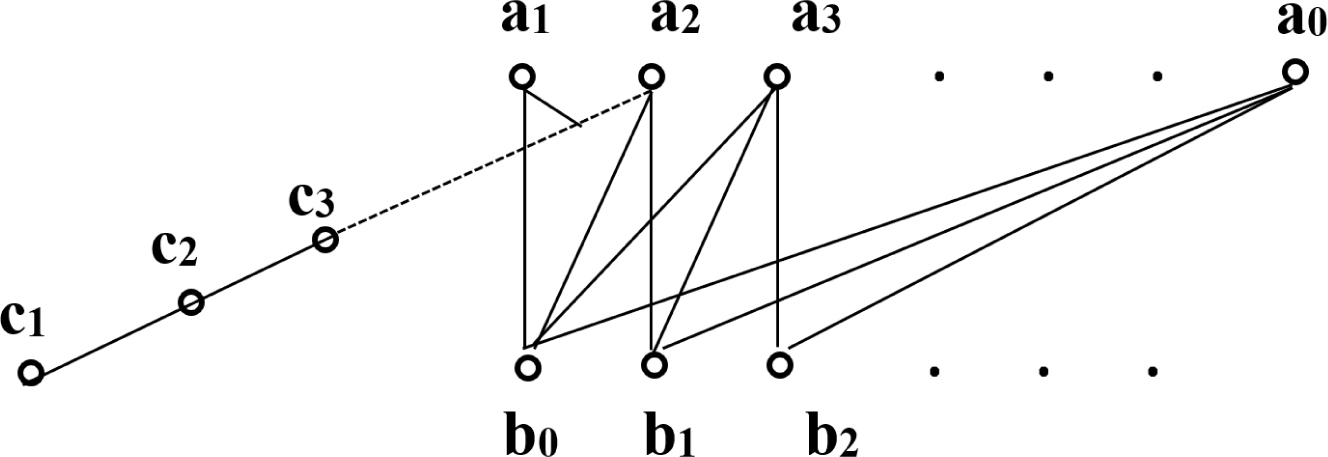
A set which is SI-open is not weakly irreducibly open.
↓ a0 = {a0} ∪ B,
↓ a1 = {a1, b0} ∪ C,
↓ a2 = {a2, b0, b1} ∪ C,
↓ an = {an} ∪ {bm : m < n}(n = 3, 4, …),
↓ bn = {bn}(n = 0, 1, 2, …),
↓ cn = {cm : m ≤ n}(n = 1, 2, …).
x ≤ y ⇔ x ∈ ↓ y. Endow P with the Alexandroff upper topology.
Then it is easy to see that ↑ b0 is open in τSI(P). C = {ck : k = 1, 2, …} is an irreducible set with b0 ∈ Cδ ∩ ↑ b0 ≠ ∅ while C ∩ ↑ b0 = ∅, and whence ↑ b0 ∉ τSI2(α(P)). Thus τSI2(α(P)) is proper contained in τSI(α(P)).
Definition 3.3
Let (X, τ) be a T0 space. X is called SI2-continuous if the following conditions are satisfied:
↡r x is directed for all x ∈ X;
x ∈ ( ↡r x)δ for all x ∈ X;
↟r x ∈ τ for all x ∈ X.
Lemma 3.2
Let P be a poset. Then SI2(P, α(P)) = (P, σ2(P)).
Remark 3.3
Let P be a poset. Then P is an s2-continuous poset if and only if it is an SI2-continuous space with respect to the Alexandroff upper topology.
Let (X, τ) be a T0 space. If X is an SI2-continuous space, then it is also an s2-continuous poset under the specialization order. But the converse may not be true.
Example 3.2
Let X be an infinite set with a cofinite topology τ. Then it is a T1 space. Clearly it is an antichain under the specialization order, and hence it is an s2-continuous poset. But ↟r x = {x} ∉ τ for all x ∈ X, then (X, τ) is not an SI2-continuous space.
Let us note that an SI2-continuous space is SI-continuous space, but the converse may not be true:
Example 3.3
Consider the Euclidean plane ℝ × ℝ under the usual topology. It is an SI-continuous space, but it is not SI2-continuous, since every lower half-plane
is a directed set with
The following theorem shows that the SI2-continuity of the topological space has the interpolation property.
Theorem 3.1
Let X be an SI2-continuous space and x, y ∈ X. If x ≪r y, then there exists z ∈ X such that x ≪r z ≪r y.
Proof
Let X be an SI2-continuous space and x ≪r y. Then we have ↡r y is directed and y ∈ (↡r y)δ. Since the union of a directed family of directed sets, E = ⋃ {↡r z : z ∈ ↡r y} is still a directed set(hence an irreducible set) and y ∈ Eδ. So there exists z ∈ ↡r y such that x ≤ u ≪r z for some u ∈ X. Thus x ≪r z ≪r y. □
Remark 3.4
In Theorem 3.1, when we prove the interpolation property, we do not need the third condition in the definition of the SI2-continuous space.
Lemma 3.3
Let X be an SI2-continuous space. Then for any x ∈ X, ↟r x ∈ τSI2(X).
Proof
It follows from Definition 3.3 and Theorem 3.1. □
Lemma 3.4
Let (X, τ) be a T0 space and y ∈ intτSI2(X) ↑ x. Then x ≪r y, where intτSI2(X) ↑ x denotes the interior of ↑ x with respect to the topology τSI2(X).
Proof
Let y ∈ intτSI2(X) ↑ x. For every irreducible set E with y ∈ Eδ, we have y ∈ Eδ ∩ intτSI2(X) ↑ x ≠ ∅, and hence intτSI2(X) ↑ x ∩ E ≠ ∅. Thus there exists e ∈ intτSI2(X) ↑ x ∩ E. Thus we have x ≤ e and e ∈ E. This shows x ≪r y. □
Theorem 3.2
Let (X, τ) be a T0 space. Then the following statements are equivalent:
X is an SI2-continuous space;
For all U ∈ τSI2(X) and x ∈ U, there exists y ∈ U such that x ∈ intτSI2(X) ↑ y ⊆ ↑ y ⊆ U;
(τSI2(X), ⊆) is a completely distributive lattice.
Proof
(1) ⇒ (2) Let X be an SI2-continuous space and U ∈ τSI2(X) with x ∈ U. Since x ∈ (↡r x)δ ⋂ U ≠ ∅, note that ↡r x is directed(hence irreducible), then we have ↡r x ⋂ U ≠ ∅. Thus there exists y ≪r x such that y ∈ U. By Lemma 3.3, ↟r y ∈ τSI2(X), we have that x ∈ ↟r y ⊆ ↑ y ⊆ U, that is, x ∈ intτSI2(X) ↑ y ⊆ ↑ y ⊆ U.
(2) ⇒ (1) For x ∈ X, consider the set E = {y ∈ X : x ∈ intτSI2(X) ↑ y}. Let y1, y2 ∈ E. Then x ∈ intτSI2(X) ↑ y1 ⋂ intτSI2(X) ↑ y2. By (2), there exists y ∈ intτSI2(X) ↑ y1 ⋂ intτSI2(X) ↑ y2 such that x ∈ intτSI2(X) ↑ y ⊆ ↑ y ⊆ intτSI2(X) ↑ y1 ⋂ intτSI2(X) ↑ y2, so y ∈ E and y1, y2 ≤ y. This shows that E is a directed set. It is not hard to show x ∈ Eδ. By Lemma 3.4, we have E ⊆ ↡r x. Thus we have that ↡r x is directed(hence irreducible) and x ∈ (↡r x)δ, so we also have ↡r x ⊆ ↓ E. Thus ↡r x = ↓ E. From the above discussion we can derive that ↟r x = ⋃y∈↑x intτSI2(X) ↑ y, which is open in τ. Hence X is an SI2-continuous space.
(2) ⇔ (3) See [4]. □
Corollary 3.1
([7]) Let P be a poset. Then the following conditions are equivalent:
P is s2-continuous;
For all U ∈ σ2(P) and x ∈ U, there exists y ∈ U such that x ∈ intσ2(P) ↑ y ⊆ ↑ y ⊆ U;
(σ2(P), ⊆) is a completely distributive lattice.
Corollary 3.2
([5]) Let (X, τ) be a T0 space. Then the following statements are equivalent:
X is an SI-continuous space;
For all U ∈ τSI(X) and x ∈ U, there exists y ∈ U such that x ∈ intτSI(X) ↑ y ⊆ ↑ y ⊆ U;
(τSI(X), ⊆) is a completely distributive lattice.
4 𝓓-convergence in SI2-continuous spaces
In this section, the concept of 𝓓-convergence in a topological space is introduced. It is proved that a space X is SI2-continuous if and only if the 𝓓-convergence with respect to the topology τSI2(X) in X is topological. In general, a space X is SI-continuous if and only if its 𝓓-convergence with respect to the topology τSI(X) in X is topological.
Definition 4.1
Let (X, τ) be a T0 space. A net (xj)j∈J in X is said to converge to x ∈ X if there exists a directed set D ⊆ X with respect to the specialization order such that
x ∈ Dδ;
For all d ∈ D, d ≤ xj holds eventually.
In this case we write x ≡𝓓 lim xj.
Let 𝓓 denote the class of those pairs ((xj)j∈J, x) with x ≡𝓓 lim xj. Then 𝓞(𝓓) = {U ⊆ X : whenever ((xj)j∈J, x) ∈ 𝓓 and x ∈ U, then eventually xj ∈ U} is a topology.
Example 4.1
Let P = {aj : j ∈ ℕ} ∪ {a, b}, where ℕ denotes the set of all natural numbers. The order on P is defined by a1 ≤ a2 ≤ ⋯ ≤ a, b ≤ a. Endow P with the Alexandroff upper topology. If xj = aj for all j ∈ ℕ, then (xj)j∈ℕ is a net. Take D = {aj : j ∈ ℕ}, and then D is a directed subset of P with b ∈ Dδ. Moreover, for all d ∈ D, d ≤ xj holds eventually, hence the net (xj)j∈ℕ converges to b.
Proposition 4.1
Let X be an SI2-continuous space. Then x ≡𝓓 lim xj if and only if the net (xj)j∈J converges to the element x with respect to the topology τSI2(X). That is, the 𝓓-convergence is topological.
Proof
Firstly, suppose that a net (xj)j∈J in X converges to x ∈ X and x ∈ U ∈ τSI2(X). Then there exists a directed set D ⊆ X (hence an irreducible set) such that d ≤ xj holds eventually for all d ∈ D and x ∈ Dδ, and hence U ⋂ D ≠ ∅, that is, there exists d ∈ U ⋂ D. Clearly, the net xj ∈ U holds eventually as U is an upper set. Conversely, assume that the net (xj)j∈J converges to an element x with respect to the topology τSI2(X). For all y ∈ ↡r x, then one has x ∈ ↟r y ∈ τSI2(X) by Lemma 3.3. Thus there exists k ∈ J such that xj ∈ ↟r y for any j ≥ k. By SI2-continuity of X, we have that x ∈ (↡r x)δ and ↡r x is directed. Thus ((xj)j∈J, x) ∈ 𝓓, that is, x ≡𝓓 lim xj. □
Proposition 4.2
Let (X, τ) be a T0 space. If the 𝓓-convergence with respect to the topology τSI2(X) is topological, then X is SI2-continuous.
Proof
Suppose that the 𝓓-convergence with respect to the topology τSI2(X) is topological. For all x ∈ X, take J = {(U, n, a) ∈ N(x) × ℕ × X : a ∈ U}, where N(x) consists of all weakly irreducibly open sets which contain x, and define an order on J as follows: (U, m, a) ≤ (V, n, b) if and only if V is proper subset of U or U = V and m ≤ n. Obviously, J is directed. Let xj = a for all j = (U, m, a) ∈ J. Then it is not hard to show that the net (xj)j∈J converges to x with respect to the weakly irreducible topology τSI2(X). By the condition, one has x ≡𝓓 lim xj. Thus there exists a directed set D with respect to the specialization order such that x ∈ Dδ and for all d ∈ D, d ≤ xj holds eventually. Then there exists k = (U, m, a) ∈ J such that (V, n, b) = j ≥ k implies d ≤ xj = b for all d ∈ D. Especially one has (U, m + 1, b) ≥ (U, m, a) = k for all b ∈ U. So x ∈ U ⊆ ↑ d. It follows that D ⊆ ↓ x and x ∈ intτSI2(X) ↑ d. By Lemma 3.4, d ≪r x, and then D ⊆ ↡r x. Thus x ∈ Dδ ⊆ (↡r x)δ. It is easy to show that ↡r x is directed. Finally, it follows that ↟r x ∈ τ for all x ∈ X. Indeed, if y ∈ ↟r x, then there exists z ∈ X such that x ≪r z ≪r y by Remark 3.4. From the above argument, as long as we replace J = {(U, n, a) ∈ N(x) × ℕ × X : a ∈ U} with I = {(U, n, a) ∈ N(y) × ℕ × X : a ∈ U}, where N(y) consists of all weakly irreducibly open sets containing y, similarly we have that (xi)i∈I converges to y with respect to the topology τSI2(X), and then there exists a directed set D1 of eventual lower bounds of the net (xi)i∈I such that y ∈
From Propositions 4.1 and 4.2, we immediately have:
Theorem 4.1
Let (X, τ) be a T0 space. Then the following statements are equivalent:
X is SI2-continuous;
The 𝓓-convergence with respect to the topology τSI2(X) is topological.
Similarly, we also have:
Theorem 4.2
Let (X, τ) be a T0 space. Then the following statements are equivalent:
X is SI-continuous;
The 𝓓-convergence with respect to the topology τSI(X) is topological.
Corollary 4.1
([17]) Let P be a poset. Then the following statements are equivalent:
P is s2-continuous;
The 𝓢-convergence in P is topological for the weak Scott topology, that is, for all x ∈ P and all nets (xj)j∈J in P, x ≡𝓢 lim xj if and only if (xj)j∈J converges to the element x with respect to the weak Scott topology.
Corollary 4.2
([3]) Let P be a dcpo. Then the following statements are equivalent:
P is a domain;
The 𝓢-convergence in P is topological for the Scott topology, that is, for all x ∈ P and all nets (xj)j∈J in P, x ≡𝓢 lim xj if and only if (xj)j∈J converges to the element x with respect to the Scott topology.
5 Conclusion
At the Sixth International Symposium on Domain Theory, J.D. Lawson encouraged the domain theory community to consider the scientific program of developing domain theory in the wider context of T0 spaces instead of restricting to posets. In this paper, we introduce a new way-below relation in T0 topological spaces based on the cuts and give the concepts of SI2-continuous spaces and weakly irreducible topologies. It is proved that a space is SI2-continuous if and only if its weakly irreducible topology is completely distributive under inclusion order. Finally, we introduce the concept of 𝓓-convergence and show that a space is SI2-continuous if and only if its 𝓓-convergence with respect to the topology τSI2(X) is topological. In general, a space is SI-continuous if and only if its 𝓓-convergence with respect to the topology τSI(X) is topological. The present paper can be seen as one of the some works towards the new direction, which may deserve further investigation. Indeed there are some questions to which we possess no answers. The following is such one.
In the first condition of the definition of the 𝓓-convergence, whether we can change directed set into irreducible set?
Acknowledgement
The research was supported by the National Natural Science Foundation of China (11661057, 11661055, 61866023, 11561046), GAN PO555 Program of Jiangxi Province and the Natural Science Foundation of Jiangxi Province (20192ACBL20045, 20151BAB201020).
References
[1] Abramsky S., Jung A., Domain theory, In: Abramsky S., Gabbay D.M., Maibaum T.S.E. (Eds.), Handbook of Logic in Computer Science, vol. 3, Oxford University Press, Oxford, 1994.Suche in Google Scholar
[2] Gierz G., Hofmann K., Keimel K., Lawson J.D., Mislove M., Scott D., A Compendium of Continuous Lattices, Springer-Verlag, Berlin-Heidelberg-New York, 1980.10.1007/978-3-642-67678-9Suche in Google Scholar
[3] Gierz G., Hofmann K., Keimel K., Lawson J.D., Mislove M., Scott D., Continuous Lattices and Domains, Encyclopedia of Mathematics and its Applications, vol. 93, Cambridge University Press, 2003.10.1017/CBO9780511542725Suche in Google Scholar
[4] Erné M., The ABC of order and topology, In: Herlich H., Porst H.E. (Eds.), Category Theory at Work, Heldermann Verlag, Berline, 1991, 57–83.Suche in Google Scholar
[5] Zhao D.S., Ho W.K., On topologies defined by irreducible sets, J. Log. Algebr. Methods Program., 2015, 84(1), 185–195.10.1016/j.jlamp.2014.10.003Suche in Google Scholar
[6] Erné M., Infinite distributive laws versus local connectedness and compactness properties, Topology Appl., 2009, 156, 2054–2069.10.1016/j.topol.2009.03.029Suche in Google Scholar
[7] Erné M., Scott convergence and Scott topology on partially ordered sets II, In: Banaschewski B., Hoffman R.-E. (Eds.), Continuous Lattices, Bremen 1979, Lecture Notes in Math., Springer-Verlag, Berlin-Heidelberg-New York, 1981, 871, 61–96.10.1007/BFb0089904Suche in Google Scholar
[8] Zhao B., Zhao D.S., Lim-inf convergence in partially ordered sets, J. Math. Anal. Appl., 2005, 309, 701–708.10.1016/j.jmaa.2004.11.028Suche in Google Scholar
[9] Zhou Y.H., Zhao B., Order-convergebce and lim-infM-convergence in posets, J. Math. Anal. Appl., 2007, 325, 655–664.10.1016/j.jmaa.2006.02.016Suche in Google Scholar
[10] Wang K.Y., Zhao B., Some further results on order-convergence in posets, Topology Appl., 2013, 160, 82–86.10.1016/j.topol.2012.09.018Suche in Google Scholar
[11] Zhao B., Li J., O2-convergence in posets, Topology Appl., 2006, 153, 2971–2975.10.1016/j.topol.2006.01.004Suche in Google Scholar
[12] Zhou L.J., Li Q.G., Convergence on quasi-continuous domain, J. Comput. Anal. Appl., 2013, 15, 381–390.Suche in Google Scholar
[13] Huang M.Q., Li Q.G., Li J.B., Generalized continuous posets and a new cartesian closed category, Appl. Categ. Structures, 2009, 17, 29–42.10.1007/s10485-008-9132-9Suche in Google Scholar
[14] Lawson J.D., Xu L.S., Posets having continuous intervals, Theoret. Comput. Sci., 2004, 316, 89–103.10.1016/j.tcs.2004.01.025Suche in Google Scholar
[15] Mislove M., Local DCPOs, local CPOs and local completions, Electron. Notes Theor. Comput. Sci., 1999, 20, 1–14.10.1016/S1571-0661(04)80085-9Suche in Google Scholar
[16] Markowsky G., A motivation and generalization of Scott’s notion of a continuous lattice, In: Banaschewski B., Hoffman R.-E. (Eds.), Continuous Lattices, Bremen 1979, Lecture Notes in Math., Springer-Verlag, Berlin-Heidelberg-New York, 1981, 871, 298–307.10.1007/BFb0089913Suche in Google Scholar
[17] Ruan X.J., Xu X.Q., Convergence in s2-quasicontinuous posets, Springerplus, 2016, 5, 218, 10.1186/s40064-016-1873-6.Suche in Google Scholar PubMed PubMed Central
[18] Mao X.X., Xu L.S., Quasicontinuity of posets via Scott topology and sobrification, Order 2006, 23, 359–369.10.1007/s11083-007-9054-4Suche in Google Scholar
[19] Venugopalan P., Quasicontinuous posets, Semigroup Forum, 1990, 41, 193–200.10.1007/BF02573390Suche in Google Scholar
[20] Zhang H., A note on continuous partially ordered sets, Semigroup Forum, 1993, 47, 101–104.10.1007/BF02573745Suche in Google Scholar
[21] Zhang W.F., Xu X.Q., s2-Quasicontinuous posets, Theoret. Comput. Sci., 2015, 574, 78–85.10.1016/j.tcs.2015.01.037Suche in Google Scholar
© 2019 Xiao-jun Ruan and Xiao-quan Xu, published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 Public License.
Artikel in diesem Heft
- Regular Articles
- On the Gevrey ultradifferentiability of weak solutions of an abstract evolution equation with a scalar type spectral operator of orders less than one
- Centralizers of automorphisms permuting free generators
- Extreme points and support points of conformal mappings
- Arithmetical properties of double Möbius-Bernoulli numbers
- The product of quasi-ideal refined generalised quasi-adequate transversals
- Characterizations of the Solution Sets of Generalized Convex Fuzzy Optimization Problem
- Augmented, free and tensor generalized digroups
- Time-dependent attractor of wave equations with nonlinear damping and linear memory
- A new smoothing method for solving nonlinear complementarity problems
- Almost periodic solution of a discrete competitive system with delays and feedback controls
- On a problem of Hasse and Ramachandra
- Hopf bifurcation and stability in a Beddington-DeAngelis predator-prey model with stage structure for predator and time delay incorporating prey refuge
- A note on the formulas for the Drazin inverse of the sum of two matrices
- Completeness theorem for probability models with finitely many valued measure
- Periodic solution for ϕ-Laplacian neutral differential equation
- Asymptotic orbital shadowing property for diffeomorphisms
- Modular equations of a continued fraction of order six
- Solutions with concentration and cavitation to the Riemann problem for the isentropic relativistic Euler system for the extended Chaplygin gas
- Stability Problems and Analytical Integration for the Clebsch’s System
- Topological Indices of Para-line Graphs of V-Phenylenic Nanostructures
- On split Lie color triple systems
- Triangular Surface Patch Based on Bivariate Meyer-König-Zeller Operator
- Generators for maximal subgroups of Conway group Co1
- Positivity preserving operator splitting nonstandard finite difference methods for SEIR reaction diffusion model
- Characterizations of Convex spaces and Anti-matroids via Derived Operators
- On Partitions and Arf Semigroups
- Arithmetic properties for Andrews’ (48,6)- and (48,18)-singular overpartitions
- A concise proof to the spectral and nuclear norm bounds through tensor partitions
- A categorical approach to abstract convex spaces and interval spaces
- Dynamics of two-species delayed competitive stage-structured model described by differential-difference equations
- Parity results for broken 11-diamond partitions
- A new fourth power mean of two-term exponential sums
- The new operations on complete ideals
- Soft covering based rough graphs and corresponding decision making
- Complete convergence for arrays of ratios of order statistics
- Sufficient and necessary conditions of convergence for ρ͠ mixing random variables
- Attractors of dynamical systems in locally compact spaces
- Random attractors for stochastic retarded strongly damped wave equations with additive noise on bounded domains
- Statistical approximation properties of λ-Bernstein operators based on q-integers
- An investigation of fractional Bagley-Torvik equation
- Pentavalent arc-transitive Cayley graphs on Frobenius groups with soluble vertex stabilizer
- On the hybrid power mean of two kind different trigonometric sums
- Embedding of Supplementary Results in Strong EMT Valuations and Strength
- On Diophantine approximation by unlike powers of primes
- A General Version of the Nullstellensatz for Arbitrary Fields
- A new representation of α-openness, α-continuity, α-irresoluteness, and α-compactness in L-fuzzy pretopological spaces
- Random Polygons and Estimations of π
- The optimal pebbling of spindle graphs
- MBJ-neutrosophic ideals of BCK/BCI-algebras
- A note on the structure of a finite group G having a subgroup H maximal in 〈H, Hg〉
- A fuzzy multi-objective linear programming with interval-typed triangular fuzzy numbers
- Variational-like inequalities for n-dimensional fuzzy-vector-valued functions and fuzzy optimization
- Stability property of the prey free equilibrium point
- Rayleigh-Ritz Majorization Error Bounds for the Linear Response Eigenvalue Problem
- Hyper-Wiener indices of polyphenyl chains and polyphenyl spiders
- Razumikhin-type theorem on time-changed stochastic functional differential equations with Markovian switching
- Fixed Points of Meromorphic Functions and Their Higher Order Differences and Shifts
- Properties and Inference for a New Class of Generalized Rayleigh Distributions with an Application
- Nonfragile observer-based guaranteed cost finite-time control of discrete-time positive impulsive switched systems
- Empirical likelihood confidence regions of the parameters in a partially single-index varying-coefficient model
- Algebraic loop structures on algebra comultiplications
- Two weight estimates for a class of (p, q) type sublinear operators and their commutators
- Dynamic of a nonautonomous two-species impulsive competitive system with infinite delays
- 2-closures of primitive permutation groups of holomorph type
- Monotonicity properties and inequalities related to generalized Grötzsch ring functions
- Variation inequalities related to Schrödinger operators on weighted Morrey spaces
- Research on cooperation strategy between government and green supply chain based on differential game
- Extinction of a two species competitive stage-structured system with the effect of toxic substance and harvesting
- *-Ricci soliton on (κ, μ)′-almost Kenmotsu manifolds
- Some improved bounds on two energy-like invariants of some derived graphs
- Pricing under dynamic risk measures
- Finite groups with star-free noncyclic graphs
- A degree approach to relationship among fuzzy convex structures, fuzzy closure systems and fuzzy Alexandrov topologies
- S-shaped connected component of radial positive solutions for a prescribed mean curvature problem in an annular domain
- On Diophantine equations involving Lucas sequences
- A new way to represent functions as series
- Stability and Hopf bifurcation periodic orbits in delay coupled Lotka-Volterra ring system
- Some remarks on a pair of seemingly unrelated regression models
- Lyapunov stable homoclinic classes for smooth vector fields
- Stabilizers in EQ-algebras
- The properties of solutions for several types of Painlevé equations concerning fixed-points, zeros and poles
- Spectrum perturbations of compact operators in a Banach space
- The non-commuting graph of a non-central hypergroup
- Lie symmetry analysis and conservation law for the equation arising from higher order Broer-Kaup equation
- Positive solutions of the discrete Dirichlet problem involving the mean curvature operator
- Dislocated quasi cone b-metric space over Banach algebra and contraction principles with application to functional equations
- On the Gevrey ultradifferentiability of weak solutions of an abstract evolution equation with a scalar type spectral operator on the open semi-axis
- Differential polynomials of L-functions with truncated shared values
- Exclusion sets in the S-type eigenvalue localization sets for tensors
- Continuous linear operators on Orlicz-Bochner spaces
- Non-trivial solutions for Schrödinger-Poisson systems involving critical nonlocal term and potential vanishing at infinity
- Characterizations of Benson proper efficiency of set-valued optimization in real linear spaces
- A quantitative obstruction to collapsing surfaces
- Dynamic behaviors of a Lotka-Volterra type predator-prey system with Allee effect on the predator species and density dependent birth rate on the prey species
- Coexistence for a kind of stochastic three-species competitive models
- Algebraic and qualitative remarks about the family yy′ = (αxm+k–1 + βxm–k–1)y + γx2m–2k–1
- On the two-term exponential sums and character sums of polynomials
- F-biharmonic maps into general Riemannian manifolds
- Embeddings of harmonic mixed norm spaces on smoothly bounded domains in ℝn
- Asymptotic behavior for non-autonomous stochastic plate equation on unbounded domains
- Power graphs and exchange property for resolving sets
- On nearly Hurewicz spaces
- Least eigenvalue of the connected graphs whose complements are cacti
- Determinants of two kinds of matrices whose elements involve sine functions
- A characterization of translational hulls of a strongly right type B semigroup
- Common fixed point results for two families of multivalued A–dominated contractive mappings on closed ball with applications
- Lp estimates for maximal functions along surfaces of revolution on product spaces
- Path-induced closure operators on graphs for defining digital Jordan surfaces
- Irreducible modules with highest weight vectors over modular Witt and special Lie superalgebras
- Existence of periodic solutions with prescribed minimal period of a 2nth-order discrete system
- Injective hulls of many-sorted ordered algebras
- Random uniform exponential attractor for stochastic non-autonomous reaction-diffusion equation with multiplicative noise in ℝ3
- Global properties of virus dynamics with B-cell impairment
- The monotonicity of ratios involving arc tangent function with applications
- A family of Cantorvals
- An asymptotic property of branching-type overloaded polling networks
- Almost periodic solutions of a commensalism system with Michaelis-Menten type harvesting on time scales
- Explicit order 3/2 Runge-Kutta method for numerical solutions of stochastic differential equations by using Itô-Taylor expansion
- L-fuzzy ideals and L-fuzzy subalgebras of Novikov algebras
- L-topological-convex spaces generated by L-convex bases
- An optimal fourth-order family of modified Cauchy methods for finding solutions of nonlinear equations and their dynamical behavior
- New error bounds for linear complementarity problems of Σ-SDD matrices and SB-matrices
- Hankel determinant of order three for familiar subsets of analytic functions related with sine function
- On some automorphic properties of Galois traces of class invariants from generalized Weber functions of level 5
- Results on existence for generalized nD Navier-Stokes equations
- Regular Banach space net and abstract-valued Orlicz space of range-varying type
- Some properties of pre-quasi operator ideal of type generalized Cesáro sequence space defined by weighted means
- On a new convergence in topological spaces
- On a fixed point theorem with application to functional equations
- Coupled system of a fractional order differential equations with weighted initial conditions
- Rough quotient in topological rough sets
- Split Hausdorff internal topologies on posets
- A preconditioned AOR iterative scheme for systems of linear equations with L-matrics
- New handy and accurate approximation for the Gaussian integrals with applications to science and engineering
- Special Issue on Graph Theory (GWGT 2019)
- The general position problem and strong resolving graphs
- Connected domination game played on Cartesian products
- On minimum algebraic connectivity of graphs whose complements are bicyclic
- A novel method to construct NSSD molecular graphs
Artikel in diesem Heft
- Regular Articles
- On the Gevrey ultradifferentiability of weak solutions of an abstract evolution equation with a scalar type spectral operator of orders less than one
- Centralizers of automorphisms permuting free generators
- Extreme points and support points of conformal mappings
- Arithmetical properties of double Möbius-Bernoulli numbers
- The product of quasi-ideal refined generalised quasi-adequate transversals
- Characterizations of the Solution Sets of Generalized Convex Fuzzy Optimization Problem
- Augmented, free and tensor generalized digroups
- Time-dependent attractor of wave equations with nonlinear damping and linear memory
- A new smoothing method for solving nonlinear complementarity problems
- Almost periodic solution of a discrete competitive system with delays and feedback controls
- On a problem of Hasse and Ramachandra
- Hopf bifurcation and stability in a Beddington-DeAngelis predator-prey model with stage structure for predator and time delay incorporating prey refuge
- A note on the formulas for the Drazin inverse of the sum of two matrices
- Completeness theorem for probability models with finitely many valued measure
- Periodic solution for ϕ-Laplacian neutral differential equation
- Asymptotic orbital shadowing property for diffeomorphisms
- Modular equations of a continued fraction of order six
- Solutions with concentration and cavitation to the Riemann problem for the isentropic relativistic Euler system for the extended Chaplygin gas
- Stability Problems and Analytical Integration for the Clebsch’s System
- Topological Indices of Para-line Graphs of V-Phenylenic Nanostructures
- On split Lie color triple systems
- Triangular Surface Patch Based on Bivariate Meyer-König-Zeller Operator
- Generators for maximal subgroups of Conway group Co1
- Positivity preserving operator splitting nonstandard finite difference methods for SEIR reaction diffusion model
- Characterizations of Convex spaces and Anti-matroids via Derived Operators
- On Partitions and Arf Semigroups
- Arithmetic properties for Andrews’ (48,6)- and (48,18)-singular overpartitions
- A concise proof to the spectral and nuclear norm bounds through tensor partitions
- A categorical approach to abstract convex spaces and interval spaces
- Dynamics of two-species delayed competitive stage-structured model described by differential-difference equations
- Parity results for broken 11-diamond partitions
- A new fourth power mean of two-term exponential sums
- The new operations on complete ideals
- Soft covering based rough graphs and corresponding decision making
- Complete convergence for arrays of ratios of order statistics
- Sufficient and necessary conditions of convergence for ρ͠ mixing random variables
- Attractors of dynamical systems in locally compact spaces
- Random attractors for stochastic retarded strongly damped wave equations with additive noise on bounded domains
- Statistical approximation properties of λ-Bernstein operators based on q-integers
- An investigation of fractional Bagley-Torvik equation
- Pentavalent arc-transitive Cayley graphs on Frobenius groups with soluble vertex stabilizer
- On the hybrid power mean of two kind different trigonometric sums
- Embedding of Supplementary Results in Strong EMT Valuations and Strength
- On Diophantine approximation by unlike powers of primes
- A General Version of the Nullstellensatz for Arbitrary Fields
- A new representation of α-openness, α-continuity, α-irresoluteness, and α-compactness in L-fuzzy pretopological spaces
- Random Polygons and Estimations of π
- The optimal pebbling of spindle graphs
- MBJ-neutrosophic ideals of BCK/BCI-algebras
- A note on the structure of a finite group G having a subgroup H maximal in 〈H, Hg〉
- A fuzzy multi-objective linear programming with interval-typed triangular fuzzy numbers
- Variational-like inequalities for n-dimensional fuzzy-vector-valued functions and fuzzy optimization
- Stability property of the prey free equilibrium point
- Rayleigh-Ritz Majorization Error Bounds for the Linear Response Eigenvalue Problem
- Hyper-Wiener indices of polyphenyl chains and polyphenyl spiders
- Razumikhin-type theorem on time-changed stochastic functional differential equations with Markovian switching
- Fixed Points of Meromorphic Functions and Their Higher Order Differences and Shifts
- Properties and Inference for a New Class of Generalized Rayleigh Distributions with an Application
- Nonfragile observer-based guaranteed cost finite-time control of discrete-time positive impulsive switched systems
- Empirical likelihood confidence regions of the parameters in a partially single-index varying-coefficient model
- Algebraic loop structures on algebra comultiplications
- Two weight estimates for a class of (p, q) type sublinear operators and their commutators
- Dynamic of a nonautonomous two-species impulsive competitive system with infinite delays
- 2-closures of primitive permutation groups of holomorph type
- Monotonicity properties and inequalities related to generalized Grötzsch ring functions
- Variation inequalities related to Schrödinger operators on weighted Morrey spaces
- Research on cooperation strategy between government and green supply chain based on differential game
- Extinction of a two species competitive stage-structured system with the effect of toxic substance and harvesting
- *-Ricci soliton on (κ, μ)′-almost Kenmotsu manifolds
- Some improved bounds on two energy-like invariants of some derived graphs
- Pricing under dynamic risk measures
- Finite groups with star-free noncyclic graphs
- A degree approach to relationship among fuzzy convex structures, fuzzy closure systems and fuzzy Alexandrov topologies
- S-shaped connected component of radial positive solutions for a prescribed mean curvature problem in an annular domain
- On Diophantine equations involving Lucas sequences
- A new way to represent functions as series
- Stability and Hopf bifurcation periodic orbits in delay coupled Lotka-Volterra ring system
- Some remarks on a pair of seemingly unrelated regression models
- Lyapunov stable homoclinic classes for smooth vector fields
- Stabilizers in EQ-algebras
- The properties of solutions for several types of Painlevé equations concerning fixed-points, zeros and poles
- Spectrum perturbations of compact operators in a Banach space
- The non-commuting graph of a non-central hypergroup
- Lie symmetry analysis and conservation law for the equation arising from higher order Broer-Kaup equation
- Positive solutions of the discrete Dirichlet problem involving the mean curvature operator
- Dislocated quasi cone b-metric space over Banach algebra and contraction principles with application to functional equations
- On the Gevrey ultradifferentiability of weak solutions of an abstract evolution equation with a scalar type spectral operator on the open semi-axis
- Differential polynomials of L-functions with truncated shared values
- Exclusion sets in the S-type eigenvalue localization sets for tensors
- Continuous linear operators on Orlicz-Bochner spaces
- Non-trivial solutions for Schrödinger-Poisson systems involving critical nonlocal term and potential vanishing at infinity
- Characterizations of Benson proper efficiency of set-valued optimization in real linear spaces
- A quantitative obstruction to collapsing surfaces
- Dynamic behaviors of a Lotka-Volterra type predator-prey system with Allee effect on the predator species and density dependent birth rate on the prey species
- Coexistence for a kind of stochastic three-species competitive models
- Algebraic and qualitative remarks about the family yy′ = (αxm+k–1 + βxm–k–1)y + γx2m–2k–1
- On the two-term exponential sums and character sums of polynomials
- F-biharmonic maps into general Riemannian manifolds
- Embeddings of harmonic mixed norm spaces on smoothly bounded domains in ℝn
- Asymptotic behavior for non-autonomous stochastic plate equation on unbounded domains
- Power graphs and exchange property for resolving sets
- On nearly Hurewicz spaces
- Least eigenvalue of the connected graphs whose complements are cacti
- Determinants of two kinds of matrices whose elements involve sine functions
- A characterization of translational hulls of a strongly right type B semigroup
- Common fixed point results for two families of multivalued A–dominated contractive mappings on closed ball with applications
- Lp estimates for maximal functions along surfaces of revolution on product spaces
- Path-induced closure operators on graphs for defining digital Jordan surfaces
- Irreducible modules with highest weight vectors over modular Witt and special Lie superalgebras
- Existence of periodic solutions with prescribed minimal period of a 2nth-order discrete system
- Injective hulls of many-sorted ordered algebras
- Random uniform exponential attractor for stochastic non-autonomous reaction-diffusion equation with multiplicative noise in ℝ3
- Global properties of virus dynamics with B-cell impairment
- The monotonicity of ratios involving arc tangent function with applications
- A family of Cantorvals
- An asymptotic property of branching-type overloaded polling networks
- Almost periodic solutions of a commensalism system with Michaelis-Menten type harvesting on time scales
- Explicit order 3/2 Runge-Kutta method for numerical solutions of stochastic differential equations by using Itô-Taylor expansion
- L-fuzzy ideals and L-fuzzy subalgebras of Novikov algebras
- L-topological-convex spaces generated by L-convex bases
- An optimal fourth-order family of modified Cauchy methods for finding solutions of nonlinear equations and their dynamical behavior
- New error bounds for linear complementarity problems of Σ-SDD matrices and SB-matrices
- Hankel determinant of order three for familiar subsets of analytic functions related with sine function
- On some automorphic properties of Galois traces of class invariants from generalized Weber functions of level 5
- Results on existence for generalized nD Navier-Stokes equations
- Regular Banach space net and abstract-valued Orlicz space of range-varying type
- Some properties of pre-quasi operator ideal of type generalized Cesáro sequence space defined by weighted means
- On a new convergence in topological spaces
- On a fixed point theorem with application to functional equations
- Coupled system of a fractional order differential equations with weighted initial conditions
- Rough quotient in topological rough sets
- Split Hausdorff internal topologies on posets
- A preconditioned AOR iterative scheme for systems of linear equations with L-matrics
- New handy and accurate approximation for the Gaussian integrals with applications to science and engineering
- Special Issue on Graph Theory (GWGT 2019)
- The general position problem and strong resolving graphs
- Connected domination game played on Cartesian products
- On minimum algebraic connectivity of graphs whose complements are bicyclic
- A novel method to construct NSSD molecular graphs

