Explicit order 3/2 Runge-Kutta method for numerical solutions of stochastic differential equations by using Itô-Taylor expansion

Yazid Alhojilan

doi:10.1515/math-2019-0124

Article Open Access

Explicit order 3/2 Runge-Kutta method for numerical solutions of stochastic differential equations by using Itô-Taylor expansion

Yazid Alhojilan

Published/Copyright: December 31, 2019

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information Explore this Subject

$Open Mathematics$

From the journal Open Mathematics Volume 17 Issue 1

Abstract

This paper aims to present a new pathwise approximation method, which gives approximate solutions of order 32 for stochastic differential equations (SDEs) driven by multidimensional Brownian motions. The new method, which assumes the diffusion matrix non-degeneracy, employs the Runge-Kutta method and uses the Itô-Taylor expansion, but the generating of the approximation of the expansion is carried out as a whole rather than individual terms. The new idea we applied in this paper is to replace the iterated stochastic integrals I_α by random variables, so implementing this scheme does not require the computation of the iterated stochastic integrals I_α. Then, using a coupling which can be found by a technique from optimal transport theory would give a good approximation in a mean square. The results of implementing this new scheme by MATLAB confirms the validity of the method.

Keywords: stochastic differential equations; pathwise approximation; Runge-Kutta method; Itô-Taylor expansion

MSC 2010: Primary 60H35; Secondary 65C30

1 Introduction

The purpose of this paper is to develop a new pathwise approximation to numerical solutions of SDEs driven by multidimensional Brownian motion. There is a standard approach, which described in [1], approximates solutions of SDEs to the required order using stochastic Taylor expansion at each time step. Nevertheless, applying this method would be difficult when the deriving Brownian motion dimension is greater than 1 to get higher order than 12 , due to hardness of generating the iterated stochastic integrals I_α. To overcome this difficulty, J. G. Gaines and T. J. Lyons [2] had introduced an effective method to deal with double stochastic integrals to get approximate solutions of order 1. However, unfortunately the method has not been extended to further dimensions higher than 2-dimensional of Brownian motion. Kloeden and Platen [1] suggest using a Fourier expansion of a Brownian bridge process to approximate stochastic integrals in any dimension. Rydén and Wiktorsson [3] have described a method that covered 2-dimensional of Brownian motion, uses the fact that the Itô integrals have an infinitely divisible distribution when are conditioned on the Wiener increments. There was a different scheme that can simulate the iterated Itô integrals for multiple independent Brownian motions. The method which derives the conditional joint characteristic function of the iterated Ito integrals given the Brownian increments, and then proposed an algorithm for the simulation of the iterated Ito integrals and the Brownian increments introduced by Wiktorsson [4]. The schemes which had introduced in [1, 3, 4] are useful for any dimension of stochastic integrals, but they need a computational cost.

In this paper, we aim to present a new pathwise approximation scheme that can be used to get a higher-order approximation for Brownian motion in dimension greater than 1. It is based on using a coupling and a version of the perturbation method. Therefore, this new scheme does not require calculating I_α, because we replace them by random variables with the same moments conditional on the linear term. Then, we get a random vector, which is a good approximation in distribution to the original Taylor expansion, and it can be generated using algorithms in MATLAB. We have used a technique from optimal transport theory [5] to give a good approximation in mean square. Other works use a coupling to approximate SDEs numerically, such that [6, 7, 8, 9]. This paper, organized as follows: section 2, gives a background material, and section 3, shows the implementation of the scheme.

2 Background

Let (Ω, 𝓕, P) be a probability space. Let σ(x̂_s : s ≤ t) denote the smallest σ-algebra such that x̂_s (a stochastic process) is σ(x̂_s : s ≤ t)-measurable for all s ≤ t. A collection of σ-algebras {𝓕_t}, satisfying (i.e. 𝓕_t ⊂ 𝓕_s ⊂ 𝓕 for all 0 ≤ t < s < ∞) is called a filtration. 𝓕_t is interpreted as corresponding to the information available at time t (the amount of information increasing as time progresses). A stochastic process x̂_t is adapted to a filtration {𝓕_t} if x̂_t is 𝓕_t-measurable for all t ≥ 0.

2.1 Stochastic Itô-Taylor expansion

Let us consider a 1-dimensional Ito stochastic differential equation in the form of an integral

x^t=x^0+∫t0ta(s,x^s)ds+∫t0tb(s,x^s)dWs,for allt∈[t0,T], (2.1)

where a(t, x) and b(t, x) are Borel measurable functions defined on [0, ∞) × ℝ) with values in ℝ. Hence, for f : 𝓡 → 𝓡 which is a twice continuously differentiable function, the Itô formula [1] gives

f(x^t)=f(x^0)+∫t0t(a(s,x^s)∂f(x^s)∂x^+12b2(s,x^s)∂2f(x^s)∂x^2)ds+∫t0tb(s,x^s)∂f(x^s)∂x^dWs=f(x^0)+∫t0tL0f(x^s)ds+∫t0tL1f(x^s)dWs,for allt∈[t0,T], (2.2)

where the operators are

L0=a∂∂x^+12b2∂2∂x^2 (2.3)

and

L1=b∂∂x^. (2.4)

Clearly, if f(x) ≡ x we have L⁰f = a and L¹f = b, in which case that there is a reduction in (2.2) to the original Itô equation for x̂_t, that is to

x^t=x^0+∫t0ta(s,x^s)ds+∫t0tb(s,x^s)dWs. (2.5)

Applying the Itô formula (2.2) to the function f = a and f = b in (2.5), we obtain

x^t=x^0+∫t0t(a(x^0)+∫t0sL0a(x^z)dz+∫t0sL1a(x^z)dWz)ds+∫t0t(b(x^0)+∫t0sL0b(x^z)dz+∫t0sL1b(x^z)dWz)dWs=x^0+a(x^0)∫t0tds+b(x^0)∫t0tdWs+R, (2.6)

where the remainder is

R=∫t0t∫t0sL0a(x^z)dzds+∫t0t∫t0sL1a(x^z)dWzds+∫t0t∫t0sL0b(x^z)dzdWs+∫t0t∫t0sL1b(x^z)dWzdWs. (2.7)

For the Taylor expansion of d-dimensional Itô stochastic differential equations, a similar expansion holds as above for

x^t=x^0+∫t0ta(s,x^s)ds+∫t0t∑j=1dbj(s,x^s)dWs(j). (2.8)

The general Itô Taylor expansion is given in (2.12).

2.2 Perturbation method

Consider the following: suppose we wish to simulate U = X + ϵ Y, where X and Y are independent, X has a smooth density, and ϵ is small. Also, suppose that X is easy to generate, while Y is hard to generate. Then, generating U by generating X and Y will be hard. Alternatively, let us suppose there is another random variable that is easy to generate to overcome this dilemma, say Z, which is independent of X. The random variable Z has the same moments up to order m − 1 as Y (i.e. E(Z^k) = E(Y^k) for k = 1, 2, 3, …, m − 1). Then, we can prove that V = X + ϵ Z is an approximation to U with the error of order ϵ^m. The justification for this can be seen by writing f_X for the density of X etc, so we have f_U(x) = Ef_X(x − ϵ Y) = f(x) + ∑k=1m−1(−ϵ)kk!f(k)(x)E(Yk) + O(ϵ^m). As Z has the same moments, we get the same expression for f_V(x), so f_U(x) − f_V(x) = O(ϵ^m). It can expect from this a Wasserstein distance estimate of the same order W(U, V) = O(ϵ^m), which gives a coupling with E(U − V)² = O(ϵ^2m). This way is an example for the bound of densities can give a Wasserstein bound between U and V, but it is not in an immediate way, the Wasserstein bound implies the coupling between U and V [10].

2.3 Construction of pathwise approximation of SDEs using stochastic Taylor expansions

Consider an Itô SDE

(dx^t)i=ai(t,x^t)dt+∑k=1dbik(t,x^t)dWtk,(x^0)i=x^i(0)i=1,...,q (2.9)

on an interval [0, T], for a q-dimensional vector x̂_t, with a d-dimensional driving Brownian path W_t. Assume (2.9) satisfies an existence and uniqueness theorem. The basic idea to get pathwise approximation is to divide [0, T] into a finite number N of subintervals, where the length of the step equals h = TN . We have used a stochastic Taylor expansion in order to approximate the equation on each subinterval.

The basic scheme which we have is Euler-Maruyama

x^i(j+1)=x^i(j)+ai(jh,x^(j))h+∑k=1dbik(jh,x^(j))ΔWk(j). (2.10)

In order to get the Milstein scheme, we add the quadratic terms

x^i(j+1)=x^i(j)+ai(jh,x^(j))h+∑k=1dbik(jh,x^(j))ΔWk(j)+∑k,l=1dρikl(jh,x^(j))Ikl(j), (2.11)

where ΔWk(j)=W(j+1)hk−Wjhk, Ikl(j)=∫jh(j+1)h{Wtk−Wjhk}dWtl and ρikl(t,x^)=∑m=1qbml(t,x^)∂bil(t,x^)∂x^m [10].

Our constructed method, which approximates SDEs at order 32 , assumes nondegeneracy of b in (2.9) and uses Itô-Taylor expansion and Runge-Kutta method. It is needed to use the following notations, which had mentioned in this reference [1] to construct the scheme for approximate solutions of SDEs at a higher order. The following discussion is derived from [10]. Let 𝓜 be the set of all multi-indices, α = (j₁, …, j_l) of length l = l(α) with 0 ≤ j_k ≤ d. The iterated integrals are defined as follows Iα,s,t=∫st∫stl...∫st2dWt1j1...dWtljl.

For m ≥ 2 in ℕ we define

Am={α∈M:l(α≥2 and either l(α)+n(α)≤m or l(α)=n(α)=m+12},

where n(α) is the number of zero indices in α.

The case l(α) = n(α) = m+12 is needed (for example when α = (00)) because I_α has non-zero mean, so we need a higher order for the local error. The order γ = m2 Taylor approximation to (2.9) is given by

x^i(j+1)=x^i(j)+ai(jh,x^(j))h+∑k=1dbik(jh,x^(j))ΔWk(j)+∑α∈Amfα,i(jh,x^(j))Iα,jh,(j+1)h, (2.12)

where ℝ^q-valued functions f_α,i(t, x̂) are defined recursively by f_v(t, x̂) = x̂ and f_jα = L^j f_α for j ∈ {0, …, d}, where v is the multi-index of zero length, and f_α,i denotes the ith component of f_α.

The main point which will be discussed in this paper; how do we generate RHS of (2.12) easily? Actually, this research has developed a scheme where to generate RHS of (2.12) by using perturbation and coupling method; how?

Let us apply this method in (2.12) in order to approximate SDEs at higher order. In order to simplify application, we will be deal with the first iteration from 0 to h of (2.12)

x^i(1)=x^i(0)+ai(0,x^(0))h+Yi, (2.13)

where

Yi=∑k=1dbik(0,x^(0))Wk(h)+∑α∈Amfi,α(0,x^(0))Iα,0,h

for i = 1, …, q, where b_ik(0, x̂⁽⁰⁾) and f_α,i(0, x̂⁽⁰⁾) are real constants.

As I_α is not independent of Δ W, so it would be difficult to generate these stochastic integrals when we want to find approximate solutions. By following the construction in [10], we can overcome this issue using the relation Wtj=h12B(th)j+th−12Vj, B1,...,Bd are independent standard Brownian bridges on (0, 1) and Vj=h−12Wj(h) are independent N(0, 1), and are independent of the B_j. We also write B₀(t) = t and Kα=∫01∫0tl...∫0t2dBt1j1...dBtljl.

For α = (j₁, …, j_l) we can replace the iterated stochastic integrals I_α using random variables with the same moments conditional on the linear term as follows

Iα=h(l(α)+n(α))2∑β=(i1,...,il)Kβ∏k:ik<jkVjk, (2.14)

where we calculate the sum over all β = (i₁, …, i_l) such that for each k ∈ {1, …, l} we have either i_k = j_k or i_k = 0 < j_k. (For examples I₀₁₃ = h²(K₀₁₃ + K₀₀₃ V₁ + K₀₁₀ V₃ + K₀₀₀ V₁ V₃)). The random variables K_β and V_k ∼ N(0, 1) are generated independently.

By setting ϵ=h12, and defining 𝓜_m = {α ∈ 𝓜 : 2 ≤ l(α) ≤ m}, we can write this

Yi=ϵ∑k=1dbik(0,x^(0))Vk+Qi(ϵ,V,(ϵl(α)Kα))α∈M, (2.15)

where V_k is independent N(0, 1) of a random variable K_α and Q_i is a polynomial, each monomial of which has overall order at least 2 in ϵ.

We have found it hard to generate Y directly by using (2.14). To tackle this problem, we use a version of the perturbation method by assuming random variables L_β and using them rather than K_β which easy to generate for α ∈ 𝓜 such that 2 ≤ l(α) ≤ m.

It will be discussed the way of construction L_β later in this section with details.

Then, (2.14) can be modified as follows

I¯α=h(l(α)+n(α))2∑β=(i1,...,il)Lβ∏k:ik<jkV¯jk, (2.16)

where we calculate the sum over all β = (i₁, …, i_l) such that for each k ∈ {1, …, l} we have either i_k = j_k or i_k = 0 < j_k. (For example Ī₀₁₃ = h² (L₀₁₃ + L₀₀₃ V̄₁ + L₀₁₀ V̄₃ + L₀₀₀ V̄₁ V̄₃)). The random variables L_β and V̄_k ∼ N(0, 1) are generated independently.

Then, we can be redefine the formula (2.5) as follows

Y¯i=ϵ∑k=1dbik(0,x^(0))V¯k+Qi(ϵ,V¯,(ϵl(α)Lα))α∈M, (2.17)

where V̄_k are independent N(0, 1) and independent of the random variable L_α.

The following theorem is essential to give the error bound in the approximation by the modified Y by considering equation (2.9) and using the notation of section (2.12).

Theorem 1

This theorem is L^p version of [10].

Assume the matrix (b_ik) has rank q. Suppose the random variables L_α have all moments finite and that 𝔼(K_α₁ … K_{α_r}) = 𝔼(L_α₁ … L_{α_r}) whenever α₁, …, α_r ∈ 𝓜_m satisfy ∑k=1r (l(α_k) − 1) ≤ m − 1. Then for p ≥ 2 we have 𝕎_p(Y, Ȳ) ≤ Cϵ^m+1, where the constant C depends only on p, d, m, upper bounds for the constants b_ik, c_i,α and a right inverse of the matrix (b_ik), and moment bounds for the L_α.

Proof

We refer the reader to [11]. □

How do we apply theorem 1 to generate approximate solution for (2.12)?

Basically, we assume coefficients a_k and b_ik are sufficiently regular (uniform bounds for the coefficients and their derivatives up to order two will certainly suffice) and the matrix (b_ik) has rank q everywhere with uniformly bounded right inverse. Then, the iterated integrals I_α,jh,(j+1)h in (2.12) are hard to generate as it has been mentioned so we should use modification of iterated integrals which are easy to generate Ī_α,jh,(j+1)h [10]. The modified formula which results is the following

x^i(j+1)=x^i(j)+ai(jh,x(j))h+∑k=1dbik(jh,x^(j))ΔWk(j)+∑α∈Amfα,i(jh,x^(j))I¯α,jh,(j+1)h. (2.18)

We now return to think about the application of coupling to the simulations of SDEs in the first step between Y and Ȳ. We have assumed the L_β satisfy the hypothesis of the theorem 1 such that 𝔼(K_α₁ … K_{α_r}) = 𝔼(L_α₁ … L_{α_r}) whenever α₁, …, α_r ∈ 𝓜_m satisfy ∑k=1r (l(α_k) − 1) ≤ m − 1. Therefore, Wasserstein bound between Y and Ȳ implies the existence of a suitable coupling between Y and Ȳ for which the following relation (2.19) holds. The coupling which has been deduced between Y and Ȳ can be extended to be between the random variables (V_k, K_α) and (V̄_k, L_α), which leads to deduce the following relation,

Wp(Y,Y¯)≤E|Y−Y¯|p=E|∑k=1dbik(0,x^(0))ϵ(V¯k(0)−Vk(0))+∑α∈Amfα(0,x^(0))(I¯α,0,h−Iα,0,h)|p≤C(p)hp(m+1)2. (2.19)

For the bound at j step, we can use the same argument as used in (2.19) to deduce the bound for (2.21), except that the coefficient functions evaluated at random variables x^i(j) such as ( (Vk(j),Kα(j)), (V¯k(j),Lα(j)), Y^(j) and Ȳ^(j)), so the extended coupling between (Vk(j), Kα(j)) and (V¯k(j),Lα(j)) are conditional on the σ-algebra 𝓕_j, where 𝓕_j = σ{V_i, K_i, L_i . i < j}. Hence, if we take an expectation w.r.t σ-algebra and conditional on (𝓕_j), then we get first a conditional bound as follows

E|∑k=1dbik(jh,x^(j))ϵ(V¯k(j)−Vk(j))+∑α∈Amfα(jh,x^(j))(I¯α,jh,(j+1)h−Iα,jh,(j+1)h)|Fj|p≤C(p)hp(m+1)2. (2.20)

Therefore, by nested expectation, we have

E|∑k=1dbik(jh,x^(j))ϵ(V¯k(j)−Vk(j))+∑α∈Amfα(jh,x^(j))(I¯α,jh,(j+1)h−Iα,jh,(j+1)h)|p≤C(p)hp(m+1)2. (2.21)

It is required to know the calculations of the relevant expectation of products of K_β for generating a suitable random variables L_β. However, before doing that, we would clarify how to construct proper random variables. First, the new random variables L_β must satisfy the moment conditions in the statement of theorem 1. Thus, once the relevant moments of the K_β are calculated, then it would be taken any choice of L_β which satisfies these moment conditions of the theorem 1. To calculate the moments, we have used the following three lemmas.

Lemma 1

[10]. Let β = (j j … j) with length l ≥ 2. Then (i) if j = 0 then K_β = 1l! , and (ii) if j > 0 then K_β = 0 if l is odd, while Kβ=(−1)r2rr! if l = 2r.

Lemma 2

[10]. If β₁, …, β_s ∈ 𝓜 and if some j ≥ 1 occurs an odd number of times in the concatenated multi-index β₁ … β_s then 𝔼(K_β₁ … K_{β_s}) = 0.

Lemma 3

[10]. (i) if 0 ≤ k < l then K_lk = −K_kl and E(Kkl2)=112. (ii) if k > 0 then 𝔼K_0kk = 𝔼K_k0k = 𝔼K_kk0 = − 16 .

K_lk = −K_kl can be proved by using integration by parts as follows ∫01 B_k dB_l = B₁ B₁ − ∫01 B_l dB_k = 0 − ∫01 B_l dB_k = − ∫01 B_l dB_k, where B_k and B_l are independent. We refer the reader to [12] for more details of how we compute the non-deterministic moments.

3 Implementation of the method

In the preceding section, it has introduced the method that can be used to get approximate solutions of higher-order for any dimension of Brownian motions. Therefore, to get numerical solutions for SDEs of order 32 , the formula (2.12) is used by putting m = 3, then using theorem 1 to determine the moments that we need for Ī_α and then using lemmas 1, 2 and 3 to compute the moments.

For β in the definition of Ī_α in (2.16), we need all indices of length 2 and 3. The random variables L_β in (2.16) must satisfy the moment condition in the statement of theorem 1, that 𝔼(K_α₁ … K_{α_r}) = 𝔼(L_α₁ … L_{α_r}) whenever α₁, …, α_r ∈ 𝓜_m satisfy ∑k=1r (l(α_k)− 1) ≤ m − 1. Hence, in order to get numerical solutions of order 32 , L_β must satisfy the moments 𝔼(L_α) for all α of length 2, α of length 3 with non zero-indices and the expectation of products 𝔼(L_α L_β) with α, β have length 2. As a result of that, we have the following moments K_β which the random variables L_β must satisfy

Deterministic K_α

K₀₀ = 12 , K₀₀₀ = 16 ,

K_kk = − 12 , K_kkk = 0, for k > 0.

Non-deterministic moments

K_lk = −K_kl, for 0 ≤ k < l,

𝔼(K_kl) = 0, for 0 ≤ k < l,

𝔼(K_nkl) = 0, for k, l, n > 0,

𝔼(K_0kk) = 𝔼(K_k0k) = 𝔼(K_kk0) = − 16 ,

𝔼(K_α) = 0 if α = 0kl or a permutation of it for k < l and k, l > 0,

𝔼(K_α) = 0 if α = 00l or a permutation of it for l > 0,

𝔼(K_kl K_k₁l₁) = 0, for k < l, k₁ < l₁ and kl ≠ k₁l₁,

E(Kkl2)=112 . for 0 ≤ k < l.

3.1 Construction of L_β

In this section, we discuss the choices that we make for L_α. Firstly, for all the deterministic α, the random variables L_α have the same values as 𝔼(K_α). For α of length 3, we only need the expectations, so we can choose them to be deterministic by making them equal to 𝔼(K_α). For the cases of the products, we can use the fact of the antisymmetry K_lk = −K_kl for k < l, so we choose the random variables L_lk with k < l which satisfy it. Therefore, the expectations for the products (L_α L_β) (α and β are distinct and not deterministic) are zeros such as 𝔼(L_lkL_l₁k₁) = 0 for k < l, k₁ < l₁ and k, l ≠ k₁, l₁.

Hence, the random variables L_kl with k < l are required to have all moments finite, mean zero, variance 112 and uncorrelated.Hence, we can take any random variable which satisfies the assumption of finite moments and has the mean zero, variance 112 , and generate independent copies. We generate L_kl with k < l using normal distribution with mean zero, variance 112 and uncorrelated, but this is not the only way of generating L_β.

As a result, we set L_lk = −L_kl for 0 ≤ k < 1, and by using lemma 1, 2 and 3, they give L₀₀ = 12 and L_kk = 12 for k > 0. By setting L₀₀₀ = 16 , L_0kk = L_k0k = L_kk0 = − 16 for k > 0, and all other L_β of length 3 to 0. As a result of these and by using (2.16) we have the following

I¯lk=h(12V¯lV¯k+L0kV¯l−L0lV¯k+Llk),I¯0k=h32(12V¯k+L0k),I¯00=h22,I¯l0=h32(12V¯l−L0l),I¯nlk=h326(V¯nV¯lV¯k−δlkV¯n−δnkV¯l−δnlV¯k), (3.1)

for k, l, n > 0.

3.2 Completion of the method

The following calculation is for finding f_α,i. The definitions of the Itô diffusion operators L⁰ (2.3) and L^j (2.4) are used to determine the f_α,i.

flk,i(jh,x^(j))=∑m=1qbml(jh,x^(j))∂bik(jh,x^(j))∂xm,f0k,i(jh,x^(j))=∂bik(jh,x^(j))∂t+∑m=1qam(jh,x^(j))∂bik(jh,x^(j))∂xm+12∑m,n=1qbmk(jh,x^(j))bnk(jh,x^(j))∂2bik(jh,x^(j))∂xm∂xn,f00,i(jh,x^(j))=∂ai(jh,x^(j))∂t+∑m=1qam(jh,x^(j))∂ai(jh,x^(j))∂xm+12∑m,n=1qbmk(jh,x^(j))bnk(jh,x^i(j))∂2ai(jh,x^(j))∂xm∂xn,fl0,i(jh,x^(j))=∑m=1qbml(jh,x^(j))∂ai(jh,x^(j))∂xm,fnlk,i(jh,x^(j))=∑p=1qbpn(jh,x^(j))(∑m=1q(∂bml(jh,x^(j))∂xp∂bik(jh,x^(j))∂xm+bml(jh,x^(j))∂2bik(jh,x^(j))∂xm∂xp)). (3.2)

Combining these in (2.18), it gives us the following formula

x^i(j+1)=x^i(j)+ai(jh,x^(j))h+h12∑k=1dbik(jh,x^(j))Vk(j)+h∑l,k=1dρilk(jh,x^(j))(12Vl(j)Vk(j)+L0k(j)Vl(j)−L0l(j)Vk(j)+Llk(j))+12h32∑k=1d(12Vk(j)+L0k(j))(∂bik(jh,x^(j))∂t+∑m=1qam(jh,x^(j))∂bik(jh,x^(j))∂xm+12∑m,n=1qbmk(jh,x^(j))bnk(jh,x^(j))∂2bik(jh,x^(j))∂xm∂xn)+h22(∂ai(jh,x^(j))∂t+∑m=1qam(jh,x^(j))∂ai(jh,x^(j))∂xm+12∑k=1d∑m,n=1qbmk(jh,x^(j))bnk(jh,x^(j))∂2ai(jh,x^(j))∂xl∂xn)+h32(∑l=1d(12Vl(j)−L0l(j))∑m=1qbml(jh,x^(j))∂ai(jh,x^(j))∂xm)+16h32(∑n,l,k=1d(Vn(j)Vl(j)Vk(j)−δlkVn(j)−δlnVk(j)−δknVl(j))∑p=1qbpn(jh,x^(j))∂ρilk(jh,x^(j))∂xp), (3.3)

where for each j the random variables Vk(j) , 1 ≤ k ≤ d and Lklj , 0 ≤ k < l ≤ d are generated independently so that the Vk(j) are each N(0, 1) and the Lkl(j) have zero mean and variance 112 ; we then set Llk(j)=−Lkl(j) for k < l, and also Lkk(j)=−12 for k > 0. The formula (3.3) is an extension to what Davie [10] had formulated where we have added a drift coefficient in (3.3) and have considered a_i and b_ik depending on t. The following formula, which uses corresponding differences quotients instead of the partial derivatives in truncated Ito-Taylor expansion, gives approximate solutions of order 32 [1].

x^(j+1)=x^(j)+ah+∑k=1mbkΔWk+12h∑l=0m∑k=1m{bl(jh,Y+k)−bl(jh,Y−k)}I¯(k,l)+1h∑k=0m{bk((j+1)h,x^(j))−bk}I¯(0,k)+12h∑l=0m∑k=1m{bl(jh,Y+k)−2bl+bl(jh,Y−k)}I¯(0,l)+12h∑k,l,n=1m{bn(jh,Φ+(k,l))−bn(jh,Φ−(k,l))−bn(jh,Y+k)+bn(jh,Y−k)}I¯(k,l,n), (3.4)

where

Y±k=x^n+1mah±bkh (3.5)

Φ±(k,l)=Y+k±bl(jh,Y+k)h (3.6)

3.3 Simulation result

The following system of SDEs had simulated by using (3.4) for the number of steps N = 200.

dx1=x1dt+(sin2⁡(x1)+1)dWt−(cos2⁡(x2))dVt,dx2=t+21+x22dt+cos2⁡(x1)dWt+(sin2⁡(x2)+1)dVt,x1(0)=1,x2(0)=2,0≤t≤1. (3.7)

Figure 1 shows the piecewise linear curve through the values for the approximate solutions at each time step.

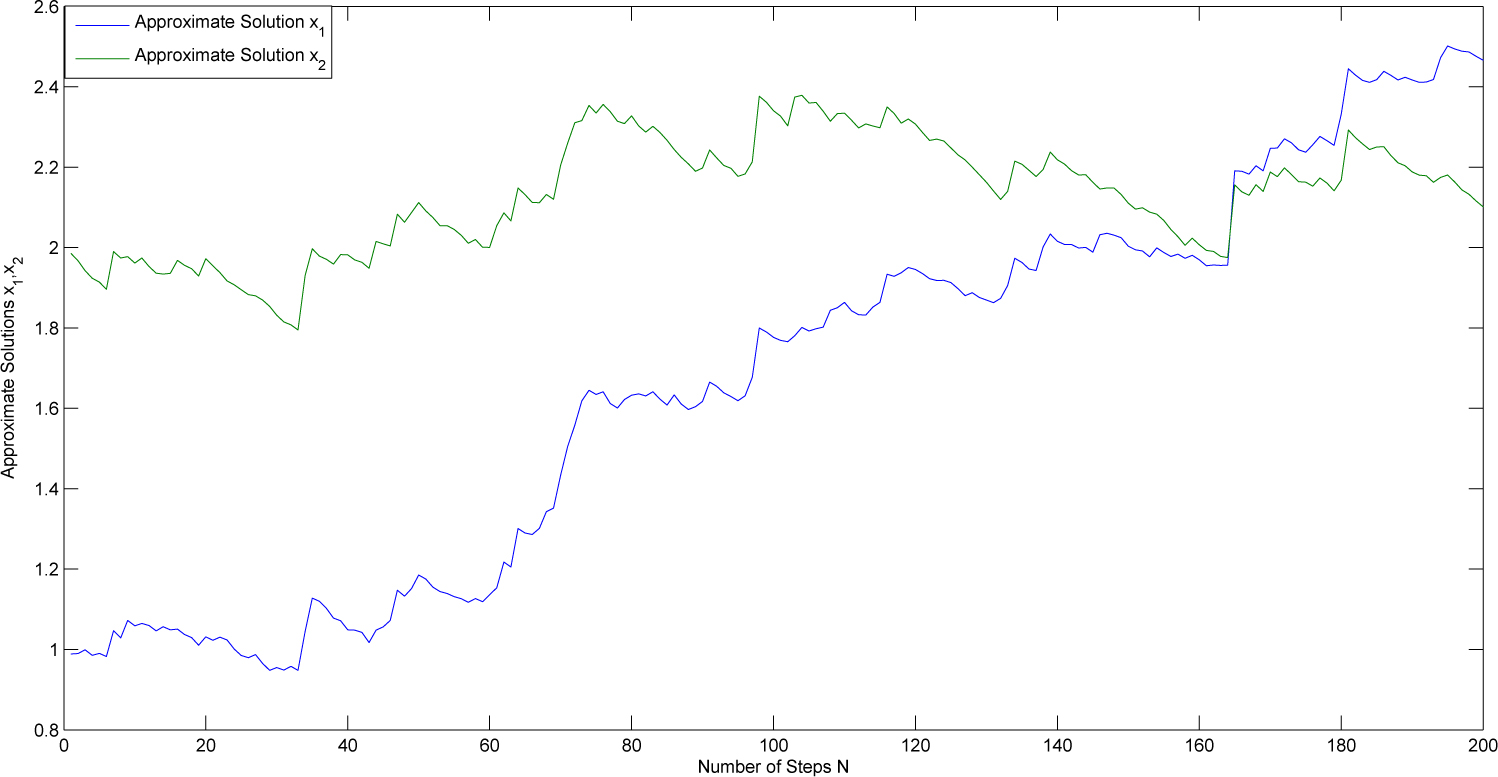
$Figure 1 Approximate solutions of (3.7).$

Figure 1

Approximate solutions of (3.7).

In Table 1, we calculate the error of the method at a time interval [0, T], where T = 1 by using the iteration numbers N = 5, 10 and 20, step sizes h = 1/5, 1/10 and 1/20 and the simulation number R = 4000000.

Table 1

Mean squared error.

N	Mean squared error E	Confidence intervals
5	0.0184	0.0146:0.0222
10	0.0050	0.0012:0.0088
20	0.0015	−0.0023:0.0058

Figure 2 shows the confidence intervals along the line of the least square for the expectations against step sizes. The blue line is the least square. The level of the confidence interval is 95%. The green line is the upper confidence bounds, while the red line is the lower confidence bounds. The red line has just two points because the lower bound of one of the confidence intervals is negative. Therefore, we swap the negative value in the confidence interval with the zero, so when we take the log for this confidence interval, then we get −∞ as the lower bound for this confidence interval, but it does not show in the graph. Therefore, we have used this method to handle the negative value in the confidence interval because if we do not do this, then the least square regression line does not pass through confidence intervals as it should be. This scheme aims to give approximation at order 32 , where the slope of the line is 1.80.

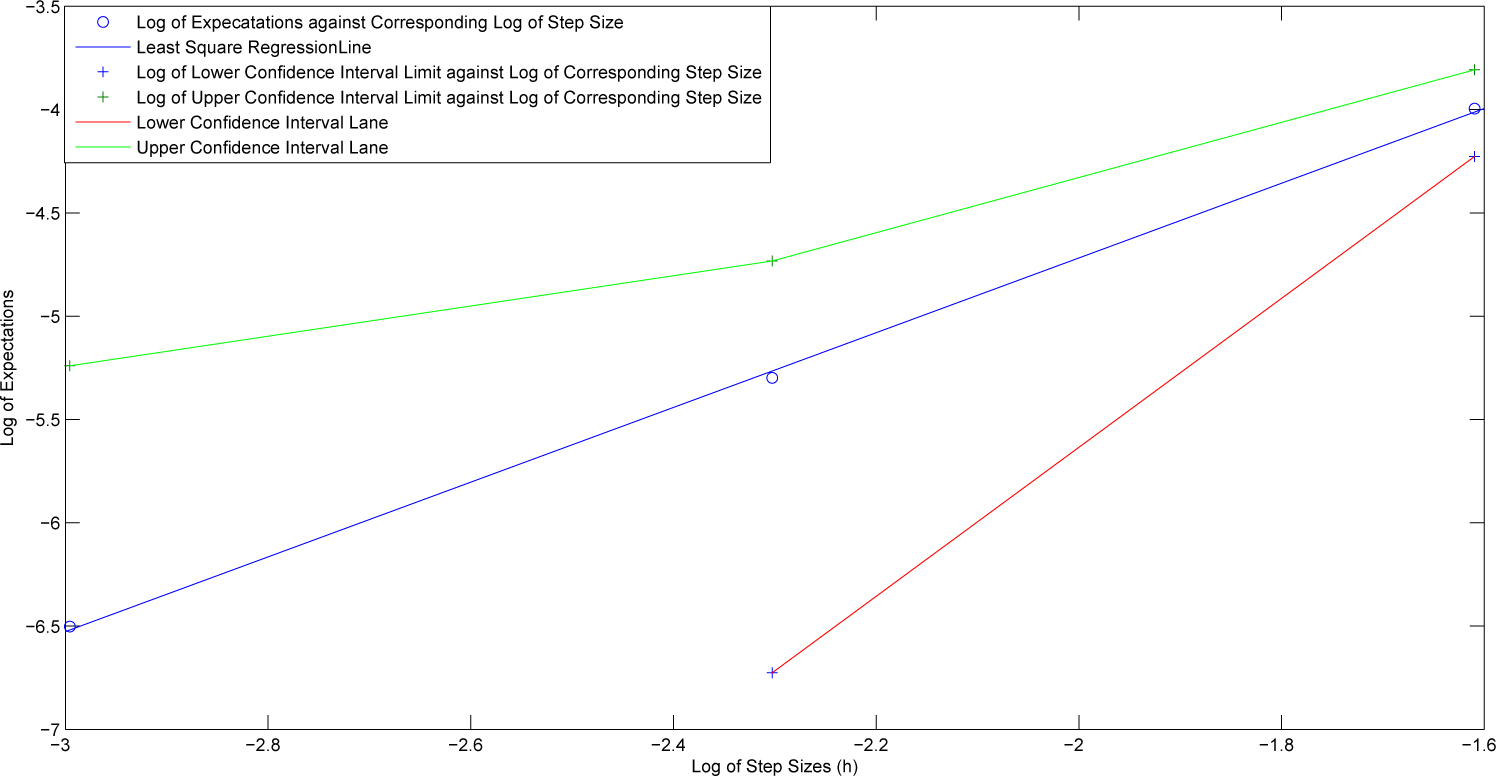
$Figure 2 Convergence of the method.$

Figure 2

Convergence of the method.

4 Conclusion

The paper presents a numerical method that gives approximate solutions of stochastic differential equations with a strong error rate of O(h32) . It is not the only method that can give this result. As mentioned in the introduction, a quiet few methods are existing, which can give approximate solutions for SDEs of order 32 , but they have a computational cost such as the one which was developed by Kloeden and Platen [1] in page 198 using Fourier series expansion. Therefore, our method does not involve a computational cost due to not requiring simulation of iterated stochastic integrals I_α. We can extend the method by adding additional terms from the formula (2.12) to achieve a higher-order of numerical solutions.

Acknowledgment

The author would like to thank Prof. Davie and Prof. Gyongy from Edinburgh University for many useful discussions, especially Prof. Davie, who answering many questions. The author is grateful for the support of Qassim University and Edinburgh University.

References

[1] Kloeden P.E., Platen E., Numerical Solution of Stochastic Differential Equations, Springer-Verlag Berlin Heidelberg New York, 1995.Search in Google Scholar

[2] Gaines J.G., Lyons T.J., Random generation of stochastic area integrals, SIAM J.Appl. Math., 1994, 54, 1132–1146.10.1137/S0036139992235706Search in Google Scholar

[3] Rydén T., Wiktorsson M., On the simulation of iterated Itô integrals, Stochastic Processes Appl, 2001, 91, 151–168.10.1016/S0304-4149(00)00053-3Search in Google Scholar

[4] Wiktorsson M., Joint characteristic function and simultaneous simulation of iterated Itô integrals for multiple independent Brownian motions, Ann. Appl. Probab., 2001, 11, 470–487.10.1214/aoap/1015345301Search in Google Scholar

[5] Villani C., Topics in Optimal Transportation, American Mathematical Society, 2003.10.1090/gsm/058Search in Google Scholar

[6] Alfonsi A., Jourdain B., Kohatsu-Higa A., Pathwise optimal transport bounds between a one-dimensional diffusion and its Euler scheme, Ann. Appl. Probab., 2014, 24, 1049–1080.10.1214/13-AAP941Search in Google Scholar

[7] Rio E., Upper bounds for minimal distances in the central limit theorem, Ann. Inst. Henri Poincar’e Probab. Stat., 2009, 45, 802–817.10.1214/08-AIHP187Search in Google Scholar

[8] Komlós J., Major P., Tusnády G., An approximation of partial sums of independent RV's and the sample DF. I, Z. Wahr. und Wer. Gebiete, 1975, 32, 111–131.10.1007/BF00533093Search in Google Scholar

[9] Rachev S.T., Ruschendorff L., Mass transportation problems, Volume 1, Theory; Volume 2, Applications, Springer-Verlag Berlin Heidelberg New York, 1998.Search in Google Scholar

[10] Davie A.M., Pathwise approximation of stochastic differential equations using coupling, http://www.maths.ed.ac.uk/∼sandy/coum.pdf.Search in Google Scholar

[11] Davie A.M., Polynomial perturbations of normal distributions, www.maths.ed.ac.uk/∼adavie/polg.pdf.Search in Google Scholar

[12] Gaines J.G., The algebra of iterated stochastic integrals, Stochastics and Stochastics Reports, 1993, 49, 169–179.10.1080/17442509408833918Search in Google Scholar

Received: 2019-02-02

Accepted: 2019-10-25

Published Online: 2019-12-31

This work is licensed under the Creative Commons Attribution 4.0 Public License.

Articles in the same Issue

https://doi.org/10.1515/math-2019-0124

Keywords for this article

stochastic differential equations; pathwise approximation; Runge-Kutta method; Itô-Taylor expansion

Creative Commons

BY 4.0

Explicit order 3/2 Runge-Kutta method for numerical solutions of stochastic differential equations by using Itô-Taylor expansion

Article

Abstract

1 Introduction

2 Background

2.1 Stochastic Itô-Taylor expansion

2.2 Perturbation method

2.3 Construction of pathwise approximation of SDEs using stochastic Taylor expansions

Theorem 1

Proof

Lemma 1

Lemma 2

Lemma 3

3 Implementation of the method

Deterministic Kα

Non-deterministic moments

3.1 Construction of Lβ

3.2 Completion of the method

3.3 Simulation result

4 Conclusion

Acknowledgment

References

Articles in the same Issue

Articles in the same Issue

Articles in the same Issue

Deterministic K_α

3.1 Construction of L_β