Home Mathematics Positivity preserving operator splitting nonstandard finite difference methods for SEIR reaction diffusion model
Article Open Access

Positivity preserving operator splitting nonstandard finite difference methods for SEIR reaction diffusion model

  • Nauman Ahmed EMAIL logo , Tahira S.S. , M. Rafiq , M.A. Rehman , Mubasher Ali and M.O. Ahmad
Published/Copyright: April 29, 2019
Download Article (PDF)
Open Mathematics
From the journal Open Mathematics Volume 17 Issue 1

Abstract

In this work, we will introduce two novel positivity preserving operator splitting nonstandard finite difference (NSFD) schemes for the numerical solution of SEIR reaction diffusion epidemic model. In epidemic model of infection diseases, positivity is an important property of the continuous system because negative value of a subpopulation is meaningless. The proposed operator splitting NSFD schemes are dynamically consistent with the solution of the continuous model. First scheme is conditionally stable while second operator splitting scheme is unconditionally stable. The stability of the diffusive SEIR model is also verified numerically with the help of Routh-Hurwitz stability condition. Bifurcation value of transmission coefficient is also carried out with and without diffusion. The proposed operator splitting NSFD schemes are compared with the well-known operator splitting finite difference (FD) schemes.

Keywords: SEIR reaction diffusion model; operator splitting techniques; positivity; bifurcation value

1 Introduction

In childhood epidemic diseases, Measles is considered as highly infectious disease, spread due to respiratory infection by a traveling virus. In 19th century, Arthur Ransom observed the unevenly recurring nature of Measles. Since 1896, age structures, contact rates and school seasons are known as critical agents for the transmission of Measles in a population. Hamer [1] in 1906 presented a model for transmission dynamics of Measles. Later, the principle of “mass action” was introduced which became a fundamental statute in present theory of infectious disease modeling [2, 3, 4, 5].

Infectious disease dynamics is an important application of dynamical systems. Fixed points, steady states or the equilibrium points of a continuous dynamical systems are the values of variables that do not change over time. If a system starts at a nearby state and converges to the equilibrium point, then this equilibrium point is attractive. Many dynamical systems in different fields of science and engineering show the chaotic behavior. If a numerical method produces chaos and it is not the feature of continuous system, then this is called contrived chaos. Many existing numerical techniques show the contrived chaos. If a continuous dynamical system demonstrates a property P, then it is necessary for the numerical method to preserve that property P. This is called dynamical consistency, in the literature, Twizzell et al and various authors [6, 7, 8, 9, 10, 11, 12, 13] discussed about the contrived chaos and loss of the dynamical consistency in the finite difference scheme. Similarly, Fernández [14] discussed about the same drawbacks exhibited in different series solution techniques. The aim of this work is to develop and investigate such numerical schemes whose equilibrium points coincide with the equilibrium points of the continuous system and preserve all the essential properties demonstrated by the continuous system.

In this work, we consider SEIR epidemic model with diffusion presented by Al-Shawaikh and Twizell [15]. This model describes the transmission dynamics of measles. In this model, the total population is taken as ‘N’ and it is categorized in four classes i.e. susceptible population, exposed population, infected population and recovered population denoted by S, E, I and R respectively. It is assumed that the total population ‘N’ is constant i.e. birth and death rates in the population are equal. Mathematical model of SEIR epidemic model with diffusion is

∂S∂t=μN−μS−βSI+dS∂2S∂x2, (1)
∂E∂t=βSI−μ+σE+dE∂2E∂x2, (2)
∂I∂t=σE−μ+γI+dI∂2I∂x2, (3)
∂R∂t=γI−μR+dR∂2R∂x2. (4)

Since R is not present in first three equations so we can write the system as

∂S∂t=μN−μS−βSI+dS∂2S∂x2, (5)
∂E∂t=βSI−μ+σE+dE∂2E∂x2, (6)
∂I∂t=σE−μ+γI+dI∂2I∂x2, (7)

with the initial conditions

S(x,0)=g1(x),E(x,0)=g2(x),I(x,0)=g3(x),0≤x≤L (8)

and homogeneous Neumann boundary conditions are

Sx0,t=SxL,t=0, (9)
Ex0,t=ExL,t=0, (10)
Ix0,t=IxL,t=0. (11)

As discussed above, the purpose of this work is to construct positivity preserving operator splitting nonstandard finite difference schemes for the system (5)-(7). Since SEIR reaction diffusion system (5)-(7) is a population model therefore negative values of susceptible, exposed and infected population is meaningless. Nonstandard finite difference method is a structural preserving numerical method which is developed by Mickens [16]. NSFD method is an important tool to solve ordinary and partial differential equations [9, 10, 11, 17, 18] as it preserves the properties possessed by continuous system.

2 Equilibrium Points

There are two steady states [15] of the system (5)-(7), disease-free and endemic steady state. Disease-free state is

(S0,E0,I0)=(N,0,0) (12)

and the endemic steady state is

(S∗,E∗,I∗)=NR0,μNμ+σ1−1R0,μβR0−1, (13)

where

R0=σβN(μ+σ)(μ+γ),when,dS=dE=dI=0

R0 is the reproductive and if R0 < 1 then the system possesses disease free state and if R0 > 1 then system possesses endemic state.

3 Stability of Equilibrium of the System

The system (5)-(7) is linearized about the equilibrium point (S*, E*, I*) to have small perturbations S(x, t), E(x, t) and I(x, t) as describe in [19]

∂S∂t=a11S1+a12E1+a13I1+dS∂2S∂x2, (14)
∂E∂t=a21S1+a22E1+a23I1+dE∂2E∂x2, (15)
∂I∂t=a31S1+a32E1+a33I1+dI∂2I∂x2. (16)

Suppose that the system (14)-(16) possesses Fourier series solution as mentioned in [19], then

S1(x,t)=∑kSkeλtcos(kx), (17)
E1(x,t)=∑kEkeλtcos(kx), (18)
I1(x,t)=∑kIkeλtcos(kx), (19)

where k represents the wave number for the node n and k = nπ/2, (n = 1, 2, 3, …). Replacing the values of S1(x, t), E1(x, t) and I1(x, t) in the system, it is transformed into

∑k(a11−dSk2−λ)Sk+∑ka12Ek+∑ka13Ik=0, (20)
∑ka21Sk+∑k(a22−dEk2−λ)Ek+∑ka23Ik=0, (21)
∑ka31Sk+∑ka32Ek+∑k(a33−dIk2−λ)Ik=0. (22)

The variational matrix 𝓥 is for the equation (20)-(22) is

V=a11−dSk2a12a13a21a22−dEk2a23a31a32a33−dIk2, (23)

where

a11=−μ−βI∗,a12=0,a13=−βS∗,a21=βI∗,a22=−μ−σ,a23=βS∗,a31=0,a32=σ,a33=−μ−γ.

The characteristics equation for matrix 𝓥 is

λ3+η1λ2+η2λ+η3=0,
η1=−a11+a22+a33−dSk2−dEk2−dIk2,
η2=−(a12a21−a11a22−a11a33+a13a31−a22a33+a23a32+a11dEk2+a11dIk2+a22dSk2+a33dSk2+a33dEk2−dSdEk4−dSdIk4−dEdIk4),
η3=−a11a22a33+a11a23a32+a12a21a33−a12a23a31−a13a21a32+a13a22a31+a11a22dEk2−a12a21dIk2+a11a33dEk2−a13a31dEk2+a22a33dSk2−a23a32dSk2−a11dEdIk4−a22dSdIk4−a33dSdEk4+dSdEdIk6.

The Routh-Hurwitz stability criterion gives

η1>0,η3>0,

and

η1η2−η3>0.

4 Bifurcation Value of Transmission Coefficient β

The values of S*, E* and I* are substituted in a11, a22, ⋅ ⋅ ⋅, to obtain

a11=−13688.874223β,a12=0,a13=−73.052026,a21=13688.87422β−0.02,a22=−45.62,a23=73.052026,a31=0,a32=45.6,a33=−73.02.

The Routh-Hurwitz criterion for stability gives

η1=13688.874223β+118.790511=f1(β),
η3=45626204.885735β−66.387278=f2(β),
η1η2−η3=22236475224.061045β2+147566036.674313β+2032.880064=f3(β).

The equation f2(β) = 0 provides the bifurcation value of β, which shifts the stability of the equilibrium point (i.e. from stable to unstable). The solution for f2(β) gives 0.000001455. The point of equilibrium is unstable for any value of β less than 0.000001455. Similarly, the bifurcation value of β for system without diffusion is 0.000001462. The equilibrium point of the system without diffusion is not stable for any value of β less than 0.000001462. It is concluded that bifurcation value of β with diffusion is less than bifurcation value of β without diffusion. In order to find the bifurcation value of β we consider case 1 in Table 1 and dS = 0.05, dE = 0.01, dI = 0.001.

Table 1

Values of parameters.

cases β σ γ μ
1 0.3×10–5 45.6 73 0.02
2 0.5×10–4 50 80 0.02
3 0.8×10–3 58 85 0.02
4 0.9×10–3 65 90 0.02
5 0.3×10–2 77 99 0.02

Al-Showaikh et al. and Jansen et al. [15, 20]

Table 2

Stability of Equilibrium.

cases Point of Equilibrium n η1 η2 η1η2–η3 Stability
1 (2.435 × 107, 1.125 × 104, 7022.67) 1 1.1883 × 102 7.0491× 10 2.4758× 103 Stable
2 (1.6010 × 106, 1.9352 × 104, 1.2092× 104) 1 130.8151 2.4215× 103 1.0579× 104 Stable
3 (1.0631 × 105, 1.7199 × 104, 1.1733× 104) 1 152.5968 4.6323× 104 1.6207× 105 Stable
4 (1.0005 × 105, 1.5349 × 104, 1.1083× 104) 1 165.1852 5.8407× 104 2.0116× 105 Stable
5 (3.3015 × 104, 1.2975 × 104, 1.0090× 104) 1 206.4796 2.3093× 105 8.7524× 105 Stable

5 Numerical Methods

In order to handle the complexity and nonlinearity of the reaction-diffusion system (5)-(7), we implement two classical and two proposed nonstandard operator splitting finite difference methods. Operator splitting FD schemes are used by various authors to solve complex problems containing differential equations [19, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30]. Generally, the SEIR reaction-diffusion equations are split into two systems of equations. The nonlinear reaction steps

12∂S∂t=μN−μS−βIS, (24)
12∂E∂t=βSI−(μ+σ)E, (25)
12∂I∂t=σE−(μ+γ)I, (26)

which are used for the first half step for time and the linear diffusion equation

12∂S∂t=dS∂2S∂x2, (27)
12∂E∂t=dE∂2E∂x2, (28)
12∂I∂t=dI∂2I∂x2, (29)

which are implemented for the second half step of time. Firstly, we present forward Euler FD and Backward Euler schemes to solve the equations.

S¯im+12=Sim+τμN−μSim−βSimIim, (30)
E¯im+12=Eim+τβSimIim−(μ+σ)Eim, (31)
I¯im+12=Iim+τσEim−(μ+γ)Iim, (32)

where Sim,Eim,Iim are the finite difference approximation values of S, E and I at 0 + ih, i = 0, 1, … and time mτ, m = 0, 1, … and S¯im+12,E¯im+12 and I¯im+12 reflect the representative values at the half time step. The procedure at first half time step is same for both forward Euler and Backward Euler FD schemes. At second half-time step, the procedure is different for both schemes. For forward Euler FD scheme, we use

Sim+1=S¯im+12+λ1S¯i−1m+12−2S¯im+12+S¯i+1m+12, (33)
Eim+1=E¯im+12+λ2E¯i−1m+12−2E¯im+12+E¯i+1m+12, (34)
Iim+1=I¯im+12+λ3I¯i−1m+12−2I¯im+12+I¯i+1m+12. (35)

The procedure for the backward Euler FD scheme is

−λ1Si−1m+1+1+2λ1Sim+1−λ1Si−1m+1=S¯im+12, (36)
−λ2Ei−1m+1+1+2λ2Eim+1−λ2Ei−1m+1=E¯im+12, (37)
−λ3Ii−1m+1+1+2λ3Iim+1−λ3Ii−1m+1=I¯im+12. (38)

Nowwe construct nonstandard FD schemes. By applying rules defined by Mickens [16], both nonstandard FD schemes at first half time step are

S¯im+12=Sim+τμN1+τμ+τβIim, (39)
E¯im+12=Eim+τβSimIim1+τ(μ+σ), (40)
I¯im+12=Iim+τσEim1+τ(μ+γ). (41)

Positivity of the solution requires that if

Sim≥0,Eim≥0,Iim≥0,thenS¯im+12≥0,E¯im+12≥0,I¯im+12≥0. (42)

The procedure is different for both NSFD operator splitting schemes at second half-time step. For explicit NSFD operator splitting scheme, we use

Sim+1=1−2λ1S¯im+12+λ1S¯i−1m+12+S¯i+1m+12, (43)
Eim+1=1−2λ2E¯im+12+λ2E¯i−1m+12+E¯i+1m+12, (44)
Iim+1=1−2λ3I¯im+12+λ3I¯i−1m+12+I¯i+1m+12. (45)

The procedure for the implicit NSFD operator splitting scheme at second half time step is

−λ1Si−1m+1+1+2λ1Sim+1−λ1Si−1m+1=S¯im+12, (46)
−λ2Ei−1m+1+1+2λ2Eim+1−λ2Ei−1m+1=E¯im+12, (47)
−λ3Ii−1m+1+1+2λ3Iim+1−λ3Ii−1m+1=I¯im+12, (48)

where

λ1=dSτh2,λ2=dEτh2,λ3=dIτh2.

5.1 Accuracy and Stability of the Numerical Methods

In operator splitting methods, the stability and consistency depends on their split solutions [21, 22]. In all the above splitting methods, the reaction step is solved exactly and time derivative has O(τ) accuracy [21, 22]. Similarly, the diffusion step has O(h2) accuracy and the cumulative accuracy of all numerical schemes is first order in time and second order in space [21, 22]. For the stability, the reaction step is unconditionally stable in all cases as it is solved exactly [21, 22]. In forward Euler method operator splitting FD method and explicit NSFD operator splitting method (32)-(34), the stability region of diffusion step is

λi≤12,(i=1,2,3). (49)

In the backward Euler method operator splitting FD method and implicit NSFD operator splitting method, the diffusion step is unconditionally stable.

5.2 Positivity of NSFD methods

It can be observed that NSFD methods in reaction step (39)-(41) preserve the positivity property of the solution. For the diffusion step, explicit NSFD method (43)-(45) gives the positive solution if

1−2λi≥0,i=1,2,3.

This implies that

λi≤12,(i=1,2,3),

which is the stability condition (49) of NSFD method (39)-(41). This proves that the first NSFD method preserves the positivity property in its stability region. In order to prove the positivity of unconditionally stable implicit NSFD method (46)-(48), we use M-matrix theory [33].

5.2.1 Theorem [31, 32]

For any h > 0 and τ > 0, the system (46)-(48) is positive, i.e. Sm > 0, Em > 0 and Im > 0 for all m = 0, 1, 2...

Proof

The system (46)-(48) can be written as

ASm+1=Sm, (50)
BEm+1=Em, (51)
CIm+1=Im, (52)

where A, B and C are the square matrices

A=a3a10⋯⋯⋯⋯0a2a3a2⋱⋮0a2a3a2⋱⋮⋮⋱⋱⋱⋱⋱⋮⋮⋱⋱⋱⋱⋱⋮⋮⋱a2a3a20⋮⋱a2a3a20⋯⋯⋯⋯0a1a3, (53)
B=b3b10⋯⋯⋯⋯0b2b3b2⋱⋮0b2b3b2⋱⋮⋮⋱⋱⋱⋱⋱⋮⋮⋱⋱⋱⋱⋱⋮⋮⋱b2b3b20⋮⋱b2b3b20⋯⋯⋯⋯0b1b3, (54)

and

C=c3c10⋯⋯⋯⋯0c2c3c2⋱⋮0c2c3c2⋱⋮⋮⋱⋱⋱⋱⋱⋮⋮⋱⋱⋱⋱⋱⋮⋮⋱c2c3c20⋮⋱c2c3c20⋯⋯⋯⋯0c1c3. (55)

The off-diagonal entries of A are a1 = −2λ1, a2 = −λ1 and a3 = 1 + 2λ1. The off-diagonal entries of B are b1 = −2λ1, b2 = −λ1and diagonal entries are b3 = 1 + 2λ2. The off-diagonal entries of C are c1 = −2λ3, c2 = −λ3and diagonal entries are c3 = 1 + 2λ3. Thus A, B and C are M-matrices. Hence equation (50), (51) and (52) become

Sm+1=A−1Sm, (56)
Em+1=B−1Em, (57)
Im+1=C−1Im. (58)

If we consider that Sm > 0, Em > 0 and Im > 0, then from the property of M-matrix and (56)-(58) we get Sm+1 > 0, Em+1 > 0 and Im+1 > 0 . So by the induction, the theorem is proved.

It follows from Theorem 5.2.1 that implicit NSFD operator splitting scheme preserve positivity property unconditionally.

6 Numerical Experiment

In this section, we perform a numerical experiment for all the methods at both equilibrium points. For the numerical test, the following values of parameters are used for disease-free equilibrium [15, 20]

N=5×107,μ=0.02,σ=45.6,γ=73,β=0.1×10−5. (59)

For endemic equilibrium points, the following parametric values are used [15, 20]

N=5×107,μ=0.02,σ=45.6,γ=73,β=0.3×10−5. (60)

In this experiment we take dS = 0.05, dE = 0.01, dI = 0.001. The initial conditions for the system (5)-(7) are

S(x,0)=12500000xif  0≤x<0.5125000001−xif  0.5≤x≤1, (61)
E(x,0)=50000xif  0≤x<0.5500001−xif  0.5≤x≤1, (62)
I(x,0)=30000xif  0≤x<0.5300001−xif  0.5≤x≤1. (63)

Now the graphs of all the schemes at disease free equilibrium point is presented. First of all we show the graphs of Forward Euler operator splitting FD scheme.

The figures 1-3 indicate the graphs of disease free equilibrium using forward Euler operator splitting FD scheme at h = 0.1 and λ1 = 0.09375, λ2 = 0.01875 and λ3 = 0.001875. Figure 2 and figure 3 show that forward Euler operator splitting FD scheme fails to preserve the positivity property.

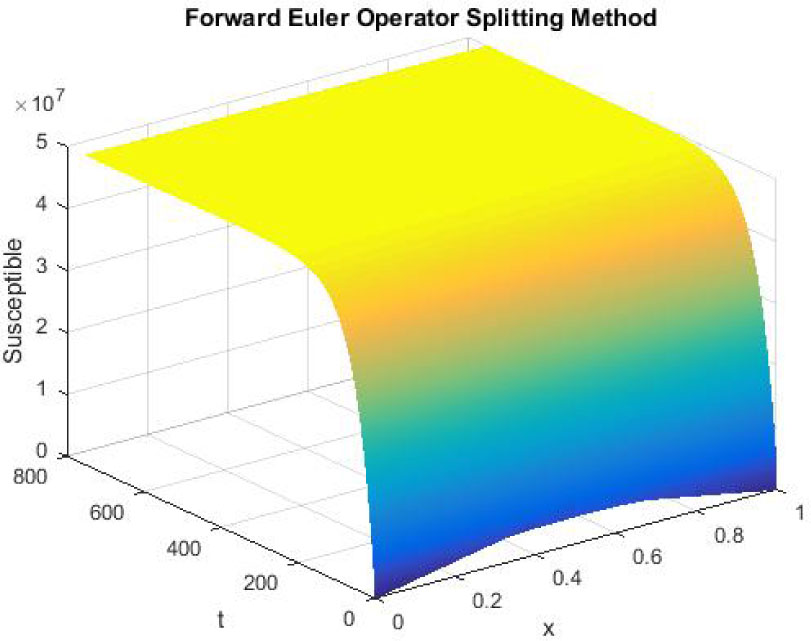
Figure 1 Mesh graph of Susceptible Individuals for DFE
Figure 1

Mesh graph of Susceptible Individuals for DFE

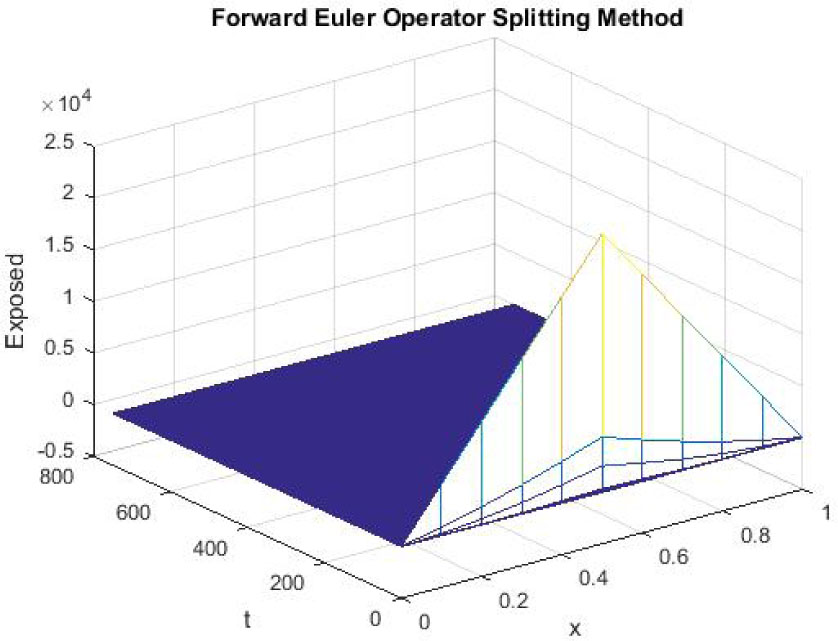
Figure 2 Mesh graph of Exposed Individuals for DFE
Figure 2

Mesh graph of Exposed Individuals for DFE

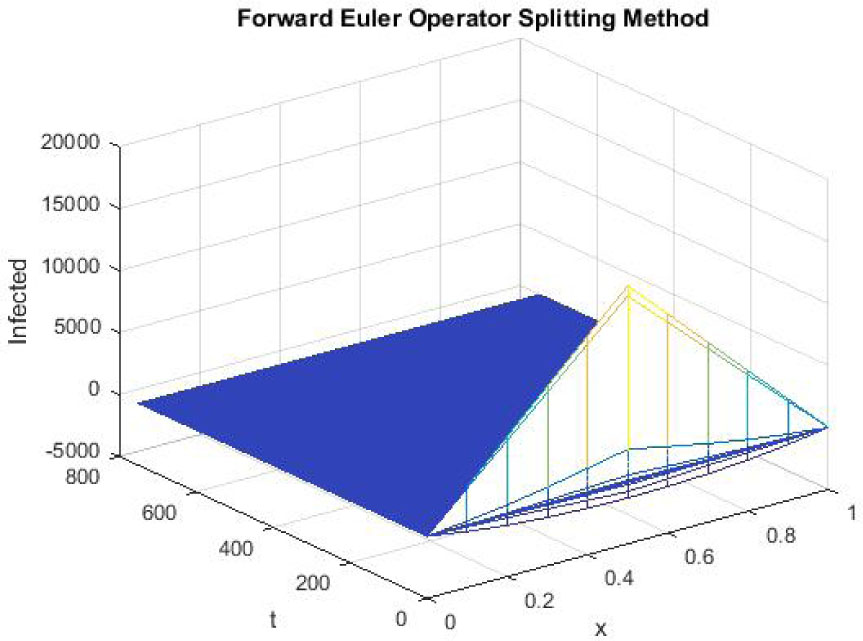
Figure 3 Mesh graph of Infected Individuals for DFE
Figure 3

Mesh graph of Infected Individuals for DFE

The figures 4-6 represent the mesh graphs of susceptible, exposed and infected individuals using forward Euler explicit operator splitting FD scheme at h = 0.1 and λ1 = 0.25, λ2 = 0.05 and λ3 = 0.005. It can be seen that all the graphs in figures 4-6 show overflow and divergence. Remember that these are the graphs at endemic equilibrium point. Forward Euler explicit operator splitting FD scheme fails to converge to the endemic equilibrium point. Secondly we present the simulation of backward Euler implicit operator splitting FD scheme.

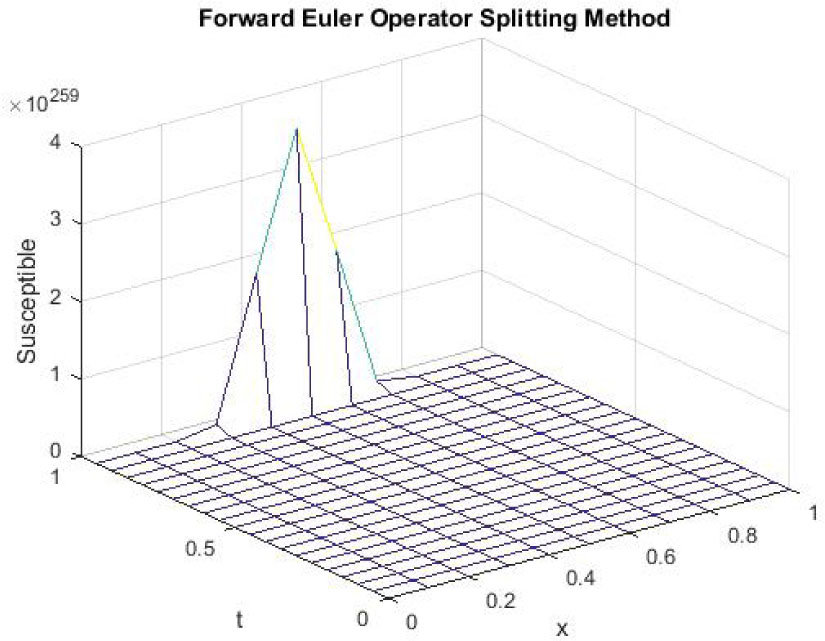
Figure 4 Mesh graph of Susceptible Individuals for EE
Figure 4

Mesh graph of Susceptible Individuals for EE

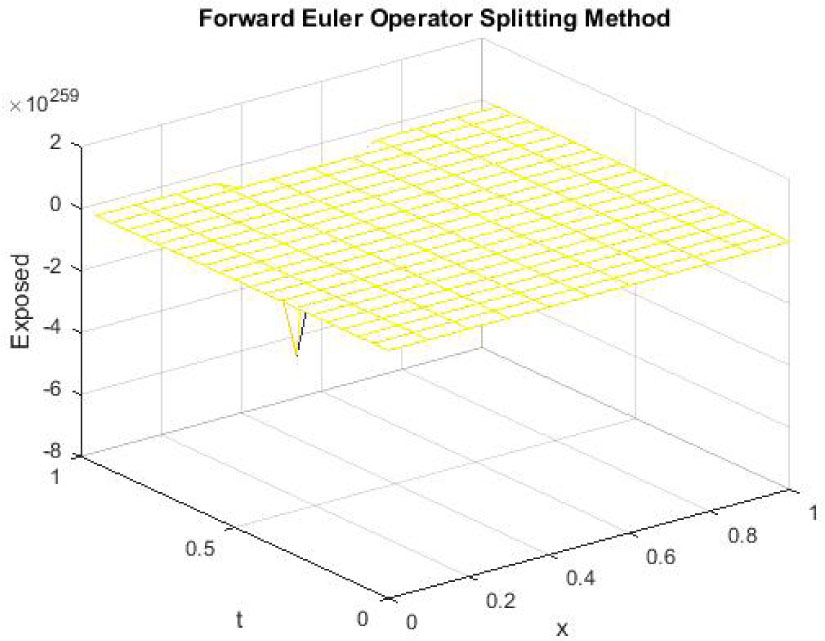
Figure 5 Mesh graph of Exposed Individuals for EE
Figure 5

Mesh graph of Exposed Individuals for EE

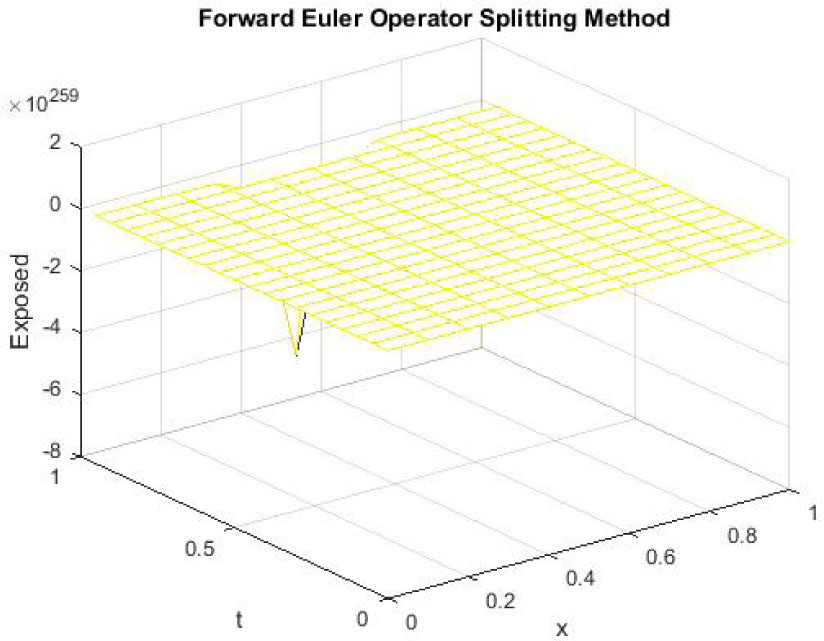
Figure 6 Mesh graph of Infected Individuals for EE
Figure 6

Mesh graph of Infected Individuals for EE

The figures 7-9 reflect the graphs of disease free equilibrium using backward Euler implicit operator splitting FD scheme at h = 0.1 and λ1 = 0.09375, λ2 = 0.01875 and λ3 = 0.001875. Figure 8 and figure 9 show that backward Euler implicit operator splitting FD scheme also fails to preserve the positivity property.

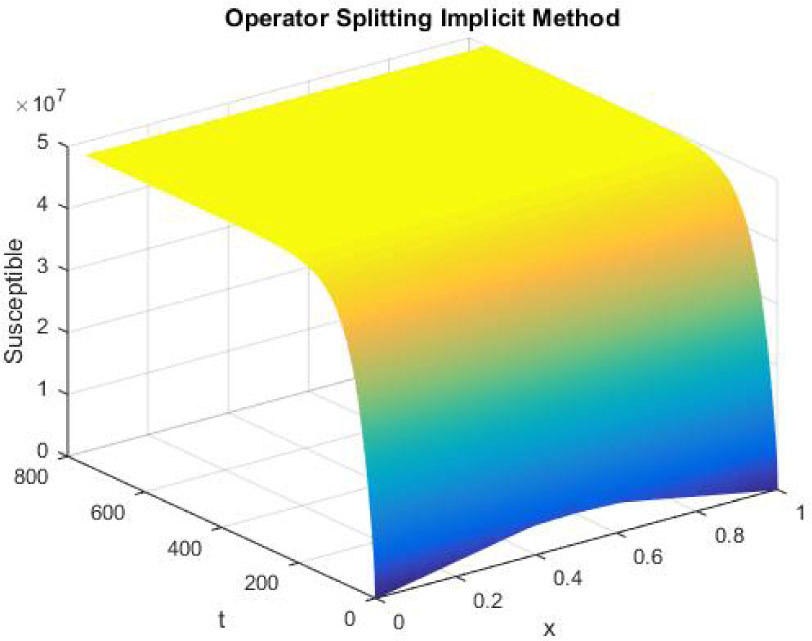
Figure 7 Mesh graph of Susceptible Individuals for DFE
Figure 7

Mesh graph of Susceptible Individuals for DFE

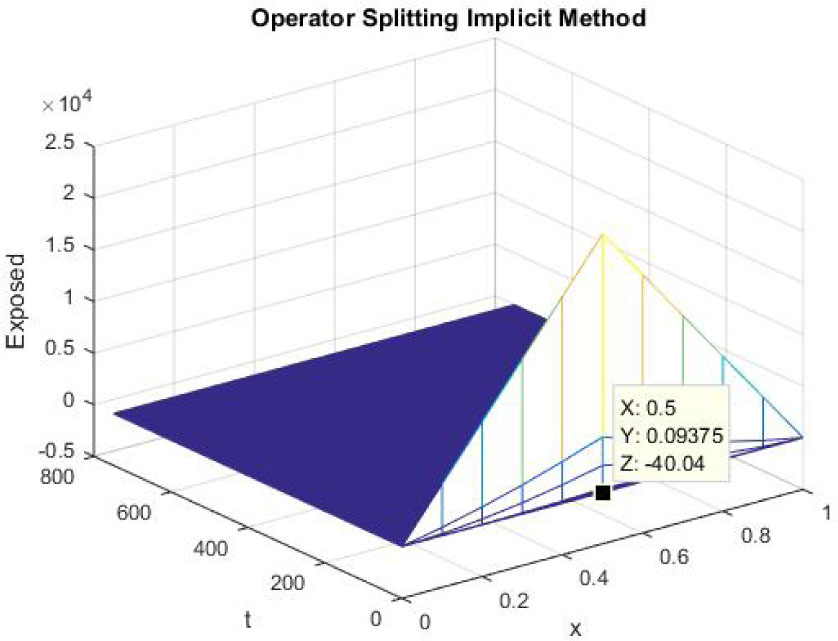
Figure 8 Mesh graph of Exposed Individuals for DFE
Figure 8

Mesh graph of Exposed Individuals for DFE

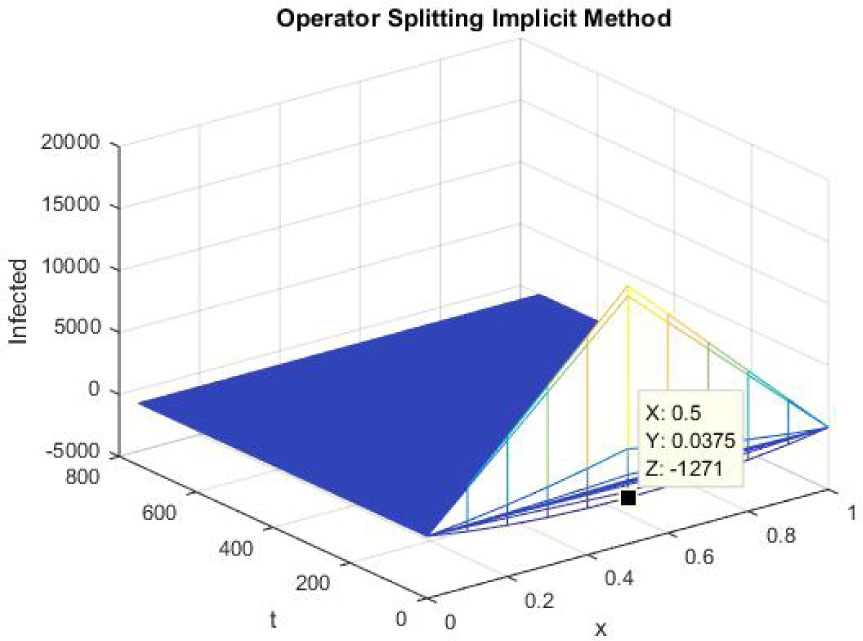
Figure 9 Mesh graph of Infected Individuals for DFE
Figure 9

Mesh graph of Infected Individuals for DFE

The figures 10-12 represent the mesh graphs of susceptible, exposed and infected individuals using backward Euler implicit operator splitting FD scheme at h = 0.1 and λ1 = 0.25, λ2 = 0.05 and λ3 = 0.005. It can be seen that all the graphs in figures 10-12 show overflow and divergence. Remember that these are the graphs at endemic equilibrium point. Backward Euler implicit operator splitting FD scheme fails to converge to the endemic equilibrium point. Thirdly, the graphs of susceptible, exposed and infected population at disease free and endemic equilibrium point using nonstandard operator splitting explicit FD method are presented.

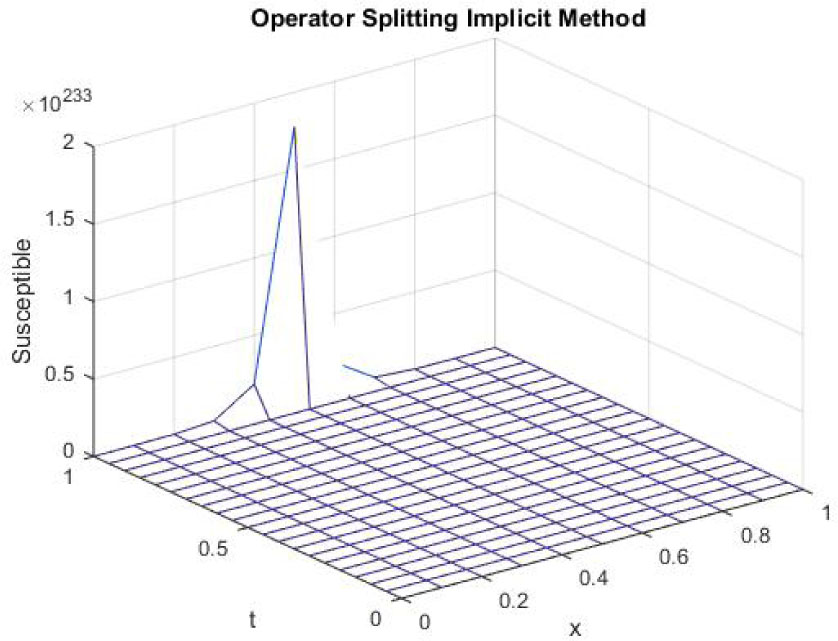
Figure 10 Mesh graph of Susceptible Individuals for EE
Figure 10

Mesh graph of Susceptible Individuals for EE

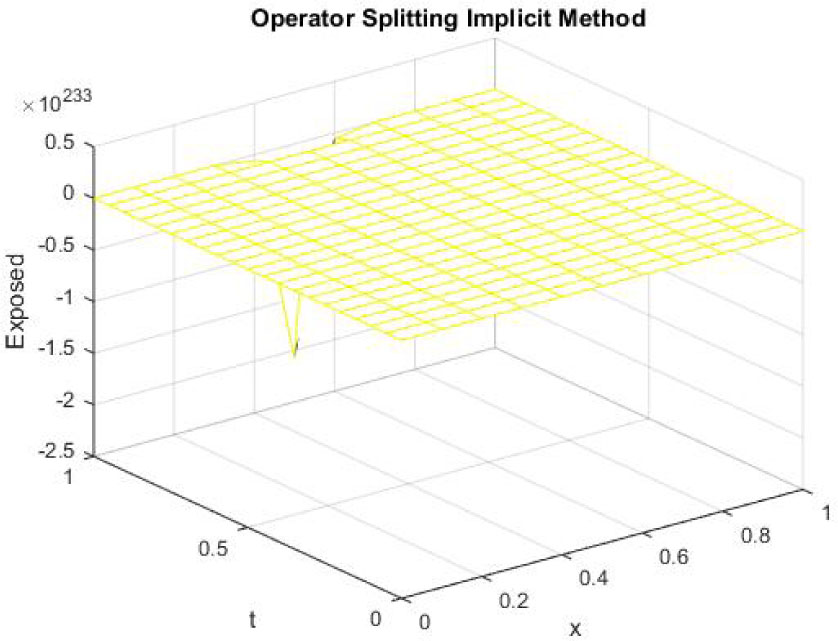
Figure 11 Mesh graph of Exposed Individuals for EE
Figure 11

Mesh graph of Exposed Individuals for EE

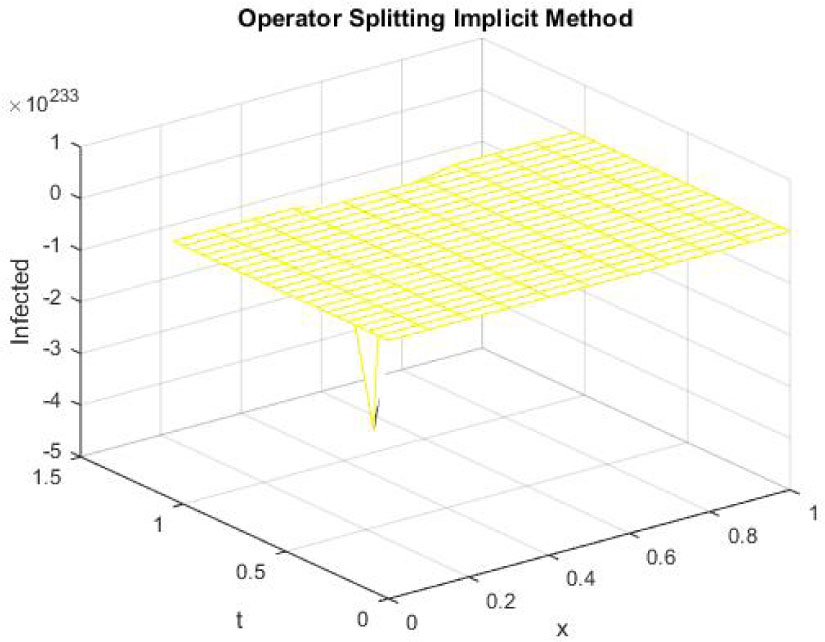
Figure 12 Mesh graph of Infected Individuals for EE
Figure 12

Mesh graph of Infected Individuals for EE

The figures 13-15 reflect the graphs of disease free equilibrium using NSFD explicit operator splitting scheme at h = 0.1 and λ1 = 0.09375, λ2 = 0.01875 and λ3 = 0.001875. Graphs clearly show that NSFD operator splitting explicit scheme preserves the positivity property and converges to the disease free equilibrium point (S0, E0, I0).

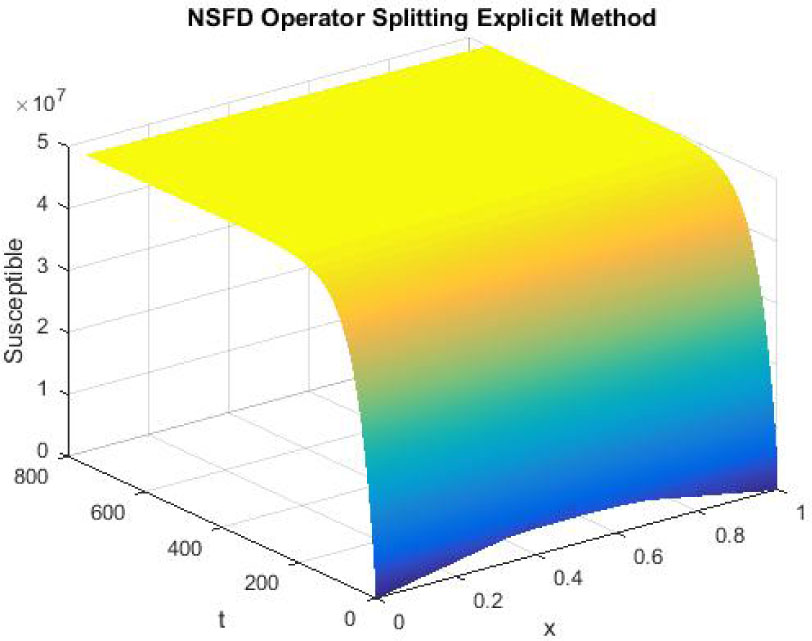
Figure 13 Mesh graph of Susceptible Individuals for DFE
Figure 13

Mesh graph of Susceptible Individuals for DFE

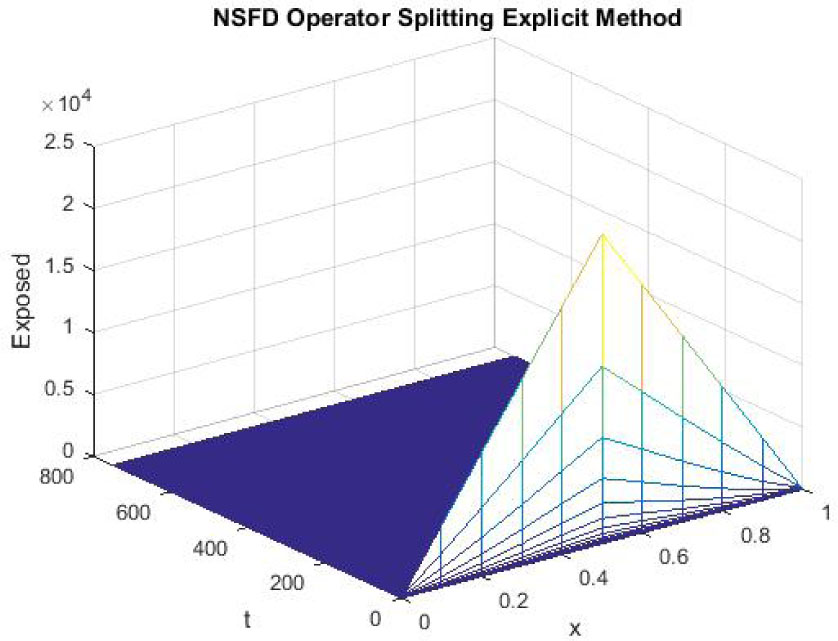
Figure 14 Mesh graph of Exposed Individuals for DFE
Figure 14

Mesh graph of Exposed Individuals for DFE

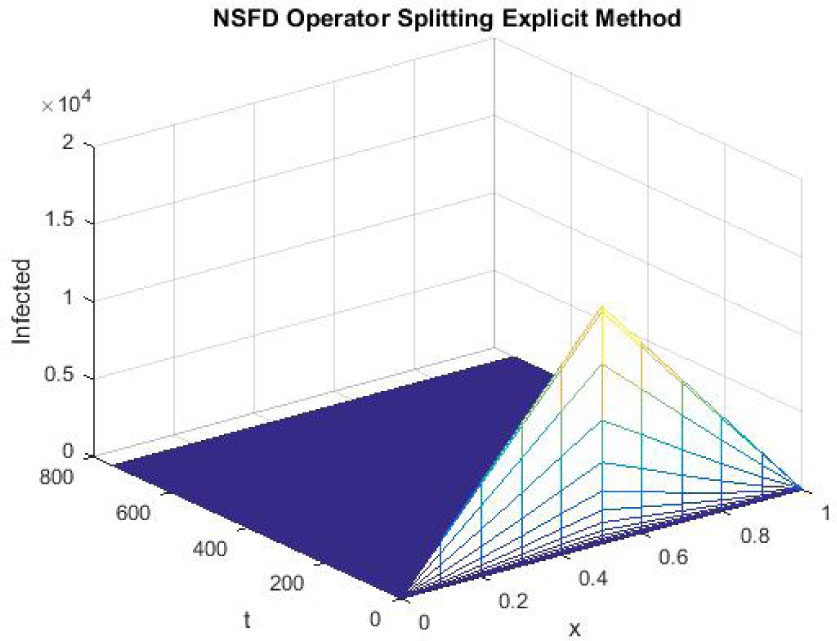
Figure 15 Mesh graph of Infected Individuals for DFE
Figure 15

Mesh graph of Infected Individuals for DFE

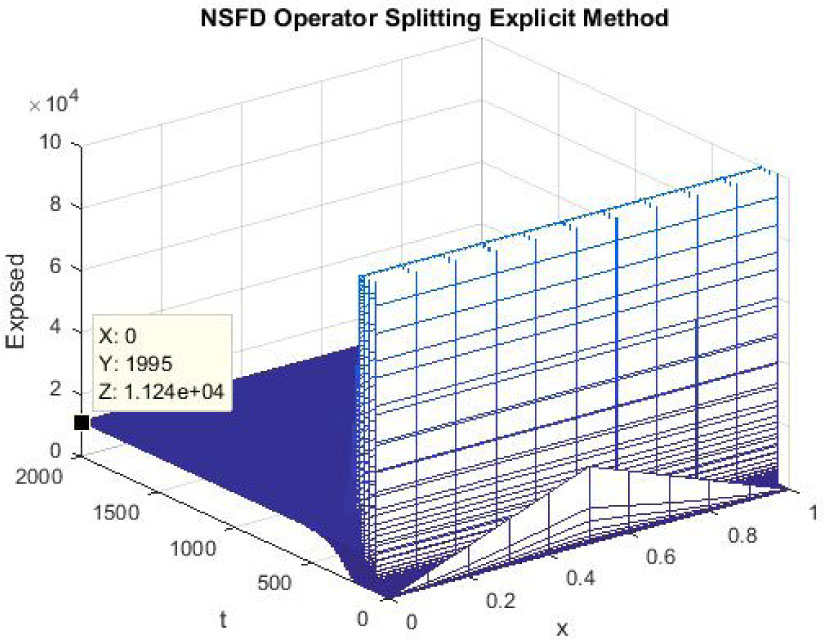
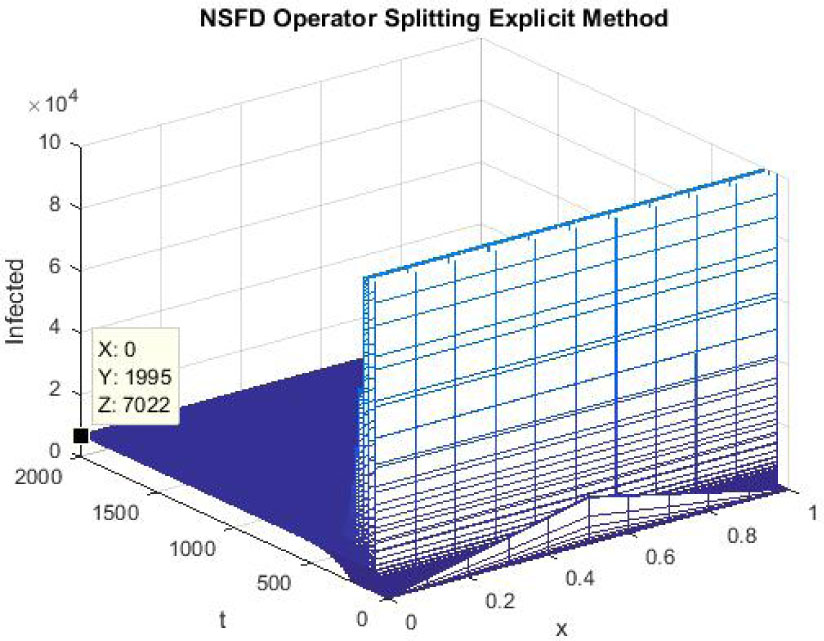
The figures 16-18 represent the graphs of endemic equilibrium point for susceptible, exposed and infected individuals using NSFD operator splitting explicit scheme at h = 0.1 and λ1 = 0.25, λ2 = 0.05 and λ3 = 0.005. Graphs show that NSFD operator splitting explicit scheme preserves the positivity property and converges to the endemic equilibrium point (S*, E*, I*). At the end, we present the simulations using NSFD operator splitting implicit method.

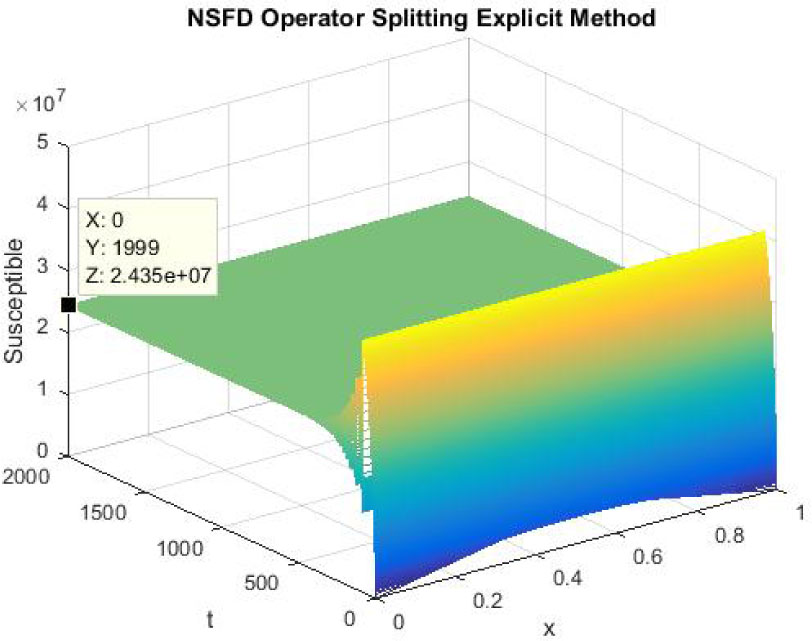
Figure 16 Mesh graph of Susceptible Individuals for EE
Figure 16

Mesh graph of Susceptible Individuals for EE

Figure 17 Mesh graph of Exposed Individuals for EE
Figure 17

Mesh graph of Exposed Individuals for EE

Figure 18 Mesh graph of Infected Individuals for EE
Figure 18

Mesh graph of Infected Individuals for EE

Figures 19-21 reflect the graphs of disease free equilibrium using NSFD operator splitting implicit scheme at h = 0.1 and λ1 = 0.09375, λ2 = 0.01875 and λ3 = 0.001875. Graphs clearly show that NSFD operator splitting implicit scheme preserves the positivity property and converges to the disease free equilibrium point (S0, E0, I0).

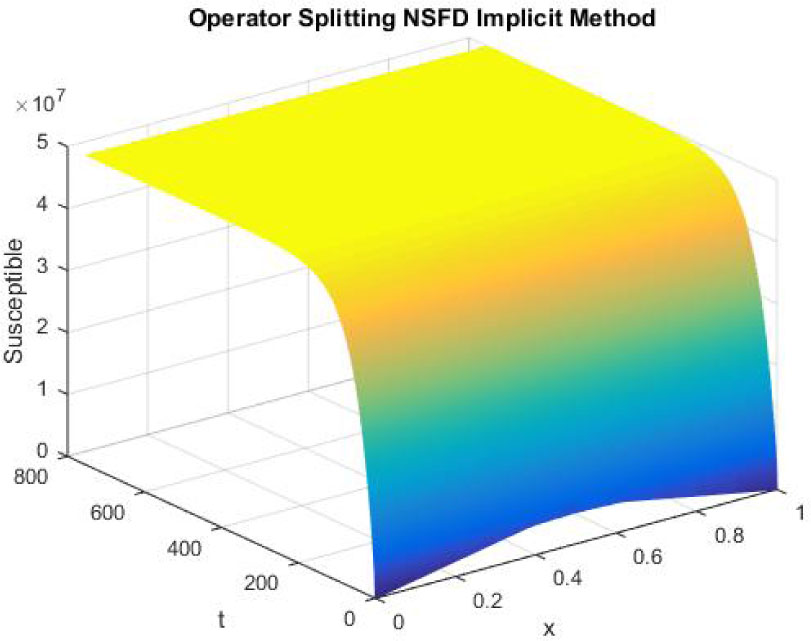
Figure 19 Mesh graph of Susceptible Individuals for DFE
Figure 19

Mesh graph of Susceptible Individuals for DFE

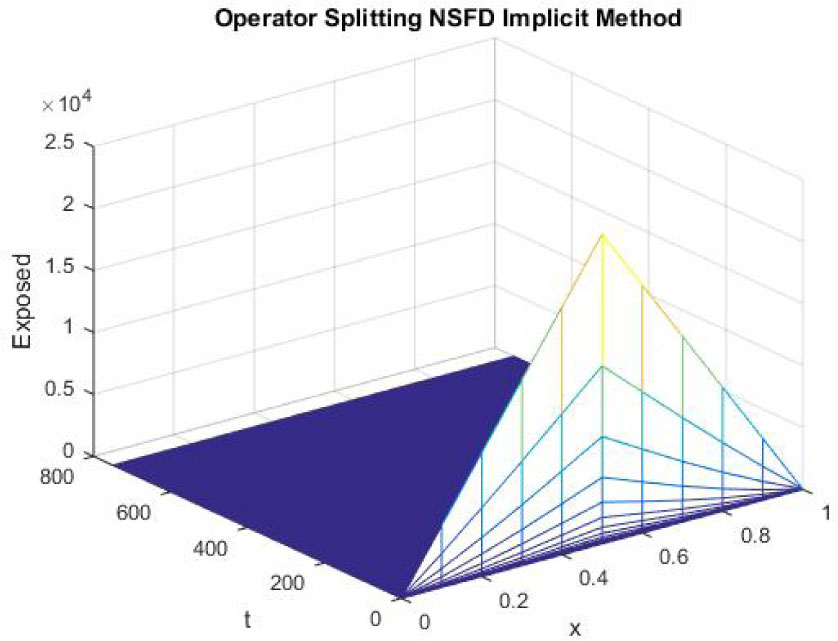
Figure 20 Mesh graph of Exposed Individuals for DFE
Figure 20

Mesh graph of Exposed Individuals for DFE

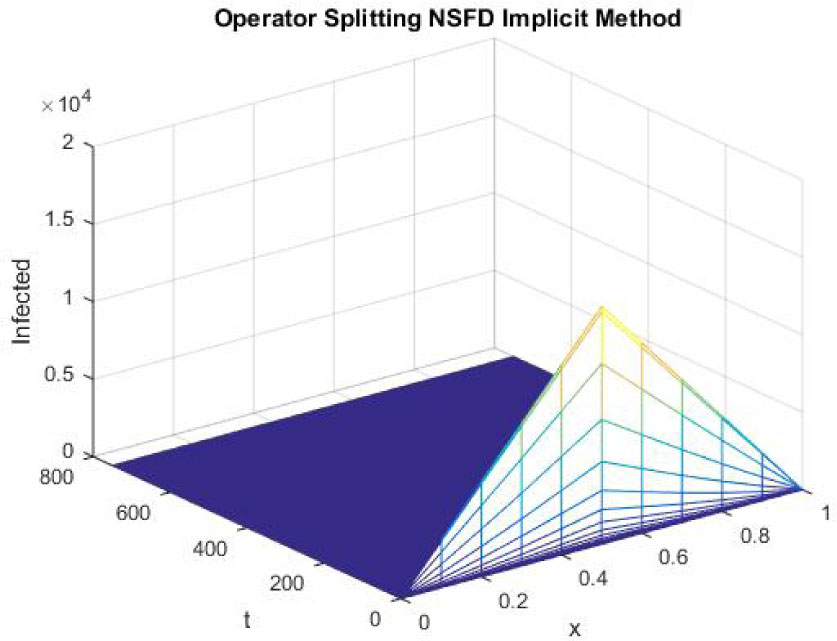
Figure 21 Mesh graph of Infected Individuals for DFE
Figure 21

Mesh graph of Infected Individuals for DFE

The figures 22-24 represent the graphs of endemic equilibrium point for susceptible, exposed and infected individuals using NSFD operator splitting implicit scheme at h = 0.1 and λ1 = 0.25, λ2 = 0.05 and λ3 = 0.005. Graphs show that NSFD operator splitting implicit method preserves the positivity property and converges to the endemic equilibrium point (S*, E*, I*).

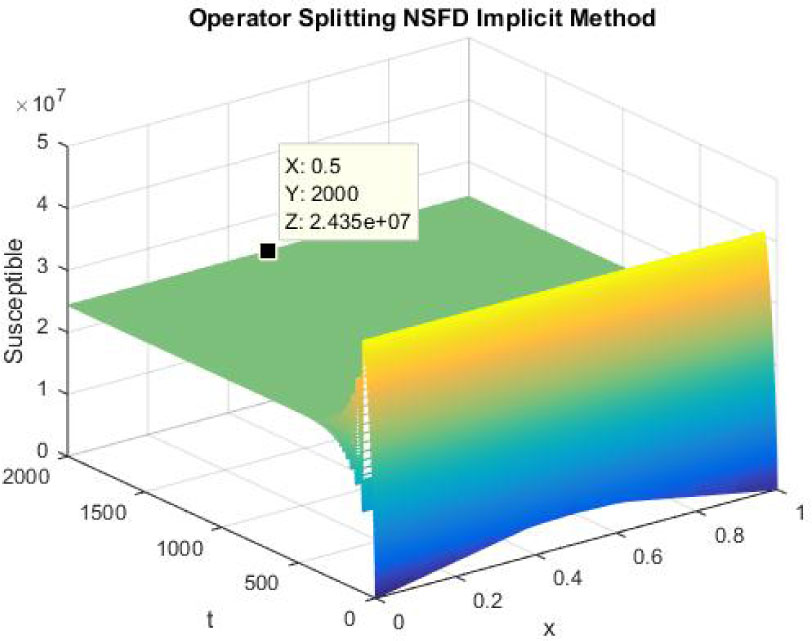
Figure 22 Mesh graph of Susceptible Individuals for EE
Figure 22

Mesh graph of Susceptible Individuals for EE

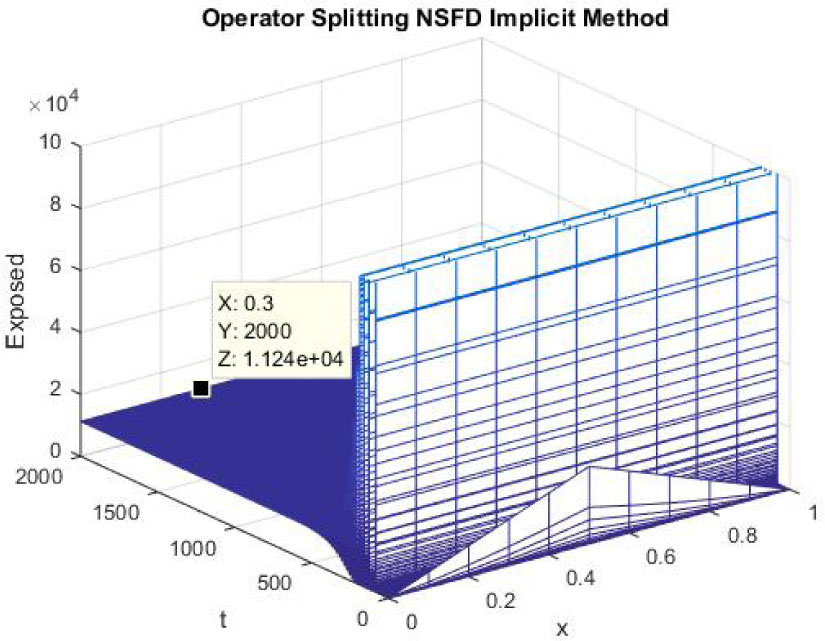
Figure 23 Mesh graph of Exposed Individuals for EE
Figure 23

Mesh graph of Exposed Individuals for EE

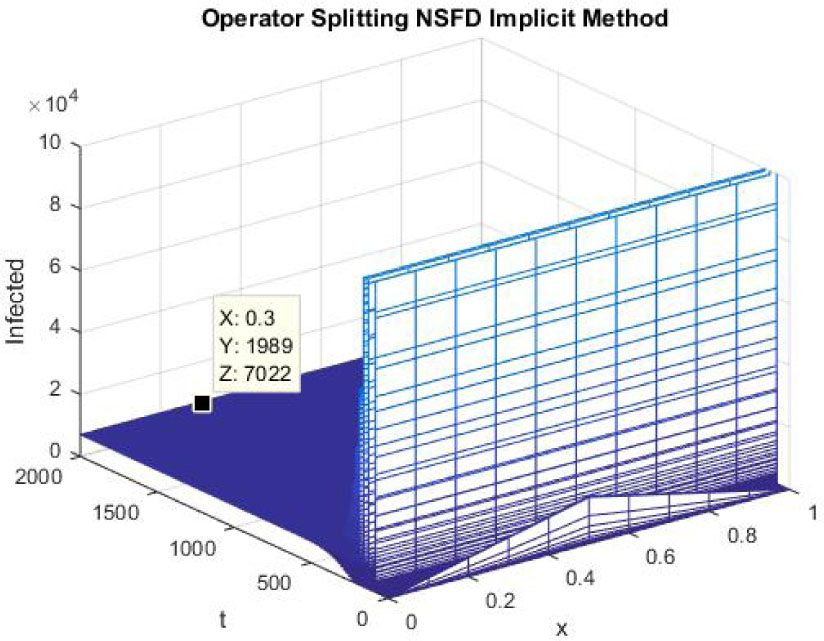
Figure 24 Mesh graph of Infected Individuals for EE
Figure 24

Mesh graph of Infected Individuals for EE

7 Conclusion

In this work, we developed two positivity preserving nonstandard finite difference schemes which did not bring contrived chaos. The proposed NSFD schemes are operator splitting FD schemes. We showed that classical operator splitting FD schemes bring the contrived chaos which lead to the numerical instabilities. We also give the stability analysis of SEIR reaction-diffusion system and find out the bifurcation value of transmission coefficient with the help of Routh-Hurwitz criteria. The proposed NSFD operator splitting schemes should prove to be of value in the solution of nonlinear continuous dynamical systems. Our future plane includes the construction of NSFD operator splitting techniques for hidden attractors in continuous dynamical systems [34, 35, 36, 37].

Acknowledgement

We are thankful to the reviewer for spending his time and giving his valuable suggestions to improve this manuscript.

References

[1] Hamer, W. H., Epidemic disease in England, Lancet, (1906), 1, 733–739.Search in Google Scholar

[2] Kaninda, A.V., Legros, D., Jataou, I.M., Malfait, P., Maisonneuve, M., Paquet, C., Moren, A., Measles vaccine Effectiveness in Standard and Early Immunization Strategies, Niger. Pediatr. Infect., (1998), 17, 1034–1039.10.1097/00006454-199811000-00014Search in Google Scholar

[3] Hethcote, H.W., Optimal ages for vaccination for Measles, Math. Biosci, (1989), 89, 29-52.10.1016/0025-5564(88)90111-3Search in Google Scholar

[4] Bakare, E. A., Adekunle, Y. A., Kadiri, K. O., Modeling and Simulation of the dynamics of the transmission of Measles, International journal of Computer Trends and Technology, (2012), 3(1), 174-177.Search in Google Scholar

[5] Okosun, K. O., Mukamuri, M., Makinde, D. O., Global stability analysis and control of leptospirosis, Open Math., (2016), 14, 567–585.10.1515/math-2016-0053Search in Google Scholar

[6] Ahmed, N., Rafiq, M., Rehman, M. A., Iqbal, M. S., Ali, M. Numerical modelling of three dimensional Brusselator reaction diffusion system, AIP Advances, (2019), 9, 01520510.1063/1.5070093Search in Google Scholar

[7] Fatima, U., Ali, M., Ahmed, N., Rafiq, M., Numerical modeling of susceptible latent breaking-out quarantine computer virus epidemic dynamics, Heliyon, (2018), 4, e00631.10.1016/j.heliyon.2018.e00631Search in Google Scholar

[8] Twizell, E.H., Wang, Y., Price, W.G., Chaos-free numerical solutions of reaction-diffusion equations, Proc.R. Soc. Lond. A, (1991), 430, 541-576.10.1098/rspa.1990.0106Search in Google Scholar

[9] Rafiq, M., Numerical Modeling of Infectious Diseases Dynamics, (PhD thesis), Lahore: University of Engineering and Technology.Search in Google Scholar

[10] Ahmed, N., Jawaz, M., Rafiq, M., Rehman, M. A., Ali, M., Ahmad, M. O., Numerical Treatment of an Epidemic Model with Spatial Diffusion, J. Appl. Environ. Biol. Sci., (2018), 8(6), 17-29.Search in Google Scholar

[11] Ahmed, N., Shahid, N., Iqbal, Z., Jawaz, M., Rafiq, M., Tahira. S. S., Ahmad, M. O., Numerical Modeling of SEIQV Epidemic Model with Saturated Incidence Rate, J. Appl. Environ. Biol. Sci., (2018), 8(4).Search in Google Scholar

[12] Ahmed, N., Rafiq, M., Rehman, M. A., Ali, M., Ahmad, M. O., Numerical Modeling of SEIR Measles Dynamics with Diffusion, Communications in Mathematics and Applications, (2018), 9(3), 315–326,Search in Google Scholar

[13] Chinviriyasit, S., Chinviriyasit, W., Numerical modeling of SIR epidemic model with diffusion, Appl. Math. Comp., (2010), 216, 395–409.10.1016/j.amc.2010.01.028Search in Google Scholar

[14] Fernández, Francisco M., On some approximate methods for nonlinear models, Applied Mathematics and Computation, (2009), 215, 168–174.10.1016/j.amc.2009.04.060Search in Google Scholar

[15] Al-Showaikh, F., Twizell, E., One-dimensional measles dynamics, Appl. Math. Comput., (2004), 152, 169-194.10.1016/S0096-3003(03)00554-XSearch in Google Scholar

[16] Mickens, R. E., Nonstandard Finite Difference Models of Differential Equations, (1994), World Scientific.10.1142/2081Search in Google Scholar

[17] Mickens, R. E., A nonstandard finite difference scheme for a Fisher PDE having nonlinear diffusion, Computer and Mathematics with Application, (2003), 45, 429-436.10.1016/S0898-1221(03)80028-7Search in Google Scholar

[18] Mickens, R. E., A nonstandard finite difference scheme for an advection-reaction equation, J. Diff. Eq. Appl., (2004), 10, 1307-1312.10.1080/10236190410001652838Search in Google Scholar

[19] Chakrabrty, A., Singh, M., Lucy, B., Ridland, P., Predator-prey model with pry- taxis and diffusion, Math. Comput. Modeling, (2007), 46, 482-498.10.1016/j.mcm.2006.10.010Search in Google Scholar

[20] Jansen, H., Twizell, E. H., An unconditionally convergent discretization of the SEIR model, MATH COMPUT SIMULAT., (2002), 58, 147-158.10.1016/S0378-4754(01)00356-1Search in Google Scholar

[21] Harwood, R. C. Operator splitting method and applications for semilinear parabolic partial differential equations (Ph.D. dissertation), (2011), Pullman: Dept. Math., Washington State Univ.Search in Google Scholar

[22] Harwood, R. C., Manoranjan, V. S., Edwards, D. B., Lead-acid battery model under discharge with a fast splitting method, IEEE Trans. Energy Convers., (2011), 26 (4), 1109-1117.10.1109/TEC.2011.2162093Search in Google Scholar

[23] Yanenko, N. N., The Method of Fractional Steps (Springer-Verlag, 1971).10.1007/978-3-642-65108-3Search in Google Scholar

[24] Zharnitsky, V., Averaging for split-step scheme, Nonlinearity, (2003), 16, 1359-1366.10.1088/0951-7715/16/4/310Search in Google Scholar

[25] Ansarizadeh, F., Singh, M., Richards, D., Modelling of tumor cells regression in response to chemotherapeutic treatment, Applied Mathematical Modeling, (2017), 48, 96-112.10.1016/j.apm.2017.03.045Search in Google Scholar

[26] Naheed, A., Singh, M., Lucy, D., Effect of Treatment on Transmission Dynamics of SARS Epidemic, J. Infect. Non. Infect. Dis., (2016).10.24966/INID-8654/100016Search in Google Scholar

[27] Naheed, A., A Study of Spatio-Temporal Spread of Infectious Disease:SARS, (Ph.D. thesis), (2015),, Australia: Swinburne University of Technology.Search in Google Scholar

[28] Naheed, A., Singh, M., Lucy, D., Numerical study of SARS epidemic model with the inclusion of diffusion in the system, Applied Mathematics and computation, (2014), 229, 480-498.10.1016/j.amc.2013.12.062Search in Google Scholar PubMed PubMed Central

[29] Samsuzzoha, Md., A Study on numerical solutions of epidemic models, (2012), (Ph.D. thesis), Australia: Swinburne University of Technology.Search in Google Scholar

[30] Wang, H. Q., Numerical studies on the split-step finite difference method for nonlinear Schrödinger equations, Applied Mathematics and Computation, (2005), 170, 17-3510.1016/j.amc.2004.10.066Search in Google Scholar

[31] Manna, K., Chakrabarty, S. P., Global stability and a non-standard finite difference scheme for a diffusion driven HBV model with capsids, J. Differ. Equ. Appl., (2015), 21, 918-933.10.1080/10236198.2015.1056524Search in Google Scholar

[32] Qin, W., Wang, L., Ding, X., A non-standard finite difference method for a hepatitis B virus infection model with spatial diffusion, J. Differ. Equ. Appl., (2014), 20(12), 1641–1651.10.1080/10236198.2014.968565Search in Google Scholar

[33] Fujimoto, T., Ranade, R., Two characterizations of inverse–positive matrices: The Hawkins–Simon condition and the Le Chatelier–Braun principle, Electron. J. Linear Algebra, (2004), 11, 59–65.10.13001/1081-3810.1122Search in Google Scholar

[34] Wei, Z.C., Moroz, I., Sprott, J.C., Akgul, A., Zhang, W., Hidden hyperchaos and electronic circuit application in a 5D self-exciting homopolar disc dynamo, Chaos, (2017), 27, 033101.10.1063/1.4977417Search in Google Scholar PubMed

[35] Wei, Z.C., Moroz, I., Sprott, J.C., Wang, Z., Zhang, W., Detecting hidden chaotic regions and complex dynamics in the self-exciting homopolar disc dynamo, Int. J. Bifurc. Chaos, (2017), 27, 1730008.10.1142/S0218127417300087Search in Google Scholar

[36] Wei, Z., Yu, P., Zhang, W., Minghui Yao, Study of hidden attractors, multiple limit cycles from Hopf bifurcation and boundedness of motion in the generalized hyperchaotic Rabinovich system, Nonlinear Dyn., (2015), 10.1007/s11071-015-2144-8.10.1007/s11071-015-2144-8Search in Google Scholar

[37] Wei, Z., Zhua B., Yanga, J., Perc, M., Slavinec, M., Bifurcation analysis of two disc dynamos with viscous friction and multiple time delays, Applied Mathematics and Computation, (2019), 347, 265–28110.1016/j.amc.2018.10.090Search in Google Scholar
Received: 2018-07-15
Accepted: 2019-02-14
Published Online: 2019-04-29

© 2019 Ahmed et al., published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 Public License.

Articles in the same Issue

  1. Regular Articles
  2. On the Gevrey ultradifferentiability of weak solutions of an abstract evolution equation with a scalar type spectral operator of orders less than one
  3. Centralizers of automorphisms permuting free generators
  4. Extreme points and support points of conformal mappings
  5. Arithmetical properties of double Möbius-Bernoulli numbers
  6. The product of quasi-ideal refined generalised quasi-adequate transversals
  7. Characterizations of the Solution Sets of Generalized Convex Fuzzy Optimization Problem
  8. Augmented, free and tensor generalized digroups
  9. Time-dependent attractor of wave equations with nonlinear damping and linear memory
  10. A new smoothing method for solving nonlinear complementarity problems
  11. Almost periodic solution of a discrete competitive system with delays and feedback controls
  12. On a problem of Hasse and Ramachandra
  13. Hopf bifurcation and stability in a Beddington-DeAngelis predator-prey model with stage structure for predator and time delay incorporating prey refuge
  14. A note on the formulas for the Drazin inverse of the sum of two matrices
  15. Completeness theorem for probability models with finitely many valued measure
  16. Periodic solution for ϕ-Laplacian neutral differential equation
  17. Asymptotic orbital shadowing property for diffeomorphisms
  18. Modular equations of a continued fraction of order six
  19. Solutions with concentration and cavitation to the Riemann problem for the isentropic relativistic Euler system for the extended Chaplygin gas
  20. Stability Problems and Analytical Integration for the Clebsch’s System
  21. Topological Indices of Para-line Graphs of V-Phenylenic Nanostructures
  22. On split Lie color triple systems
  23. Triangular Surface Patch Based on Bivariate Meyer-König-Zeller Operator
  24. Generators for maximal subgroups of Conway group Co1
  25. Positivity preserving operator splitting nonstandard finite difference methods for SEIR reaction diffusion model
  26. Characterizations of Convex spaces and Anti-matroids via Derived Operators
  27. On Partitions and Arf Semigroups
  28. Arithmetic properties for Andrews’ (48,6)- and (48,18)-singular overpartitions
  29. A concise proof to the spectral and nuclear norm bounds through tensor partitions
  30. A categorical approach to abstract convex spaces and interval spaces
  31. Dynamics of two-species delayed competitive stage-structured model described by differential-difference equations
  32. Parity results for broken 11-diamond partitions
  33. A new fourth power mean of two-term exponential sums
  34. The new operations on complete ideals
  35. Soft covering based rough graphs and corresponding decision making
  36. Complete convergence for arrays of ratios of order statistics
  37. Sufficient and necessary conditions of convergence for ρ͠ mixing random variables
  38. Attractors of dynamical systems in locally compact spaces
  39. Random attractors for stochastic retarded strongly damped wave equations with additive noise on bounded domains
  40. Statistical approximation properties of λ-Bernstein operators based on q-integers
  41. An investigation of fractional Bagley-Torvik equation
  42. Pentavalent arc-transitive Cayley graphs on Frobenius groups with soluble vertex stabilizer
  43. On the hybrid power mean of two kind different trigonometric sums
  44. Embedding of Supplementary Results in Strong EMT Valuations and Strength
  45. On Diophantine approximation by unlike powers of primes
  46. A General Version of the Nullstellensatz for Arbitrary Fields
  47. A new representation of α-openness, α-continuity, α-irresoluteness, and α-compactness in L-fuzzy pretopological spaces
  48. Random Polygons and Estimations of π
  49. The optimal pebbling of spindle graphs
  50. MBJ-neutrosophic ideals of BCK/BCI-algebras
  51. A note on the structure of a finite group G having a subgroup H maximal in 〈H, Hg〉
  52. A fuzzy multi-objective linear programming with interval-typed triangular fuzzy numbers
  53. Variational-like inequalities for n-dimensional fuzzy-vector-valued functions and fuzzy optimization
  54. Stability property of the prey free equilibrium point
  55. Rayleigh-Ritz Majorization Error Bounds for the Linear Response Eigenvalue Problem
  56. Hyper-Wiener indices of polyphenyl chains and polyphenyl spiders
  57. Razumikhin-type theorem on time-changed stochastic functional differential equations with Markovian switching
  58. Fixed Points of Meromorphic Functions and Their Higher Order Differences and Shifts
  59. Properties and Inference for a New Class of Generalized Rayleigh Distributions with an Application
  60. Nonfragile observer-based guaranteed cost finite-time control of discrete-time positive impulsive switched systems
  61. Empirical likelihood confidence regions of the parameters in a partially single-index varying-coefficient model
  62. Algebraic loop structures on algebra comultiplications
  63. Two weight estimates for a class of (p, q) type sublinear operators and their commutators
  64. Dynamic of a nonautonomous two-species impulsive competitive system with infinite delays
  65. 2-closures of primitive permutation groups of holomorph type
  66. Monotonicity properties and inequalities related to generalized Grötzsch ring functions
  67. Variation inequalities related to Schrödinger operators on weighted Morrey spaces
  68. Research on cooperation strategy between government and green supply chain based on differential game
  69. Extinction of a two species competitive stage-structured system with the effect of toxic substance and harvesting
  70. *-Ricci soliton on (κ, μ)′-almost Kenmotsu manifolds
  71. Some improved bounds on two energy-like invariants of some derived graphs
  72. Pricing under dynamic risk measures
  73. Finite groups with star-free noncyclic graphs
  74. A degree approach to relationship among fuzzy convex structures, fuzzy closure systems and fuzzy Alexandrov topologies
  75. S-shaped connected component of radial positive solutions for a prescribed mean curvature problem in an annular domain
  76. On Diophantine equations involving Lucas sequences
  77. A new way to represent functions as series
  78. Stability and Hopf bifurcation periodic orbits in delay coupled Lotka-Volterra ring system
  79. Some remarks on a pair of seemingly unrelated regression models
  80. Lyapunov stable homoclinic classes for smooth vector fields
  81. Stabilizers in EQ-algebras
  82. The properties of solutions for several types of Painlevé equations concerning fixed-points, zeros and poles
  83. Spectrum perturbations of compact operators in a Banach space
  84. The non-commuting graph of a non-central hypergroup
  85. Lie symmetry analysis and conservation law for the equation arising from higher order Broer-Kaup equation
  86. Positive solutions of the discrete Dirichlet problem involving the mean curvature operator
  87. Dislocated quasi cone b-metric space over Banach algebra and contraction principles with application to functional equations
  88. On the Gevrey ultradifferentiability of weak solutions of an abstract evolution equation with a scalar type spectral operator on the open semi-axis
  89. Differential polynomials of L-functions with truncated shared values
  90. Exclusion sets in the S-type eigenvalue localization sets for tensors
  91. Continuous linear operators on Orlicz-Bochner spaces
  92. Non-trivial solutions for Schrödinger-Poisson systems involving critical nonlocal term and potential vanishing at infinity
  93. Characterizations of Benson proper efficiency of set-valued optimization in real linear spaces
  94. A quantitative obstruction to collapsing surfaces
  95. Dynamic behaviors of a Lotka-Volterra type predator-prey system with Allee effect on the predator species and density dependent birth rate on the prey species
  96. Coexistence for a kind of stochastic three-species competitive models
  97. Algebraic and qualitative remarks about the family yy′ = (αxm+k–1 + βxm–k–1)y + γx2m–2k–1
  98. On the two-term exponential sums and character sums of polynomials
  99. F-biharmonic maps into general Riemannian manifolds
  100. Embeddings of harmonic mixed norm spaces on smoothly bounded domains in ℝn
  101. Asymptotic behavior for non-autonomous stochastic plate equation on unbounded domains
  102. Power graphs and exchange property for resolving sets
  103. On nearly Hurewicz spaces
  104. Least eigenvalue of the connected graphs whose complements are cacti
  105. Determinants of two kinds of matrices whose elements involve sine functions
  106. A characterization of translational hulls of a strongly right type B semigroup
  107. Common fixed point results for two families of multivalued A–dominated contractive mappings on closed ball with applications
  108. Lp estimates for maximal functions along surfaces of revolution on product spaces
  109. Path-induced closure operators on graphs for defining digital Jordan surfaces
  110. Irreducible modules with highest weight vectors over modular Witt and special Lie superalgebras
  111. Existence of periodic solutions with prescribed minimal period of a 2nth-order discrete system
  112. Injective hulls of many-sorted ordered algebras
  113. Random uniform exponential attractor for stochastic non-autonomous reaction-diffusion equation with multiplicative noise in ℝ3
  114. Global properties of virus dynamics with B-cell impairment
  115. The monotonicity of ratios involving arc tangent function with applications
  116. A family of Cantorvals
  117. An asymptotic property of branching-type overloaded polling networks
  118. Almost periodic solutions of a commensalism system with Michaelis-Menten type harvesting on time scales
  119. Explicit order 3/2 Runge-Kutta method for numerical solutions of stochastic differential equations by using Itô-Taylor expansion
  120. L-fuzzy ideals and L-fuzzy subalgebras of Novikov algebras
  121. L-topological-convex spaces generated by L-convex bases
  122. An optimal fourth-order family of modified Cauchy methods for finding solutions of nonlinear equations and their dynamical behavior
  123. New error bounds for linear complementarity problems of Σ-SDD matrices and SB-matrices
  124. Hankel determinant of order three for familiar subsets of analytic functions related with sine function
  125. On some automorphic properties of Galois traces of class invariants from generalized Weber functions of level 5
  126. Results on existence for generalized nD Navier-Stokes equations
  127. Regular Banach space net and abstract-valued Orlicz space of range-varying type
  128. Some properties of pre-quasi operator ideal of type generalized Cesáro sequence space defined by weighted means
  129. On a new convergence in topological spaces
  130. On a fixed point theorem with application to functional equations
  131. Coupled system of a fractional order differential equations with weighted initial conditions
  132. Rough quotient in topological rough sets
  133. Split Hausdorff internal topologies on posets
  134. A preconditioned AOR iterative scheme for systems of linear equations with L-matrics
  135. New handy and accurate approximation for the Gaussian integrals with applications to science and engineering
  136. Special Issue on Graph Theory (GWGT 2019)
  137. The general position problem and strong resolving graphs
  138. Connected domination game played on Cartesian products
  139. On minimum algebraic connectivity of graphs whose complements are bicyclic
  140. A novel method to construct NSSD molecular graphs
https://doi.org/10.1515/math-2019-0027
Keywords for this article
SEIR reaction diffusion model; operator splitting techniques; positivity; bifurcation value
Creative Commons
BY 4.0

Articles in the same Issue

  1. Regular Articles
  2. On the Gevrey ultradifferentiability of weak solutions of an abstract evolution equation with a scalar type spectral operator of orders less than one
  3. Centralizers of automorphisms permuting free generators
  4. Extreme points and support points of conformal mappings
  5. Arithmetical properties of double Möbius-Bernoulli numbers
  6. The product of quasi-ideal refined generalised quasi-adequate transversals
  7. Characterizations of the Solution Sets of Generalized Convex Fuzzy Optimization Problem
  8. Augmented, free and tensor generalized digroups
  9. Time-dependent attractor of wave equations with nonlinear damping and linear memory
  10. A new smoothing method for solving nonlinear complementarity problems
  11. Almost periodic solution of a discrete competitive system with delays and feedback controls
  12. On a problem of Hasse and Ramachandra
  13. Hopf bifurcation and stability in a Beddington-DeAngelis predator-prey model with stage structure for predator and time delay incorporating prey refuge
  14. A note on the formulas for the Drazin inverse of the sum of two matrices
  15. Completeness theorem for probability models with finitely many valued measure
  16. Periodic solution for ϕ-Laplacian neutral differential equation
  17. Asymptotic orbital shadowing property for diffeomorphisms
  18. Modular equations of a continued fraction of order six
  19. Solutions with concentration and cavitation to the Riemann problem for the isentropic relativistic Euler system for the extended Chaplygin gas
  20. Stability Problems and Analytical Integration for the Clebsch’s System
  21. Topological Indices of Para-line Graphs of V-Phenylenic Nanostructures
  22. On split Lie color triple systems
  23. Triangular Surface Patch Based on Bivariate Meyer-König-Zeller Operator
  24. Generators for maximal subgroups of Conway group Co1
  25. Positivity preserving operator splitting nonstandard finite difference methods for SEIR reaction diffusion model
  26. Characterizations of Convex spaces and Anti-matroids via Derived Operators
  27. On Partitions and Arf Semigroups
  28. Arithmetic properties for Andrews’ (48,6)- and (48,18)-singular overpartitions
  29. A concise proof to the spectral and nuclear norm bounds through tensor partitions
  30. A categorical approach to abstract convex spaces and interval spaces
  31. Dynamics of two-species delayed competitive stage-structured model described by differential-difference equations
  32. Parity results for broken 11-diamond partitions
  33. A new fourth power mean of two-term exponential sums
  34. The new operations on complete ideals
  35. Soft covering based rough graphs and corresponding decision making
  36. Complete convergence for arrays of ratios of order statistics
  37. Sufficient and necessary conditions of convergence for ρ͠ mixing random variables
  38. Attractors of dynamical systems in locally compact spaces
  39. Random attractors for stochastic retarded strongly damped wave equations with additive noise on bounded domains
  40. Statistical approximation properties of λ-Bernstein operators based on q-integers
  41. An investigation of fractional Bagley-Torvik equation
  42. Pentavalent arc-transitive Cayley graphs on Frobenius groups with soluble vertex stabilizer
  43. On the hybrid power mean of two kind different trigonometric sums
  44. Embedding of Supplementary Results in Strong EMT Valuations and Strength
  45. On Diophantine approximation by unlike powers of primes
  46. A General Version of the Nullstellensatz for Arbitrary Fields
  47. A new representation of α-openness, α-continuity, α-irresoluteness, and α-compactness in L-fuzzy pretopological spaces
  48. Random Polygons and Estimations of π
  49. The optimal pebbling of spindle graphs
  50. MBJ-neutrosophic ideals of BCK/BCI-algebras
  51. A note on the structure of a finite group G having a subgroup H maximal in 〈H, Hg〉
  52. A fuzzy multi-objective linear programming with interval-typed triangular fuzzy numbers
  53. Variational-like inequalities for n-dimensional fuzzy-vector-valued functions and fuzzy optimization
  54. Stability property of the prey free equilibrium point
  55. Rayleigh-Ritz Majorization Error Bounds for the Linear Response Eigenvalue Problem
  56. Hyper-Wiener indices of polyphenyl chains and polyphenyl spiders
  57. Razumikhin-type theorem on time-changed stochastic functional differential equations with Markovian switching
  58. Fixed Points of Meromorphic Functions and Their Higher Order Differences and Shifts
  59. Properties and Inference for a New Class of Generalized Rayleigh Distributions with an Application
  60. Nonfragile observer-based guaranteed cost finite-time control of discrete-time positive impulsive switched systems
  61. Empirical likelihood confidence regions of the parameters in a partially single-index varying-coefficient model
  62. Algebraic loop structures on algebra comultiplications
  63. Two weight estimates for a class of (p, q) type sublinear operators and their commutators
  64. Dynamic of a nonautonomous two-species impulsive competitive system with infinite delays
  65. 2-closures of primitive permutation groups of holomorph type
  66. Monotonicity properties and inequalities related to generalized Grötzsch ring functions
  67. Variation inequalities related to Schrödinger operators on weighted Morrey spaces
  68. Research on cooperation strategy between government and green supply chain based on differential game
  69. Extinction of a two species competitive stage-structured system with the effect of toxic substance and harvesting
  70. *-Ricci soliton on (κ, μ)′-almost Kenmotsu manifolds
  71. Some improved bounds on two energy-like invariants of some derived graphs
  72. Pricing under dynamic risk measures
  73. Finite groups with star-free noncyclic graphs
  74. A degree approach to relationship among fuzzy convex structures, fuzzy closure systems and fuzzy Alexandrov topologies
  75. S-shaped connected component of radial positive solutions for a prescribed mean curvature problem in an annular domain
  76. On Diophantine equations involving Lucas sequences
  77. A new way to represent functions as series
  78. Stability and Hopf bifurcation periodic orbits in delay coupled Lotka-Volterra ring system
  79. Some remarks on a pair of seemingly unrelated regression models
  80. Lyapunov stable homoclinic classes for smooth vector fields
  81. Stabilizers in EQ-algebras
  82. The properties of solutions for several types of Painlevé equations concerning fixed-points, zeros and poles
  83. Spectrum perturbations of compact operators in a Banach space
  84. The non-commuting graph of a non-central hypergroup
  85. Lie symmetry analysis and conservation law for the equation arising from higher order Broer-Kaup equation
  86. Positive solutions of the discrete Dirichlet problem involving the mean curvature operator
  87. Dislocated quasi cone b-metric space over Banach algebra and contraction principles with application to functional equations
  88. On the Gevrey ultradifferentiability of weak solutions of an abstract evolution equation with a scalar type spectral operator on the open semi-axis
  89. Differential polynomials of L-functions with truncated shared values
  90. Exclusion sets in the S-type eigenvalue localization sets for tensors
  91. Continuous linear operators on Orlicz-Bochner spaces
  92. Non-trivial solutions for Schrödinger-Poisson systems involving critical nonlocal term and potential vanishing at infinity
  93. Characterizations of Benson proper efficiency of set-valued optimization in real linear spaces
  94. A quantitative obstruction to collapsing surfaces
  95. Dynamic behaviors of a Lotka-Volterra type predator-prey system with Allee effect on the predator species and density dependent birth rate on the prey species
  96. Coexistence for a kind of stochastic three-species competitive models
  97. Algebraic and qualitative remarks about the family yy′ = (αxm+k–1 + βxm–k–1)y + γx2m–2k–1
  98. On the two-term exponential sums and character sums of polynomials
  99. F-biharmonic maps into general Riemannian manifolds
  100. Embeddings of harmonic mixed norm spaces on smoothly bounded domains in ℝn
  101. Asymptotic behavior for non-autonomous stochastic plate equation on unbounded domains
  102. Power graphs and exchange property for resolving sets
  103. On nearly Hurewicz spaces
  104. Least eigenvalue of the connected graphs whose complements are cacti
  105. Determinants of two kinds of matrices whose elements involve sine functions
  106. A characterization of translational hulls of a strongly right type B semigroup
  107. Common fixed point results for two families of multivalued A–dominated contractive mappings on closed ball with applications
  108. Lp estimates for maximal functions along surfaces of revolution on product spaces
  109. Path-induced closure operators on graphs for defining digital Jordan surfaces
  110. Irreducible modules with highest weight vectors over modular Witt and special Lie superalgebras
  111. Existence of periodic solutions with prescribed minimal period of a 2nth-order discrete system
  112. Injective hulls of many-sorted ordered algebras
  113. Random uniform exponential attractor for stochastic non-autonomous reaction-diffusion equation with multiplicative noise in ℝ3
  114. Global properties of virus dynamics with B-cell impairment
  115. The monotonicity of ratios involving arc tangent function with applications
  116. A family of Cantorvals
  117. An asymptotic property of branching-type overloaded polling networks
  118. Almost periodic solutions of a commensalism system with Michaelis-Menten type harvesting on time scales
  119. Explicit order 3/2 Runge-Kutta method for numerical solutions of stochastic differential equations by using Itô-Taylor expansion
  120. L-fuzzy ideals and L-fuzzy subalgebras of Novikov algebras
  121. L-topological-convex spaces generated by L-convex bases
  122. An optimal fourth-order family of modified Cauchy methods for finding solutions of nonlinear equations and their dynamical behavior
  123. New error bounds for linear complementarity problems of Σ-SDD matrices and SB-matrices
  124. Hankel determinant of order three for familiar subsets of analytic functions related with sine function
  125. On some automorphic properties of Galois traces of class invariants from generalized Weber functions of level 5
  126. Results on existence for generalized nD Navier-Stokes equations
  127. Regular Banach space net and abstract-valued Orlicz space of range-varying type
  128. Some properties of pre-quasi operator ideal of type generalized Cesáro sequence space defined by weighted means
  129. On a new convergence in topological spaces
  130. On a fixed point theorem with application to functional equations
  131. Coupled system of a fractional order differential equations with weighted initial conditions
  132. Rough quotient in topological rough sets
  133. Split Hausdorff internal topologies on posets
  134. A preconditioned AOR iterative scheme for systems of linear equations with L-matrics
  135. New handy and accurate approximation for the Gaussian integrals with applications to science and engineering
  136. Special Issue on Graph Theory (GWGT 2019)
  137. The general position problem and strong resolving graphs
  138. Connected domination game played on Cartesian products
  139. On minimum algebraic connectivity of graphs whose complements are bicyclic
  140. A novel method to construct NSSD molecular graphs
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 24.12.2025 from https://www.degruyterbrill.com/document/doi/10.1515/math-2019-0027/html
Scroll to top button