A concise proof to the spectral and nuclear norm bounds through tensor partitions

Xu Kong

doi:10.1515/math-2019-0028

Artikel Open Access

A concise proof to the spectral and nuclear norm bounds through tensor partitions

Xu Kong

Veröffentlicht/Copyright: 16. Mai 2019

Veröffentlicht von

Veröffentlichen auch Sie bei De Gruyter Brill

Manuskript einreichen Informationen für Autor*innen Erkunden Sie dieses Fachgebiet

$Open Mathematics$

Aus der Zeitschrift Open Mathematics Band 17 Heft 1

Abstract

On estimations of the lower and upper bounds for the spectral and nuclear norm of a tensor, Li established neat bounds for the two norms based on regular tensor partitions, and proposed a conjecture for the same bounds to be hold based on general tensor partitions [Z. Li, Bounds on the spectral norm and the nuclear norm of a tensor based on tensor partition, SIAM J. Matrix Anal. Appl., 37 (2016), pp. 1440-1452]. Later, Chen and Li provided a solution to the conjecture [Chen B., Li Z., On the tensor spectral p-norm and its dual norm via partitions]. In this short paper, we present a concise and different proof for the validity of the conjecture, which also offers a new and simpler proof to the bounds of the spectral and nuclear norms established by Li for regular tensor partitions. Two numerical examples are provided to illustrate tightness of these bounds.

Keywords: tensor norm; spectral norm; nuclear norm; tensor partition

MSC 2010: 15A60; 15A69

1 Introduction

Tensor is the main subject in multilinear algebra [1, 2, 3, 4, 5, 6]. Let ℝ be the field of real numbers. Specially, a tensor 𝓣 = (t_{i₁i₂⋯i_d}) ∈ ℝ^{n₁×n₂×⋯×n_d} is a d-way array, i.e., its entries t_{i₁i₂⋯i_d} are represented via d indices, say i₁, i₂, ⋯, i_d with each index ranging from 1 to n_j, 1 ≤ j ≤ d. 𝓣 is also called as an n₁ × n₂ × ⋯ × n_d tensor. Similar to the definition of the submatrix of a matrix, a p₁ × p₂ × ⋯ × p_d subtensor of a tensor 𝓣 ∈ ℝ^{n₁×n₂×⋯×n_d} is a p₁ × p₂ × ⋯ × p_d tensor formed by taking a block of the entries from the original tensor 𝓣.

Some general notations are in place: tensors are denoted by the calligraphic letters (e.g. 𝓣 or 𝓧), scalars are denoted by plain letters, and matrices and vectors are denoted by bold letters (e.g. X and x).

Let ∥⋅∥₁, ∥⋅∥₂, and ∥⋅∥_∞ denote the conventional 1-norm, 2-norm, and ∞-norm of a vector, respectively, i.e.,

∥x∥1=∑i=1n|xi|,∥x∥2=∑i=1nxi2,

and

∥x∥∞=max1≤i≤n{|xi|},

where x = (x₁, x₂, ⋯, x_n)^T ∈ ℝⁿ.

Definition 1.1

Let 𝓣 ∈ ℝ^{n₁×n₂×⋯×n_d}. The spectral norm of 𝓣 denoted by ∥𝓣∥_σ is defined as

∥T∥σ=maxxj∈Rnj,∥xj∥2=1,1≤j≤d〈T,x1∘x2∘⋯∘xd〉1/2,

where 〈⋅, ⋅〉 is the classical Euclidean inner product, and the symbol “∘” denotes the outer product operation of vectors such that the entries of x₁∘ x₂ ∘ ⋯ ∘ x_d are x_i₁1x_i₂2 ⋯ x_{i_dd}, and x_k = (x_1k, x_2k, ⋯, x_{n_kk})^T, 1 ≤ i_k ≤ n_k, and 1 ≤ k ≤ d.

Definition 1.2

Let 𝓣 ∈ ℝ^{n₁×n₂×⋯×n_d}. The nuclear norm of 𝓣 denoted by ∥𝓣∥_∗ is defined as

∥T∥∗=maxX∈Rn1×n2×⋯×nd,∥X∥σ≤1〈T,X〉 =maxX∈Rn1×n2×⋯×nd,∥X∥σ=1〈T,X〉.

With the wide applications of the spectral and nuclear norm of a matrix, the research on the tensor spectral and nuclear norm has also attracted much attention recently. Unlike the computation of the spectral and nuclear norm of a matrix that can be done easily, the tensor spectral and nuclear norm are both NP-hard to compute; see [7] and [8]. Therefore, estimating these bounds, especially the polynomial-time approximation bounds has been a hot issue [7, 8, 9, 10, 11, 12, 13, 14].

In [15], Li proposed an efficient way for the estimation of the tensor spectral and nuclear norms based on tensor partitions, which is defined as follows.

Definition 1.3

[15] A partition {𝓣₁, 𝓣₂, ⋯, 𝓣_m} is called a general tensor partition of a tensor 𝓣 ∈ ℝ^{n₁×n₂×⋯×n_d} if

every 𝓣_j (j = 1, 2, ⋯, m) is a subtensor of 𝓣,
every pair of subtensors {𝓣_i, 𝓣_j} with i ≠ j has no common entry of 𝓣, and
every entry of 𝓣 belongs to one of the subtensors in {𝓣₁, 𝓣₂, ⋯, 𝓣_m.

Furthermore, let 𝓧 ∈ ℝ^{n₁×n₂×⋯×n_d} and {𝓧₁, 𝓧₂, ⋯, 𝓧_m} be a general tensor partition of 𝓧. If each 𝓧_j has the same partition way as 𝓣_j for 1 ≤ j ≤ m, then 𝓣 and 𝓧 are said to have the same partition pattern.

Li also proposed a special tensor partition called regular tensor partition based on which the bounds of tensor norms were established [15]. The partition is obtained via several tensor cuts. We omit the details as it is not relevant to our discussion here. For illustration, Fig. 1 depicts a general tensor partition of a third order tensor.

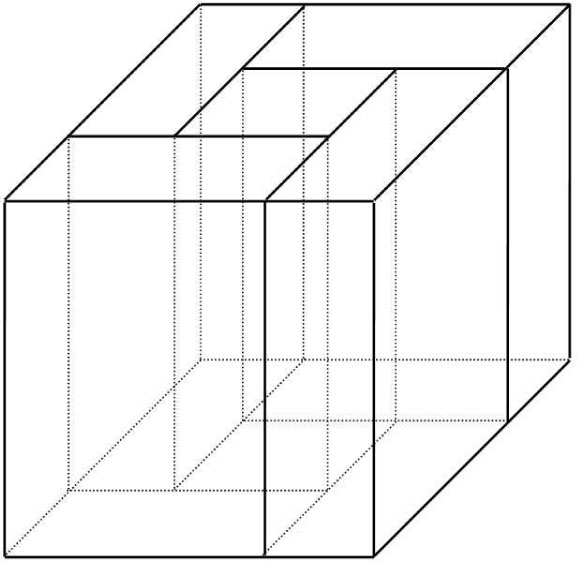
$Figure 1 A general tensor partition of a third order tensor.$

Figure 1

A general tensor partition of a third order tensor.

For a general tensor partition of a tensor, Li presented the following conjecture, which was answered in affirmative via a lengthy proof and also extended to a generalized tensor spectral and nuclear norms in a recent manuscript [11]. Some applications and general tightness results on rank-one tensors are discussed as well.

Conjecture 1.1

[15] If {𝓣₁, 𝓣₂, ⋯, 𝓣_m} is a general tensor partition of a tensor 𝓣 ∈ ℝ^{n₁×n₂×⋯×n_d}, then

∥(∥T1∥σ,∥T2∥σ,⋯,∥Tm∥σ)T∥∞≤∥T∥σ≤∥(∥T1∥σ,∥T2∥σ,⋯,∥Tm∥σ)T∥2,

and

∥(∥T1∥∗,∥T2∥∗,⋯,∥Tm∥∗)T∥2≤∥T∥∗≤∥(∥T1∥∗,∥T2∥∗,⋯,∥Tm∥∗)T∥1.

In the current paper, we, in an independent work^[1], propose a much simpler way to prove this conjecture. We also provide some nontrivial examples to show the tightness of these bounds. Since a regular tensor partition is a special type of a general tensor partition, naturally, the way for the solution to the conjecture also offers a new proof to the bounds for the spectral and nuclear norm established in [15].

The rest of this paper is organized as follows: In Section 2, we simply recall some definitions and results required for the subsequent sections. In Section 3, the main results of the paper are presented. A short conclusion is given in Section 4.

2 Preliminaries

The main objective of this section is to review some basic definitions and simple results relating to the tensor.

Definition 2.1

Let 𝓣 = (t_{i₁i₂⋯i_d}) ∈ ℝ^{n₁×n₂×⋯×n_d}. The Frobenius norm of 𝓣 denoted by ∥𝓣∥_F is defined as

∥T∥F=〈T,T〉1/2=∑i1=1n1∑i2=1n2⋯∑id=1nd(ti1i2⋯id)21/2.

Definition 2.2

A tensor 𝓦 = (w_{i₁i₂⋯i_d}) ∈ ℝ^{n₁×n₂×⋯×n_d} is called a rank-one tensor if there exist nonzero vectors w_j ∈ ℝ^n_j (1 ≤ j ≤ d) such that

W=w1∘w2∘⋯∘wd.

Definition 2.3

Let 𝓣 = (t_{i₁i₂⋯i_d}) ∈ ℝ^{n₁×n₂×⋯×n_d}. u₁ ∘ u₂ ∘ ⋯ ∘ u_d is called as a best rank-one approximation of 𝓣 if

∥T−u1∘u2∘⋯∘ud∥F=minxj∈Rnj,1≤j≤d∥T−x1∘x2∘⋯∘xd∥F. (1)

Relating to the spectral norm of a tensor and the best rank-one approximation tensor, the following conclusion is straightforward.

Lemma 2.1

[8, 16] Let 𝓣 ∈ ℝ^{n₁×n₂×⋯×n_d}. Suppose that u₁ ∘ u₂ ∘ ⋯ ∘ u_d is a best rank-one approximation to 𝓣, then

∥T∥σ=∥u1∘u2∘⋯∘ud∥F

and

∥T−u1∘u2∘⋯∘ud∥F2=∥T∥F2−∥u1∘u2∘⋯∘ud∥F2=∥T∥F2−∥T∥σ2.

For the sake of convenience, we may write an n₁ × n₂ × n₃ tensor 𝓣 in the following form (T₁|T₂| ⋯ |T_n₃), where T_i ∈ ℝ^n₁×₂, 1 ≤ i ≤ n₃. For example, let 𝓣 = (t_ijk) ∈ ℝ^2×3×3. Then 𝓣 is expressed as the following form:

T=t111t121t131t211t221t231t112t122t132t212t222t232t113t123t133t213t223t233.

3 Main results

In this section, we provide a new proof to the Conjecture 1.1. Meanwhile, simple examples are given to illustrate the main result.

Let us first propose a lemma.

Lemma 3.1

Let 𝓦 ∈ ℝ^{n₁×n₂×⋯×n_d} be a rank-one tensor. If {𝓦₁, 𝓦₂, ⋯, 𝓦_m} is a general tensor partition of 𝓦, then every 𝓦_i (i = 1, 2, ⋯, m) is a rank-one tensor or a zero tensor.

Proof

Since 𝓦 is a rank-one tensor, 𝓦 can be written as

W=w1∘w2∘⋯∘wd, (2)

where w_j ∈ ℝ^n_j, j = 1, 2, ⋯, d.

According to the definition of the general partition, we know that every 𝓦_i (i = 1, 2, ⋯, m) is a subtensor of 𝓦. Without loss of generality, suppose that 𝓦_i ∈ ℝ^{n_i,1×n_i,2×⋯×n_i,d}, then it follows from (2) that 𝓦_i can be written as the following form:

Wi=wi,1∘wi,2∘⋯∘wi,d,

where every w_i,j ∈ ℝ^n_i,j is a subvector of w_j, i = 1, 2, ⋯, m and j = 1, 2, ⋯, d. This implies that every 𝓦_i (i = 1, 2, ⋯, m) is a rank-one tensor or a zero tensor. □

We are ready to prove the Conjecture 1.1. For the sake of clarity, the Conjecture 1.1 is written as the Theorem 3.1.

Theorem 3.1

If {𝓣₁, 𝓣₂, ⋯, 𝓣_m} is a general tensor partition of a tensor 𝓣 ∈ ℝ^{n₁×n₂×⋯×n_d}, then

∥(∥T1∥σ,∥T2∥σ,⋯,∥Tm∥σ)T∥∞≤∥T∥σ≤∥(∥T1∥σ,∥T2∥σ,⋯,∥Tm∥σ)T∥2, (3)

and

∥(∥T1∥∗,∥T2∥∗,⋯,∥Tm∥∗)T∥2≤∥T∥∗≤∥(∥T1∥∗,∥T2∥∗,⋯,∥Tm∥∗)T∥1. (4)

Proof

Without loss of generality, we suppose that

∥(∥T1∥σ,∥T2∥σ,⋯,∥Tm∥σ)T∥∞=∥T1∥σ.

Based on the fact that the Frobenious norm of the best rank-one approximation to the subtenor of a tensor is less than or equal to the Frobenious norm of the best rank-one approximation to this tensor, the left hand side of inequality (3) is obviously true. Thus, we only need to prove the right hand side of inequality (3).

Suppose that 𝓦 ∈ ℝ^{n₁×n₂×⋯×n_d} is a best rank-one approximation to 𝓣 ∈ ℝ^{n₁×n₂×⋯×n_d}. By Lemma 2.1, we get

∥T∥σ=∥W∥F.

Furthermore, suppose that {𝓦₁, 𝓦₂, ⋯, 𝓦_m} is a general tensor partition of 𝓦 with the same partition pattern as 𝓣, then it follows from the Lemma 2.1 that

∑j=1m∥Tj−Wj∥F2=∥T−W∥F2=∥T∥F2−∥W∥F2=∥T∥F2−∥T∥σ2. (5)

Noting that every 𝓦_j (j = 1, 2, ⋯, m) is a rank-one tensor or a zero tensor (by Lemma 3.1), we get

∑j=1m∥Tj−Wj∥F2≥∑j=1m(∥Tj∥F2−∥Tj∥σ2)=∥T∥F2−∑j=1m∥Tj∥σ2. (6)

Comparing (5) with (6), we get

∥T∥σ2≤∑j=1m∥Tj∥σ2.

This implies that the right hand side of inequality (3) is true.

In what follows we will prove the inequality (4).

Firstly, we prove the right hand side of the inequality (4). As mentioned in [15], the upper bound for the nuclear norm can be obtained through the definition of the nuclear norm.

It follows from the definition of the nuclear norm that

∥T∥∗=max∥X∥σ≤1〈T,X〉.

Suppose that {𝓧₁, 𝓧₂, ⋯, 𝓧_m} is a general tensor partition of the arbitrary tensor 𝓧 with the same partition pattern as 𝓣, then

∥Xj∥σ≤∥X∥σ,1≤j≤m,

and

∥T∥∗=max∥X∥σ≤1∑j=1m〈Tj,Xj〉≤∑j=1mmax∥X∥σ≤1〈Tj,Xj〉≤∑j=1mmax∥Xj∥σ≤1〈Tj,Xj〉=∑j=1m∥Tj∥∗.

Secondly, we prove the left hand side of the inequality (4).

It follows from the right hand side of inequality (3) that

∥X∥σ2≤∑j=1m∥Xj∥σ2.

Then, according to the definition of the nuclear norm of a tensor, we get

∥T∥∗=max∥X∥σ≤1〈T,X〉≥max∑j=1m∥Xj∥σ2≤1∑j=1m〈Tj,Xj〉. (7)

Based on the arbitrariness of the tensor 𝓧, we can ensure that all its sub-tensors are non-zero tensors. Let ∥𝓧_j∥_σ = σ_j, then σ_j ≠ 0. Furthermore, let Yj=1σjXj , then ∥𝓨_j∥_σ = 1 and the inequality (7) can be written as

∥T∥∗≥max∑j=1m∥Xj∥σ2≤1∑j=1m〈Tj,Xj〉=max∑j=1mσj2≤1,∥Yj∥σ=1∑j=1m〈Tj,σjYj〉=max∑j=1mσj2≤1max∥Yj∥σ=1,1≤j≤m∑j=1mσj〈Tj,Yj〉=max∑j=1mσj2≤1∑j=1mσjmax∥Yj∥σ=1,1≤j≤m〈Tj,Yj〉=max∑j=1mσj2≤1∑j=1mσj∥Tj∥∗. (8)

By using the Cauchy-Schwarz inequality, we get

∑j=1mσj∥Tj∥∗≤∑j=1mσj2∑j=1m∥Tj∥∗2. (9)

Noting the inequality (9), if ∑j=1mσj2≤1 , then it holds

∑j=1mσj∥Tj∥∗≤∑j=1m∥Tj∥∗2.

Thus, we get

max∑j=1mσj2≤1∑j=1mσj∥Tj∥∗=∑j=1m∥Tj∥∗2. (10)

It follows from (8) and (10) that

∑j=1m∥Tj∥∗2≤∥T∥∗.◻

□

At last of this section, we give two simple examples to illustrate the validity of the main result.

Example 3.1

Let

T=1111011111−1110−1−11−1∈R3×3×2.

By applying the following general partition,

1111011111−1110−1−11−1,

the tensor 𝓣 is partitioned into five subtensors, each corresponding to one of the five colors. Specifically, let

T1=111−1∈R1×2×2,T2=111−1∈R2×1×2,T3=111−1∈R1×2×2,T4=111−1∈R2×1×2,

and

T5=00∈R1×1×2.

Then {𝓣₁, 𝓣₂, 𝓣₃, 𝓣₄, 𝓣₅} is a general tensor partition of 𝓣.

By a simple computation, we get

∥T1∥σ=∥T2∥σ=∥T3∥σ=∥T4∥σ=2,∥T5∥σ=0,∥T1∥∗=∥T2∥∗=∥T3∥∗=∥T4∥∗=22,

and

∥T5∥∗=0.

Then according to the Theorem 3.1, we get

2=max{∥T1∥σ,∥T2∥σ,⋯,∥T5∥σ}≤∥T∥σ≤∥T1∥σ2+∥T2∥σ2+⋯+∥T5∥σ2=22, (11)

and

42=∥T1∥∗2+∥T2∥∗2+⋯+∥T5∥∗2≤∥T∥∗≤∥T1∥∗+∥T2∥∗+⋯+∥T5∥∗=82. (12)

Using the same method above, other upper bounds for the spectral norm and lower bounds for the nuclear norm can be obtained. For the sake of simplicity, we omit the corresponding discussions.

Let

W=111111111000000000.

Then

W=111∘111∘10

is a rank-one tensor and

〈T,W〉=22.

Thus, the Frobenius norm of the best rank-one approximation to the tensor 𝓣 is larger than or equal to

∥W∥F=22.

Then it follows from (11) that

∥T∥σ=22.

This implies that for the tensor 𝓣 in this simple example, the tensor partition {𝓣₁, 𝓣₂, 𝓣₃, 𝓣₄, 𝓣₅} is the best choice of all tensor partitions for the estimation of the spectral norm of 𝓣. However, we do not know whether the lower bound of the nuclear norm, estimated by (12), is tight, since, there is no an effective way for estimating the nuclear norm [8].

For the sake of completeness, in what follows, we give another example to illustrate that a tight lower bound of the nuclear norm can be obtained by the Theorem 3.1.

Example 3.2

Let

T=1111111111−1−111−1−1−1−111−1−11111111111∈R4×2×4.

Similar to the discussion above, the tensor 𝓣 can be partitioned into eight subtensors 𝓣_i (1 ≤ i ≤ 8),

T=1111111111−1−111−1−1−1−111−1−11111111111∈R4×2×4.

where

T1=T2=T3=T4=111−1∈R2×1×2,T5=T6=T7=T8=−1111∈R2×1×2.

Then, by using Theorem 3.1, we get

8=∥T1∥∗2+∥T2∥∗2+⋯+∥T8∥∗2≤∥T∥∗≤∥T1∥∗+∥T2∥∗+⋯+∥T8∥∗=162. (13)

Furthermore, the tensor 𝓣 can be decomposed into a sum of two rank-one tensors. That is

T=1111∘11∘1001+1−11−1∘11∘01−10.

Thus, it holds

∥T∥∗≤12+12+12+1212+1212+12+12+(−1)2+12+(−1)212+1212+(−1)2=8. (14)

It follows from (13) and (14) that

∥T∥∗=8.

This implies that a tight lower bound of the nuclear norm is obtained.

By Theorem 3.1, the following estimates about the spectral norm can also be obtained,

2=max{∥T1∥σ,∥T2∥σ,⋯,∥T8∥σ}≤∥T∥σ≤∥T1∥σ2+∥T2∥σ2+⋯+∥T8∥σ2=82. (15)

However, neither the lower bound nor the upper bound given by (15) are tight. Actually, through a series of calculations, we get

∥T∥σ=4.

As discussed above, how to choose a better tensor partition for the estimation of the spectral norm and nuclear norm of a general tensor is no fixed format, and it could be one of the future research.

4 Conclusions

In this paper, by considering the structure of the subtensors of rank-one tensors, we present a new proof to the conjecture proposed by Li [15]. The proof is different and simper than the method for proving the main results relating to the bounds for the spectral norm and nuclear norm in [11]. As discussed in [15], we believe these inequalities will have great potential in various applications. In the future, we will find more applications of these inequalities.

Acknowledgement

The author would like to thank Prof. Yao-lin Jiang and Zhening Li for their valuable suggestions and constructive comments on the manuscript, and also to the two anonymous referees for their enormously helpful comments.

Funding: This research work was supported by the Natural Science Foundation of China (NSFC) (Nos: 11401286, 11871393, 61663043), and Natural Science Foundation of Shandong Province (No: K17LB2501).

References

[1] Chang K., Pearson K., Zhang T., Perron-Frobenius theorem for nonnegative tensors, Commu. Math. Sci., 2008, 6, 507-52010.4310/CMS.2008.v6.n2.a12Suche in Google Scholar

[2] Che M., Cichocki A., Wei Y., Neural networks for computing best rank-one approximations of tensors and its applications, Neurocomputing, 2017, 267, 114-13310.1016/j.neucom.2017.04.058Suche in Google Scholar

[3] Cichocki A., Mandic D., De Lathauwer L., et al., Tensor decompositions for signal processing applications: From two-way to multiway component analysis, IEEE. Signal Proc. Mag., 2015, 32, 145-16310.1109/MSP.2013.2297439Suche in Google Scholar

[4] De Lathauwer L., De Moor B., Vandewalle J., On the best rank-1 and rank-(R₁, …, R_N) approximation of higher-order tensors, SIAM J. Matrix Anal. Appl., 2000, 21, 1324-134210.1137/S0895479898346995Suche in Google Scholar

[5] Kolda T. G., Bader B. W., Tensor decompositions and applications, SIAM Rev., 2009, 51, 455-50010.1137/07070111XSuche in Google Scholar

[6] Qi L., Luo Z., TENSOR ANALYSIS: Spectral Theory and Special Tensor, SIAM Press, Philadelphia, 201710.1137/1.9781611974751Suche in Google Scholar

[7] He S., Li Z., Zhang S., Approximation algorithms for homogeneous polynomial optimization with quadratic constraints, Math. Program., 2010, 125, 353-38310.1007/s10107-010-0409-zSuche in Google Scholar

[8] Friedland S., Lim L.-H., Nuclear norm of higher-order tensors, Math. Comput., 2018, 87, 1255-128110.1090/mcom/3239Suche in Google Scholar

[9] Li C, Li Y., Kong X., New eigenvalue inclusion sets for tensors, Numer. Linear Algebra Appl., 2014, 51, 39-5010.1002/nla.1858Suche in Google Scholar

[10] Li W., Ng M. K., Some bounds for the spectral radius of nonnegative tensors, Numer. Math., 2015, 130, 315-33510.1007/s00211-014-0666-5Suche in Google Scholar

[11] Chen B., Li Z., On the tensor spectral p-norm and its dual norm via partitions, Preprint, 2018Suche in Google Scholar

[12] Nikiforov V., Combinatorial methods for the spectral p-norm of hypermatrices, Linear Algebra App., 2017, 529, 324-35410.1016/j.laa.2017.04.023Suche in Google Scholar

[13] Yuan M., Zhang C.-H., On tensor completion via nuclear norm minimization, Found. Comput. Math., 2016, 16, 1031-106810.1007/s10208-015-9269-5Suche in Google Scholar

[14] Zhao Q., Meng D., Kong X., et al., A novel sparsity measure for tensor recovery, In ICCV, 2015, 271-27910.1109/ICCV.2015.39Suche in Google Scholar

[15] Li Z., Bounds on the spectral norm and the nuclear norm of a tensor based on tensor partition, SIAM J. Matrix Anal. Appl., 2016, 37, 1440-145210.1137/15M1028777Suche in Google Scholar

[16] Jiang Y.-L., Kong X., On the uniqueness and purturbation to the best rank-one approximation of a tensor, SIAM J. Matrix Anal. Appl., 2015, 36, 775-79210.1137/140975577Suche in Google Scholar

Received: 2018-10-23

Accepted: 2019-03-02

Published Online: 2019-05-16

This work is licensed under the Creative Commons Attribution 4.0 Public License.

Artikel in diesem Heft

https://doi.org/10.1515/math-2019-0028

Schlagwörter für diesen Artikel

tensor norm; spectral norm; nuclear norm; tensor partition

Creative Commons

BY 4.0