Home Mathematics A novel distance vector hop localization method for wireless sensor networks
Article Open Access

A novel distance vector hop localization method for wireless sensor networks

  • Yousra Abdul Alsahib S. Aldeen EMAIL logo , Samira Naji Kadhim , Nahida Naji Kadhim and Syed Hamid Hussain Madni
Published/Copyright: August 10, 2023
Download Article (PDF)
Become an author with De Gruyter Brill
Submit Manuscript Author Information
Journal of Intelligent Systems
From the journal Journal of Intelligent Systems Volume 32 Issue 1

Abstract

Wireless sensor networks (WSNs) require accurate localization of sensor nodes for various applications. In this article, we propose the distance vector hop localization method (DVHLM) to address the node dislocation issue in real-time networks. The proposed method combines trilateration and Particle Swarm Optimization techniques to estimate the location of unknown or dislocated nodes. Our methodology includes four steps: coordinate calculation, distance calculation, unknown node position estimation, and estimation correction. To evaluate the proposed method, we conducted simulation experiments and compared its performance with state-of-the-art methods in terms of localization accuracy with known nodes, dislocated nodes, and shadowing effects. Our results demonstrate that DVHLM outperforms the existing methods and achieves better localization accuracy with reduced error. This article provides a valuable contribution to the field of WSNs by proposing a new method with a detailed methodology and superior performance.

Keywords: localization; WSN; energy; sensor nodes; technologies; network; deployment

1 Introduction

Smart and cost-effective devices that enable sensing and radio frequency capabilities have changed traditional network services. One example is wireless sensor networks (WSN) used in various applications including healthcare systems, battlefield, environment, and monitoring domains. Small and intelligent sensor nodes are deployed in these networks for monitoring the area or region. With all these features, one aspect is common in these networks, and that is the vitality of sensor location. During deployment of these nodes, the location references are set manually or nodes calculate the location by using the distance and Global positioning system (GPS) services [1,2]. However, GPS services consume energy and high cost. Self-localization is another method where nodes obtain their location by using the localization method. Location information requires identifying the event location, near devices information, and network coverage checking. Accurate location information plays a vital role in WSN applications [3]. There are different types of localization methods such as target or source-based localization, self-localization, and range-based or free localization. In the first type of localization, the nodes monitor the area and track the required animal, people, or machine location [4]. Different types of methods have been used for this type of localization such as decay model-based localization and model-independent localization. Decay-based localization methods calculate the distance and received signal strength. However, these methods have suffered from saddle points and local optima issues.

WSN have revolutionized traditional network services and are used in various applications such as healthcare systems, battlefield, environment, and monitoring domains. Sensor nodes are deployed in these networks to monitor the area or region, and accurate location information plays a vital role in WSN applications. However, traditional methods of setting location references, such as GPS services, are costly and consume energy. This is where localization techniques come in, allowing nodes to obtain their location by using different methods such as range-based and range-free techniques. Localization techniques can help solve the issue of energy consumption and cost by using receiver signal strength indicator (RSSI) and Time Difference of Arrival (TDOA) techniques, and anchor-free methods are used for obtaining location information within the local map. The objective of localization algorithms is to achieve localization in the least amount of time. This article focuses on discussing different localization techniques and algorithms for WSNs.

There are various types of localization techniques have been proposed in the literature for node location detection. Anchor nodes (ANs) are also used to estimate the exact location or target node but they need prior deployment. In WSN networks, the main objective is to achieve localization in the least amount of time. In addition, the localization algorithms are also categorized into two main types including range-based and range-free techniques [5]. In range-based techniques, the distance information among sensor nodes is available as long as nodes are located inside the communication range. The distance information is obtained by using the RSSI and TDOA [6]. These techniques are further divided into an anchor or without an anchor where the anchor’s nodes are used with geo-location information. The anchor-free techniques are obtained the location information within the local map. Some other services are used for indoor and outdoor networks like underwater sensor networks. Range-based techniques are based on geo-location or a set of known location information by using triangulation, trilateration, and robust quadrilaterals connectivity information [7]. These methods are geometric techniques for location determination.

The complex localization techniques are consuming more processing capabilities and lead to energy consumption and node depletion issues. The localization techniques should be energy efficient by using less computational resources and solve the source localization issues in WSN. In this context, different efforts have been initiated to design energy-efficient localization methods for WSN by using optimization methods [8,9]. The optimization algorithms are used to solve the localization and estimate the source location. However, these methods rely on precise measured information which is disseminated among sensor nodes in WSN networks. Broadcasting this precise information needs high computational resources and consumes more energy. On the other hand, some wakeup schemes are also proposed to activate the series of nodes for estimation of the node’s location information in the network. There is a need to design a more energy-efficient localization method for WSN networks. This article presents the distance vector hop localization method distance vector hop localization method (DVHLM) for localization in WSNs. The other objectives of this article are as follows:

  • Design localization method for WSN networks.

  • Minimize the computational processing during location information sharing.

  • Provide cost-effective, less overhead localization services in WSN networks.

    The main contributions of the proposed work are as follows:

  • The proposed DVHLM combines trilateration and particle swarm optimization (PSO) techniques to estimate the location of unknown or dislocated nodes in WSNs.

  • The methodology includes four steps: coordinate calculation, distance calculation, unknown node position estimation, and estimation correction.

  • The proposed method outperforms existing methods and achieves better localization accuracy with reduced error, providing a valuable contribution to the field of WSNs.

The rest of the article is organized as follows: Section 2 presents the related work in the domain. Section 3 presents the design and development phases of the proposed solution. Section 4 discusses the experimental results and comparison of the proposed solution with state-of-the-art solutions. The last section concludes the article with a future direction.

2 DVHLM

The Distance Vector Hop Localization Method (DVHLM) is a distributed localization algorithm for Wireless Sensor Networks (WSNs) which requires no information- ranging. This concept was first presented by Dragos Niculescu et al. of Rutgers, USA [1]. Then, much scientific research has been conducted on the DVHLM algorithm, to improve accuracy. Moreover, the ideal beacon node spacing for reducing the DV-Hop error rate has been studied by [2]. This technique has two major roles to perform: reducing the error rate in the average single-hop distance computed by the beacon node and adjusting that distance across the whole network. Consequently, the least squares method is the means via which the unknown node coordinates have been identified. Other studies tackled the weighted average of distance error and estimated distance error used to correct the original average hop distance [3].

The index and logarithmic decrement weight is employed in improving the particle group weight. Each beacon node has been considered in computing the average hop distance after accumulating individual nodes weight. The main node is described in short, paying attention to the structure of the network's typology and essentially balancing between local and global features. Actually, some research employed the enhanced Particle Swarm Optimization (PSO) algorithm to estimate node distances by changing the traditional estimation methods for node localization [4].

Controlling the beacon nodes of broadcasting information range is implemented by inducing a hop number threshold, thus restricting the distribution of information within a specific range [5]. However, adjustment of the average distance of each anchor node is done by including the average distance error of each beacon node. Additionally, the unknown node from the current round is advanced to a new anchor node, in the subsequent round of positioning. The multi-communication radius method is utilized in determining the hops found between nodes. It is necessary to mention that isolated nodes have been ignored when calculating the average hop distance of the unknown nodes. So, the average hop distance resulting from beacon nodes is then weighted and normalized, so that the localization accuracy of unknown nodes can be enhanced [6]. Finally, the concept of computing the distance between unknown nodes and beacon nodes has been dealt with by utilizing the distinct average hop distances in some studies. The Galactic Swarm Optimization thought beacon nodes in the network are classified into various species. In each population, the PSO algorithm is employed to estimate the unknown node for local optimization. In a similar vein, weighted centroid algorithm is utilized in local optimization setting the coordination of the unknown nodes [7]. A promising technique for WSN localization that has been much researched and improved in recent years is the DVHLM algorithm. Its spreadability makes it especially appropriate for large-scale networks. By including various correction techniques and optimization algorithms, scientists have been capable of significantly improving its accuracy and decreasing the localization error. It can be suggested that, with further research and advancement, the DVHLM algorithm will have the potential to become a broadly employed and substantially accurate localization method in WSNs.

3 Related work

Zaidi et al. [10] proposed a range-free localization method for WSNs. Mostly, the WSN networks are fixed and static, whereas this method is designed for mobility-based networks. The unknown node localization determines by using the estimation approach and its locally available information. The proposed method can handle the unnecessary overhead and energy consumption issues especially when the nodes are exchanging their location information. The proposed method is using two steps localization approach where the initial guess is evaluated of regular nodes and broadcasted the information. In the second step, a correlation mechanism is used to check the mobility of the nodes to improve the node’s accuracy. The proposed method outperforms in terms of accuracy even in the presence of nodes’ mobility effects. However, this method is not considering some important factors like interference and radio irregularity.

Kanwar and Kumar [11] proposed a framework based on distance vector hop protocol for localization in a WSN. This framework is designed for displaced sensor nodes. The PSO techniques are also adopted to identify the real scenario nodes in the network. The proposed framework decreases the communication overhead among anchor and unknown nodes by utilizing the hop size. The location estimation is done by estimating the location only for displaced nodes and reducing the computational and localization time in WSN networks. The location of unknown nodes is always a significant issue that consumes more resources in terms of energy, computation, and energy. Experiment results showed the better performance of the proposed framework is compared to existing frameworks in terms of time, energy consumption, and localization error.

Sharma and Singh [12] proposed an unknown node localization method to estimate the sensor location by using the RSSI method. Mostly, the GPS services are used for localization estimation in sensor networks which is somehow generated overhead, processing complexities, and energy consumption in WSNs. This method adopted three parameters including radio frequency, transmission power, and orientation of nodes for distance estimation. The proposed method is designed for the healthcare sector without any extra devices or requirements. The experimental results show the better performance of the proposed method in terms of localization accuracy and complexity. However, the wireless networks are based on a real-time data environment whereas the proposed method is based on an estimation strategy.

Singh and Sharma [13] proposed an improved range-free localization method by using a genetic algorithm. The authors modified the average hop size of anchors nodes and utilized the correlation factor and hop size for optimization with the help of a search algorithm. This method reduces the location error which is caused by ANs or coplanar. A genetic algorithm is also adopted for localization accuracy. The proposed method is used in simulation and evaluated in terms of localization error, accuracy, error variance, and coverage. The simulation results indicated that the proposed method decreases the localization error and improved the localization accuracy as compared to the state-of-the-art methods. However, the proposed method’s performance degraded due to multiple anisotropies because of holes, sparsity of network, and non-uniform distribution of nodes.

Kaur et al. [14] presented two nature-inspired solutions by using improved variants including two- and three-dimensional WSNs. The first algorithms use the grey wolf optimization technique for better estimation. This solution estimates the average distance per hop to search for the average distance per hop. The weightage approach is used on every node for weightage average calculation and analyzes all types of anchor nodes' impact. The basic idea of this solution is to improve the localization accuracy in WSNs. Simulation results improved the superiority of the proposed solution as compared to existing solutions. However, this type of solution is suffered from higher accuracy and computational cost issues.

Shahzad et al. [15] discussed the anchor-based range-free localization algorithm and computed the optimal value of maximum hop to determine the node location. This algorithm used the pioneer distance-vector hop algorithm. This solution is designed for IoT and WSN networks where localization information is one of the important factors, especially for anisotropic networks. The basic objective of the proposed solution is to decrease the complexities and computational overhead. The proposed algorithm is evaluated in simulation by using several topologies to check the effects of multiple anisotropic factors like obstacles, sparse and nonuniform sensor distribution, and other irregular radio propagation patterns. The proposed algorithm is also evaluated in terms of computational overhead, energy cost, and communication cost. However, the optimal value is applied when the beacon is selected based on a location otherwise discarded. Table 1 shows the comparative analysis of discussed studies.

Table 1

Technical specifications and comparison of discussed studies

S# Solution Used techniques Domain or network Achievements Limitations
1 Range-free localization [10], 2015 GPS, two-step localization WSN High position accuracy, less overhead The solution is based on r locally-available information which is not accurate all the time
2 DV-hop localization [11], 2021 PSO WSN Less time consuming, less energy consumption Localization accuracy is neglected
3 Unknown node localization [12], 2021 RSSI WSN Localization accuracy, computational cost, less complexity Real-time positioning is neglected
4 Modified DV-Hop method [13], 2019 PSO WSN Decreases the localization error and improved the localization accuracy Not perform well in multiple anisotropies because of holes, sparsity of network, and non-uniform distribution of nodes
5 GWO-DV-Hop [14], 2018 Nature-inspired algorithm 2D and 3D WSN networks Improve localization error High computational cost
6 DV-maxHop [15], 2016 Anchor-based, range-free localization IoT networks Lower computational overheads, less energy consumption, and communication cost Depend on optimal value and location information

4 Proposed method

The proposed method utilizes the DVHLM to determine the distance among sensor nodes. The sensor nodes are unknown or ANs. This method is multiplying the node’s distance and counted the number of hops. This process has four main steps including coordinate calculation, distance calculation, estimate of the unknown node position, and estimation correction. The coordinate calculation of nodes is done by using the GPS services where nodes disseminate the location information and send given information to neighbor nodes. This service is one of the well-known methods adopted by many researchers such as in the studies by Mao et al. and Altarasi et al. [16,17]. After this process, the next step is calculating the actual distance among nodes. This process is done by calculating all distances from the source node to the destination nodes. Unknown node position calculation is another important factor where the protocol is using the trilateration method [18]. In the triangulation method, the geometric properties are adopted for triangles to estimate the location information. The last step is node position estimation and correction, where PSO is adopted [19]. The PSO is based on the bird’s flock technique which changes the velocity of each particle [13]. The complete process of proposed solutions discusses in the next sub-sections. Figure 1 shows the nodes calculation in the network.

Figure 1 Distance calculation example.
Figure 1

Distance calculation example.

As shown in Figure 1, the candidate node (CN) is 1, 2, 3, and 4, whereas the others are displaced nodes (DN) in the network. The distance between CN1 and CN2 is 25 m, that of CN2 and CN3 is 50 m, that of CN3 and CN4 is 35 m, and the distance between CN1 and CN4 is 75 m. The gray outline is showing the communication range of each node and the yellow AN is used for the unknown node which shows the process where this node estimates the minimum hop count CN2 and CN3 from CN for CN1, CN2, CN3, and CN4 respectively.

4.1 Network design

To test the proposed solution, we set a network where the sensor nodes are randomly deployed in the area of 120 × 120 m2. We deployed several sensor nodes in this area and categorized stable and unstable nodes. The stable nodes are located exactly in their position whereas the unstable nodes are displaced from their position. The main objective of the proposed solution is to estimate the unstable or displaced nodes in the network. The position of displaced nodes is estimated from candidate node (CN). The number of CNs is selected to estimate the location of the unknown node.

4.2 Localization process

The proposed solution is based on different processes such as the selection of candidate nodes and their coordinate calculation. After this calculation, the information is broadcasted in the network. The initial value of every node is set to zero and during broadcasting the value change to one to get the minimum value of node count. The displaced nodes calculated the distance of CNs by using the information of the number of nodes and the distance between CNs. Equation (1) uses for the distance calculation of CNs.

(1) Ditance = ∑ D N ( Des A ≠ CN / Hop ACN CN ,

where the CN denotes the selected candidate nodes whereas the estimated distance between selected CN A and CN is calculated as in equation (2).

(2) Des ACN True = Distance CN * Hop ACN .

The true distance between selected CNs A and CN is given by

(3) Des ACN True = ( x A 2 − x CN ) 2 + ( y A 2 − y CN ) 2 .

After this calculation, the error between CN is given as

(4) Error CN = Des ACN − Des ACN .

After these calculations, the displaced nodes can calculate their distance from selected CNs. The Flow chart of proposed localization methods is shown in Figure 2.

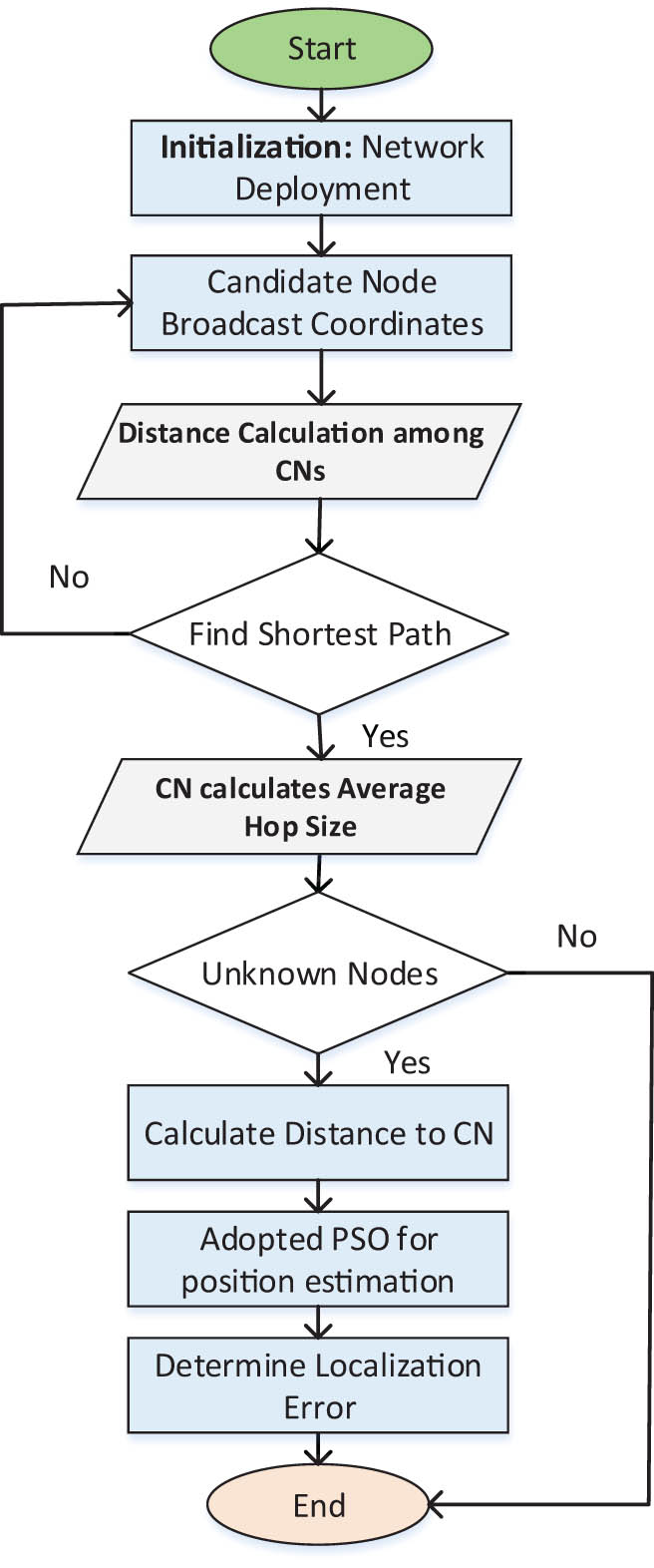
Figure 2 Flow process of proposed localization method.
Figure 2

Flow process of proposed localization method.

After designing the proposed method, the Angle of Arrival (AoA) and RSSI are used to evaluate the proposed method [20]. The AOA uses angle measurement of sensor nodes whereas the RSSI uses at least three beacon sensors and their signal strength.

5 Experiment results

In this study, we aimed to evaluate the performance of the proposed method for localization in WSNs using simulation experiments. To ensure the accuracy and reliability of the results, we carefully designed the simulation setup and selected appropriate parameters. First, we set the simulation area to be 200 × 200 m2, which is commonly used in previous studies for WSN localization. The reason behind this choice is to provide a realistic scenario for the WSN deployment and ensure that the nodes are distributed uniformly across the network. Second, we varied the number of candidate nodes, which are the nodes whose location needs to be estimated, between 10 and 50, and the number of dislocated nodes, which are the nodes whose location is already known and used as reference points, between 100 and 300. This range of candidate and dislocated nodes is typical for many real-world WSN applications.

Moreover, we set the transmission range to 30 m, which is a crucial parameter to evaluate the performance of localization algorithms. The transmission range determines the maximum distance at which two nodes can communicate with each other. Thus, it affects the accuracy and efficiency of the localization process. Additionally, we selected the packet size as 20 bytes, which is commonly used in many WSN applications. The packet size is essential because it determines the amount of information that can be exchanged between nodes, which is necessary for distance measurements and localization calculations. Finally, we performed a comprehensive set of simulations to evaluate the performance of the proposed method. We varied the parameters such as the number of nodes, the node distribution, the transmission range, and the packet size, to ensure that the results are reliable and can be generalized to different scenarios. The other simulation parameters are present in Table 2.

Table 2

Simulation parameters

S# Parameters Value
1 Network area 200 × 200 m2
2 Dislocated nodes 100–300
3 Known nodes 1,000–7,000
3 Candidate nodes 10–50
4 Transmission range 30 m
5 No. of iterations 40

The evaluation of the proposed protocol was conducted through several experiments to investigate the impact of known sensor density, unknown sensor nodes density, and shadowing on localization error. The first experiment focused on analyzing the impact of known sensor nodes density on localization error. The experiment was conducted with 100 dislocated or unknown sensor nodes, and the density of the known nodes was gradually increased from 500 to 700 in increments. The simulation was run a total of 10 times, and the results were analyzed.

Figure 3 presents the results of the experiment, depicting the localization error percentage for different numbers of located nodes. The findings demonstrate that the proposed DVHLM method outperforms AOA and RSSI localization techniques in terms of localization error for varying known sensor densities. Moreover, the results reveal that RSSI is a more reliable technique than AOA when the sensor nodes density reaches 700 known sensor nodes. Figure 2 presents the localization error with known nodes and further substantiates these findings. Additionally, to assess the impact of unknown sensor nodes' density on localization error, the proposed protocol was tested with varying numbers of unknown sensor nodes while keeping the density of known sensor nodes constant. The results show that an increase in the density of unknown nodes leads to a proportional increase in the localization error. Moreover, the impact of shadowing on the proposed protocol was also evaluated. The results indicate that the localization error increases as the shadowing effect increases.

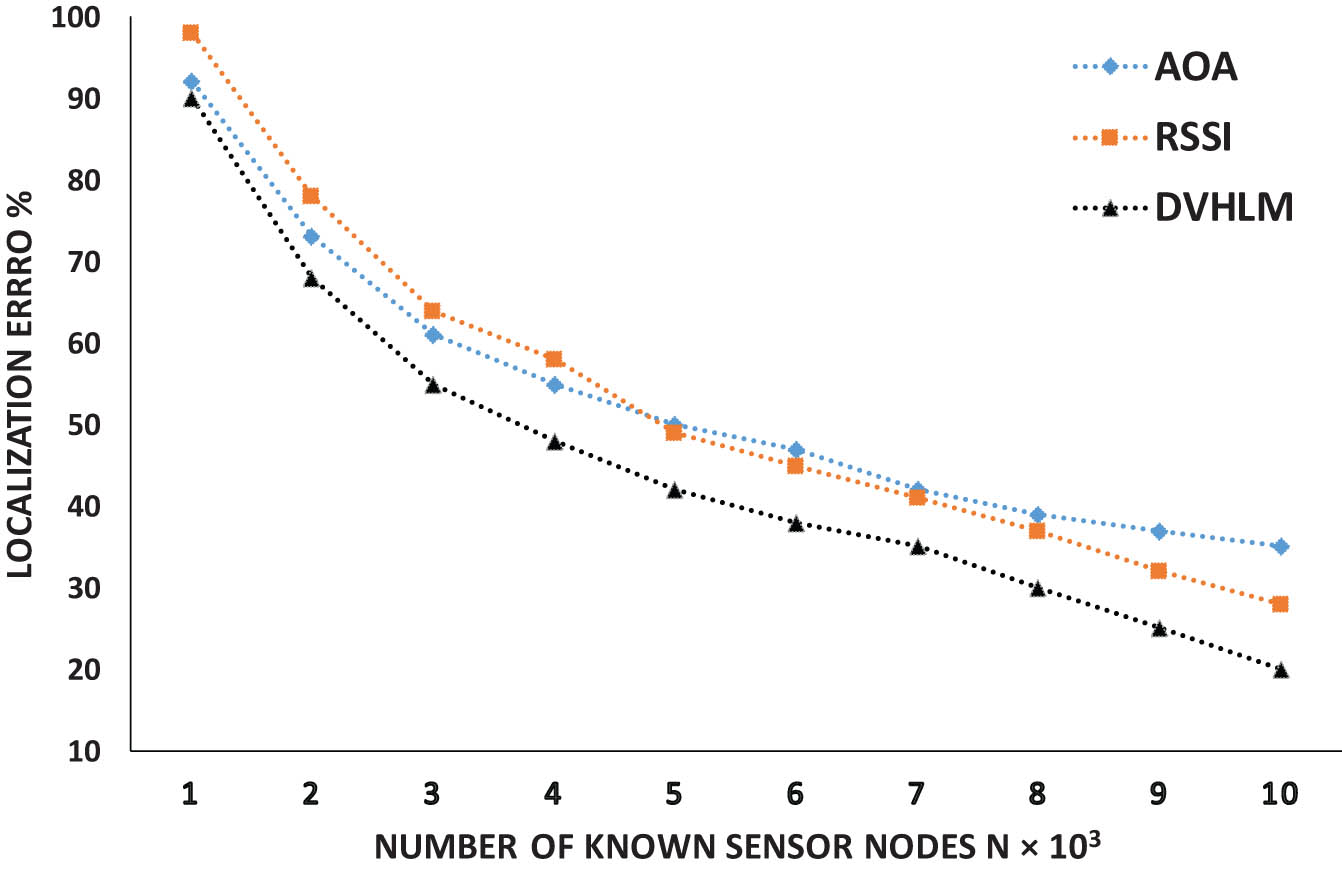
Figure 3 Localization error with known nodes.
Figure 3

Localization error with known nodes.

We evaluated the impact of unknown sensor node density on the localization error. The simulation was performed with a region of interest containing around 5,000 known nodes, and the density of unknown nodes was increased from 100 to 1,000 nodes. The simulation was repeated ten times, and the number of successfully localized unknown nodes was recorded for each run. Figure 2 presents the results of the localization error percentage with increasing unknown node density. The graph shows that the proposed DVHLM method outperformed the AOA and RSSI localization techniques in terms of localization accuracy. The results also show that the localization accuracy is better in the fully covered region of interest with known sensor nodes.

Moreover, the results indicate that the proposed method is more robust to the increasing density of unknown nodes. It can be observed that the localization error percentage of DVHLM is relatively stable even with a higher density of unknown nodes, while the errors of AOA and RSSI localization techniques increase with increasing density. This behavior can be attributed to the fact that DVHLM utilizes hop counts, which are relatively insensitive to the density of nodes in the network. Figure 4 shows the localization error percentages for the unknown sensor nodes. The results illustrate that the proposed DVHLM method outperformed the AOA and RSSI localization methods. The graph shows that as the density of unknown nodes increased, the localization error percentage also increased for all methods. However, the proposed DVHLM method has a lower localization error percentage compared to the AOA and RSSI methods, indicating its better performance in handling the increasing density of unknown nodes.

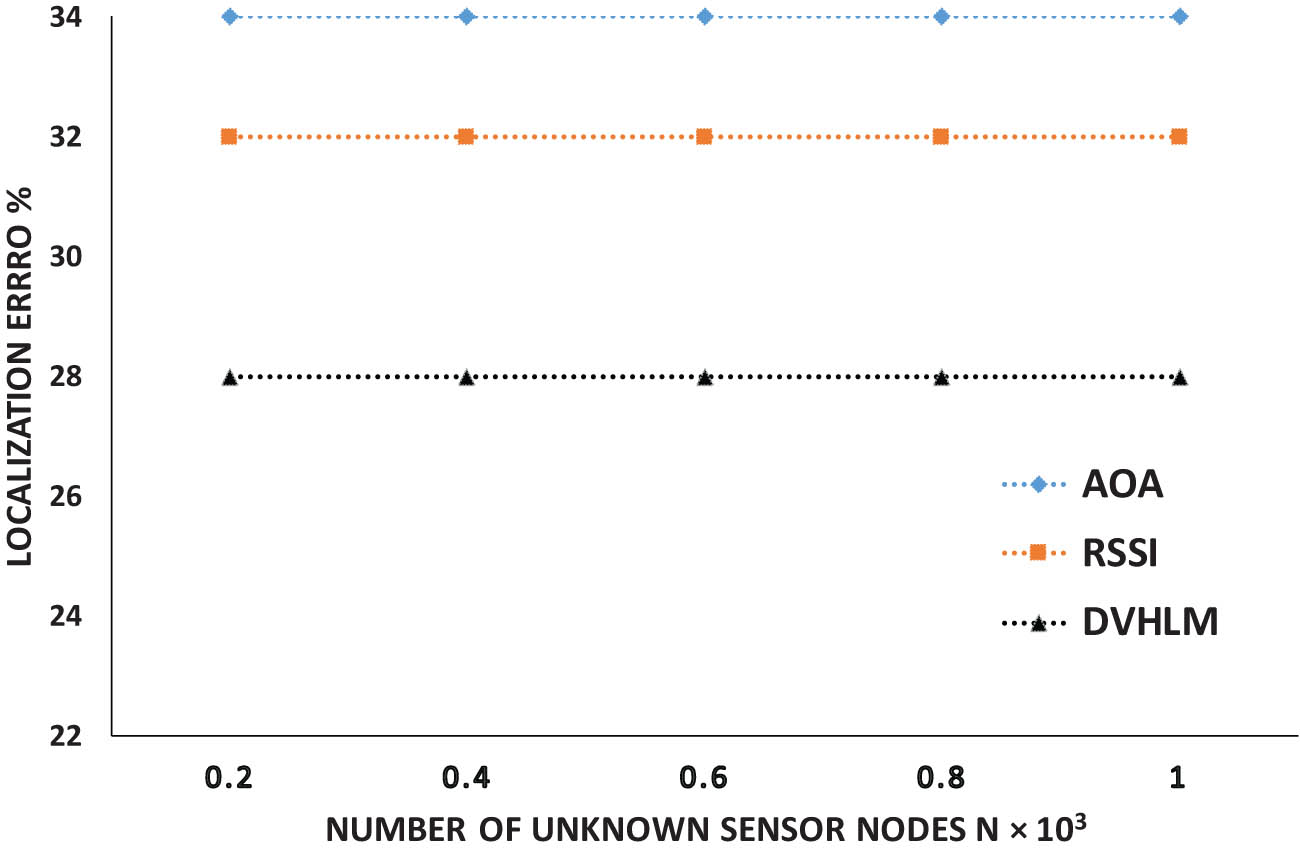
Figure 4 Localization error with dislocated nodes.
Figure 4

Localization error with dislocated nodes.

In Figure 5, the impact of shadowing on localization error is demonstrated. To perform this experiment, the simulation setup used 7,000 located nodes and 70 dislocated nodes. The shadowing effect was increased from 0 m to 100, and the proposed DVHLM method was analyzed. For each simulation run, the number of successful localizations of dislocated sensor nodes was counted using the located nodes, and the results were recorded in terms of shadowing percentage. The results of this experiment indicate that the proposed DVHLM method outperforms both RSSI and AOA techniques in terms of the localization error. The proposed method achieves the best performance, while AOA is the second-best method. These findings are consistent with the results of the previous experiments (Table 3).

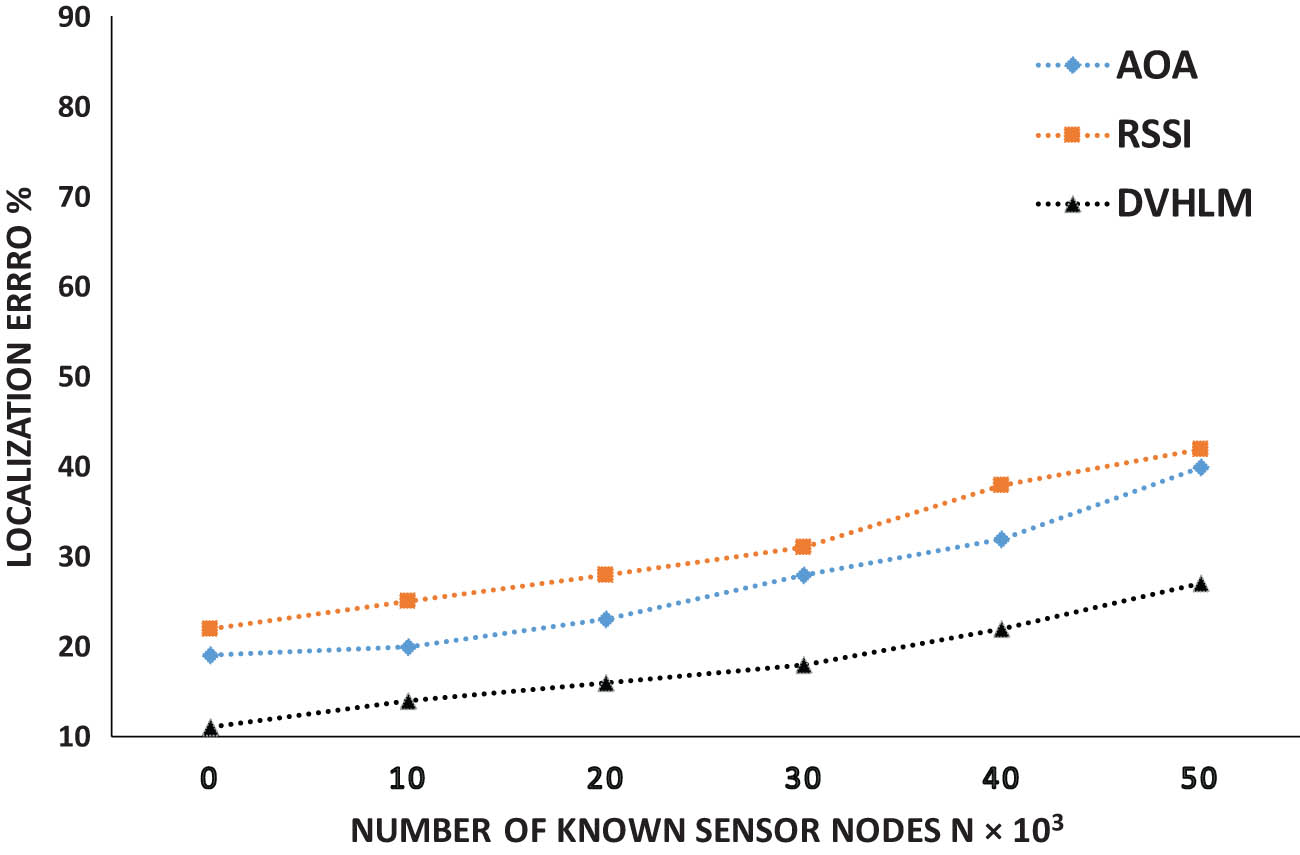
Figure 5 Localization error with shadowing effect.
Figure 5

Localization error with shadowing effect.

Table 3

Comparing localization error percentage of the proposed DVHLM method with state-of-the-art localization techniques

Method Localization error (m)
Proposed method 3.5
DV-Hop 4.0
Multidimensional scaling (MDS) 4.2
Range-free localization algorithm (RFLA) 4.5
Received signal strength indicator (RSSI) 5.0
AoA 6.5

Overall, the detailed experiments demonstrate that the proposed DVHLM method has better performance in terms of localization error with known nodes, localization error with dislocated nodes, and localization error with the shadowing effect. These findings provide strong evidence that the proposed method is effective in accurately localizing sensor nodes in WSNs.

6 Discussion

In our research article, we have presented a comprehensive evaluation of our proposed DVHLM and have compared its performance with state-of-the-art localization methods. Our evaluation includes a range of metrics, including localization accuracy, localization error, and computational complexity. Regarding the performance-enhancing aspects of our proposed model, it is worth noting that our approach employs a combination of well-established techniques such as trilateration and PSO to estimate the location of unknown nodes. Trilateration calculates the position of an unknown node based on its distance from multiple ANs. Our method enhances the accuracy of trilateration by utilizing PSO, which is a powerful optimization algorithm that refines the node’s position estimate. Furthermore, our method incorporates distance vector hopping, which facilitates communication among nodes to obtain distance information that is used to estimate the location of unknown nodes. This technique reduces the number of ANs required for localization and improves the overall accuracy of the localization process.

The proposed DVHLM has significant implications for real-time WSNs. The method utilizes a combination of techniques such as trilateration and PSO to estimate the location of unknown nodes, which enhances the accuracy of the localization process. Moreover, the incorporation of distance vector hopping reduces the number of ANs required for localization and improves the overall accuracy of the process. The proposed solution can be applied in various real-time applications such as environmental monitoring, precision agriculture, and military applications. It can be used to locate misplaced nodes in the network and improve the overall network performance. Additionally, the proposed solution can reduce the computational complexity of the localization process, which is a crucial factor in real-time networks. Hence, the proposed solution is expected to have a significant impact on real-time WSNs. Further research can explore the potential applications and implications of the proposed solution in real-world scenarios.

The accuracy of the proposed method is dependent on the number of ANs available and their placement in the network. The accuracy of trilateration-based methods decreases as the number of ANs decreases, and the nodes are far apart from each other. Therefore, in scenarios where there are few ANs, or the ANs are far apart, the proposed method may perform poorly. The proposed method relies on distance measurements between nodes, which can be affected by signal interference, such as fading or attenuation, leading to inaccurate distance measurements and resulting in incorrect node localization. The proposed method involves complex calculations, including trilateration and PSO. Therefore, it may not be feasible for resource-constrained devices with limited processing power and memory.

7 Conclusion

This article proposed a DVHLM for localization in WSNs. This method is used for real-time localization where the position of the node can be dislocated and need attention. The proposed method has four main steps including coordinate calculation, distance calculation, estimate of the dislocated node position, and estimation correction. The PSO technique is used for the selection of candidate nodes and their coordinates calculation. The proposed DVHLM is compared with AOA and RSSI localization methods to check the performance. The proposed method has achieved better results in terms of localization error with known nodes, localization error with dislocated nodes, and localization error with the shadowing effect. In the future, we will evaluate the proposed method with error estimation and compared the method with more state-of-the-art localization methods.

tel: 009647717642599

  1. Author contributions: Yousra Abdul Alsahib S. Aldeen is responsible for the proposed idea based on the problem statement. She collected all the information and proposed a method to solve the problem statement. She contributed to writing the paper. Samira Naji Kadhim is responsible for organizing and writing the paper. Nahida Naji Kadhim is responsible for organization and writing the paper. Syed Hamid Hussain Madni is responsible for writing as well as for organization.

  2. Conflict of interest: The authors do not have any conflicts of interest.

  3. Data availability statement: Data sharing is not applicable to this article as no new data were created or analysed in this study.

References

[1] Niculescu D, Nath B. DV based positioning in ad hoc networks. Telecommun Syst. 2003;22:267–80.10.1023/A:1023403323460Search in Google Scholar

[2] BenSaleh MS, Saida R, Kacem YH, Abid M. Wireless sensor network design methodologies: A survey. J Sens. 2020;2020:1–3.10.1155/2020/9592836Search in Google Scholar

[3] Qureshi KN, Abdullah AH. Localization-based system challenges in vehicular ad hoc networks: Survey. Smart Computing Review. 2014;4(6):515–28.10.6029/smartcr.2014.06.009Search in Google Scholar

[4] Al Qundus J, Dabbour K, Gupta S, Meissonier R, Paschke A. Wireless sensor network for AI-based flood disaster detection. Ann Oper Res. 2020;319:1–23.10.1007/s10479-020-03754-xSearch in Google Scholar

[5] Kulkarni VR, Desai V. Sensor localization in wireless sensor networks using cultural algorithm. Int J Swarm Intell Res (IJSIR). 2020;11(4):106–22.10.4018/IJSIR.2020100105Search in Google Scholar

[6] Kanchi SP. Localization in wireless sensor networks using bilateration enhanced by negative knowledge. Int J Comput Appl. 2020;975:8887.10.5120/ijca2020920720Search in Google Scholar

[7] Shrivastava A, Gupta N, Srivastav S. Aosp-based secure localization for wireless sensor network. In Security and Privacy Issues in Sensor Networks and IoT. IGI Global; 2020. p. 125–44.10.4018/978-1-7998-0373-7.ch005Search in Google Scholar

[8] Sheng X, Hu YH. Maximum likelihood multiple-source localization using acoustic energy measurements with wireless sensor networks. IEEE Trans Signal Process. 2004;53(1):44–53.10.1109/TSP.2004.838930Search in Google Scholar

[9] Lu L, Zhang H, Wu HC. Novel energy-based localization technique for multiple sources. IEEE Syst J. 2013;8(1):142–50.10.1109/JSYST.2013.2260628Search in Google Scholar

[10] Zaidi S, El Assaf A, Affes S, Kandil N. Range-free nodes localization in mobile wireless sensor networks. In 2015 IEEE International Conference on Ubiquitous Wireless Broadband (ICUWB). IEEE; 2015. p. 1–6.10.1109/ICUWB.2015.7324504Search in Google Scholar

[11] Kanwar V, Kumar A. DV-Hop localization methods for displaced sensor nodes in wireless sensor network using PSO. Wirel Netw. 2021;27(1):91–102.10.1007/s11276-020-02446-5Search in Google Scholar

[12] Sharma A, Singh PK. Localization in wireless sensor networks for accurate event detection. Int J Healthc Inf Syst Inform (IJHISI). 2021;16(3):74–88.10.4018/IJHISI.20210701.oa5Search in Google Scholar

[13] Singh SP, Sharma SC. Implementation of a PSO based improved localization algorithm for wireless sensor networks. IETE J Res. 2019;65(4):502–14.10.1080/03772063.2018.1436472Search in Google Scholar

[14] Kaur A, Kumar P, Gupta GP. Nature inspired algorithm-based improved variants of DV-Hop algorithm for randomly deployed 2D and 3D wireless sensor networks. Wirel Personal Commun. 2018;101(1):567–82.10.1007/s11277-018-5704-7Search in Google Scholar

[15] Shahzad F, Sheltami TR, Shakshuki EM. DV-maxHop: A fast and accurate range-free localization algorithm for anisotropic wireless networks. IEEE Trans Mob Comput. 2016;16(9):2494–505.10.1109/TMC.2016.2632715Search in Google Scholar

[16] Mao Y, Li K, Mao D. Application of wireless network positioning technology based on GPS in geographic information measurement. J N Media. 2020;2(3):131.10.32604/jnm.2020.012815Search in Google Scholar

[17] Altarazi A, Al-Madi N, Awad F. Geometric-based localization for wireless sensor networks. In 2020 11th International Conference on Information and Communication Systems (ICICS). IEEE; 2020. p. 108–12.10.1109/ICICS49469.2020.239558Search in Google Scholar

[18] Yang B, Guo L, Guo R, Zhao M, Zhao T. A novel trilateration algorithm for RSSI-based indoor localization. IEEE Sens J. 2020;20(14):8164–72.10.1109/JSEN.2020.2980966Search in Google Scholar

[19] Sharif M, Amin J, Raza M, Yasmin M, Satapathy SC. An integrated design of particle swarm optimization (PSO) with fusion of features for detection of brain tumor. Pattern Recognit Lett. 2020;129:150–7.10.1016/j.patrec.2019.11.017Search in Google Scholar

[20] Panwar A, Kumar SA. Localization schemes in wireless sensor networks. In 2012 Second International Conference on Advanced Computing & Communication Technologies. IEEE; 2012. p. 443–9.10.1109/ACCT.2012.67Search in Google Scholar
Received: 2023-03-04
Revised: 2023-04-13
Accepted: 2023-05-05
Published Online: 2023-08-10

© 2023 the author(s), published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Research Articles
  2. Salp swarm and gray wolf optimizer for improving the efficiency of power supply network in radial distribution systems
  3. Deep learning in distributed denial-of-service attacks detection method for Internet of Things networks
  4. On numerical characterizations of the topological reduction of incomplete information systems based on evidence theory
  5. A novel deep learning-based brain tumor detection using the Bagging ensemble with K-nearest neighbor
  6. Detecting biased user-product ratings for online products using opinion mining
  7. Evaluation and analysis of teaching quality of university teachers using machine learning algorithms
  8. Efficient mutual authentication using Kerberos for resource constraint smart meter in advanced metering infrastructure
  9. Recognition of English speech – using a deep learning algorithm
  10. A new method for writer identification based on historical documents
  11. Intelligent gloves: An IT intervention for deaf-mute people
  12. Reinforcement learning with Gaussian process regression using variational free energy
  13. Anti-leakage method of network sensitive information data based on homomorphic encryption
  14. An intelligent algorithm for fast machine translation of long English sentences
  15. A lattice-transformer-graph deep learning model for Chinese named entity recognition
  16. Robot indoor navigation point cloud map generation algorithm based on visual sensing
  17. Towards a better similarity algorithm for host-based intrusion detection system
  18. A multiorder feature tracking and explanation strategy for explainable deep learning
  19. Application study of ant colony algorithm for network data transmission path scheduling optimization
  20. Data analysis with performance and privacy enhanced classification
  21. Motion vector steganography algorithm of sports training video integrating with artificial bee colony algorithm and human-centered AI for web applications
  22. Multi-sensor remote sensing image alignment based on fast algorithms
  23. Replay attack detection based on deformable convolutional neural network and temporal-frequency attention model
  24. Validation of machine learning ridge regression models using Monte Carlo, bootstrap, and variations in cross-validation
  25. Computer technology of multisensor data fusion based on FWA–BP network
  26. Application of adaptive improved DE algorithm based on multi-angle search rotation crossover strategy in multi-circuit testing optimization
  27. HWCD: A hybrid approach for image compression using wavelet, encryption using confusion, and decryption using diffusion scheme
  28. Environmental landscape design and planning system based on computer vision and deep learning
  29. Wireless sensor node localization algorithm combined with PSO-DFP
  30. Development of a digital employee rating evaluation system (DERES) based on machine learning algorithms and 360-degree method
  31. A BiLSTM-attention-based point-of-interest recommendation algorithm
  32. Development and research of deep neural network fusion computer vision technology
  33. Face recognition of remote monitoring under the Ipv6 protocol technology of Internet of Things architecture
  34. Research on the center extraction algorithm of structured light fringe based on an improved gray gravity center method
  35. Anomaly detection for maritime navigation based on probability density function of error of reconstruction
  36. A novel hybrid CNN-LSTM approach for assessing StackOverflow post quality
  37. Integrating k-means clustering algorithm for the symbiotic relationship of aesthetic community spatial science
  38. Improved kernel density peaks clustering for plant image segmentation applications
  39. Biomedical event extraction using pre-trained SciBERT
  40. Sentiment analysis method of consumer comment text based on BERT and hierarchical attention in e-commerce big data environment
  41. An intelligent decision methodology for triangular Pythagorean fuzzy MADM and applications to college English teaching quality evaluation
  42. Ensemble of explainable artificial intelligence predictions through discriminate regions: A model to identify COVID-19 from chest X-ray images
  43. Image feature extraction algorithm based on visual information
  44. Optimizing genetic prediction: Define-by-run DL approach in DNA sequencing
  45. Study on recognition and classification of English accents using deep learning algorithms
  46. Review Articles
  47. Dimensions of artificial intelligence techniques, blockchain, and cyber security in the Internet of medical things: Opportunities, challenges, and future directions
  48. A systematic literature review of undiscovered vulnerabilities and tools in smart contract technology
  49. Special Issue: Trustworthy Artificial Intelligence for Big Data-Driven Research Applications based on Internet of Everythings
  50. Deep learning for content-based image retrieval in FHE algorithms
  51. Improving binary crow search algorithm for feature selection
  52. Enhancement of K-means clustering in big data based on equilibrium optimizer algorithm
  53. A study on predicting crime rates through machine learning and data mining using text
  54. Deep learning models for multilabel ECG abnormalities classification: A comparative study using TPE optimization
  55. Predicting medicine demand using deep learning techniques: A review
  56. A novel distance vector hop localization method for wireless sensor networks
  57. Development of an intelligent controller for sports training system based on FPGA
  58. Analyzing SQL payloads using logistic regression in a big data environment
  59. Classifying cuneiform symbols using machine learning algorithms with unigram features on a balanced dataset
  60. Waste material classification using performance evaluation of deep learning models
  61. A deep neural network model for paternity testing based on 15-loci STR for Iraqi families
  62. AttentionPose: Attention-driven end-to-end model for precise 6D pose estimation
  63. The impact of innovation and digitalization on the quality of higher education: A study of selected universities in Uzbekistan
  64. A transfer learning approach for the classification of liver cancer
  65. Review of iris segmentation and recognition using deep learning to improve biometric application
  66. Special Issue: Intelligent Robotics for Smart Cities
  67. Accurate and real-time object detection in crowded indoor spaces based on the fusion of DBSCAN algorithm and improved YOLOv4-tiny network
  68. CMOR motion planning and accuracy control for heavy-duty robots
  69. Smart robots’ virus defense using data mining technology
  70. Broadcast speech recognition and control system based on Internet of Things sensors for smart cities
  71. Special Issue on International Conference on Computing Communication & Informatics 2022
  72. Intelligent control system for industrial robots based on multi-source data fusion
  73. Construction pit deformation measurement technology based on neural network algorithm
  74. Intelligent financial decision support system based on big data
  75. Design model-free adaptive PID controller based on lazy learning algorithm
  76. Intelligent medical IoT health monitoring system based on VR and wearable devices
  77. Feature extraction algorithm of anti-jamming cyclic frequency of electronic communication signal
  78. Intelligent auditing techniques for enterprise finance
  79. Improvement of predictive control algorithm based on fuzzy fractional order PID
  80. Multilevel thresholding image segmentation algorithm based on Mumford–Shah model
  81. Special Issue: Current IoT Trends, Issues, and Future Potential Using AI & Machine Learning Techniques
  82. Automatic adaptive weighted fusion of features-based approach for plant disease identification
  83. A multi-crop disease identification approach based on residual attention learning
  84. Aspect-based sentiment analysis on multi-domain reviews through word embedding
  85. RES-KELM fusion model based on non-iterative deterministic learning classifier for classification of Covid19 chest X-ray images
  86. A review of small object and movement detection based loss function and optimized technique
https://doi.org/10.1515/jisys-2023-0031
Keywords for this article
localization; WSN; energy; sensor nodes; technologies; network; deployment
Creative Commons
BY 4.0

Articles in the same Issue

  1. Research Articles
  2. Salp swarm and gray wolf optimizer for improving the efficiency of power supply network in radial distribution systems
  3. Deep learning in distributed denial-of-service attacks detection method for Internet of Things networks
  4. On numerical characterizations of the topological reduction of incomplete information systems based on evidence theory
  5. A novel deep learning-based brain tumor detection using the Bagging ensemble with K-nearest neighbor
  6. Detecting biased user-product ratings for online products using opinion mining
  7. Evaluation and analysis of teaching quality of university teachers using machine learning algorithms
  8. Efficient mutual authentication using Kerberos for resource constraint smart meter in advanced metering infrastructure
  9. Recognition of English speech – using a deep learning algorithm
  10. A new method for writer identification based on historical documents
  11. Intelligent gloves: An IT intervention for deaf-mute people
  12. Reinforcement learning with Gaussian process regression using variational free energy
  13. Anti-leakage method of network sensitive information data based on homomorphic encryption
  14. An intelligent algorithm for fast machine translation of long English sentences
  15. A lattice-transformer-graph deep learning model for Chinese named entity recognition
  16. Robot indoor navigation point cloud map generation algorithm based on visual sensing
  17. Towards a better similarity algorithm for host-based intrusion detection system
  18. A multiorder feature tracking and explanation strategy for explainable deep learning
  19. Application study of ant colony algorithm for network data transmission path scheduling optimization
  20. Data analysis with performance and privacy enhanced classification
  21. Motion vector steganography algorithm of sports training video integrating with artificial bee colony algorithm and human-centered AI for web applications
  22. Multi-sensor remote sensing image alignment based on fast algorithms
  23. Replay attack detection based on deformable convolutional neural network and temporal-frequency attention model
  24. Validation of machine learning ridge regression models using Monte Carlo, bootstrap, and variations in cross-validation
  25. Computer technology of multisensor data fusion based on FWA–BP network
  26. Application of adaptive improved DE algorithm based on multi-angle search rotation crossover strategy in multi-circuit testing optimization
  27. HWCD: A hybrid approach for image compression using wavelet, encryption using confusion, and decryption using diffusion scheme
  28. Environmental landscape design and planning system based on computer vision and deep learning
  29. Wireless sensor node localization algorithm combined with PSO-DFP
  30. Development of a digital employee rating evaluation system (DERES) based on machine learning algorithms and 360-degree method
  31. A BiLSTM-attention-based point-of-interest recommendation algorithm
  32. Development and research of deep neural network fusion computer vision technology
  33. Face recognition of remote monitoring under the Ipv6 protocol technology of Internet of Things architecture
  34. Research on the center extraction algorithm of structured light fringe based on an improved gray gravity center method
  35. Anomaly detection for maritime navigation based on probability density function of error of reconstruction
  36. A novel hybrid CNN-LSTM approach for assessing StackOverflow post quality
  37. Integrating k-means clustering algorithm for the symbiotic relationship of aesthetic community spatial science
  38. Improved kernel density peaks clustering for plant image segmentation applications
  39. Biomedical event extraction using pre-trained SciBERT
  40. Sentiment analysis method of consumer comment text based on BERT and hierarchical attention in e-commerce big data environment
  41. An intelligent decision methodology for triangular Pythagorean fuzzy MADM and applications to college English teaching quality evaluation
  42. Ensemble of explainable artificial intelligence predictions through discriminate regions: A model to identify COVID-19 from chest X-ray images
  43. Image feature extraction algorithm based on visual information
  44. Optimizing genetic prediction: Define-by-run DL approach in DNA sequencing
  45. Study on recognition and classification of English accents using deep learning algorithms
  46. Review Articles
  47. Dimensions of artificial intelligence techniques, blockchain, and cyber security in the Internet of medical things: Opportunities, challenges, and future directions
  48. A systematic literature review of undiscovered vulnerabilities and tools in smart contract technology
  49. Special Issue: Trustworthy Artificial Intelligence for Big Data-Driven Research Applications based on Internet of Everythings
  50. Deep learning for content-based image retrieval in FHE algorithms
  51. Improving binary crow search algorithm for feature selection
  52. Enhancement of K-means clustering in big data based on equilibrium optimizer algorithm
  53. A study on predicting crime rates through machine learning and data mining using text
  54. Deep learning models for multilabel ECG abnormalities classification: A comparative study using TPE optimization
  55. Predicting medicine demand using deep learning techniques: A review
  56. A novel distance vector hop localization method for wireless sensor networks
  57. Development of an intelligent controller for sports training system based on FPGA
  58. Analyzing SQL payloads using logistic regression in a big data environment
  59. Classifying cuneiform symbols using machine learning algorithms with unigram features on a balanced dataset
  60. Waste material classification using performance evaluation of deep learning models
  61. A deep neural network model for paternity testing based on 15-loci STR for Iraqi families
  62. AttentionPose: Attention-driven end-to-end model for precise 6D pose estimation
  63. The impact of innovation and digitalization on the quality of higher education: A study of selected universities in Uzbekistan
  64. A transfer learning approach for the classification of liver cancer
  65. Review of iris segmentation and recognition using deep learning to improve biometric application
  66. Special Issue: Intelligent Robotics for Smart Cities
  67. Accurate and real-time object detection in crowded indoor spaces based on the fusion of DBSCAN algorithm and improved YOLOv4-tiny network
  68. CMOR motion planning and accuracy control for heavy-duty robots
  69. Smart robots’ virus defense using data mining technology
  70. Broadcast speech recognition and control system based on Internet of Things sensors for smart cities
  71. Special Issue on International Conference on Computing Communication & Informatics 2022
  72. Intelligent control system for industrial robots based on multi-source data fusion
  73. Construction pit deformation measurement technology based on neural network algorithm
  74. Intelligent financial decision support system based on big data
  75. Design model-free adaptive PID controller based on lazy learning algorithm
  76. Intelligent medical IoT health monitoring system based on VR and wearable devices
  77. Feature extraction algorithm of anti-jamming cyclic frequency of electronic communication signal
  78. Intelligent auditing techniques for enterprise finance
  79. Improvement of predictive control algorithm based on fuzzy fractional order PID
  80. Multilevel thresholding image segmentation algorithm based on Mumford–Shah model
  81. Special Issue: Current IoT Trends, Issues, and Future Potential Using AI & Machine Learning Techniques
  82. Automatic adaptive weighted fusion of features-based approach for plant disease identification
  83. A multi-crop disease identification approach based on residual attention learning
  84. Aspect-based sentiment analysis on multi-domain reviews through word embedding
  85. RES-KELM fusion model based on non-iterative deterministic learning classifier for classification of Covid19 chest X-ray images
  86. A review of small object and movement detection based loss function and optimized technique
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 16.12.2025 from https://www.degruyterbrill.com/document/doi/10.1515/jisys-2023-0031/html
Scroll to top button