Effect of curved geometrical aspects of Savonius rotor on turbine performance using factorial design analysis

2.1 Savonius rotor

1920 was the year that saw the publication of the Savonius rotor’s initial design, and this rotor was later used in fluids that were composed of water and wind [46]. One type of vertical-axis turbine is known as a Savonius turbine. The conventional Savonius is composed of blades formed from cut pipe cylinders, positioned on opposite sides to form the letter “S” [47]. The Savonius shape, as seen in Figure 3a, is a straightforward design consisting of a blade, a shaft, and an endplate. The Savonius design is inspired by the concept of the Flanner ship turbine, which enables the rotation of two semi-circular blades in a sideways direction. This principle is illustrated in the schematic shown in Figure 3b [48]. It is possible to enhance the performance of the Savonius rotor by conducting extensive research on its advantages, including its straightforward shape, which facilitates easy construction [49].

Figure 3

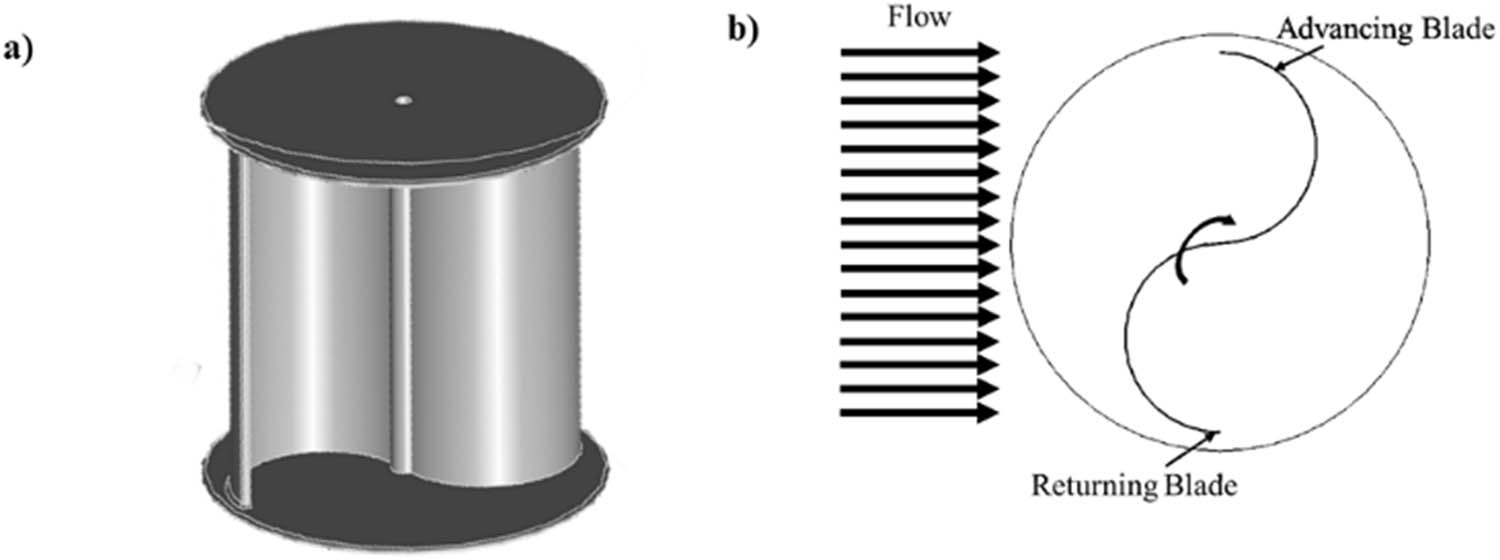
(a) Design of Savonius, and (b) working principle of Savonius.

Savonius’s research is facilitated by the ability to use CFD modeling, as many of his developments are driven by geometric changes and are progressing rapidly. Table 1 summarizes several advancements in wind-Savonius rotor design over the past 5 years, emphasizing geometry factors and utilizing CFD techniques. Lajnef et al. [50] investigated the modification of the helix rotor using two methods: modeling and experimentation. The validation of the modeling research conducted is demonstrated through both methods. The research aimed to enhance comprehension of the aerodynamic working principles of blade modification by analyzing the pressure distribution contours. Therefore, the optimal angle for the geometry change in this analysis remains to be determined due to deficiencies in comparing helix angle variations. Patel et al. [51] researched the effect of changing the blade’s shape to elliptical and applying it to a two-stage Savonius. The research was conducted experimentally and using numerical 3D modeling. The results show that the two-stage elliptical shape performs better than the single-stage.

In another study, Prabowoputra et al. [36] examined the stage ratio of a two-stage Savonius turbine with a PSA of 30°. The choice of a 30° PSA was made based on the findings of Prabowoputra and Prabowo [28], who concluded that a 30° PSA was the optimal choice. Research on the stage ratio [36] indicates that optimal performance is achieved at a ratio of 2:1. However, this research is limited to a PSA of 30°. Hence, the relationship between the PSA factor and stage ratio remains uncertain. The CFD research employs a mesh-independent investigation phase to select the most suitable mesh for modeling [32].

Chegini et al. [52] performed CFD simulations on a hybrid rotor system consisting of Savonius and Darrieus rotors. This study demonstrates that incorporating a Savonius rotor enhances the Darrieus turbine’s ability to start independently and improves its overall efficiency when combined with a deflector. Nevertheless, this research continues to prioritize high TSR. Modifications to the design of the “divergent slot” and “convergent slot” have been implemented in the Savonius rotor investigation [53]. This study focused on examining the parameters related to the slot position on the blade. In general, the research being conducted on the Savonius rotor focuses on optimizing rotor design to examine the influence of rotor geometry on turbine performance. Table 1 shows various studies conducted to develop geometry modifications to improve Savonius performance. The research optimizes several geometric ratios or changes the shape of the main rotor components, such as blades, and adds guide blades or deflectors.

2.2 Rotor design and design parameters

This research uses three-dimensional modeling with the CFD method. The factors used in this study are PSA, blade shape, and TSR. The purpose of varying the PSA on the Savonius rotor is to investigate its effect on fluid flow around the rotating body. The PSA influences pressure distribution, flow pattern, and forces acting on the rotor. By testing from various angles, it is possible to understand how the air or fluid flow functions around the rotor under different conditions. TSR significantly influences rotor performance [59]; therefore, this factor is considered in this study with four levels. Previous research has shown that the PSA influences the performance of two-stage Savonius turbines [12]. Based on this research, the PSA factor was retested in combination with modifications to the blade shape. The PSA in this research employed three levels: 0°, 25°, and 35°. The two-stage Savonius rotor’s PSA is varied to 0°, 25°, and 35° to understand the influence of different angles on fluid flow, pressure distribution, and rotational efficiency. This research is crucial for determining the optimal angle to maximize the power generated by the rotor, enhance energy efficiency, and enable the turbine to adapt to varying fluid flow speeds and directions. The shape of the blade used in this study is categorized into three types based on its size, height, and length, as shown in Figure 3. The dimensions of the Savonius rotor used are shown in Table 2. Figure 4 shows the three-dimensional shape of the rotor used in this study. The AR of this Savonius rotor is 1 using Eq. (1) [60]. For the overlap ratio design parameter, an overlap ratio value of 0 was used, as specified in Eq. (2) [60]. The endplate ratio (ER) used in this study is 1.095, as calculated using Eq. (3) [60]. Figure 4 also illustrates the three-dimensional forms of rotor type-1 at PSA angles of 0°, 25°, and 35°, rotor type-2 at PSA angles of 0°, 25°, and 35°, and rotor type-3 at PSA angles of 0°, 25°, and 35°. The blade shape in this variation can be expressed in terms of an elliptical ratio (ELR), as shown in Eq. (4), where the ELR used is 0.5, 0.33, and 0.25. The stage ratio used here is 1, which is obtained from Eq. (5) [36]. The variation design shown in Figure 5 was obtained using a factorial design with factors of PSA, TSR, and blade shape.

Figure 4

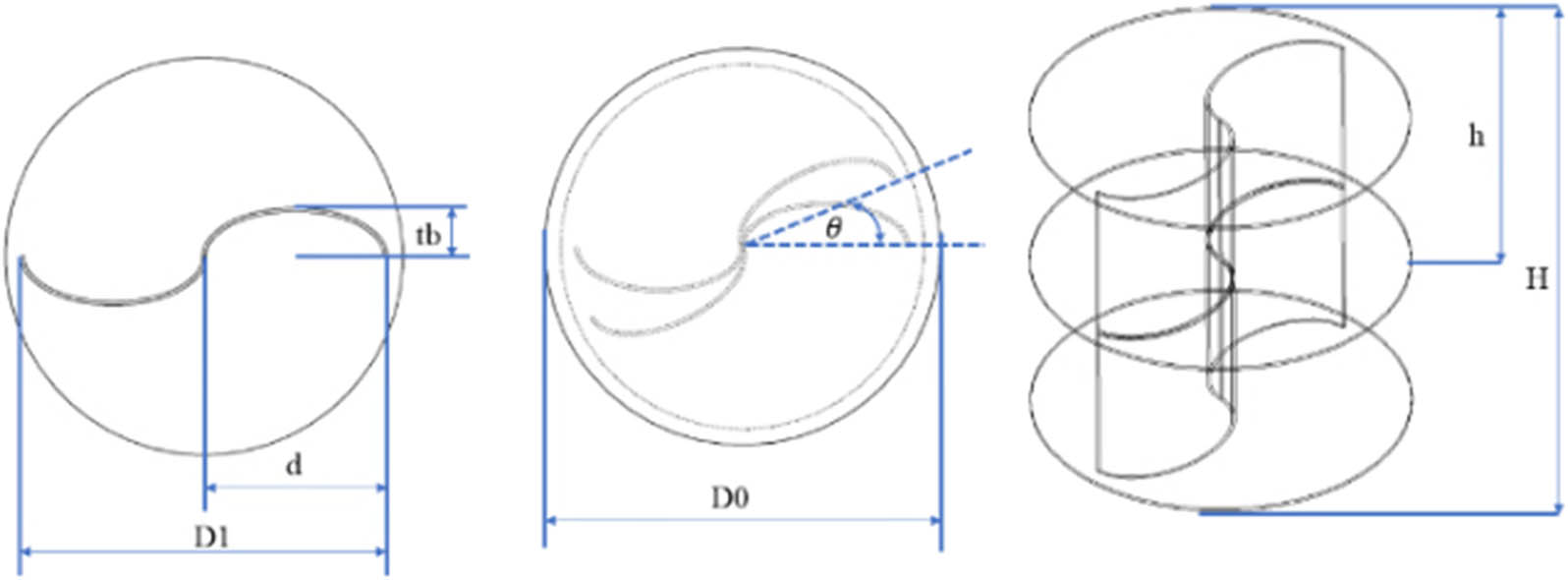
Savonius rotor design with dimension information.

Figure 5

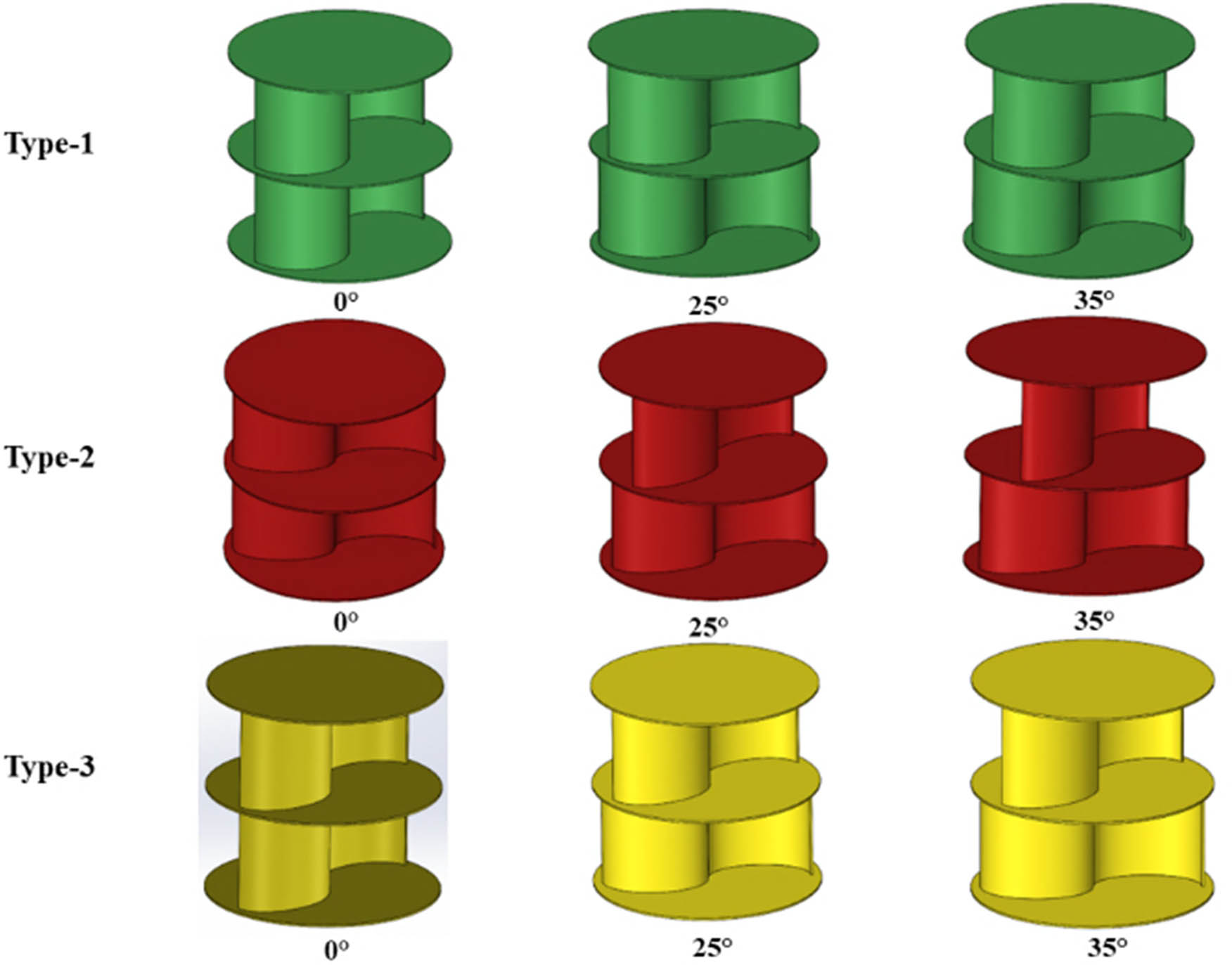
The three-dimensional design of the Savonius rotor.

AR:

Overlap ratio (OR):

ER:

ELR:

SR:

Turbine performance in fluid energy systems, such as wind and hydrokinetic turbines, is primarily governed by the interaction between the fluid’s mass flow rate and the turbine’s swept area. The mass flow rate, expressed in Eq. (6), quantifies the rate at which kinetic energy is transferred to the turbine. This leads to the theoretically available power, as shown in Eq. (7), which depends on the cube of the free stream velocity [60].

where V is the free flow speed, and ρ is the fluid density. Nevertheless, due to aerodynamic and hydrodynamic losses, only a fraction of this power is converted into sound mechanical energy. The power coefficient C p , introduced in Eq. (8), captures this efficiency and varies with the TSR λ , defined in Eq. (9) as the ratio between blade tip speed and free stream speed. Moreover, torque efficiency is also essential and is represented by the torque coefficient C m , as shown in Eq. (10). These performance metrics, C p and C m , are fundamental for evaluating the aerodynamic behavior of turbines such as the Savonius rotor under varying flow and geometric conditions.

where C p depends on a speed factor λ also known as TSR, which is the ratio between rotational speed ω and free flow speed V , as expressed in Eq. (9).

Hence, plotting C p against λ could assess the turbine performance. Another critical performance parameter is the moment or torque coefficient, C m , developed by the turbine, which directly relates to power and is expressed in Eq. (10).

where R stands for the turbine radius. AR is a dimensionless parameter defined as the ratio of the turbine height ( H ) to its diameter ( D t ) as shown in Eq. (11). It is a key factor influencing the aerodynamic performance and efficiency of vertical-axis turbines.

The ER describes its size compared with the rotor diameter, and the ratio is expressed in Eq. (12).

One last important Savonius parameter is the OR ; it defines the gap distance between the inner ends of the blades and is expressed as Eq. (13).

Bézier curves are widely used in geometric modeling due to their mathematical elegance and intuitive control. These curves are generated by a set of control points that form a polygon, defining the curve’s general shape. The Bézier curve P ( t ) is calculated as a linear combination of control points B i , each weighted by the Bernstein polynomial J n , i ( t ) , as defined in Eq. (14). The Bernstein basis function itself is a function of the parameter t and the binomial coefficient, as given in Eq. (15). The binomial coefficient n i utilized in the formulation is described by Eq. (16).

The t variable describes from 0 to 1 the trajectory from the initial to the final vertices, representing the interpolation variable. The lower the t step in the calculations, the greater the sensitivity or definition of the curve becomes. Figure 6 graphically illustrates a third-order curve, defined by points B 0 , B 1 , B 2 , B 3 .

Figure 6

Third-order Bézier curve representation [60].

To guarantee continuity between two adjacent Bézier curves, defined by P i and C j , the first derivative in the joint vertex must be equal for both of them; besides, the vertices next to the joint must be colinear. Hence, both the direction and magnitude of the tangent vectors at the joint must be equal, and P n = C 0 must be the midpoint of the line that joins P n − 1 and C 1 .

Eqs. (17) and (18) describe the conditions to make continuous two-degree curves, one defined by P i points and another defined by C j points, as illustrated in Figure 7. The neuron’s output signal y k and a neuron k are described by Eqs. (19) and (20).

Figure 7

First derivative continuity for third-order Bézier curves [60].

An n-degree Bezier curve of order n + 1 is represented by Eq. (21) [24].

The coefficients P i are the control points, and together with the basis function B i , n ( t ) determine the shape of the curve. The control polygon’s control points are connected by lines drawn between them.

where the function i n is the binomial coefficient defined as n ! i ! ( n − i ) ! . The blending functions are referred to as the i th Bernstein basis polynomial of degree n , and t is the number of time intervals.

A general expression for cubic polynomial forms can be written as Eq. (23).

2.3 Turbine performance

The CP value shows the rotor performance parameter, as shown in Eq. (24) [61]. P _t is the rotor power and is shown in Eq. (25) [62]. A non-dimensional TSR indicates the speed ratio between angular and fluid velocities. The TSR formula is shown in Eq. (26), and the torque coefficient is shown in Eq. (27) [63], where T is the torque, ρ is the fluid density, ω is the angular velocity, A is the projection area, and U is the fluid velocity.

2.4 Numerical modeling

The research was conducted using three-dimensional modeling with the CFD method. The governing equation of CFDs comprises several equations, including the continuity and Navier-Stokes equations. The continuity equation is shown in Eq. (28), and the Navier-Stokes equation is shown in Eqs. (29)–(31), where x, y, and z are coordinate axes. Eq. (29) is the x-axis direction, Eq. (30) is the y-axis direction, and Eq. (31) is the z-axis direction. The equation variables are as follows: p represents density, t represents time, u, v, w represent velocities in three Cartesian coordinates, and x, y, and z represent the Cartesian coordinates [62,63].

Savonius modeling consists of two rotary and stationary zones. Figure 8 shows the zone design in the modeling. The next step is to perform the meshing process. Meshing utilizes the tetrahedral method, which offers the advantage of being able to adjust the shape of complex geometries compared to other meshing methods [64,65]. Figure 9 shows the meshing results for the rotary and stationary zones.

Figure 8

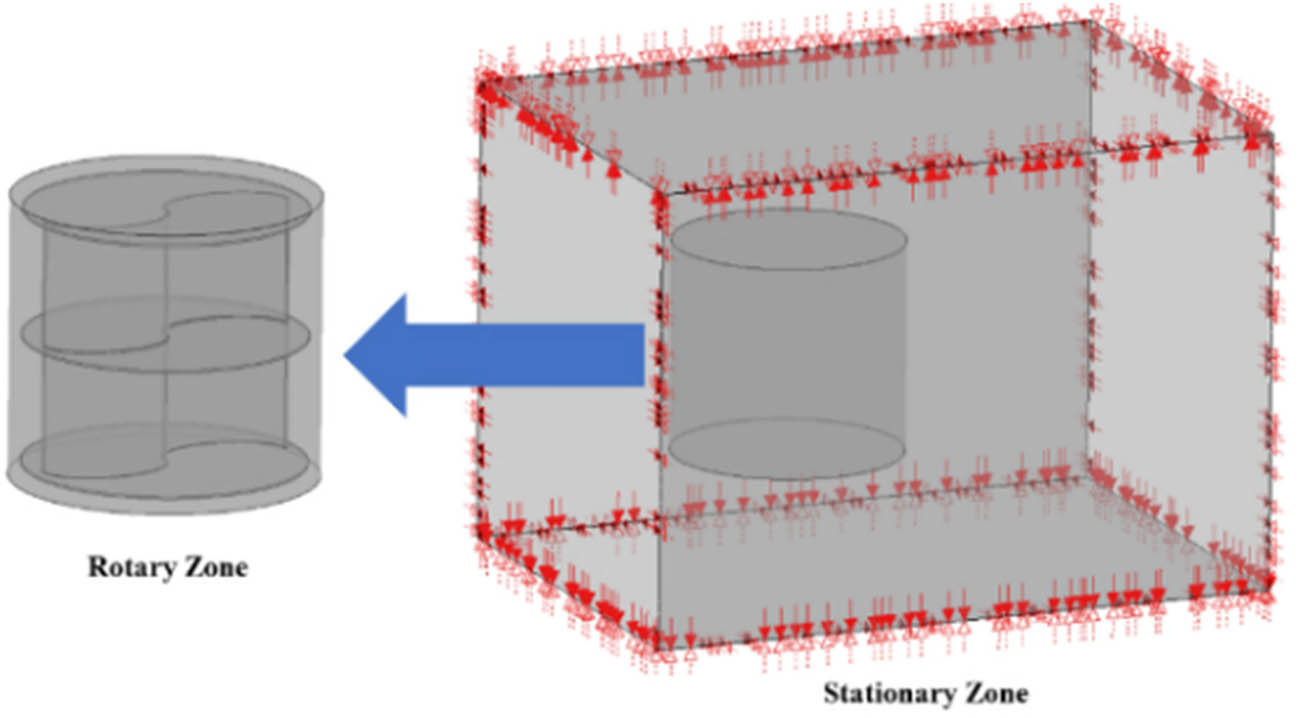
Rotary zone and stationary zone.

Figure 9

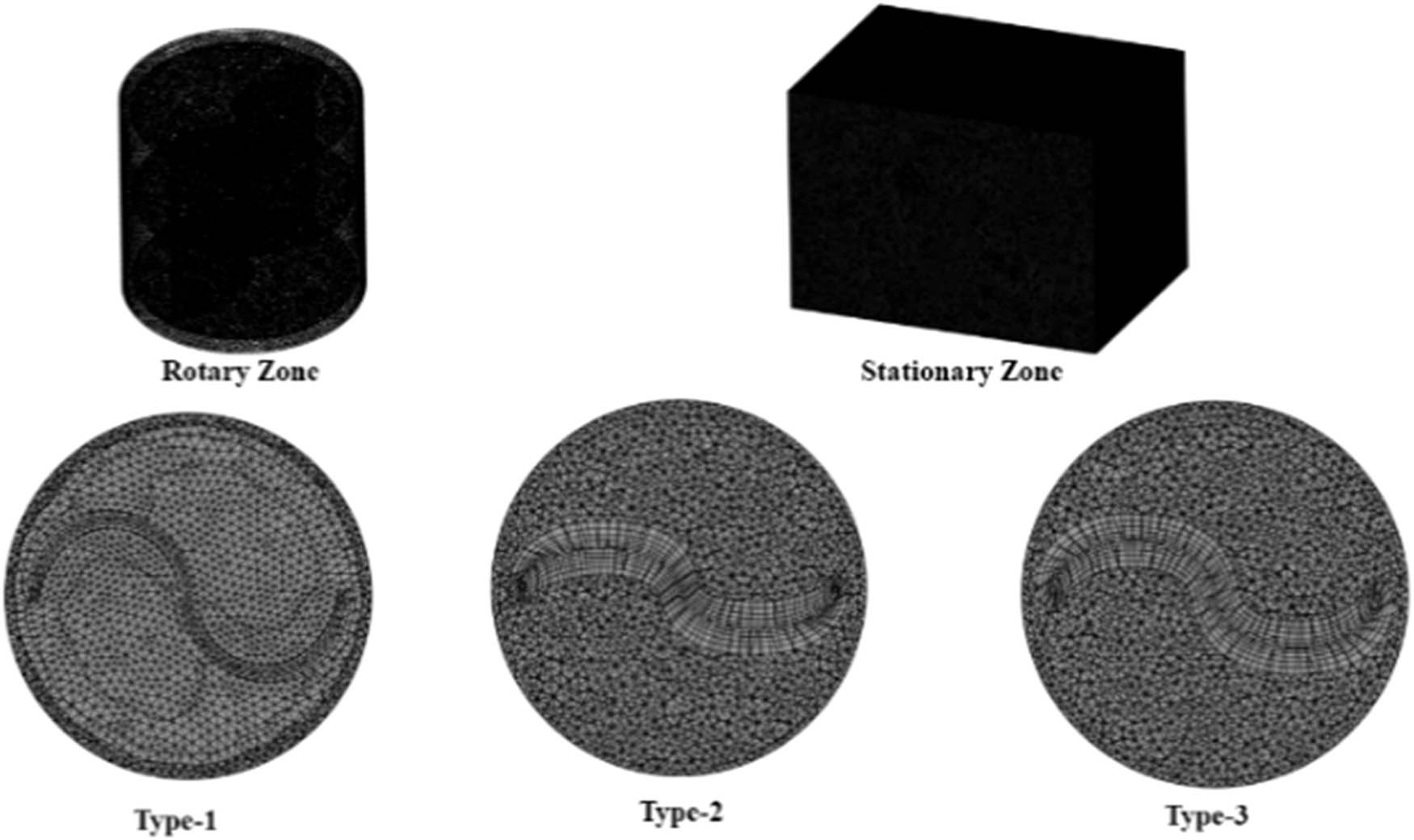
Results of the meshing process.

Modeling boundary conditions is found in the stationary zone. The boundary conditions used are inlet, outlet, and wall. The inlet has a wind speed of 6 m/s, and the outlet uses a static pressure of 1 atm. The modeling schematic is shown in Figure 10, where the wall uses symmetry conditions. This study employs the shear stress transport (SST) turbulence model. Modeling is done at a steady state. The fluid properties used and boundary conditions are shown in Table 3. This study was conducted at a TSR with values of 0.2–1.1.

Figure 10

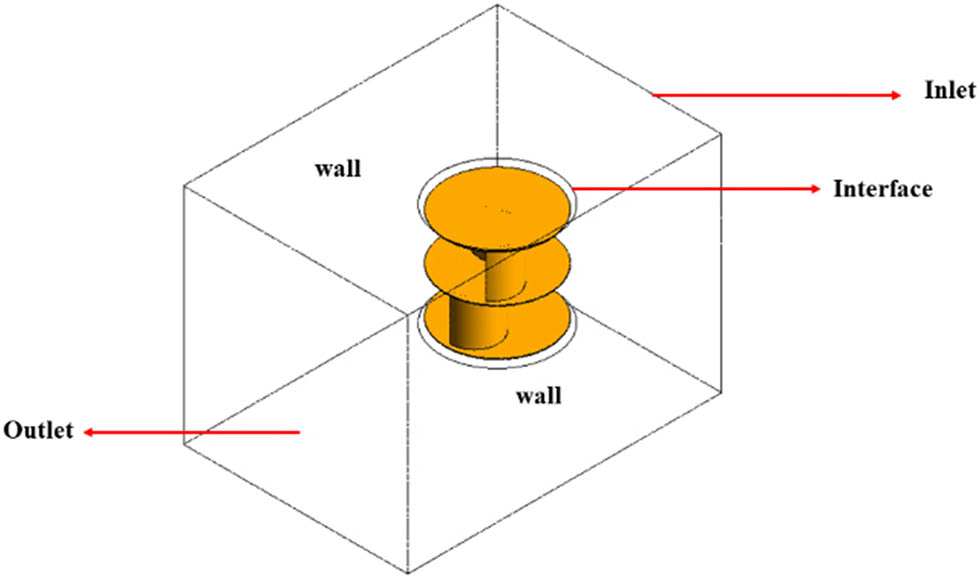
Schematic illustration of the Savonius modeling and simulation.

2.5 Mesh study and benchmarking

Most modeling research using the CFD method involves a mesh study. This mesh study aims to determine the optimal mesh. Some methods for conducting mesh studies, as employed by researchers, are presented in Table 4. Multiple adjustments are made when determining the appropriate meshing settings. This is done to determine the optimal number of meshes in the modeling process, commonly referred to as a mesh study. The number of meshes will affect the modeling’s running time. Figure 11 shows the ratio of the mesh study process graph, where the setting ratio with 713,385 elements produces the optimal mesh.

Figure 11

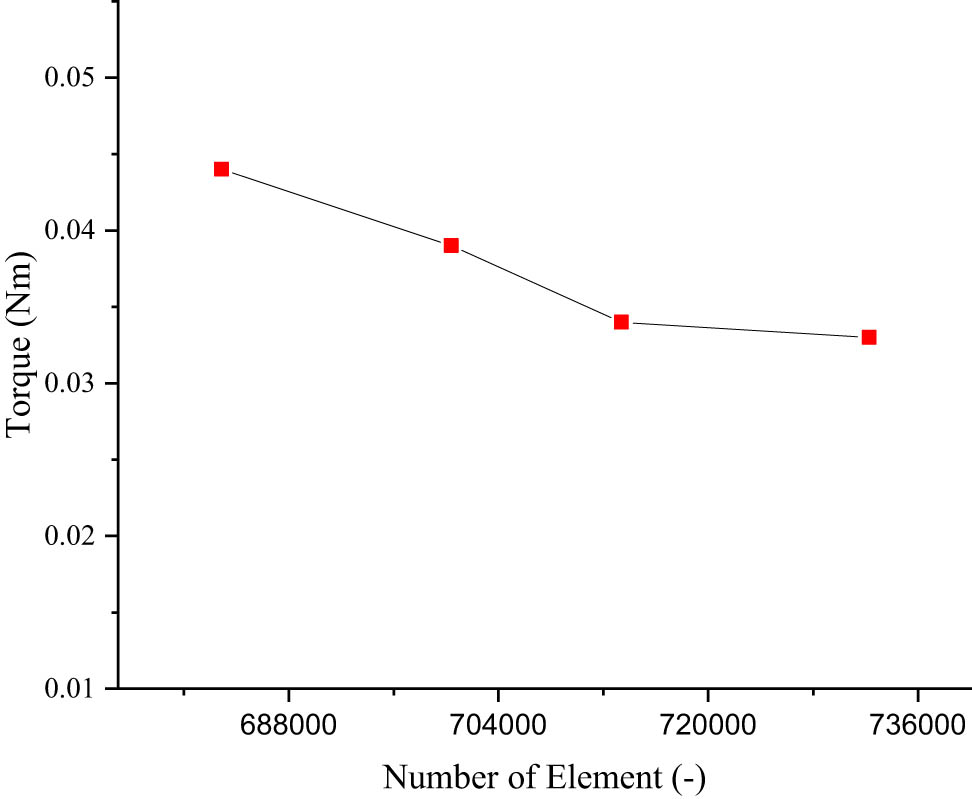
Graph of the mesh convergence study.

Roy and Saha conducted experimental research to conduct benchmarking [68]. The benchmarking results are presented in Figure 12. The difference between the benchmarking results of the modeling performed and Roy’s experiment is 3%. Benchmarking errors are calculated by determining the difference between the simulation results and those of other studies, using the mean absolute error (MAE), as presented in Eq. (32).

where f i is the value of the simulation results, y i is the experimental value, and n is the number of variants. This difference is lower than that reported in some other studies, such as research conducted by Lajnef et al. [50] and Abdullah and Ismail [69], by 5 and 5.5%, respectively. Because its error value is below that of other studies, this modeling can be used for testing in further modeling.

Figure 12

Benchmarking of the numerical model with experiment [27].

2.6 Factorial design approach

Factorial design is an experimental method used to study the effects of several factors simultaneously, and it is constructive in strengthening the conclusions of the research [70,71,72,73,74,75,76]. Through this analysis, it is possible to determine the significance of a factor and the involvement of interactions between factors, thereby deepening the analysis. On the other hand, analysis of variance (ANOVA) can be used to determine the main effects and interactions between factors [77,78,79,80,81]. In ANOVA, the F-value is calculated and compared with the F-table value at a 95% confidence level. The 95% confidence level or α value of 0.05 is commonly used in analyzing the significance test of a factor. The three variables analyzed in this investigation using a factorial design are the rotational speed factor, blade shape, and PSA. Using a factorial design, we can determine the interaction between the two factors and assess the significance of each factor. To conclude from the FDA results, compare the F value of the results to the F value in the table, which is based on the degrees of freedom for that factor. The fundamental calculations are provided in Eqs. (33)–(40) and are subsequently presented in Table 5 [60,61,62]. The sum of squares equation for each effect is [70]

When referring to a research factor denoted by A, B, and C, the notations “a,” “b,” and “c” denote its degree of freedom. The AB notation is used to estimate the interaction between components A and B. The AC notation is used to assess the interaction of components A and C. The BC notation is used to assess the interaction of components B and C. Table 6 shows the results of the computations performed using Eqs. (33)–(40) [70].

3.1 Aerodynamic performance of Savonius turbine

The modeling results are torque values and pressure contours in the fluid. The torque value is converted to CP, where CP is the performance parameter of the rotor. Then, the results of the CP are analyzed using factorial design and ANOVA to determine the significance of these factors. Figure 13 illustrates the modeling results in a graph that displays the relationship between CP and TSR. The type-1 rotor reaches CPmax at TSR 0.8 for all PSA variations. The CPmax values for each PSA are 0.27 at 0° PSA, 0.32 at 25° PSA, and 0.26 at 35° PSA. Unlike the type-1 rotor, the CPmax on the type-2 rotor is achieved at TSR 0.5 for all PSA variations. PSA 0° produces a CPmax of 0.14, PSA 25° of 0.22, and PSA 35° of 0.158. The type-3 rotor produces a CPmax of 0.178 at PSA 0° and a CPmax of 0.26 at PSA 25°. PSA 0° and PSA 25° reached CPmax at TSR 0.8, while PSA 35° reached TSR 0.5 at 0.192. This research shows an increase when compared to previous research [32], where research on PSA variations obtained a CPmax value of only 0.29 at a 30° PSA rotor. when compared to this research, there is an increase in Cpmax by 10%.

Figure 13

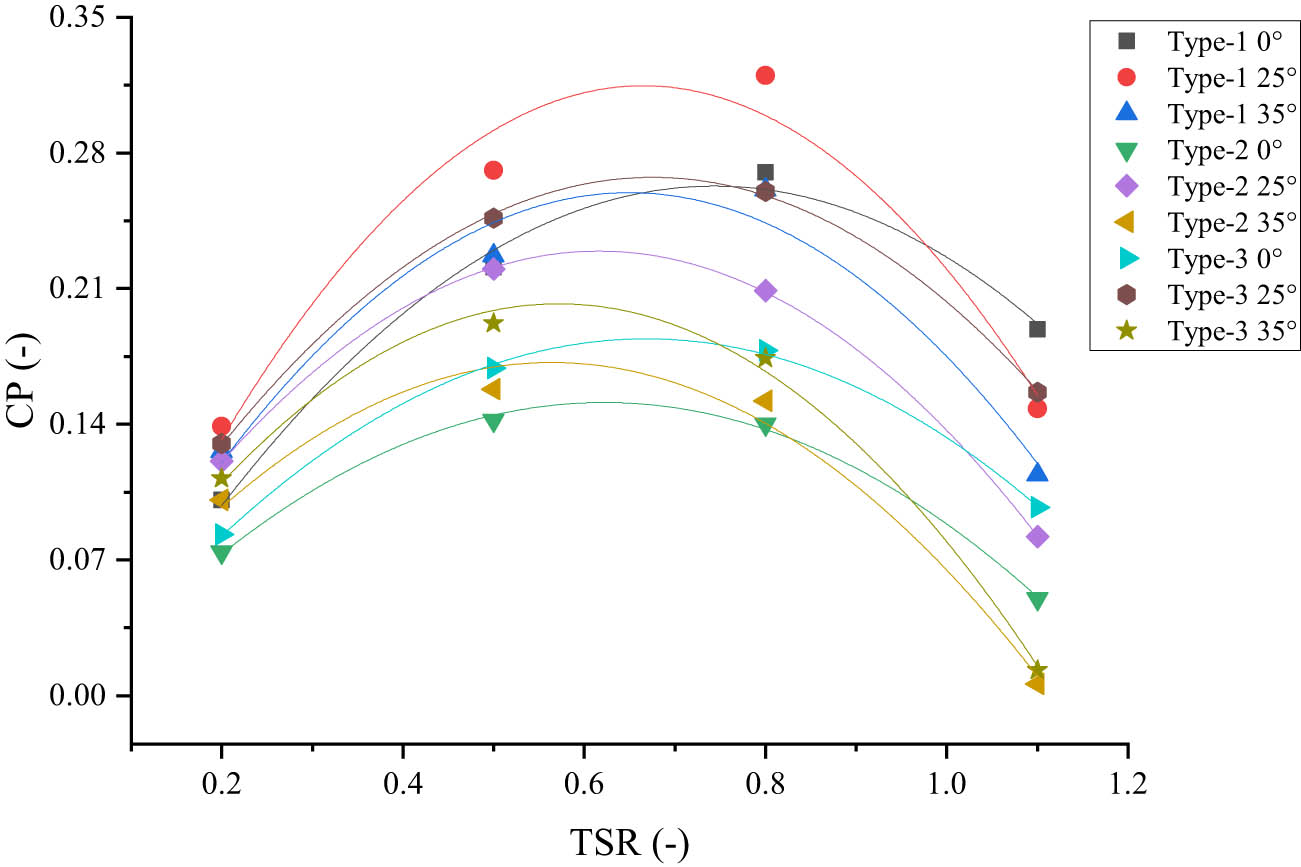
Relationship graph of TSR and CP on the Savonius rotor.

The performance of the Savonius turbine can also be assessed by examining the coefficient of thrust (C _t), as depicted in Figure 14. The maximum Coefficient of Torque (CTmax) was achieved at a pressure of 25° PSA for rotor types 1 and 2. Type-1 achieved a CTmax of 0.695 at a phase-shift angle (PSA) of 25°, 0.63 at a PSA of 35°, and 0.505 at a PSA of 0°. Type-2 achieved a CTmax of 0.605 at a PSA of 25°. In type-2, the pattern is analogous to type-1, with PSA 25° followed by the production of PSA 35° and finally PSA 0° in consecutive order. The specific figures for these PSAs are 0.505 and 0.37, respectively. Type-1 achieved a CTmax of 0.65 at a PSA of 25°. At a PSA of 35 °, it yielded a CTmax of 0.56; at a PSA of 0 °, it yielded a CTmax of 0.415.

Figure 14

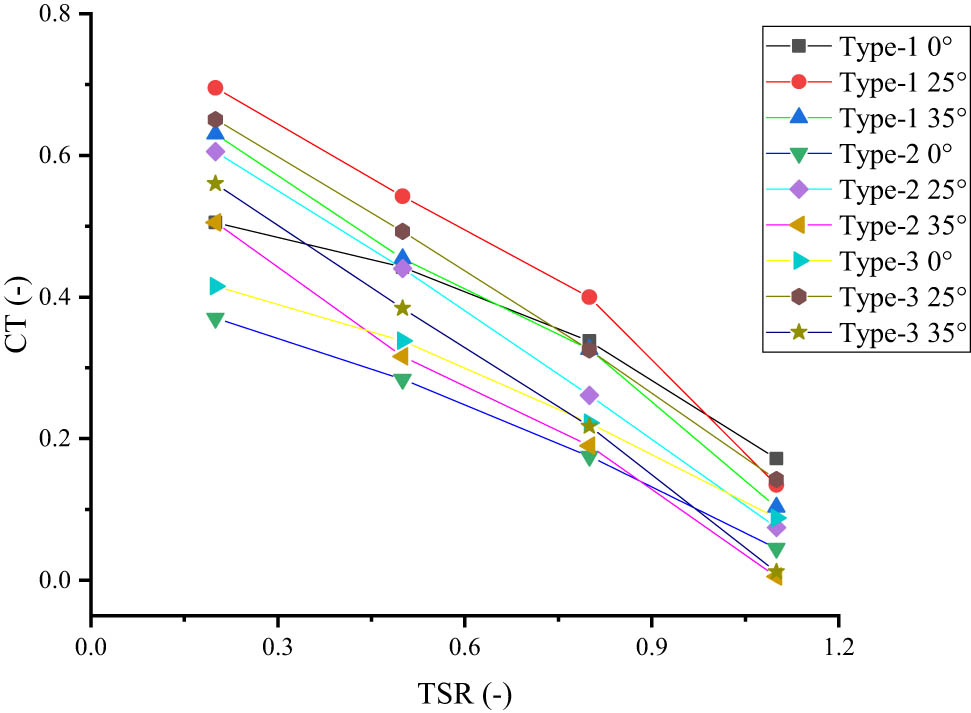
Relationship graph of TSR and Ct on the Savonius rotor.

3.2 Pressure contours

Modeling performed on the Savonius rotor, in addition to generating torque, also produces pressure contours. The pressure contours of type-1 rotor are shown in Figure 15, type-2 in Figure 16, and type-3 in Figure 17. Stage 1 in Figure 15 displays similar pressure contours, with the maximum pressures at PSA 0°, PSA 25°, and PSA 35° being 64.4, 67.1, and 68.2 MPa, respectively. The maximum pressure in each variation at stage 1 is located at the same position, which is at the bottom edge of the blade. The contour shape at stage 2 is different due to the change in angle at the PSA formed at stage 2. The maximum pressure at stage 2 includes 64.6 MPa at PSA 0°, 66.6 MPa at PSA 25°, and 57.57 MPa at PSA 35°. Stage 2 shows the maximum pressure position at the bottom of the blade for all PSA variations; however, at this stage, there are differences in the wake zone area. The 35° PSA has the most expansive wake zone among other variations. Particularly at PSA angles of 0° and 25°, stage 1 exhibits a pressure distribution that is somewhat centered on the rotor’s leading edge. This can suggest the first phase of the rotor’s contact with the fluid flow, where the high pressure is more confined to one side. Particularly at 35°, stage 2 exhibits a more diffuse high-pressure pattern. This could mean that the rotor has turned so that the lift force exceeds the drag force, distributing the high pressure more fairly around the rotor.

Figure 15

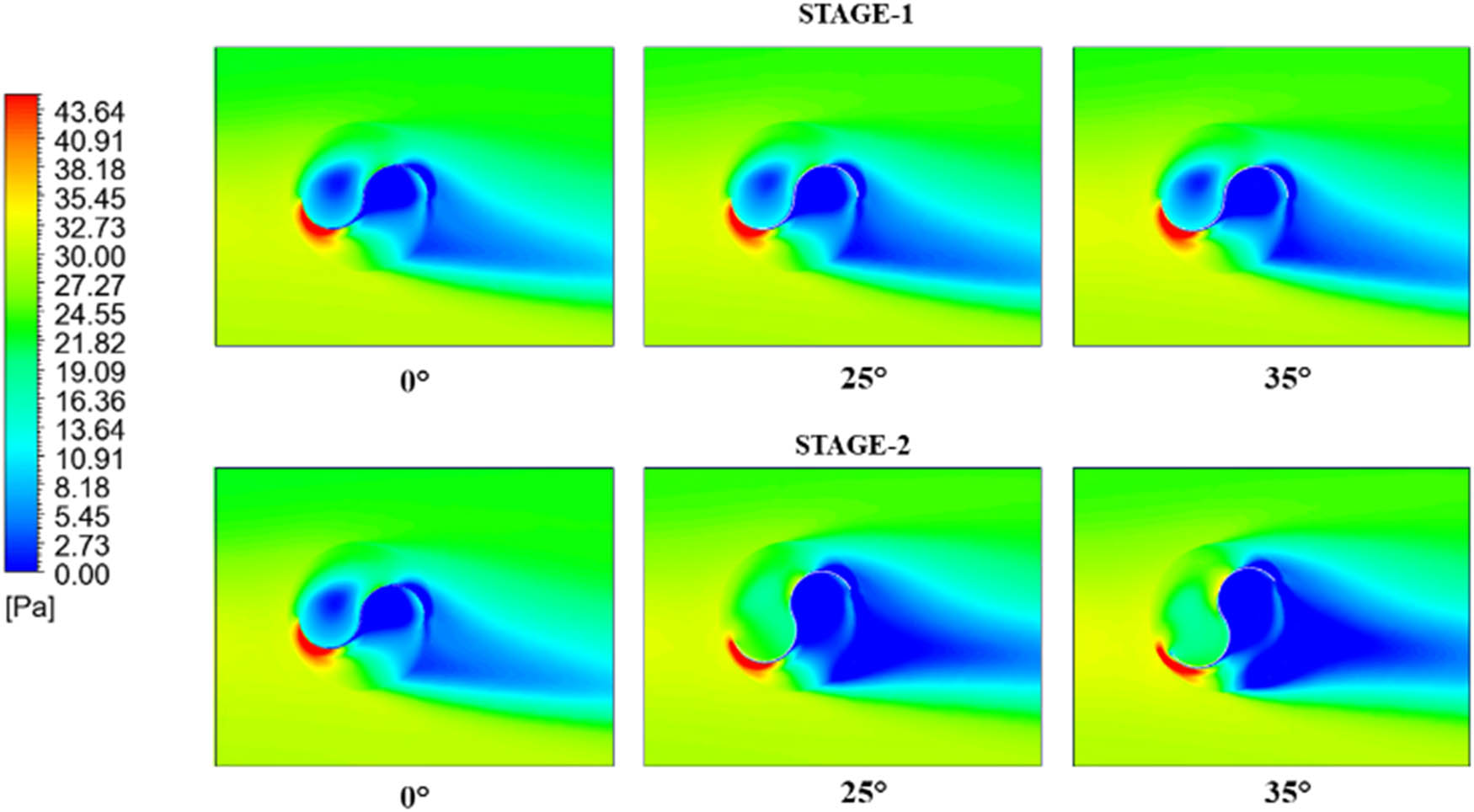
Pressure contour of Savonius type-1 rotor.

Figure 16

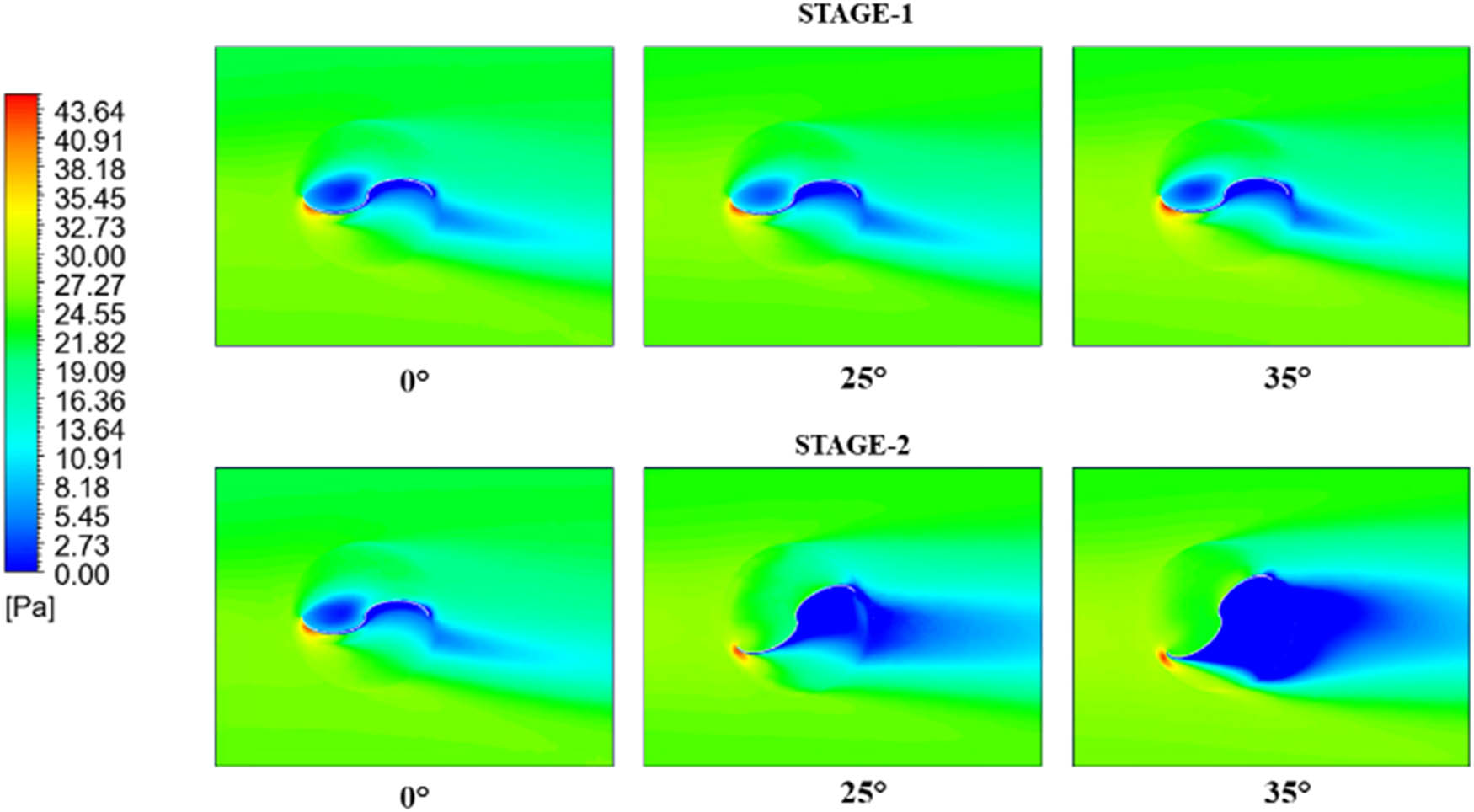
Pressure contour of Savonius type-2 rotor.

Figure 17

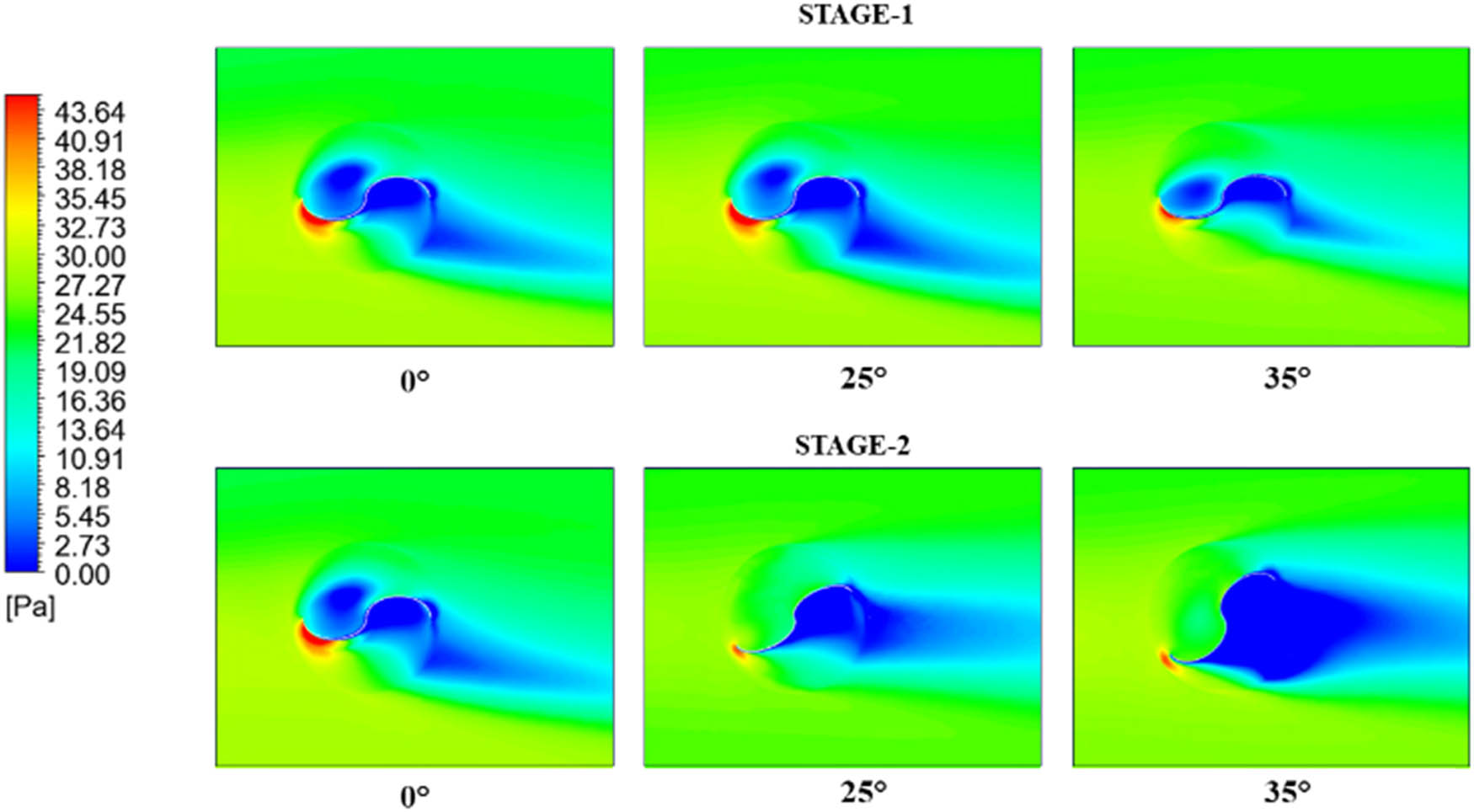
Pressure contour of Savonius type-3 rotor.

The maximum pressure on stage-1 type-2 rotor shown in Figure 15 is 43.7 MPa at PSA 0°, 45.36 MPa at PSA 25°, and 50.8 MPa at PSA 35°. Savonius type-2 shows similar contours at stage 1, and stage 2 shows that the 35° PSA variation has the most expansive wake zone among other variations. The maximum pressure at stage 2 is 46.6 MPa at PSA 0°, 42.8 MPa at PSA 25°, and 50.8 MPa at PSA 35°. Stage 1 in Figure 16 displays similar pressure contours, with the maximum pressures at PSA 0°, PSA 25°, and PSA 35° being 61.6, 62.5, and 50.7 MPa, respectively. The location of the maximum pressure at stage 1 for rotors of types 1, 2, and 3 is similar, positioned at the lower edge of the blade. The maximum pressure at stage 2 is 60.3 MPa at PSA 0°, 59 MPa at PSA 25°, and 42.9 MPa at PSA 35°.

3.3 Factorial analysis design

The results of the CPmax calculation for each variation were analyzed using a factorial design and analysis of variance to reinforce conclusions from existing results. The results of the variance analysis are shown in Table 6. The plot of the response is shown in Figure 18. The plot indicates that the best performance is achieved with rotor type-1, at a PSA of 0° and a TSR of 0.8. The plot shows the same thing as the graph in Figure 13. The results of the variance analysis show that the rotor shape factor, PSA, and TSR have a significant influence on the performance of the Savonius rotor. This is significant because the F-value on the rotor shape factor, PSA, and TSR are higher than those on the F-table [58]. Table 6 shows that the TSR factor is the most dominant, followed by the rotor shape factor, and finally, the PSA factor is based on the F-value of each factor. This confirms that these factors influence the performance of the Savonius rotor.

Figure 18

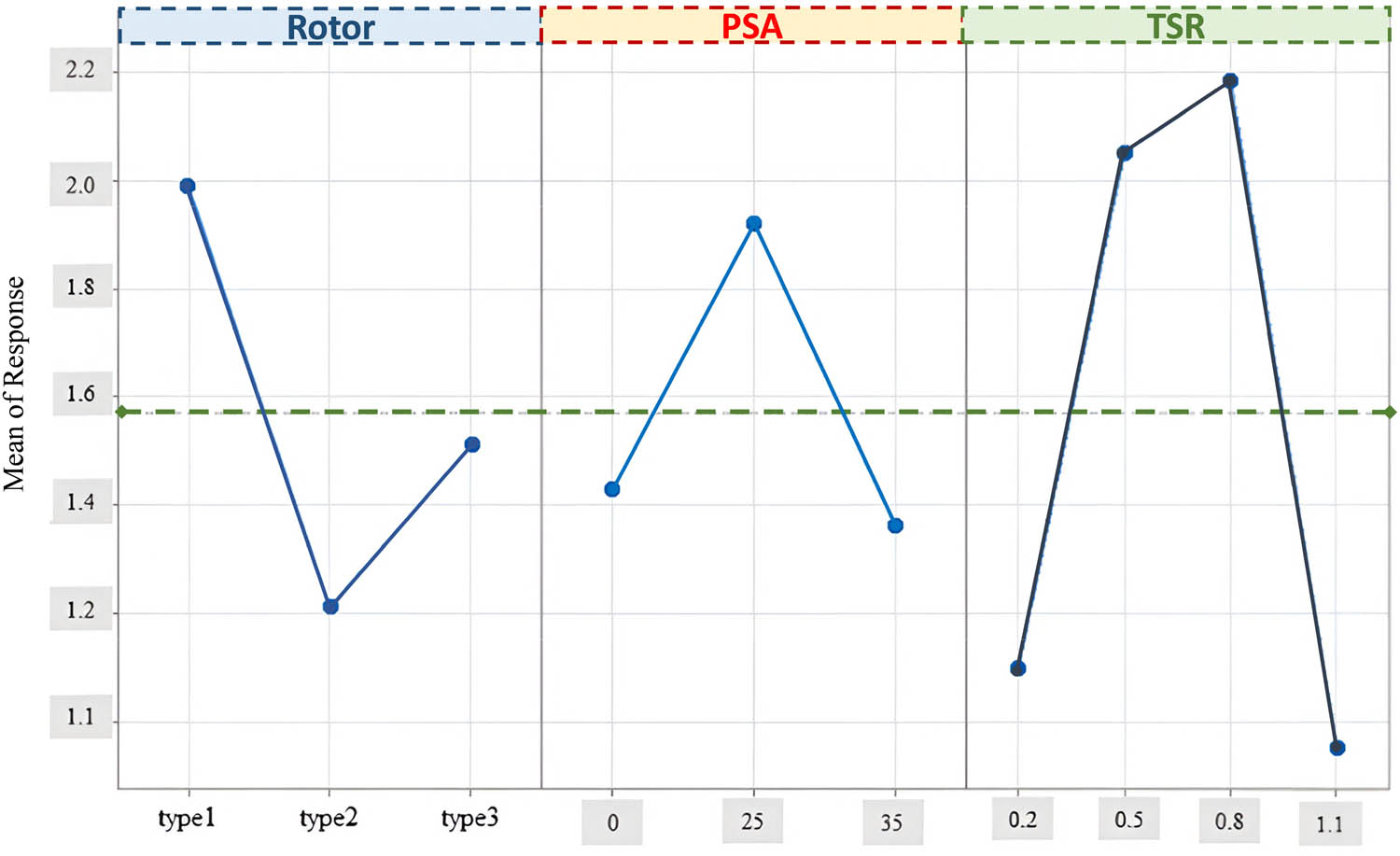
Main effect plot for a response.

Then, the interaction between factors shows an insignificant interaction between the rotor shape factor and PSA. This is indicated by the fact that the F-value of the interaction of the two factors is smaller than the F-table [60]. However, the rotor and TSR factors show a significant interaction. This also occurs in the interaction of the PSA factor with TSR. The interaction between rotor vs TSR and PSA vs TSR shows an F-value greater than the F-table, and the PSA vs TSR interaction is more significant than rotor vs TSR.

Since the F-value is greater than the F-table (90.28 > 3.89), the rotor factor is statistically significant at the 95% confidence level. This suggests that variations in rotor design or type have a significant influence on the responses measured in this research. The TSR factor has a high F value and is well above the critical value (177.72 > 3.49). This indicates that the variation in the TSR significantly influences the system response, perhaps even the most significant factor in this experiment. The interaction between rotor and PSA is insignificant (2.97 < 3.26), which means the variation in rotor type and PSA has no significant influence on the response in this context. The interaction between the rotor and TSR is significant (6.82 > 3), indicating that the combination of rotor type and TSR has a significant effect on the response. This means that the effect of TSR on performance may differ depending on the type or design of the rotor used. The interaction between PSA and TSR is also significant (7.82 > 3), indicating that variations in PSA and TSR jointly affect performance. This indicates that changes in PSA can influence the effect of TSR on the rotor.

The data analysis reveals that the three main factors – rotor, PSA and TSR – have a significant influence on the measured responses. In particular, the effect of each factor proved to be significant and needs to be considered individually in process optimization. Furthermore, the interactions between rotor and TSR, as well as PSA and TSR, also showed significance, indicating that the effect of TSR on the response highly depends on the levels of rotor and PSA used. The interaction between rotor and PSA did not provide any significant additional influence, so the combined effect is additive. Thus, adjusting the TSR according to the rotor and PSA levels is necessary to achieve optimal results in practical applications. At the same time, the insignificant interaction can be simplified in the analysis model.