Layerwise generalized formulation solved via boundary discontinuous method for multilayered structures. Part 2: Shells

Ronaldo Walter Laureano; José Luis Mantari

doi:10.1515/cls-2024-0022

Article Open Access

Layerwise generalized formulation solved via boundary discontinuous method for multilayered structures. Part 2: Shells

Ronaldo Walter Laureano and José Luis Mantari

Published/Copyright: April 2, 2025

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information

From the journal Curved and Layered Structures Volume 12 Issue 1

Abstract

This article introduces a unique analytical solution with a layerwise approach for cross-ply laminated composite cylindrical and doubly curved panels with clamped boundary conditions at all four edges. Under a layerwise (LW) description, from lower- to higher-order models based on the Carrera unified formulation are built with Legendre polynomials. The strong-form governing equations are obtained by employing the principle of virtual displacements displacement-based statement. The boundary discontinuous Fourier-based method is employed to yield purely analytical solutions. The high accuracy and efficiency of our proposed methodology are evaluated by comparing the results against those from the 3D finite element method and the literature for various side-to-thickness and radius-to-depth ratios. As a conclusion, the numerical results presented can be used as a benchmark for future comparative analyses and finite elements.

Keywords: shell; CUF; layerwise theory; clamped; boundary discontinuous; analytical

1 Introduction

Over the last few years, researchers have increasingly focused their efforts on exploring the potential of multilayered structures, drawn by remarkable attributes such as an impressive stiffness-to-weight ratio, low density, exceptional resilience against impact and corrosion, and the capacity to tailor material properties to meet specific requirements [1]. As a result, laminated composites have gained widespread acceptance across a multitude of engineering disciplines, encompassing aerospace, mechanical, biomedical, marine, automotive design, and civil structures. Notably, the application of multilayered curved structures, often referred to as shells, stands out due to their intrinsic curvature and aesthetically pleasing geometric shapes. These characteristics endow them with outstanding load-bearing capabilities, making them highly covered in the industry.

Theories for composite multilayered structures are mostly classified as three-dimensional (3D) theories [2,3,4,5,6,7,8,9,10], which are developed by employing the 3D elasticity equilibrium equations and exhibit a high accuracy in exchange for computational cost, and two-dimensional (2D) theories, which emerge through the adoption of axiomatic hypotheses derived from conjectures and practical experiences. Within 2D theories, classical models such as classical shell theory [11,12,13,14], based on Kirchhoff–Love [15,16,17] assumptions, first-order shear deformation theory [18], based on the Reissner and Mindlin [19,20] assumptions, and higher-order shell theories [21,22,23,24,25,26,27,28,29] mostly adopt two different approaches: equivalent single layer (ESL) and layer-wise (LW) approaches. ESL-based theories [30,31,32,33] consider multilayered structures as a single layer with homogenized properties, i.e., the variables are independent of the number of layers, reducing the computational resources required. However, ESL models encounter challenges in accurately reproducing the characteristic Zig-Zag (ZZ) effects observed in laminates. Conversely, LW models can accurately capture this behavior, as demonstrated by Reddy [34], where his so-called generalized LW theory is presented. Carrera [35,36] utilized Legendre polynomials to expand the displacement field at a layer level. He employed the principal virtual of displacement (PVD) and Reissner’s mixed variational theorem statements to build displacement-based and mixed shell theories, respectively. Displacement-based LW theories consider independent displacement fields within each layer. They then enforce compatibility conditions at the interfaces of laminae, effectively reducing the number of unknown variables in the analysis. Carrera [37,38] introduces his unified formulation (Carrera unified formulation [CUF]), which allows us to express the displacement field as an arbitrary and hierarchical expansion of the primary unknowns along the thickness of both the plate and the shell. Carrera and Brischetto [39,40] investigated the thickness locking for a large variety of ESL and LW theories. An interesting extension was developed in previous studies [41,42,43], where Demasi presents a generalized unified formulation (CUF) based on either PVD or the Reissner mixed variational theorem (RMVT). Ferreira [44] and Ferreira et al. [45] discretized an LW shear deformation theory for composite laminated plates using a meshless method called multiquadrics. Tornabene et al. [46] investigated the static behavior of doubly curved laminated composite shells and panels by using CUF and the differential quadrature method. Plagianakos and Papadopoulos [47] presented a novel higher-order LW theoretical and the finite-element method (FEM) for shallow cylindrical composite and sandwich simply supported shells. Li [48] and Li and Zhang [49] described an accurate description of the multiple delamination and transverse cracks in doubly curved laminated composite shells by using the extended finite-element method and an LW theory, previously developed for beams in the study of Li et al. [50]. Carrera and Valvano [51] performed static analysis of multilayered shells using ESL and LW theories and even further variable kinematic models that combine ESL and LW approaches. Carrera et al. [52] extended the last work to multilayered shell structures embedding piezoelectric layers. Kumar et al. [53] considered the modal analysis of delaminated composite shell structures with double curvature geometry by employing CUF and mixed interpolation of tensorial components. Petrolo and Carrera [54] provided guidelines for the modeling approaches adopted over the years to develop shell theories for composite structures. Recently, Carrera et al. [55] proposed hierarchical expansions built using Jacobi polynomials in the CUF framework to derive beam, plate, and shell models. Petrolo et al. [56] implemented three types of structural theories based on Taylor, Lagrange, and Jacobi polynomials in both ESL and LW ways and exploited the stress recovery technique to analyze composite structures.

As noted, there has been considerable advancement in the investigation of cylindrical and doubly-curved panels using 3D, ESL, and LW theories. However, a predominant emphasis in these investigations has been on structures with simply supported boundary conditions, resulting in a comparatively limited examination of clamped shells. Specifically, there is a notable lack of analytical solutions for these types of structures. Chaudhuri and Kabir [57,58] developed analytical solutions for moderately thick cross-ply laminated doubly curved panels under diverse boundary conditions, such as SS1- and SS2-type simply supported and C4-type clamped constraints. They employed their boundary-discontinuous double-Fourier series-based method, which was developed in previous studies [59,60]. The boundary-discontinuous methodology alongside a higher-order theory allowed Oktem and Chaudhuri to model a cross-ply thick rectangular plate [61] and a doubly-curved panel [62]. They studied a shell structure with C4-type clamped support on two opposing edges, while the remaining two edges were subjected to SS3-type constraints. Moreover, Oktem and Chaudhuri [63] extended their analysis to a cross-ply-laminated plate with C3-type clamped boundary conditions at all four edges. Canales and Mantari [64,65] combined CUF and the boundary-discontinuous method to develop a static analysis of cross-ply laminated beams. Laureano et al. successfully applied this technique and extended it to isotropic, cross-ply laminated, and sandwich plates [66] and functionally graded (FG) structures [67], obtaining accurate numerical results. For more details about the boundary-discontinuous double Fourier series-based method, refer to previous studies [68,69,70,71]. Excellent and comprehensive reviews of composite shell theories can be found in the literature [72,73,74,75,76].

This article presents analytical closed-form solutions for analyzing the static behavior of cylindrical and doubly curved panels with clamped boundary conditions applied to all four edges. The governing equations for doubly curved panels are derived from the PVD. The core innovation of this research lies in a unique methodology that integrates CUF with the boundary-discontinuous double-Fourier series method, implemented under the LW approach, to yield quasi-3D numerical results. To the authors’ best knowledge, the boundary-discontinuous is expressed at a layer level of a shell structure for the very first time in the literature. The present analytical modeling clearly shows robustness and superior performance over the ESL-based shell models in accurately capturing displacement behavior and stress distributions across the entire thickness.

2 Analytical modeling

In Figure 1, (α, β, z) is a curvilinear reference coordinate system where α and β are orthogonal coordinates of the multilayered panel. The radii of curvature, R_α and R_β , are constant at each point of the middle (reference) cross section (z = 0). In some other studies [48,57,58], the global thickness coordinate is alternatively denoted by ζ. k signifies the layer starting from the bottom. N l is the total number of layers. The region occupied by the midsurface of the shell is:

0 ≤ α ≤ a , 0 ≤ β ≤ b , − h 2 ≤ z ≤ h 2

Figure 1

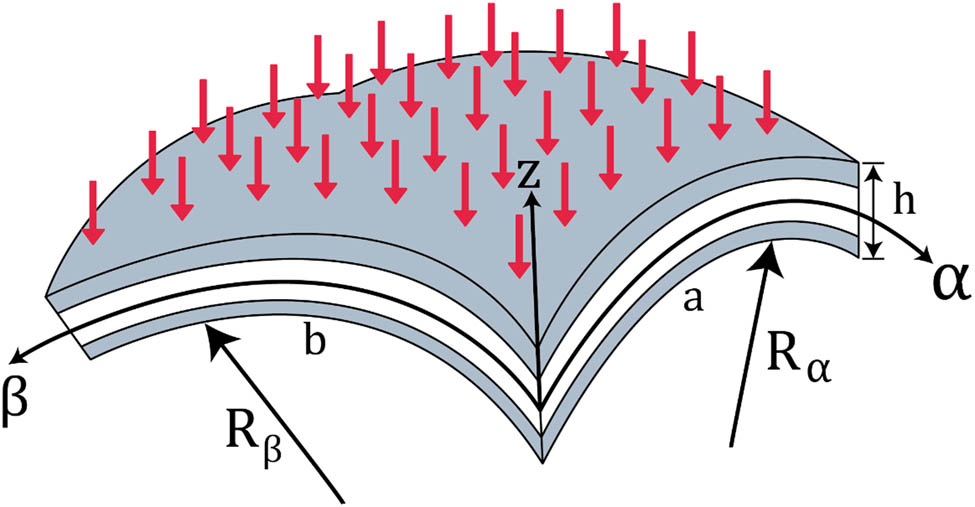
Geometry and reference system of a doubly curved panel.

In order to develop an LW model, the following local variables are required:

(1) − h k 2 ≤ z k ≤ h k 2 ,

(2) − 1 ≤ ζ k ≤ 1 ,

where z k and ζ k are the physical coordinate and non-dimensioned layer coordinate, respectively. Both correspond to crucial terms to work with each layer. In this work, doubly curved panels and cylindrical panels (either R α → ∞ or R β → ∞ ) are considered.

2.1 Elastic stress–strain relations

The transposed displacement vector u k for each layer is introduced in the following:

(3) u k = { u k v k w k } T .

The components of linear normal and shear stress and strain in the orthogonal curvilinear coordinate system are expressed as:

(4) σ k = { σ α α k σ β β k τ α β k τ α z k τ β z k σ z z k } T ,

(5) ε k = { ε α α k ε β β k γ α β k γ α z k γ β z k ε z z k } T ,

Note that Eqs. (4) and (5) use analogous notations to distinguish between normal (σ and ε) and shear (τ and γ) components.

The stress and strain vectors in Eqs. (4) and (5) are divided into in-plane ( σ p k , ε p k ) and out-of-plane ( σ n k , ε n k ) components:

(6a) σ p k = { σ α α k σ β β k τ α β k } T ,

(6b) σ n k = { τ α z k τ β z k σ z z k } T ,

(7a) ε p k = { ε α α k ε β β k γ α β k } T ,

(7b) ε n k = { γ α z k γ β z k ε z z k } T .

In the case of shells with constant radii of curvature, the in-plane ε p k and out-plane ε n k are linearly related to the displacement u k :

(8a) ε p k = ( D p + A p ) u k ,

(8b) ε n k = ( D n p + D n z − A n ) u k ,

where D p , D n p , D n z , A p , A n denote in-plane and out-of-plane differential operators:

(9a) D p = 1 H α ∂ ∂ α 0 0 0 1 H β ∂ ∂ β 0 1 H β ∂ ∂ β 1 H α ∂ ∂ α 0 , A p = 0 0 1 H α R α 0 0 1 H β R β 0 0 0 ,

(9b) D n p = 0 0 1 H α ∂ ∂ α 0 0 1 H β ∂ ∂ β 0 0 0 , D n z = ∂ ∂ z 0 0 0 ∂ ∂ z 0 0 0 ∂ ∂ z , A n = 1 H α R α 0 0 0 1 H β R β 0 0 0 0 .

Details of Eqs. (8a), (8b), (9a), and (9b) are given in the study of Carrera [38]. The parametric coefficients used in Eqs. (9a) and (9b) are

(10a) H α = 1 + z k R α ,

(10b) H β = 1 + z k R β ,

where R α and R β are the radii of curvature in the α , β directions, respectively.

Then, the stress-strain relation can be written as below:

(11a) σ p k = C ˜ p p k ε p k + C ˜ p n k ε n k ,

(11b) σ n k = C ˜ n p k ε p k + C ˜ n n k ε n k .

In the above equations, C ˜ p p k , C ˜ p n k , C ˜ n p k , and C ˜ n n k are matrices of material coefficients of the k -layer. As orthotropic layers with cross-ply lamination are considered, each matrix is defined as follows:

(12) C ˜ p p k = C ˜ 11 k C ˜ 12 k 0 C ˜ 12 k C ˜ 22 k 0 0 0 C ˜ 66 k , C ˜ n n k = C ˜ 55 k 0 0 0 C ˜ 44 k 0 0 0 C ˜ 33 k , C ˜ p n k = C ˜ n p k T = 0 0 C ˜ 13 k 0 0 C ˜ 23 k 0 0 0 .

Since orthotropic materials are the focus of this study, the mathematical relationships between the stiffness coefficients and the material properties are detailed in Reddy’s book [1]. Fibers are oriented on planes parallel to the (α, β) plane.

2.2 Displacement field

Based on Carrera [38], the CUF-based model introduces a free parameter, denoted as N, which represents the order of the model under the LW description (for each layer). In this way, several theories can be built in a compact form as follows:

(13a) u k = F b ( ζ ) u b k ( α , β ) + F r ( ζ ) u r k ( α , β ) + F t ( ζ ) u t k ( α , β ) ,

(13b) v k = F b ( ζ ) v b k ( α , β ) + F r ( ζ ) v r k ( α , β ) + F t ( ζ ) v t k ( α , β ) ,

(13c) w k = F b ( ζ ) w b k ( α , β ) + F r ( ζ ) w r k ( α , β ) + F t ( ζ ) w t k ( α , β ) ,

where b and t denote the bottom and the top of the shell, respectively. Eq. (12) can also be written in a compact form:

u k = F τ ( ζ ) u τ k ( α , β ) ,

(14) δ u k = F s ( ζ ) δ u s k ( α , β ) , τ , s = t , b , r ( r = 2 , 3 , … , N ) ,

in which thickness functions F τ and F s are Legendre polynomials, defined in Table 1.

Table 1

Thickness expansion functions

F τ ( τ = b , 2 , 3 , 4 , t )	F ( ζ k )
F _b	ζ k ‒ 1 2
F ₂	3 ζ k 2 ‒ 3 2
F ₃	5 ζ k 3 ‒ 5 ζ k 2
F ₄	35 ζ k 4 ‒ 42 ζ k 2 + 7 8
F _t	ζ k + 1 2

The displacement components should be linked in the interfaces (compatibility) as follows:

(15a) u t k = u b k + 1 , k = 1 , N l − 1 ,

(15b) v t k = v b k + 1 , k = 1 , N l − 1 ,

(15c) w t k = w b k + 1 , k = 1 , N l − 1 .

2.3 Governing equations

In order to extract the governing equations, the static version of the PVD statement is used as follows:

(16) δ L int = δ L ext ,

L int and L ext denote the virtual variation of internal and external energy, respectively.

Considering strain–displacement relations (Eqs. (8a) and (8b)), constitutive equations (Eqs. (11a) and (11b)), the compact form of CUF (Eq. (14)), and integrating by parts to obtain strong form equations [38]:

(17) δ L int = ∑ k = 1 N l ∫ Ω k ∫ A k ( δ ε p k T σ p k + δ ε n k T σ n k ) d z dΩ k = ∑ k = 1 N l ∫ Ω k δ u s k T K k τ s u τ k dΩ k + ∫ Γ k δ u s k T Π k τ s u τ k dΓ k ,

where K k τ s is a 3 × 3 matrix called fundamental nucleus and Π k τ s is the matrix of the natural boundary conditions. Unlike the version for plates, additional operators containing curvature terms are included, e.g., A_p and A_n . The components of K k τ s and Π k τ s are provided in Appendix A, where the following integral parameter is defined in the thickness direction:

(18) J a b α β τ , ϕ s , θ = ∫ A k C ˜ a b F τ , ϕ F s , θ H α H β d z

Eq. (18) includes curvature terms H_α and H_β . This is due to the nature of panels, unlike the generic parameter used for beams and plates in [65–67]. Functions F τ and F s are used as in Table 1.

Moreover, RHS of Eq. (16), which is related to the mechanical loading, is defined as follows:

(19) δ L ext = ∑ k = 1 N l ∫ Ω k δ u s k T P s k dΩ k ,

where P s k = 0 0 F s z = h 2 q z T is the external load applied at the top surface z = h 2 of the shell.

Then, the explicit form of the differential equations is given by:

(20) δ u s k T : K k τ s u τ k = P s k .

2.4 Boundary conditions

Eqs. (21a)–(21h) list the geometric boundary conditions of displacements for simply-supported (SSSS) shells:

(21a) u τ , α k ( 0 , β ) = 0 ,

(21b) u τ , α k ( a , β ) = 0 ,

(21c) v τ , β k ( α , 0 ) = 0 ,

(21d) v τ , β k ( α , b ) = 0 ,

(21e) w τ k ( 0 , β ) = 0 ,

(21f) w τ k ( a , β ) = 0 ,

(21g) w τ k ( α , 0 ) = 0 ,

(21h) w τ k ( α , b ) = 0 .

Additional constraints have to be added if clamped (CCCC) boundary conditions are treated:

(22a) u τ k ( 0 , β ) = 0 ,

(22b) u τ k ( a , β ) = 0 ,

(22c) v τ k ( α , 0 ) = 0 ,

(22d) v τ k ( α , b ) = 0 .

Likewise, Eqs. (21a)–(21d) need to be rewritten as inequalities:

(23a) u τ , α k ( 0 , β ) ≠ 0 ,

(23b) u τ , α k ( a , β ) ≠ 0 ,

(23c) v τ , β k ( α , 0 ) ≠ 0 ,

(23d) v τ , β k ( α , b ) ≠ 0 .

2.5 Boundary-discontinuous solution

The well-known Navier-type solution is a commonly used method for solving differential equations of simply supported structures. However, it is not applicable to fully clamped shells, as it fails to satisfy the boundary conditions specified in Eqs. (22a)–(22d) and (23a)–(23d). Therefore, the robust boundary-discontinuous Fourier-based method emerges as an alternative analytical approach. Based on previous studies [59,60], the displacement variables u τ k , v τ k , and w τ k are expanded as follows:

(24a) u τ k = ∑ m = 0 m ∑ n = 1 n U τ m n k cos ( α ¯ α ) sin ( β ¯ β ) , 0 < α < a ; 0 ≤ β ≤ b ,

(24b) v τ k = ∑ m = 1 m ∑ n = 0 n V τ m n k sin ( α ¯ α ) cos ( β ¯ β ) , 0 ≤ α ≤ a ; 0 < β < b ,

(24c) w τ k = ∑ m = 1 m ∑ n = 1 n W τ m n k sin ( α ¯ α ) sin ( β ¯ β ) , 0 ≤ α ≤ a ; 0 ≤ β ≤ b .

The load q z is also expanded in the Fourier series:

(24d) q z = ∑ m = 1 m ∑ n = 1 n Q m n sin ( α ¯ α ) sin ( β ¯ β ) , 0 ≤ α ≤ a ; 0 ≤ β ≤ b ,

where

(25a) U τ m n k = 4 a b ∫ 0 b ∫ 0 a u τ k cos ( α ¯ α ) sin ( β ¯ β ) d α d β ,

(25b) V τ m n k = 4 a b ∫ 0 b ∫ 0 a v τ k sin ( α ¯ α ) cos ( β ¯ β ) d α d β ,

(25c) ( W τ m n k , Q m n ) = 4 a b ∫ 0 b ∫ 0 a ( w τ k , q z ) sin ( α ¯ α ) sin ( β ¯ β ) d α d β ,

(25d) α ¯ = m π a ,

(25e) β ¯ = n π b .

This step introduces [ N l ( N u − 1 ) + 1 ] ( 3 m n + m + n ) unknown variables, where m and n represent the wave number of each trigonometric term in Eqs. (24a)–(24d) and (25a)–(25e). Note that the load is considered transversal to the cross-section, e.g., only bending phenomena is studied. The Fourier-expansion is commonly used to analyze several kinds of loads (see Reddy [1]).

The explicit form of the governing equations provided in Appendix A highlights the presence of several partial derivatives of displacements in Eqs. (24a)–(24c). It is important to note that discontinuities arise due to the inequalities in Eqs. (23a)–(23d). In the next lines, the core aspects of the proposed approach and its procedure are explained. For instance, according to Eqs. (23a) and (23b), u τ , α k is forced not to vanish at α = 0 and α = a , whereas v τ , β k at β = 0 and β = b . This idea should be removed, as it reflects basic concepts of infinitesimal calculus. In that scenario, u τ , α k is expanded in the Fourier series:

(26a) u τ , α k = ∑ m = 1 m ∑ n = 1 n U τ m n , α k sin ( α ¯ α ) sin ( β ¯ β ) , 0 < α < a ; 0 ≤ β ≤ b ,

The amplitude term U τ m n , α k is defined as:

(26b) U τ m n , α k = 4 a b ∫ 0 b ∫ 0 a u τ , α k sin ( α ¯ α ) sin ( β ¯ β ) d α d β .

The determination of whether to use term-by-term differentiation or Fourier coefficients is analyzed through the following procedure:

(27a) U τ m n , α k = 2 b ∫ 0 b 2 a u τ k sin ( α ¯ α ) ∣ α = 0 α = a − α ¯ 2 a ∫ 0 a u τ k cos ( α ¯ α ) d α sin ( β ¯ β ) d β ,

(27b) U τ m n , α k = − α ¯ 4 a b ∫ 0 b ∫ 0 a u τ , α k cos ( α ¯ α ) sin ( β ¯ β ) d α d β ,

(27c) U τ m n , α k = − α ¯ U τ m n k .

Replacing Eq. (27c) in Eq. (24a):

(28) u τ , α k = − α ¯ ∑ m = 1 m ∑ n = 1 n U τ m n k sin ( α ¯ α ) sin ( β ¯ β ) , 0 < α < a ; 0 ≤ β ≤ b .

Therefore, Eq. (28) shows that u τ , α k can be obtained by term-by-term differentiation.

Since discontinuities are presented for u τ , α k , the second derivative is expressed as follows:

(29a) u τ , α α k = 1 2 ∑ n = 1 n a ¯ τ n k sin ( β ¯ β ) + ∑ m = 1 m ∑ n = 1 n U τ m n , α α k cos ( α ¯ α ) sin ( β ¯ β ) , 0 < α < a ; 0 ≤ β ≤ b ,

where the amplitude associated with the displacement variable is:

(29b) U τ m n , α α k = 4 a b ∫ 0 b ∫ 0 a u τ , α α k cos ( α ¯ α ) sin ( β ¯ β ) d α d β .

An analogous procedure of Eq. (26b), by applying integration by parts in Eq. (27b), the following is obtained:

(30) U τ m n , α α k = 2 b ∫ 0 b 2 a u τ , α k cos ( α ¯ α ) ∣ α = 0 α = a + α ¯ 2 a ∫ 0 a u τ , α k sin ( α ¯ α ) d α sin ( β ¯ β ) d β .

Since discontinuities are well-stablished in Eqs. (23a) and (23b) as inequalities, no vanishing conditions can be applied here:

(31a) U τ m n , α α k = 4 a b ∫ 0 b [ ( − 1 ) m u τ , α k ( a , β ) − u τ , α k ( 0 , β ) ] sin ( β ¯ β ) d β + α ¯ 4 a b ∫ 0 b ∫ 0 a u τ , α k sin ( α ¯ α ) sin ( β ¯ β ) d α d β ,

(31b) U τ m n , α α k = 4 a b ∫ 0 b [ ( − 1 ) m u τ , α k ( a , β ) − u τ , α k ( 0 , β ) ] sin ( β ¯ β ) d β + α ¯ U τ m n , α k ,

(31c) U τ m n , α α k = 4 a b ∫ 0 b [ ( − 1 ) m u τ , α k ( a , β ) − u τ , α k ( 0 , β ) ] sin ( β ¯ β ) d β − α ¯ 2 U τ m n k .

Replacing Eq. (31c) into Eq. (29a):

(32) u τ , α α k = 1 2 ∑ n = 1 n a ¯ τ n k sin ( β ¯ β ) + ∑ m = 1 m ∑ n = 1 n [ − α ¯ 2 U τ m n k + γ m a ¯ τ n k + ψ m b ¯ τ n k ] cos ( α ¯ α ) sin ( β ¯ β ) ,

where a ¯ τ n k , b ¯ τ n k introduce [ N l ( Nu − 1 ) + 1 ] ( 2 n ) new unknown variables. According to Chaudhuri and Kabir [57,58], they are defined as:

(33) ( a ¯ τ n k , b ¯ τ n k ) = 4 a b ∫ 0 b [ ± u τ , α k ( a , β ) − u τ , α k ( 0 , β ) ] sin ( β ¯ β ) d β .

In the inverse manner, the derivatives of the longitudinal displacement can be expressed in terms of the new Fourier coefficients:

(34) ( u τ , α k ( 0 , β ) , u τ , α k ( a , β ) ) = − a 4 ∑ n = 1 n ( ± a ¯ τ n k + b ¯ τ n k ) sin ( β ¯ β ) .

And γ m , ψ m are defined as

(35) ( γ m , ψ m ) = ( 1 , 0 ) , m = even ( 0 , 1 ) , m = odd .

Furthermore, for the latitudinal displacement v τ k , an analogous procedure is developed.

(36) v τ , β k = − ∑ m = 1 m ∑ n = 1 n β ¯ V τ m n k sin ( α ¯ α ) sin ( β ¯ β ) .

The second partial derivative v τ , β β k is written as follows:

(37) v τ , β β k = 1 2 ∑ m = 1 m c ¯ τ m k sin ( α ¯ α ) + ∑ m = 1 m ∑ n = 1 n [ − β ¯ 2 V τ m n k + γ n c ¯ τ m k + ψ n d ¯ τ m k ] sin ( α ¯ α ) cos ( β ¯ β ) ,

where c ¯ τ m k , d ¯ τ m k introduce [ N l ( Nu − 1 ) + 1 ] ( 2 n ) new unknown variables. These coefficients are given by

(38) ( c ¯ τ m k , d ¯ τ m k ) = 4 a b ∫ 0 a [ ± v τ , β k ( α , β ) − v τ , β k ( α , 0 ) ] sin ( α ¯ α ) d α .

As in Eq. (34), the inverse manner of Eq. (38) is:

(39) ( v τ , β k ( α , 0 ) , v τ , β k ( α , b ) ) = − b 4 ∑ m = 1 m ( ± c ¯ τ m k + d ¯ τ m k ) sin ( α ¯ α ) .

γ n , ψ n are similar functions as Eq. (35).

The remaining partial derivatives can be obtained through term-by-term differentiation as they do not deal with discontinuities.

In order to match the number of equations, Eqs. (22a)–(22d) are required:

After substituting the longitudinal amplitudes in Eqs. (22a)–(22b), the clamped boundary conditions are developed as follows:

(40a) ∑ m = 1 , 3 , 5 , … ∞ U τ mn k = 0 ,

(40b) U τ 0 n k + ∑ m = 2 , 4 , 6 , … ∞ U τ mn k = 0 .

Analogous procedure with lateral amplitudes replaced in Eqs. (22c)–(22d):

(41a) ∑ n = 1 , 3 , 5 , … ∞ V τ mn k = 0 ,

(41b) V τ m 0 k + ∑ n = 2 , 4 , 6 , … ∞ V τ mn k = 0 .

Finally, this procedure results in a linearly determined algebraic system, yielding an analytical boundary-discontinuous solution to the static problem.

3 Numerical results and discussion

In this section, the level of accuracy of the proposed LW approach is investigated. The assessment is developed within four problems including cross-ply laminated and sandwich panels subjected to uniform distributed load. The clamped boundary condition is set at all four edges for all cases. The mechanical properties of the materials employed in this study are reported in Table 2. The following dimensionless parameters are used for displacements and stresses:

( u ¯ , v ¯ ) = E 2 bottom h 2 q z a 3 ( u , v ) ,

w ¯ = E 2 bottom h 3 q z a 4 w ,

( σ ¯ α α , σ ¯ β β , τ ¯ α β ) = h 2 q z a 2 ( σ α α , σ β β , τ α β ) ,

( τ ¯ α z , τ ¯ β z ) = h q z a ( τ α z , τ β z ) ,

σ ¯ z z = 1 q z σ z z .

Table 2

List of materials

Material	E ₁	E ₂	E ₃	G ₁₂	G ₁₃	G ₂₃	ν ₁₂	ν ₁₃	ν ₂₃
Material	(GPa)						ν ₁₂	ν ₁₃	ν ₂₃
1	172.5	6.9	6.9	3.45	3.45	1.38	0.25	0.25	0.25
2 (Al)	70			26.92			0.3
3 (Zr)	168			64.62			0.3
4	0.7			0.269			0.3

The proposed approach was implemented in a MATLAB code, where stress components are computed through constitutive relations (Eqs. (11a) and (11b)). Both past semi-analytical [26] and analytical [56] solutions are utilized for comparison purposes. Furthermore, 3D FEM and EDZ4 through-the-thickness distributions, which were provided by Tornabene et al. [46], are also used to assess the validity of the shell models presented.

3.1 Convergence analysis

The accuracy of the boundary-discontinuous method is highly dependent by the number of trigonometric terms, denoted as m , n . Figure 2 shows the variation of both transversal displacement ( w ¯ ) and normal stress ( σ ¯ α α ) as m , n are increased. The structure in the study is a [0°/90°] cross-ply laminated spherical panel made of material 1. Particularly for higher order models such as LD3 and LD4, an oscillatory pattern of σ ¯ α α is noticeable in Figure 2b even for the highest values m , n ≥ 200 . Then, it is crucial to select an appropriate value for m , n , considering that higher values of m , n lead to increased computational expenses. Hence, for the upcoming tables and figures, a choice of 150 is made for both m and n . This selection strikes a good balance between achieving accuracy and managing the necessary computational resources.

$Figure 2 Problem I. Convergence of non-dimensional (a) transverse displacement 10 3 w ¯ ( z = 0 ) {10}^{3}{\bar{w}}_{(z=0)} and (b) in-plane stress 10 2 σ ¯ α α z = h 2 {10}^{2}{\bar{\sigma }}_{\alpha \alpha \left(,z=\frac{h}{2}\right)} of two-layer antisymmetric [0°/90°] spherical panel at the point α = a 4 , β = b 4 \left(\phantom{\rule[-0.75em]{}{0ex}},\alpha =\frac{a}{4},\hspace{.25em}\beta =\frac{b}{4}\right) as m , n m,n are increased. a h = 4 , R a = 5 \left(\phantom{\rule[-0.75em]{}{0ex}},\frac{a}{h}=4,\hspace{.25em}\frac{R}{a}=5\right) .$

Figure 2

Problem I. Convergence of non-dimensional (a) transverse displacement 10 3 w ¯ ( z = 0 ) and (b) in-plane stress 10 2 σ ¯ α α z = h 2 of two-layer antisymmetric [0°/90°] spherical panel at the point α = a 4 , β = b 4 as m , n are increased. a h = 4 , R a = 5 .

3.2 Problem I: Cross-ply laminated spherical panel

For the initial problem, symmetric [0°/90°/0° and 0°/90°/90°/0°] and antisymmetric [0°/90°] lamination schemes, which are made of material 1, are studied. The numerical results of central transversal displacement ( w ¯ ) of the present LW models and those of the literature [26,56] are reported in Table 3. From shallow to deep spherical shells and various length-to-thickness ratios are considered. A strong agreement for thin structures is achieved. Moreover, a good concordance with the study by Petrolo et al. [56] for the moderately thick three-layer symmetric case [0°/90°/0°] is obtained. Figure 3 shows the through-the-thickness distribution of w ¯ , σ ¯ β β , τ ¯ α z , σ ¯ z z of a two-layer [0°/90°] moderately thick and moderately deep R a = 10 , a h = 10 cross-ply laminated case at the point α = a 4 , β = b 4 . The performance of low-order and higher-order theories (from LD1 to LD4) are plotted. It is worth mentioning that only constitutive equations were employed to obtain the out-of-plane stresses. As it is seen in Figure 3c, the interlaminar continuity (IC) for the shear stress τ ¯ α z is met at the top and the bottom only for higher-order models such as LD3 and LD4. Furthermore, the best performance of normal stress σ ¯ z z is achieved with LD4 as the free boundary conditions is fulfilled at the bottom and the top of the structure. The through-the-thickness distribution of u ¯ , w ¯ , σ ¯ β β , τ ¯ β z , and σ ¯ z z the symmetric case [0°/90°/0°] is shown in Figure 4. Figure 4a illustrates the capability of all LW models to capture the ZZ effect of the longitudinal displacement u ¯ at the interfaces. As is seen in Figure 4d and e, for out-of-plane components τ ¯ β z , σ ¯ z z , there is a slight discontinuity at the interfaces; hence, the IC conditions are not fulfilled a priori and a post-process stress recovery technique might be required.

Table 3

Problem I. Numerical results of the dimensionless central transversal displacement ( 10 3 w ¯ ) for different values of a / h and R / a

R/a	Model	a/h = 10			a/h = 20			a/h = 50
R/a	Model	0°/90°	0°/90°/0°	0°/90°/90°/0°	0°/90°	0°/90°/0°	0°/90°/90°/0°	0°/90°	0°/90°/0°	0°/90°/90°/0°
2	Bigdeli and Aghdam [26]	—	1.715	1.723	—	0.518	0.523	—	0.092	0.092
	Present LD1	1.960	1.786	1.773	0.620	0.519	0.539	0.090	0.090	0.092
	Present LD2	1.966	1.800	1.783	0.619	0.520	0.539	0.090	0.090	0.092
	Present LD3	1.976	1.798	1.783	0.617	0.519	0.538	0.089	0.090	0.092
	Present LD4	1.976	1.798	1.783	0.617	0.519	0.538	0.089	0.090	0.092
3	Bigdeli and Aghdam [26]	—	2.715	2.688	—	0.943	0.956	—	0.209	0.217
	Present LD1	3.203	2.883	2.831	1.252	0.965	0.996	0.228	0.202	0.214
	Present LD2	3.226	2.922	2.866	1.253	0.971	0.998	0.228	0.202	0.214
	Present LD3	3.270	2.929	2.869	1.253	0.970	0.998	0.227	0.202	0.214
	Present LD4	3.270	2.929	2.869	1.253	0.970	0.998	0.227	0.202	0.214
5	Bigdeli and Aghdam [26]	—	3.777	3.685	—	1.535	1.556	—	0.492	0.521
	Present LD1	4.622	4.105	3.984	2.365	1.622	1.653	0.646	0.482	0.514
	Present LD2	4.678	4.185	4.058	2.375	1.643	1.665	0.646	0.483	0.514
	Present LD3	4.785	4.207	4.069	2.385	1.644	1.666	0.645	0.483	0.514
	Present LD4	4.785	4.208	4.069	2.385	1.644	1.666	0.645	0.483	0.514
10	Chaudhuri and Kabir [57]	5.580	4.730	—	—	—	—	—	—	—
	Bigdeli and Aghdam [26]	5.970	4.493	4.345	—	2.049	2.075	—	1.018	1.069
	Present LD1	5.644	4.963	4.780	3.653	2.229	2.249	1.814	1.020	1.072
	Present LD2	5.733	5.081	4.892	3.681	2.269	2.273	1.818	1.025	1.074
	Present LD3	5.900	5.120	4.909	3.715	2.273	2.276	1.819	1.025	1.075
	Present LD4	5.901	5.120	4.909	3.715	2.273	2.276	1.819	1.025	1.075
20	Bigdeli and Aghdam [26]	—	4.715	4.545	—	2.231	2.259	—	1.356	1.416
	Present LD1	5.968	5.233	5.029	4.212	2.452	2.466	3.075	1.379	1.438
	Present LD2	6.069	5.364	5.154	4.251	2.501	2.497	3.090	1.388	1.443
	Present LD3	6.258	5.408	5.173	4.299	2.506	2.500	3.094	1.388	1.443
	Present LD4	6.260	5.409	5.173	4.299	2.506	2.500	3.094	1.388	1.443

$Figure 3 Problem I. Through-the-thickness variation of w ¯ \bar{w} , σ ¯ β β {\bar{\sigma }}_{\beta \beta } , τ ¯ α z {\bar{\tau }}_{\alpha z} , σ ¯ z z {\bar{\sigma }}_{zz} at the point α = a 4 , β = b 4 \left(\phantom{\rule[-0.75em]{}{0ex}},\alpha =\frac{a}{4},\hspace{.25em}\beta =\frac{b}{4}\right) of a two-layer [0°/90°] moderately thick and moderately deep cross-ply laminated shell R a = 10 , a h = 10 \left(\phantom{\rule[-0.75em]{}{0ex}},\frac{R}{a}=10,\frac{a}{h}=10\right) .$

Figure 3

Problem I. Through-the-thickness variation of w ¯ , σ ¯ β β , τ ¯ α z , σ ¯ z z at the point α = a 4 , β = b 4 of a two-layer [0°/90°] moderately thick and moderately deep cross-ply laminated shell R a = 10 , a h = 10 .

$Figure 4 Problem I. Through-the-thickness variation of u ¯ \bar{u} , w ¯ \bar{w} , σ ¯ β β {\bar{\sigma }}_{\beta \beta } , τ ¯ β z {\bar{\tau }}_{\beta z} , σ ¯ z z {\bar{\sigma }}_{zz} at the point α = a 4 , β = b 4 \left(\phantom{\rule[-0.75em]{}{0ex}},\alpha =\frac{a}{4},\hspace{.25em}\beta =\frac{b}{4}\right) of a three-layer symmetric [0°/90°/0°] moderately thick and very deep cross ply laminated shell R a = 2 , a h = 10 \left(\phantom{\rule[-0.75em]{}{0ex}},\frac{R}{a}=2,\frac{a}{h}=10\right) .$

Figure 4

Problem I. Through-the-thickness variation of u ¯ , w ¯ , σ ¯ β β , τ ¯ β z , σ ¯ z z at the point α = a 4 , β = b 4 of a three-layer symmetric [0°/90°/0°] moderately thick and very deep cross ply laminated shell R a = 2 , a h = 10 .

3.3 Problem II: Sandwich (Zr/Al/Zr) spherical panel

For the second problem, a three-layer sandwich spherical panel ( R α = R β = 1 ) case is investigated in this work. The external layers are made of material 2 (zirconia), whereas the core is made of material 3 (aluminum). The thickness of each layer is considered h _skin = 0.03 m and h _core = 0.04 m. The side dimensions are as follows: a = 1.0472 m and b = 2.0944 m. The through-the-thickness distribution of u ¯ , w ¯ , σ ¯ α α , τ ¯ α z , and σ ¯ z z at the point α = a 4 , β = b 4 are shown in Figure 5. For comparison purposes, the 3D FEM and EDZ4 results provided by Tornabene et al. [46] are also plotted. An excellent agreement is exhibited for the longitudinal displacement u ¯ , whereas for the deflection w ¯ , a slight deviation is presented. For in-plane σ ¯ α α and out-of-plane σ ¯ z z , stress components are described accurately by the LD4 shell model. Furthermore, the shear stress τ ¯ α z is captured accurately all along the thickness except at the interfaces where the discontinuities are exhibited as only constitutive equations are employed. Moreover, LD3 and LD4 exhibit superior performance as they fulfilled the free-surface boundary conditions at the top and the bottom surfaces. In Table 4, the displacements and the in-plane and shear stresses calculated by LW models are presented. Clearly, LD4 is capable to accurately describe the transverse displacement w ¯ and normal stress σ ¯ α α as the maximum relative errors are less than 2.2 and 1.2%, respectively.

$Figure 5 Problem II. Through-the-thickness variation of u ¯ \bar{u} , w ¯ \bar{w} , σ ¯ α α {\bar{\sigma }}_{\alpha \alpha } , τ ¯ α z {\bar{\tau }}_{\alpha z} at the point α = a 4 , β = b 4 \left(\phantom{\rule[-0.75em]{}{0ex}},\alpha =\frac{a}{4},\hspace{.25em}\beta =\frac{b}{4}\right) of a spherical panel with a zirconia/aluminum/zirconia lamination scheme.$

Figure 5

Problem II. Through-the-thickness variation of u ¯ , w ¯ , σ ¯ α α , τ ¯ α z at the point α = a 4 , β = b 4 of a spherical panel with a zirconia/aluminum/zirconia lamination scheme.

Table 4

Problem II. Numerical results of displacements and stress components at the point α = a 4 , β = b 4

Theories	10 2 u ¯ z = − h 2	10 2 w ¯ ( z = 0 )	10 2 σ ¯ α α ( z = 0 )	10 2 τ ¯ α β z = − h 2	10 2 τ ¯ α z z = h 2	10 2 σ ¯ z z z = h 2
FEM 3D [46]	1.004	0.347	2.083	1.088	4.066	47.390
EDZ4 [46]	1.006	0.347	2.077	1.003	4.064	46.350
Present LD1	1.052	0.337	2.051	0.873	4.246	42.682
Present LD2	1.052	0.339	2.058	0.864	4.170	42.564
Present LD3	1.051	0.339	2.059	0.864	4.256	42.612
Present LD4	1.051	0.339	2.059	0.864	4.255	42.613

3.4 Problem III: Sandwich (Zr/Al/Zr) cylindrical panel

As the previous problem, Tornabene et al. [46] provided reference results which are compared with the proposed LW shell theories in this work. In this case, a three-layer sandwich cylindrical ( R α → ∞ , R β = 2 ) panel is investigated. The thickness of each layer is considered: h _skin = 0.018 m and h _core = 0.024 m. The side dimensions are the same as the previous spherical problem. Figure 6 shows the through-the-thickness distribution of u ¯ , w ¯ , σ ¯ β β , τ ¯ α β , τ ¯ α z , and τ ¯ β z at the point α = a 4 , β = b 4 . As it is seen, there is an excellent agreement by all LW models with the references for the longitudinal displacement u ¯ . For transverse displacement w ¯ , the relative error is less than 3.2% in almost all along the thickness between LD4 and references. Both normal σ ¯ β β and shear τ ¯ α β stresses are captured accurately even by lower order models, e.g., LD1 and LD2. Furthermore, an excellent response of shear stresses τ ¯ α z , τ ¯ β z with the reference solution is exhibited by LD4 as the IC and free-boundary conditions are fulfilled. The numerical values of displacements and stresses are reported in Table 5. For the selected points, LD4 clearly achieves the best description for all components, exhibiting a relative error of 1% for shear stress τ ¯ α z and less than 3.5% for σ ¯ α α .

$Figure 6 Problem III. Through-the-thickness variation of u ¯ \bar{u} , w ¯ \bar{w} , σ ¯ β β {\bar{\sigma }}_{\beta \beta } , τ ¯ α β {\bar{\tau }}_{\alpha \beta } , τ ¯ α z {\bar{\tau }}_{\alpha z} , τ ¯ β z {\bar{\tau }}_{\beta z} at the point α = a 4 , β = b 4 \left(\phantom{\rule[-0.75em]{}{0ex}},\alpha =\frac{a}{4},\hspace{.25em}\beta =\frac{b}{4}\right) of a cylindrical panel with a zirconia/aluminum/zirconia lamination scheme.$

Figure 6

Problem III. Through-the-thickness variation of u ¯ , w ¯ , σ ¯ β β , τ ¯ α β , τ ¯ α z , τ ¯ β z at the point α = a 4 , β = b 4 of a cylindrical panel with a zirconia/aluminum/zirconia lamination scheme.

Table 5

Problem III. Numerical results of displacements and stress components at the point α = a 4 , β = b 4

Theories	10 2 u ¯ z = − h 2	10 2 w ¯ ( z = 0 )	10 2 σ ¯ α α z = h 2	10 2 τ ¯ α β z = − h 2	10 2 τ ¯ α z z = h 2	10 2 σ ¯ z z z = h 2
FEM 3D [46]	1.468	0.620	5.501	3.909	10.570	44.480
EDZ4 [46]	1.470	0.621	5.432	3.898	10.580	43.460
Present LD1	1.421	0.598	5.913	3.792	10.253	41.581
Present LD2	1.437	0.606	5.673	3.832	10.248	41.818
Present LD3	1.437	0.607	5.691	3.832	10.465	41.751
Present LD4	1.437	0.607	5.690	3.832	10.465	41.757

3.5 Problem IV: Sandwich (Zr/Soft Core/Zr) cylindrical panel with a soft core

For the last problem, the same geometry of the previous case is studied: a three-layer sandwich cylindrical panel. However, the core utilized for this case is made of material 4, which is softer than aluminum. Figure 7 shows the through-the-thickness distribution of u ¯ , w ¯ , σ ¯ α α , and τ ¯ β z at the point α = a 4 , β = b 4 . The main difference when a softer core is utilized is the presence of the ZZ effect in the longitudinal displacement u ¯ , which is well captured by all LW models. Furthermore, the behavior of transverse displacement w ¯ presents different slopes at each layer. An interesting situation occurs for the normal stress σ ¯ α α as the value of this component is 0 in the core region. This indicates the superior capabilities of this material to absorb more efficiently and manage the loads applied to the structure. LD3 and LD4 exhibit a superior performance capturing the shear stress τ ¯ β z as the IC and the free-boundary conditions are met.

$Figure 7 Problem IV. Through-the-thickness variation of u ¯ \bar{u} , w ¯ \bar{w} , σ ¯ α α {\bar{\sigma }}_{\alpha \alpha } , τ ¯ β z {\bar{\tau }}_{\beta z} at the point α = a 4 , β = b 4 \left(\phantom{\rule[-0.75em]{}{0ex}},\alpha =\frac{a}{4},\hspace{.25em}\beta =\frac{b}{4}\right) of a cylindrical panel with a zirconia/soft core/zirconia lamination scheme.$

Figure 7

Problem IV. Through-the-thickness variation of u ¯ , w ¯ , σ ¯ α α , τ ¯ β z at the point α = a 4 , β = b 4 of a cylindrical panel with a zirconia/soft core/zirconia lamination scheme.

4 Conclusions

In this article, the static behavior of clamped cylindrical and spherical panels is investigated using a robust analytical methodology that leverages the versatility of CUF and the high precision of the boundary-discontinuous Fourier-based method. Several lower- to higher-order models based on CUF are implemented to predict the displacements and stresses when a uniform load is applied to the top of the structure. The strong form of governing equations is obtained by using the PVD statement. The boundary-discontinuous Fourier-based method is used to solve the governing equations of shells at a layer level for the very first time achieving highly-accurate numerical results. The following main conclusions can be drawn:

The numerical investigation concludes that LW shell models have superior capabilities compared to ESL models as they are able to obtain quasi-3D results and reproduce the typical ZZ effect in composite laminated shells.
An appropriate value for the number of trigonometric terms m, n leads to highly accurate results as the boundary discontinuous method is strongly dependent on this value.
As demonstrated in the previous section, higher-order LW shell theories are capable of fulfilling the free surface boundary conditions and the interlaminar continuity in almost all cases without requiring a post-process stress recovery technique.
The closed-form solutions for fully clamped shells obtained through LW theories and the boundary discontinuous Fourier-based method require higher computational cost than ESL-based theories. However, the computational time is significantly reduced in comparison to finite-element solutions.

Future works can include other types of polynomials such as Chebyshev and Jacobi in the CUF-based displacement field. Furthermore, the development of mixed shell theories by employing the RMVT would be quite interesting as the C z 0 requirements are fulfilled a priori.

tel: +51 964358966

Acknowledgements

The authors would like to thank the University of Engineering and Technology, Barranco, Peru, for supporting present work.

Funding information: Authors state no funding involved.
Author contributions: All authors have accepted responsibility for the entire content of this manuscript and consented to its submission to the journal, reviewed all the results and approved the final version of the manuscript. Ronaldo Walter Laureano: writing draft, date analysis, editing. José Luis Mantari: conceptualization, writing, revision.
Conflict of interest: Authors state no conflict of interest.
Ethical approval: This work does not contain any experiments with human participants or animals undertaken.
Data availability statement: The data supporting this study will be made available upon reasonable request.

Appendix A

The complete explicit form of the fundamental nucleus is presented below. The following integrations over the thickness are considered:

(A1a) J k τ s , J α k τ s , J β k τ s , J α β k τ s , J β α k τ s , J α β k τ s = ∫ A k F τ F s 1 , H α , H β , H α H β , H β H α , H α H β d z ,

(A1b) J k τ z s , J α k τ z s , J β k τ z s , J α β k τ z s , J β α k τ z s , J α β k τ z s = ∫ A k F τ , z F s 1 , H α , H β , H α H β , H β H α , H α H β d z ,

(A1c) J k τ s z , J α k τ s z , J β k τ s z , J α β k τ s z , J β α k τ s z , J α β k τ s z = ∫ A k F τ F s , z 1 , H α , H β , H α H β , H β H α , H α H β d z ,

(A1d) J k τ z s z , J α k τ z s z , J β k τ z s z , J α β k τ z s z , J β α k τ z s z , J α β k τ z s z = ∫ A k F τ , z F s , z 1 , H α , H β , H α H β , H β H α , H α H β d z .

The fundamental nucleus of dimension (3 × 3) is defined as follows:

(A2a) δ u s k : C ˜ 55 k J α β k τ z s z − 1 R α J β k τ z s − 1 R α J β k τ s z + 1 R α 2 J β α k τ s u τ k − C ˜ 11 k J β α k τ s u τ , α α k − C ˜ 66 k J α β k τ s u τ , β β k − ( C ˜ 12 k + C ˜ 66 k ) J k τ s v τ , α β k + C ˜ 55 k J β k τ s z − C ˜ 55 k R α J β α k τ s − C ˜ 11 k R α J β α k τ s − C ˜ 12 k R β J k τ s − C ˜ 13 k J β k τ z s w τ , α k = 0 ,

(A2b) δ v s k : − ( C ˜ 12 k + C ˜ 66 k ) J k τ s u τ , α β k + C ˜ 44 k J α β k τ z s z − 1 R β J α k τ z s − 1 R β J α k τ s z + 1 R β 2 J α β k τ s v τ k − C ˜ 66 k J β α k τ s v τ , α α k − C ˜ 22 k J α β k τ s v τ , β β k + C ˜ 44 k J α k τ s z − C ˜ 44 k R β J α β k τ s − C ˜ 22 k R β J α β k τ s − C ˜ 12 k R α J k τ s − C ˜ 23 k J α k τ z s w τ , β k = 0 ,

(A2c) δ w s k : C ˜ 13 k J β k τ s z + C ˜ 55 k R α J β α k τ s + C ˜ 11 k R α J β α k τ s + C ˜ 12 k R β J k τ s − C ˜ 55 k J β k τ z s u τ , α k + C ˜ 23 k J α k τ s z + C ˜ 44 k R β J α β k τ s + C ˜ 22 k R β J α β k τ s + C ˜ 12 k R α J k τ s − C ˜ 44 k J α k τ z s v τ , β k + C ˜ 33 k J α β k τ z s z + C ˜ 13 k R α J β k τ s z + C ˜ 13 k R α J β k τ z s + C ˜ 11 k R α 2 J β α k τ s + 2 R α R β C ˜ 12 k J k τ s + C ˜ 23 k R β J α k τ s z + C ˜ 23 k R β J α k τ z s + C ˜ 22 k R β 2 J α β k τ s w τ k − C ˜ 55 k J β α k τ s w τ , α α k − C ˜ 44 k J α β k τ s w τ , β β k = F ¯ s q z .

Appendix B

(B1a) ∑ m = 1 m ∑ n = 1 n cos ( α ¯ α ) sin ( β ¯ β ) { α ¯ 2 C ˜ 11 k J β α k τ s + β ¯ 2 C ˜ 66 k J α β k τ s + C ˜ 55 k J α β k τ z s z − C ˜ 55 k R α J β k τ z s − C ˜ 55 k R α J β k τ s z + C ˜ 55 k R α 2 J β α k τ s U τ mn k + [ α ¯ β ¯ ( C ˜ 12 k + C ˜ 66 k ) J k τ s ] V τ mn k + α ¯ C ˜ 55 k J β k τ s z − C ˜ 55 k R α J β α k τ s − C ˜ 11 k R α J β α k τ s − C ˜ 12 k R β J k τ s − C ˜ 13 k J β k τ z s W τ mn k − C ˜ 11 k J β α k τ s ( γ m a ¯ τ n k + ψ m b ¯ τ n k ) } = 0 ,

(B1b) ∑ m = 1 m ∑ n = 1 n sin ( α ¯ α ) cos ( β ¯ β ) [ α ¯ β ¯ ( C ˜ 12 k + C ˜ 66 k ) J k τ s ] U τ mn k + α ¯ 2 C ˜ 66 k J β α k τ s + C ˜ 22 k J α β k τ s + C ˜ 44 k J α β k τ z s z − C ˜ 44 k R β J α k τ z s − C ˜ 44 k R β J α k τ s z + C ˜ 44 k R β 2 J α β k τ s V τ mn k + β ¯ C ˜ 44 k J α k τ s z − C ˜ 44 k R β J α β k τ s − C ˜ 22 k R β J α β k τ s − C ˜ 12 k R α J k τ s − C ˜ 23 k J α k τ z s W τ mn k − C ˜ 22 k J α β k τ s ( γ n c ¯ τ m k + ψ n d ¯ τ m k ) = 0 ,

(B1c) ∑ m = 1 m ∑ n = 1 n sin ( α ¯ α ) sin ( β ¯ β ) α ¯ C ˜ 55 J β τ z s − C ˜ 55 k R α J β α k τ s − C ˜ 11 k R α J β α k τ s − C ˜ 12 k R β J k τ s − C ˜ 13 k J β k τ s z U τ mn k + β ¯ C ˜ 44 k J α k τ z s − C ˜ 44 k R β J α β k τ s − C ˜ 22 k R β J α β k τ s − C ˜ 12 k R α J k τ s − C ˜ 23 k J α k τ s z V τ mn k + α ¯ 2 C ˜ 55 k J β α k τ s + β ¯ 2 C ˜ 44 k J α β k τ s + C ˜ 33 k J α β k τ z s z + C ˜ 13 k R α J β k τ s z + C ˜ 13 k R α J β k τ z s + C ˜ 11 k R α 2 J β α k τ s + 2 R α R β C ˜ 12 k J k τ s + C ˜ 23 k R β J α k τ s z + C ˜ 23 k R β J α k τ z s + C ˜ 22 k R β 2 J α β k τ s W τ mn k − F ¯ s Q m n } = 0 ,

(B1d) ∑ n = 1 n sin ( β ¯ β ) β ¯ 2 C ˜ 66 k J α β k τ s + C ˜ 55 k J α β k τ z s z − C ˜ 55 k R α J β k τ z s − C ˜ 55 k R α J β k τ s z + C ˜ 55 k R α 2 J β α k τ s U τ 0 n k − C ˜ 11 k 2 J β α k τ s a ¯ τ n k = 0 ,

(B1e) ∑ m = 1 m sin ( α ¯ α ) α ¯ 2 C ˜ 66 k J β α k τ s + C ˜ 44 k J α β τ z s z − C ˜ 44 k R β J α k τ z s − C ˜ 44 k R β J α k τ s z + C ˜ 44 k R β 2 J α β k τ s V τ m 0 k − C ˜ 22 k 2 J α β k τ s c ¯ τ m k = 0 .

References

[1] Reddy JN. Mechanics of laminated composite plates and shells: theory and analysis. Boca Raton: CRC Press; 2004.10.1201/b12409Search in Google Scholar

[2] Ren JG. Exact solutions for laminated cylindrical shells in cylindrical bending. Compos Sci Technol. 1987;29:169–87.10.1016/0266-3538(87)90069-8Search in Google Scholar

[3] Varadan TK, Bhaskar K. Bending of laminated orthotropic cylindrical shells - an elasticity approach. Compos Struct. 1991;17:141–56.10.1016/0263-8223(91)90067-9Search in Google Scholar

[4] Bhimaraddi A. Three-dimensional elasticity solution for static response of simply supported orthotropic cylindrical shells. Compos Struct. 1992;20:227–35.10.1016/0263-8223(92)90028-BSearch in Google Scholar

[5] Bhimaraddi A. Three-dimensional elasticity solution for static response of orthotropic doubly curved shallow shells on rectangular planform. Compos Struct. 1993;24:67–77.10.1016/0263-8223(93)90056-VSearch in Google Scholar

[6] Fan J, Ding K. Exact solutions for thick laminated closed cylindrical shells with two clamped edges. Appl Math Model. 1993;17:632–41.10.1016/0307-904X(93)90073-PSearch in Google Scholar

[7] Brischetto S. Exact three-dimensional static analysis of single- and multi-layered plates and shells. Compos Part B. 2017;119:230–52.10.1016/j.compositesb.2017.03.010Search in Google Scholar

[8] Monge JC, Mantari JL. 3D elasticity numerical solution for the static behavior of FGM shells. Eng Struct. 2020;208:110159.10.1016/j.engstruct.2019.110159Search in Google Scholar

[9] Monge JC, Mantari JL, Arciniega RA. Computational semi-analytical method for the 3D elasticity bending solution of laminated composite and sandwich doubly-curved shells. Eng Struct. 2020;221:110938.10.1016/j.engstruct.2020.110938Search in Google Scholar

[10] Monge JC, Mantari JL. Exact solution of thermo-mechanical analysis of laminated composite and sandwich doubly-curved shell. Compos Struct. 2020;245:112323.10.1016/j.compstruct.2020.112323Search in Google Scholar

[11] Flügge W. Stresses in shells. Berlin: Springer-Verlag; 1960.10.1007/978-3-662-29731-5Search in Google Scholar

[12] Leissa AW. Vibrations of shells. NASA Sp; 1973. p. 288.Search in Google Scholar

[13] Kraus H. Thin elastic shells. New York: John Wiley & Sons; 1967.Search in Google Scholar

[14] Gould PL. Analysis of shells and plates. Berlin: Springer-Verlag; 1988.10.1007/978-1-4612-3764-8Search in Google Scholar

[15] Kirchhoff G. Über das gleichgewicht und die bewegung einer elastischen scheibe. J Reine Angew Math. 1850;1850(40):51–88.10.1515/crll.1850.40.51Search in Google Scholar

[16] Love AEH. On the small free vibrations and deformations of the elastic shells. Philos Trans R Soc A. 1888;17:491–546.10.1098/rsta.1888.0016Search in Google Scholar

[17] Love AEH. A treatise on the mathematical theory of elasticity. Cambridge: Cambridge University Press; 1927.Search in Google Scholar

[18] Naghdi WT. The theory of shells and plates. Handb Phys. 1972;6:425–640.10.1007/978-3-642-69567-4_5Search in Google Scholar

[19] Reissner E. The effect of transverse shear deformation on the bending of elastic plates. ASME J Appl Mech. 1945;12:69–76.10.1115/1.4009435Search in Google Scholar

[20] Mindlin RD. Influence of rotatory inertia and shear in flexural motions of isotropic elastic plates. ASME J Appl Mech. 1951;18:1031–6.10.1115/1.4010217Search in Google Scholar

[21] Whitney JM, Sun CT. A higher order theory for extensional motion of laminated anisotropic shells and plates. J Sound Vib. 1973;30:85.10.1016/S0022-460X(73)80052-5Search in Google Scholar

[22] Whitney JM, Sun CT. A refined theory for laminated anisotropic cylindrical shells. J Appl Mech. 1974;41:471–6.10.1115/1.3423312Search in Google Scholar

[23] Reddy JN, Liu CF. A higher-order shear deformation theory for laminated elastic shells. Int J Eng Sci. 1985;23:319–30.10.1016/0020-7225(85)90051-5Search in Google Scholar

[24] Khdeir AA, Librescu L, Frederick D. A shear deformable theory of laminated composite shallow shell-type panels and their response analysis II: Static response. Acta Mech. 1989;77:1–12.10.1007/BF01379740Search in Google Scholar

[25] Alijani F, Aghdam MM, Abouhamze M. Application of the extended Kantorovich method to the bending of clamped cylindircal panels. Eur J Mech. 2008;27:378–88.10.1016/j.euromechsol.2007.05.011Search in Google Scholar

[26] Bigdeli K, Aghdam MM. A semianalytical solution for the bending of clamped laminated doubly curved or spherical panels. J Mech Mater Struct. 2010;5:855–73.10.2140/jomms.2010.5.855Search in Google Scholar

[27] Mantari JL, Oktem AS, Guedes Soares C. Bending and free vibration analysis of isotropic multilayered plates and shells by using a new accurate higher order shear deformation theory. Compos B. 2012;43:3348–60.10.1016/j.compositesb.2012.01.062Search in Google Scholar

[28] Tornabene F, Liverani A, Caligiana G. Static analysis of laminated composite curved shells and panels of revolution with a posteriori shear and normal stress recovery using generalized differential quadrature method. Int J Mech Sci. 2012;61:71–87.10.1016/j.ijmecsci.2012.05.007Search in Google Scholar

[29] Tornabene F, Liverani A, Caligiana G. Laminated composite rectangular and annular plates: A GDQ solution for static analysis with a posteriori shear and normal stress recovery. Compos B. 2012;43:1847–72.10.1016/j.compositesb.2012.01.065Search in Google Scholar

[30] Fares ME, Youssif YG. A refined equivalent single-layer model of geometrically non-linear doubly curved layered shells using mixed variational approach. Int J Non-Linear Mech. 2001;36:117–24.10.1016/S0020-7462(99)00091-8Search in Google Scholar

[31] Reddy JN. On the generalization of displacement-based laminate theories. Appl Mech Rev. 1989;42:213–22.10.1115/1.3152393Search in Google Scholar

[32] Dennis ST. A Galerkin solution to geometrically nonlinear laminated shallow shell equations. Comput Struct. 1997;63:859–74.10.1016/S0045-7949(96)00380-XSearch in Google Scholar

[33] Balah M, Al-Ghamedy HN. Finite element formulation of a third order laminated finite rotation shell element. Comput Struct. 2002;80:1975–90.10.1016/S0045-7949(02)00222-5Search in Google Scholar

[34] Reddy J. A generalization of two-dimensional theories of laminated composite plates. Commun Appl Numer Methods. 1987;3:173–80.10.1002/cnm.1630030303Search in Google Scholar

[35] Carrera E. Multilayered shell theories accounting for layerwise mixed description, Part 1: Governing equations. AIAA J. 1999;37:1107–16.10.2514/2.821Search in Google Scholar

[36] Carrera E. Multilayered shell theories accounting for layerwise mixed description, Part 2: Numerical evaluations. AIAA J. 1999;37:1117–24.10.2514/2.822Search in Google Scholar

[37] Carrera E. Theories and finite elements for multilayered, anisotropic, composite plates and shells. Arch Comput Methods Eng. 2002;9(2):87–140.10.1007/BF02736649Search in Google Scholar

[38] Carrera E. Theories and finite elements for multilayered plates and shells: a unified compact formulation with numerical assessment and benchmarking. Arch Comput Methods Eng. 2003;10:215–96.10.1007/BF02736224Search in Google Scholar

[39] Carrera E, Brischetto S. Analysis of thickness locking in classical, refined and mixed multilayered plates theories. Compos Struct. 2008;82(4):549–62.10.1016/j.compstruct.2007.02.002Search in Google Scholar

[40] Carrera E, Brischetto S. Analysis of thickness locking in classical, refined and mixed theories for layered shells. Compos Struct. 2008;85:83–90.10.1016/j.compstruct.2007.10.009Search in Google Scholar

[41] Demasi L. 6 mixed plate theories based on the generalized unified formulation Part I: governing equations. Compos Struct. 2009;87:1–11.10.1016/j.compstruct.2008.07.013Search in Google Scholar

[42] Demasi L. ∞ 6 mixed plate theories based on the generalized unified formulation. Part III: advanced mixed high order shear deformation theories. Compos Struct. 2009;87:183–94.10.1016/j.compstruct.2008.07.011Search in Google Scholar

[43] Demasi L. 6 Mixed plate theories based on the Generalized Unified Formulation Part V: results. Compos Struct. 2009;88:1–16.10.1016/j.compstruct.2008.07.009Search in Google Scholar

[44] Ferreira AJM. Analysis of composite plates using a layerwise theory and multiquadrics discretization. Mech Adv Mater Struct. 2005;12:99–112.10.1080/15376490490493952Search in Google Scholar

[45] Ferreira AJM, Roque CMC, Jorge RMN, Kansa EJ. Static deformations and vibration analysis of composite and sandwich plates using a layerwise theory and multiquadrics discretizations. Eng Anal Bound Elem. 2005;29:1104–14.10.1016/j.enganabound.2005.07.004Search in Google Scholar

[46] Tornabene F, Fantuzzi N, Viola E, Carrera E. Static analysis of doubly-curved anisotropic shells and panels using CUF approach, differential geometry and differential quadrature method. Compos Struct. 2014;107:675–97.10.1016/j.compstruct.2013.08.038Search in Google Scholar

[47] Plagianakos TS, Papadopoulos EG. Coupled higher-order layerwise mechanics and finite element for cylindrical composite and sandwich shells with piezoelectric transducers. Eur J Mech A Solids. 2015;54:11–23.10.1016/j.euromechsol.2015.06.003Search in Google Scholar

[48] Li DH. Extended layerwise method of laminated composite shells. Compos Struct. 2016;136:313–44.10.1016/j.compstruct.2015.08.141Search in Google Scholar

[49] Li DH, Zhang F. Full extended layerwise method for the simulation of laminated composite plates and shells. Comput Struct. 2017;187:101–13.10.1016/j.compstruc.2016.10.023Search in Google Scholar

[50] Li DH, Liu Y, Zhang X. An extended layerwise method for composite laminated beams with multiple delaminations and matrix cracks. Int J Numer Methods Eng. 2015;101(6):407–34.10.1002/nme.4803Search in Google Scholar

[51] Carrera E, Valvano S. Analysis of laminated composite structures with embedded piezoelectric sheets by variable kinematic shell elements. J Intell Mater Syst Struct. 2017;28:2959–87.10.1177/1045389X17704913Search in Google Scholar

[52] Carrera E, Pagani A, Valvano S. Shell elements with through-the-thickness variable kinematics for the analysis of laminated composite and sandwich structures. Compos Part B Eng. 2017;111:294–314.10.1016/j.compositesb.2016.12.001Search in Google Scholar

[53] Kumar SK, Harursampath D, Carrera E, Cinefra M, Valvano S. Modal analysis of delaminated plates and shells using Carrera Unified Formulation – MITC9 shell element. Mech Adv Mater Struct. 2017;25:681–97.10.1080/15376494.2017.1302024Search in Google Scholar

[54] Petrolo M, Carrera E. Methods and guidelines for the choice of shell theories. Acta Mech. 2020;231(2):395–434. 10.1007/s00707-019-02601-w.Search in Google Scholar

[55] Carrera E, Augello R, Pagani A, Scano D. Refined multilayered beam, plate and shell elements based on Jacobi polynomials. Compos Struct. 2023;304:116275.10.1016/j.compstruct.2022.116275Search in Google Scholar

[56] Petrolo M, Augello R, Carrera E, Scano D, Pagani A. Evaluation of transverse shear stresses in layered beams/plates/shells via stress recovery accountng for various CUF-based theories. Compos Struct. 2023;307:116625.10.1016/j.compstruct.2022.116625Search in Google Scholar

[57] Chaudhuri RA, Kabir HRH. Sensitivity of the response of moderately thick cross-ply doubly-curved panels to lamination and boundary constraint-I. Theory. Int J Solids Struct. 1993;30(2):263–72.10.1016/0020-7683(93)90065-FSearch in Google Scholar

[58] Chaudhuri RA, Kabir HRH. Sensitivity of the response of moderately thick cross-ply doubly-curved panels to lamination and boundary constraint-II. application. Int J Solids Struct. 1993;30:273–86.10.1016/0020-7683(93)90066-GSearch in Google Scholar

[59] Chaudhuri RA. On boundary-discontinuous double Fourier series solution to a system of completely coupled PDE’s. Int J Eng Sci. 1989;27:1005–22.10.1016/0020-7225(89)90080-3Search in Google Scholar

[60] Chaudhuri RA. On the roles of complementary and admissible boundary constraints in Fourier solutions to boundary-value problems of completely coupled r-th order PDE’s. J Sound Vib. 2002;251:261–313.10.1006/jsvi.2001.3913Search in Google Scholar

[61] Oktem AS, Chaudhuri RA. Fourier solution to a thick cross-ply Levy type clamped plate problem. Compos Struct. 2007;79:481–92.10.1016/j.compstruct.2006.02.007Search in Google Scholar

[62] Oktem AS, Chaudhuri RA. Fourier analysis of thick cross-ply Levy type clamped doubly-curved panels. Compos Struct. 2007;80:489–503.10.1016/j.compstruct.2006.05.028Search in Google Scholar

[63] Oktem AS, Chaudhuri RA. Boundary discontinuous Fourier analysis of thick cross-ply clamped plates. Compos Struct. 2008;82:539–48.10.1016/j.compstruct.2007.02.001Search in Google Scholar

[64] Canales FG, Mantari JL. Boundary discontinuous Fourier analysis of thick beams with clamped and simply supported edges via CUF. Chin J Aeronaut. 2017;30(5):1708–18.10.1016/j.cja.2017.06.014Search in Google Scholar

[65] Canales FG, Mantari JL. A boundary-discontinuous based Fourier analysis of thick laminated beam via a robust 1D-CUF model. Int J Solids Struct. 2017;118–119:109–18.10.1016/j.ijsolstr.2017.04.017Search in Google Scholar

[66] Laureano RW, Mantari JL, Yarasca J, Oktem AS, Monge J, Zhou X. Boundary Discontinuous Fourier analysis of clamped isotropic and cross-ply laminated plates via Unified Formulation. Compos Struct. 2024;328:117736.10.1016/j.compstruct.2023.117736Search in Google Scholar

[67] Laureano RW, Mantari JL, Yarasca J, Oktem AS, Zhou X, Hinostroza MA. Closed-form solutions for clamped FGM plates via the unified formulation and boundary discontinuous method. Mech Adv Mater Struct. 2024;31(26):8546–63. 10.1080/15376494.2023.2261000.Search in Google Scholar

[68] Chaudhuri RA, Kabir HRH. A boundary discontinuous Fourier solution for clamped transversely isotropic (pyrolytic graphite) Mindlin plates. Int J Solid Struct. 1993;30:287–97.10.1016/0020-7683(93)90067-HSearch in Google Scholar

[69] Oktem AS, Mantari JL, Soares CG. Static response of functionally graded plates and doubly-curved shells based on a higher order shear deformation theory. Eur J Mech A/Solids. 2012;36:163–72.10.1016/j.euromechsol.2012.03.002Search in Google Scholar

[70] Oktem AS, Chaudhuri RA. Higher-order theory based boundary-discontinuous Fourier analysis of simply supported thick cross-ply doubly curved panels. Compos Struct. 2009;89:448–58.10.1016/j.compstruct.2008.09.007Search in Google Scholar

[71] Oktem AS, Chaudhuri RA. Levy type analysis of cross-ply plates based on higher-order theory. Compos Struct. 2007;78:243–53.10.1016/j.compstruct.2005.09.012Search in Google Scholar

[72] Reddy JN, Robbins DH. Theories and computational models for composite laminates. Appl Mech Rev. 1994;47:147–65.10.1115/1.3111076Search in Google Scholar

[73] Varadan TK, Bhaskar K. Review of different theories for the analysis of composites. J Aerosp Soc India. 1997;49:202–8.Search in Google Scholar

[74] Carrera E. Developments, ideas and evaluation based upon Reissner's mixed variational theorem in the modeling of multilayered plates and shells. Appl Mech Rev. 2001;54:301–29.10.1115/1.1385512Search in Google Scholar

[75] Kreja I. A literature review on computational models for laminated composite and sandwich panels. Open Eng. 2011;1:59–80.10.2478/s13531-011-0005-xSearch in Google Scholar

[76] Caliri MF, Ferreira AJM, Tita V. A review on plate and shell theories for laminated and sandwich structures highlighting the Finite Element Method. Compos Struct. 2016;156:63–77.10.1016/j.compstruct.2016.02.036Search in Google Scholar

Received: 2024-07-05

Accepted: 2024-10-23

Published Online: 2025-04-02

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/cls-2024-0022

Keywords for this article

shell; CUF; layerwise theory; clamped; boundary discontinuous; analytical

Creative Commons

BY 4.0