An optimized solution to the course scheduling problem in universities under an improved genetic algorithm

1 Introduction

With the development of the social economy and the introduction of compulsory education, more and more people are able to receive education, the population base receiving basic education has increased, and the number of people willing to receive higher education has also greatly increased [1]. As a result, the enrollment scale of universities becomes increasingly larger, and the limited educational facilities and teachers’ resources on the campus can hardly meet the growing demand. Therefore, multi-campus operation and sharing of educational facilities and faculty resources among different campuses have become a way to solve the demand for education [2]. Although the sharing of teaching resources across multiple campuses can meet the growing demand, the increased teaching resources also make the management more difficult and require the coordinated adjustment of the sequence of course arrangements to maximize the use of limited resources [3]. Hossain et al. [4] proposed a particle swarm algorithm to solve the highly constrained university course scheduling problem and added a forceful swap operation with a repair mechanism to the particle swarm algorithm. The experimental results showed the effectiveness of the proposed method. Herawatie et al. [5] solved the course scheduling problem with a genetic algorithm and avoided local optimum with a replacement policy. The experimental results showed that the algorithm functioned well. Yang and Xie [6] proposed a course scheduling algorithm based on a particle swarm optimization algorithm, designed a model of university ideological and political course scheduling system based on this algorithm, and verified the effectiveness and usability of the system by experimental and test results. In this study, the course scheduling problem in universities was briefly introduced. A genetic algorithm was proposed to optimize the scheduling scheme. The genetic algorithm was improved by using the principle of coevolution. The novelty of this study is scheduling courses with a genetic algorithm instead of manpower and using coevolution to improve the performance of the genetic algorithm in finding the best solution. The advantage of using a genetic algorithm for scheduling courses is that it can give multiple scheduling solutions more quickly and select the best solution from them.

2 Course scheduling problem in universities

Higher education institutions teach students according to a course schedule. A scientific and standardized course schedule can maximize the mobilization and utilization of teaching resources, thus improving teaching quality. After excluding various restrictions, the scheduling problem can be regarded as a problem of arranging and combining different courses, and different arrangements and combinations will bring different teaching qualities [7]. However, in the actual scheduling problem, the optimization of the scheduling scheme is subject to various constraints, including the type of courses, the number of classes required for every course, the number of teachers, the size of classrooms, the number and size of classes, and the duration of courses.

In addition to the various restrictions mentioned above, the difficulties of the scheduling problem also include the large number of optional permutations and combinations caused by the large number of courses, class time slots, and teachers. Some of these permutations and combinations violate the restrictions, but even for the remaining combinations, the huge number makes it difficult to find a suitable scheduling solution by human effort. Therefore, this study uses a genetic algorithm to optimize the scheduling solution.

The factors involved in the mathematical description of the scheduling problem are:

where T _t refers to the t-th period, T refers to the set of time periods, M _m refers to the m-th course (there are z _m classes for this course), M refers to the set of courses, C _c refers to the c-th class (this class includes k _c students), C refers to the set of classes, R _r refers to the r-th classroom (this class can tolerate y _r people), R refers to the set of classrooms, P _p refers to the p-th teacher (this teacher has x _p courses to teach), and P is the set of teachers [8].

In the actual scheduling problem, the values of the factors involved in equation (1) will be restricted. To facilitate calculation, we default that every classroom can accommodate students in every class in equation (1). Restrictions for the scheduling problem are:

1. only one M _m can be taught by P _p at T _t ;

2. C _c can only take one M _m at T _t ;

3. only one M _m can be taught in R _r at T _t .

The above restrictions are converted into a mathematical form:

where V is the set of allocation events with the teacher, student, and course bound in the scheduling scheme, v _q is the q-th allocation event with the teacher, student, and course bound (teacher is an element of P, student is an element of C, and course is an element of M), T ₁, T ₂, and T ₃ are the judgment values for the corresponding three restrictions (the value is 1 if the restriction is not met; otherwise, the value is 0), and f ₁, f ₂, and f ₃ are the total judgement values of V for the above three restrictions. When the sum of f ₁, f ₂, and f ₃ is 0, it indicates that there is no scheduling conflict [9].

3 Scheduling optimization based on the improved genetic algorithm

As we can see from Section 2, the goal of the course scheduling problem in universities is to make the scheduling scheme more reasonable without scheduling conflicts. Traditionally, manual course scheduling involves scheduling courses with high priorities or scheduling difficulty first, arrange time periods for every course according to the course hours, and arrange courses with lower priorities in the same way, and the goal of no conflict is eventually achieved through continuous backtracking and adjustment [10]. However, in universities with a large number of faculty, students, and course programs, the workload of course scheduling is heavy. Manual course scheduling for universities is tedious and more prone to scheduling conflicts. The traditional genetic algorithm [11] uses a single population for evolution. Small population size is ineffective in finding the optimal solution, while a large population size will lead to too much computation and difficult convergence. In addition, although the iterative process of the genetic algorithm will increase the number of solution candidates by mutation operation, it will still fall into the optimal local solution [12].

The traditional genetic algorithm was improved by multi-population coevolution, and the flow of the improved genetic algorithm for scheduling is shown in Figure 1.

Figure 1

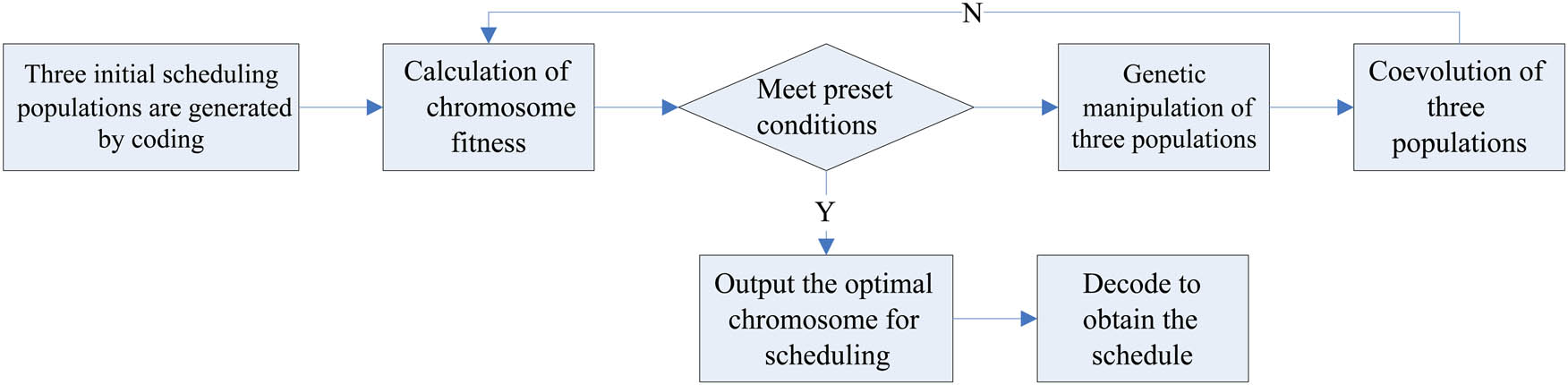
The improved process.

Three initial populations of the same size are generated through coding. Every chromosome in the population represents one scheduling scheme. In general, the teaching schedule is based on a week-long cycle, and Saturday and Sunday are holidays, so the scheduling scheme spans from Monday to Friday, which means that the schemes represented by the chromosomes are for a week. The gene coding pattern of the chromosome is “time period code + classroom code + course code + class code + teacher code,” and non-conflicting plural segments following the above pattern constitute the scheduling scheme, i.e., a chromosome. The choice of gene locus code is not random. There are 25 time periods, so the time period code is chosen from “01, 02, 03, …, 25.” The classroom code is chosen from the classroom codes owned by the school. The course code, class code, and teacher code are provided by the school [13]. The coding rules for chromosomes within the initial population are as described in Section 2. Under the premise of following the coding rules, the initial population is generated according to the custom of manual course scheduling. Step 1, the corresponding teacher codes of one class are added to fixed time periods. Then, the codes of other teachers of that class are added to different time periods randomly to obtain the initial course schedule of the class, and the initial class schedule of all classes is combined to form an initial chromosome. The plural chromosomes obtained as above constitute the initial population.

Step 2 The fitness of chromosomes in the population is calculated. Since the random generation of chromosomes, i.e., scheduling schemes, has already taken into account the problem of course conflicts and actively excluded conflicting schemes in the subsequent genetic operation, the main consideration in the calculation of fitness is to make the existing conflict-free scheduling schemes better, so the calculation formula of fitness is:

where g is the chromosome fitness, g ₁, g ₂, and g ₃ are the course sequence priority, course duration discrete uniformity, and classroom utilization, ω ₁, ω ₂, and ω ₃ are weights of g ₁, g ₂, and g ₃, α _j is the weight value (importance) of the j-th course, t _i is the sequence weight of the i-th period, and d _j is the schedule discrete degree of the j-th course.

Step 3 Whether the predefined conditions (reaching the maximum number of iterations or population fitness converging to stability) are met is determined based on the calculated population chromosome fitness. If the predefined conditions are met, the optimal chromosome is selected, and the chromosome is decoded to obtain the schedule. As shown in Figure 2, every row in this two-dimensional schedule represents a classroom, every column represents a course time period, and the intersection of the rows and columns is an array of courses, classes, and teachers, (M _m , C _c , P _p ).

Figure 2

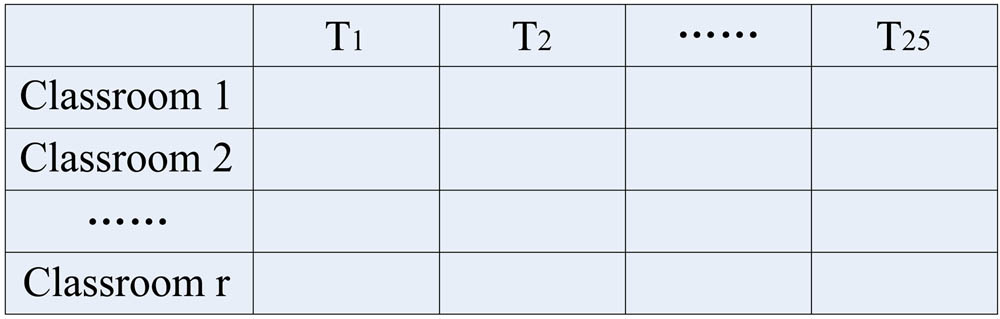
Two-dimensional course schedule.

The genetic operation is conducted when the population chromosome fitness does not meet the pre-defined conditions.

Step 4 In genetic iteration [14], crossover means randomly selecting two chromosomes according to the crossover probability and exchanging the gene fragment of the same position. In this study, the single-point crossover was used, i.e., only one gene at one gene locus was exchanged in one crossover. In addition, the conflict between the two chromosomes after crossover is determined using equation (2), and if a conflict occurs, another gene locus is randomly selected again for crossover until there is no conflict. Mutation means randomly selecting a chromosome according to the mutation probability and exchanging genes at the same type of gene locus until the mutated chromosome is conflict-free.

Step 5 After all three populations have undergone one genetic operation, the three populations are subjected to a coevolutionary [15] operation, as shown in Figure 3. The updated populations are arranged in ascending order by the value of the fitness function, and half of the worst chromosomes are replaced by half of the best chromosomes in the other population (order: population 1 → population 2 → population 3 → population 1). Then, the best and worst chromosomes in every population are selected, and the worst chromosomes are replaced by the best chromosomes.

Figure 3

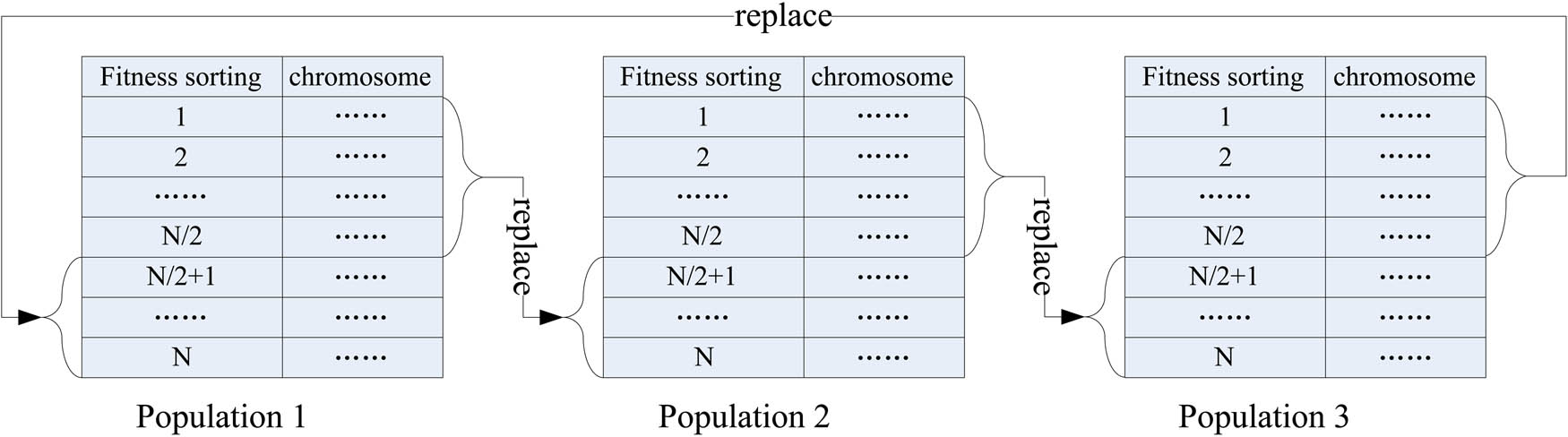
The operation flow of coevolutionary operation of three populations.

Step 6 Return to step 2 until one of the termination conditions is satisfied. There are two termination conditions. The first termination condition is that the number of iterations reaches the preset maximum number, avoiding the unnecessary computation time caused by difficult convergence. The second termination condition is that the fitness value of the algorithm converges to stable. The difference between the fitness value after the current time of iteration and the fitness value after the last time of iteration is calculated. The algorithm is considered as converging to stable when the difference reduces to within the preset range and no longer exceeds the preset range in the following 100 times of iterations.

4 Simulation experiments

4.2 Experimental results

Figure 4 shows the change in the average fitness value of population chromosomes during iterations of the traditional genetic algorithm and the improved genetic algorithm. It is seen from Figure 4 that the average fitness value of the populations of both genetic algorithms increased with the increase in the number of iterations and converged gradually. The improved genetic algorithm converged to a stable fitness value (48) after about 750 iterations, and the traditional genetic algorithm converged to a stable fitness value (44) after about 900 iterations. It was found that the improved genetic algorithm converged faster and yielded better chromosomes, i.e., better scheduling solutions.

Figure 4

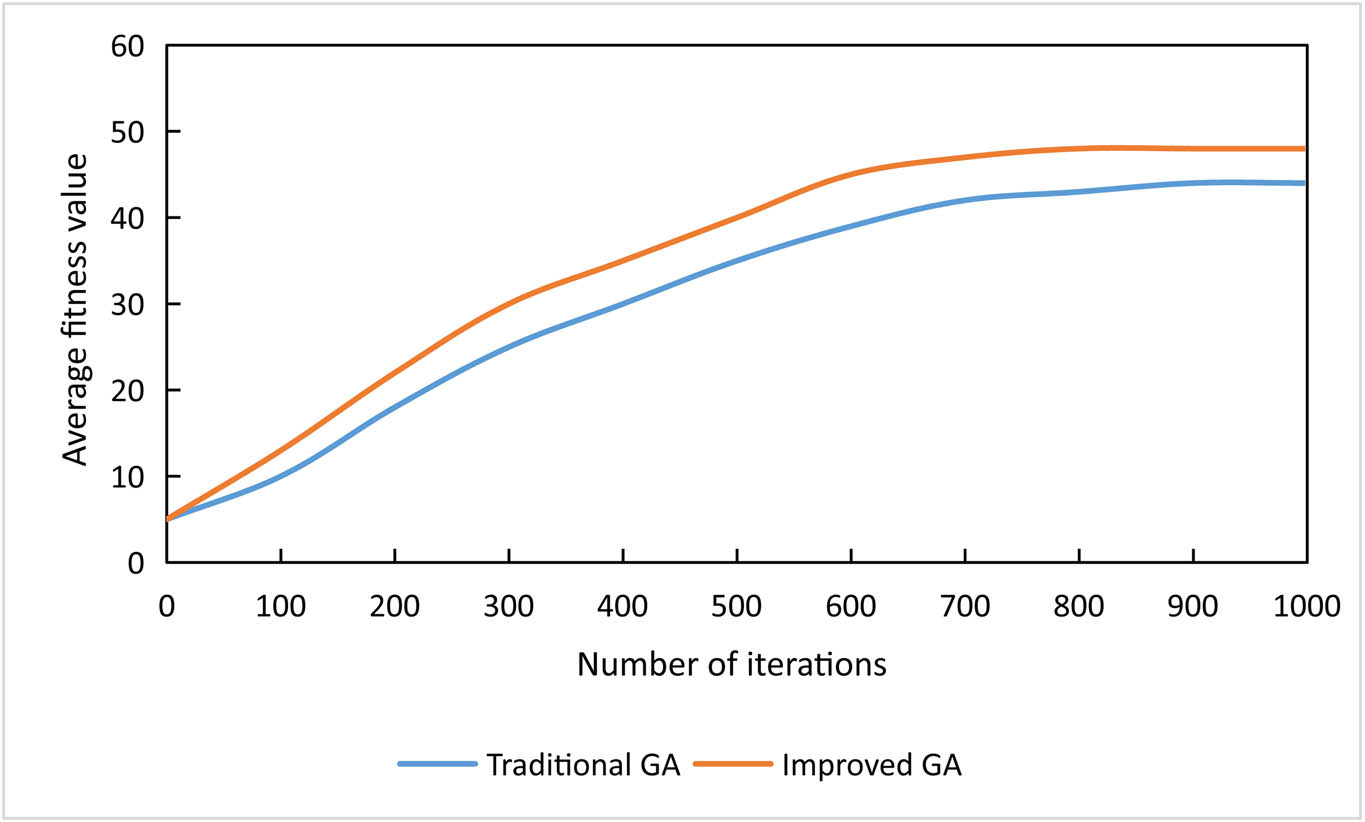
Comparison of traditional and improved genetic algorithms.

Figure 5 shows the average population fitness values and computational time of the two genetic algorithms under 0.4, 0.5, 0.6, 0.7, and 0.8 crossover probabilities when the mutation probability was 0.1. It is seen from Figure 5 that as the crossover probability increased from 0.4 to 0.8, the average fitness value of the two genetic algorithms tended to increase and then decrease, and the computational time of both algorithms tended to decrease and then increase. The comparison of the two genetic algorithms under the same crossover probability showed that the improved genetic algorithm had a larger fitness value and shorter computational time. The reason for the trend of the average fitness value and computational time of the two genetic algorithms with the crossover probability was that when the crossover probability was low, fewer new chromosomes were generated, leading to a slow search, and when it was high, the excellent chromosomes were easily split, leading to a slow search.

Figure 5

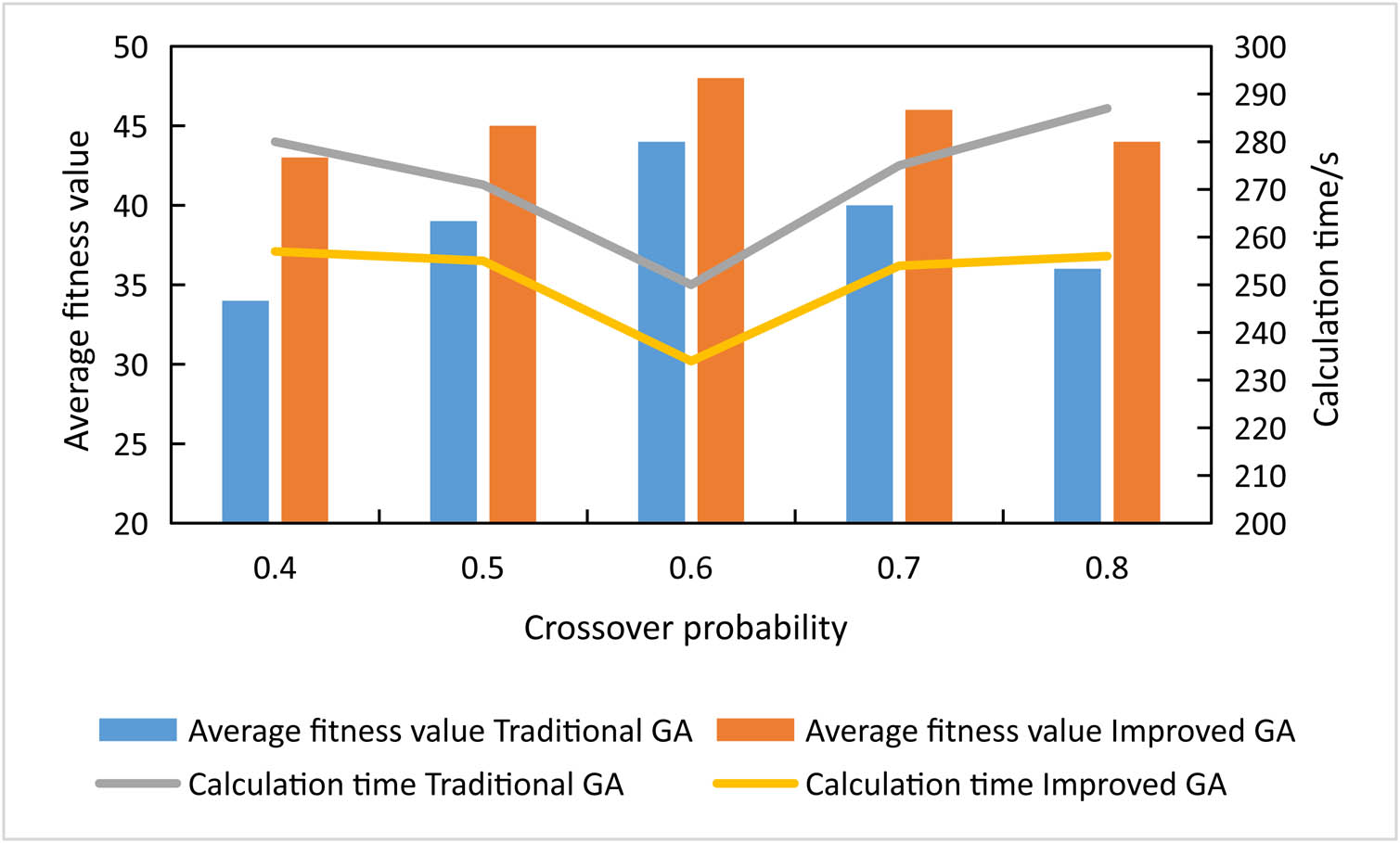
Performance of two genetic algorithms under different crossover probabilities when the mutation probability is 0.1.

Figure 6 shows the average population fitness values and computational time of the two genetic algorithms at 0.1, 0.2, 0.3, 0.4, and 0.5 mutation probabilities when the crossover probability was 0.6. It is seen from Figure 6 that as the variation probability increased from 0.1 to 0.5, the average fitness value of the two genetic algorithms tended to decrease and the detection time tended to increase. The improved genetic algorithm showed a higher fitness value and shorter computational time than the traditional algorithm under the same variance probability. The reason for the trend of the average fitness value and computational time of the two genetic algorithms with the mutation probability was that the variation in chromosomes generated new gene fragments to increase the diversity of population genes, and when the variation probability increased, the diversity of population genes increased, but it also resulted in the unstable inheritance of good genes.

Figure 6

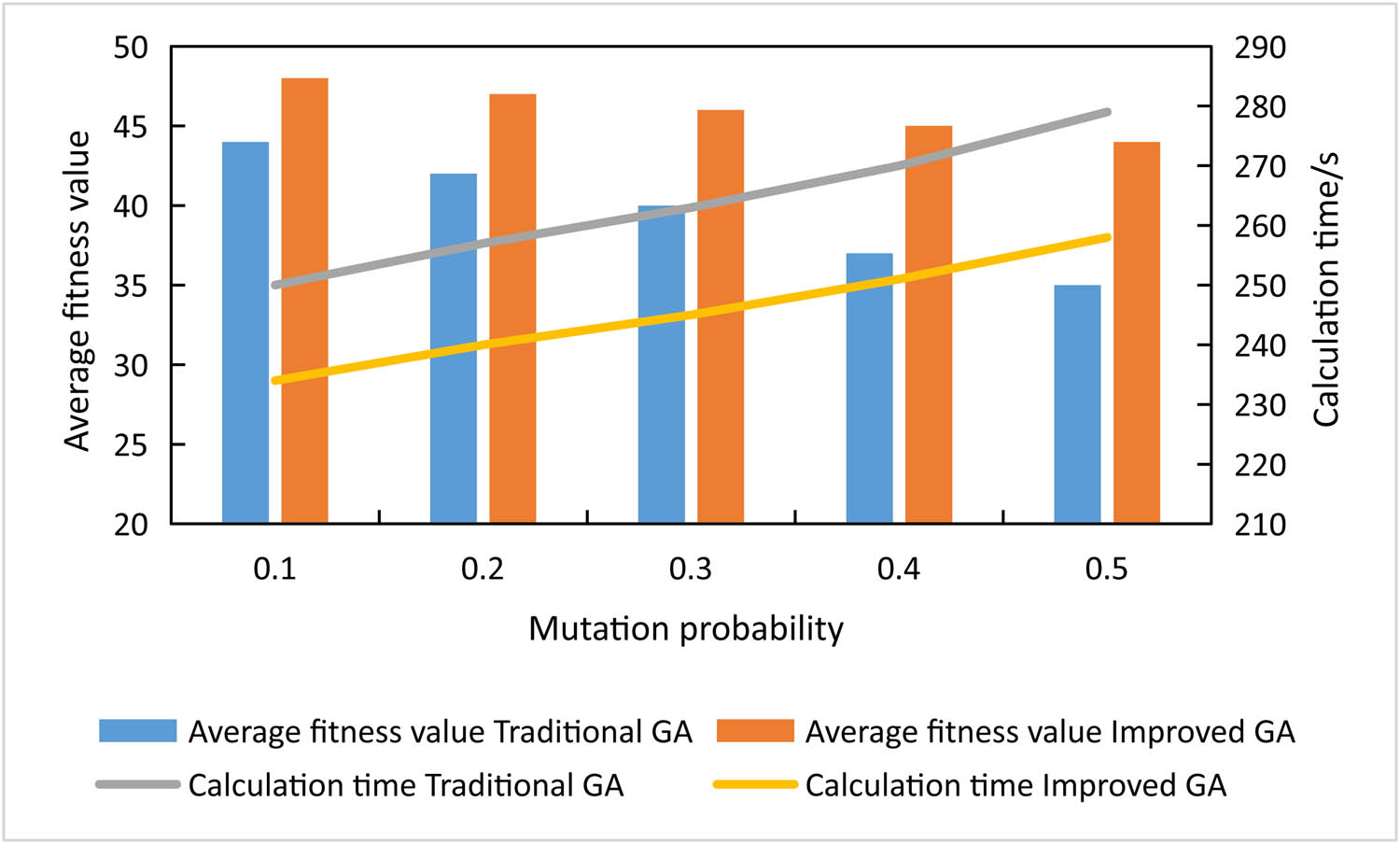
Performance of two genetic algorithms under different variation probabilities when the crossover probability is 0.6.

Both Figures 5 and 6 reflect that the improved genetic algorithm outperformed the traditional genetic algorithm in terms of average fitness value and computational time under the same crossover and mutation probabilities. The reason for the above result was that the improved genetic algorithm used the principle of multi-population coevolution to make the three populations evolve independently and replaced poor chromosomes with excellent chromosomes to enhance the diversity of high-quality chromosomes and jump out of the locally optimal solution.

5 Discussion

For higher education institutions, it is an important task to arrange courses for teachers and students in a reasonable manner. A reasonable scheduling plan can effectively improve the teaching management efficiency of colleges. As the education reform progresses and the importance of higher education is emphasized, the enrollment scale of colleges has increased. However, the teaching resources of universities are limited, and a reasonable scheduling plan is needed to meet the growing demand of students. The increase in the number of students makes the traditional manual scheduling methods increasingly difficult to cope with more complex scheduling problems.

The optimization of the scheduling scheme can be regarded as the search for an optimal scheduling scheme in different candidates, so this study used a genetic algorithm to optimize the scheduling scheme and also used coevolution to improve the genetic algorithm. Finally, simulation experiments were conducted to verify the performance difference between the traditional and improved genetic algorithms under different mutation and crossover probabilities, and the final experimental results are shown above.

Under the same crossover and variation probabilities, the coevolution-improved genetic algorithm converged to stability faster, and the corresponding scheduling scheme was better when convergence was stable. In addition, under the same mutation probability, with the increase in the crossover probability, the fitness values of the scheduling solutions of both traditional and improved genetic algorithms increased first and then decreased, and the computation time decreased first and then increased. Under the same crossover probability, with the increase in the mutation probability, the fitness values of the scheduling schemes of both traditional and improved genetic algorithms tended to decrease, while the computational time tended to increase. The reasons for these results are as follows. Under the same crossover and mutation probabilities, due to the introduction of coevolution, the three populations executed crossover and mutation operations independently and replaced poor chromosomes with excellent ones in turn. The independent evolution of the three populations made it possible to get rid of one of the populations even if it fell into a local optimum by the other population, and the parallel optimization search of the three populations also accelerated the convergence. Therefore, the improved genetic algorithm not only converged faster but also had a larger fitness value after the convergence was stable. Under a fixed mutation probability, a low crossover probability might reduce the efficiency of optimization search due to insufficient chromosome “exchange” within the population, but a high crossover probability might result in too much “exchange” and loss of good chromosomes, which would also reduce the efficiency of optimization search. Therefore, increasing the crossover probability made the fitness value of the two genetic algorithms increase first and then decrease and the computational time decrease first and then increase. If the crossover probability was fixed, the increase in mutation probability would make the chromosomes more likely to produce new genes, but it would also lead to the unstable inheritance of good genes, which would eventually result in slow convergence and lower fitness value in the iterative results.

6 Conclusion

This study briefly introduced the course scheduling problem in universities, proposed the use of a genetic algorithm to optimize the scheduling scheme, improved the genetic algorithm with the principle of coevolution, and finally conducted simulation experiments on the traditional and improved genetic algorithms. The results are as follows. The improved genetic algorithm converged to a stable fitness value (48) after about 750 iterations, and the traditional genetic algorithm converged to a stable fitness value (44) after about 900 iterations. When the mutation probability was fixed at 0.1 and the crossover probability was between 0.4 and 0.8, the average fitness value of the two genetic algorithms tended to increase first and then decrease, and the computation time tended to decrease first and then increase. When the crossover probability was fixed at 0.6 and the crossover probability was between 0.1 and 0.5, the average fitness value of the 2 genetic algorithms tended to decrease, and the detection time tended to increase. The improved genetic algorithm had a higher average fitness value and shorter computation time than the traditional one under the same crossover probability and mutation probability.