Convex optimization for additive noise reduction in quantitative complex object wave retrieval using compressive off-axis digital holographic imaging

1 Introduction

The research studies on three-dimensional (3D) information processing systems based on optical, digital, and hybrid architectures have got empowered with machine intelligence, which is rapidly advancing these days [1,2,3, 4,5]. The advancements in 3D information processing systems play a pivotal role in the development of next generation machine vision and robotics. The design and development of such robust systems involve the need of efficient 3D object data acquisition systems, accurate and noise-free 3D object reconstruction techniques from the sensed data, and finally the development of prudent algorithms that impart intelligence to process the 3D information on a real-time basis. Digital holography [6,7, 8,9] is a hybrid opto-electronic technique used for sensing the quantitative 3D object information by a digital image sensor in the form of a two-dimensional (2D) real-valued image – a “digital hologram.” The numerical reconstruction of such optically generated and electronically sensed hologram gives a quantitative measure of the intensity and phase of the object wavefront as digital complex images. The 3D information processing may be achieved by processing the retrieved 2D digital complex images for machine vision and other robotics applications. A digital hologram is acquired using a charge-coupled device/complementary metal-oxide semiconductor image sensor and stored in a digital format. Therefore, the noises [10,11, 12,13,14, 15,16,17, 18,19,20, 21,22] such as photon noise, dark current, shot noise, additive noise, and speckle noise are imposed during the process of recording the digital hologram. The recorded digital hologram is numerically reconstructed by means of numerical computational algorithms. On reconstructing one gets a complex-valued digital image of the 3D object information. The amplitude part of the object wavefield gives intensity information and phase part of the object wavefield gives depth or 3D information of the object. The noise intruded in the digital hologram will lower the image quality of the reconstructed object wavefront, particularly the phase information. The additive noise arouses mainly due to the conversion of the interference patterns to a digital output and due to the camera characteristics. The additive noise is one of the major reasons behind the reduced quality of the reconstructed object wavefront and it is at this particular issue the article is focused.

Compressive sensing (CS) [23,24,25,27,28,29, 30,31,32, 33,34,35] is a paradigm shift in the sampling theorem, which suggests a much lesser sampling rate than the Nyquist rate. CS has been applied in the fields of autonomous mobile robots [31,32,33], wireless sensor networks [34,35], image processing [27,28, 29,30], digital holography [6,7, 8,9], etc. for data compression and transmission. Integration of optics with CS model is an emerging research field for data acquisition based on the condition that a small number of samples can recover a sparse original signal without losing any information using optimization techniques. In compressive Fresnel digital holography [36,37, 38,39,40, 41,42,43, 44,45], the object wavefield is reconstructed from a lesser number of hologram samples. The CS is an iterative procedure to reconstruct the original signal from the incomplete linear measurements exploiting the sparsity of the signal. If signal is said to be sparse, then it has a very less number of non-zero samples. The signal shall be sparse either in the spatial or transform domains like fast fourier transform, wavelet, discrete cosine transform, etc. The sparse signal learning is achieved by using convex optimization based on l1-norm minimization [23,24, 25,26,27, 28,29] and iterative process as a trial-and-error method. The convex optimization searches for recovery of object wave closer to the original signal from noisy and incomplete measurements.

Memmolo et al. [15] have proposed a sparsity-based noise reduction (SPADEDH) algorithm in digital holography. In this method, the denoising of digital hologram is performed without any prior knowledge of noise characteristics or parameters. The results show that the SPADEDH method effectively minimizes the noise and improved the reconstructed quality of object intensity image. Verpillat et al. [16] have examined the noise-level limits in digital holography using the Monte Carlo method. The experimental results show that the Monte Carlo noise method is able to reconstruct the object wavefield information accurately from low light illumination and short noise. Pandey and Hennelly [17] have investigated the effect of additive Gaussian noise and Poisson noise on quantitative phase reconstruction in digital holographic microscopy using the Fourier filtering method. The results show that the Poisson noise has more impact on reconstructed image quality than the gaussian noise. This filtering method performs better reconstruction and reduces the phase error for both the noise models. Gong et al. [18] have discussed the influence of noise and bias in off-axis digital holography to study acoustic pressure phenomenon. The influence of noise on the characterization of the quantitative phase has been studied using the analytical model. Montresor and Picart [19] have proposed a block-matching and 3D filtering (BM3D) approach for the phase denoising method in digital holography interferometry. The BM3D method has shown that it effectively minimizes the additive or Gaussian noise in the reconstructed image compared to other conventional denoising methods. Choi et al. [20] have presented comparative study of various noise reduction algorithm approaches, i.e., average filtering, Butterworth low-pass filtering, and Histogram modification filtering, to minimize the noise and enhance the reconstructed image reconstruction quality of object wavefront. The experimental results show that the Histogram modification filtering method provides improved reconstruction quality compared to other filtering methods. Sharma et al. [21] have proposed a noise reduction in digital holographic image reconstruction using a modified median filtering method. In this approach, the reconstructed results have shown good improvement in the signal to noise ratio of the reconstruction image quality compared to the conventional holographic image reconstruction. Che et al. [22] have proposed a non-local mean filtering approach by averaging the different noise pattern holograms to minimize the noise in the reconstruction process. This method has shown that minimizing the noise in the reconstructed image is more than 90% when compared to conventional Fourier filtering approach. Various image processing methods [15,16,17, 18,19,20, 21,22] such as Fourier filtering, noise-removal filters, and wavelet filters have been implemented in digital holography to remove the noise in the reconstructed image. These filtering techniques are effective for good quality intensity image reconstruction from a noisy digital hologram, however, not suitable for phase reconstruction. The CS has been applied in many in-line and off-axis digital holographic schemes [36,37, 38,39,40, 41,42,43, 44,45] and is gaining attention in reconstruction of sparse complex object wave from a 2D digital hologram. Some recent studies [46,47, 48,49,50, 51,52] have proposed the use of CS approach to replace the noise removal techniques in digital holography. In these methods, only intensity reconstruction has been addressed and hence required to extend CS application further for the phase reconstruction.

The present article numerically demonstrates the complex object wavefront reconstruction accuracy (both intensity and phase) of CS-based off-axis digital holography from a noisy digital Fresnel hologram. The choice of off-axis digital holographic geometry employed in this method enables the recording of a single exposure hologram and also helps in the noise-free image reconstruction. The robustness of the proposed CS method is shown by applying to object wavefield using only 50% of the hologram pixels detection. The reconstruction of complex object wavefront by the CS method is studied using the “Gradient projection sparse representation (GPSR) algorithm [27].” The proposed CS model mathematical framework is discussed, and the results from the numerical simulations are quantitatively analysed.

2 Methodology

In this section, we consider the compressive Fresnel holography framework for the object wavefront reconstruction from a noisy digital hologram. In this article, off-axis holography is utilized for the simulation procedure of data acquisition and complex object wave retrieval. An off-axis digital holographic system allows the recording of single-shot digital hologram by the superposition between the object wave O and reference wave R at an off-set angle θ . A DC and twin image-free object wavefront can be reconstructed from the single digital hologram using the “complex wave retrieval method” [53]. Let us consider the complex object function O located at d distance from the recording plane can be related by a Fresnel transform U .

Here λ is the laser wavelength used for propagating the object wavefront. The intensity distribution of the resulting hologram at the recoding plane is as follows,

where I is the sensed digital Fresnel hologram by the digital sensor with sampling period “T” to give 2D real-valued discrete hologram. Now, consider the noise that originates from the image sensor can be modelled as additive noise N ( μ , σ ) , where N ( . ) is an additive noise [16,17,18, 19,20,21] with mean μ and standard deviation σ . Thus, the digital hologram given in equation (2) and noise are added to obtain a noisy hologram. The noisy digital hologram is expressed as follows:

Let us examine only K measurements of the simulated noisy digital hologram H and K ≪ M . In the reconstruction process, the Fresnel field U ˜ on the recording plane is retrieved using complex wave retrieval method. In this method “a practical assumption that the amplitude of the reference wave is greater than that of the object wave and followed by a non-linear change of variables. Thus, the non-linear holography is approximated to a linear process that can be solved by linear algorithm to determine the Fresnel field at the recording plane [53].”

The process of the proposed CS method for additive noise reduction in complex object wave reconstruction is shown in Figure 1. To implement the CS algorithm, let the reconstructed U ˜ from equation (4) be a noisy and approximated version of U . The retrieved U ˜ is inverse Fresnel propagated by a distance d to reconstruct the approximated object wavefront.

The sparse object wavefield O can be reconstructed from noisy and incomplete measurements by minimizing the unconstrained optimization problem as given in the following equation:

Here τ is a non-negative parameter, ℱ ˜ d termed as sensing matrix. In this work, the intensity and phase reconstruction of the sparse object wave O is reconstructed by solving CS optimization equation (6) using GPSR algorithm [27]. Equation (6) is minimized iteratively by using the GPSR algorithm, which uses the forward operator ℱ ˜ d and ℱ ˜ d − 1 as its inverse operator for faithful reconstruction of object wavefield. The mean square error (MSE) between the original and the reconstructed object wavefronts with the variations of standard deviation of the additive gaussian noise is investigated to quantify the quality of the reconstructed images. The CS algorithm is basically developed for processing the real-valued matrices. The main advantage of the proposed CS method is to deal with the reconstruction of both intensity and phase information of the object wave with proper selection of the sensing matrix. Additionally, the CS optimization using the GPSR algorithm enables an accurate original complex object wave reconstruction using only 50% of the hologram pixel detection ( M ≪ N ). The computational time involved in this method can be minimized using very high-speed processor for real-time applications.

Figure 1

Flowchart of the proposed CS method.

3 Numerical experiments, results and discussion

A USAF resolution chart image of size 1,024 × 1,024 pixels was used as an input complex object wave. The simulated phase information of the object wave was randomly generated in the ranges of [0–1]. The amplitude and the phase of the input complex USAF chart are shown in Figure 2.

Figure 2

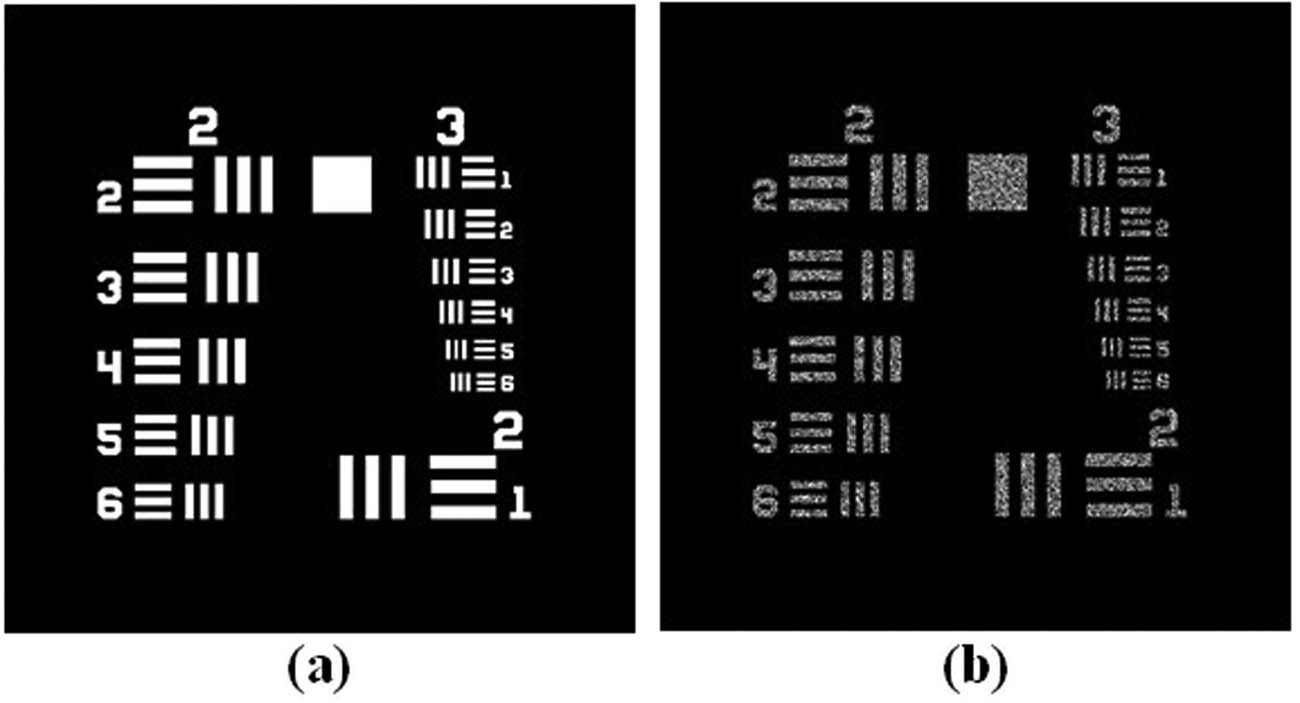
Original USAF resolution chart (a) amplitude and (b) corresponding phase.

In the computer simulation, the Fresnel field U of the input object wavefield at the hologram plane was obtained using Fresnel propagation. The simulation parameters used were propagation distance, d = 20 mm , wavelength λ = 532 nm , angle θ = 1.32 ∘ , and pixel pitch of the detector Δ x = Δ y = 5 μ m . Figure 3(a–c) shows the numerically computed off-axis digital Fresnel hologram of size 1,024 × 1,024 pixel measurements was corrupted by adding additive noise with a standard deviation of σ = 0.1 , 0.5, and 1.0, respectively. Here, only 50% of the pixels were considered in the hologram detection process, and the remaining 50% of the pixels were randomly discarded.

Figure 3

Simulated noisy digital Fresnel holograms with different standard deviations: (a) σ = 0.1 , (b) σ = 0.5 , and (c) σ = 1.0 .

The approximated Fresnel field was computed numerically by solving equation (4) from the noisy digital Fresnel hologram. Figure 4 shows the retrieved intensity and phase of the complex USAF chart using conventional complex wave retrieval method. It can be observed that the retrieved intensity and phase of the USAF chart shown in Figure 4 are degraded due to approximation used in the conventional complex wave retrieval algorithm. This implies that the USAF chart O ˜ reconstructed from the U ˜ using the conventional method is an approximated version of the original USAF chart. Thus, the Fresnel filed U ˜ is considered as noisy and incomplete measurement to implement the proposed CS method. The CS method was implemented by solving equation (6) considering object wave as sparse, and the reconstruction results are shown in Figure 5. From Figures 4 and 5, it can be deduced that the reconstructed USAF chart results of CS method are superior when compared to the conventional method in terms of both intensity and phase accuracy. The reconstructed intensity and phase in the CS method were similar to the original input USAF chart.

Figure 4

Reconstructed USAF chart using conventional method (a–c) intensity and (d–f) the corresponding phases.

Figure 5

Reconstructed complex object wave using CS method (a–c) intensity and (d–f) the corresponding phases.

The MSE value calculated between the original and the reconstructed USAF chart for both conventional and proposed CS method is tabulated in Table 1. It can be deduced from Table 1 that the proposed CS technique is the most superior in reconstruction quality of the USAF resolution chart and the MSE giving the least deviation compared to the conventional method. In addition, the CS-based algorithm reconstructs the original complex object wave using only 50% of the hologram pixel detection. The reconstruction algorithm is executed with MATLAB software (version R2014a). Table 2 shows the reconstruction time for all the computations using the GPSR algorithm.

Figure 6 shows the MSE deviation on the reconstructed object wavefront with different standard deviations of the additive noise. Figure 6(a) shows the MSE of reconstructed intensity of USAF chart with the various additive noise-levels and the CS approach has least error. Similarly, Figure 6(b) shows the MSE of reconstructed phase of USAF chart with the various additive noise-levels and the phase MSE error is minimal in the CS approach. Clearly, it can be seen from Figure 6 that the MSE decreases as the standard deviation increases in the case of CS method and the conventional method has a high noise influence on the reconstructed intensity and phase compared with the CS method.

Figure 6

MSE between original and reconstructed USAF resolution chart versus the standard deviation of the additive noise (a) intensity deviation and (b) phase deviation.

4 Conclusion

The presence of additive noise in digital hologram reduces the quality of both intensity and phase information of the reconstructed complex image. In this study, the digital holography method and CS framework are integrated for high-quality intensity and phase information reconstruction from only 50% of the pixel measurements. This article has demonstrated a CS method to denoise and to accurately reconstruct the complex object wavefront from a noisy off-axis digital Fresnel hologram. The linear reconstruction approach in the complex wave retrieval method has fulfilled the linearity condition of the proposed CS algorithm. Simulation results show that the performance of the proposed CS denoising method has provided good quality reconstruction of object wavefront. Both intensity and phase reconstructed using the CS method is of higher quality as compared to that of the traditional method. The proposed CS denoising approach shown in this work is based on the sparse sampling, which reconstructs both intensity and phase images with minimal noise. The proposed CS approach has shown better reconstruction performance in minimizing the additive noise with zero mean and various combinations of standard deviation of additive Gaussian noise. We have numerically studied the additive noise in the recording and image plane and have verified our proposed CS model with appropriate quantifying metrics. The proposed CS method finds applications in quantitative phase contrast imaging of microscopic 3D objects, live-cell imaging of static or dynamic events, 3D data compression and transmission, etc.