The application of an artificial neural network for 2D coordinate transformation

Ahmed Imad Abbas; Oday Y. M. Alhamadani; Mamoun Ubaid Mohammed

doi:10.1515/jisys-2022-0033

Article Open Access

The application of an artificial neural network for 2D coordinate transformation

Ahmed Imad Abbas , Oday Y. M. Alhamadani and Mamoun Ubaid Mohammed

Published/Copyright: July 7, 2022

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information

From the journal Journal of Intelligent Systems Volume 31 Issue 1

Abstract

Clark1880, WGS1984, and ITRF08 are the reference systems used in Iraq. The ITRF08 and WGS84 represent the global reference frames. In the majority of instances, the transformation from one coordinate system to another is required. The ability of the artificial neural network (ANN) to identify the connection between two coordinate systems without the need for a mathematical model is one of its most significant benefits. In this study, an ANN was employed for two-dimensional coordinate transformation from local Clark1880 to the global reference system ITRF08. To accomplish so, 68 stations with known coordinates in both systems were utilized in this research and were split into two groups: the first set of data (38 stations) was used as the training data and the second set of data (38 stations) was used as the validation data. A root-mean-square error (RMSE) was used to examine the performance of each transformation. The results showed that the RMSE using the ANN was 0.08 m in the east and 0.17 m in the north. The results indicated that the ANN can be used for 2D coordinate transformation with the results that are better than those of the authorized techniques such as 2D conformal transformation and 2D conformal least square.

Keywords: 2D coordinate transformation; feed-forward back propagation; geodetic datum; neural network

1 Introduction

Just after the first Gulf War, the forces of the United States and the United Kingdom initiated a project for the establishment of the Iraqi Geospatial Reference System (IGRS) in cooperation with the Iraqi Ministry of Water Resources, which played a major role in this project. Many of the first-order stations of the Karbala 1979 network, which are still functional and used for precise observations, were re-positioned using high-precision GNSS techniques. Additionally, several new control stations were created to compensate for the destroyed or unusable stations for precise applications. The IGRS’s backbone is a network of six continuously operating reference stations (CORS), which were utilized to expand and densify the IGRS’s control network. The International Terrestrial Reference System (ITRF2000) is used to create the IGRS geodetic datum [1].

Several studies have been conducted over the last few decades on the subject of two- and three-dimensional coordinate transformations between different geographic coordinate reference systems (CRSs), particularly WGS 84 and/or ITRF. The coordinate changes between different CRSs are referred to as datum shifts, datum transformations, and geographic transformations, among other terms.

In general, a coordinate transformation is used to solve the problem of transforming data from one reference frame to another. Although coordinate transformations are simple mathematically, they can generate a variety of issues when used for many reasons, such as a lack of understanding of the local datum’s distortions and inconsistencies, or even a lack of appropriate expertise in geodesy among those who use them [2]. In addition, because local networks serve as the foundation for many engineering projects, such as dam monitoring and border stabilization, and with the development of technology, the field observation is performed using a global navigational satellite system (GNSS) and a laser scanner. This modern technology gives the observation of the ITRF reference frame. For that reason, it is vital to establish a relationship between global and local reference systems. ANNs are represented as a solution to this problem where they can determine the relationship between two completely different reference systems without any mathematical model. Additionally, ANNs have recently gained popularity in the field of geodetic sciences, particularly for coordinate transformation applications [3].

ANNs are computer models based on the nervous systems of live organisms. They have the capacity to train and predict based on regression (information-based) and may be characterized as a collection of processing units characterized by artificial neurons, interconnected by a large number of interconnections (artificial synapses), and implemented by synaptic weight vectors and matrices [4].

The problem with neural networks is that they need more training data to give more accurate results [5]. Most authors used a large amount of data to get an accurate result using the ANN; this may take a long time and effort to collect data, there is a trend in employing neural networks to obtain accurate results using a small amount of data for training. Because of the ability of the ANN to compensate for any mathematical model that links different data sets, several studies have employed the ANN for coordinate transformation. ANN is employed by Lin and Wang [6] to coordinate the transformation from Taiwan Datum 1967 (TWD67) to Taiwan Datum 1997 (TWD97) in Taiwan. The authors demonstrated the coordinate transformation based on the ANN and compared the results to those calculated using the affine transformation technique. The comparison showed that the results of ANNs are more precise than those of affine results. The authors used 74% of the available data as training data and 26% as the validation data on an area of about 2,500 km². On the other hand, Gullu and Essays [7] performed a coordinate transformation using the ANN technique between WGS84 and ED50 in Turkey. The authors showed that the ANN gave results with an accuracy of approximately ±1 cm, while other transformation methods yielded results with a lower level of accuracy. In addition, the authors used approximately 57% of the available data as the training data and 43% as the validation data on an area of about 2,700 km². A software attempt using the ANN was performed by Tierra and Romero [8]. The authors computerized the ANN for easting and northing transformations between PSAD56 and SIRGAS.2, results showed that the ANN is capable of producing more precise transformation results than other conventional methods. On the other hand, the authors used approximately 67% of the available data as the training data and 33% as the validation data on an area of about 372.4 km². Konakoglu, Cakir et al. [9] used the ANN to coordinate transformation between the European Datum 1950 (ED50) used in Turkey and the International Terrestrial Reference Frame 1996 (ITRF96). The transformation results showed that the accuracy obtained from the ANN method was within ±1 cm. Additionally, the authors used approximately 73% of the available data as the training data and 27% as the validation data on an area of about 188.8 km². Kumi-Boateng and Ziggah [10] employed Radial Basis Function Neural Networks for 2D coordinate transformation between Accra and Leigon datum used in Ghana. Results showed that the RBFNN has the capacity to realize more dependable and accurate results with a maximum error in differences between the predicted value and actual value of about 0.7768 m and a minimum error of 0.1795 m, making it more appropriate for modeling distortions in local geodetic networks than older approaches (six-parameter and four-parameter). The authors used approximately 74% of the available data as the training data and 26% as the validation data on an area of about 107,000 km². The ANN was utilized for coordinate transformation [11] between Ghana’s Accra datum based on the War Office 1926 ellipsoid and the World Geodetic System 1984 (WGS84) ellipsoid, with deviation estimates ranging from 20 to 80 cm for the modified coordinates. The authors used approximately 74% of the available data as training data and 26% as the validation data on an area of about 68,000 km². The least-square support vector machine (LS-SVM) and RBFNN were utilized by Ziggah et al. [12] to carry out a 2D coordinate transformation in Ghana. According to the results, the LS-SVM and RBFNN produced equivalent results and were superior to the other approaches. The results acquired from the ANN were 0.382 m for the east and 0.296 m for the north in terms of RMSE. The authors used approximately 67% of the available data as the training data and 33% as the validation data on an area of about 122,000 km².

The current study presents a novel approach for converting coordinates from global to local by linking two separate geodetic references (ITRF08 and Karbala 1979). In this research, a new technique for choosing the training data and validation data is performed by reducing the amount of training data within a large study area. In addition, up to date, the literature has not converted the ITRF08 to Clark 1880 earlier. Most of the past studies used a large amount of training data with a small study area, so the results of the ANN were better than any traditional method [13]. In this research, despite using a small amount of training data related to the area of the study area, the results were also better than the traditional methods such as 2D conformal transformation and 2D least square. The gap in this research is that the transformation is applied just in the study area, with a limitation. This means that the transformation is performed at a specific location, which is Baghdad, Wasit, Babel, Karbala, Misan, Qadisia, Najaf, Di-Qar, Muthana, and Basra. In this investigation, the easting limitation of the ANN ranged from 397394.89 to 770000.00 m. In comparison, from 3328967.933 to 3692767.624 m north, this constraint arises from the lack of training data.

The contribution of this study was as follows:

The present work provides a novel method to link two different geodetic references for coordinate transformation from global to local.
This study presented a new interaction technique by reducing the amount of training data and increasing the amount of validation data to test the performance of the ANN.
This study applies the ANN to a large area with small data, contrary to what was previously stated.
This study employed a modern tool that has never been used before for 2D coordinate transformation, which is the Python programming language.

In the related work, it can be noticed that all the authors used a high percentage of the amount of training data when compared with the validation data. This study evaluates the accuracy of 2D coordinate transformation from Karbala 1979 (Clark1880) and ITRF08 using the ANN. On an area of approximately 140,000 km², 50% of the available data was used as the training data and 50% as the validation data. This paper is divided into four main parts. The first part includes the methodology of working with the study area, the second part includes the working principle of the ANN for 2D coordinate transformation, the third part includes the results that were obtained from the ANN and compares the results with the traditional methods used for 2D coordinate transformations, and the final part includes the conclusion of this study.

2 Methodology

2.1 Study area

The 2D coordinate transformation is carried out based on 68 stations of the first-order network, which have known geographic coordinates in both coordinate systems, Karbala 1979 (Clark1880) and ITRF08. These selected stations are distributed in the middle and southern parts of Iraq, which represent a study area and limitation for the ANN. Figure 1 shows the distribution of the 68 stations among the 10 provinces, which are Baghdad, Wasit, Babel, Karbala, Misan, Qadisia, Najaf, Di-Qar, Muthana, and Basra.

Figure 1

Location of the study area in Iraq.

2.2 Used station and the study area limitation

In this paper, 68 stations with known coordinates in both systems were used. 50% of the available data was employed as the training data and represents 34 stations. On the other hand, 50% of the data was used as the validation data and represents 34 stations. To acquire the best prediction result, many scenarios were run to pick the training data using a trial and error process. The points that were used for training and validation are shown in Figure 2.

Figure 2

Training and validation data in the study area.

Furthermore, because the research region is quite large in contrast to the available training data, it was divided into zones to calculate precise ANN parameters for each zone. The author determined each zone for the east–west and south–north directions based on the two training points selected previously in each direction, which contain a midpoint used for verifying the results. For example, the first zone in the east–west direction is determined between 397394.89 E and 438351.5 E based on the available data. As a result, there are 23 east–west zones and 23 south–north zones in the east–west direction.

2.3 Software used

In this study, the Python programming language is used to perform the processing of estimating the coordinate transformation parameters between Clark1880 and ITRF08 based on an ANN. It is worth mentioning here that Python significantly supports the ANN applications due to the availability of the libraries that are continuously updated. In addition, many authors perform the coordinate transformation using an ANN algorithm based on MATLAB, Visual Basic, etc. [3,6,14,15]. This represents a novel technique for employing the ANN to coordinate transformations. Furthermore, the code for coordinate transformation is ready and available as open-source for the majority of coordinate transformations, whereas the code in this paper is built from the ground up.

2.4 ANN for 2D coordinate transformation

ANN is a collection of information-processing methods that are similar to the biological nerve systems [16,17,18]. ANN consists of “neurons,” which are parallel elementals, and “links” that connect these neurons. The neurons are linked by a high number of information-transmitting weighted connections. An ANN is something like artificial intelligence that works according to what it is coded to do. ANN has been applied successfully in a wide field of life [19], see Figure 3.

Figure 3

General design of ANN.

2.5 Feed forward back propagation neural network (FFBPNN)

The backpropagation artificial neural network (BPANN) is widely utilized for different geodetic surveying applications. In an ANN, there are three types of layers that make up the whole ANN [20]: the input layer, one or more hidden layers, and the output layer. The training data is received by the input layer, which is delivered for processing to the hidden layers, and the results are yielded by the output layer [21], see Figure 4. The number of hidden layers and neurons in each layer can vary depending on the trial and error process [22]. A sequential trial-and-error method was used in this study to find the optimal number of neurons in the hidden layer [23]. A Relu activation function was selected for the hidden layer, while a linear function [24] was used for the output layer. The weights for the structure of the neural network were selected using different methods. The optimizer parameter is widely used for generating neural network weights in various scenarios Sarang [25]. The optimizer parameter that is employed in this study is Adamax, which is consistent with the trial and error procedure. Furthermore, the mean-squared error (MSR) is used in this study as a loose function to measure the quality of an estimator and give an indication of the efficiency of the proposed ANN.

Figure 4

Structure of the used ANN.

The proposed ANN in this study is a fully connected network, which is significantly used to find the complex relationship between remarkably different two data sets Rungta [26]. The structure of the proposed ANN used in this study consists of one input layer and three hidden layers, with six neurons in the first hidden layer and four neurons in the next two hidden layers and one output layer to yield the predicted data, which are the predicted easting and northing components in ITRF08, see Figure 4.

The training data that go first through the input layer is defined as the (X) parameter, which is delivered later to the first hidden layer through the link between nodes as activation values (a, z). The yielded activation values (a, z) are considered later as an input value to the next layer based on equations (1) and (2):

(1) a 1 [ 1 ] = σ ( z [ 1 ] ) ,

(2) σ ( z [ 1 ] ) = ( w 1 x + b 1 ) ,

(3) z i i + 1 = ( w j k i ⁎ x 1 + b 1 ) + ( w j k i ⁎ x 2 + b 1 ) + ( w j k i ⁎ x 3 + b 1 ) + ( w j k i ⁎ x n + b 1 ) ,

where a 1 [ 1 ] is the activation function for the first neuron in the first hidden layer, w 1 stands for the weight parameters, and, b ₁ is the bias parameter, which equals 1, w represents the weight parameter, i stands for the number of layers, X ₁, X ₂, X ₃…X _n stands for input values, j is a symbol that denotes the first layer (previous), k is a symbol that denotes the second layer (next layer).

Equations (1) and (2) are applied to the other neurons in the first hidden layer to predict all the activation functions for the next hidden layers, which represent the input values for the next hidden layer as it is shown in Figure 5:

Figure 5

Process of transfer activation function in forwarding iteration.

To be more clear, assume that the (X) value shown in the first input layer in Figure 5 is the training data (ITRF08) for the neural network and is passed through the input layer to elucidate the ANN process. An activation function is the input data that is passed to the first hidden layer and is indicated as (a) parameter in Figure 5. In general, the activation function uses an equation to present the input values for the next layer (the first hidden layer) [27] using equation (1).

The evaluation of the proposed ANN for 2D coordinate transformation in this study is carried out based on the comparison between the predicted data set that yields from the backward iteration and the corresponding data set that was initially used as input data. The output predicted result in the last node’s layer is applied again as an input data set to go back in the iteration and produce a predicted input data set that should be close to the input data set (observed data). The difference between the predicted value and the observed value is represented as a delta ( δ ) as shown in equation (4) (see Figure 6).

(4) δ = a − y ,

where a is the predicted values and y stands for actual values (input data set).

Figure 6

Backward iteration of neural network.

The statistical analysis for assessing the ANN model is calculated through different tools in Python. In this study, the mean-square error (MSE) is used to calculate the performance of the proposed ANN. The number of iterations used in this study was obtained by a trial and error procedure of 1,000 epochs.

3 Result

The Forward Back Propagation Neural Network (FBBNN) is used in this study to execute 2D coordinate transformations between the Karbala 1979 and ITRF08 coordinate systems in Iraq’s middle and southern regions, see Figure 1.

The selected control stations, which have known positions in two reference systems (the Karbala 1979 and ITRF08), were divided into two data sets. The first data set, which comprises 34 stations, is considered as the training data, while the second data set, which involves 34 stations, is considered a check data set. (See Figure 7).

Figure 7

Distribution of training and validation data.

3.1 Results from ANN’s method

In the case of the easting and northing components, the RMSE using the ANN is 0.08 and 0.17 m, respectively. Figure 8a and b visually depicts the RMSE values of coordinate differences for the easting and northing components, respectively. To show the variations in the coordinate values for the ANN solution, the coordinate difference values for the Easting and Northing components are scaled from −0.4 to 0.8 m.

Figure 8

(a) Color scale accuracy for the ANN method for easting. (b) Color scale accuracy for the ANN method for northing.

In Figure 8a, it can be seen that the accuracy of the scale ranged between (−40 cm) and (80 cm), represented by dark blue, which is the minimum range of scale, to red, which is the highest range of scale.

33 points represent a high accuracy in transformation, which ranges from (0–20 cm). On the other hand, there is one point located in Al-Muthana Province that ranges from (−20 cm) to (−30 cm) and colored in yellow.

The accuracy of the northing coordinate transformation can be seen in Figure 8b.

As shown in Figure 8b, 28 points fall within the range of zero accuracy and are mentioned in Figure 8b in blue sky color, while five points range between (−20 to 20 cm) and are illustrated in blue. In addition, there is one point that falls within the range of 60–80 cm and can be found in the red color in Figure 8b. The RMSE for the ANN transformation northing accuracy was found to be 0.17 m.

3.2 Results from a 2D conformal transformation

To do a two-dimensional (2D) conformal coordinate transformation, users should first know the coordinates of at least two points in both coordinate systems. When translating two separate surveys into a single reference coordinate system, the 2D conformal coordinate transformation is often used in surveying [28].

In terms of comparisons, the 2D conformal transformation method was employed in this study to compare the results with the proposed method. The RMSE for easting and northing using 2D conformal mid-point was 1.94 and 1.99, respectively. The distribution of the accuracy of points in the transformation was illustrated using a color scale, as shown in Figure 9a and b.

Figure 9

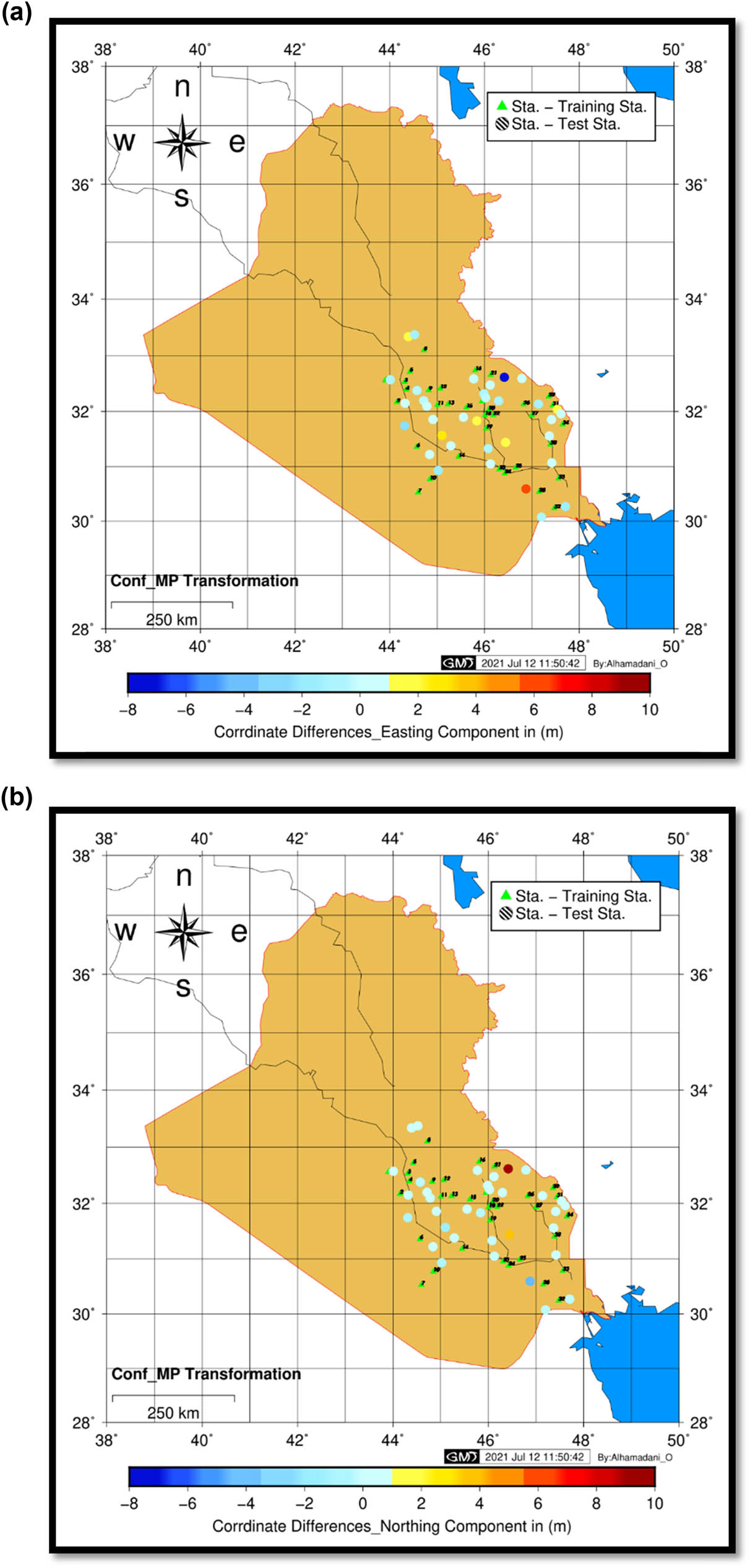
(a) Color scale accuracy for the 2D conformal method for easting. (b) Color scale accuracy for the 2D conformal method for northing.

As it is illustrated in Figure 9a, the accuracy of the transformation ranged between (−7 to 6 m) in terms of differences between the predicted and observed values. Only 11 points were below 10 cm in accuracy, while in the ANN, it was 25 points below 10 cm in accuracy. The accuracy of the northing coordinate transformation can be seen in Figure 9b.

The accuracy of the transformation in the north using 2D conformal transformation mid-point ranged between (−4 to 9 m) in terms of differences between predicted and observed values, see Figure 9b. Only three points had an accuracy of less than 10 cm, whereas the ANN had 19 points with an accuracy of less than 10 cm.

3.3 Results from 2D conformal transformation least square

If there are more than two control points, the least squares method can be used to improve a solution [28].

It follows the same scenario for training the ANN to perform the least square method. 34 stations with known coordinates in both systems were used as training data to apply the least square method. Figure 10a shows the color scale for the accuracy of the transformation for easting. It can be seen that only 6 points were felt with accuracy in the range of 0–4 m, 4 points were felt in the range of 6–12 m, and the remaining points were felt in the range of 0–12 m for all the easting data.

Figure 10

(a) Color scale accuracy for the 2D conformal least square method for easting. (b) Color scale accuracy for the 2D conformal least square method for northing.

For the northing coordinate accuracy that is shown in Figure 10b, it indicates that the range of accuracy lies between −10 m and 11 m.

Figure 10b shows that most of the points are felt in the range of 4–12 m with accuracy, and compared to the other methods that take over, it seems that this method is the weakest method in accuracy for 2D coordinate transformation.

From the results, it can be seen that the ANN can be represented as the most accurate method for 2D coordinate transformation from ITRF08 to Clark1880. Table 1 shows the results that were obtained from the three methods.

Table 1

Root mean square error for the applied methods

Method	(RMSE) for East	(RMSE) for North
2D conformal transformation	1.94	1.99
2D conformal least square	4.19	6.41
ANN	0.08	0.17

A histogram indicates the accuracy of the methods being used. Other than that, the other method is shown in the histogram as a way to compare the accuracy of the methods that were used, as shown in Figure 11.

Figure 11

RMSE for the applied methods.

4 Conclusion

Geodetic research has made extensive use of the ANN applications. The goal of this study was to use feed-forward backpropagation to investigate a 2D coordinate transformation problem between the Karbala 1979 and ITRF08 systems. 68 stations with known coordinates in both systems were employed to demonstrate the ANN for 2D coordinate transformation. In addition, two traditional methods for 2D coordinate transformation were performed to compare the results with the proposed method which is 2D conformal transformation and 2D conformal transformation least square. Results indicated that the ANN represents the most accurate method for linking ITRF08 and Karbala 1979 and can be used for coordinate transformation with an accurate result. The RMSE estimates for the easting and northing components of the ANN solution were 8 and 17 cm, respectively, which shows that the ANN can be used to transform 2D coordinates in Iraq rather than other methods.

This study employs the ANN for linking two completely different reference systems. This is due to the complexity of finding an algorithm to link global and local reference systems for coordinate transformation.

Furthermore, this study has provided a clearer understanding of the significance of Iraq’s national geodetic networks, which serve as the foundation for various engineering projects such as dam monitoring and monitoring earthquakes. Furthermore, this paper sets the framework for future research into employing the ANN coordinate transformation on stations with known coordinates in their coordinate systems in the north and west of Iraq because it is not covered in the present study due to the available stations. In a broader sense, research is required to adopt many scenarios for selecting training data through trial and error. There needs to be more research into different structures for ANNs, like using different numbers of hidden layers with different neurons to get more accurate results.

acc0022@mtu.edu.iq

Conflict of interest: Authors state no conflict of interest.

References

[1] IOGP. Guidance Note 22 geodetic referencing in Iraq. International Association of Oil & Gas Producers; 2015.Search in Google Scholar

[2] Mitsakaki C. Coordinate transformatin [Online]. https://www.fig.net/resources/proceedings/fig_proceedings/athens/papers/ts07/ts07_2_mitsakaki.pdf.Search in Google Scholar

[3] Konakoglu B, Cakır L, Gökalp E. 2D coordinate transformation using artificial neural networks. Int Arch Photogram, Remote Sens Spat Inf Sci. 2016;42:183–6.10.5194/isprs-archives-XLII-2-W1-183-2016Search in Google Scholar

[4] Nunes I, Dasilva HS. Artificial neural networks: a practical course. Brazil: Springer; 2018.Search in Google Scholar

[5] Bhasin H. Python basics: a self-teaching Introduction. LLC: Stylus Publishing; 2018.10.1515/9781683923541Search in Google Scholar

[6] Lin L-S, Wang Y-J. A study on cadastral coordinate transformation using artificial neural network. In Proceedings of the 27th Asian conference on remote sensing, Ulaanbaatar, Mongolia; 2006. Citeseer. p. 1–6.Search in Google Scholar

[7] Gullu M. Coordinate transformation by radial basis function neural network. Sci Res Essays. 2010;5(20):3141–6.Search in Google Scholar

[8] Tierra A, Romero RJ. Planes coordinates transformation between PSAD56 to SIRGAS using a multilayer artificial neural network. Geodesy Cartograp. 2014;63.10.2478/geocart-2014-0014Search in Google Scholar

[9] Konakoglu B, Cakır L, Gökalp E. 2D coordinate transformation using artificial neural networks. Remote Sensing Spatial Inform Sci. 10/26 2016;XLII–2/W1:183–6. 10.5194/isprs-archives-XLII-2-W1-183-2016.Search in Google Scholar

[10] Kumi-Boateng B, Ziggah YYJ. Horizontal coordinate transformation using artificial neural network technology–A case study of Ghana geodetic reference network. J Geomatics. 2017;11(1):1–11.Search in Google Scholar

[11] Ziggah YY, Youjian H, Tierra AR, Laari PB. Coordinate transformation between global and local data based on artificial neural network with K-fold cross-validation in Ghana. Earth Sci Res J. 2019;23(1):67–77.10.15446/esrj.v23n1.63860Search in Google Scholar

[12] Ziggah YY, Hu Y, Issaka Y, Laari PBJ. Least squares support vector machine model for coordinate transformation. Geodesy Cartograp. 2019;45(1):16–27.10.3846/gac.2019.6053Search in Google Scholar

[13] Dutta P, Kumar A. Modeling and optimization of a liquid flow process using an artificial neural network-based flower pollination algorithm. J Intell Syst. 2020;29(1):787–98. 10.1515/jisys-2018-0206 Search in Google Scholar

[14] Yilmaz M, Turgut B, Gullu M, Yilmaz I. Application of artificial neural networks to height transformation. Tech Gaz. 2017;24(2):443–8.Search in Google Scholar

[15] Gullu M, Yilmaz M, YILMAZ I. Application of back propagation artificial neural network for modelling local GPS/levelling geoid undulations: A comparative study. FIG Working Week. 2011;18–22. https://www.researchgate.net/publication/322358029_Application_of_Back_Propagation_Artificial_Neural_Network_for_Modelling_Local_GPSLevelling_Geoid_Undulations_A_Comparative_Study.Search in Google Scholar

[16] Kuznetsov SV, Siswanto WA, Sabirova FM, Pustokhina IG, Melnikova LA, Zakieva RR, et al. Emotional artificial neural network (EANN)-based prediction model of maximum A-weighted noise pressure level. Noise Mapp. 2022;9(1):1–9. 10.1515/noise-2022-0001.Search in Google Scholar

[17] Köroğlu MA. Artificial neural network for predicting the flexural bond strength of FRP bars in concrete. Sci Eng Composite Mater. 2019;26(1):12–29. 10.1515/secm-2017-0155.Search in Google Scholar

[18] Imoru O, Nelwamondo FV, Jimoh A, Ayodele TR. A neural network approach to detect winding faults in electrical machine. Int J Emerg Electr Power Syst. 2021;22(1):31–41. 10.1515/ijeeps-2020-0161.Search in Google Scholar

[19] Hagan MT, Demuth HB, Beale MH, De Jesús O. Neural network design. 2nd edn. Martin Hagan: Oklahoma; 2014.Search in Google Scholar

[20] Ansari K, Gyawali P, Pradhan PM, Park K-D. Coordinate transformation parameters in Nepal by using neural network and SVD methods. J Geodetic Sci. 2019;9(1):22–8. 10.1515/jogs-2019-0003. Search in Google Scholar

[21] Hagan MT, Demuth H, Beale M, Jesus O. Neural network design. Hagan MT, Demuth HB, Beale MH. Orlando De Jesus. 2nd edn; 2014. p. 1012.Search in Google Scholar

[22] Sarkar D, Bali R, Ghosh T. Hands-on transfer learning with python: implement advanced deep learning and neural network models using TensorFlow and KerasPackt. Birmingham, UK: Packt Publishing Ltd; 2018.Search in Google Scholar

[23] Hussein Z, Alhamadani O, Hussein W. Application of artificial neural networks for 2D coordinate transformation of coordinate reference system of Iraq. 2020. https://www.researchgate.net/publication/353243537_Application_of_Artificial_Neural_Networks_for_2D_Coordinate_Transformation_of_Coordinate_Reference_System_of_Iraq.Search in Google Scholar

[24] Qiu Q. The application of neural network algorithm and embedded system in computer distance teach system. J Intell Syst. 2022;31(1):148–58. 10.1515/jisys-2022-0004.Search in Google Scholar

[25] Sarang P. Artificial neural networks with TensorFlow 2; 2021. p. 228. 10.1007/978-1-4842-6150-7.Search in Google Scholar

[26] Rungta K. TensorFlow in 1 Day: Make your own Neural Network. Independently Published; 2018. p. 367. Search in Google Scholar

[27] Arce-Medina E, Paz-Paredes JI. Artificial neural network modeling techniques applied to the hydrodesulfurization process. Math Computer Model. 2009;49(1–2):207–14.10.1016/j.mcm.2008.05.010Search in Google Scholar

[28] Paul PD, Wolf R, Bon PD, Dewitt A, Benjamin PD, Wilkinson E. Coordinate transformations. Fourth edn. New York: McGraw-Hill Education; 2014.Search in Google Scholar

Received: 2021-12-29

Revised: 2022-02-28

Accepted: 2022-03-03

Published Online: 2022-07-07

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/jisys-2022-0033

Keywords for this article

2D coordinate transformation; feed-forward back propagation; geodetic datum; neural network

Creative Commons

BY 4.0