Abstract
In this article, we study the problem of Nash implementation in private good economies with single-peaked, single-plateaued, and single-dipped preferences in the presence of at least one minimally honest agent. We prove that all solutions of the problem of fair division satisfying unanimity can be implemented in Nash equilibria as long as there are at least three agents participating in the mechanism (game form). To justify this result, we provide a list of solutions which violate the condition of no-veto power.
Acknowledgments
We would like to thank Michele Lombardi for his suggestions and helpful comments. We would also like to thank the seminar participants at Maastricht University in Netherland. We are particularly grateful to two anonymous referees of the journal for comments that greatly improved this article. Of course any error is our own responsibility.
References
Doghmi, A.. 2013a. “Nash Implementation in Allocation Problem with Single-Dipped Preferences.” Games4:38–49.10.3390/g4010038Suche in Google Scholar
Doghmi, A.. 2013b. “Nash Implementation in Private Good Economies When Preferences Are Single-Dipped with Best Indifferent Allocations.” Mathematical Economics Letters. DOI 10.1515/mel-2013-0003.10.1515/mel-2013-0003Suche in Google Scholar
Doghmi, A., and A.Ziad. 2008a. “Reexamination of Maskin’s Theorem on Nash Implementability.” Economics Letters100:150–2.10.1016/j.econlet.2007.12.009Suche in Google Scholar
Doghmi, A., and A.Ziad. 2008b. “Nash Implementation in Exchange Economies with Single-Peaked Preferences.” Economics Letters100:157–60.10.1016/j.econlet.2007.12.010Suche in Google Scholar
Doghmi, A., and A.Ziad. 2013a. “Nash Implementation in Private Good Economies with Single-Plateaued Preferences.” Working Paper.Suche in Google Scholar
Doghmi, A., and A.Ziad. 2013b. “Nash Implementation in Domain Restrictions with Indifferences.” Working Paper. DOI 10.1515/mel-2013-0003.Suche in Google Scholar
Dutta, B., and A.Sen. 2009[2012]. “Nash Implementation with Partially Honest Individuals.” Working Paper. Published 2012 in Games and Economic Behavior74:154–69.10.1016/j.geb.2011.07.006Suche in Google Scholar
Holden, R., N.Kartik, and O.Tercieux. 2012. “Simple Mechanisms and Preferences for Honesty.” Working Paper.Suche in Google Scholar
Korpela, V. 2012. “Bayesian Implementation with Partially Honest Individuals.” Working paper, University of Turku.Suche in Google Scholar
Lombardi, M., and N.Yoshihara. 2011. “Partially-Honest Nash Implementation: Characterization Results.” Working Paper, Hitotsubashi University.10.2139/ssrn.1759924Suche in Google Scholar
Lombardi, M., and N.Yoshihara. 2012. “Natural Implementation with Partially Honest Agents.” Working Paper, Hitotsubashi University.10.2139/ssrn.2172419Suche in Google Scholar
Maskin, E.1977[1999]. “Nash Equilibrium and Welfare Optimality.” M.I.T. mimeo. Published 1999 in the Review of Economic Studies66:23–38.10.1111/1467-937X.00076Suche in Google Scholar
Matsushima, H. 2008a. “Role of Honesty in Full Implementation.” Journal of Economic Theory139:353–9.10.1016/j.jet.2007.06.006Suche in Google Scholar
Matsushima, H. 2008b. “Behavioral Aspects of Implementation Theory.” Economics Letters100:161–4.10.1016/j.econlet.2007.12.008Suche in Google Scholar
Moore, J., and R.Repullo. 1990. “Nash Implementation: A Full Characterization.” Econometrica58:1083–100.10.2307/2938301Suche in Google Scholar
Thomson, W. 1990. “Manipulation and Implementation to Solutions to the Problem of Fair Allocations When Preferences Are Single-Peaked.” mimeo, University of Rochester.Suche in Google Scholar
Thomson, W.. 2010. “Implementation to Solutions to the Problem of Fair Allocations When Preferences Are Single-Peaked.” Review of Economic Design14:1–15.10.1007/s10058-009-0092-9Suche in Google Scholar
- 1
The strict weak no-veto power condition has been introduced by Doghmi and Ziad (2008a, 2008b). An SCC F satisfies strict weak no-veto power, if for i,
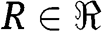 , and
, and 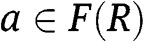 , for
, for 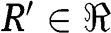 ,
, 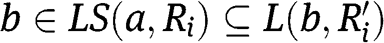 and
and 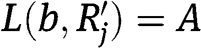 for all
for all 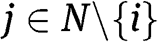 , then
, then 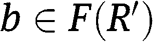 .
. - 2
The proof of the no-logical relationship between I-weak no-veto power and strict weak no-veto power is in Doghmi and Ziad (2013a).
- 3
For all
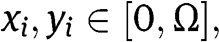
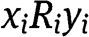 means that, for the agent i, to consume a share
means that, for the agent i, to consume a share 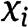 is as good as to consume the quantity
is as good as to consume the quantity 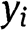 . The asymmetrical part is written
. The asymmetrical part is written 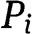 and the symmetrical part
and the symmetrical part 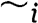 .
. - 4
The monotonic correspondences in our examples in the case of private good economies with single-peaked preferences are Pareto correspondence, no-envy correspondence, individually rational correspondence from equal division, and all intersections of them. For more details, see Thomson (1990, 2010).
- 5
In standard Nash implementation, Doghmi (2013b) and Doghmi and Ziad (2013b) proved that many important monotonic correspondences studied in private good economies with single-dipped preferences by Doghmi (2013a) become no-monotonic when we allow multiple best/worst indifferent allocations. Thus, these correspondences can be examined in partially honest environment.
©2013 by Walter de Gruyter Berlin / Boston
Artikel in diesem Heft
- Masthead
- Masthead
- Advances
- Dependence and Uniqueness in Bayesian Games
- Monopolistic Signal Provision†
- Multi-task Research and Research Joint Ventures
- Transparent Restrictions on Beliefs and Forward-Induction Reasoning in Games with Asymmetric Information
- A Simple Bargaining Procedure for the Myerson Value
- On the Difference between Social and Private Goods
- Optimal Use of Rewards as Commitment Device When Bidding Is Costly
- Labor Market and Search through Personal Contacts
- Contributions
- Learning, Words and Actions: Experimental Evidence on Coordination-Improving Information
- Are Trust and Reciprocity Related within Individuals?
- Optimal Contracting Model in a Social Environment and Trust-Related Psychological Costs
- Contract Bargaining with a Risk-Averse Agent
- Academia or the Private Sector? Sorting of Agents into Institutions and an Outside Sector
- Topics
- Poverty Orderings with Asymmetric Attributes
- Dictatorial Mechanisms in Constrained Combinatorial Auctions
- When Should a Monopolist Improve Quality in a Network Industry?
- On Partially Honest Nash Implementation in Private Good Economies with Restricted Domains: A Sufficient Condition
- Revenue Comparison in Asymmetric Auctions with Discrete Valuations
Artikel in diesem Heft
- Masthead
- Masthead
- Advances
- Dependence and Uniqueness in Bayesian Games
- Monopolistic Signal Provision†
- Multi-task Research and Research Joint Ventures
- Transparent Restrictions on Beliefs and Forward-Induction Reasoning in Games with Asymmetric Information
- A Simple Bargaining Procedure for the Myerson Value
- On the Difference between Social and Private Goods
- Optimal Use of Rewards as Commitment Device When Bidding Is Costly
- Labor Market and Search through Personal Contacts
- Contributions
- Learning, Words and Actions: Experimental Evidence on Coordination-Improving Information
- Are Trust and Reciprocity Related within Individuals?
- Optimal Contracting Model in a Social Environment and Trust-Related Psychological Costs
- Contract Bargaining with a Risk-Averse Agent
- Academia or the Private Sector? Sorting of Agents into Institutions and an Outside Sector
- Topics
- Poverty Orderings with Asymmetric Attributes
- Dictatorial Mechanisms in Constrained Combinatorial Auctions
- When Should a Monopolist Improve Quality in a Network Industry?
- On Partially Honest Nash Implementation in Private Good Economies with Restricted Domains: A Sufficient Condition
- Revenue Comparison in Asymmetric Auctions with Discrete Valuations


