On the Difference between Social and Private Goods

Alvaro Sandroni; Sandra Ludwig; Philipp Kircher

doi:10.1515/bejte-2012-0008

Enjoy 40% off

academic books on De Gruyter Brill *

Article

On the Difference between Social and Private Goods

Alvaro Sandroni , Sandra Ludwig and Philipp Kircher

Published/Copyright: June 29, 2013

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information Explore this Subject

From the journal The B.E. Journal of Theoretical Economics Volume 13 Issue 1

Abstract

Standard economic models have long been applied to choices over private consumption goods, but have recently been extended to incorporate social situations as well. We challenge the applicability of standard decision-theoretic models to social settings. In an experiment where choices affect the payoffs of someone else, we find that a large fraction of subjects prefer randomization over any of the deterministic outcomes. This tendency prevails whether the other party knows about the choice situation or not. Such randomization violates standard decision theory axioms that require that lotteries are never better than their best deterministic component. For conceptually similar choices in classical non-social situations, we do not find much evidence for such violations, suggesting the need for theories of uncertainty that are targeted to social settings.

Keywords: risky choice; betweenness axiom; social preferences; preference for randomness

JEL Classification: D81; C91; D63

Appendix – Instructions basic social good experiment

Welcome to this experiment. You can earn money in this experiment. At the end of the experiment, you will be paid in cash according to your decisions and the decisions of the other participants. Each participant receives a payment of 5 Euro. Your additional payments are explained in these instructions.

During the whole experiment, you are not allowed to speak to other participants, to use cell phones, or to start any other program on the computer. If you have questions, please raise your hand. An instructor of the experiment will then come to your seat to answer your questions.

During the experiment, we do not speak of Euros but of the fictitious currency “Taler”. At the end of the experiment, your actual amount of Taler will be converted into Euro according to the following exchange rate:

1 Taler 0.50 Euro.

The payment at the end of the experiment is anonymous. This means, no participant is informed about the payment of the other participants.

In this experiment, half of the participants are in role A and the other half in role B. The roles have been assigned randomly.

Course of the experiment:

In the beginning of the experiment, each participant in role A (participant A) is randomly matched with another participant B.

No participant learns during or after the experiment which other participant was matched with him.

Participant A decides, which payment he himself and his matched participant B receive in this experiment. There are the following options:

Participant A receives 15 Taler, and participant B receives 0 Taler.
Participant A receives 10 Taler, and participant B receives 10 Taler.
The computer chooses randomly one of the two aforementioned options. Both options are equally likely.

Participant

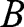does not make a decision which affects his own or participant A's payment. He answers several hypothetical questions. His answers are irrelevant for the payment and are not told other participants.

Participant A also answers several hypothetical questions after his decision. His answers are irrelevant for the payment and are not told other participants.

End

Finally, each participant B is informed which of the three aforementioned options participant A has chosen. In addition, all participants are informed about their payment in the experiment. This ends the experiment.

Appendix – Instructions mug experiments

The introductory part of the instructions is exactly as in the social good experiment besides two changes: The show-up fee is not mentioned and instead of “half of the participants are in role A the other half in role B”, we say “some of the participants are in role A and some in role B”. Below we give the remaining part of the instructions. Those parts that are related to the voting experiment, which is not in our interest here, are in small italic fonts.

Course of the experiment:

In the beginning of the experiment, groups consisting of six participants are formed. Each group consists of five randomly chosen participants A and one participant B. No participant learns during or after the experiment which other participant was matched with him.

Each participant A has an endowment of 20 Taler; each participant B has an endowment of 0 Taler. In each group, the participants A vote on the following two alternatives. The alternative that gets the majority of votes in a group determines the payoffs of all participants in this group.

Alternative 1:

Each participant A gives up 6 Taler. For each participant A, the payoff reduces to 14 Taler, but the payoff of participant B increases to 14 Taler.

Alternative 2:

Each participant A gives up 0 Taler. For each participant A, the payoff remains 20 Taler, and the payoff of participant B remains 0 Taler.

Each participant A has one vote. The alternative which receives most of the votes is implemented for the group. Participant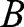makes a hypothetical decision which is not payoff relevant. All participants answers several hypothetical questions[…].

In addition, each participant receives a fixed payment. He can choose between the following three options:

He can choose to receive 15 Taler or to receive 10 Taler and a mug (including tea), or that the computer randomly chooses one of the two aforementioned options. Both options are equally likely.

End:

Finally, each participant is informed which alternative is implemented for his group and his payment in the experiment. This ends the experiment.

Appendix – The coffee mug in the mug experiments

Acknowledgments

The authors thank Michèle Belot, Shachar Kariv, Alexander Koch, Martin Kocher, Ehud Lehrer, Axel Ockenfels, and Klaus Schmidt for helpful comments. Financial support from LMUexcellent, the National Science Foundation, grant SES-0922404, and SFB/TR 15 is gratefully acknowledged. The authors kindly thank MELESSA of the University of Munich for providing laboratory resources.

References

Allais, M. 1953. “Le comportement de l’homme rationnel devant le risque: Critique des postulats et axiomes de l’ecole Americane.” Econometrica 21:503–46.10.2307/1907921Search in Google Scholar

Andreoni, J., and J. Miller. 2002. “Giving According to GARP: An Experimental Test of the Consistency of Preferences for Altruism.” Econometrica 70:737–53.10.1111/1468-0262.00302Search in Google Scholar

Andreoni, J., and B. D. Bernheim. 2009. “Social Image and the 50–50 Norm: A Theoretical and Experimental Analysis of Audience Effects” Econometrica 77:1607–36.10.3982/ECTA7384Search in Google Scholar

Bartling, B., and U. Fischbacher. 2011. “Shifting the Blame: On Delegation and Responsibility.” Review of Economic Studies 79:67–87.10.1093/restud/rdr023Search in Google Scholar

Battigalli, P., and M. Dufwenberg 2009. “Dynamic Psychological Games.” Journal of Economic Theory 144:1–35.10.1016/j.jet.2008.01.004Search in Google Scholar

Bohnet, I., F. Greig, B. Herrmann and R. Zeckhauser. 2004. “Betrayal Aversion: Evidence from Brazil, China, Oman, Switzerland, Turkey, and the United States.” American Economic Review 98(1):294–310.10.1257/aer.98.1.294Search in Google Scholar

Bohnet, I., and R. Zeckhauser. 2004. “Trust, Risk and Betrayal.” Journal of Economic Behavior and Organization 55:467–84.10.1016/j.jebo.2003.11.004Search in Google Scholar

Bolton, G., J. Brandts, and A. Ockenfels. 2005. “Fair Procedures: Evidence from Games Involving Lotteries.” The Economic Journal 115:1054–76.10.1111/j.1468-0297.2005.01032.xSearch in Google Scholar

Bolton, G., and A. Ockenfels. 2000. “ERC A Theory of Equity, Reciprocity and Competition.” American Economic Review 90(1):166–93.10.1257/aer.90.1.166Search in Google Scholar

Bolton, G., and A. Ockenfels. 2010. “Betrayal Aversion: Evidence from Brazil, China, Oman, Switzerland, Turkey, and the United States: Comment.” American Economic Review 100:628–33.10.1257/aer.100.1.628Search in Google Scholar

Borah, A. 2009. “Other Regarding Preferences in Environments of Risk.” Mimeo, University of Pennsylvania.Search in Google Scholar

Brock, M., A. Lange, and E. Ozbay. 2013. “Dictating the Risks – Experimental Evidence on Norms of Giving in Risky Environments.” American Economic Review 103:415–37.10.1257/aer.103.1.415Search in Google Scholar

Broom, J. 1984. “Uncertainty and Fairness.” The Economic Journal 94:624–32.10.2307/2232707Search in Google Scholar

Camerer, C., and T-H. Ho. 1994. “Violations of the Betweenness Axiom and Nonlinearity in Probability.” Journal of Risk and Uncertainty 8:167–96.10.1007/BF01065371Search in Google Scholar

Charness, G., and M. Dufwenberg. 2011. “Participation.” American Economic Review 101:1211–37.10.1257/aer.101.4.1211Search in Google Scholar

Charness, G., and M. Rabin. 2002. “Understanding Social Preferences with Simple Tests.” The Quarterly Journal of Economics 117:817–69.10.1162/003355302760193904Search in Google Scholar

Chew, S., and J. Sagi. 2006. “Event Exchangeability: Probabilistic Sophistication without Continuity or Monotonicity.” Econometrica 74–73:771–86.Search in Google Scholar

Chew, S. H. 1983. “A generalization of The Quasilinear Mean with Applications to the Measurement of the Income Inequality and Decision Theory Resolving the Allais Paradox.” Econometrica 53:1065–92.Search in Google Scholar

Cooper, D., and J. Kagel. 2013. “Other Regarding Preferences: A Selective Survey of Experimental Results.” In The Handbook of Experimental Economics, vol. 2, edited by J. Kagel, and A. Roth. Princeton, NJ: Princeton University Press.Search in Google Scholar

Dana, J., D. M. Cain, and R. M. Dawes. 2006. “What You Don’t Know Won’t Hurt Me: Costly (but Quiet) Exit in Dictator Games.” Organizational Behavior and Human Decision Processes 100:193–201.10.1016/j.obhdp.2005.10.001Search in Google Scholar

Dana, J., R. A. Weber, and J. X. Kuang. 2007. “Exploiting Moral Wiggle Room: Experiments Demonstrating an Illusory Preference for Fairness.” Economic Theory 33:67–80.10.1007/s00199-006-0153-zSearch in Google Scholar

Dekel, E. 1986. “An Axiomatic Characterization of Preference under Uncertainty: Weakening the Independence Axiom.” Journal of Economic Theory 40:304–18.10.1016/0022-0531(86)90076-1Search in Google Scholar

Diamond, P. A. 1967. “Cardinal Welfare, Individualistic Ethics, and Intertemporal Comparisons of Utility: Comment.” Journal of Political Economy 75:765–6.10.1086/259353Search in Google Scholar

Ellsberg, D. 1961. “Risk, Ambiguity, and the Savage Axioms.” Quarterly Journal of Economics 75:643–69.10.2307/1884324Search in Google Scholar

Fehr, E., and K. Schmidt. 1999. “A Theory of Fairness, Competition, and Cooperation.” The Quarterly Journal of Economics 114:817–68.10.1162/003355399556151Search in Google Scholar

Fischbacher, U. 2007. “z-Tree: Zurich Toolbox for Readymade Economic Experiments.” Experimental Economics 10(2):171–178.10.1007/s10683-006-9159-4Search in Google Scholar

Fishburn, P. 1988. Nonlinear Preference and Utility Theory. Baltimore, MD: Johns Hopkins University Press.Search in Google Scholar

Fudenberg, D., and D. K. Levine. 2012. “Fairness, Risk Preferences and Independence: Impossibility Theorems.” Journal of Economic Behaviour and Organization 81:606–12.10.1016/j.jebo.2011.09.004Search in Google Scholar

Gneezy, U., J. A. List, and G. Wu. 2006. “The Uncertainty Effect: When a Risky Prospect is Valued Less than Its Worst Outcome.” The Quarterly Journal of Economics 121(4):1283–309.10.1093/qje/121.4.1283Search in Google Scholar

Grant, S. 1995. “Subjective Probability without Monotonicity: Or How Machina’s Mom May also Be Probabilistically Sophisticated.” Econometrica 63–61:159–89.10.2307/2951701Search in Google Scholar

Grant, S., A. Kajii, B. Polak, and Z. Safra. 2010. “Generalized Utilitarianism and Harsanyi’s Impartial Observer Theorem.” Econometrica 78–6:1939–71.Search in Google Scholar

Greiner, B. 2004. “An Online Recruitment System for Economic Experiments” in Forschung und wissenschaftliches Rechnen 2003, GWDG Bericht 63, eds. Kurt Kremer and Volker Macho. GesellschaftfLuer Wissenschaftliche Datenverarbeitung, GLoettingen: 79–93.Search in Google Scholar

Gul, F. 1991. “A Theory of Disappointment in Decision Making under Uncertainty.” Econometrica LIX:667–86.10.2307/2938223Search in Google Scholar

Hamman, J., G. Loewenstein, and R. A. Weber. 2010. “Self-interest Through Delegation: An Additional Rationale for the Principal-Agent Relationship.” American Economic Review 100:1826–46.10.1257/aer.100.4.1826Search in Google Scholar

Harsanyi, J. 1955. “Cardinal Welfare, Individualistic Ethics, and Interpersonal Comparisons of Utility.” Journal of Political Economy 63:309–21.10.1086/257678Search in Google Scholar

Harsanyi, J. 1975. “Nonlinear Social Welfare Functions: Do Welfare Economists Have a Special Exemption from Bayesian Rationality?” Theory and Decision 6:311–32.10.1007/BF00136200Search in Google Scholar

Harsanyi, J. 1978. “Bayesian Decision Theory and Utilitarian Ethics.” American Economic Review 68:223–8.Search in Google Scholar

Kahneman, D., J. Knetsch, and R. Thaler. 1990. “Experimental Tests of the Endowment Effect and the Coase Theorem.” Journal of Political Economy 98(6):1325–48.10.1086/261737Search in Google Scholar

Kahneman, D., and A. Tversky. 1979. “Prospect Theory: An Analysis of Decision under Risk.” Econometrica 47:263–92.10.2307/1914185Search in Google Scholar

Karni, E., and Z. Safra. 2002. “Individual Sense of Justice: A Utility Representation.” Econometrica 70:263–84.10.1111/1468-0262.00275Search in Google Scholar

Karni, E., T. Salmon, and B. Sopher. 2008. “Individual Sense of Fairness: An Experimental Study.” Experimental Economics 11(2):174–89.10.1007/s10683-007-9165-1Search in Google Scholar

Keren, G., and M. C. Willemsen. 2009. “Decision Anomalies, Experimenter Assumptions, and Participants’ Comprehension: Revaluating the Uncertainty Effect.” Journal of Behavioral Decision Making 22(3):301–17.10.1002/bdm.628Search in Google Scholar

Kirchsteiger, G. 1994. “The Role of Envy in Ultimatum Games.” Journal of Economic Behavior and Organization 25:373–89.10.1016/0167-2681(94)90106-6Search in Google Scholar

Krawczyk, M., and F. Le Lec. 2008. “Social Decisions under Risk. Evidence from the Probabilistic Dictator Game.” Mimeo, University of Amsterdam.Search in Google Scholar

Levine, D. K. 1998. “Modeling Altruism and Spitefulness in Experiments.” Review of Economic Dynamics 1:593–622.10.1006/redy.1998.0023Search in Google Scholar

Maccheroni, F., M. Marinacci, and A. Rustichini. 2008. “Social Decision Theory: Choosing Within and between Groups.” Mimeo.Search in Google Scholar

Machina, M. 1982. “Expected Utility Analysis without the Independence Axiom.” Econometrica 50:277–323.10.2307/1912631Search in Google Scholar

Machina, M. 1987. “Choice under Uncertainty: Problems Solved and Unsolved.” Journal of Economic Perspectives 1:121–54.10.1257/jep.1.1.121Search in Google Scholar

Machina, M. 1989. “Dynamic Consistency and Non-expected Utility Models of Choice under Uncertainty.” Journal of Economic Literature XXVII:1622–68.Search in Google Scholar

Neilson. W. 2006. “Axiomatic Reference-dependence in Behavior Toward others and Toward Risk. Economic Theory 28:681–92.10.1007/s00199-005-0643-4Search in Google Scholar

Ok, E., and L. Kockesen. 2000. “Negatively Interdependent Preferences.” Social Choice and Welfare 17:533–58.10.1007/s003550050177Search in Google Scholar

Rydval, O., A. Ortmann, S. Prokosheva, and R. Hertwig. 2009.” How Certain Is the Uncertainty Effect?” Experimental Economics 12(4):473–87.10.1007/s10683-009-9224-xSearch in Google Scholar

Quiggin, J. 1982. “A Theory of Anticipated Utility.” Journal of Economic Behavior and Organization 3:323–43.10.1016/0167-2681(82)90008-7Search in Google Scholar

Rohde, K. 2010. “A Preference Foundation for Fehr and Schmidt’s Model of Inequity Aversion.” Social Choice and Welfare 34:537–47.10.1007/s00355-009-0413-5Search in Google Scholar

Saito, K. 2010. “Preferences for Randomization – Ambiguity Aversion and Inequality Aversion.” Mimeo, Northwestern University.Search in Google Scholar

Sandbu, M. 2008. “Axiomatic Foundations for Fairness-Motivated Preferences.” Social Choice and Welfare 31(4):589–619.10.1007/s00355-008-0296-xSearch in Google Scholar

Spector, Y., M. Leshno, and M. Ben Horin. 1996. “Stochastic Dominance in an Ordinal World.” European Journal of Operational Research 93(3):620–7.10.1016/0377-2217(95)00118-2Search in Google Scholar

Starmer, C. 2000. “Developments in Non-expected Utility Theory: The Hunt for a Descriptive Theory of Choice under Risk.” Journal of Economic Literature XXXVIII:332–82.10.1257/jel.38.2.332Search in Google Scholar

Tadelis, S. 2008. “The Power of Shame and the Rationality of Trust.” Mimeo, University of California, Berkeley.10.2139/ssrn.1006169Search in Google Scholar

Trautmann, S. 2009. “Fehr-Schmidt Process Fairness and Dynamic Consistency.” Journal of Economic Psychology 30:803–13.10.1016/j.joep.2009.07.002Search in Google Scholar

Weber, M., and C. Camerer. 1987. “Recent Developments in Modelling Preferences under Risk.” OR Spektrum 9:129–51.10.1007/BF01721094Search in Google Scholar

1
The particular functional forms for the utility function that have been suggested differ. For example, Fehr and Schmidt (1999) and Bolton and Ockenfels (2000) suggest specifications designed to capture inequality aversion. Charness and Rabin (2002) incorporate a concern for efficiency. Kirchsteiger (1994) incorporates envy. Each of these articles shows evidence that such specifications improve the ability to accommodate various dimensions of observed behavior, in particular if both fairness-motivated and selfish types exist.
2
Andreoni and Miller (2002) find that only a quarter of the subjects display preferences that are consistent with pure selfishness, another quarter are consistent with either an equal split of resources or the most efficient outcome, and another quarter spend own resources to reduce the others’ payoff in line with spite or envy. It should be noted that in our verbal explanations we often refer to the case where more resources to the other player increases utility, but this need not hold in general, similar to standard utility functions over non-social goods that need not increase with more of a particular good. None of our arguments hinges on the exact form of the utility function, and in particular it does not rely on the same utility function across individuals.
3
Andreoni and Miller (2002) vary the budget set and the price at which personal monetary payoff can be exchanged for higher monetary payoff of another person. They find that only 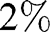of subjects violate the weak axiom of revealed preference, which means that the choices of 98% can be represented by some utility function.
4
Gneezy, List, and Wu (2006) refer to a similar property as the “internality axiom”.
5
In this definition, we restrict attention to tangible outcomes such as the joint monetary payoffs of all agents. In the discussion section, we return to this point and elaborate on larger state spaces where utility over outcomes may involve intangibles such as psychological states or beliefs (see, for example, Andreoni and Bernheim 2009; and Battigalli and Dufwenberg 2009).
6
It is weaker than the monotonicity axiom as it only refers to outcomes in the support of the lottery (i.e. elementary lotteries are considered) and not any other outcome. It is weaker than the betweenness axiom, because it does not involve compound lotteries. To compare with first-order stochastic dominance, the underlying space of outcomes first needs an order, which naturally arises by ordering outcomes by the utility 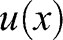of the certain outcome. Such a notion is present for example in the ordinal first-order stochastic dominance approach in Spector, Leshno, and Ben Horin (1996) and in the approach to dominance in probabilities in Karni and Safra (2002).
7
In the tradition of Kahneman, Knetsch, and Thaler (1990), who analyzed the endowment effect with coffee mugs, we use coffee mugs, because there are no apparent norms in favor or against buying such mugs.
8
This subsumes motives like shifting responsibilities as, for example, observed by Bartling and Fischbacher (2011) and Hamman, Loewenstein, and Weber (2010).
9
If the utility of a lottery L over outcomes 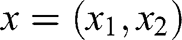specifying the realization for each of two players can be written as the utility over expected realizations 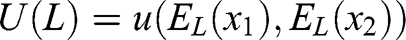with u non-linear, then it cannot be represented as expected utility 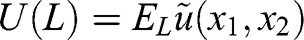for any function 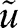because this is linear in probabilities.
10
See also Chew and Sagi (2006), Grant (1995), and Grant et al. (2010) for related work.
11
See, however, Keren and Willemsen (2009), and Rydval et al. (2009), for empirical evidence suggesting that Gneezy et al.’s findings may not be very robust.
12
Since we are not aware of an implementation of this thought experiment, we included hypothetical versions of Machina’s parental example in another, unrelated experiment. We asked 56 participants to imagine they are a mother with 2 kids and to have only 1 candy. They had to decide whether to give kid 1 or kid 2 the candy or let a coin toss decide. About 95% chose the coin toss. One hundred and one participants faced a modified version, in which we tried to break indifference: the mother now has a green candy and knows that kid 1 likes green candies best, while kid 2 likes red candies. Here, still 67% choose the coin toss and the remainder to give the candy to kid 1.
13
Original instructions are written in German and are available from the authors upon request. See the Appendix for translated instructions.
14
The random allocation to a cubicle also determined an individual’s role in the experiment.
15
We chose the magnitude of these payments to be well within the range used in other experiments on social preferences.
16
On average, participants earned 9.4 € including a 5 € show-up fee.
17
The first choice is between the lotteries 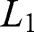: 500,000 € with 100% and 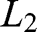: 2.5 million € with 10%, 500,000 € with 89% and 0 € with 1%; the second between 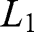: 500,000 € with 11%, 0 € with 89% and 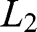: 2.5 million € with 10%, and 0 € with 90%. A violation of EUT involves choosing 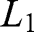in one situation but 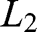in the other.
18
A chi-square test comparing all three options also yields no significant difference ().
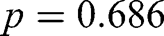19
If we had chosen another individual as the uninformed receiver, we would have had to make sure in the instructions that the subjects know and believe that the receiver is indeed uninformed.
20
Individuals made the mug choice before they knew their earnings. Since the mug choice is so trivial, they made in addition a decision in an unrelated voting experiment in which they could earn 0, 7, or 10 Euro. The complete (translated) instructions are in the Appendix.
21
Given the small number of subjects that randomize in the mug experiment, a Fisher exact test seems more appropriate than a Pearson chi-square test. The latter however yields a similar result (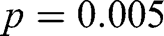). Instead of bundling those who take the money or buy the good, we can test for a relation between experiments using all three choice options (randomization, take the money, or buy the good). Again, both tests indicate a significant difference (Fisher exact test: 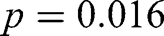; Pearson chi-square test ).
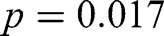22
However, in the latter two comparisons, the social good experiment differs from the mug experiment due to the cost of randomization and the receiver being a charity.
23
Mann–Whitney U tests do not indicate significant differences: 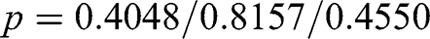when testing decision times for all three choice options/for those who keep the money/for those who buy the social good or the mug. Since too few people choose to randomize in the mug experiment, we cannot test for differences in the time for randomized choices.
24
Generalizations which do not assume betweenness are those in the quadratic class (e.g. Machina 1982) and those in the rank dependent or cumulative class (e.g. Quiggin 1982).
25
See e.g. Kirchsteiger (1994), Levine (1998), Fehr and Schmidt (1999), Bolton and Ockenfels (2000), Ok and Kockesen (2000), and Charness and Rabin (2002) for specific functional forms. See, e.g., Maccheroni, Marinacci, and Rustichini (2008), Sandbu (2008), and Rohde (2010) for specifications founded in the axiomatic tradition of decision-theory.
26
See also Neilson (2006).
27
Since these works were concerned with signaling to the receiver, the settings were not double blind. Neither was our experiment. That leaves open the possibility of signaling to the experimenter.
28
In Bolton and Ockenfels (2010), depending on the treatment, the outcomes of the safe option are (7,7), (7,0), (7,16), (9,9), (9,0), or (9,16) – where in each case the first (second) entry denotes the dictator’s (receiver’s) payoff. The outcomes of the risky option are either (16,16) and (0,0) or (16,0) and (0,16). Since the outcomes of the safe option differ from the outcomes of the risky choice, it is possible to assign utility values to the outcomes that rationalize the findings even within the framework of expected utility theory. Whether such utility values reflect one’s intuition about fairness or inequality aversion is a different matter.
29
Bolton, Brandts, and Ockenfels (2005) study a different environment and document that responders often reject unfavorable offers if the sender could have chosen an unbiased offer, while the rejection rates go down substantially if no unbiased offer is in the choice set of the sender. This part of their study does not deal with preferences for randomization directly, though.
30
In Andreoni and Bernheim (2009), decision makers do not choose among lotteries, but choose after the lottery is executed. Charness and Dufwenberg (2011) and Tadelis (2008) have decisions only between one deterministic outcome and one lottery. Dana, Cain, and Dawes (2006) and most of Dana, Weber, and Kuang (2007) consider settings without uncertainty.
This article circulated under the title “Fairness: A Critique to the Utilitarian Approach”.