Abstract: We analyze forward-induction reasoning in games with asymmetric information assuming some commonly understood restrictions on beliefs. Specifically, we assume that some given restrictions Δ on players’ initial or conditional first-order beliefs are transparent, that is, not only do the restrictions Δ hold but there is also common belief in Δ at every node. Most applied models of asymmetric information are covered as special cases whereby Δ pins down the probabilities initially assigned to states of nature. But the abstract analysis also allows for transparent restrictions on beliefs about behavior, e.g. independence restrictions or restrictions induced by the context behind the game. Our contribution is twofold. First, we use dynamic interactive epistemology to formalize assumptions that capture foward-induction reasoning given the transparency of Δ, and show that the behavioral implications of these assumptions are characterized by the Δ-rationalizability solution procedure of Battigalli (1999, 2003). Second, we study the differences and similarities between this solution concept and a simpler solution procedure put forward by Battigalli and Siniscalchi (2003). We show that the two procedures are equivalent if Δ is “closed under compositions” a property that holds in all the applications considered by Battigalli and Siniscalchi (2003). We also show that when Δ is not closed under compositions, the simpler solution procedure of Battigalli and Siniscalchi (2003) may fail to characterize the behavioral implications of forward-induction reasoning.
5 Appendix
Subsection 5.1 provides a complete forward-induction analysis of the Beer–Quiche game under different scenarios and related restrictions on beliefs; 5.2 derives the epistemic justifications of Δ-rationalizability; 5.3 proves the equivalence between Δ-rationalizability and the naïve reduction algorithm when Δ is closed under compositions.
5.1 Two scenarios for Δ-rationalizability in the Beer–Quiche game
Complete information scenario We formalize the informal argument provided in Section 1 for the Beer–Quiche game of Figure 1 and Example 1 (1). As formally described in Example 2, assume the following restrictions Δ are transparent:
Players ex ante assign 90% (10%) probability to the surly (wimp) state,
According to the ex ante beliefs of Player 1, the chance move and the strategy of Player 2 are independent.
The behavioral implications of (correct) common strong belief of rationality and transparency of Δ can be derived with the (naïve) Δ-rationalizability algorithm (Theorem 1, Corollary 1). To apply the latter, we first note that we may add wlog further restriction that, according to the beliefs of Player 2, the strategy of Player 1 and the chance move are independent.43 With this, Δ-rationalizability is a refinement of rationalizability on the ex ante strategic form of the Bayesian game defined by the first restriction.44 In the Table 4, we multiply all the expected payoffs by a factor of 10:
Ex ante strategic form of the Beer and Quiche game.
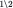 | 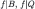 | 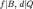 | 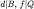 | 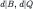 |
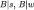 | 9, 1 | 9, 1 | 29, 9 | 29, 9 |
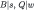 | 10, 1 | 12, 0 | 28, 10 | 30, 9 |
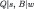 | 0, 1 | 18, 10 | 2, 0 | 20, 9 |
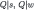 | 1, 1 | 21, 9 | 1, 1 | 21, 9 |
Iterated weak dominance on this strategic form deletes f.f and Q.B in step 1, f.d in step 2, Q.Q in step 3, d.d in step 4, and B.Q in step 5.45 This is equivalent (for this game) to iterated conditional dominance on the strategic form, which gives the Δ-rationalizability solution. We summarize the procedure in Table 5. For intuitive explanations based on the epistemic analysis see Section 1.
Solution of the Beer and Quiche game for the complete information scenario.
| Steps | Player 1 | Player 2 |
| 1 | 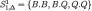 | 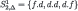 |
| 2 | 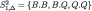 | 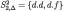 |
| 3 | 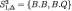 | 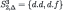 |
| 4 | 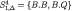 | 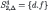 |
| 5 | 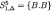 | 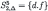 |
Incomplete-information scenario In this scenario, there is no chance move, the game begins at the “interim” stage, when Player 1 knows the true state; see Example 1 (2). Now there are two conceivable information types of Player 1, s and w, each with strategy space 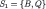 . Thus,
. Thus,
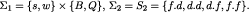
In this scenario, Player 1 has no belief on {s, w}. Intuitively, the reason is that 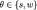 is just an attribute of Player 1 known to him, not something that he learns. Formally, his primitive uncertainty space is
is just an attribute of Player 1 known to him, not something that he learns. Formally, his primitive uncertainty space is 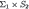 . With this, the independence assumption of the complete-information scenario cannot be expressed as a property of his first-order beliefs. As we mentioned in Section 1, there is a property of the second-order beliefs of Player 2 that could replace the independence property expressible in the complete-information scenario: according to the second-order beliefs of Player 2, the information type of Player 1 and his first-order belief about the strategy of Player 2 are independent. We could provide an epistemic analysis of the game based on the transparency of first and second-order restrictions and derive results similar to those obtained for the complete-information scenario. But in this paper we restricted our attention to transparency of first-order restrictions. Therefore, as an illustration of our approach we assume the following first-order restrictions Δ to be transparent:
. With this, the independence assumption of the complete-information scenario cannot be expressed as a property of his first-order beliefs. As we mentioned in Section 1, there is a property of the second-order beliefs of Player 2 that could replace the independence property expressible in the complete-information scenario: according to the second-order beliefs of Player 2, the information type of Player 1 and his first-order belief about the strategy of Player 2 are independent. We could provide an epistemic analysis of the game based on the transparency of first and second-order restrictions and derive results similar to those obtained for the complete-information scenario. But in this paper we restricted our attention to transparency of first-order restrictions. Therefore, as an illustration of our approach we assume the following first-order restrictions Δ to be transparent:
Player 2 initially assigns 90% probability to θ = s,
conditional on B, Player 2 believes that s is more likely than w.
Formally,
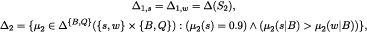
where we used obvious abbreviations for unconditional, conditional, and marginal probabilities. Note, this is just meant to be an example; we do not claim that the assumption in the second bullet is more plausible, or “nicer” than the assumption about the second-order beliefs of Player 2 described above.
The behavioral implications of (correct) common strong belief in rationality and transparency of the restrictions are characterized by a solution procedure that deletes profiles from the set 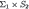 . We summarize the steps in Table 6 and then comment.
. We summarize the steps in Table 6 and then comment.
Solution of the Beer and Quiche game for the incomplete information scenario.
| Steps | Player 1 | Player 2 |
| 1 | 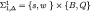 | 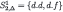 |
| 2 | 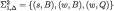 | 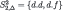 |
| 3 |  | 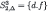 |
| 4 | 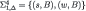 | 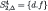 |
Step 1, Player 2: We delete f.f (as in the complete-information scenario) and also f.d (fight if and only if Beer); the reason for the latter is that it is rational to fight if and only if the conditional probability of the surly type is no more that 50%, therefore, given the restrictions on beliefs, if it is rational to fight after B then it is a fortiori rational to fight after Q. To sum up, Player 2 does not fight after B.
Step 2, Player 1: Given the above, the surly type has his preferred meal, i.e., type/strategy pair (s,Q) is deleted.
Step 3, Player 2: By a forward-induction argument similar to Step 4 of the complete-information scenario (see Section 1), d.d is deleted.
Step 4: Each type of Player 1 is certain of d.f, therefore both types choose Beer.
5.2 Proofs of the characterization results
The proof of the main result (Theorem 1) is adapted from Battigalli and Siniscalchi (2007). First, we need some preliminaries. Fix a belief-complete type structure and a collection of compact subsets Δ. 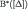 is a belief-closed subset of this structure that can be constructed as follows (recall we introduced the singleton
is a belief-closed subset of this structure that can be constructed as follows (recall we introduced the singleton 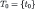 for notational convenience): let
for notational convenience): let
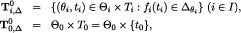
for each  and
and 
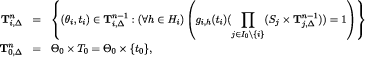
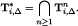
Clearly, 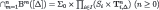 ,46 thus
,46 thus 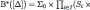
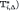 . Note that we had to define
. Note that we had to define 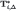 as a subset of
as a subset of 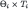 rather than
rather than  , because the restrictions on first-order beliefs may depend on the information type θi. Elements of
, because the restrictions on first-order beliefs may depend on the information type θi. Elements of 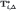 will be simply called “types”.
will be simply called “types”.
We begin with a few preliminary results. Let 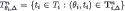 and
and 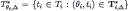 denote the θi-section of, respectively,
denote the θi-section of, respectively, 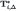 and
and 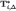 . Clearly,
. Clearly, 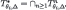 .
.
Lemma 1For all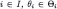 and
and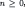 , the sets
, the sets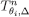 ,
, 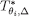 ,
, 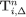 and
and 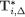 are closed.
are closed.
Proof For every 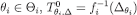 is closed because fi is continuous and Δθi is closed. Therefore,
is closed because fi is continuous and Δθi is closed. Therefore,  is closed because it is the union of finitely many closed sets.
is closed because it is the union of finitely many closed sets.
Now suppose by way of induction that 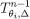 is closed for every i and θi, so that
is closed for every i and θi, so that 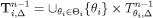 is closed for every i. Then the set of probability measures
is closed for every i. Then the set of probability measures
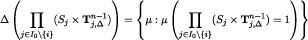
is closed. This implies that the set of conditional beliefs that fully believe 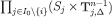 , that is,
, that is,
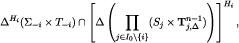
is closed as well, because 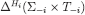 is closed. Since gi is continuous,
is closed. Since gi is continuous,
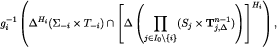
is closed. This implies that, for every 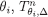 is closed, because
is closed, because 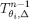 is closed (inductive hypothesis) and
is closed (inductive hypothesis) and
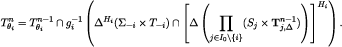
Hence, 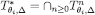 is closed as well. ■
is closed as well. ■
Lemma 2For every , projΘi
, projΘi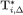 =Θi, therefore there exists a function
=Θi, therefore there exists a function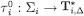 such that
such that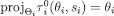 .
.
Proof We prove below by induction that 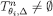 for every
for every 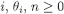 . By Lemma 1,
. By Lemma 1,  is a decreasing sequence of non-empty closed subsets of a compact space. By the finite intersection property,
is a decreasing sequence of non-empty closed subsets of a compact space. By the finite intersection property, 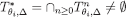 . Hence, for every i
. Hence, for every i
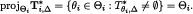
Then, we can define 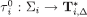 as follows: for each
as follows: for each 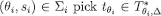 and let
and let 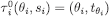 .
.
Now we prove by induction that, for every 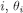 , and
, and 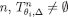 .
.
Basis step First, for every 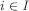 and
and 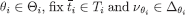 arbitrarily. Also, let
arbitrarily. Also, let 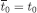 . Now define an array of probability measures
. Now define an array of probability measures 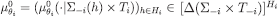 as follows: for every measurable subset
as follows: for every measurable subset 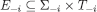 and
and 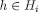
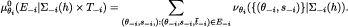
It can be checked that 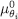 is a CPS, that is,
is a CPS, that is, 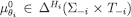 . Since
. Since 
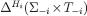 is onto (belief-completeness), there is some
is onto (belief-completeness), there is some 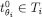 such that
such that 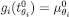 . By construction,
. By construction, 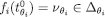 thus,
thus, 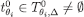 .
.
As a matter of notation, let 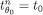 for every
for every 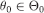 and
and 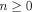 .
.
Induction step Now suppose that, for every i and 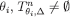 and pick for each
and pick for each 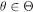 a profile
a profile 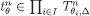 . For every
. For every 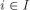 and θi, define an array of probability measures
and θi, define an array of probability measures 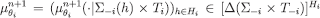 as follows: for every measurable subset
as follows: for every measurable subset 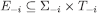 and
and 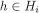
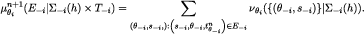
As in the basis step, it can be checked that 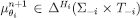 . Since gi is onto, there is some
. Since gi is onto, there is some 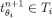 such that
such that 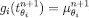 . By construction,
. By construction, 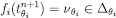 . Furthermore, for every
. Furthermore, for every 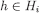 and
and 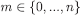
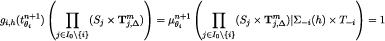
(the equalities hold by construction for 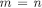 , then they also hold for
, then they also hold for  because
because 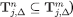 ). Since
). Since
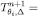
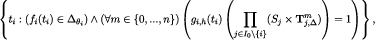
it follows that 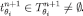 . ■
. ■
Lemma 3Fix compact restrictions Δ and maps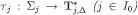 such that
such that , where
, where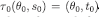 . Fix a player
. Fix a player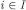 and, for eachθi, a first-order
and, for eachθi, a first-order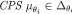 . Then, for eachθi, there exists an epistemic type
. Then, for eachθi, there exists an epistemic type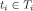 such that
such that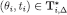 and, for each
and, for each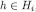 ,
, 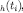 has finite support and
has finite support and
![[7]](/document/doi/10.1515/bejte-2012-0005/asset/graphic/bejte-2012-0005_eq61.png)
Proof. Define a candidate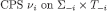 by setting
by setting
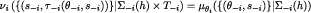
for every and 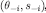 and
and 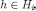 , extending the assignments by additivity. Axioms 1 and 2 follow immediately from the observation that the map
, extending the assignments by additivity. Axioms 1 and 2 follow immediately from the observation that the map 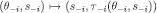 yields an embedding of
yields an embedding of 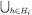 supp
supp 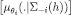 (a finite sub setset of
(a finite sub setset of  ∑‒i) in
∑‒i) in 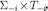 , so that, for every
, so that, for every 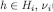
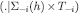 is indeed a probability measure on
is indeed a probability measure on 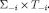 . By the same argument, νi must also satisfy Axiom 3, i.e. it must be a CPS; of course, each
. By the same argument, νi must also satisfy Axiom 3, i.e. it must be a CPS; of course, each 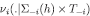 has finite support by construction. Since gi is onto, there exists a type
has finite support by construction. Since gi is onto, there exists a type 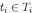 such that
such that
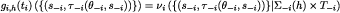
for every 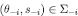 and
and 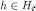 . To see that
. To see that 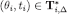 note that by construction
note that by construction 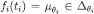 and
and 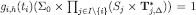 for each h, which implies
for each h, which implies 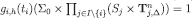 for each h and n. ■
for each h and n. ■
We can now prove our main result.
Proof of Theorem 1: To prove the first part, we rely on Lemma 2 and Lemma 3 to recursively define, for each 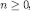 , a profile of functions
, a profile of functions 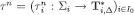 such that, for each
such that, for each 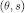 ,
, 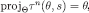 and
and 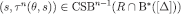 whenever
whenever 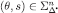 .
.
For the reader’s convenience, we report below the conditions for surviving the (n+1)-th step of Δ-rationalizability:
For every 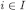 and
and 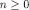 ,
, 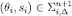 if and only if there exists a CPS
if and only if there exists a CPS 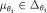 such that
such that
![[8]](/document/doi/10.1515/bejte-2012-0005/asset/graphic/bejte-2012-0005_eq64.png)
![[9]](/document/doi/10.1515/bejte-2012-0005/asset/graphic/bejte-2012-0005_eq65.png)
The maps for Player 0 are trivial: 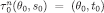 for every and n. As for the real players, let
for every and n. As for the real players, let 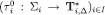 be any profile of functions such that
be any profile of functions such that  such functions exist by Lemma 2. Next, assuming that
such functions exist by Lemma 2. Next, assuming that 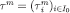 has been defined and satisfies
has been defined and satisfies 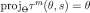 for every m = 0, … n, define
for every m = 0, … n, define 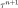 as follows: for each i and
as follows: for each i and 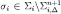 let
let 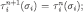 for each
for each 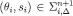 there is first-order
there is first-order 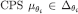 such that eqs. [8] and [9] hold and, by Lemma 3, there is an epistemic type
such that eqs. [8] and [9] hold and, by Lemma 3, there is an epistemic type 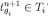 with
with 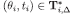 such that eq. [7] holds (for each
such that eq. [7] holds (for each 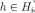 ) with
) with 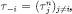 , so that – in particular
, so that – in particular 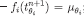 then let
then let 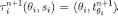 . Clearly,
. Clearly, 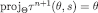 .
.
Claim 1For every and
and 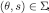 ,
,
![[10]](/document/doi/10.1515/bejte-2012-0005/asset/graphic/bejte-2012-0005_eq66.png)
![[11]](/document/doi/10.1515/bejte-2012-0005/asset/graphic/bejte-2012-0005_eq67.png)
Equation [10] implies
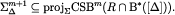
Equation [11] implies
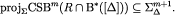
Therefore, the claim implies that
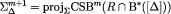
for every m.
Proof of the claim Recall that 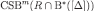 is a Cartesian product. To ease notation, for each
is a Cartesian product. To ease notation, for each 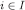 and
and 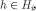 , we write
, we write
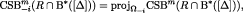
Basis step Fix (θ, s) arbitrarily. Suppose that 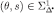 . By construction of
. By construction of 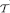 1, for each
1, for each 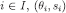
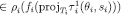 and
and 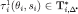 . Therefore,
. Therefore, 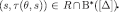 . Since
. Since 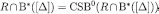 , this proves eq. [10] for m= 0. Next, fix any
, this proves eq. [10] for m= 0. Next, fix any 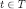 such that
such that 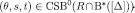 . Then, for each
. Then, for each 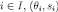
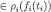 and
and 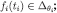 ; therefore
; therefore 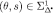 . This proves eq. [11] for m = 0.
. This proves eq. [11] for m = 0.
Induction step Assume that eqs. [10] and [11] hold for each 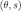 and m = 0, …, n‒1. Then, for each m = 0, …, n – 1,
and m = 0, …, n‒1. Then, for each m = 0, …, n – 1,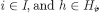 ,
,
![[12]](/document/doi/10.1515/bejte-2012-0005/asset/graphic/bejte-2012-0005_eq72.png)
Fix (θ, s) arbitrarily. Suppose that 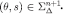 . By construction of
. By construction of 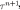 , for every
, for every 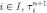
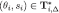 and
and 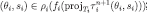 ; therefore
; therefore 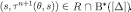 . By the inductive hypothesis and the construction of
. By the inductive hypothesis and the construction of 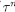 , for every
, for every 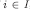 ,
, 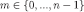 and
and 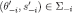
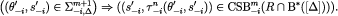
Hence, by construction of 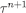 and eq. [12], for every
and eq. [12], for every 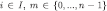 and
and 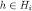 ,
,
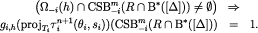
Next, note that
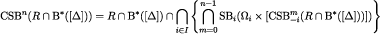
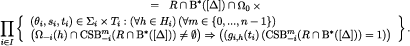
It follows that 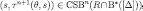 , showing that eq. [10] holds for m = n.
, showing that eq. [10] holds for m = n.
Now fix any 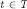 such that
such that 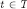 . Then, for every
. Then, for every 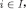
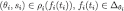 , and (by the inductive hypothesis) for every
, and (by the inductive hypothesis) for every 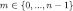 and
and 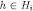
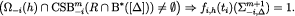
By eq. [12], the formula above is equivalent to
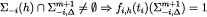
for every 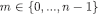 and
and 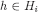 . Therefore,
. Therefore, 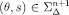 , showing that eq. [11] holds with m = n. □
, showing that eq. [11] holds with m = n. □
Next, we prove the second part of the thesis: 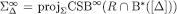 . Pick any
. Pick any 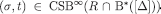 . Since,
. Since, 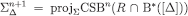 for every
for every 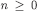 , we conclude that
, we conclude that 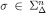 for every
for every 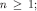 so
so 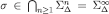 . Hence,
. Hence, 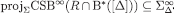 . Now pick any
. Now pick any 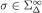 and consider the sequence of sets
and consider the sequence of sets 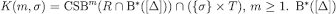 is closed and (by standard arguments) R is closed as well. For every closed event E, i, and
is closed and (by standard arguments) R is closed as well. For every closed event E, i, and 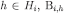 is closed, therefore
is closed, therefore 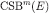 is also closed.
is also closed. 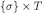 is obviously closed. Therefore, each
is obviously closed. Therefore, each 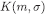 is non-empty (because
is non-empty (because 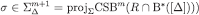 and closed subset of the compact space
and closed subset of the compact space 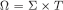 ; also, the sequence of sets
; also, the sequence of sets 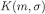 is decreasing, and hence has the finite intersection property. Then
is decreasing, and hence has the finite intersection property. Then 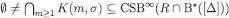 and
and 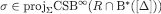 . Therefore,
. Therefore, 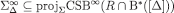 . ■
. ■
Proof of Theorem First observe that the set of states of player i in 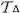 is
is
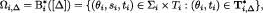
where 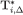 is the set of information/epistemic types defined at the beginning of this subsection.
is the set of information/epistemic types defined at the beginning of this subsection.
Proof of eq. [3] Fix i, θi. By definition of 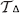 , the right-hand-side of eq. [3] is contained in the left-hand-side. To see that also the converse holds, fix
, the right-hand-side of eq. [3] is contained in the left-hand-side. To see that also the converse holds, fix 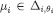 ; by Lemma 3 there is a type
; by Lemma 3 there is a type 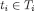 such that
such that 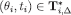 and
and 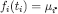 . By construction,
. By construction, 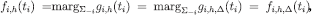 , for each
, for each 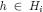 (the second equality holds because
(the second equality holds because 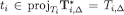 and
and 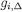 is the restriction of
is the restriction of 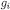 on
on 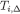 ). Thus,
). Thus,  for some
for some 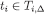 such that
such that 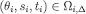 for every si.
for every si.
Proof of eq. [4]Basis step. Each first-order belief map 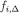 is the restriction of
is the restriction of 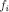 on
on 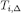 and
and 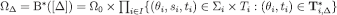 ; therefore
; therefore
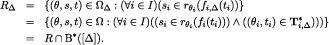
Induction step. Suppose that 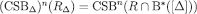 . Then
. Then
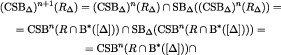
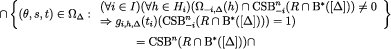
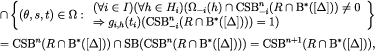
where the second equality follows from the induction hypothesis, the fourth holds because 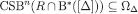 and
and 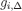 is the restriction of gi on
is the restriction of gi on 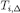 , and the other equalities hold by definition. □
, and the other equalities hold by definition. □
Proof of eqs. [5] and [6]. Given eqs. [4], [5] and [6] follow from Theorem 1. ■
Proof of Theorem 3. To shorten the proof, we take advantage of the result due to Battigalli and Siniscalchi (2007) mentioned in Section 1:
Theorem 5Fix a collection 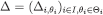 of compact subsets of first-order CPS’s and a belief-complete type structure
of compact subsets of first-order CPS’s and a belief-complete type structure 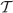 . Then, for every n ≥ 0,
. Then, for every n ≥ 0,
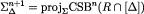
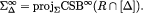
Sketch of proof of Theorem 5. By inspection of the proof of the main characterization result in Battigalli and Siniscalchi (2007), it is clear that a separate lemma47 shows the equivalence of naïve Δ-rationalizability 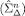 and Δ-rationalizability
and Δ-rationalizability 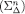 under the assumption that Δ is regular, whereas the rest of the proof shows that Theorem 5 holds. This is done within the observable-actions framework, but it is clear that the arguments of the rest of the proof are unaffected by considering the more general framework of this paper. □
under the assumption that Δ is regular, whereas the rest of the proof shows that Theorem 5 holds. This is done within the observable-actions framework, but it is clear that the arguments of the rest of the proof are unaffected by considering the more general framework of this paper. □
Theorems 1 and 5 imply
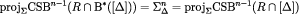
for each 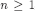 , including
, including 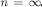 . An induction argument shows that all the claimed inclusions hold. Indeed,
. An induction argument shows that all the claimed inclusions hold. Indeed,
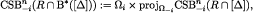
Suppose that 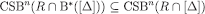 . Recall from subsection 3.2 that, for each
. Recall from subsection 3.2 that, for each 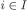 and
and 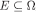 , we let
, we let 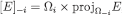 ,
,
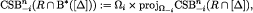
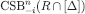 is similarly defined. Since
is similarly defined. Since 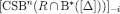 and
and 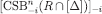 have the same projection on
have the same projection on 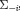 , they are consistent with the same information sets of Player i, even if
, they are consistent with the same information sets of Player i, even if  . Let
. Let 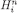 denote the collection of such information sets; then, by the inductive hypothesis and monotonicity of the Bi, h operators,
denote the collection of such information sets; then, by the inductive hypothesis and monotonicity of the Bi, h operators,
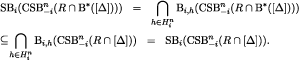
Recall that, for each 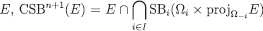 . Therefore, given the above definitions and inclusions,
. Therefore, given the above definitions and inclusions,
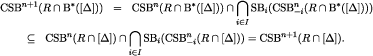
■
5.3 Equivalence of Δ-rationalizability and naïve Δ-rationalizability
We begin with a preliminary result about closedness under compositions.
Definition 11A finite sequence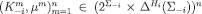 is admissible if
is admissible if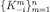 is a decreasing sequence of product sets with
is a decreasing sequence of product sets with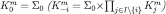 and, for every
and, for every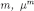 strongly believes
strongly believes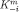 (for each
(for each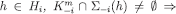
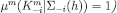 .
.
Definition 12Fix an admissible sequence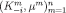 and let
and let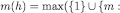
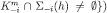 . A system of beliefs
. A system of beliefs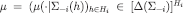 is the composition of
is the composition of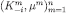 if
if
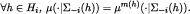
Lemma 4The compositionμof an admissible sequenceis a CPS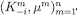 such that
such that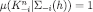 for each
for each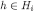 with
with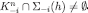 .
.
Proof. We only have to prove that μ satisfies the chain rule, the rest follows immediately by inspection of Definition 12. Fix  , and E‒i so that
, and E‒i so that 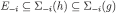 (g is a prefix of h); then
(g is a prefix of h); then 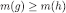 . If
. If 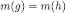 then
then
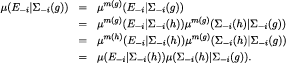
If 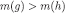 then, by definition of
then, by definition of 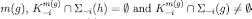 . By admissibility of the sequence,
. By admissibility of the sequence, 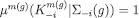 . Therefore,
. Therefore, 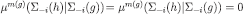 and
and
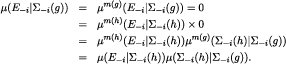
■
Lemma 5Let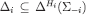 be closed under compositions and fix an admissible sequence
be closed under compositions and fix an admissible sequence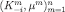 such that
such that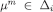 for each m. Then also the composition of
for each m. Then also the composition of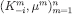 gives a CPS in
gives a CPS in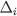 .
.
Proof. The statement is true by definition for admissible sequences of length 2. Assume by way of induction that the result holds for admissible sequences of length  and consider an admissible sequence of length n, viz.
and consider an admissible sequence of length n, viz. 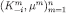 . Let μ be the composition of the (admissible) prefix
. Let μ be the composition of the (admissible) prefix 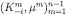 . By the inductive hypothesis,
. By the inductive hypothesis, 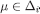 . The pair
. The pair 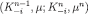 is admissible since
is admissible since 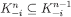 and μ is a composition of
and μ is a composition of 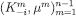 so that, in particular, μ is a CPS such that
so that, in particular, μ is a CPS such that 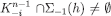 implies
implies 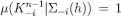 for each
for each 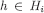 (Lemma 4). Now let
(Lemma 4). Now let 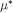 be the composition of
be the composition of 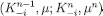 . Since
. Since 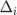 is closed under compositions,
is closed under compositions, 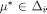 . By construction,
. By construction, 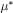 is the composition of
is the composition of 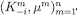 . ■
. ■
Proof of Proposition 1. The statement is obvious for 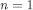 . Now pick
. Now pick 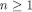 and assume by way of induction that the statement it is true for each positive integer up to n. We have to show that
and assume by way of induction that the statement it is true for each positive integer up to n. We have to show that 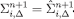 .
.
If 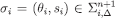 then there is some
then there is some 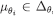 satisfying Eqs. [8] and [9]; since
satisfying Eqs. [8] and [9]; since 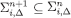 , then by the inductive hypothesis
, then by the inductive hypothesis 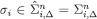 ; moreover, since
; moreover, since 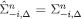 (again by the inductive hypothesis), eq. [9] implies
(again by the inductive hypothesis), eq. [9] implies 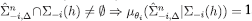 1. We conclude that
1. We conclude that 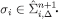 .
.
In the other direction, suppose 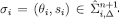 . Then also
. Then also 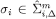 for
for 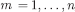 , so we can find CPS’s
, so we can find CPS’s 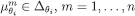 , such that, for each m,
, such that, for each m, 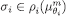 and,
and, 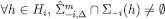 implies
implies  and,
and, 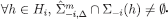 . Therefore, the sequence
. Therefore, the sequence 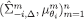 is admissible. Now let
is admissible. Now let 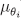 be the composition of this sequence. Clearly,
be the composition of this sequence. Clearly, 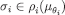 and
and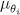 satisfies eq. [9]. Moreover, by Lemma 5
satisfies eq. [9]. Moreover, by Lemma 5 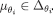 . Therefore
. Therefore  . ■
. ■
Acknowledgments
The authors thank an anonymous referee for his or her thoughtful and constructive review of an earlier draft of this paper. The authors gratefully acknowledge useful comments by Emiliano Catonini, Nicodemo De Vito, Amanda Friedenberg, Elena Manzoni, Sara Negrelli, Jacopo Perego, and Pietro Tebaldi. All errors are their own. Pierpaolo Battigalli thanks NYU-Stern for its hospitality and gratefully acknowledges financial support from ERC grant 324219.
References
Aradillas-Lopez, A., and E.Tamer. 2008. “The Identification Power of Equilibrium in Simple Games.” Journal of Business & Economics Statistics26:261–83.10.1198/073500108000000105Search in Google Scholar
Aumann, R. J.1987. “Correlated Equilibrium as an Expression of Bayesian Rationality.” Econometrica55:1–18.10.2307/1911154Search in Google Scholar
Battigalli, P.1996. “Strategic Rationality Orderings and the Best Rationalization Principle.” Games and Economic Behavior13:178–200.10.1006/game.1996.0033Search in Google Scholar
Battigalli, P.1997. “On Rationalizability in Extensive Form Games.” Journal of Economic Theory74:40–61.10.1006/jeth.1996.2252Search in Google Scholar
Battigalli, P.1991. “Rationalizability in Incomplete Information Games.” EUI working papers, ECO 99/17.Search in Google Scholar
Battigalli, P.2003. “Rationalizability in Infinite Dynamic Games with Incomplete Information.” Research in Economics57:1–38.10.1016/S1090-9443(02)00054-6Search in Google Scholar
Battigalli, P.2006. “Rationalization in Signaling Games: Theory and Applications.” International Game Theory Review8:1–27.10.1142/S0219198906000795Search in Google Scholar
Battigalli, P., and A.Friedenberg. 2009. “Context-Dependent Forward Induction Reasoning.” IGIER working paper 351, Bocconi University.Search in Google Scholar
Battigalli, P., and A.Friedenberg. 2012. “Forward Induction Reasoning Revisited.” Theoretical Economics7:57–98.10.3982/TE598Search in Google Scholar
Battigalli, P., and M.Siniscalchi. 1999. “Hierarchies of Conditional Beliefs and Interactive Epistemology in Dynamic Games.” Journal of Economic Theory88:188–230.10.1006/jeth.1999.2555Search in Google Scholar
Battigalli, P., and M.Siniscalchi. 2002. “Strong Belief and Forward Induction Reasoning.” Journal of Economic Theory106:356–91.10.1006/jeth.2001.2942Search in Google Scholar
Battigalli, P., and M.Siniscalchi. 2003. “Rationalization and Incomplete Information.” Advances in Theoretical Economics3(1), Article 3, http://www.bepress.con/bejte/advances/vol3/iss1/art3.Search in Google Scholar
Battigalli, P., and M.Siniscalchi. 2007. “Interactive Epistemology in Games with Payoff Uncertainty.” Research in Economics61:165–84.10.1016/j.rie.2007.10.003Search in Google Scholar
Battigalli, P., and P.Tebaldi. 2012. “Interactive Epistemology in Simple Dynamic Games with a Continuum of Strategies.” typescript.Search in Google Scholar
Battigalli, P., A.Di Tillio, and D.Samet. 2011. “Strategies and Interactive Beliefs in Dynamic Games,” IGIER w.p. n. 375 (2011), forthcoming in Advances in Economics and Econometrics (D.Acemoglu, M.Arellano, E.Dekel Eds.)Search in Google Scholar
Battigalli, P., A.Di Tillio, E.Grillo, and A.Penta. 2011. “Interactive Epistemology and Solution Concepts for Games with Asymmetric Information.” The B.E. Journal of Theoretical Economics11(1)(Advances), Article 6.Search in Google Scholar
Bergemann, D., and S.Morris. 2012. “Robust Mechanism Design.” The Role of Private Information and Higher Order Beliefs. Singapore: World Scientific Publishing.10.1142/8318Search in Google Scholar
Brandenburger, A., and E.Dekel. 1987. “Rationalizability and Correlated Equilibria.” Econometrica55:1391–402.10.2307/1913562Search in Google Scholar
Brandenburger, A., and E.Dekel. 1993. “Hierarchies of Beliefs and Common Knowledge.” Journal of Economic Theory59:189–98.10.1006/jeth.1993.1012Search in Google Scholar
Brandenburger, A., and A.Friedenberg. 2010. “Self-Admissible Sets.” Journal of Economic Theory145:785–811.10.1016/j.jet.2009.11.003Search in Google Scholar
Brandenburger, A., A.Friedenberg, and H. J.Keisler. 2008. “Admissibility in Games.” Econometrica76:307–52.10.1111/j.1468-0262.2008.00835.xSearch in Google Scholar
Cappelletti, G.2010. “A Note on Rationalizability and Restrictions on Beliefs.” B.E. Journals in Theoretical Economics10(1) (Topics), Article 40.Search in Google Scholar
Catonini, E.2012. “Non-Binding Agreements and Forward Induction Reasoning.” typescript (2012), Bocconi University.Search in Google Scholar
Cho, I. K., and D.Kreps. 1987. “Signaling Games and Stable Equilibria.” Quarterly Journal of Economics102:179–222.10.2307/1885060Search in Google Scholar
Dekel, E., D.Fudenberg, and S.Morris. 2007. “Interim Correlated Rationalizability.” Theoretical Economics2:15–40.Search in Google Scholar
De Vito, N.2012. “Complete Conditional Type Structures.” typescript, Bocconi University.Search in Google Scholar
Friedenberg. 2010. “When Do Type Structures Contain All Hierarchies of Beliefs?” Games and Economic Behavior68:108–29.10.1016/j.geb.2009.05.005Search in Google Scholar
Harsanyi, J.1967–68. “Games of Incomplete Information Played by Bayesian Players.” Parts I, II, III, Management Science14:159–82, 320–34, 486–502.Search in Google Scholar
Mertens, J.-F., and S.Zamir. 1985. “Formulation of Bayesian Analysis for Games with Incomplete Information.” International Journal of Game Theory14:1–29.10.1007/BF01770224Search in Google Scholar
Mueller, C.2012. “Robust Virtual Implementation Under Common Strong Belief in Rationality.” typescript, Carnegie Mellon University.Search in Google Scholar
Osborne, M., and A.Rubinstein. 1994. A Course in Game Theory. Cambridge, MA: MIT Press.Search in Google Scholar
Pearce, D.1984. “Rationalizable Strategic Behavior and the Problem of Perfection.” Econometrica52:1029–50.10.2307/1911197Search in Google Scholar
Renyi, A.1955. “On a New Axiomatic Theory of Probability.” Acta Mathematica Academiae Scientiarum Hungaricae6:285–335.10.1007/BF02024393Search in Google Scholar
Schweinzer, P., and M.Shimoji. 2012. “Implementation without Incentive Compatibility: Two Stories with Partially Informed Planners.” typescript, University of York, 2012.Search in Google Scholar
Tan, T., and S.Werlang. 1988. “The Bayesian Foundation of Solution Concepts of Games.” Journal of Economic Theory45:370–91.10.1016/0022-0531(88)90276-1Search in Google Scholar
Tebaldi, P.2011. “Non-Binding Agreements in Dynamic games.” MSc Thesis, Bocconi University.Search in Google Scholar
- 1
For a result of this sort see, for example, Battigalli et al. (2011, Theorem 3): absent independent restrictions, rationality and common belief in rationality have equivalent behavioral implications in the two scenarios.
- 2
The strategies and conditional beliefs pinned down by this argument concide with the sequential equilibrium selected by the Intuitive Criterion of Cho and Kreps (1987).
- 3
We refrain from saying that such restrictions are “common knowledge”. We find the use of the “common knowledge” terminology much too casual in economic theory, as there is often either a terminological or even a conceptual conflation of (common) knowledge and (common, probability one) belief. We find it semantically and conceptually useful to reserve “knowledge” for the justified true belief that comes from observation and logical deduction.
- 4
We distinguish between states of nature, that parametrize payoff functions, and states of the world that describe every relevant aspect of the situation of strategic interaction.
- 5
On extensive-form rationalizability see Pearce (1984) and Battigalli (1996, 1997).
- 6
Battigalli (1999, 2003) and Battigalli and Siniscalchi (2007) also analyze a less demanding solution concept that only requires initial common belief in rationality and the restrictions Δ. To stress the difference between these two solution concepts, these papers call “weak Δ-rationalizability” the one based on assumptions about initial beliefs, and “strong Δ-rationalizability” the one capturing forward-induction reasoning. Like other papers that only analyze the latter solution concept (e.g. Battigalli and Siniscalchi 2003; Battigalli and Friedenberg 2012), here we simply call it “Δ-rationalizability.”
- 7
For applications of the Δ-rationalizability approach to economic models see, e.g., Battigalli (2003, 2006), Battigalli and Siniscalchi (2003) and references therein; for applications to robust mechanism design see Schweinzer and Shimoji (2012) and Mueller (2012) and the survey by Bergemann and Morris (2012), for applications to non-binding agreeements see Catonini (2012) and Tebaldi (2011); for empirical applications see Aradillas-Lopez and Tamer (2008). Attention is restricted to first-order beliefs for the sake of simplicity, as Δ-rationalizability is meant to be a relatively simple reduction procedure whose implementation does not involve type structures and beliefs about beliefs. But restrictions on higher-order beliefs (not implied by the transparency of first-order beliefs restrictions) may well be appropriate in some applications; taking higher-order belief restrictions into account does not change the essential features of the approach. See, for example, the rationalizability analysis of Spence’s model by Battigalli (2006). Also, Theorem 4 (a straightforward extension of results due to Battigalli and Friedenberg 2012) provides a kind of equivalence between forward-induction reasoning under transparency of first-order and of higher-order beliefs.
- 8
Informally, we call “expressible” an assumption that can be stated using primitive terms and terms derived from primitive terms or other derived terms (see Battigalli et al. 2011).
- 9
More formally, we say that a collection of expressible assumptions justifies a solution concept, or equivalently that characterizes the behavioral implications of A, if for each player i and each piece of private information θi, the set of strategies allowed by for θi coincides with the set of strategies allowed by for θi.
- 10
On the other hand, the conjunction of strong belief in E and strong belief in F implies strong belief in.
- 11
Indeed, considering the same events and informational setup as above,E ∩ FE ∩ F ⊆, but we have just shown that strong belief in E ∩ F does not imply strong belief in both E and F. Thus, monotonicity does not hold.
- 12
Cf. Osborne-Rubinstein (1994), chapters 6, 11.
- 13
For any given set Y, Y<N denotes the set of finite sequences of elements of Y, including the empty sequence ∅, that is,
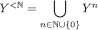 with
with 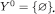 .
. - 14
No information set
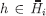 contains two ordered histories; furthermore, whenever
contains two ordered histories; furthermore, whenever 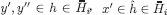 and
and 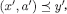 , there is a history
, there is a history 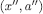 such that
such that 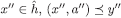 and
and 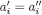 .
. - 15
This is not to be confused with “complete information,” which means that all the rules of the game and players’ preferences over consequences are common knowledge. Indeed, we allow for the opposite, if there is payoff uncertainty, there is incomplete information.
- 16
Battigalli (2003) allows for type-dependent actions sets.
- 17
Our framework allows for the possibility that players do not have common beliefs about the probabilities of chance moves.
- 18
The construction of a canonical type structure à la Battigalli and Siniscalchi applies to this more general setting (see Battigalli and Siniscalchi 1999; Battigalli 2003). The extension of the main epistemic characterization result of this paper involves, directly or indirectly, a measurable selection argument (see Battigalli and Tebaldi 2012).
- 19
Г exhibits complete information if the payoff map
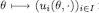 is constant (which is trivially true when Θ is a singleton), otherwise Г has incomplete information.
is constant (which is trivially true when Θ is a singleton), otherwise Г has incomplete information. - 20
Compactness of the relevant spaces is assumed for simplicity, it can be relaxed with some additional technical complications.
- 21
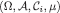 is called conditional probability space in Renyi (1955).
is called conditional probability space in Renyi (1955). - 22
That is,
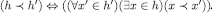 .
. - 23
If the information set of i containing also contained another node, then it would contain two nodes on the same path, thus violating perfect recall.
- 24
If two information sets
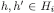 differ only because of moves of i, then
differ only because of moves of i, then 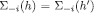 . Thus, the cardinality of Hi may be smaller than the cardinality of
. Thus, the cardinality of Hi may be smaller than the cardinality of  . This redundancy is innocuous in our analysis.
. This redundancy is innocuous in our analysis. - 25
History h is inconsistent with (or counterfactual at)
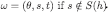 .
. - 26
Battigalli and Siniscalchi (1999) uses a slightly different definition of type structure. But all the arguments in Battigalli and Siniscalchi (1999) can be easily adapted to the present framework.
- 27
The representation of a type structure as a belief-closed substructure of the canonical one eliminates redundant types, i.e. types that yield the same hierarchy of CPS’s. Redundant types do not play any role in our analysis.
- 28
A result by Friedenberg (2010) implies that in static games (games where
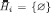 for each i) every compact-continuous complete structure contains all the “conceivable” hierarchies of beliefs and is in a precise sense equivalent to the canonical structure. It can be shown that the same holds more generally for all the dynamic games considered here (De Vito 2012).
for each i) every compact-continuous complete structure contains all the “conceivable” hierarchies of beliefs and is in a precise sense equivalent to the canonical structure. It can be shown that the same holds more generally for all the dynamic games considered here (De Vito 2012). - 29
See the discussion section in Battigalli, Di Tillio, and Samet (2011).
- 30
For any measurable (closed) subset
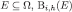 is measurable (closed).
is measurable (closed). - 31
We can prove our main results without assuming compactness of [Δ], but we are not able to do it without complicating the analysis. Clearly, compactness of [Δ] may not hold in interesting applications. In the incomplete-information scenario of the Beer–Quiche example analyzed in Section 5, Δ2 is not compact. But exactly the same analysis goes through with any compact subset of Δ2 sufficiently close to Δ2 (that is, sufficiently close in the Hausdorff topology to the closure of Δ2).
- 32
See Lemma 1 in Section 5.
- 33
Battigalli and Siniscalchi (2007) also put forward an incorrectly stated conjecture, the correct version of which is Theorem 1 above.
- 34
With this notation,
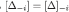 .
. - 35
We conjecture that if Δ is regular and each Δi,h is closed and convex, then the characterization of Δ-rationalizability as iterated Δ-dominance (Cappelletti 2010) can be extended to the present extensive-form setting.
- 36
If the reader is wondering why a complete information game corresponds to a Bayesian game, he should remember that in our terminology (which we claim to be the correct one) “complete information” is a substantive assumption, i.e. common knowledge of the payoff functions. On the other hand, Bayesian games are just mathematical structures that may be used to analyze both games with incomplete information and games with asymmetric, imperfect information about an initial chance move, such as poker. The interpretation of such mathematical structures is immaterial for Harsanyi’s equilibrium analysis, but not for rationalizability analysis. The reason is that standard notions of rationalizability for Bayesian games implicitly incorporate independence restrictions, and different restrictions are relevant under different interpretations (see Battigalli et al. 2011).
- 37
Our original example showing the difference between Δ-rationalizability and naive Δ-rationalizability did not have the latter feature. We thank Amanda Friedenberg for providing this example.
- 38
We use the following notation: O is the class of realization-equivalent strategies choosing Out, otherwise strategies are denoted by lists of action labels in an obvious way.
- 39
Note that in games with complete information Σ = S.
- 40
Battigalli and Friedenberg (2012) provide examples of complete information games where the inclusion also fails for the corresponding sets of paths, that is,
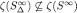 for some game and some restrictions Δ.
for some game and some restrictions Δ. - 41
Battigalli and Friedenberg (2012) is the abridged published version of Battigalli and Friedenberg (2009). The latter elab-orates more on the context interpretation of incomplete type structures and how they are related to transparent restrictions on beliefs. Battigalli and Friedenberg build on previous work on admissibility by Brandenburger, Friedenberg, and Keisler (2008) and Brandenburger and Friedenberg (2010).
- 42
The equivalences stated in the Theorem 4 adapt results of Battigalli and Friedenberg as follows:
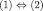 adapts Proposition 1 of Battigalli and Friedenberg (2012);
adapts Proposition 1 of Battigalli and Friedenberg (2012); 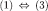 adapts Theorem 1 of Battigalli and Friedenberg (2012);
adapts Theorem 1 of Battigalli and Friedenberg (2012); 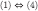 adapts Proposition A1 of Battigalli and Friedenberg (2009) applied to the E-restriction TE of a belief-complete type structure T; finally
adapts Proposition A1 of Battigalli and Friedenberg (2009) applied to the E-restriction TE of a belief-complete type structure T; finally 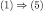 follows from Theorem 2 and (the adaptation of) Proposition 1 in Battigalli and Siniscalchi (2012) (the set Δ constructed in the proof is finite, hence compact),
follows from Theorem 2 and (the adaptation of) Proposition 1 in Battigalli and Siniscalchi (2012) (the set Δ constructed in the proof is finite, hence compact), 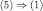 follows from Theorem 1 and
follows from Theorem 1 and 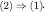 .
. - 43
The coalition formed by the chance player and Player 1 has perfect recall. Therefore, a correlated strategy of the coalition is realization equivalent to a behavioral strategy of the coalition, which is in turn equivalent to a product measure.
- 44
As observed by Battigalli et al. (2011), the application of solution concepts (such as rationalizability, or iterated dominance) to the ex ante strategic form implicitly relies on the independence assumption described above.
- 45
We write X.Y for the strategy of Player 1 that selects X in the surly state and Y in the wimp state; similarly we write x.y for the strategy of Player 2 that selects x if B and y if Q.
- 46
Since
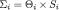 and
and 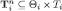 we are abusing notation here. This should cause no confusion.
we are abusing notation here. This should cause no confusion. - 47
Lemma 7 of Battigalli and Siniscalchi (2007), which is a special case of our Proposition 1.
©2013 by Walter de Gruyter Berlin / Boston
Articles in the same Issue
- Masthead
- Masthead
- Advances
- Dependence and Uniqueness in Bayesian Games
- Monopolistic Signal Provision†
- Multi-task Research and Research Joint Ventures
- Transparent Restrictions on Beliefs and Forward-Induction Reasoning in Games with Asymmetric Information
- A Simple Bargaining Procedure for the Myerson Value
- On the Difference between Social and Private Goods
- Optimal Use of Rewards as Commitment Device When Bidding Is Costly
- Labor Market and Search through Personal Contacts
- Contributions
- Learning, Words and Actions: Experimental Evidence on Coordination-Improving Information
- Are Trust and Reciprocity Related within Individuals?
- Optimal Contracting Model in a Social Environment and Trust-Related Psychological Costs
- Contract Bargaining with a Risk-Averse Agent
- Academia or the Private Sector? Sorting of Agents into Institutions and an Outside Sector
- Topics
- Poverty Orderings with Asymmetric Attributes
- Dictatorial Mechanisms in Constrained Combinatorial Auctions
- When Should a Monopolist Improve Quality in a Network Industry?
- On Partially Honest Nash Implementation in Private Good Economies with Restricted Domains: A Sufficient Condition
- Revenue Comparison in Asymmetric Auctions with Discrete Valuations
Articles in the same Issue
- Masthead
- Masthead
- Advances
- Dependence and Uniqueness in Bayesian Games
- Monopolistic Signal Provision†
- Multi-task Research and Research Joint Ventures
- Transparent Restrictions on Beliefs and Forward-Induction Reasoning in Games with Asymmetric Information
- A Simple Bargaining Procedure for the Myerson Value
- On the Difference between Social and Private Goods
- Optimal Use of Rewards as Commitment Device When Bidding Is Costly
- Labor Market and Search through Personal Contacts
- Contributions
- Learning, Words and Actions: Experimental Evidence on Coordination-Improving Information
- Are Trust and Reciprocity Related within Individuals?
- Optimal Contracting Model in a Social Environment and Trust-Related Psychological Costs
- Contract Bargaining with a Risk-Averse Agent
- Academia or the Private Sector? Sorting of Agents into Institutions and an Outside Sector
- Topics
- Poverty Orderings with Asymmetric Attributes
- Dictatorial Mechanisms in Constrained Combinatorial Auctions
- When Should a Monopolist Improve Quality in a Network Industry?
- On Partially Honest Nash Implementation in Private Good Economies with Restricted Domains: A Sufficient Condition
- Revenue Comparison in Asymmetric Auctions with Discrete Valuations


