Abstract
The paper shows that, whenever the completion of a research project requires the overcoming of more than one research obstacle, then Research Joint Ventures enjoy an intrinsic advantage relative to independent firms. This advantage, which has hitherto escaped attention in the RJV literature, relates to the RJV’s ability to organize research more efficiently than independent firms. The fact that RJVs can be both more profitable and yield higher expected net welfare than independent firms is surprising because it is derived from a model in which RJVs do not optimize over R&D investment. The paper exploits a basic result in systems reliability theory to establish the organizational superiority of RJVs.
Appendix
A1 Proof of Theorem 1
The basic result that a series of parallel arrangements of components is more likely to succeed than a parallel arrangement of series of components has a status akin to the Folk Theorem in game theory and is similarly tricky to pin down to a definite source. Perhaps the simplest version can be found in Ross (1996, Theorem 9.1) which can be adapted to prove Theorem 1 in the paper as follows:
Theorem 1 (after Ross (1996)):
For any ,
, 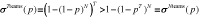 .
.
The above theorem is both a special case and a trivial extension of Theorem 9.1 in Ross (1996).
For anyS(.) and T-dimensional vectorsp, p’: 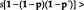
 , where
, where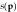 is the probability that a series of T components with individual probability of successpsucceeds.
is the probability that a series of T components with individual probability of successpsucceeds.
Theorem 1 follows from the above by setting 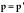 and by iterating Theorem 9.1 N times (and not just twice as in Theorem 9.1).
and by iterating Theorem 9.1 N times (and not just twice as in Theorem 9.1).
A2 The bridge structure as a general model of information flows
Consider the “bridge” structure depicted earlier in Figure 1and assume that the probabilities of individual task success for firms A and B are respectively  and
and 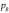 , as in Figure 5. Moreover, for reasons that will become apparent shortly, introduce a “connecting” unit that succeeds with probability
, as in Figure 5. Moreover, for reasons that will become apparent shortly, introduce a “connecting” unit that succeeds with probability  .
.
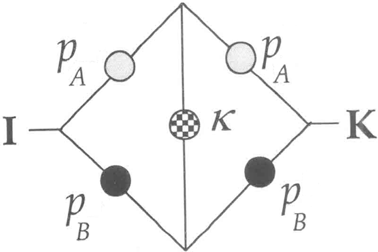
The bridge structure and information flows.
It is straightforward to compute the overall probability of success of the “bridge” structure, 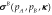 , as:
, as:
![[19]](/document/doi/10.1515/bejte-2012-0004/asset/graphic/bejte-2012-0004_eq19.png)
Notice that under symmetry (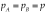 ) eq. [19] simplifies to:
) eq. [19] simplifies to:
![[20]](/document/doi/10.1515/bejte-2012-0004/asset/graphic/bejte-2012-0004_eq20.png)
Equation [20] shows that the “bridge” structure encompasses both types of RJV organizations (inefficient, with N teams; efficient, with T teams) as special cases:
![[21]](/document/doi/10.1515/bejte-2012-0004/asset/graphic/bejte-2012-0004_eq21.png)
![[22]](/document/doi/10.1515/bejte-2012-0004/asset/graphic/bejte-2012-0004_eq22.png)
>
This observation is interesting for three reasons: (i) the organization-efficient RJV, by assigning a team to each task, effectively introduces additional information flows across tasks, which explains why it dominates the alternative arrangement (assigning each team to the full series of tasks); (ii) even when inter-task information flows are imperfect (i.e.,  ), organization-efficient RJVs are more likely to achieve overall success than independent firms; (iii) the superiority of efficient RJVs may hold also in the case (not examined in this paper) when the probabilities of individual success are not statistically independent.
), organization-efficient RJVs are more likely to achieve overall success than independent firms; (iii) the superiority of efficient RJVs may hold also in the case (not examined in this paper) when the probabilities of individual success are not statistically independent.
Using eq. [19] we can get an insight into the quantitative superiority of RJVs compared to independent research. Recalling that in a tournament model the profits from independent research are the same as from membership of an inefficient RJV, we can compute the rate of return from forming an efficient RJV as:
![[23]](/document/doi/10.1515/bejte-2012-0004/asset/graphic/bejte-2012-0004_eq23.png)
Figure 6 shows that, for the relevant case when success in individual tasks is “difficult” (i.e.,  ), this rate of return ranges from nearly 100% to 10%:
), this rate of return ranges from nearly 100% to 10%:

Rate of return for efficient RJVs.
The formulation of the alternative organizational structures open to an RJV in terms of the “bridge structure” provides a simple way of comparing the results in this paper with the vast literature on RJVs spawned by d’Aspremont and Jacquemin (1988) and Kamien et al. (1992). A distinctive feature of this literature is to regard the formation of an RJV as a means of endogenizing any spillover effect. For single-task research, this effectively amounts to assuming that any RJV member agrees to share its successful innovation with all other members. Under multi-task research there is a richer network of potential information flows, some of which can be formalized by means of our bridge structure. The canonical RJV model, where members share information about completed projects is captured by setting 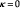 in eq. [19], whereas an organizationally-efficient RJV would share information about completed tasks, i.e., would set
in eq. [19], whereas an organizationally-efficient RJV would share information about completed tasks, i.e., would set 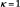 . Notice also that the bridge structure can be used to model the case where different research tasks undertaken by different RJV members may not be fully compatible, i.e., success in task i by member A when combined with success in task j by member B leads to the whole project succeeding with probability
. Notice also that the bridge structure can be used to model the case where different research tasks undertaken by different RJV members may not be fully compatible, i.e., success in task i by member A when combined with success in task j by member B leads to the whole project succeeding with probability 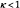 .
.
Acknowledgments
I wish to thank the Editor in charge and two referees for their extensive comments that led to a complete re-drafting of the paper.
- 1
Recent surveys include Caloghirou et al. (2003), Sena (2004), Silipo (2003).
- 2
Obviously, neither of the above characteristics of the research process would matter if the outcomes of projects were non-stochastic and thus in what follows it will be assumed that success in research is uncertain.
- 3
The seminal paper in this area is “Probabilistic logics” (1956) where John von Neumann (who else?) showed how to combine unreliable devices (the so-called “Sheffer stroke”) so that they can function as a system of higher reliability.
- 4
To mention an example familiar to the reader, suppose that the aim is to write a publishable paper in mathematical economics where the first “obstacle” may be proving an existence theorem (which can be established either by topological means (x1) or constructively)** (x4) and the second obstacle may be proving a uniqueness theorem (which, again, can be done topologically)** (x2) or constructively (x5), with (x3) being a way of translating a topological story into a constructive argument.
- 5
As modelled, for example, in Weitzman (1979) and Weitzman and Roberts (1981).
- 6
My use if the term modular is related to, but different from, two standard uses: in mathematical economics a function
 , which, for simplicity we can assume smooth, is modular if
, which, for simplicity we can assume smooth, is modular if 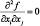 for
for 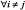 (see the classic treatment in Topkis (1998)). In management science, and especially in product design, the notion of modularity is similar to Simon’s concept of decomposable systems, meaning the extent to which large complex problems can be broken down into smaller sub-problems. The connection between the two concepts is that if the interactions between variables/subsets are weak or non-existent, then the search for optimal solutions can be achieved in a piece-meal fashion (see Brusoni et al. (2007) for an example and algorithm).
(see the classic treatment in Topkis (1998)). In management science, and especially in product design, the notion of modularity is similar to Simon’s concept of decomposable systems, meaning the extent to which large complex problems can be broken down into smaller sub-problems. The connection between the two concepts is that if the interactions between variables/subsets are weak or non-existent, then the search for optimal solutions can be achieved in a piece-meal fashion (see Brusoni et al. (2007) for an example and algorithm). - 7
Here superscripts refer to tasks, not to firms.
- 8
By making this symmetry assumption we are ignoring some interesting applications of the “systems reliability” approach to research organization, in so far as the approach sketched here yields some sharp implications on the optimal assignment of R&D resources when tasks are not equally difficult to accomplish.
- 9
Notice that this assumption biases the analysis against RJVs in so far as an RJV would never try the same method more than once and therefore could achieve a resource saving with no decrease in the overall probability of success compared to independent firms following identical methods.
- 10
As mentioned later, the model also applies to the case where only one method succeeds (with certainty), but it is not distinguishable ex ante from the other M–1 useless methods, so that ex ante
 .
. - 11
In systems reliability terminology this is a parallel-series arrangement, whereby N series of T components each are arranged in parallel.
- 12
This is a series-parallel arrangement whereby T arrangements of N components are each arranged in series.
- 13
References
Baldwin, C. Y., and K.Clark.2000. Design Rules: The Power of Modularity. London: MIT Press.10.7551/mitpress/2366.001.0001Suche in Google Scholar
Brusoni, Stefano, Marengo Luigi, Principe Andrea, and Valente Marco.2007. “The value and costs of modularity: a problem-solving perspective.” European Management Review4:121–32.10.1057/palgrave.emr.1500079Suche in Google Scholar
Caloghirou, Yannis, Stavros Ioannides, and Vonortas Nicholas.2003. “Research Joint Ventures.” Journal of Economic Surveys17:541–70.10.1111/1467-6419.00204Suche in Google Scholar
Dasgupta, P.1986. “The Theory of Technological Competition.” In New Developments in the Analysis of Market Structure, edited byJ. E.Stiglitz and G. F.Mathewson,519–47. London: Macmillan.10.1007/978-1-349-18058-5_17Suche in Google Scholar
D’Aspremont, C., and A.Jacquemin.1988. “Cooperative and Non-cooperative R&D in a Duopoly with Spillovers.” American Economic Review78:1133–137.Suche in Google Scholar
Kamien, M., E.Muller, and I.Zang.1992. “Research Joint Ventures and R&D Cartels.” American Economic Review82:1293–306.Suche in Google Scholar
Ross, S. M.1996. Introduction to Probability Models, 6th edition. San Diego and London: Academic Press.Suche in Google Scholar
Sena, Vania.2004. “The return of the Prince of Denmark: A Survey on Recent Developments in the Economics of Innovation.” The Economic Journal114:312–32.10.1111/j.1468-0297.2004.00225.xSuche in Google Scholar
Silipo, Damiano Bruno.2003. “The Economics of Cooperation and Competition in Research and Development: A Survey.” Discussion Paper 37, Dipartimento di Economia e Statistica, Universitá della Calabria.Suche in Google Scholar
Topkis, D. M.1998. Supermodularity and Complementarity. Princeton, NJ: Princeton University Press.Suche in Google Scholar
von Neumann, John.1956. “Probabilistic Logics.” In Automata Studies, edited by C. E.Shannon and J.McCarthy, 329–78. Princeton, NJ: Princeton University Press. Reprinted in von Neumann, J.,Collected Works,vol. V, Pergamon Press,1963.Suche in Google Scholar
Weitzman, M.1979. “Optimal search for the best alternative.” Econometrica47:641–54.10.2307/1910412Suche in Google Scholar
Weitzman, M. and K.Roberts.1981. “Funding Criteria for Research, Development, and Exploration Projects.” Econometrica49:1261–288.10.2307/1912754Suche in Google Scholar
©2013 by Walter de Gruyter Berlin / Boston
Artikel in diesem Heft
- Masthead
- Masthead
- Advances
- Dependence and Uniqueness in Bayesian Games
- Monopolistic Signal Provision†
- Multi-task Research and Research Joint Ventures
- Transparent Restrictions on Beliefs and Forward-Induction Reasoning in Games with Asymmetric Information
- A Simple Bargaining Procedure for the Myerson Value
- On the Difference between Social and Private Goods
- Optimal Use of Rewards as Commitment Device When Bidding Is Costly
- Labor Market and Search through Personal Contacts
- Contributions
- Learning, Words and Actions: Experimental Evidence on Coordination-Improving Information
- Are Trust and Reciprocity Related within Individuals?
- Optimal Contracting Model in a Social Environment and Trust-Related Psychological Costs
- Contract Bargaining with a Risk-Averse Agent
- Academia or the Private Sector? Sorting of Agents into Institutions and an Outside Sector
- Topics
- Poverty Orderings with Asymmetric Attributes
- Dictatorial Mechanisms in Constrained Combinatorial Auctions
- When Should a Monopolist Improve Quality in a Network Industry?
- On Partially Honest Nash Implementation in Private Good Economies with Restricted Domains: A Sufficient Condition
- Revenue Comparison in Asymmetric Auctions with Discrete Valuations
Artikel in diesem Heft
- Masthead
- Masthead
- Advances
- Dependence and Uniqueness in Bayesian Games
- Monopolistic Signal Provision†
- Multi-task Research and Research Joint Ventures
- Transparent Restrictions on Beliefs and Forward-Induction Reasoning in Games with Asymmetric Information
- A Simple Bargaining Procedure for the Myerson Value
- On the Difference between Social and Private Goods
- Optimal Use of Rewards as Commitment Device When Bidding Is Costly
- Labor Market and Search through Personal Contacts
- Contributions
- Learning, Words and Actions: Experimental Evidence on Coordination-Improving Information
- Are Trust and Reciprocity Related within Individuals?
- Optimal Contracting Model in a Social Environment and Trust-Related Psychological Costs
- Contract Bargaining with a Risk-Averse Agent
- Academia or the Private Sector? Sorting of Agents into Institutions and an Outside Sector
- Topics
- Poverty Orderings with Asymmetric Attributes
- Dictatorial Mechanisms in Constrained Combinatorial Auctions
- When Should a Monopolist Improve Quality in a Network Industry?
- On Partially Honest Nash Implementation in Private Good Economies with Restricted Domains: A Sufficient Condition
- Revenue Comparison in Asymmetric Auctions with Discrete Valuations


