Abstract
Based on the exit temperature in the aluminium extrusion process, the quality of the aluminium bars is obtained in the industries. Control of temperature plays a significant role to obtain the quality of the aluminium bars or rods. Problems are still encountered in the design of proper temperature control schemes in the industries. A new control scheme is presented here, to address the temperature control in the aluminium extrusion process. Spider-based fractional-order PID controller scheme is simulated for the aluminium extrusion plant using MATLAB and its toolbox. It gives the improved result for reducing the time delay, rise time and settling time in the process. Integral square error performance criteria are considered an objective function. The minimization of objective function gives good results. Comparisons of the presented control scheme with the conventional control methods are presented.
1 Introduction
Modern scenario aluminium products are used for various industries like Building & Construction, Solar panel, Modular applications, Transmission & Distribution, Electrical & Electronics, Textiles, Automobiles, Medical equipment’s, Defence, Robotic manufacturing, Air conditioning and other applications also [1]. In the aluminium industry, the output process is continuously obtained. So, this continuous control is extremely important. In the extrusion process, the heating and cooling process of temperature control is monitored in all stages. The industrial thermal process is a continuous process and repeatedly turns into a productivity blockage and quality limitation. Also, the complications are being increased on account of various dimensions, different loading patterns, several grades, and lack of contactless thermal sensors steers to the experimental design of various temperature–time cycles in an industrial metal heat treatment operation [2,3], control of the batch process, robotic control and extruder control etc.
In Robot tracking, control input is obtained by linear repetitive learning control. During the process of aluminium, optimal repetitive learning control for temperature control extruder is considered in ref. [4]. The extrusion process of die trial and aluminium profiles is simulated in ref. [5]. Considering the current automation in industries, optimization of operations must be taken as major importance. The mathematical models yield a fair alternative to optimize these processes due to cost, high risk, and time involved in the industrial plant trials based on empirical methods. Latterly, a many number of industrial heat treating operations, including carburizing [6], reheating [7,8] and annealing [9,10,11], have been efficiently optimized by utilizing process models.
Conventional closed loop controller is used to maintain the desired output. The proportional–integral–derivative (PID) controller is prolonged in use for controlling the temperature in industrial processes. In general, it is a complex duty to tune the controller parameters and to get optimum performance for a system. Zieglor-Nicholos tuning methodology is used to tune PID controller parameters for temperature control of plants [12]. After conventional controllers, many intelligent controllers are developed and used in a practical scenario. One of among is ant colony optimization, which is built on Fuzzy predictive control for many nonlinear processes [13]. Temperature control for heat-treating furnaces was achieved by Fuzzy logic PID controller with accurate temperature overshoot and minimized steady-state error [14,15]. Fuzzy PID is utilized to control the furnace temperature. The temperature control system, which works on an expert fuzzy PID algorithm, has the merits of quick response, reduced overshoot and elevated robustness than classical PID.
Fractional order (FO) controller is an alternate solution of control technology, because its real-world FOs considered for the analysis. FO controllers rely on the basis of FO calculus. It is a computative method based on integrals and derivatives of arbitrary and complex orders. Hence, it provides a new feature to identify and sketch the fundamental nature and behaviour of complex systems in an enhanced way [16]. In real-time systems, the order of the integration and differentiation is fractional. Because of the unavailability of the solution methods for FO differential equation, the Integer order derivative of the ordinary differential equation is used in almost every case for the analysis of the system. The applications of FO controller are widely used in many fields such as power system, control system, signal processing and motion control theory [17,18].
An artificial neural network (ANN) is used in an aluminium alloy manufacturing process. The three-layer neural networks with the Levenberg Marquardt algorithm are trained with the experimental data from the industrial temperature control process. The temperature profile, which is predicted by the neural network, closely matches the experimental temperature profile values [19]. ANFIS (Adaptive Neuro Fuzzy Inference System) controller tuned with PSO (Particle Swarm Optimization) algorithm was created to provide continuous temperature control during the industrial process called extrusion process. To show and confirm the robustness of the created controller, it was compared and contrasted with other conventional as well as intelligent controllers such as the ANFIS, Fuzzy-PI, Fuzzy and Proportional Integral (PI), controller [20]. ZA27 (aluminium zinc material) squash casting process parameter optimization method utilizing ANN incorporated with the PSO is presented in ref. [21].
PSO algorithm for spotting out of thermal contact resistance is presented in ref. [22]. Because of the efficient performance for solving optimization problems Swarm intelligence (SI) optimization algorithms have attracted researchers. These algorithms are described by a combination of deterministic rules and randomness. It imitates animal groups in nature’s warm [23]. The Social Spider Optimization (SSO) algorithm is a population-dependent algorithm which produces the supportive performance of the social spider. SSO considers two search agents, that is spider’s namely female and male candidates. Each candidate is contacted with a various non-identical set of evolutionary operators’ accordance with its gender that imitates dissimilar supportive performance found in the social colony [24].
The traditional PID controllers represent the most applicable types of industrial controllers so far. Some reasons for the widespread use of these controllers in industrial applications include the simplicity of structure, existing simple tuning procedures, and robustness against parameter uncertainties. On the other hand, in recent years, the design of parameter fractional-order PID (FOPID) controllers has drawn much interest amongst researchers, because they are more flexible than traditional PID controllers and can improve the robustness of the closed-loop system against parameter uncertainties [12]. This is the reason why the studies about the tuning of these controllers for controlling the industrial and experimental processes have been on the rise. Up to now, tuning of FOPID controllers based on certain performance criteria in the time domain such as Integral Square Error (ISE), Integral Absolute Error (IAE), Integral Time Absolute Error (ITAE), and Integral Square Time Error (ISTE) or the frequency domain such as gain crossover frequency and phase margin specifications remain the most popular subjects in the area of fractional-order control systems.
A set of tuning rules is used for both integer-order and FOPID controllers in order to optimally control integral and unstable processes based on the ISE criterion. Their results pointed to the higher performance of the systems controlled by FOPID controller than the same ones controlled by standard PID. Therefore, finding an analytical method to solve the optimization problems resulting from satisfying the above-mentioned objectives may be laborious (particularly in the cases where we encounter high-dimensional and multi-objective optimization problems). Accordingly, various heuristic algorithms can be employed to solve these complex optimization problems.
Tuning the parameters of FOPID controllers, the enhanced PSO algorithm was applied in conjunction with minimizing a cost function defined as a weighted combination of the ITAE and the control effort. Also, there are different tuning methods for FOPID controllers obtained by mathematical optimizations.
FOPID-like fuzzy controller addresses the improvements in FO system performance. Although the classical PID fuzzy controller can provide adequate results for both transient and steady-state responses in both linear and nonlinear systems, the FOPID fuzzy controller has been proven to provide better results [25]. The properly set values of the controller played a vital role in the system’s performance. The optimal parameters of the controller relative to its gains and the FOs were obtained using SSO.
From the literature, it is found that there is a need to provide a fractional controller. A set of algebraic rules for tuning the fractional-order based integer-order controller can be progressed by considering the ISE performance index. Also, the quality of the output product from the extruder depends on the thermal process involved in the aluminium extrusion process is updated according to the convergence rate of the algorithm. In other words, fuzzy linguistic variables and membership functions are employed to conduct the swarm towards the global optimum point. Therefore, temperature control is very important in all stages of the extrusion process. To maintain the output temperature as constant and error must be zero, here a spider-based PID, Fuzzy PID and Fractional order PID (FOPID) controller is proposed. To validate the proposed method, the results are compared and contrasted with those of the PSO-based PID, FOPID and Fuzzy PID controller. The results show that the proposed controller algorithm gives an improved result.
2 Aluminium extrusion process
2.1 Extruder temperature control
Figure 1 shows the manufacturing process for aluminium products by extrusion in plants. At 500°C in an electric furnace, billet (B) of the metal is heated and loaded or stacked into the receptacle (R) in the extruder. A hydraulic ram (Ra) squashes the metal via an orifice with the appropriate geometry in a die (D) and forms the desired product as bars (Ba). Consequently, the next billet is loaded or stacked into the extruder and the process is repeated sequentially. When the die is maintained at a constant temperature value of 540°C, then the quality of the output product is good. This exit temperature Y(t) is influenced by changing the temperature to which the billets are preheated. This exit temperature Y(t) influenced by changing the velocity with which the ram squashes the metal out of the die.

Extruder model.
The extruder output temperature must be sustained at a constant temperature in the range of 500–525°C. This can be achieved by measuring the open loop output temperature value. The temperature process is slow and also has a long dead time. Based on the open loop response, we have to consider the closed feedback control loop to maintain the constant temperature output. Conventionally in industries, PID controller has been used. But it does not give optimized output. Therefore, to enhance the performance of the process, various controllers like artificial intelligent controller, FO controller, Model predictive controller, Adaptive controller, robust controller have been used tremendously. Even though various controllers are used in plants, the controller parameters also contribute to the fine output tuning of the process. For that fine-tuning, many optimization algorithms are used such as genetic algorithm (GA), ant colony algorithm, PSO, and Bee algorithm can be used.
2.2 Mathematical model of temperature control in aluminium extrusion process
Any complex system can be illustrated by mathematical modelling for easy understanding and get simulated desired output before we go for the real-time implementation. Here, also aluminium extrusion process can be converted into mathematical modelling for the analysis of temperature controllers with various controllers and various algorithms.
The output temperature of the extruder Y
o(t) depends on the initial temperature in the deformation zone
The initial temperature
Similarly, the temperature change
K
1, C
1, C
2, C
3, and C
4 are constants, and they are based on aluminium alloy, geometry of the profile, material properties and die. The nexus between input u which is congruous to the velocity of ram
Figure 2 shows the Simulink diagram for the temperature control process. Maintaining the output temperature as constant means, the change in temperature, i.e., the difference between reference temperature and output temperature value is minimized to zero. Practically this can be done by integrating all the errors, and this error output is given to the controller input. This is generally called integral errors.

Simulation model.
2.3 Objective function
For getting the optimum value of controller output, this integral error must be minimized to zero. In this work, minimizing ISE is taken as an objective function. The main role of this system is to create a parametric solution of the ISE for linear continuous feedback control systems, while the closed-loop system is stable and the difference between reference and output, or error, is strictly proper. It is well adapted when a parametric solution of the ISE for optimal control problems is needed.
where Y
r(t) is the reference temperature and
In this work, ISE can be minimized by spider-based PID, Fuzzy PID and FOPID controller algorithms. All the results are compared by the PSO algorithm.
3 Methodology
3.1 Controller design
3.1.1 PID Controller
Basic structure of the PID controller is given by
where
In the PID controller, the summation of the proportional error signal, the integral error signal and its derivative error signal gives the system output. Here, the error signal is the subtraction between the reference input temperature and the actual plant output temperature. Adding a controller leads to an increment in order and type of the system, which results in lowering steady-state error. Thus, the PID controller improves the stability of the system. For a linear time-invariant temperature plant, the PID controller equation is written as,
where e(t) = r(t) – y(t) and K = 0, 1, 2, …, n.
If k tends to ∞, the error is minimized to zero.
Controller parameters and minimization of the objective function are tuned by PSO and Spider algorithms.
3.1.2 Fuzzy PID Controller
The conventional PI and Derivative controller can be extended into a Fuzzy PID controller by making adjustments in the PID parameters by fuzzy control. The above equation can be rewritten into a fuzzy PID controller, and the equations are as follows:
Where
A fuzzy set of error e, and rate of change of error de is utilized to define the PID parameters. The fuzzy membership function can be formed as negative big (NB), negative small (NS), zero (Z), positive small (PS), and positive big (PB). Based on nonlinear Gaussian distribution [15], the membership function is defined. Then, using these membership functions, suitable fuzzy rules of k p, k i, k d are formed according to the experiences. The fuzzy rule of k p is shown in Table 1.
Fuzzy rules for K P
| Error (e) | NB | NS | Z | PS | PB | |
|---|---|---|---|---|---|---|
| Rate of change of error (d e ) | NB | PB | PS | PS | PS | Z |
| NS | PS | PS | PS | Z | NS | |
| Z | PS | PS | Z | NS | NS | |
| PS | PS | Z | NS | NS | NB | |
| PB | Z | NS | NB | NB | NB | |
According to fuzzy tables, 25 × 3 fuzzy rules are formed with the following statements.
If error (e) = A i and rate of change of error (de) = B j then k p (k i, k d) = C ij .
where A i is the fuzzy sets of error; B j is the rate of change of error; and C ij is the PID parameters K p, K i, K d.
With these Fuzzy rules, the fuzzy PID parameters K p, K i, K D are obtained. For tuning, gain values of PID controller and minimization of error PSO and proposed Spider algorithms are used.
3.1.3 FO controller
In order to implement the fractional controllers in practice, the integer-order approximation of the fractional derivatives and integrators is used because the exact implementation of fractional-order operators in online applications is not possible due to their infinite memory characteristics [26]. This approximation may cause a difference between the behaviour of the implemented system and the expected behaviour of the closed-loop system. Therefore, the use of an appropriate approximation is necessary for the proper implementation of fractional-order operators. The main purpose of this study is to concentrate on providing a set of tuning rules for the implementable form of FOPID controller by using the algebraic formulation of ISE cost functions in terms of free parameters of the fractional-based controller. In doing so, first, the integer-order realization of the FOPID controller, which is referred to as an implementable form, is obtained.
Li et al. have expressed that the fractional calculus is globalization of integration and differentiation for a number that is not a whole number, a negative whole number, or zero-order fundamental operators [18].
where
Based on Equations (2) and (3), the FO system has been defined as
FOPID structure for aluminium extrusion process is given by
where
e(t) = ISE =
Instead of three controller parameters in the PID controller k p, k i, k d, five controller parameters are tuned in FOPID controller k p, k i, k d, λ, μ where λ and μ are the integral and derivative orders. This value lies between 0 and 1. If the orders are equal to 1, then FOPID works on the conventional PID. Similarly, PSO and spider algorithms are used to tune these parameters and finally, and ISE gets minimized.
3.1.4 PSO Algorithm
PSO is an uncomplicated optimization algorithm, and it has been effectively applied to a number of applications in several fields of engineering and science such as operations research, mesh processing, data mining. A new method for optimal control of parameters in PSO based on fuzzy rules is presented. In other words, fuzzy linguistic variables and membership functions are employed to conduct the swarm towards the global optimum point. Several computational simulations are carried out to demonstrate the high performance and stability of this method. Simulation results reveal superior optimality and stability and lower computational cost of the new algorithm compared to the traditional meta-heuristics such as standard PSO, which justifies its advantages for PSOs. It is mainly applicable for continuous search spaces. In other words, to apply this algorithm in some state spaces, modifications to standard formulation are required. Thus, in the proposed system, the optimized controller gain and order parameters can be obtained from the search space.
The position and velocity equations are given by
where
PSO parameters
| Parameter | Number of iterations | Number of runs | Swarm size | Acceleration constants (c 1 = c 2) |
|---|---|---|---|---|
| Value | 100 | 20 | 20 | 1 |
Conventional PID, Fuzzy PID, and FOPID controller parameters gain values and order values are tuned by the PSO algorithm. Therefore, the ISE can be minimized with the tuned values.
3.1.5 Spider-based controller algorithm
Spider algorithm is different from other algorithms like PSO, GA, and EA. Unlike all SI algorithms, the spider is self-organized, because solutions are processed based on their gender. Since the female and male spiders accomplish wide examination and extensive exploitation, the algorithm avoids premature convergence and incorrect exploration. All particles pursue their own best position and a common global best position in PSO. On the other hand, social spiders in algorithms chase positions through the knowledge of others’ current positions and those positions which it is not sure to be already visited by the population before. This feature improves its ability to solve optimization problems with many local optimums but makes its convergence slower. While all particles in PSO are conscious of the system information without any loss, the spiders communicating through vibrations form an all-purpose information scheme with information loss.
In the Spider algorithm, the spider is symbolized by widespread search space from a spider web. Among the total population, all candidate solution is represented by a spider. Based on the fitness solution, all individual spiders collect a weight from the fitness function. In a colony, two-non identical sets of evolutionary operators imitate the different mutual performances of the spider. Nonlinear global optimization problem having box constraint was assumed for spider algorithm. The optimization problem was represented by
Minimize
where f: R d → R is a nonlinear function
which is a minimized feasible space bounded by the lower (

Flowchart for spider algorithm.
The optimization problem is solved from S of N candidates. From X search space, spider position represents the solution. In this method, the population S is segregated into two search representatives, namely, Male (M) and Female (F). Let us assume
Each spider's weight we i is calculated based on a fitness function, and that weight is planned as follows:
where
In SSO optimization, information swapping is the basic mechanism. From vibrations produced on the spider web, it is simulated. The vibration equation is modelled by
where we j is the weight of the jth spider and d is the distance between two spiders.
Each and every spider “i” can be distinguished by three types of vibration,
A population of N spiders is steered at initial stage k = 0 to
where k is the iteration number;
Male spiders are categorized into two categories namely D (dominant) and ND (non-dominant) spiders. Generally, D is the set which is consolidated with the male spider fitness value set. Also, ND is a group which is constructed by the rest of the male spiders. Based on the following equation, the male spiders
where
Figure 4 illustrates the complete evolutionary process in the form of a flowchart. In the suggested algorithm, dominant male

Weight updating process for spider algorithm.
In the spider-based controller, the algorithm gets input from the sensors of the aluminium extrusion plant and feedback output from the aluminium extrusion plant. Then, the error output signal is found, which is a switching sequence akin to a web-building behaviour of a spider. In the spider’s web-building process, in the beginning, it forms a silky thread from its mouth. Akin to that, the controller receives input signals such as input temperature Y i(t) from the thermal sensor output. Then, after forming silk, the spider thrust it in the air to cling to some fixed place. The place where it clings to is based upon the parameters such as the distance from the spider and the strength of the silk [28].
In the beginning, the spider has the temperature output (thread), it peruses the value of the temperature at each and every instant (explore the place to fix silk), and after that, it moves to the zero crossing, which is the most suitable place where it can fix the silk. And again, it moves to another location which forms the duty ratio and fixes the silk. It moves back to the past location by eating the old thread. This operation gives the temperature ON and OFF cyclic process. Using equations (20) and (21), the minimization of the objective function and also the controller parameters are obtained. The flowchart for the spider algorithm is shown in Figure 5.

Temperature control flowchart using spider algorithm.
4 Results and discussions
From Jindal Aluminium Ltd., the 6063 Aluminium alloy extruded real-time data have been obtained in the Aluminium Extrusion plant. The supporting document is attached at the end. With these data and MATLAB system identification toolbox, the following input parameters such as Billet Temperature, Die Temperature and Ram Speed linearized second order system are to be obtained. The transfer functions are as follows:
With the assistance of MATLAB Simulink, the output exit profile temperature control of the aluminium extrusion process is analysed. Figure 1 is taken as the structure and parameters of the model. The analysis is carried out with the spider-based PID control algorithm. The performance of the proposed spider FOPID controller yields a good result compared to the conventional PID and Fuzzy PID controllers. For reference, a sample simulation model with a conventional PID controller is shown in Figure 6.

PID Simulink model.
Figure 7 shows the control input given to the plant. With this control action, the performances of the spider-based FOPID control output and PSO-based FOPID control outputs are shown in Figures 8 and 9.

Control action given to the controller.
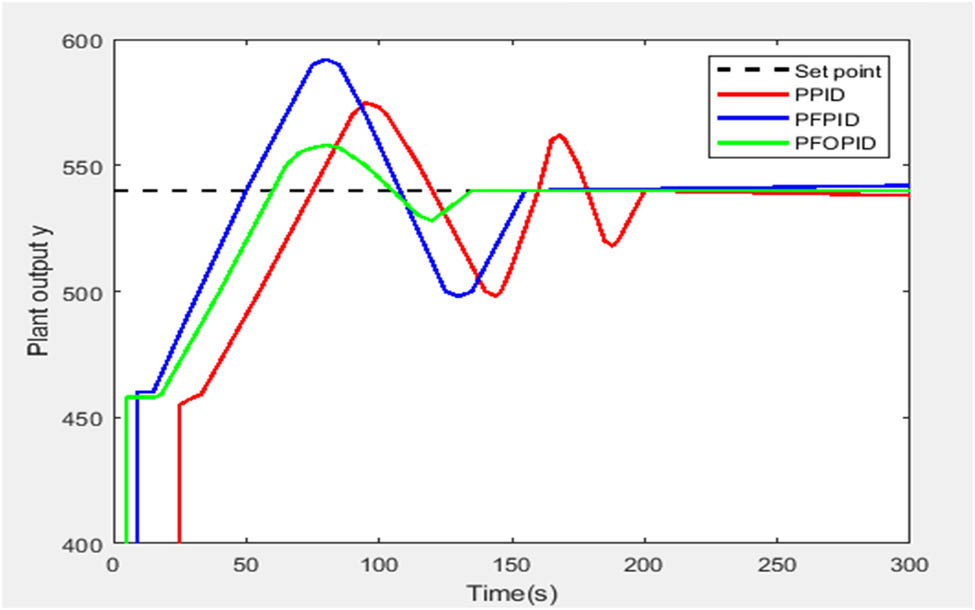
PSO-based controller output.

Proposed spider-based controller output.
4.1 Controller algorithms
Figure 8 gives the comparative results of PSO-dependent conventional PID, Fuzzy PID and proposed FOPID controller performance results. The temperature process dead time is reduced by the proposed controller. The oscillations were reduced compared to the PID controller. Settling time can be more or less equal to the Fuzzy PID controller. Table 3 shows the complete analysis of the temperature control in the aluminium extrusion process. Figure 9 gives the output of the proposed spider-based controller.
Instead of three controller parameters in the PID controller, FOPID utilizes five parameters to get the optimized output. For that fine-tuning, improved results are obtained. In MATLAB FOMCON, toolbox is used to get the FOPID outputs. The proposed Spider-based controller output is shown in Figure 9. The results show that spider-based controller minimizes the dead time of the process and reaches the settling time earlier. The following Table gives the completer analysis of the process.
Tables 3–6 give the complete analysis of how the extruder temperature controller works for the various controller algorithms. From the Figures and Tables, the proposed spider-based FOPID controller gives reduced dead time and less settling time.
PSO-based controller parameters
| Controller/Parameters | K p | K I | K D | λ | μ |
|---|---|---|---|---|---|
| PPID | 8.846 | 61.313 | 0.9 | — | — |
| PFPID | 7.802 | 30.12 | 0.7 | — | — |
| PFOPID | 6.746 | 0.802 | 0.3 | 0.769 | 0.899 |
Performance criteria
| Controller/Parameters | Rise time (s) | Peak time (s) | Settling time (s) | ISE |
|---|---|---|---|---|
| PPID | 25 | 100 | 200 | 0.3 |
| PFPID | 10 | 80 | 150 | 0.1 |
| PFOPID | 7 | 70 | 130 | 0.001 |
SPIDER-based controller parameters
| Controller/Parameters | K P | K I | K D | λ | μ |
|---|---|---|---|---|---|
| SPID | 5.473 | 20.56 | 0.5 | — | — |
| SFPID | 3.432 | 5.45 | 0.2 | — | — |
| SFOPID | 1.746 | 2.21 | 0 | 0.9 | 0.897 |
Performance criteria
| Controller/Parameters | Rise time (s) | Peak time (s) | Settling time (s) | ISE |
|---|---|---|---|---|
| SPID | 20 | 80 | 180 | 0.123 |
| SFPID | 5 | 70 | 120 | 0.00235 |
| SFOPID | 1 | 50 | 80 | 0.00035 |
Convergence plots of PSO-based controllers and proposed Spider-based controllers are shown in Figures 10 and 11. The proposed controller has a faster convergence compared to the other controllers.

Convergence plot of PSO-based controllers.

Convergence plot of Spider-based controllers.
Also, for our easy visualization and understanding, the results are summarized in Figure 12 and Table 6.

Comparison controller output.
Figure 12 shows the outputs of conventional PID controller, Fuzzy PID Controller, FOPID controller, PSO-based PID controller (PPID), PSO-based Fuzzy PID controller (PFPID), PSO-based FOPID controller (PFOPID), Spider-based PID controller (SPID), Spider-based Fuzzy PID controller (SFPID), and Spider-based FOPID controller (SFOPID). The result shows that the proposed spider-based controller gives an improved result (Table 7).
Overall comparison table
| Controller/Parameters | K P | K I | K D | Rise time (s) | Peak time (s) | Settling time (s) | ISE |
|---|---|---|---|---|---|---|---|
| PID | 15.92 | 55.76 | 1.2 | 50 | 150 | 280 | 0.5 |
| FPID | 10.54 | 39.54 | 1 | 45 | 135 | 250 | 0.3 |
| FOPID | 9.45 | 15.65 | 0.8 | 35 | 100 | 220 | 0.1 |
| PPID | 8.846 | 50.31 | 0.9 | 25 | 100 | 200 | 0.3 |
| PFPID | 7.802 | 30.12 | 0.7 | 10 | 80 | 150 | 0.1 |
| PFOPID | 6.746 | 5.802 | 0.3 | 7 | 70 | 130 | 0.001 |
| SPID | 5.473 | 20.56 | 0.5 | 20 | 80 | 180 | 0.123 |
| SFPID | 3.432 | 5.45 | 0.2 | 5 | 70 | 120 | 0.00235 |
| SFOPID | 1.746 | 2.21 | 0 | 1 | 50 | 80 | 0.00035 |
The table gives the summarized output performance criteria for the exit profile temperature in aluminium extruder.
5 Conclusion
In this work, a new control scheme SPIDER-based FOPID controller is addressed. The performance of this controller is evaluated by one of the performance criteria ISE. The results are validated in two ways. First PSO-dependent conventional PID, PSO-based FUZZY PID and PSO-based FOPID control outputs are taken. The simulated extruder plant works well for the above controller.
On the basis of these forms, algebraic rules are proposed for tuning the free parameters of FOPID controllers. Based on these rules, it is guaranteed that the resultant performance is superior to that of any conventional PID controller.
Second, the proposed SPIDER control algorithm is implemented similarly, and the outputs are figured out and tabulated. Its remarkable performance is associated with two different reasons: (i) their operators permit a superior particle distribution in the search space, growing the algorithm’s ability to evaluate the global optima; and (ii) the partition of the population into several individual types offers the usage of different rates between exploitation and exploration, throughout the evolution process.
The results show the Spider-based FOPID controller gives an improved result compared to the conventional controller by suppressing the dead time, cyclic disturbances and faster settling time. Thus, the proposed controller maintains the extruder output temperature at 525°C to get the quality aluminium product output.
Various performance criteria, namely, IAE, ITAE, and ISTE and in the frequency domain namely gain crossover frequency and phase margin specifications are still in the area of fractional-order control systems. Thus, in our future work, we can also consider these types of performances to further enhance our implementation sections. Real-time implementation will also be considered practically.
Acknowledgments
I thank Jindal Aluminium Ltd. for my practical study carried out on their aluminium extrusion plant and provided data for research purposes on the topic “Design and Development of Optimal Controller for Aluminium Extrusion Process.”
-
Funding information: The author state no funding involved.
-
Author contributions: Ramasubramanian Murugesan conducting the practical study and Experiments, process design and modelling, writing the original draft; Thirumarimurugan Marimuthu: methodology and reviewing the document.
-
Conflict of interest: Author states no conflict of interest.
-
Data availability statement: All authors can confirm that all data used in this article can be published in High Temperature Materials and Processes.
References
[1] Jindal Manual. https:\\jindalaluminium.com.Search in Google Scholar
[2] Jaluria, Y. Thermal processing of materials: From basic research to engineering. Journal of Heat and Mass Transfer, Vol. 125, 2003, pp. 957–979.10.1115/HT2003-47600Search in Google Scholar
[3] Sahay, S. S. Opportunities and challenges for process modelling in surface and heat treatment operations. Surface Engineering, Vol. 20, 2004, pp. 401–403.10.1179/174329404X29087Search in Google Scholar
[4] Arimoto, S., S. Kawamura, and F. Miyazaka. Bettering operation of dynamic systems by learning. Proc. 23rd IEEE CDC, Las Vegas, 1984, pp. 1064–1069.Search in Google Scholar
[5] Zhao, H. E., H. N. Wang, M. J. Wang, and G. Y. Li. Simulation of extrusion process of complicated aluminium profile and die trial. Trans Nonferrous Met Soc China, Vol. 22, No. 7, 2012, pp. 1732–1737.10.1016/S1003-6326(11)61380-0Search in Google Scholar
[6] Sahay, S. S. and K. Mitra. Cost model-based optimization of carburizing operation. Surface Eng, Vol. 20, 2004, pp. 379–384.10.1179/026708404X1143Search in Google Scholar
[7] Malhotra, C. P., N. R. Pedanekar, and S. S. Sahay. Cost model for the steel reheating operation. Industrial Heating, Vol. 69, March 2002, pp. 67–71.Search in Google Scholar
[8] Leden, B. A control system for fuel optimization of reheating furnaces. Scandinavian Journal of Metallurgy, Vol. 15, 1986, pp. 16–24.Search in Google Scholar
[9] Sahay, S. S., A. M. Kumar, and A. Chatterjee. Development of integrated model for batch annealing of cold rolled steels. Ironmaking Steelmaking, Vol. 31, 2004, pp. 144–152.10.1179/030192304225010990Search in Google Scholar
[10] Sahay, S. S., K. Krishnan, M. Kulthe, A. Chodha, A. Bhattacharya, and A. K. Das. Model-based optimization of a highly automated industrial batch annealing operation. Ironmaking Steelmaking, Vol. 33, 2006, pp. 306–314.10.1179/174328106X94799Search in Google Scholar
[11] Sahay, S. S. and K. Krishnan. Model-based optimisation of a continuous annealing operation for a bundle of packed rods. Ironmaking Steelmaking, Vol. 34, 2007, pp. 89–94.10.1179/174328106X118170Search in Google Scholar
[12] Palaniyappan, T. K., V. Yadav, V. K. Tayal, and P. Choudekar. PID control design for a temperature control system. In 2018 International Conference on Power Energy, Environment and Intelligent Control (PEEIC), IEEE, Greater Noida, India, 2018, pp. 632–637.10.1109/PEEIC.2018.8665469Search in Google Scholar
[13] Bououden, S., M. Chadli, and H. R. Karimi. An ant colony optimization-based fuzzy predictive control approach for nonlinear processes. Information Sciences, Vol. 299, 2015, pp. 143–158.10.1016/j.ins.2014.11.050Search in Google Scholar
[14] Mugisha, J. C., B. Munyazikwiye, and H. R. Karimi. Design of temperature control system using conventional PID and Intelligent Fuzzy Logic controller. International Conference on Fuzzy Theory and Its Applications (iFUZZY), IEEE, Yilan, Taiwan, 2015.10.1109/iFUZZY.2015.7391893Search in Google Scholar
[15] Dequan, S. H., G. A. Guili, G. A. Zhiwei, and X. Peng. Application of expert fuzzy PID method for temperature control of heating furnace. Procedia Engineering, Vol. 29, 2012, pp. 257–261.10.1016/j.proeng.2011.12.703Search in Google Scholar
[16] Luo, Y., Y. Quan, C. Yang, and Y. Guo. Tuning fractional order proportional integral controllers for fractional order systems. Journal of Process Control, Vol. 20, 2010, pp. 823–831.10.1016/j.jprocont.2010.04.011Search in Google Scholar
[17] Li, H., Y. Luo, and Y. Chen. A fractional order proportional and derivative (FOPD) motion controller: Tuning rule and experiments. IEEE Transactions on Control Systems Technology, Vol. 18, No. 2, 2010, pp. 516–520.10.1109/TCST.2009.2019120Search in Google Scholar
[18] Li, Z., L. Liu, S. Dehghan, Y. Chen, and D. Xue. A review and evaluation of numerical tools for fractional calculus and fractional order controls. International Journal of Control, Vol. 90, No. 6, 2017, pp. 1165–1181.10.1080/00207179.2015.1124290Search in Google Scholar
[19] Lucignano, C., R. Montanari, V. Tagliaferri, and N. Ucciardello. Artificial neural networks to optimize the extrusion of an aluminium alloy. Journal of Intell Manufacturing, Vol. 21, 2010, pp. 569–574. 10.1007/s10845-009-0239-0.Search in Google Scholar
[20] Agyare, O. R., E. Normanyo, and O. Lydia. Temperature control of heaters in cable extrusion machine using PSO-ANFIS controller. 2019 IEEE AFRICON, 2019, pp. 1–9. 10.1109/africon46755.2019.9134027.Search in Google Scholar
[21] Fu-hua, S. H. Aluminum-zinc alloy squeeze casting technological parameters optimization based on PSO and ANN. China Foundry, Vol. 4, No. 3, 2007, pp. 202–205.Search in Google Scholar
[22] Maamir, F., M. Guiatni, Y. Morsly, A. Kheddar. 22nd Mediterranean Conference on Control and Automation, 2014, pp. 499–504. 10.1109/MED.2014.6961422.Search in Google Scholar
[23] Cuevas, E. and M. Cienfuegos. A new algorithm inspired in the behavior of the social-spider for constrained optimization. Expert Systems with Applications, Vol. 41, No. 2, 2014, pp. 412–425.10.1016/j.eswa.2013.07.067Search in Google Scholar
[24] Cuevas, E., M. Cienfuegos, D. Zaldívar, and M. Pérez-Cisneros. A swarm optimization algorithm inspired in the behavior of the social-spider. Expert Systems with Applications, Vol. 40, No. 16, 2013, pp. 6374–6384.10.1016/j.eswa.2013.05.041Search in Google Scholar
[25] Nassef, A. M. and H. Rezk. Optimal tuning of FOPID-like fuzzy controller for high-performance fractional-order systems. CMC-Computers Materials & Continua, Vol. 70, No. 1, 2022, pp. 171–180.10.32604/cmc.2022.019347Search in Google Scholar
[26] Ashjaee, M. and M. S. Tavazoei. Tuning the implementable structures of fractional-order PID controllers for control of FOPDT processes. Scientia Iranica, Vol. 29, No. 2, 2022, pp. 660–675.10.24200/sci.2019.51703.2321Search in Google Scholar
[27] Salakhutdinov, R., and S. T. Roweis. Adaptive overrelaxed bound optimization methods. Proceedings of the 20th International Conference on Machine Learning (ICML-03), 2003, pp. 664–671.Search in Google Scholar
[28] Muneeswaran, V. and M. P. Rajasekaran. Automatic segmentation of gallbladder using the bio-inspired algorithm based on a spider web construction model. J Supercomput, Vol. 75, No. 6, 2019, pp. 3158–3183.10.1007/s11227-017-2230-4Search in Google Scholar
© 2022 Ramasubramanian Murugesan and Thirumarimurugan Marimuthu, published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Research Articles
- Numerical and experimental research on solidification of T2 copper alloy during the twin-roll casting
- Discrete probability model-based method for recognition of multicomponent combustible gas explosion hazard sources
- Dephosphorization kinetics of high-P-containing reduced iron produced from oolitic hematite ore
- In-phase thermomechanical fatigue studies on P92 steel with different hold time
- Effect of the weld parameter strategy on mechanical properties of double-sided laser-welded 2195 Al–Li alloy joints with filler wire
- The precipitation behavior of second phase in high titanium microalloyed steels and its effect on microstructure and properties of steel
- Development of a huge hybrid 3D-printer based on fused deposition modeling (FDM) incorporated with computer numerical control (CNC) machining for industrial applications
- Effect of different welding procedures on microstructure and mechanical property of TA15 titanium alloy joint
- Single-source-precursor synthesis and characterization of SiAlC(O) ceramics from a hyperbranched polyaluminocarbosilane
- Carbothermal reduction of red mud for iron extraction and sodium removal
- Reduction swelling mechanism of hematite fluxed briquettes
- Effect of in situ observation of cooling rates on acicular ferrite nucleation
- Corrosion behavior of WC–Co coating by plasma transferred arc on EH40 steel in low-temperature
- Study on the thermodynamic stability and evolution of inclusions in Al–Ti deoxidized steel
- Application on oxidation behavior of metallic copper in fire investigation
- Microstructural study of concrete performance after exposure to elevated temperatures via considering C–S–H nanostructure changes
- Prediction model of interfacial heat transfer coefficient changing with time and ingot diameter
- Design, fabrication, and testing of CVI-SiC/SiC turbine blisk under different load spectrums at elevated temperature
- Promoting of metallurgical bonding by ultrasonic insert process in steel–aluminum bimetallic castings
- Pre-reduction of carbon-containing pellets of high chromium vanadium–titanium magnetite at different temperatures
- Optimization of alkali metals discharge performance of blast furnace slag and its extreme value model
- Smelting high purity 55SiCr automobile suspension spring steel with different refractories
- Investigation into the thermal stability of a novel hot-work die steel 5CrNiMoVNb
- Residual stress relaxation considering microstructure evolution in heat treatment of metallic thin-walled part
- Experiments of Ti6Al4V manufactured by low-speed wire cut electrical discharge machining and electrical parameters optimization
- Effect of chloride ion concentration on stress corrosion cracking and electrochemical corrosion of high manganese steel
- Prediction of oxygen-blowing volume in BOF steelmaking process based on BP neural network and incremental learning
- Effect of annealing temperature on the structure and properties of FeCoCrNiMo high-entropy alloy
- Study on physical properties of Al2O3-based slags used for the self-propagating high-temperature synthesis (SHS) – metallurgy method
- Low-temperature corrosion behavior of laser cladding metal-based alloy coatings on EH40 high-strength steel for icebreaker
- Study on thermodynamics and dynamics of top slag modification in O5 automobile sheets
- Structure optimization of continuous casting tundish with channel-type induction heating using mathematical modeling
- Microstructure and mechanical properties of NbC–Ni cermets prepared by microwave sintering
- Spider-based FOPID controller design for temperature control in aluminium extrusion process
- Prediction model of BOF end-point P and O contents based on PCA–GA–BP neural network
- Study on hydrogen-induced stress corrosion of 7N01-T4 aluminum alloy for railway vehicles
- Study on the effect of micro-shrinkage porosity on the ultra-low temperature toughness of ferritic ductile iron
- Characterization of surface decarburization and oxidation behavior of Cr–Mo cold heading steel
- Effect of post-weld heat treatment on the microstructure and mechanical properties of laser-welded joints of SLM-316 L/rolled-316 L
- An investigation on as-cast microstructure and homogenization of nickel base superalloy René 65
- Effect of multiple laser re-melting on microstructure and properties of Fe-based coating
- Experimental study on the preparation of ferrophosphorus alloy using dephosphorization furnace slag by carbothermic reduction
- Research on aging behavior and safe storage life prediction of modified double base propellant
- Evaluation of the calorific value of exothermic sleeve material by the adiabatic calorimeter
- Thermodynamic calculation of phase equilibria in the Al–Fe–Zn–O system
- Effect of rare earth Y on microstructure and texture of oriented silicon steel during hot rolling and cold rolling processes
- Effect of ambient temperature on the jet characteristics of a swirl oxygen lance with mixed injection of CO2 + O2
- Research on the optimisation of the temperature field distribution of a multi microwave source agent system based on group consistency
- The dynamic softening identification and constitutive equation establishment of Ti–6.5Al–2Sn–4Zr–4Mo–1W–0.2Si alloy with initial lamellar microstructure
- Experimental investigation on microstructural characterization and mechanical properties of plasma arc welded Inconel 617 plates
- Numerical simulation and experimental research on cracking mechanism of twin-roll strip casting
- A novel method to control stress distribution and machining-induced deformation for thin-walled metallic parts
- Review Article
- A study on deep reinforcement learning-based crane scheduling model for uncertainty tasks
- Topical Issue on Science and Technology of Solar Energy
- Synthesis of alkaline-earth Zintl phosphides MZn2P2 (M = Ca, Sr, Ba) from Sn solutions
- Dynamics at crystal/melt interface during solidification of multicrystalline silicon
- Boron removal from silicon melt by gas blowing technique
- Removal of SiC and Si3N4 inclusions in solar cell Si scraps through slag refining
- Electrochemical production of silicon
- Electrical properties of zinc nitride and zinc tin nitride semiconductor thin films toward photovoltaic applications
- Special Issue on The 4th International Conference on Graphene and Novel Nanomaterials (GNN 2022)
- Effect of microstructure on tribocorrosion of FH36 low-temperature steels
Articles in the same Issue
- Research Articles
- Numerical and experimental research on solidification of T2 copper alloy during the twin-roll casting
- Discrete probability model-based method for recognition of multicomponent combustible gas explosion hazard sources
- Dephosphorization kinetics of high-P-containing reduced iron produced from oolitic hematite ore
- In-phase thermomechanical fatigue studies on P92 steel with different hold time
- Effect of the weld parameter strategy on mechanical properties of double-sided laser-welded 2195 Al–Li alloy joints with filler wire
- The precipitation behavior of second phase in high titanium microalloyed steels and its effect on microstructure and properties of steel
- Development of a huge hybrid 3D-printer based on fused deposition modeling (FDM) incorporated with computer numerical control (CNC) machining for industrial applications
- Effect of different welding procedures on microstructure and mechanical property of TA15 titanium alloy joint
- Single-source-precursor synthesis and characterization of SiAlC(O) ceramics from a hyperbranched polyaluminocarbosilane
- Carbothermal reduction of red mud for iron extraction and sodium removal
- Reduction swelling mechanism of hematite fluxed briquettes
- Effect of in situ observation of cooling rates on acicular ferrite nucleation
- Corrosion behavior of WC–Co coating by plasma transferred arc on EH40 steel in low-temperature
- Study on the thermodynamic stability and evolution of inclusions in Al–Ti deoxidized steel
- Application on oxidation behavior of metallic copper in fire investigation
- Microstructural study of concrete performance after exposure to elevated temperatures via considering C–S–H nanostructure changes
- Prediction model of interfacial heat transfer coefficient changing with time and ingot diameter
- Design, fabrication, and testing of CVI-SiC/SiC turbine blisk under different load spectrums at elevated temperature
- Promoting of metallurgical bonding by ultrasonic insert process in steel–aluminum bimetallic castings
- Pre-reduction of carbon-containing pellets of high chromium vanadium–titanium magnetite at different temperatures
- Optimization of alkali metals discharge performance of blast furnace slag and its extreme value model
- Smelting high purity 55SiCr automobile suspension spring steel with different refractories
- Investigation into the thermal stability of a novel hot-work die steel 5CrNiMoVNb
- Residual stress relaxation considering microstructure evolution in heat treatment of metallic thin-walled part
- Experiments of Ti6Al4V manufactured by low-speed wire cut electrical discharge machining and electrical parameters optimization
- Effect of chloride ion concentration on stress corrosion cracking and electrochemical corrosion of high manganese steel
- Prediction of oxygen-blowing volume in BOF steelmaking process based on BP neural network and incremental learning
- Effect of annealing temperature on the structure and properties of FeCoCrNiMo high-entropy alloy
- Study on physical properties of Al2O3-based slags used for the self-propagating high-temperature synthesis (SHS) – metallurgy method
- Low-temperature corrosion behavior of laser cladding metal-based alloy coatings on EH40 high-strength steel for icebreaker
- Study on thermodynamics and dynamics of top slag modification in O5 automobile sheets
- Structure optimization of continuous casting tundish with channel-type induction heating using mathematical modeling
- Microstructure and mechanical properties of NbC–Ni cermets prepared by microwave sintering
- Spider-based FOPID controller design for temperature control in aluminium extrusion process
- Prediction model of BOF end-point P and O contents based on PCA–GA–BP neural network
- Study on hydrogen-induced stress corrosion of 7N01-T4 aluminum alloy for railway vehicles
- Study on the effect of micro-shrinkage porosity on the ultra-low temperature toughness of ferritic ductile iron
- Characterization of surface decarburization and oxidation behavior of Cr–Mo cold heading steel
- Effect of post-weld heat treatment on the microstructure and mechanical properties of laser-welded joints of SLM-316 L/rolled-316 L
- An investigation on as-cast microstructure and homogenization of nickel base superalloy René 65
- Effect of multiple laser re-melting on microstructure and properties of Fe-based coating
- Experimental study on the preparation of ferrophosphorus alloy using dephosphorization furnace slag by carbothermic reduction
- Research on aging behavior and safe storage life prediction of modified double base propellant
- Evaluation of the calorific value of exothermic sleeve material by the adiabatic calorimeter
- Thermodynamic calculation of phase equilibria in the Al–Fe–Zn–O system
- Effect of rare earth Y on microstructure and texture of oriented silicon steel during hot rolling and cold rolling processes
- Effect of ambient temperature on the jet characteristics of a swirl oxygen lance with mixed injection of CO2 + O2
- Research on the optimisation of the temperature field distribution of a multi microwave source agent system based on group consistency
- The dynamic softening identification and constitutive equation establishment of Ti–6.5Al–2Sn–4Zr–4Mo–1W–0.2Si alloy with initial lamellar microstructure
- Experimental investigation on microstructural characterization and mechanical properties of plasma arc welded Inconel 617 plates
- Numerical simulation and experimental research on cracking mechanism of twin-roll strip casting
- A novel method to control stress distribution and machining-induced deformation for thin-walled metallic parts
- Review Article
- A study on deep reinforcement learning-based crane scheduling model for uncertainty tasks
- Topical Issue on Science and Technology of Solar Energy
- Synthesis of alkaline-earth Zintl phosphides MZn2P2 (M = Ca, Sr, Ba) from Sn solutions
- Dynamics at crystal/melt interface during solidification of multicrystalline silicon
- Boron removal from silicon melt by gas blowing technique
- Removal of SiC and Si3N4 inclusions in solar cell Si scraps through slag refining
- Electrochemical production of silicon
- Electrical properties of zinc nitride and zinc tin nitride semiconductor thin films toward photovoltaic applications
- Special Issue on The 4th International Conference on Graphene and Novel Nanomaterials (GNN 2022)
- Effect of microstructure on tribocorrosion of FH36 low-temperature steels

