Unveiling Ecological Unequal Exchange: The Role of Biophysical Flows as an Indicator of Ecological Exploitation in the North-South Relations

3.1 Equality of Resource Flows Versus Equality of Welfare

The relationship between biophysical flows and trade flows can be well developed within the extended Ricardo trade model^[10] developed by Dornbusch et al. (1977).^[11] We use this model not in terms of labor but in terms of natural resources as only fixed input. This allows us to focus solely on resources, as the focus of the EUE approach is set by the construction of aggregated metrics of natural resources. While this assumption of fixity would undoubtedly be problematic for a model focusing on the labor market it makes sense for many countries endowed with natural resources, especially those in the Global South with structurally lower exploration capacities.

The production of goods in both the South and the North is based on using only one input, namely, a resource or an aggregate of resources. There is a continuum of goods indexed z on an interval [0, 1]. Required resources per output of z are a J ( z ) , where J = { S , N } , where S is South and N = North, i.e. a J ( z ) are constant input–output coefficients with regard to the produced quantity of the good z . The comparative advantage of producing z in the South compared to the North is A ( z ) = a N ( z ) ∕ a S ( z ) , z ∈ [ 0 , 1 ] . The index z is ordered such that A ( z ) decreases in z , i.e., the comparative advantage of the South decreases in z . Therefore, A ′ ( z ) < 0 .

International production specialization depends on the prices of goods. Under the (usual) assumption of the basic Ricardian model, there is perfect competition, so the product supply prices follow from the following price equations.

where q J refer to the resource price of the South and the North, respectively. The South will produce those goods with a lower price compared to the North, i.e.,

From equation (3.2), it follows

where ω is the factoral terms of trade,^[12] which indicates the exchange ratio of the resources embodied in the goods traded. Subsequently, we show that this exchange ratio is the decisive indicator for determining ecologically unequal exchange.^[13]

From equation (3.3), we can find the borderline commodity

which divides the product space into goods z ≤ z ¯ with the South having a comparative advantage and goods z > z ¯ where the North produces comparatively cheaper.

The demand for the commodities are derived from a Cobb-Douglas utility function for both, the South and the North, assuming identical preferences.^[14] This task is simple also for the case of a continuous spectrum of goods.^[15] The demand functions are as follows:

where Y J is the income and p ( z ) the market price for z . Under free trade without transportation costs, a uniform price p ( z ) applies for z . Depending on which country group offers product z , the offer price p J ( z ) is equal to the market price p ( z ) . Hence, due to the decreasing comparative advantage of the South, i.e., A ′ ( z ) < 0 , there exists a z ˜ , 0 < z ˜ < 1 , such that South produces all commodities z within the interval [ 0 , z ˜ ] , whereas the North produces the remaining products z ∈ [ z ˜ , 1 ] . Resource market equilibria are achieved if total demand equals the supply, i.e.,

where z ¯ indicates the equilibrium value of z ˜ and where a J ( z ) , J = { S , N } are the input–output–coefficients. From equation (3.1), it follows for z ∈ [ 0 , z ˜ ] that p ( z ) = p S ( z ) = a S ( z ) q S , i.e., the prices of the commodities produced by the South depend on the respective input-output coefficients and the price for the resource R ¯ S . Similar, the prices for the products produced in the North z ∈ [ z ˜ , 1 ] are p ( z ) = p N ( z ) = a N ( z ) q N . Inserting these relations and equation (3.5) into equation (3.6) yields:

Income in the South and North is generated in the factor market. Therefore, Y J = q J R ¯ J applies where R ¯ J symbolizes the fixed supply of resources in both country groups. This supply is exogenously given, and in this pure trading model, it is open whether it is sustainable or associated with an over-exploitation of resources.

Define

and utilizing ω = q S ∕ q N together with Y J = q J R ¯ J yields after insertion into equation (3.6)

Equation (3.10) shows the factoral terms of trade as function of the relative endowment of resources and as a function of the range of products the South is producing in trade equilibrium, i.e., z ¯ . The bandwith of the range depend on the comparative advantages as defined in equation (3.4). In the following figure we depict both functions, A ( z ) and ω ( z ) and determine graphically^[16] the equilibrium value of z ¯ along the x -axis (point E).

The range of commodities z ∈ [ 0 , z ¯ ] are produced by the South, all z ∈ [ z ¯ , 1 ] are produced by the North. The trade equilibrium adjusts the input prices q J such that the factoral terms of trade are ω ¯ = ω ( z ¯ ) defined in equation (3.10). The welfare distribution between the South and the North is expressed as Ψ ( z ¯ ) = U S ( z ¯ ) ∕ U N ( z ¯ ) and depends on the trade equilibrium z ¯ . Ψ ( z ¯ ) is a positively monotone function with respect to z ¯ , indicating that the welfare of the South rises disproportionally high as the range of commodities produced in the South increases. The horizontal line marks the case of ecologically balanced exchange, i.e., the case were the net flow of resources of the South to the North are zero.

Figure 1 and the following figures are based on numerical parameter values^[17] that have not been determined empirically but are chosen to reflect the results of the empirical literature about trade patterns and international production specialization. For example, Debaere (2014) shows that relatively water-rich countries export water-intensive products. The results of the EUE literature also show that resource-rich countries export resource-intensive goods so that they are net exporters of their resources (Dorninger and Hornborg, 2015). In addition, we have chosen the numerical values such that the trade equilibrium leads to ecologically unequal exchange between the South and the North since the factoral terms of trade are less than unity.

Figure 1

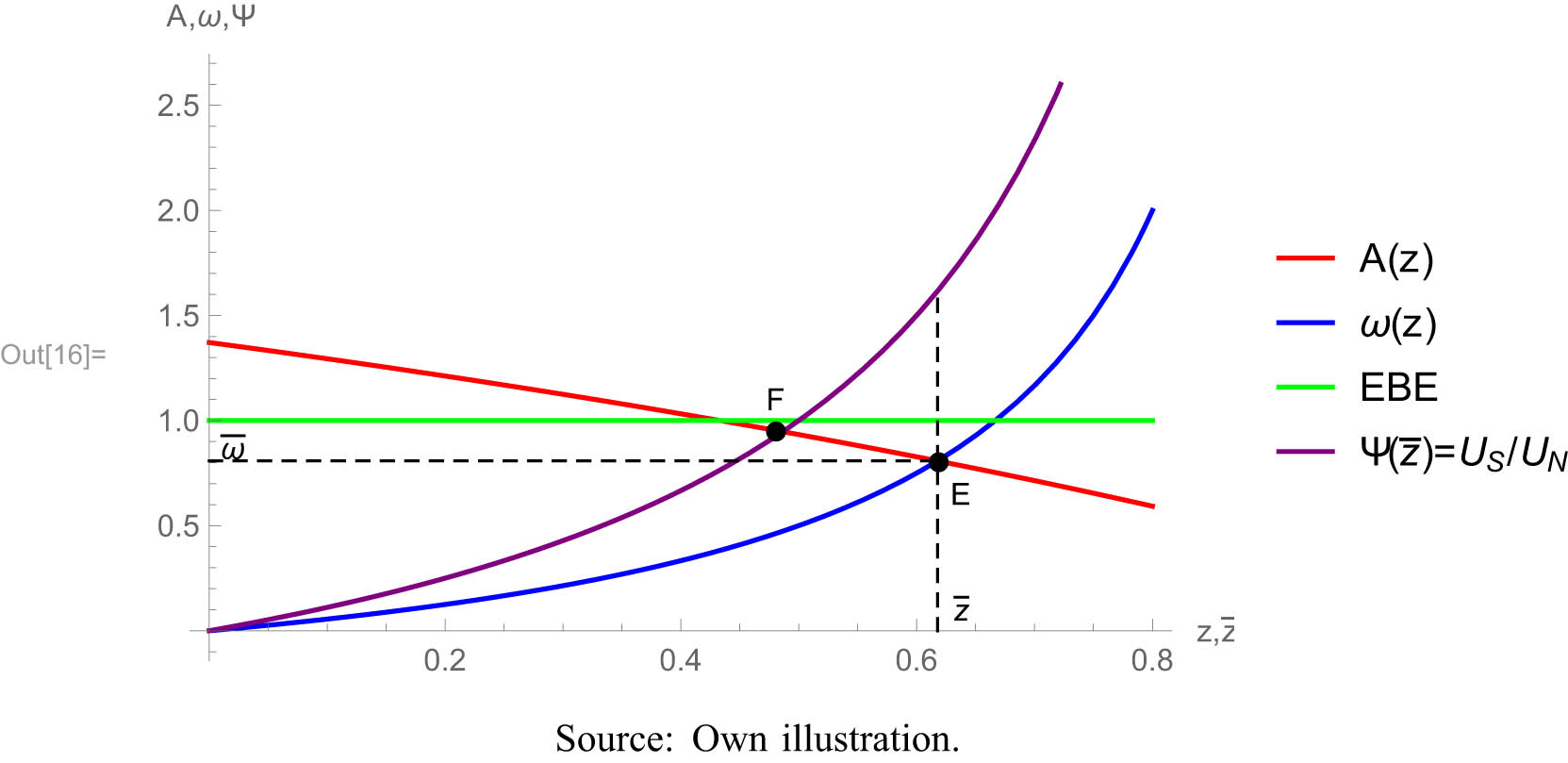
Factoral terms of trade and the production range of the South. Source: Own illustration.

The result follows from the fact that trading in the Ricardo model is voluntary. Exploitation can only exist if trade is forced because the state of autarky would make the South better off. In our numerical example, on which the figure is based, gains of trade are realized for both, the South and the North, even though the factoral terms of trade are to the South’s disadvantage.^[18] If ω < 1 , there is a net flow of biophysical matter from the South to the North. The level of net biophysical flows, therefore, does not indicate ecological exploitation. This would only be the case if the South were to give up the possibility of realizing trade advantages in the future due to an excessive outflow of resources today. Thus, the level of factoral terms of trade ω < 1 cannot per se be used to infer the exploitation of resources in the South. To infer exploitation requires further independent information relating to the sustainability of the resource consumption of R ¯ S and R ¯ N .

The fairness of the welfare distribution is shown in Figure 1 by the Ψ -function. The more comprehensive the range of goods produced in the South is, i.e. the higher z ¯ is, the greater is the welfare of the South compared to the North. Figure 2 shows two scenarios that illustrate the non-monotonicity of the relationship between the factoral terms of trade and welfare distribution.

Figure 2

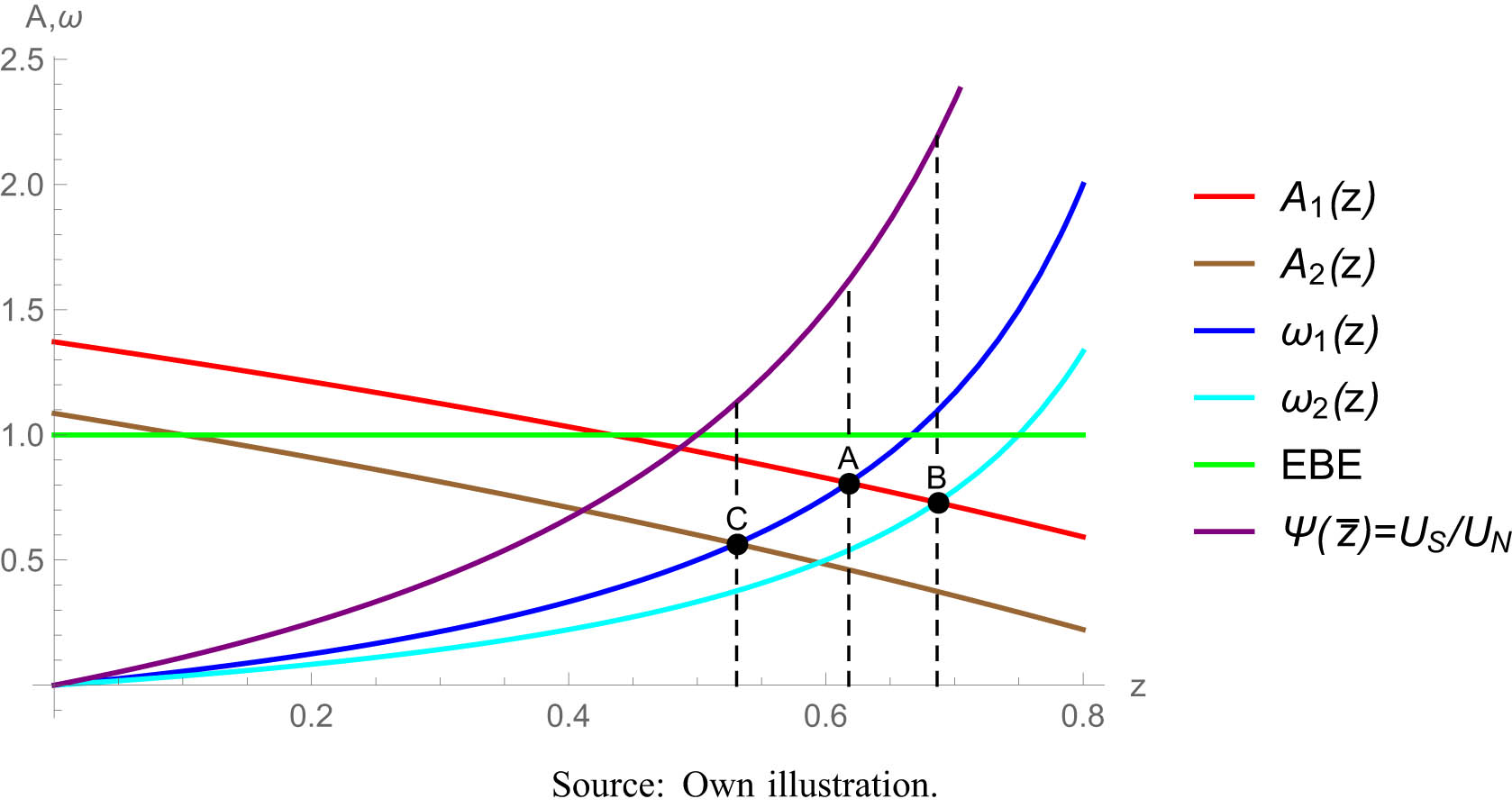
Factoral terms of trade and welfare distribution. Source: Own illustration.

In the first case, the factor input of the South increases such that the trade equilibrium shifts from A to B implying that the factoral terms of trade have fallen to the disadvantage of the South. At the same time, however, the welfare distribution improves in favor of the South since z ¯ has increased. Thus, increased resource consumption, provided it is ecologically sustainable, is beneficial overall for the South, although the factoral terms of trade are falling. Welfare of the South rises not only in absolute terms but also in relative terms. This means that a deterioration in the factoral terms of trade leads to an improvement in the distribution of welfare in favor of the South. In the second scenario beginning at point A, all-encompassing technological progress in the North causes a reduction in the input–output coefficients of the North so that the A ( z ) curve shifts downwards. In this case, a new equilibrium is established with lower factoral terms of trade for the South (point C). At the same time, the distribution worsens to the disadvantage of the South. The decline in the terms of trade is associated with a deterioration in the distribution of welfare. The reason for this is the advancement of technologies in the North, a relationship that not only representatives of the EUE have pointed out^[19] but also other economists^[20] referring to the heading of a “technology gap.”

The two cases show that there is no clear monotonic relationship between biophysical flows and the distribution of trade gains between the two blocks of countries. Whether there is a positive or negative correlation between the welfare distribution and the factoral terms of trade depends on the exogenous determinants that influence the relative resource flows expressed by ω and the welfare distribution.

3.2 Technological Gaps and Asymmetric Technological Progress

According to the EUE approach, asymmetric technological progress, i.e., the faster technological development of the North, leads to an increasing exploitation of resources in the South because technological progress displaces the production of the South into resource extraction (Althouse et al., 2023). This relationship is illustrated in Figure 2 for the scenario 2 (the shift in equilibrium from A to C). Although the welfare of both hemispheres increases in the course of technical progress in the North, the distribution changes to the disadvantage of the South. As the technological progress of the North increases, the A ( z ) -curve shifts downward because the input–output coefficients of the North decrease.^[21] As a result, the relative position of the South in terms of welfare distribution decreases. This argument assumes that technical progress relates to the production of all goods, including those that the North does not produce.

However, technical progress will relate more to those production processes that are used in both hemispheres, i.e., technical progress will be directed towards the respective domestic production. There is a similarity here with the concept of neutral technical progress in growth theory (Hicks neutrality). This approach has been criticized by Atkinson and Stiglitz (1969), who argue that technical progress depends on factor proportions.^[22] Instead, they have developed the concept of “localized technical progress,” which in our context means that technical progress has only an impact on the actual production processes.

The localized technical concept can also explain why the North’s one-sided, continuous innovation process leads to a technological gap. The A ( z ) -curve falls steeply after a critical threshold value^[23] because the input–output coefficients of the North only decrease after this threshold value. This leads to an entrenchment in the global production division: the South tends to produce technologically simple goods, while the North produces high-tech goods. This technology gap can be expressed as a smooth approximation of a step in the A ( z ) -curve (Figure 3).

Figure 3

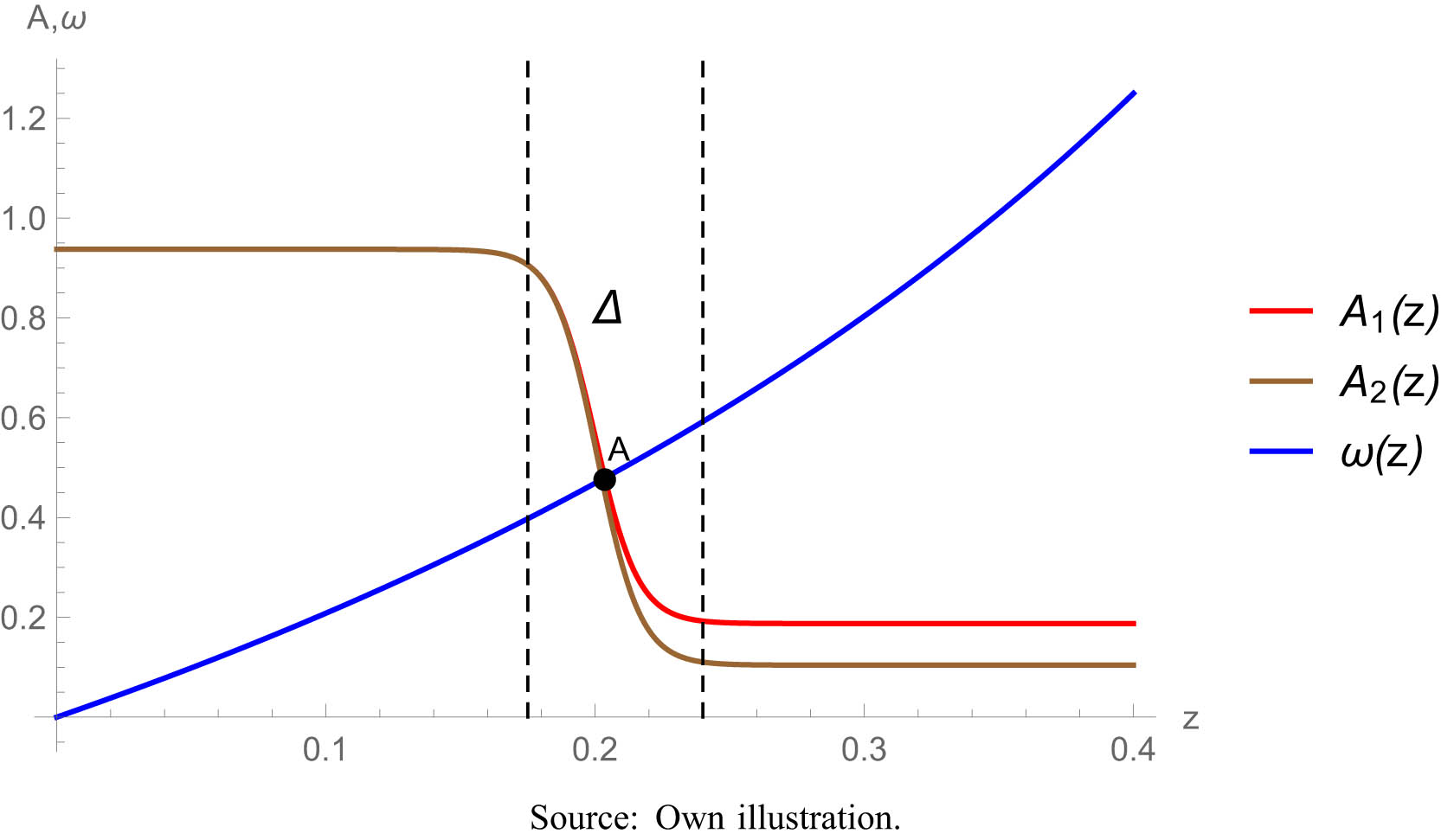
Technological progress in the North. Source: Own illustration.

The curve drops steeply in the Δ -range of z . To the right of the Δ -range, the comparative cost advantages of the North are considerable. This does not apply to the leftside. Technologically simple products can be produced more cheaply in the South than in the North with the help of low labor costs. The figure now analyzes how technological progress in the North affects the terms of trade and the welfare distribution. We assume that technological progress does not relate to the production of goods manufactured in the South. This assumption is based on the fact that technological progress tends to take place in the area of actual production processes. Technological progress in the North is now characterized by the A ( z ) -curve shifting asymmetrically from A 1 ( z ) to A 2 ( z ) leading to the result:

Thus, technological progress in the North is not necessarily at the expense of the South as claimed in the EUE-literature. Although the terms of trade are falling to the disadvantage of the South, the distribution of welfare is not changing. Here, the technological divide even provides protection against a shift in value creation from the South to the North ( z ¯ remains stationary). However, if technological progress takes place in such a way that the North can also produce the goods of the South more cheaply, this can lead to a deterioration in the terms of trade and an associated negative shift in welfare distribution for the South. Still, both hemispheres benefit from technological progress, albeit to varying degrees.

3.3 A neo-Ricardian reconstruction of EUE within the DFS model

In contrast to the standard two-factor neoclassical foreign trade models, which include the DFS model, in neo-Marxist theory, the distribution of income between labor and capital is not determined according to the scarcity and productivity of the two factors but is the result of political–economic power relations, which Emmanuel refers to as “extra-economic factors.”^[24] The exchange relations of internationally traded goods between the periphery and the center (barter terms of trade) then follow from the predetermined wage-profit-rate ratio. The unequal exchange about the exchange of labor values is, therefore, the result of these power relations, which do not result from the relative factor endowments as derived, e.g., in the H-O-model. The neoclassical interpretation of the Ricardian one-factor model of international trade is also rejected. There, the international exchange relationships are determined by different production techniques and the relative factor endowments between the trading partners. Analytically, the neo-Marxist approach is expressed using the Marxian value and price determination scheme. However, by using the Marxian scheme leads to problems with consistent separation between labor values and market prices. In a later contribution^[25] Emmanuel therefore also transferred his theory of unequal exchange into a neo-Ricardian framework.^[26]

His basic conclusion is^[27]

that the inequality of wages as such, all other things being equal, is alone the cause of the inequality of exchange.

where wage levels are not the result of supply and demand in a free labor market, but are formed in a political-economic process, i.e., are model-exogenous. If we transfer this labor value theory approach to the resource exchange relationship between the South and the North, we can represent this approach by the following modifications of the price equation (3.1) of the DFS model:

where the bars indicate that resource prices are fixed and r is the global rate of return on capital. An essential element of the global economy for Emmanuel is the unrestricted mobility of capital. Therefore, the returns on capital in the North and South are equalized. It should also be noted that, in contrast to the modern neo-Marxist approach, intermediary goods are not taken into account in the DFS-model. The return, therefore, relates to the wage bill paid, i.e., it is a simple wage fund model.^[28]

Since the rate of return is identical across the trading partners, it plays no role in determining the international distribution of production because the relative costs advantages are not affected by the uniform rate of return. To determine the trade equilibrium, we can, therefore, proceed directly to equation (3.4). If we also consider the demand side, assuming that resource owners and capital owners have the same consumption preferences, we arrive at equation (3.10), which together with equation (3.4) determines both z ¯ and ω ¯ . In the neo-Ricardian context, however, there is an overdetermination because the exogenous resource prices already predetermine ω ¯ . The overdetermination becomes visible in the DFS model because the goods demand side and the trade balance are taken into account in this model. In the neo-Marxist approaches to unequal exchange, the quantity relationships and, thus, the balance of trade are not taken into account because the linear price model for closed economies is applied to international trade. In these models, the quantity system and the price system are completely separated. However, it is known from the simple Ricardian foreign trade model that the terms of trade in a linear production model are also determined by demand because the production factor labor or, in our case, the natural resources are internationally immobile. Exploitation relationships, therefore, do not solely determine the exchange ratio of traded goods. Bacha (1978) has pointed out in the context of a two-country-two-goods model that the assumption of a fixed exchange of labor values – in our case the resource exchange ratio – can only prevail if there is a quantity adjustment of the resource inputs.^[29] In our case, it is sufficient if the resource input in the South R ¯ S adjusts accordingly so that the balance of trade remains balanced for each exchange ratio. This relationship is shown in Figure 4.

Figure 4

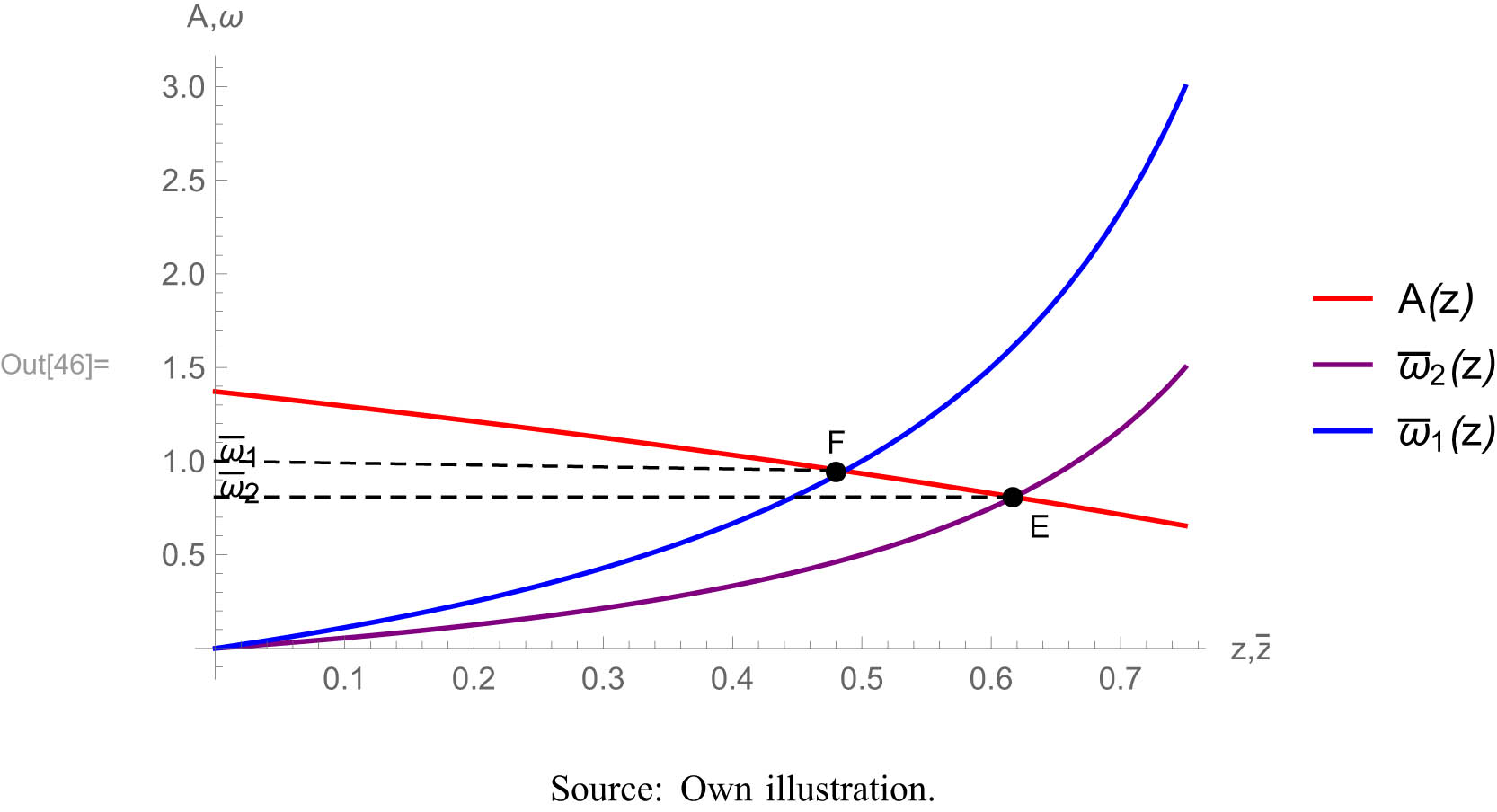
Fixed factoral terms of trade and resource use. Source: Own illustration.

At point F, there is a trade equilibrium with factoral terms of trade of ω ¯ 1 . This corresponds to a factoral terms of trade ratio of R ¯ N ∕ R ¯ S (equation (3.10)). If, in the course of further exploitation of the South, the factoral terms of trade deteriorates to ω ¯ 2 , a new trade equilibrium can only arise if the resource input in the South increases^[30]. R ¯ S increases so that the ω -curve runs exactly through point E. The core statement of the EUE can then be summarized as follows.^[31]

From the perspective of labor theory of value, this conclusion is understandable. The factoral terms of trade also reflect the relative income per worker ( ω = q S ∕ q N ). However, if the theory of unequal exchange is applied to the exchange of resources, the factoral terms of trade cannot be interpreted as an indicator of an exploitative relationship, as summarized in Section 3.1. In this case, the ratio of the total income of both countries must be set in proportion, i.e., ( q S R S ) ∕ ( q N R N ) . This quotient can be used to determine the ratio in which the income of the two countries is exchanged.^[32] Equation (3.10) and equation (A16) immediately show that the income ratio is nothing other than Ψ . Thus, if the factoral terms of trade fall exogenously due to political–economic forces, this even improves the income situation in the South. A comprehensive political-economic analysis should therefore include the functional income distribution between labor, capital, and land ownership (resource ownership) in the South and North to assess exploitative relationships. The factoral terms of trade are not suitable as a measure of exploitation as long as the distribution mechanisms within both economies have not been clarified. This finding applies to both types of model, the neoclassical Ricardian foreign trade model and the ecological neo-Ricardian model, in which the factoral terms of trade are exogenously given.

Another criticism of the EUE approach is the unspoken implication that a deterioration in the factoral terms of trade results in the overexploitation of nature. The fact that an exogenous deterioration in the terms of trade leads to an increase in the use of resources does not mean that nature’s regenerative capacities have been exceeded. This question can only be answered if the institutional framework of resource use is clarified.^[33] The assumption of exogenous resource prices is taken from the neo-Marxist model of labor exploitation. The workers receive their fixed subsistence wage. Lewis adopted this relationship for dual economies with an agricultural subsistence sector and an industrial sector. The fixed labor wage is the result of an oversupply of labor that is offered if the wage exceeds the subsistence income.^[34] However, it is not clear whether these characteristics of the labor market in the South can simply be transferred to the resource market in the South. The neoclassical modeling approach with a fixed supply of resources at a flexible resource price approximates reality better because the extraction of natural resources is limited by capacities whose expansion requires investments. Thus, the supply of resources is presumably not completely elastic.

3.4 Fair Trade, Transfers, and EUE

Beyond the neo-Marxian literature, there is also an extensive literature on the relation between inequality and international trade.^[35] In this section, we discuss some criteria of international distributive justice and their policy instruments for its implementation within the DFS model. We show that justice-oriented trade policy should not make its instruments dependent on biophysical flows.

In the Ricardian one-factor model, distribution problems can only relate to the endowment of factors and the ownership of technologies. When applying the model to natural factors, migration cannot be used as a means of distribution policy.^[36] Thus, natural resources cannot be allocated directly to countries according to equity criteria. Their endowment is subject to geographical randomness, be it resources that are used as inputs or natural capacities for absorbing emissions and waste. However, resources can be redistributed virtually by assigning property rights^[37] and the question remains as to the normative basis on which claims can be legitimized.^[38] There are two opposing fundamental criteria: self-ownership and joint ownership. Applied to countries, the first principle considers a country to be the rightful owner of a natural resource because the population has legitimately appropriated it. This position implies that the appropriation is not to the detriment of others. The second principle considers the geographical distribution of natural resources across countries’ territories to be (morally) random or arbitrary.^[39] This view concludes that all natural resources are owned jointly by all countries (joint ownership) and gives rise to a claim by resource-poor countries to the proceeds of trade based on the utilization of resources of resource-rich countries. The issue of fair trade, therefore, does not relate to the exchange ratio of goods or virtual resource content, as in the theory of ecologically unequal exchange, but to the fair distribution of resource ownership.^[40] The principle of joint ownership can also be applied to the ownership of productivity-enhancing technologies of economies.^[41] Exclusive ownership claims can be legitimized if production technologies have not come to their owners by chance but due to their efforts. This also applies if technological disadvantages do not result from the systematic prevention of development opportunities. If, on the other hand, technological differences are the result of historical randomness or power constellations, then technologies should also be jointly owned.

Before we analyze the welfare-theoretical implications of the distributive justice criteria within the framework of the DFS model, we examine the effect of distributive policy instruments. These transfers between the South and the North can take place in various ways: Technology transfers, direct investments (capital transfers), the assignment of property rights to natural resources, and transfers of purchasing power. Here, we do not pursue the first two transfers further because they would require a model of higher complexity. We only consider the allocation of property rights that lead to corresponding transfers of scarcity rents, i.e., purchasing power. The effects of transfers have been extensively analyzed in the literature and goes back to Keynes’ classic analysis.^[42] In the simple, pure foreign trade models of Ricardian provenance and the multifactor models of Heckscher and Ohlin, transfers do not change the factoral terms of trade if the preferences of the trading countries are identical. This can be shown for the DFS-model (Section A.4) and is illustrated in Figure 5.

Figure 5

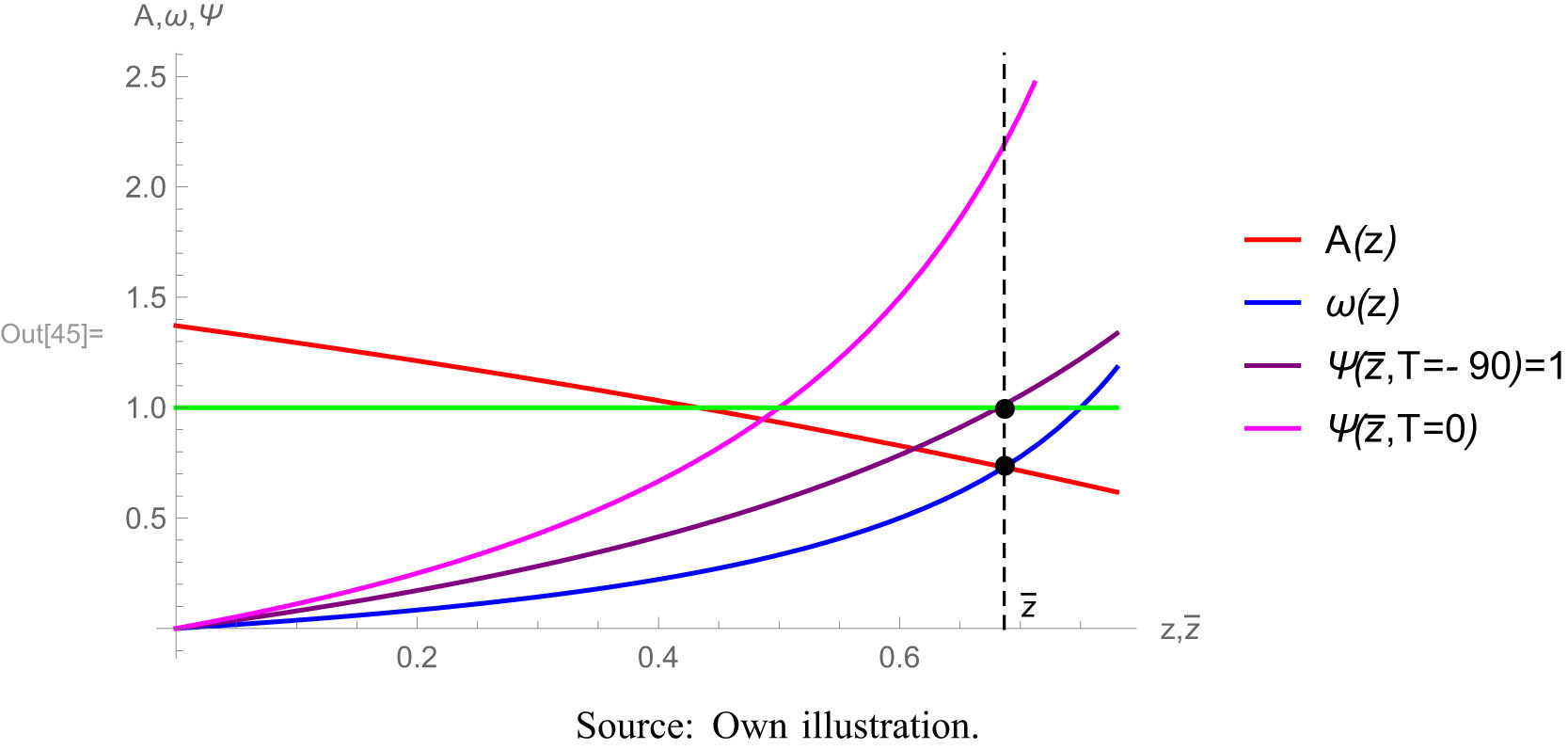
Effects of transfers from South to North. Source: Own illustration.

The figure contains the two functions A ( z ) and ω ( z ) . The intersection point denotes the trading equilibrium ω ¯ or z ¯ that remains unaffected by the transfer. So the net transfer of biophysical material does not change either. Only Ψ , the relative welfare of the South, changes from Ψ ( T = 0 ) to Ψ ( T = − 80 ) as a result of the transfer from the South to the North.^[43] The transfer T = − 80 leads to equal welfare of both regions, i.e., Ψ ( z ¯ , T = − 80 ) = 1 .

Thus, constructing a fair trade system should not be based on the physical net position of international trade. Distribution policy should not be linked to physical flows because there is no monotonic relationship between welfare distribution and the net ecological position of trade relations.

It remains to determine the amount of transfers with the help of equity criteria. Here, we follow Roemer’s approach^[44] and relate the question of justice to the distribution of natural resources and technological equipment. If the level of endowments is not the result of the deliberate efforts of the acting societies, i.e., if they are morally arbitrary, they should be collectively owned. Therefore, the trade equilibrium derived in Section 3.1 is unjust if R S is unequal to R N generally implying^[45] ψ ( z ) ≠ 1 . The principle of joint ownership can be well defined and derived with the help of the Nash-bargaining approach. In the context of the DFS model, this means that natural resources by both countries can only be utilized if South and North have agreed on the distribution of ownership. Otherwise, no production is possible. Therefore, there is a negotiation game in which the threat points are zero. The utility functions of the South and the North for given transfer T in trade equilibrium are given as follows:

where L i ( z ¯ ) , i = S , N are defined in equations (A12) and (A13). The Nash solution, then, follows from the following program:^[46]

It follows from this approach that the transfer amount should be chosen so that the incomes of both countries are equal, i.e., R N − ω ¯ T = ( R S + T ) ω ¯ , which also results in equality of welfare, i.e., ψ = 1 . This extremely egalitarian result follows from the principle of joint ownership. Although the technologies are different and are owned exclusively by the two groups of countries, welfare equality prevails. This is because the two threat points are zero, i.e., without agreement, there is no production and no consumption in autarky. Of course, this approach can only serve as a normative reference point, as no country can be denied the retreat position of autarky resulting from the principle of sovereignty. The determination of an acceptable transfer perceived as fair will, therefore, have to mediate between the principles of equity and sovereignty what can be referred to as cursive joint ownership.

For example, if we consider both the principle of joint ownership and that of sovereignty equally, we arrive at a transfer determination that takes into account the autarky starting point of both countries. The South and North remain in autarky if no agreement is reached on a possible transfer. The corresponding Nash bargaining approach is expressed as follows:

where U ¯ i ( A ) , i = { S , N } are the welfare levels in the case of autarky. Here, the explicit determination of the optimal and fair transfer is only possible numerically in the DFS-model. However, for the normative discussion, it is sufficient to describe the qualitative properties of the solution. In contrast to pure joint ownership, the negotiation outcome here does not provide for an egalitarian solution U ¯ S ( T ) = U ¯ N ( T ) . The two negotiating partners agree on a transfer that provides equality in the trade’s welfare gains, i.e.,

With different starting positions in autarky, this principle means that welfare in both blocs differs even after a transfer has been implemented.

The combined principle^[47] of joint ownership and sovereignty (autarky as starting point and fallback position) legitimizes different starting positions as morally justified. As a rule, the transfer calculated from the equation does not equal zero. This means that pure trade equilibrium without an accompanying transfer is considered unfair from this normative perspective, although the approach is also committed to self-ownership of initial resource endowments. This is because the bargaining approach contains an element of equality. The distribution of trade benefits will not be left to the mechanics of supply and demand alone, but the welfare gains of the North and the South will be distributed equally. The positive welfare effect of trade resulting from specialization in comparative cost advantages is joint ownership. Finally, it should be emphasized once again, whichever principle is considered morally acceptable, cursive joint ownership or the mediated principle of cursive joint ownership, both relate the issue of fair trade to the distribution of natural resources and technologies and not to the exchange ratio of ecological values.