Dictatorial Mechanisms in Constrained Combinatorial Auctions
-
Anat Lerner
und
Rica Gonen
Abstract
We study the possibility space of deterministic, dominant-strategy incentive compatible, individually rational, and Pareto efficient combinatorial auctions in a model with two players and two nonidentical items (four outcomes). Our model has multidimensional types, private values, nonnegative prices, and quasilinear preferences for the players with one relaxation – the players are subject to publicly known budget constraints. We show that the space we study essentially includes one type of mechanisms: autocratic mechanisms (a form of dictatorship). Furthermore, we prove that there are families of autocratic mechanisms that uniquely fulfill the basic properties of deterministic, dominant-strategy incentive compatible, individually rational, and Pareto efficient. The mechanisms in the autocratic families are identical except for two to three price parameters that differentiate them.
References
Arrow, K.J. 1950. “A Difficulty in the Concept of Social Welfare.” Journal of Political Economy 58 (4):328–46.10.1086/256963Suche in Google Scholar
Ashlagi, I., M. Braverman, A. Hassidim, R. Lavi, and M. Tennenholtz. 2010. “Position Auctions with Budgets: Existence and Uniqueness.” The B.E. Journal of Theoretical Economics (Advances) 10 (1).10.2202/1935-1704.1648Suche in Google Scholar
Bartal, Y., R. Gonen, and N. Nisan. 2003. Incentive Compatible Multi-unit Combinatorial Auctions.” In Proceedings of TARK, 72–87. Bloomington, Indiana: USA, June 20–22.Suche in Google Scholar
Bhattacharya, S., V. Conitzer, K. Munagala, and L. Xiax. 2010. “Incentive Compatible Budget Elicitation in Multi-unit Auctions.” In Proceedings of SODA. Austin, Texas: USA, January 17–19.Suche in Google Scholar
Budish, E., and E. Cantillon. 2010. “The Multi-unit Assignment Problem: Theory and Evidence from Course Allocation at Harvard.” In ECARES Working Paper.Suche in Google Scholar
Clarke, E.H. 1971. “Multipart Pricing of Public Goods.” Public Choice 2:17–33.10.1007/BF01726210Suche in Google Scholar
Dobzinski, S., R. Lavi, and N. Nisan. 2012. “Multi-unit Auctions with Budget Limits.” Games and Economic Behavior 74:486–503.10.1016/j.geb.2011.08.003Suche in Google Scholar
Dobzinski, S., and N. Nisan. 2011. “Multi-unit Auctions: Beyond Roberts.” In Proceedings of EC’11, 233–42. San Jose, CA: USA, June 5–9.Suche in Google Scholar
Fiat, A., S. Leonardi, J. Saia, and P. Sankowski. 2011. “Combinatorial Auctions with Budgets.” In Proceedings of EC’11.10.1145/1993574.1993609Suche in Google Scholar
Gibbard, A. 1973. “Manipulation of Voting Schemes: A General Result.” Econometrica 41:587–601.10.2307/1914083Suche in Google Scholar
Groves, T. 1973. “Incentives in Teams.” Econometrica 41:617–31.10.2307/1914085Suche in Google Scholar
Hatfield, J.W. 2009. “Strategy-Proof, Efficient, and Non Bossy Quota Allocations.” Social Choice and Welfare 33:505–15.10.1007/s00355-009-0376-6Suche in Google Scholar
Lavi, R., and M. May. 2012. “A Note on the Incompatibility of Strategy-proofness and Pareto-Optimality in Quasi-linear Settings with Public Budgets.” Economics Letters 115:100–03.10.1016/j.econlet.2011.11.043Suche in Google Scholar
Lehmann, D., L.I. O’Callaghan, and Y. Shoham. 2002. “Truth Revelation in Approximately Efficient Combinatorial Auctions.” Journal of ACM 49 (5):577–602.10.1145/585265.585266Suche in Google Scholar
Nisan, N., and A. Ronen. 2007. “Computationally Feasible VCG-Based Mechanisms.” Journal of Artificial Intelligence Research 29:19–47.10.1613/jair.2046Suche in Google Scholar
Roberts, K. 1979. “The Characterization of Implementable Choice Rules.” In Aggregation and Revelation of Preferences, edited by J.-J. Laffont. North-Holland: North-Holland Publishing Company.Suche in Google Scholar
Satterthwaite, M. 1975. “Strategy-Proofness and Arrow’s Condition: Existence and Correspondence Theorems for Voting Procedures and Social Welfare Functions.” The Journal of Economic Theory 10:187–217.10.1016/0022-0531(75)90050-2Suche in Google Scholar
Vickrey, W. 1961. “Counterspeculation, Auctions and Competitive Sealed Tenders.” Journal of Finance 16:8–37.10.1111/j.1540-6261.1961.tb02789.xSuche in Google Scholar
- 1
We call the mechanisms autocratic and not dictatorial, as our domain of preferences is monetary and in that domain Groves has defined dictatorial mechanisms to allow for negative prices, which are not included in our model. A thorough discussion of the difference between Groves’s dictatorial mechanism and our autocratic mechanism is deferred to Section 2
- 2
Dictatorship cannot be efficient.
- 3
This article considers valuation spaces where not all valuations are included in the valuation space.
- 4
y can be either a constant or a function
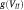. The function 
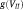must satisfy 
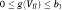. - 5
An example for a non-constant
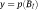that satisfies the conditions when player 1 is the autocrat, 
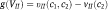, which is 
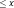and, therefore, within the range of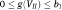 
- 6
Note that the cases of equality in D2 and D3 can be randomly chosen. In such cases of equality, the players are indifferent to the alternative allocations of D2 and D3.
©2013 by Walter de Gruyter Berlin / Boston
Artikel in diesem Heft
- Masthead
- Masthead
- Advances
- Dependence and Uniqueness in Bayesian Games
- Monopolistic Signal Provision†
- Multi-task Research and Research Joint Ventures
- Transparent Restrictions on Beliefs and Forward-Induction Reasoning in Games with Asymmetric Information
- A Simple Bargaining Procedure for the Myerson Value
- On the Difference between Social and Private Goods
- Optimal Use of Rewards as Commitment Device When Bidding Is Costly
- Labor Market and Search through Personal Contacts
- Contributions
- Learning, Words and Actions: Experimental Evidence on Coordination-Improving Information
- Are Trust and Reciprocity Related within Individuals?
- Optimal Contracting Model in a Social Environment and Trust-Related Psychological Costs
- Contract Bargaining with a Risk-Averse Agent
- Academia or the Private Sector? Sorting of Agents into Institutions and an Outside Sector
- Topics
- Poverty Orderings with Asymmetric Attributes
- Dictatorial Mechanisms in Constrained Combinatorial Auctions
- When Should a Monopolist Improve Quality in a Network Industry?
- On Partially Honest Nash Implementation in Private Good Economies with Restricted Domains: A Sufficient Condition
- Revenue Comparison in Asymmetric Auctions with Discrete Valuations
Artikel in diesem Heft
- Masthead
- Masthead
- Advances
- Dependence and Uniqueness in Bayesian Games
- Monopolistic Signal Provision†
- Multi-task Research and Research Joint Ventures
- Transparent Restrictions on Beliefs and Forward-Induction Reasoning in Games with Asymmetric Information
- A Simple Bargaining Procedure for the Myerson Value
- On the Difference between Social and Private Goods
- Optimal Use of Rewards as Commitment Device When Bidding Is Costly
- Labor Market and Search through Personal Contacts
- Contributions
- Learning, Words and Actions: Experimental Evidence on Coordination-Improving Information
- Are Trust and Reciprocity Related within Individuals?
- Optimal Contracting Model in a Social Environment and Trust-Related Psychological Costs
- Contract Bargaining with a Risk-Averse Agent
- Academia or the Private Sector? Sorting of Agents into Institutions and an Outside Sector
- Topics
- Poverty Orderings with Asymmetric Attributes
- Dictatorial Mechanisms in Constrained Combinatorial Auctions
- When Should a Monopolist Improve Quality in a Network Industry?
- On Partially Honest Nash Implementation in Private Good Economies with Restricted Domains: A Sufficient Condition
- Revenue Comparison in Asymmetric Auctions with Discrete Valuations
