The extension of thixotropy of cement paste under vibration: a shear-vibration equivalent theory

1 Introduction

Cement paste is a particle stream formed by mixing water and cement particles and concrete consists of cement paste and aggregates. Research on cement paste and fresh concrete is closely linked. The change of rheological properties of fresh concrete under vibration mainly comes from cement paste. Both cement paste and fresh concrete can be streamlined as water-containing particles. The internal structures of the two vary over time due to their internal chemical reactions, which in turn changes the rheological properties. In the case of external force, its internal structures are destroyed and the rheological properties are also changed. Therefore, it can be observed in the experiment that the same proportion of cement paste and fresh concrete exhibit different behaviors [1, 2]. Barnes et al. [3, 4] defines thixotropy as “a gradual decrease of the viscosity under shear stress followed by a gradual recovery of the structure when the stress is removed”. It can be considered that the cement paste has thixotropic properties. Hattori and Izumi [5], Tattersall and Banfill [6] studied the thixotropic properties of cement paste, and established Hattori-Izumi theory (HI theory). Based on the research of Hattori et al., Wallevik [7, 8] made some necessary improvements to HI theory. According to HI theory, the thixotropy of cement paste is related to coagulation, dispersion, and re-coagulation between cement particles. It shows that without external force, the coagulation of cement particles makes the junctions of cement paste increase with time. When the shearing action is applied, it leads to dispersion of the coagulated particles, resulting in the reduction of viscosity. When the shearing action is removed, re-coagulation happens and the viscosity rises again.

On the other hand, many researches have showed that the rheological properties of concrete change under vibration [9, 10, 11, 12]. Tattersall used a vertical tube method to study fresh concrete under vibration. Fresh concrete without vibration remained in the straight pipe due to the existence of the yield value, while it flowed under vibration because the yield value of fresh concrete decreased. The fluidity of fresh concrete will be significantly improved under vibration. Popovics [13] suggested that the effect of arch bridges produced by aggregates in fresh concrete would be destroyed during vibration and then improved the workability of fresh concrete. On the other hand, cement paste in fresh concrete flows under vibration, which makes the distribution of aggregates more uniform and improves the workability of fresh concrete as well. In most literature, fresh concrete was considered as a Bingham fluid, and under low-intensity vibration, the rheological model would be transformed to Hershel-Bulkley model and finally to Power-Law model.

As is mentioned above, the rheological properties of concrete will change under vibration. Since the main influence of rheological properties of concrete comes from cement paste, it’s reasonable to suppose that there are rheological changes of cement paste under vibration. HI theory and Wallevik proposed a simple way to estimate the rheological properties change under shear. However, they obtained the results by measuring the rheological properties of cement paste with rotational rheometers, which means the theory can be acceptable only in shear condition. Current study established the rheological model through data fitting and ignored the internal structure of fresh concrete, more specifically, the change of rheological properties of cement paste. In this paper, the shear-vibration equivalent theory is proposed, which makes HI theory applicable under vibration. It is verified by a series of experiments which considers both the shear effect and vibration effect. Combined with the shear-vibration equivalent theory with HI theory, the process that the rheological model of cement paste changes from Bingham model to Hershel-Bulkley model and finally to Power-Law model is explained.

2 Shear-Vibration Equivalent theory

2.1 Traditional rheological test method of cement paste

For non-Newtonian fluids, the ratio of shear stress to shear rate is defined as the apparent viscosity. As Bingham fluid, the apparent viscosity of the cement paste can be calculated by the following formula [14, 15, 16, 17]:

(1)η=τγ˙=τ0γ˙+μ

Where η is the apparent viscosity of cement paste, τ and γ˙are respectively shear stress and shear rate, τ₀ is the yield value and μ is the plastic viscosity of cement paste.

In most researches, the apparent viscosity of cement paste is usually measured by the rotational rheometers, as is the same in this paper. The schematic diagram of the rotary viscometer is shown in Figure 1.

Figure 1

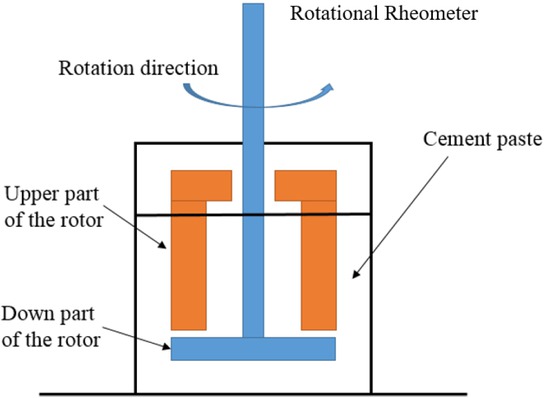
The schematic of rotational rheometers

When the rotor rotates, the cement paste in contact with the rotor will maintain the same speed as the rotor, and the speed of fluid in contact with the vessel wall will be zero due to the action of friction. The shear strain will generate inside the fluid which will cause shear stress. The following relationship will be obtained:

(2)M=2πr2hτ=2πr2h(τ0+μrdωdr)

Where M is the torque of viscometer rotor, h is immersion depth of the rotor in cement paste, r is the horizontal distance from one point in the fluid to the center of the rotor and ω is the angular velocity at this point.

By transforming formula (2), the Reiner-Riwlin equation [15] is obtained:

(3)Ω=M4πhμ1R12−1R22−τ0μlnR2R1

2.2 Experiment procedure under vibration

2.2.1 Experiment procedure

The method of measuring the viscosity of cement paste under vibration is to place the self-made viscometer on the vibrator and measure the viscosity of the cement paste during the vibrating process, as is shown in Figure 2.

Figure 2

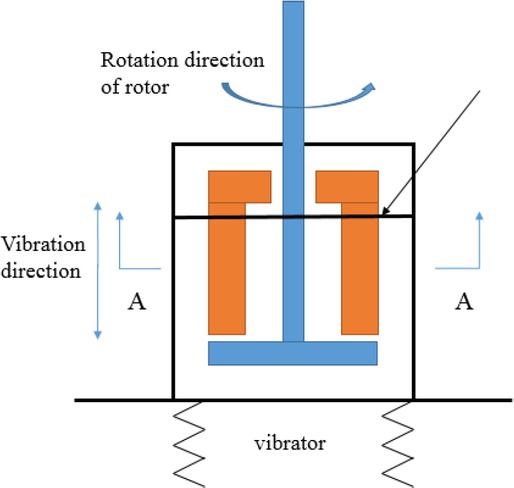
Viscosity measurement of cement paste under vibration

The container is fixed on the vibrating table, and the speed of the container is the same as the vibrator obviously. During the vibration process, the energy generated by the vibrator is transmitted in the form of waves. Due to the limited size of the container, the intensity of vibration can be assumed as the equivalent inside the container. When the vibrator starts, the cement paste in contact with the inner wall of the container will maintain the same speed as the vibrator and the speed of fluid in contact with the rotor will be zero in vibration direction due to the interaction of friction, which will result in uneven internal movement of the cement paste. Thus shear stress will be generated inside the cement paste and the inner structure of the cement paste will be destroyed. As a result, the rheology changes during the process.

2.2.2 A brief introduction of HI theory

HI theory assumes that the apparent viscosity is related to the number of junctions in the cement paste, as is shown in formula (4):

(4)ηHI=B3Jt2/3+{othernegligiblerelatedterms}≈B3Jt2/3

Where η_HI is the apparent viscosity calculated by HI theory, B₃ is the friction coefficient between cement paste particles and has a physical unit of N·s. J_t is the number of junctions between particles, and is calculated as formula (5):

(5)Jt=n3[U0γ˙Ht2+1+Ht](Ht+1)(γ˙t+1)

Where n₃ is particle numbers in a unit volume of cement paste. H is coagulation rate. t represents for time and U₀ is the ratio of the number of bonded particles to the total number of particles in the fluid. Combining formula (4) and (5), the viscosity of fluid is calculated as follows:

(6)ηHI=B3n3[U0γ˙Ht2+1+Ht](Ht+1)(γ˙t+1)2/3

Due to the difficulty to obtain the parameters in formula (6), Wallevik made some necessary modifications, and expressed the plastic viscosity and yield value of cement paste as a function of shear rate and time, providing a method to calculate the viscosity of cement paste under shear. The parameters m_a, m_b, a₁, a₂, U₀, τ₀, η are only determined by the characteristics of cement paste, also known as HI parameters. The detailed deduction can be referred to literatures [5, 7, 8].

2.2.3 Introduction of shear-vibration equivalent theory

Unfortunately, the HI theory is not suitable in the vibration process mentioned above, because the vibration of the vibrator also leads to relative movement of the cement particles and changes the rheological properties of the fluid, namely, the viscosity and yield stress.

This thesis proposes a shear-vibration equivalent theory which considers that the effect of the vibration process of cement paste is as the same with the effect of the shear process. In other words, the vibration process can be transformed into the shear process. The following is the analysis of the cement paste under both vibration and shear.

According to Li [18], the flow field of cement paste without vibration (A-A section of Figure 2. without vibration) is shown in Figure 3(a), which is layered radially according to the central symmetry of the flow field. The viscosity of cement paste in each layer is considered the same. It is proved that this simplification is reliable. Based on the simplification of Li, the isometric of Figure 2 A-A section is shown in Figure 3(b). It should be noted that the flow field of Figure 3(b) is under both shear and vibration. A and B represent for two adjacent points in the radial direction. The distance between the two points is dr. Then the shear rate between two points can be approximated as formula (7) and (8).

Figure 3

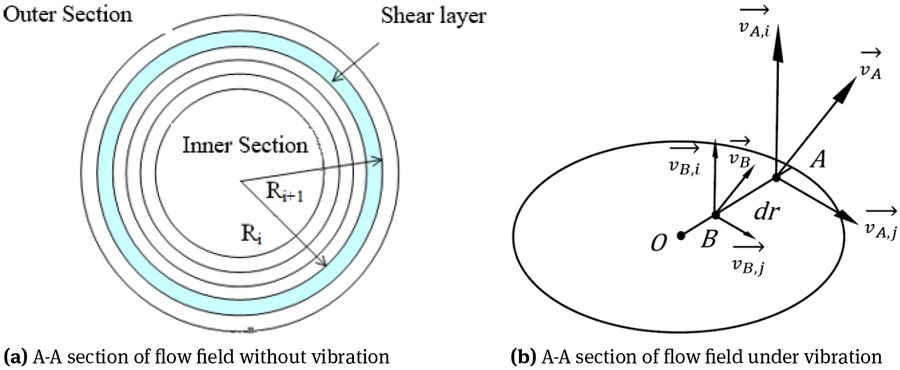
Flow field of cement paste

(7)γ˙A,B→=V→A−V→B/dr

(8)γ˙A,B→=VA,i→−VB,i→i→dr+VA,j→−VB,j→i→dr

Where VA→is the speed of cement paste in point A, VB→is the speed of cement paste in point B, γ˙A,B→is the relative shear rate between point A and point B, VA,i→ and VB,i→are respectively the speed of fluid in point A and B in direction i→(direction of vibration), VA,j→ and VB,j→are respectively the speed of cement paste in point A and point B in direction j→.

The vibration process and shear process can be transferred into pure shear process. The total shear rate is composed of shear rate generated by vibration process and shear rate generated by shear process, as is shown in formula (9).

(9)γ˙total→=γ˙vibration→+γ˙shear→

Where γ˙total→is the total shear rate, γ˙vibration→ is the shear rate generated by vibration, γ˙shear→is shear rate generated by shear. The shear rate generated by vibration is related to

the intensity of vibration. However, for a sinusoidal vibration process, it is difficult to calculate its vibration intensity directly, so a new parameter γvib˙is introduced to describe the vibration intensity. On the other hand,when the direction of vibration is perpendicular to the direction of rotation of the rotor, as is illustrated in Figure 2, formula (7) and formula (8) are simplified as formula (10).

(10)γ˙total=γ˙vib2+γ˙shear2

Now, HI theory is suitable under both vibration and shear condition. However, there is still something to modify in the calculation. First, the memory modules Γ and coagulation rate H are calculated by the total shear rate, which are shown in formula (11) and (12):

(11)Γ=∫0te−(t−t′)/maγ˙total(t′)dt′

(12)Hγ˙total,t=K(t)γ˙total2+l,t>0Hγ˙total,0=k1(1−U0)4l,t=0

At last, replacing γ˙withγ˙total,formula (1) is translated to formula (13), and is suitable to calculate the viscosity of cement paste under both shear and vibration condition.

(13)η=τγ˙=τ0γ˙total+μ

3 Results

Based on the shear-vibration equivalent theory and HI theory mentioned above, we designed the experiment described below. Firstly, measuring the apparent viscosity of cement paste at 20Hz vibration frequency using a self-made viscometer to calibrate the parameters of the logarithmic calculation in Table 1 and the newly added parameter γ˙vib.The settings of the experiment are given in Table 2. Then keeping the experimental setting unchanged, another experiment under 30Hz vibration frequency is performed and the apparent viscosity of the cement paste is also obtained. At last, only change the value of newly added parameter γ˙vib.to obtain the corresponding numerical calculated apparent viscosity.

The measured viscosity in experiment and numerical calculation of cement paste under vibration of 20Hz frequency is shown in Figure 4(a). The parameter settings of numerical calculation are given in Table 3. It can be seen from Figure 4(a) that the error of the whole process is less than 7%, and the experiment results agree well with the numerical results. Keeping the experiment settings unchanged and only adjusting the numerical calculation parameter γ˙vibto 21, the experiment and numerical results are obtained as Figure 4(b). Since the rotational rheometer rotates unstably at first, the error is relatively large in the first 5 seconds. When the rheometer rotates stably, the error begins to drop less than 8%.

Figure 4

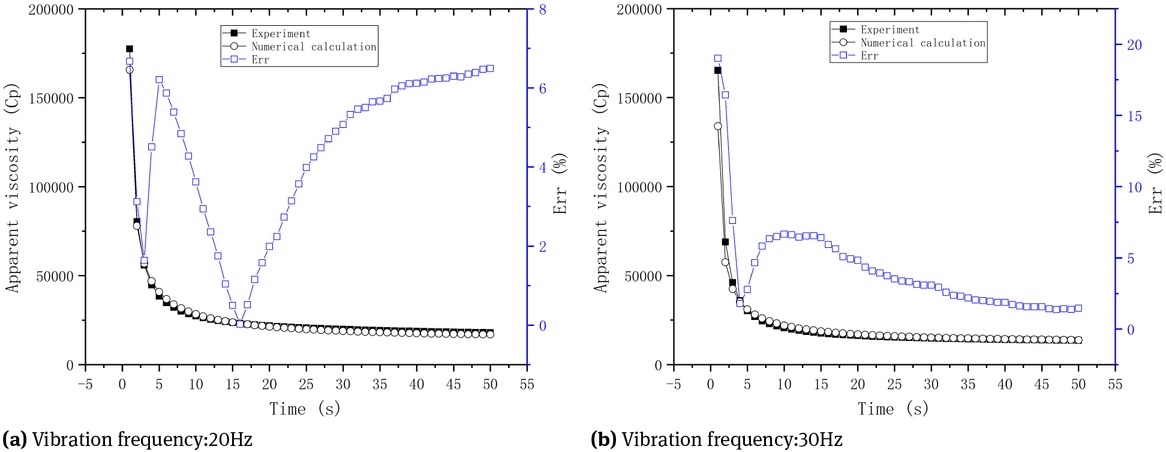
Experiment and numerical calculation of apparent viscosity

Through the calibration and comparison of Figure 4(a), it is proved that the shear-vibration equivalent theory is reliable when applied with HI theory. And the consistency of apparent viscosity in experiment and numerical calculation by only changing the newly added parameter γ˙vibindicates the success of simplification of the vibration intensity. Above all, the feasibility of shear-equivalent theory applied to cement paste under vibration is verified.

4 Discussion

In this chapter, we use the combination of shear-vibration equivalent theory and HI theory to study the effect of vibration intensity on the rheological properties of cement paste. In other words, the parameter γ˙vibrepresenting for vibration intensity is changed in the following numerical calculation. The process of rheological model of cement paste changing from Bingham model to Hersey-Bulkley model under vibration, and finally to Power-Law fluid is also presented.

In Figure 5, curves of apparent viscosity calculated under the conditions γ˙vib = 0, 10, 20, 30, 40 are obtained. As the increase of rotation speed, the apparent viscosity of cement paste is gradually decreasing, and as the increase of vibration intensity, namely γ˙vib,the apparent viscosity of vibrating cement paste will gradually approach to the curve without vibration

Figure 5

Apparent viscosity at γ˙vib= 0, 10, 20, 30, 40

Since the viscosity of the cement paste is affected by the combination of time and shearing action, it is not reasonable to use only one test to change the rotational speed of the rotary viscometer to obtain multiple sets of data, because the data measured by this method are affected by the previous shear history.

In this paper, a set of simulation tests is used to obtain only a set of data at one single speed to reduce the impact of other factors on the data. The details are as follows:

1. Select the rotary viscometer and get its dimension parameters. Select the type and proportion of cement and vibration state. Based on the above selection, obtain the parameters of PFI theory.

2. The rotational speed is selected to calculate the change of apparent viscosity and torque of cement paste with time until the apparent viscosity and torque of the cement paste tend to be stable.

3. Calculate the average value of the viscosity of the cement paste and the average value of the torque.

Repeat steps 2 and 3, obtain the torque and viscosity values at a series of speeds, which are shown in Figure 6.

Figure 6

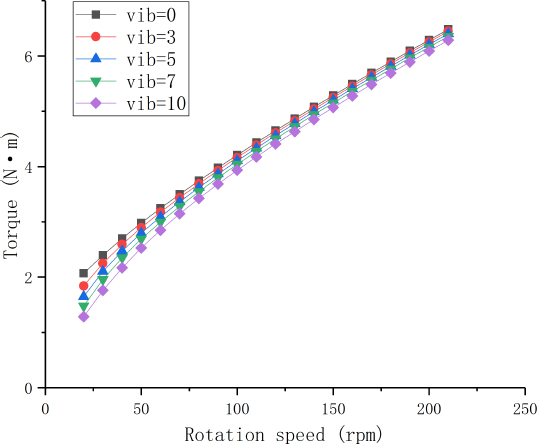
Torque at γ˙vib = 0, 3, 5, 7, 10

When γ˙vibis 0,3,5,7,10,20 respectively, the curves acquired by numerical calculations are shown in Figure 6, whose fit functions are given in Table 4.

Through the above description, the following conclusions can be obtained:

1. Non-vibration cement paste can be considered as Bingham fluid approximately. When vibration is applied to cement paste, its rheological properties obey Hershel-Bulkley model. With the further increase of vibration intensity, it can be approximated as Power-Law model.

2. As the intensity of vibration increases, the difference between the apparent viscosity under vibration and without vibration increases.

3. As shear rate increases, the curve of apparent viscosity under vibration approaches to the curve without vibration.

The above conclusions are consistent with the conclusions which Tattersall [1] suggested in the experiment. It can be considered that combining vibration with the thixotropy of cement paste is able to express the rheological changes of cement paste to some extent.

5 Conclusion

Cement paste is a suspension of cement particles in water. It shows different characteristics compared to pure fluid, namely, the viscosity and yield value of cement paste change with time. In this paper, the combination of vibration and shearing action is utilized to obtain the viscosity change process of cement paste. From the microscopic structure, the mechanism of the change of rheological properties of cement paste under vibration is explained, and the calculation method of viscosity of cement paste under vibration is acquired. A consistent theory is proposed for cement paste under vibration and without vibration. The correctness and credibility of this theory are verified by experiments.

In conclusion, cement paste under vibration has the following characteristics:

1. As the intensity of vibration increases, the rheological model of cement paste changes from Bingham model to Hershel-Bulkley model and then to Power-Law model.

2. When measuring the viscosity of cement paste under vibration state by rotational rheometer, as the intensity of vibration increases, the measured viscosity can be regarded as the viscosity of the cement paste under vibration, for the reason that the shear rate produced by the rotational rheometer is negligible.

3. As the intensity of vibration increases, the effect from vibration is getting smaller and smaller on the apparent viscosity of cement paste. In other words, there is a peak in the effect of vibration on the viscosity of cement paste. Above this value, the apparent viscosity no longer decreases with increasing vibration intensity.

The peak value of the effect of vibration intensity on apparent viscosity of cement paste is not given in this paper, and further study is needed in the future.