Molecular aromaticity: a quantum phenomenon

Introduction

The United Nations has declared 2025 the International Year of Quantum Science and Technology (IYQ). ¹ In this paper, we contribute to the special issue of the Pure and Applied Chemistry journal that celebrates the IYQ. And we do so by discussing an important property in chemistry, which is aromaticity. In the realm of aromaticity, misunderstandings and disagreements over the definition of aromaticity and the aromatic nature of specific systems are frequent. ² Despite the abundance of studies, reviews, and conferences published, there is still no universally accepted definition of aromaticity. In these cases, it is useful to resort to the simplest models in which aromaticity could play a role, and from them learn the foundations of the concept before starting to analyze more complex situations.

In a recent publication, Solà and Bickelhaupt ³ compared the solutions of the particle on a ring (POR) and the particle in a box (PIB) simple physical models to demonstrate that the phenomenon of aromaticity is deeply rooted in fundamental quantum mechanics. The particle in the cyclic POR model is more stable than that of the corresponding PIB model for a box and a ring of the same length. The main reasons for this are that the cyclic system has a much more stable lowest-energy eigenvalue and degenerate higher-energy eigenvalues that allow it to hold twice as many particles per “shell” before the subsequent higher-energy eigenfunctions are populated (see Fig. 1). Consequently, a zeroth-order approximation to the so-called aromatic stabilization energy (ASE) is recovered by the POR and PIB model systems. Not only that, but also with the molecular orbital distribution obtained with the POR model, closed-shell electronic structures are obtained with 2, 6, 10, 14… π-electrons, i.e., with 4 N + 2 π-electrons (N = 1, 2, 3…), resulting in the Hückel rule. ⁴ Moreover, a last shell half-filled with same-spin electrons is reached with 4 N π-electrons leading to aromaticity in the lowest triplet state, which is nothing but the Baird rule. ⁵ Therefore, the two most important rules of aromaticity ⁶ can already be derived from the POR model.

Fig. 1:

Energy levels for a particle in a 1-dimensional box and for a particle on a ring of the same length as the box.

The wavefunction for the POR is completely delocalized and the energy of the ground state is zero (particle at rest with zero kinetic energy), whereas that of the PIB is partially localized and the energy of the ground state is h²/8 mL² (particle moving even at 0 K). The PIB is stabilized by just closing the two ends of a cage and generating a POR. A given particle delocalized in a closed circuit is more stable than the same particle in an open circuit. This has no classical explanation and can only be understood by applying the laws of quantum mechanics. Therefore, aromaticity is a quantum phenomenon. What we can learn from the comparison between the PIB and POR is that molecular aromaticity is reached when one has energetic stabilization due to electron delocalization in a closed circuit. This conclusion is already contained in what is likely the most widely accepted definition nowadays, which was provided in 2005 by Chen et al. ⁷ who defined aromaticity as “a manifestation of electron delocalization in closed circuits, either in two or in three dimensions. This results in energy lowering, often quite substantial, and a variety of unusual chemical and physical properties. These include a tendency toward bond length equalization, unusual reactivity, and characteristic spectroscopic features”.

According to our discussion in the preceding paragraphs, it makes sense to focus on the two primary characteristics of aromaticity – aromatic stabilization and electronic delocalization – while classifying the bond length equalization, ring currents (diatropic for aromatic species), and lack of reactivity as secondary features.

The energetic stability of the delocalized structure of cyclic π-conjugated molecules obtained just by being cyclic is one of the most significant features of the aromaticity phenomenon. The ASE is a well-established metric for determining whether cyclic conjugated compounds are aromatic or antiaromatic. ⁸ Theoretically or empirically, this amount can be obtained from suitable homodesmotic processes. Homodesmotic reactions are a particular case of isodesmic reactions (reactions with equal number of formal single and double bonds in products and reactants) in which there is a same number of bonds between given atoms in each hybridization state in products and reactants. Homodesmotic reactions minimize different sources of errors, like lack of compensation in strain, hyperconjugation, anomeric effects, etc. ⁹ The main problem in ASE calculations is the choice of appropriate reference molecules. If one can find a suitable reference, the ASE should be provided in aromaticity studies because it is one of the primary properties of (anti)aromatic compounds.

Cyclic delocalization of mobile electrons in closed circuits of two or three dimensions is the second of the key aspects that characterize aromatic compounds. There is no experimental attribute that permits direct measurement of electronic delocalization as it is not an observable and, consequently, there is not a single, generally accepted method to measure this property from a theoretical standpoint. Numerous methods have been devised to ground this idea in theoretically correct quantum mechanics, many of which are based on the electron-pair density. The most used methods to quantify electronic delocalization in aromatic compounds are: ¹⁰

1. The multicenter DI or multicenter electron sharing index (Mc-ESI), the so-called I_ring, ¹¹ between the M centers A ₁ to A _M of a given ring, which is a generalization of the delocalization index (DI) ¹² providing a measure of the electron sharing between two atoms in the molecule. And the multicenter index (MCI), which was defined by Bultinck and coworkers ¹³ using the I_ring expression but taking into account all possible permutations of the M atoms in the ring.

2. The electron localization function (ELF), which has been proved so far a valuable tool to determine the location of electrons pairs. ¹⁴ When the ELF value defining a reducible localization domain is increased, this latter is split for a given ELF value giving rise to two new domains sharing a (3,-1) critical point. The ELF value where a domain splits is called a bifurcation point. The ELF value at the bifurcation points can be used as an indirect measure of aromaticity. ¹⁵

3. The electron density of delocalized bonds (EDDB) method, which decomposes the one-electron density (ED) in several ‘layers’ representing different levels of electron delocalization. ¹⁶ These layers include the electron density of localized bonds (EDLB), which represents typical (2-center 2-electron) Lewis-like bonds; the density of electrons localized on atoms (EDLA), which represents inner shells, lone pairs, etc.; and EDDB, which represents electron density that cannot be assigned to atoms or bonds because of its (multicenter) delocalized nature.

4. Other indices such as the para-delocalization index (PDI), ¹⁷ the bond-order index of aromaticity (BOIA), ¹³ the aromatic fluctuation index (FLU) ¹⁸ or the θ aromaticity index, ¹⁹ which are also frequently used to analyze electron delocalization in (anti)aromatic species.

In the Valence Bond language, electron delocalization in closed 2D or 3D circuits, which is a condition for a system to be classified as aromatic, is present in systems that require the use of several resonance structures with similar or equal weights to represent their structure (Fig. 2). The most obvious example is benzene with the two resonance structures depicted in Fig. 2a that are needed to have a good description of the molecule. It is worth mentioning that there is no clear relation between the number of resonance structures and aromaticity. For instance, C₆₀ has 12.500 covalent resonance structures ²⁰ and it is not considered an aromatic molecule. The reason is that a single resonance structure in C₆₀ (that with a radialene-type bonding pattern) describes reasonably well the molecule. Therefore, it is not only the number of resonance structures but also their weights, which should be similar in aromatic compounds.

Fig. 2:

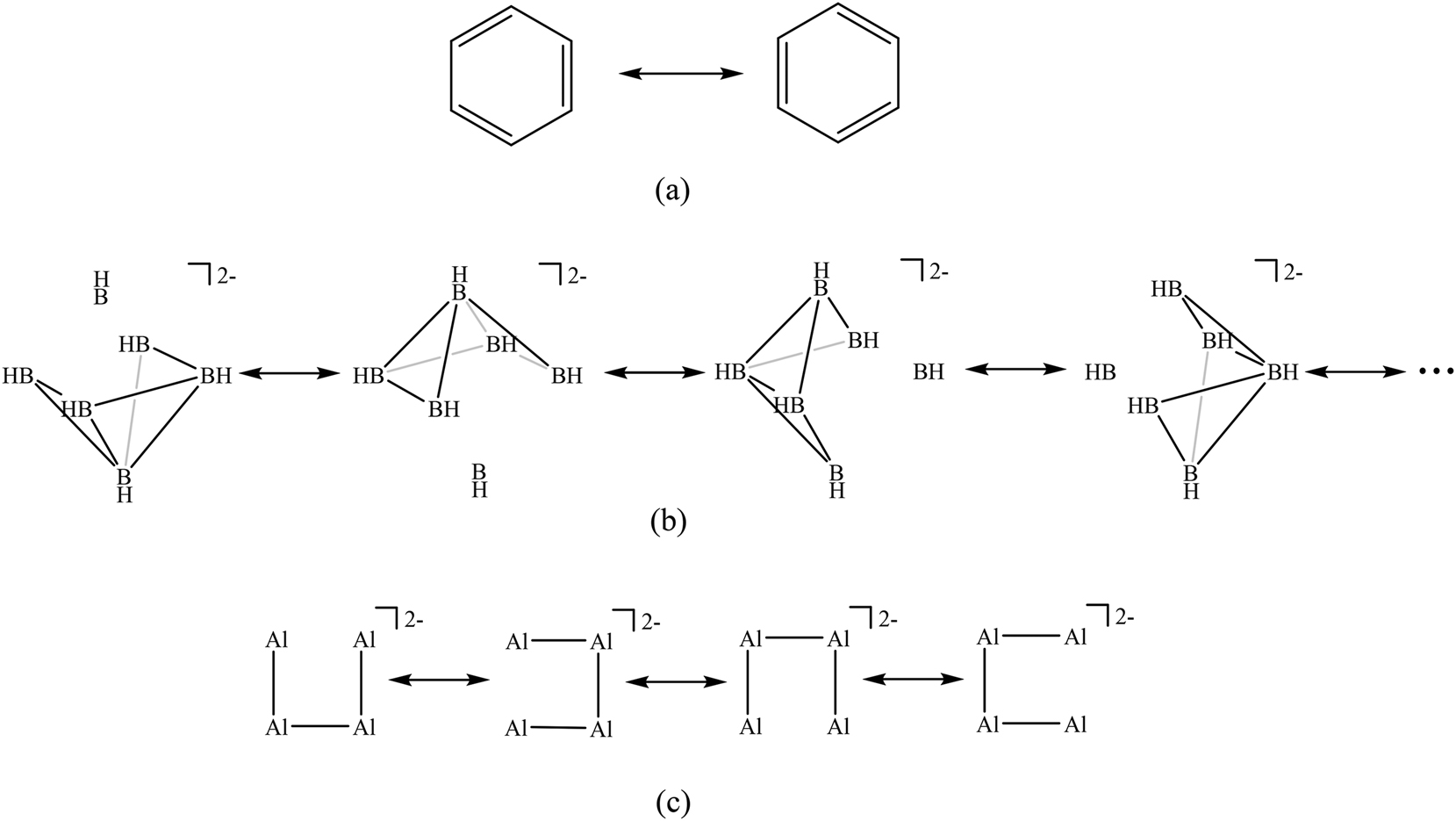
Same weight resonance structures for (a)benzene with 6π-electrons, (b) B₆H₆ ²⁻ with 14 cage electrons (only 4 out of the 792 possible resonance structures are depicted), and (c) Al₄ ²⁻ with 14 valence electrons (8 out of 14 valence electrons remain in the 2s orbitals of Al atoms).

C₁₈ as an example

In 1989, cyclo[18]carbon (C₁₈) was generated and detected for the first time with time-of-flight mass spectroscopy. ²¹ The C₁₈ allotrope has only two-coordinated carbon atoms, as opposed to three-coordinated carbon atoms found in fullerenes, carbon nanotubes, and graphene. It has been consistently shown that C₁₈ exists in the gas phase as a highly reactive species. ²² C₁₈’s high reactivity made it impossible to determine its shape experimentally and prompted multiple quantum-mechanical calculations of its structure. ^{23 , 24 , 25 , 26 , 27} Out-of-plane and in-plane π-molecular orbitals (MOs) characterize the two π-conjugated (π_in and π_out) systems of C₁₈, which contribute differently to its stability. For C₁₈, two symmetric geometries have been taken into consideration: a doubly cumulenic (D_18h) and a D_9h polyynic structure with alternating single and triple bonds or, preferably, alternating short and long bonds. ²⁸ Kaiser et al. ²⁹ in 2019 used high-resolution atomic force microscopy (AFM) to analyze C₁₈ and their results supported the polyynic structure of C₁₈ on the NaCl surface. From a theoretical point of view, most DFT calculations of C₁₈ predict the D_18h symmetry ²³ whereas the Hartree–Fock (HF) and Coupled Cluster methods give the D_9h structure, ^{24 , 25} the D_18h structure being a transition state between two D_9h species with a barrier of ca. 10 kcal/mol. ^{26 , 30} The coupled cluster method predicts a polyynic structure of C₁₈ with bond lengths of 1.238 and 1.383 Å. ²⁵ Increasing the amount of the exact HF exchange in a DFT functional stabilizes the correct polyynic structure comparing to the cumulenic one. ²⁷

The aromaticity of C₁₈ has been computationally analyzed in several works. ^{28 , 30 , 31 , 32} All these studies focused on the calculated magnetic measures of aromaticity such as the nucleus-independent chemical shift (NICS) and ring currents with few exceptions. ^{28 , 32} Ring currents indicate that D_9h polyynic and D_18h cumulenic structures of C₁₈ are both diatropic, and, consequently, aromatic. Indeed, the cumulenic and polyynic structures are classified as double aromatic with two orthogonal π-systems of 18 π-electrons each, although some authors point out that bond-length alternating polyynic structure is less aromatic than the non-alternating transition state structure. ³⁰ For the D_18h cumulenic structure of C_18, there are two resonance structures of the same weight, which seems to support its aromatic character (Fig. 3b). However, for the D_9h polyynic structure of C₁₈, one does not need more than a single resonance structure to have a reasonable representation of the molecule (Fig. 3a). Therefore, the conclusion that the D_9h polyynic structure of C₁₈ is aromatic is surprising because the π-electrons are localized in the triple bonds and not delocalized through the whole ring. If there is no π-delocalization, there is no aromaticity.

Fig. 3:

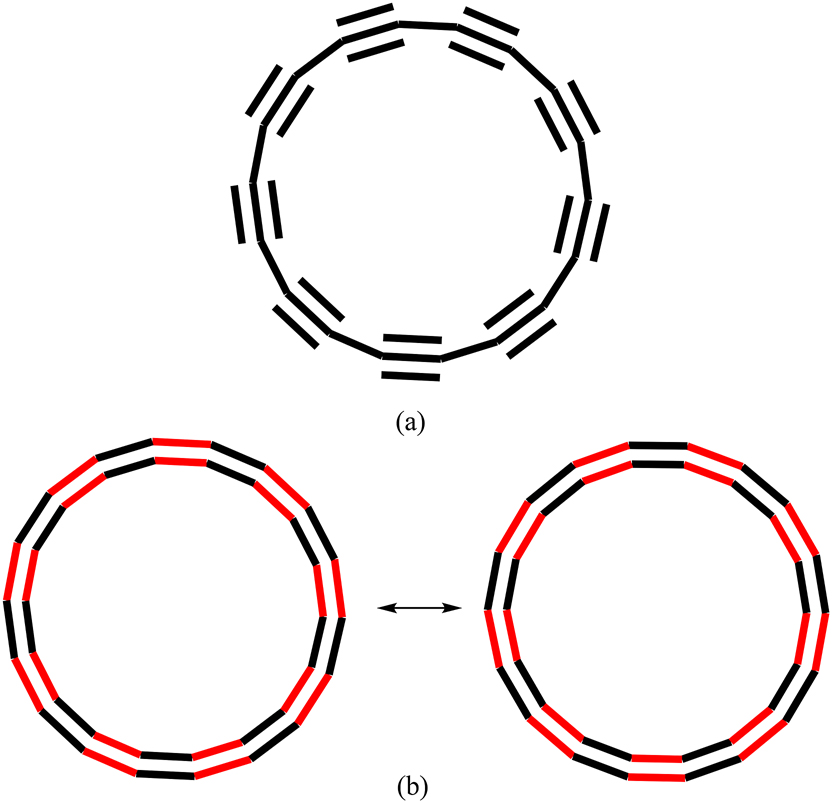
Main resonance structures for (a) D_9h polyynic and (b) D_18h cumulenic structures (red π_in and black π_out) of C₁₈.

As said before, ring currents should be considered a secondary characteristic of aromaticity. To make more reliable conclusions about the aromaticity of a given system, one should compute the ASE and/or analyze the electron delocalization. As in many other molecules, the calculation of the ASE in C₁₈ is not easy because the lack of a clear system of reference (although calculation of extra cyclic resonance energy (ECRE_π) shows residual stabilization in C₁₈ ³³ ). However, the electron delocalization can be easily computed using the EDDB method (calculation of I_ring or MCI is not affordable for rings of this size). A previous work ²⁸ has analyzed the electron delocalization with the ELF and LOL functions, but still the conclusion mainly based on the ring current was that C₁₈ is a doubly aromatic molecule.

The EDDB results obtained with the DLPNO-CCSD(T)/CBS//ωB97M-V/def2-QZVPP method are shown in Fig. 4. At this level of theory, the polyynic structure is more stable than the cumulenic one by 9.8 kcal/mol (T₁diag < 0.014). The total π-electron population is separated into the π-electrons in localized bonds (EDLB) and the delocalized π-electrons (EDDB). Let us discuss first the D_18h cumulenic structure. As can be seen in Fig. 4, both the π_out and π_in systems have ca. 18 delocalized electrons (99 % of the total population of electrons in the π-cloud is delocalized). Therefore, from an electronic viewpoint, the D_18h cumulenic structure, i.e. the transition structure between two D_9h polyynic structures, could to be considered aromatic. If we now move to the D_9h polyynic structure, we find that about 14 electrons are localized in both the π_out and π_in systems, that is a 78 % of the π-electrons are localized in the short bonds of the D_9h C₁₈ species. Only 22 % of the electrons (about 4 e) are delocalized. Such a small percentage indicates prevalence of a single resonance form and hence lack of aromaticity. Admittedly, there is some conjugation effect, typical for acyclic systems (like for instance in 1,3-butadiyne), that makes the formal triple (single) bonds longer (shorter) than expected, but it is obviously not enough to claim aromaticity in the polyynic structure of C₁₈.

Fig. 4:

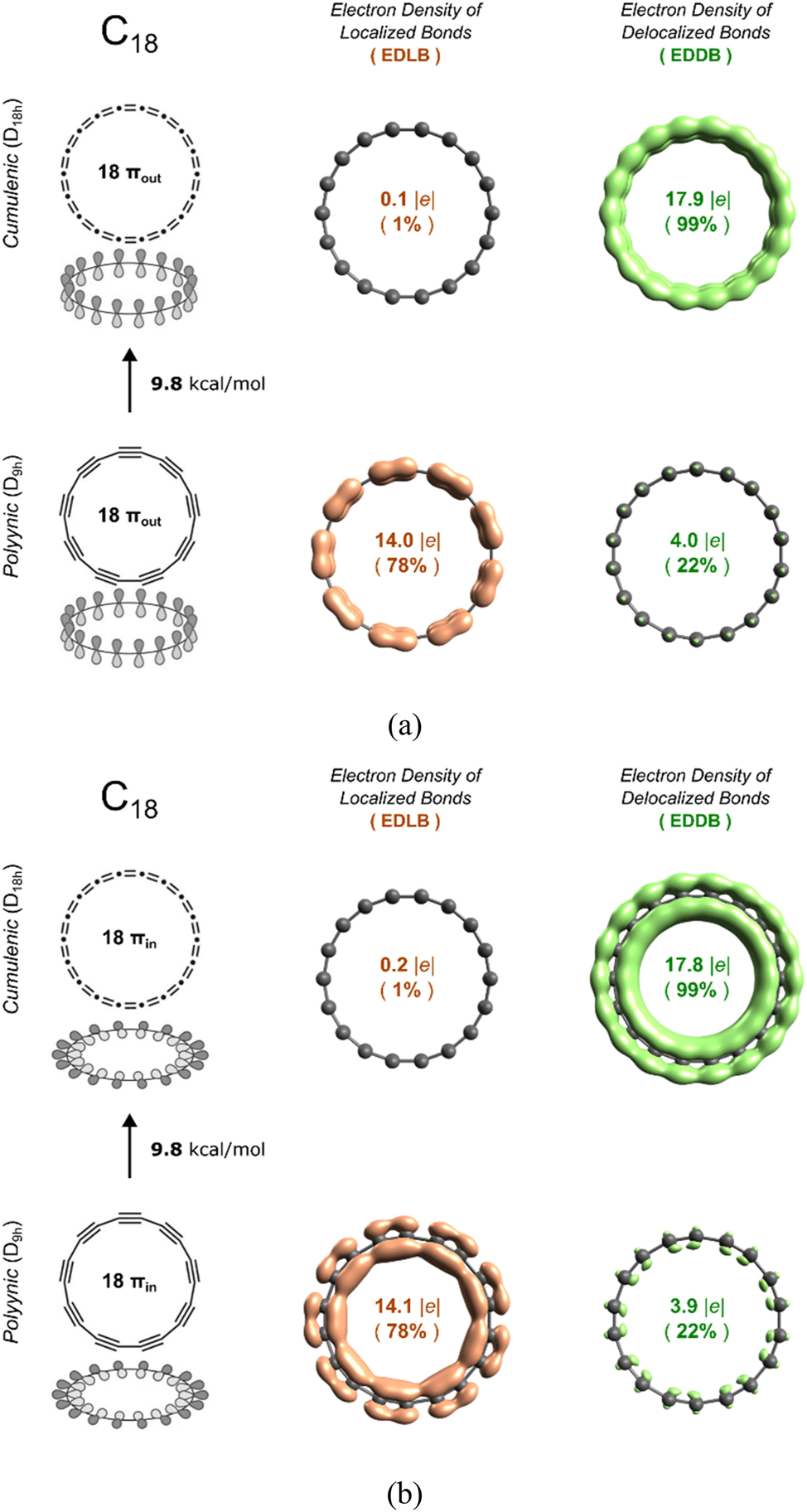
EDLB and EDDB results for (a) the π_out system of D_18h cumulenic and D_9h polyynic structures and (b) the πin system of D_18h cumulenic and D_9h polyynic structures.

Based on the mere fact that the delocalized cumulenic structure of C₁₈ has significantly higher electronic energy than the localized polyynic one can conclude that electron delocalization in C₁₈ is not associated with aromatic stabilization effect, and thus such species should be classified as non-aromatic. But which are the physical reasons for the higher stabilization of the localized polyynic structure of C₁₈ as compared to the delocalized cumulenic structure? As shown in the POR model, under the periodic boundary conditions hypothetical non-interacting particles prefer the delocalized situation because of the reduction in their kinetic energy. In molecular rings, a uniform distribution of electrons in the π-cloud and the resulting kinetic energy decrease are associated with a much tighter electron binding effect due to increased Coulomb interactions between electrons and the cyclically arranged nuclei. This extra stabilization of cyclic over acyclic molecular topology is particularly important in small systems, where it determines the specific (delocalized) bonding pattern and lower reactivity. However, in larger molecular rings, the extra stability due to uniform distribution of charge and coherence of the wavefunction is counterbalanced by the extra cost of the exchange correlation between electrons of the same spin, which is distortive in nature. In other words, the more cyclically delocalized π-electrons in the ring, the higher the cost of the exchange-correlation at large distances, ³⁴ and, at some point, breaking the symmetry and localizing π-bonds is the best way to minimize these destabilizing interactions (cf. the second-order Jahn–Teller effect in C₁₈). ³⁵ This effect is also present in annulenes, C _n H _n . ^{36 , 37} When n increases, the ASE decreases and starting from n ≈ 34, the ASE value is less than 1 kJ/mol, ³⁷ not enough to consider these species aromatic. Then, it is not surprising that a species like C₁₈ with 36 π-electrons prefers the localized to the delocalized structure. For this reason, C₁₈ has to be classified as a non-aromatic molecule. This conclusion is in line with a recent study by Baranac-Stojanović ³³ on cyclo [2n]carbons (n = 3 – 12), where the author concluded that starting from n = 8, the π_in and π_out systems are nearly localized and energetically almost unaffected by (anti)aromaticity.

Conclusions

As happens with many other important concepts in chemistry, aromaticity is not well defined. However, it is a phenomenon deeply rooted in fundamental quantum mechanics, as can be demonstrated by solving the Schrödinger equation for the particle in a box and particle on a ring models. In this contribution, we consider that aromatic compounds are those species that are stabilized because of their electronic delocalization in closed 2D or 3D circuits. If we take this definition as granted, then the C₁₈ molecule has to be considered a non-aromatic molecule, in contradiction with a number of studies that consider this molecule aromatic based on magnetic criteria. Finally, it is worth noting that the conclusion whether C₁₈ is aromatic or not depends on the definition of aromaticity. This is why, we consider it important to revise and update the current IUPAC definition of aromaticity. ³⁸