Finite vertex-based resolvability of supramolecular chain in dialkyltin

Xiujun Zhang; Muhammad Tanzeel Ali Kanwal; Muhammad Azeem; Muhammad Kamran Jamil; Muzammil Mukhtar

doi:10.1515/mgmc-2022-0027

Article Open Access

Finite vertex-based resolvability of supramolecular chain in dialkyltin

Xiujun Zhang , Muhammad Tanzeel Ali Kanwal , Muhammad Azeem , Muhammad Kamran Jamil and Muzammil Mukhtar

Published/Copyright: December 31, 2022

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information Explore this Subject

From the journal Main Group Metal Chemistry Volume 45 Issue 1

Abstract

For mammals, l-valine, which is a glycogen, is an essential amino acid. A protein made of 20 amino acids, salicylidene and l-valine make the carboxylate ligand which is the base of chiral Schiff. On a large scale, complexes with the ligand are utilized to help in the research work. To locate the exact location of a specific node from all the nodes, the entire node set is developed in a specific manner by choosing a particular subset and this subset is known as the resolving/locating set. This study contributed to the metric dimension of chemical complexes of supramolecular chain in dialkyltin from N-salicylidene-l-valine. We considered the complexes of 2,3,4 and ( C λ ⁎ ) chains and proved that the members of resolving sets are highly dependent on the number of vertices.

Keywords: N-salicylidene-l-valine; complex 2, 3, 4; supramolecular chain in dialkyltin; resolving set; finite metric dimension; complex chemical structures

MSC 2010: 05C12; 05C76

1 Introduction

In mathematics, graph theory means the study of graphs. The graph represents the set of vertices connected by the edges. Similarly, in the chemical graph theory, the atoms are represented by the nodes/vertices that are connected by the bonds/edges called the molecular graphs (Ahsan et al., 2020). Some chemical structures are more complicated and large such that these structures are not understandable. The chemical graph theory is defined as the study of graph theory with mathematics and chemical graphs (Imran et al., 2019; Siddiqui and Imran, 2015; Siddiqui et al., 2016).

To obtain the unique representations of the whole chemical structure, in structure, each atom/node is connected with bonds/edges that have distinct positions. A subset that gives the unique representations of the entire node set of a graph is called a resolving set, locating set, and metric basis in computer science applied sciences, and in pure mathematical terminologies, the minimum cardinality of resolving a set of unique representations is called locating number/metric dimension. The concept of metric basis and resolving sets was first introduced by Slater (1975) and later by Harary and Melter (1976).

2 Literature review

In the research work of Singh et al. (2021), authors discussed windmill graphs in terms of metric basis and their generalization. In the study by Moreno et al. (2021), authors discussed the generalized version of the metric dimension graph and they defined this parameter on two variables. In the work by Pirzada and Aijaz (2021), researchers computed metrics and their upper bounds on some generalized families of graphs. In the work of Azeem and Nadeem (2021), polycyclic hydrocarbons are detailed with the concept of metric and their generalizations. In the research work of Imran et al. (2018), symmetric graphs are obtained by the rooted product and they studied metrics and their generalizations. In the study by Koam et al. (2021), researchers give the idea of hollow coronoids on metric dimension and their generalization. In the research work by Koam et al. (2021a), the authors measured the resolvability of quartz structure, and particularly they computed metric parameters for the structure of quartz without considering the pendant nodes outside the circle. In the work by Anitha et al. (2021), the authors detailed the rough graphs on the topics of metric dimensions and their generalized parameters. In the research of Moscarini (2021), the author discussed hereditary bipartite and computing the metric basis of this generalized class of complex networks. In the study by Koam et al. (2019), the authors suggested the idea of pseudo valuation on KU-algebras and investigated the relationship between pseudo-valuations and KU-algebras and their generalizations. More reports on chemical networks and metric parameters of different chemical structures and networks are available in recent articles by Ahmad and Sultan (2017), Ahmad et al. (2018, 2020a, 2020b), Mahapatra et al. (2020), Raza et al. (2018, 2019a, 2019b), and Vetrik and Ahmad (2017).

There are shortlisted articles cited here to give some knowledge to the reader. Some articles show the chemical structure, and in that works of literature, most of the authors discussed the resolving sets in detail. Metric dimension is also important in any field to study the different structures such as chemical structures, computer networks/structures, and electric circuits, and also to build structures and networks forms. In pharmaceutical chemistry, drugs are represented in graph form. For mammals, l-valine, which is a glycogen, is an essential amino acid. A protein is made of 20 amino acids, salicylidene and l-valine make the carboxylate ligand which is the base of chiral Schiff. On a large scale, complexes with the ligand are utilized to help in the research work Belokon et al. (2009), Chen et al. (2004, 2007), Ucar et al. (2017), and Yu et al., (2015). To choose a unique shortest path of a structure for navigating a robot/submarine, metric parameters played an important role (Khuller et al., 1996). Process and recognition of patterns also utilized the concept of resolving set (Slater, 1975). Some concepts utilized in the electric field (Ahmad et al., 2022) and in the polymer industry (Nadeem et al., 2021) are recent discoveries of metric dimensions. For further details on this parameter, we refer to see papers by Azeem et al. (2021, 2022), Koam et al. (2021), Raza et al. (2021), Shabbir and Azeem (2021), and Wang et al., (2021).

3 Preliminaries

Some definitions giving idea to understand this work are given below.

Definition 1

(Nadeem et al., 2020)

Let G be a connected graph with vertex set V ( G ) , the distance between two vertices v 1 , v 2 ∈ V ( G ) is the length of shortest path between v 1 , v 2 , and it is denoted by d ( v 1 , v 2 ) .

Definition 2

(Nadeem et al., 2020)

Let R = { v 1 , v 2 , … v m } be an ordered set of vertices of G and let v ∈ V ( G ) . The representation r ( v | R ) of ( d ( v , v 1 ) , d ( v , v 2 ) , … , d ( v , v m )) . If different vertices of G have different representations with respect to R , it is called a resolving set/positioning set of G . A resolving set R of minimum cardinality is called metric dimension/locating number of G and is denoted by dim ( G ) .

4 Finite vertex-based resolvability of supramolecular chain in dialkyltin complex-2, C_2,λ

The supramolecular chain dialkyltin has four types of complexes, but we will discuss here three types of complexes 2, 3, and 4. Complex-2 of N-salicylidene-l-valine is shown in Figure 1. There are λ units, the first unit is connected with the vertices of the second unit and the second unit is connected with the vertices of the third, and the ( λ − 1) unit is connected with the vertices of λ unit. The order of C_2,λ is | V ( C 2, λ ) | = 21 λ and the size of C_2,λ is | E ( C 2, λ ) | = 25 λ − 2 . The vertex set and edge set of the complex is given in Figure 1. For more details, on this complex network, please refer the research work of Siddiqui et al. (2022).

V ( C 2, λ ) = { v i λ :1 ≤ i ≤ 21; λ ≥ 1},

E ( C 2, λ ) = { v i λ v i + 1 λ :1 ≤ i ≤ 12; λ ≥ 1} ∪ { v 1 λ v 13 λ , v 3 λ v 11 λ , v 5 λ v 9 λ , v 4 λ v 14 λ , v 6 λ v 18 λ , v 7 λ v 19 λ , v 9 λ v 20 λ , v 9 λ v 21 λ , v 6 λ v 16 λ } ∪ { v i λ v i + 1 λ : i = 15, 16; λ ≥ 1} ∪ { v 8 λ v 14 λ + 1 , v 19 λ v 18 λ + 1 ; λ ≥ 1} .

Figure 1

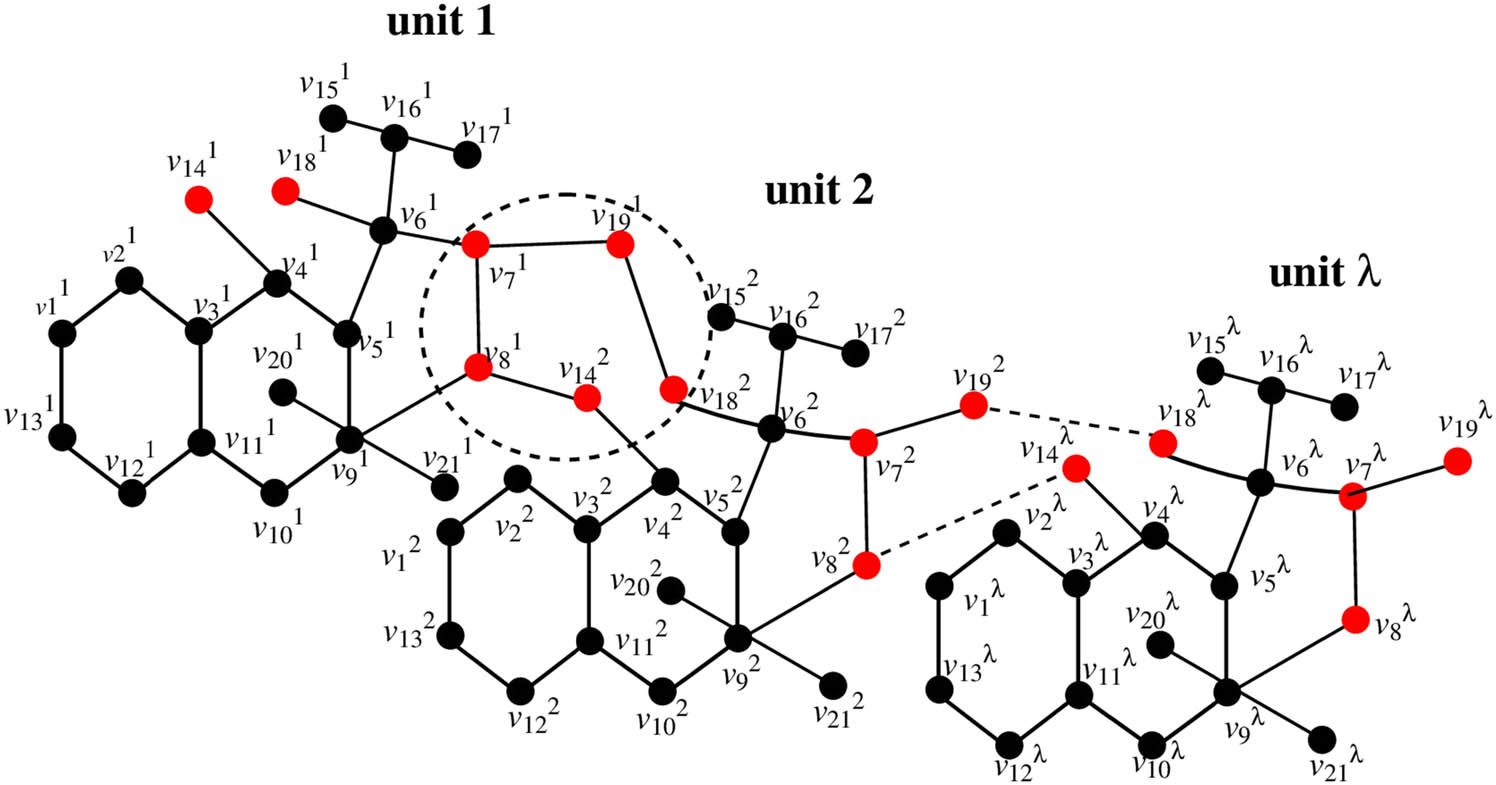
Supramolecular chain of complex-2.

Theorem 1

If λ = 1, then d i m ( C 2,1 ) is 3.

Proof. To prove that d i m ( C 2,1 ) ≤ 3, for this assume a resolving set R = { v 1 1 , v 15 1 , v 20 1 } . We construct the following cases on the vertex set of ( C 2,1 ) :

r ( v i 1 | R ) = ( d ( v i 1 , v 1 1 ) , d ( v i 1 , v 15 1 ) , d ( v i 1 , v 20 1 )) .

r ( v i 1 | R ) = ( i − 1,8 − i ,7 − i ) , i f i = 1,2, … ,5; ( i − 1,8 − i ,3 ) , i f i = 6; ( i − 1, i − 4,3 ) , i f i = 7; ( 14 − i , i − 4,2 ) , i f i = 8; ( 14 − i , i − 5, i − 8 ) , i f i = 9,10, … ,13; ( 4,5,4 ) , i f i = 14; ( 7, i − 15,5 ) , i f i = 15,17; ( 6, i − 15,4 ) , i f i = 16,18; ( 7, i − 15,4 ) , i f i = 19; ( 6, i − 15, i − 20 ) , i f i = 20; ( 6,5, i − 20 ) , i f i = 21;

Hence, it follows from the above arguments in the form of representation that dim ( C 2,1 ) ≤ 3 because all the vertices of ( C 2,1 ) have the unique representations with respect to resolving set R .

Now we prove that dim ( C 2,1 ) ≥ 3 . On contradictory, we assume dim ( C 2,1 ) = 2 . For this, consider the resolving set R ' with cardinality 2 . The discussion for this assumption as follows.

Case 1: Let R ' = { v 1 , v 2 } with cardinality 2 . The same is represented as follows: r ( v 13 | R ' ) = r ( v 15 | R ' ) .

Case 2: Let R ' = { v 1 , v 3 } with cardinality 2 . The same is represented as follows: r ( v 13 | R ' ) = r ( v 15 | R ' ) .

Case 3: Let R ' = { v i , v 12 } with cardinality 2 . The same is represented as follows: r ( v 13 | R ' ) = r ( v 15 | R ' ) , where 2 ≤ i ≤ 12 .

Case 4: Let R ' = { v i , v 13 } with cardinality 2 . The same is represented as follows: r ( v 8 | R ' ) = r ( v 12 | R ' ) , where 13 ≤ i ≤ 15 .

Case 5: Let R ' = { v 1 , v 16 } with cardinality 2 . The same is represented as follows: r ( v 13 | R ' ) = r ( v 15 | R ' ) .

Case 6: Let R ' = { v 1 , v i } with cardinality 2 . The same is represented as follows: r ( v 13 | R ' ) = r ( v 15 | R ' ) , where 16 ≤ i ≤ 21 .

Case 7: Let R ' = r ( v 1 , v i ) with cardinality 2 . The same is represented as follows: ⇒ r ( v α | R ' ) = r ( v β | R ' ) , where α = 8,13, and β = 12,15 .

Case 8: Let R ' = { v 4 , v 16 } with cardinality 2 . The same is represented as follows: r ( v 1 | R ' ) = r ( v 3 | R ' ) .

Case 9: Let R ' = { v i , v j } , i ≠ j with cardinality 2 . The identical representation is as follows: r ( v 13 | R ' ) = r ( v 15 | R ' ) , where 2 ≤ i , j ≤ 21 .

Correspondingly, there is no single possibility from the possible cases made by the whole vertex of C 2,1 . This shows that two metric dimension of C 2,1 is not possible. Hence, dim ( C 2,1 ) ≥ 3 . Thus,

(1) d i m ( C 2,1 ) = 3

Theorem 2

If λ ≥ 2, then dim ( C 2, λ ) is 3 λ .

Proof. To show that dim ( C 2, λ ) = 3 λ , we will apply the induction method on λ , the number of units of complexes. The case of λ = 1 is proved in Theorem 1.

dim ( C 2,1 ) = 3

Now we assume that this assertion is true for λ = m .

(2) dim ( C 2, m ) = 3 m

We will show that it is true for λ = m + 1 . Suppose

(3) dim ( C 2, m + 1 ) = dim ( C 2, m ) + dim ( C 2,1 )

Using Eqs. 1–3, we will get

dim ( C 2, m + 1 ) = dim ( C 2, m ) + dim ( C 2,1 ) , = 3 m + 3, = 3( m + 1)

Hence, the result is true for all the positive integers λ ≥ 1 .

5 Finite vertex-based resolvability of supramolecular chain in dialkyltin complex-3, C _3,λ

The complex-3 of N-salicylidene-l-valine has the λ units. The vertex of the second unit is connected with the vertex of the first unit and so on all the λ units are connected with the λ − 1 units. Figure 2 shows the generalized form of λ units. Each unit is labeled and the order of C 3, λ is | V ( C 3, λ ) | = 26 λ and the size of C 3, λ is | E ( C 3, λ ) | = 30 λ − 1 . The vertex set and edge set of complex-3 are given in Figure 2. For more details on this complex network, please refer the research workof Siddiqui et al., 2022.

V ( C λ ,3 ) = { v i λ :1 ≤ i ≤ 26; λ ≥ 1},

E ( C λ ,3 ) = { v i λ v i + 1 λ :1 ≤ i ≤ 14; λ ≥ 1} ∪ { v 1 λ v 15 λ , v 2 λ v 13 λ , v 4 λ v 9 λ , v 10 λ v 13 λ , v 8 λ v 19 λ , v 19 λ v 20 λ , v 12 λ v 21 λ , v 13 λ v 22 λ , v 22 λ v 23 λ , v 13 λ v 24 λ , v 24 λ v 25 λ , v 1 λ v 17 λ , v 15 λ v 26 λ } ∪ { v i λ v i + 1 λ : i = 6,17; λ ≥ 1} ∪ { v 25 λ v 26 λ : λ ≥ 1}

Figure 2

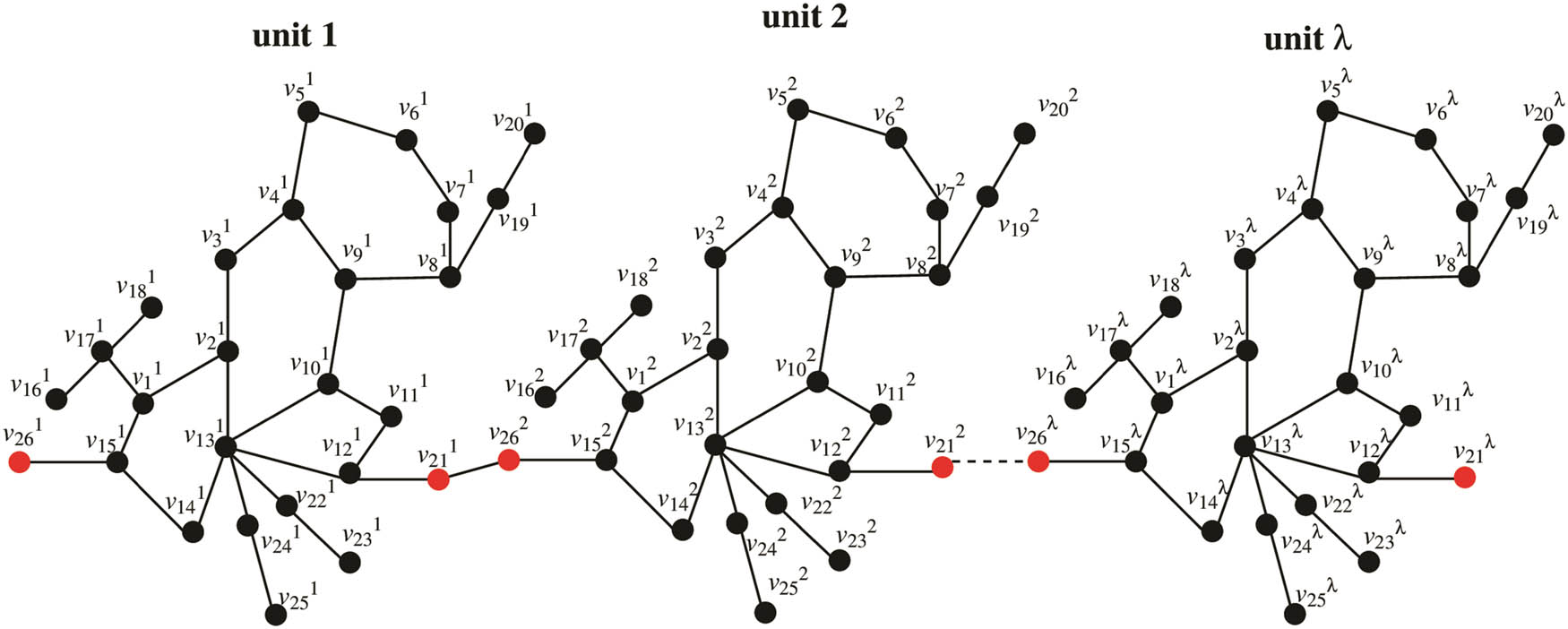
Supramolecular chain of complex-3.

Theorem 3

If λ =1, then dim ( C 3,1 ) is 5.

Proof. To prove that dim ( C 3,1 ) ≤ 5, assume a resolving set R = { v 5 1 , v 11 1 , v 18 1 , v 20 1 , v 24 1 } . We construct the following cases on vertex set of ( C 3,1 ) :

r ( v i 1 | R ) = ( d ( v i 1 , v 5 1 ) , d ( v i 1 , v 11 1 ) , d ( v i 1 , v 18 1 ) d ( v i 1 , v 20 1 ) , d ( v i 1 , v 24 1 ) ) ,

r ( v i 1 | R ) = ( |5 − i |,5 − i , i + 1,8 − i ,4 − i ) , if i = 1,2; ( |5 − i |,7 − i , i + 1,8 − i , i ) , if i = 3,4; ( |5 − i | , i − 1, i + 1,10 − i ,6 ) , if i = 5; ( |5 − i | , i − 1, i + 1,10 − i ,12 − i ) , if i = 6; ( |5 − i |,11 − i , i + 1,10 − i ,12 − i ) , if i = 7; ( |5 − i |,11 − i ,15 − i ,10 − i ,12 − i ) , if i = 8; ( i − 7,11 − i ,17 − i , i − 6,14 − i ) , if i = 9,10; ( i − 7,11 − i ,17 − i , i − 6,14 − i ) , if i = 11,12; ( i − 9,11 − i ,17 − i , i − 8,14 − i ) , if i = 13; ( i − 9,11 − i ,18 − i , i − 8, i − 12 ) , if i = 14; ( i − 10,11 − i ,18 − i , i − 8, i − 12 ) , if i = 15; ( i − 10,24 − i ,18 − i ,25 − i ,21 − i ) , if i = 16; ( i − 11,24 − i ,18 − i ,25 − i ,21 − i ) , if i = 17; ( i − 11,18,18 − i ,9,5 ) , if i = 18; ( i − 15, i − 15, i − 11,20 − i , i − 14 ) , if i = 19,20; ( i − 15, i − 19,27 − i ,7,24 − i ) , if i = 21; ( i − 17, i − 19,27 − i , i − 16,24 − i ) , if i = 22; ( i − 17, i − 19,29 − i , i − 16,3 ) , if i = 23; ( i − 19, i − 21,29 − i , i − 18, i − 24 ) , if i = 24; ( i − 19, i − 21,2(28 − i ) , i − 18, i − 24 ) , if i = 25; ( 6, i − 21,2(28 − i ) , i − 18,4 ) , if i = 26;

Hence, it follows from the above arguments in the form of representation that dim ( C 3,1 ) ≤ 5 because all the vertices of ( C 3,1 ) have the unique representations with respect to resolving set R.

Now we prove that dim ( C 3,1 ) ≥ 5 . On the contrary, we consider resolving set R ' of cardinality 4 . Following are the discussions for this assumption.

Case 1: Let R ' = { v 1 , v 2 , v 3 , v 4 } with cardinality 4 . The same is represented as follows: r ( v 21 | R ' ) = r ( v 25 | R ' ) .

Case 2: Let R ' = { v 1 , v 2 , v 3 , v i } with cardinality 4 . The same is represented as follows: r ( v 21 | R ' ) = r ( v 25 | R ' ) , where 5 ≤ i ≤ 20 .

Case 3: Let R ' = { v 1 , v 2 , v 3 , v 2 1} with cardinality 4 . The same is represented as follows: r ( v 9 | R ' ) = r ( v 16 | R ' ) .

Case 4: Let R ' = { v 1 , v 2 , v 3 , v i } with cardinality 4 . The same is represented as follows: r ( v 9 | R ' ) = r ( v 16 | R ' ) , where 23 ≤ i ≤ 26 .

Case 5: Let R ' = { v 1 , v 2 , v 3 , v i } with cardinality 4 . The same is represented as follows: r ( v α | R ' ) = r ( v β | R ' ) , where α =9,21 and β =16,25 .

Case 6: Let R ' = { v 1 , v 2 , v 4 , v 5 } with cardinality 4 . The same is represented as follows: r ( v 21 | R ' ) = r ( v 25 | R ' ) .

Case 7: Let R ' = { v 1 , v 2 , v i , v j } , i ≠ j with cardinality 4 . The same representation are; r ( v 21 | R ' ) = r ( v 25 | R ' ) , where 3 ≤ i ≤ 20 and 5 ≤ j ≤ 20 .

Case 8: Let R ' = { v 1 , v 2 , v 4 , v 2 1} with cardinality 4 . The same is represented as follows: r ( v 9 | R ' ) = r ( v 16 | R ' ) .

Case 9: Let R ' = { v 1 , v 2 , v i , v j } ; i ≠ j with cardinality 4 . The same is represented as follows: r ( v 9 | R ' ) = r ( v 16 | R ' ) , where 3 ≤ i ≤ 26 and 21 ≤ j ≤ 26 .

Case 10: Let R ' = { v 1 , v 2 , v i , v j } r ( v α | R ' ) = r ( v β | R ' ) , where α = 9,21 and β = 16,25 .

Case 11: Let R ' = { v 1 , v 2 , v 5 , v 9 } with cardinality 4 . The same is represented as follows: r ( v 21 | R ' ) = r ( v 25 | R ' ) .

Case 12: Let R ' = { v 1 , v i , v j , v k } with cardinality 4 . The same is represented as follows: r ( v 21 | R ' ) = r ( v 25 | R ' ) , where 2 ≤ i ≤ 26, 3 ≤ j ≤ 26 and 4 ≤ k ≤ 26 .

Case 13: Let R ' = { v 1 , v i , v j , v k } with cardinality 4 . The same is represented as follows: ⇒ r ( v α | R ) = r ( v β | R ) , where α = 9,21, and β = 16,25 .

Case 14: Let R ' = { v i , v j , v k , v l } with cardinality 4 . The same is represented as follows: r ( v 21 | R ' ) = r ( v 25 | R ' ) , where 1 ≤ i ≤ 20, 2 ≤ j ≤ 20, 3 ≤ k ≤ 20 and 4 ≤ k ≤ 20 .

Case 15: Let R ' = { v i , v j , v k , v l } with cardinality 4 . The same is represented as follows: r ( v 9 | R ' ) = r ( v 16 | R ' ) , where 1 ≤ i ≤ 20, 2 ≤ j ≤ 20, 3 ≤ k ≤ 20, and 4 ≤ k ≤ 20 .

Case 16: Let R ' = { v i , v j , v k , v l } with cardinality 4 . The same is represented as follows: ⇒ r ( v α | R ) = r ( v β | R ) , where α = 9,21, and β = 16,25 .

Similarly, there is no single possibility from the feasible cases made by the entire vertex of C 3,1 . This shows that four metric dimension of C 3,1 is not possible. So d i m ( C 3,1 ) ≥ 5 .

Hence,

(4) dim ( C 3 , 1 ) = 5

Theorem 4

If λ ≥ 2, then dim ( C 3, λ ) is 4 λ + 1 .

Proof. To show that dim ( C 3, λ ) = 4 λ + 1 . We will apply the induction method on λ , the number of units of complexes. The case of λ = 1 is proved in Theorem 3.

dim ( C 3,1 ) = 5

Now, we assume that this assertion is true for λ = m .

(5) dim ( C 3, m ) = 4 m + 1

We will show that it is true for λ = 4 ( m + 1) + 1 = 4 m + 5 . Suppose

(6) dim ( C 3, m + 1 ) = dim ( C 3, m ) + dim ( C 3,1 ) − 1

Using Eqs. 4–6, we will get

dim ( C 3, m + 1 ) = dim ( C 3, m ) + dim ( C 3,1 ) − 1, = 4 m + 1 + 5 − 1, = 4 m + 5

Hence, the result is true for all the positive integers λ ≥ 1.

6 Finite vertex-based resolvability of supramolecular chain in dialkyltin complex-4, C _4,λ

The supramolecular chain in dialkyltin complex-4 of N-salicylidene-l-valine also has copies of λ units. In Figure 3, similar to complex-2 and complex-3, the second unit is connected with the vertices of first unit and similarly go on with the copies of λ units. The order of C 4, λ is | V ( C 4, λ ) | = 28 λ and the size of C 4, λ is | E ( C 4, λ ) | = 31 λ − 1 . The vertex set and edge set of complex-4 are given in Figure 3. For more details on this complex network, please the study by Siddiqui et al. (2022).

V ( C λ ,4 ) = { v i λ :1 ≤ i ≤ 28; λ ≥ 1},

E ( C λ ,4 ) = { v i λ v i + 1 λ :1 ≤ i ≤ 5; λ ≥ 1} ∪ { v i λ v i + 1 λ :7 ≤ i ≤ 9; λ ≥ 1} ∪ { v i λ v i + 1 λ :11 ≤ i ≤ 12; λ ≥ 1} ∪ { v i λ v i + 1 λ :14 ≤ i ≤ 16; λ ≥ 1} ∪ { v i λ v i + 1 λ :18 ≤ i ≤ 20; λ ≥ 1} ∪ { v i λ v i + 1 λ : 25 ≤ i ≤ 26; λ ≥ 1} ∪ { v 1 λ v 6 λ , v 3 λ v 7 λ , v 4 λ v 10 λ , v 8 λ v 11 λ , v 9 λ v 13 λ , v 11 λ v 26 λ , v 1 λ v 23 λ , v 5 λ v 22 λ , v 9 λ v 14 λ , v 9 λ v 18 λ , v 12 λ v 28 λ , v 7 λ v 24 λ ; λ ≥ 1} ∪ { v 28 λ v 24 λ + 1 ; λ ≥ 1}

Figure 3

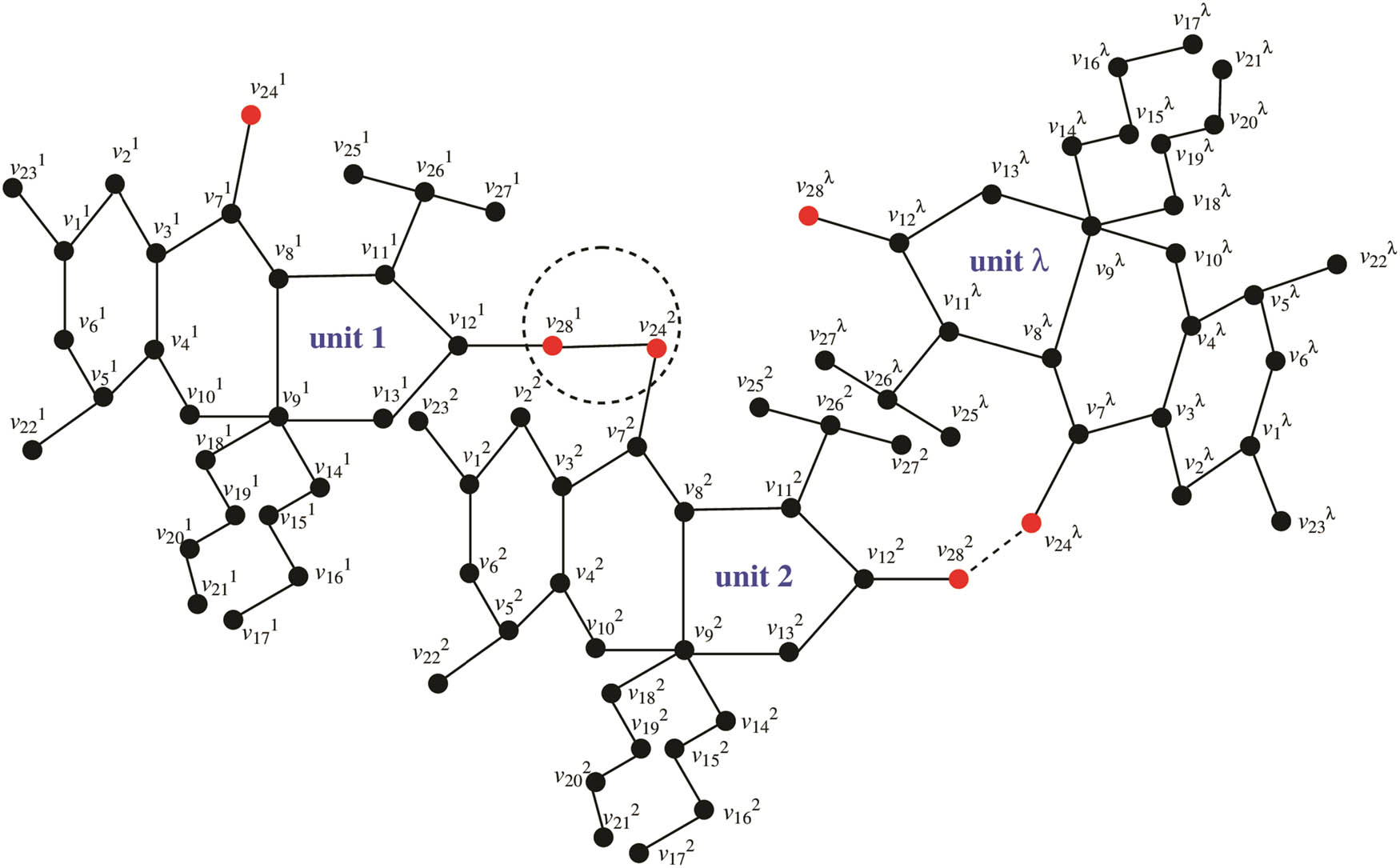
Supramolecular chain of complex-4.

Theorem 5

If λ =1, then dim ( C 4,1 ) is 3 .

Proof. To prove that dim ( C 4,1 ) ≤ 3, assume a resolving set R = { v 23 1 , v 21 1 , v 25 1 } . We create the following cases on the vertex set of ( C 4,1 ) : r ( v i 1 | R ) = ( d ( v i 1 , v 23 1 ) , d ( v i 1 , v 21 1 ) , d ( v i 1 , v 25 1 )) .

r ( v i 1 | R ) = ( i ,10 − i ,8 − i ) , if i = 1,2,3; ( i ,10 − i ,2 + i ) , if i = 4; ( 8 − i ,2 + i ,2 + i ) , if i = 5,6; ( i − 3,13 − i ,11 − i ) , if i = 7,8; ( i − 3,13 − i , i − 5 ) , if i = 9; ( i − 5, i − 5, i − 5 ) , if i = 10; ( i − 5, i − 5, i − 9 ) , if i = 11; ( i − 5,18 − i , i − 9 ) , if i = 12; ( 7,18 − i , i − 9 ) , if i = 13; ( i − 7, i − 9, i − 9 ) , if i = 14, … ,17; ( i − 11,21 − i , i − 13 ) , if i = 18, … ,21; ( 4,8,8 ) , if i = 22; ( 0,10,8 ) , if i = 23; ( 5,7,5 ) , if i = 24; ( 33 − i ,8, i − 25 ) , if i = 25; ( 33 − i ,7, i − 25 ) , if i = 26; ( 8,8, i − 25 ) , if i = 27; ( 8,7,4 ) , if i = 28;

Hence, it follows from the above arguments in the form of representation that d i m ( C 4,1 ) ≤ 3 because all the vertices of C 4, λ have the unique representations with respect to resolving set R.

Now we prove that d i m ( C 4,1 ) ≥ 3 . On the contradictory, we assume d i m ( C 4,1 ) = 2 . For this, consider the resolving set R ' with cardinality 2 . For this assumption, we discuss the following cases:

Case 1: Let R ' = { v 1 , v 2 , } with cardinality 2 . The same is represented as follows: r ( v 21 | R ' ) = r ( v 22 | R ' ) .

Case 2: Let R ' = { v 1 , v i , } with cardinality 2 . The same is represented as follows: r ( v 21 | R ' ) = r ( v 22 | R ' ) , where 2 ≤ i ≤ 20 .

Case 3: Let R ' = { v 1 , v 21 , } with cardinality 2 . The same is represented as follows: r ( v 9 | R ' ) = r ( v 11 | R ' ) .

Case 4: Let R ' = { v 1 , v i , } with cardinality 2 . The same is represented is as follows: r ( v 9 | R ' ) = r ( v 11 | R ' ) , where 21 ≤ i ≤ 28 .

Case 5: Let R ' = { v 1 , v 2 , } with cardinality 2 . The same represented as follows: r ( v α | R ' ) = r ( v β | R ' ) , where α = 9,21 and β = 11,22 .

Case 6: Let R ' = { v 2 , v 5 , } ; i ≠ j with cardinality 2 . The same is represented as follows: r ( v 21 | R ' ) = r ( v 22 | R ' ) , where 2 ≤ i , j ≤ 20 .

Case 7: Let R ' = { v 21 , v 22 , } with cardinality 2 . The same is represented as follows: r ( v 9 | R ' ) = r ( v 11 | R ' ) , where 22 ≤ i , j ≤ 28 .

Case 8: Let R ' = { v i , v j , } with cardinality 2 . The same is represented as follows: ⇒ r ( v α | R ' ) = r ( v β | R ' ) , where α = 9,21 and β = 11,22 .

Correspondingly, there is no single possibility from the possible cases constructed by the entire vertex of C 4,1 . This shows that two metric dimensions of C 4,1 is not possible. So, d i m ( C 4,1 ) ≥ 3 .

Hence,

(7) dim ( C 4,1 ) = 3

Theorem 6

If λ ≥ 2, then dim ( C 4, λ ) is 3 λ .

Proof. To show that dim ( C 4, λ ) = 3 λ . We will apply the induction method on λ , the number of units of complexes. The case of λ = 1 is proved in Theorem 5.

(8) dim ( C 4,1 ) = 3

Now, we assume that this assertion is true for λ = m .

(9) dim ( C 4, m ) = 3 m

We will show that it is true for λ = m + 1 . Suppose

(10) dim ( C 4, m + 1 ) = dim ( C 2, m ) + dim ( C 2,1 )

Using Equations 8–10, we will get

dim ( C 4, m + 1 ) = dim ( C 2, m ) + dim ( C 2,1 ) , = 3 m + 3, = 3( m + 1)

Hence, the result is true for all the positive integer λ ≥ 1.

7 Finite vertex-based resolvability of polyhedron generalized sheet of C 28, λ ∗

The structure of polyhedron generalized sheet of C 28 ∗ shown in Figure 4 is made by generalizing a C 28 ∗ polyhedron structure. The vertex of unit 2 is also connected with the vertex of unit 1 and vertex of unit 3 is connected with the vertex 2 and so on forming the generalized λ unit of C 28, λ ∗ . The order of C 28, λ ∗ is | V ( C 28, λ ∗ ) | = 26 λ + 2 and the size of C 28, λ ∗ is | E ( C 28, λ ∗ ) | = 34 λ + 1 . The vertex set and edge set of C 28, λ ∗ are given in Figure 4. This particular structure of C 28, λ ∗ polyhedron is given by Diudea and Nagy (2013).

V ( C 28, λ ∗ ) = { v i , u i ;1 ≤ i ≤ 13 λ + 1}

E ( C 28, λ ∗ ) = { v i v i + 1 , u i u i + 1 ;1 ≤ i ≤ 13 λ + 1} ∪ { v 14 u 14 , v 1 v 6 , v 13 λ + 1 v 13 λ + 6 , v 13 λ − 5 v 13 λ − 1 , u 1 u 6 , u 13 λ + 1 u 13 λ + 6 , u 13 λ − 5 u 13 λ − 1 } ∪ { v i u i ; i =1,6,8,12,13 λ + k & k =6,8,12,14: λ ≥ 1}

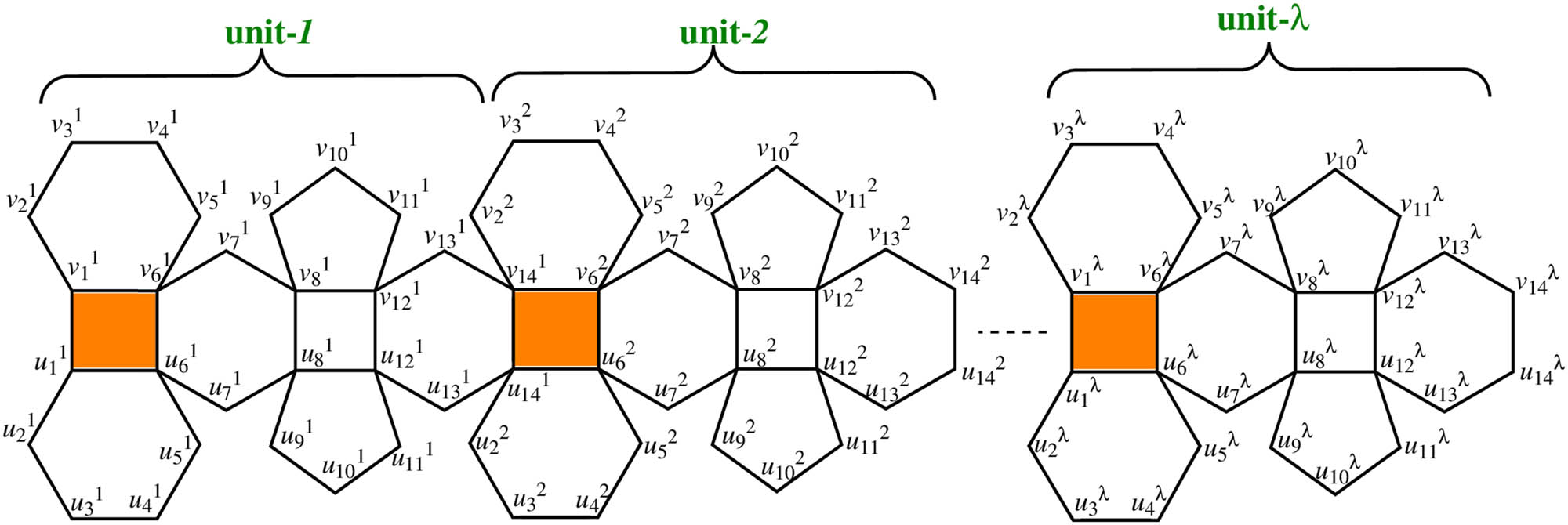
$Figure 4 Structure of polyhedron generalized sheet of C 28 ∗ {C}_{28}^{\ast } .$

Figure 4

Structure of polyhedron generalized sheet of C 28 ∗ .

Theorem 7

If λ ≥ 1, then ( C 28, λ ∗ ) is 3 .

Proof. To prove that d i m ( C 28, λ ∗ ) ≤ 3, assume a resolving set R = { v 2 , u 2 , v 13 λ + 1 } . We construct the following cases on vertex set of ( C 28, λ ∗ ) .

r ( v i | R ) = ( d ( v i , v 2 ) , d ( v i , u 2 ) , d ( v i , v 13 λ + 1 )) .

r ( v i | R ) = ( i , i + 1, i − 13 λ + 18 ) , if i = k + 13 ( λ − 1, ) i = 1; ( i − 7 λ + 5, i − 7 λ + 8, i − 13 λ + 18 ) , if i = k + 13 ( λ − 1, ) i = 2,3; ( i − 7 λ + 5, i − 7 λ + 8,13 λ − i − 2 ) , if i = k + 13 ( λ − 1, ) i = 4; ( i − 7 λ + 5, i − 7 λ + 6,13 λ − i − 2 ) , if i = k + 13 ( λ − 1, ) i = 5; ( i − 7 λ + 3, i − 7 λ + 4,13 λ − i − 2 ) , if i = k + 13 ( λ − 1, ) i = 6, … ,8; ( i − 7 λ + 3, i − 7 λ + 4, i − 13 λ + 8 ) , if i = k + 13 ( λ − 1, ) i = 9,10; ( 19 λ − i − 2,19 λ − i − 1,13 λ − i + 1 ) , if i = k + 13 ( λ − 1, ) i = 11,12; ( i − 7 λ , i − 7 λ + 1,13 λ − i + 1 ) , if i = k + 13 ( λ − 1, ) i = 13,14;

r ( u i | R ) = ( d ( u i , v 2 ) , d ( u i , u 2 ) , d ( u i , v 13 λ + 1 )) .

r ( u i | R ) = ( i , i + 1, i − 13 λ + 19 ) , if i = k + 13 ( λ − 1, ) i = 1; ( i − 7 λ + 5, i − 7 λ + 8, i − 13 λ + 19 ) , if i = k + 13 ( λ − 1, ) i = 2,3; ( i − 7 λ + 5, i − 7 λ + 8,13 λ − i − 1 ) , if i = k + 13 ( λ − 1, ) i = 4; ( i − 7 λ + 5, i − 7 λ + 6,13 λ − i − 1 ) , if i = k + 13 ( λ − 1, ) i = 5; ( i − 7 λ + 3, i − 7 λ + 4,13 λ − i − 1 ) , if i = k + 13 ( λ − 1, ) i = 6, … ,8; ( i − 7 λ + 3, i − 7 λ + 4, i − 13 λ + 9 ) , if i = k + 13 ( λ − 1, ) i = 9,10; ( 19 λ − i − 2,19 λ − i − 1,13 λ − i + 2 ) , if i = k + 13 ( λ − 1, ) i = 11,12; ( i − 7 λ , i − 7 λ + 1,13 λ − i + 2 ) , if i = k + 13 ( λ − 1, ) i = 13,14;

Hence, it follows the above arguments in the form of representation that dim ( C 28, λ ∗ ) ≤ 3 because all the vertices of C 28, λ ∗ have the unique representation with respect to resolving set R .

Now we prove that dim ( C 28, λ ∗ ) ≥ 3 . On the contrary, consider the resolving set R ' with cardinality 2 . Following are the discussion for this assumption.

Case 1: Let R ' = { v 1 , v 2 } with cardinality 2 . The same is represented as follows r ( v 5 | R ' ) = r ( v 7 | R ' ) .

Case 2: Let R ' = { v 1 , v 3 } with cardinality 2 . The same is represented as follows: r ( v 10 | R ' ) = r ( v 11 | R ' ) .

Case 3: Let R ' = { v 1 , v 5 } with cardinality 2 . The same is represented as follows: r ( v 2 | R ' ) = r ( u 2 | R ' ) .

Case 4: Let R ' = { v 1 , v i } with cardinality 2 . The same is represented as follows: r ( v 5 | R ' ) = r ( v 7 | R ' ) . 5 ≤ i ≤ 2(13 λ + 1)

Case 5: Let R ' = { v 1 , v i } with cardinality 2 . The same is represented as follows: r ( v α | R ' ) = r ( v β | R ' ) , with α =2,5,10; and β =6,7,11 . OR r ( v 2 | R ' ) = r ( u 1 | R ' ) .

Case 6: Let R ' = { v 2 , v 4 } with cardinality 2 . The same is represented as follows: r ( v 9 | R ' ) = r ( v 12 | R ' ) .

Case 7: Let R ' = { v i , v j } with cardinality 2 . The same is represented as follows: r ( v 9 | R ' ) = r ( v 12 | R ' ) , where 2 ≤ i , j ≤ 8 .

Case 8: Let with cardinality 2 . The same representation are; r ( v 2 | R ' ) = r ( v 4 | R ' ) .

Case 9: Let R ' = { v i , v j } with cardinality 2 . The same is represented as follows: r ( v 2 | R ' ) = r ( v 4 | R ' ) , where 9 ≤ i , j ≤ 2(13 λ + 1) .

Case 10 (result): Let R ' = { v i , v j } with cardinality 2 . The same is represented as follows: r ( v α | R ' ) = r ( v β | R ' ) , where α = 2,9, and β = 4,12 .

Case 11: Let R ' = { v 1 , u i } with cardinality 2 . The same is represented as follows: r ( v 3 | R ' ) = r ( v 5 | R ' ) .

Case 12: Let R ' = { v 1 , u 2 } with cardinality 2 . The same is represented as follows: r ( v 3 | R ' ) = r ( v 5 | R ' ) , where 2 ≤ i ≤ 3 .

Case 13: Let R ' = { v 1 , u 4 } with cardinality 2 . The same isrepresented as follows: r ( v 4 | R ' ) = r ( v 8 | R ' ) .

Case 14: Let R ' = { v 1 , u i } with cardinality 2 . The same is represented as follows: r ( v | R ' ) = r ( v 8 | R ' ) , where 4 ≤ i ≤ 6 .

Case 15: Let R ' = { v 1 , u 7 } with cardinality 2 . The same is represented as follows: r ( v 5 | R ' ) = r ( v 7 | R ' ) .

Case 16: Let R ' = { v 1 , u i } with cardinality 2 . The same is represented as follows: r ( v 10 | R ' ) = r ( v 11 | R ' ) , where 8 ≤ i ≤ 9 .

Case 17: Let R ' = { v 1 , u i } with cardinality 2 . The same is represented as follows: r ( v 4 | R ' ) = r ( u 3 | R ' ) , where 10 ≤ i ≤ 2(13 λ + 1) .

Case 18 (result): Let R ' = { v 1 , u i } with cardinality 2 . The same is represented as follows: r ( v α | R ' ) = r ( v β | R ' ) , where α = 3,4,5,10; and β = 5,7,8,11 . OR

Case 19: Let R ' = { v i , u 1 } with cardinality 2 . The same is represented as follows: r ( u 3 | R ' ) = r ( u 5 | R ' ) , where 2 ≤ i ≤ 3 .

Case 20: Let R ' = { v i , u 1 } with cardinality 2 . The same is represented as follows: r ( u 4 | R ' ) = r ( u 8 | R ' ) , where 4 ≤ i ≤ 6 .

Case 21: Let R ' = { v 7 , u 1 } with cardinality 2 . The same is represented as follows: r ( u 5 | R ' ) = r ( u 7 | R ' ) .

Case 22: Let R ' = { v 7 , u 1 } with cardinality 2 . The same is represented as follows: r ( u 5 | R ' ) = r ( u 7 | R ' ) .

Case 23: Let R ' = { v i , u 1 } with cardinality 2 . The same is represented as follows: r ( u 10 | R ' ) = r ( u 11 | R ' ) , 8 ≤ i ≤ 9 .

Case 24: Let R ' = { v i , u 1 } with cardinality 2 . The same is represented as follows: r ( u 4 | R ' ) = r ( v 3 | R ' ) , where 10 ≤ i ≤ 2(13 λ + 1) .

Case 25 (result): Let R ' = { v i , u 1 } with cardinality 2 . The same is represented as follows: r ( u α | R ' ) = r ( u β | R ' ) , where α = 3,4,5,10; and β = 5,7,8,11 . OR r ( u 10 | R ' ) = r ( v 3 | R ' ) .

Case 26: Let R ' = { v 2 , u 3 } with cardinality 2 . The same is represented as follows: r ( v 5 | R ' ) = r ( v 7 | R ' ) .

Case 27: Let R ' = { v 5 , u 7 } with cardinality 2 . The same is represented as follows: r ( v 1 | R ' ) = r ( v 7 | R ' ) .

Case 28: Let R ' = { v 9 , u 3 } with cardinality 2 . The same is represented as follows: r ( u 2 | R ' ) = r ( u 4 | R ' ) .

Case 29 (result): Let R ' = { v i , u j } with cardinality 2 . The same is represented as follows: r ( v α | R ' ) = r ( v β | R ' ) , where α = 1,5; and β = 7 . OR r ( u 2 | R ' ) = r ( 4 4 | R ' ) .

Case 30: Let R ' = { u 1 , u 2 } with cardinality 2 . The same is represented as follows: r ( v 5 | R ' ) = r ( v 7 | R ' ) .

Case 31: Let R ' = { u 1 , u j } with cardinality 2 . The same is represented as follows: r ( v 10 | R ' ) = r ( v 11 | R ' ) , where 3 ≤ i ≤ 9 .

Case 32: Let R ' = { u 1 , u j } with cardinality 2 . The same is represented as follows: r ( v 11 | R ' ) = r ( v 13 | R ' ) , where 10 ≤ i ≤ 13 .

Case 33: Let R ' = { u 1 , u 14 } with cardinality 2 . The same is represented as follows: r ( v 5 | R ' ) = r ( v 7 | R ' ) .

Case 34: Let R ' = { u 1 , u j } with cardinality 2 . The same is represented as follows: r ( v α | R ' ) = r ( v β | R ' ) , where α = 5,10,11 and β = 7,11,13 .

Case 35: Let R ' = { u i , u j } with cardinality 2 . The same is represented as follows: where 2 ≤ i ≤ 7, and 1 ≤ j ≤ 8 .

Case 36: Let R ' = { u i , u j } with cardinality 2 . The same is represented as follows: r ( u 2 | R ' ) = r ( u 4 | R ' ) , where 9 ≤ i ≤ 13, and 8 ≤ j ≤ 14 .

Case 37: Let R ' = { u i , u j } with cardinality 2 . The same is represented as follows: r ( u α | R ' ) = r ( u β | R ' ) , where α = 2,9 and β = 4,12 .

Analogously, there is no single possibility from the possible cases made by the entire vertex of C λ ,1 ' . This shows that two metric dimension of C λ , 1 * is not possible. So, dim ( C λ , 1 ⁎ ) ≥ 3 .

Hence:

dim ( C λ , 1 ⁎ ) ≥ 3

8 Conclusion

This work contributed the metric dimension of chemical complexes of supramolecular chain in dialkyltin from N-salicylidene-l-valine. We considered the complexes of 2, 3, and 4 chains, and proved that the members of resolving sets are highly dependent on the number of vertices. Moreover, We computed the metric of a polyhedron generalized sheet of C 28, λ ∗ resulting in dim ( C 28, λ ∗ ) = 3, and it has a constant metric dimension.

woodszhang@hotmail.com

Funding information: This work was supported by the National Key Research and Development Program under Grant 2018YFB0904205.
Author contributions: Muhammad Azeem: writing – original draft; Muhammad Kamran Jamil: writing – review and editing; Muhammad Tanzeel Ali Kanwal: methodology, formal analysis; and visualization; Muzammil Mukhtar: project administration; Xiujun Zhang: resources.
Conflict of interest: Authors state no conflict of interest.
Data availabilty statement: All the data supporting the results are included in the manuscript.

References

Ahmad A., Bača M., Sultan S., Minimal doubly resolving sets of Necklace graph. Math. Rep., 2018, 20(70), 123–129.Search in Google Scholar

Ahmad A., Bača M., Sultan S., Computing the metric dimension of Kayak Paddles graph and cycles with chord. Proyecciones J. Math., 2020a, 39, 287–300. 10.22199/issn.0717-6279-2020-02-0018.Search in Google Scholar

Ahmad A., Bača M., Sultan S., On Metric Dimension and Minimal doubly resolving sets of Harary graph. Acta Math. Univ. Comen., 2020b, 89, 123–129.Search in Google Scholar

Ahmad A., Koam A.N.A., Siddiqui M.H.F., Azeem M., Resolvability of the starphene structure and applications in electronics. Ain Shams Eng. J., 2022, 13(2), 101587. 10.1016/j.asej.2021.09.014.Search in Google Scholar

Ahmad A., Sultan S., On minimal doubly resolving sets of circulant graphs. Acta Mech. Slov., 2017, 20, 6–11. 10.21496/ams.2017.002.Search in Google Scholar

Ahsan M., Zahid Z., Zafar S., Rafiq A., Sarwar Sindhu M., Umar M., Computing the edge metric dimension of convex polytopes related graphs. J. Math. Comput. Sci., 2020, 22(2), 174–188.10.22436/jmcs.022.02.08Search in Google Scholar

Anitha K., Aruna Devi R., Munir M., Nisar K.S., Metric dimension of rough graphs. Int. J. Nonlinear Anal. Appl., 2021, 12, 1793–1806. 10.22075/IJNAA.2021.5891.Search in Google Scholar

Azeem M., Imran M., Nadeem M.F., Sharp bounds on partition dimension of hexagonal Möbius ladder. J. King Saud. Univ-Sci., 2021, 34(2), 101779. 10.1016/j.jksus.2021.101779.Search in Google Scholar

Azeem M., Jamil M.K., Javed A., Ahmad A., Verification of some topological indices of Y-junction based nanostructures by M-polynomials. J. Math., June 2022, 2022, 8238651. 10.1155/2022/8238651.Search in Google Scholar

Azeem M., Nadeem M.F., Metric-based resolvability of polycyclic aromatic hydrocarbons. Eur. Phys. J. Plus, 2021, 136(4), 1–14. 10.1140/epjp/s13360-021-01399-8.Search in Google Scholar

Belokon Y.N., Maleev V.I., Kataev D.A., Saveleva T.F., North M., Chiral ion pairs in catalysis: lithium salts of chiral metallo-complex anions as catalysts for asymmetric C–C bond formation. Tetrahedron-Asymmetric., 2009, 20, 1746–1752. 10.1016/j.tetasy.2009.06.006.Search in Google Scholar

Chen C.T., Bettigeri S., Weng S.S., Pawar V.D., Lin Y.H., Liu C.Y., Asymmetric aerobic oxidation of α-hydroxy acid derivatives by C4-symmetric, vanadate-centered, tetrakisvanadyl(V) QJ;clusters derived from N-salicylidene-α-aminocarboxylates. J. Org. Chem., 2007, 72, 8175–8185. 10.1021/jo070575f.Search in Google Scholar PubMed

Chen C.T., Lin J.S., Kuo J.H., Weng S.S., Cuo T.S., Lin Y.W., Site-selective DNA photocleavage involving unusual photoinitiated tautomerization of chiral tridentate vanadyl(V) complexes derived from N-salicylidene α-amino acids. Org. Lett., 2004, 6, 4471–4474. 10.1021/ol048156h.Search in Google Scholar PubMed

Diudea M.V., Nagy C.L., Diamond and Related Nanostructures. Springer, Netherlands, 2013. 10.1007/978-94-007-6371-5.Search in Google Scholar

Harary F., Melter R.A., On the metric dimension of a graph. Ars Combinatoria, 1976, 2, 191–195.Search in Google Scholar

Imran S., Siddiqui M.K., Hussain M., Computing the upper bounds for the metric dimension of cellulose network. Appl. Math. e-notes, 2019, 19, 585–605.Search in Google Scholar

Imran S., Siddiqui M.K., Imran M., Hussain M., On metric dimensions of symmetric graphs obtained by rooted product. Mathematics, 2018, 6(10), 191. 10.3390/math6100191.Search in Google Scholar

Khuller S., Raghavachari B., Rosenfeld A. Landmarks in graphs. Discret. Appl. Math., 1996, 70(3), 217–229.10.1016/0166-218X(95)00106-2Search in Google Scholar

Koam A.N., Ahmad A., Abdelhag M.E., Azeem M., Metric and fault-tolerant metric dimension of hollow coronoid. IEEE Access., 2021, 9, 81527–81534. 10.1109/ACCESS.2021.3085584.Search in Google Scholar

Koam A.N., Ahmad A., Alatawi M.S., Nadeem M.F., Azeem M., Computation of metric-based resolvability of quartz without pendant nodes. IEEE Access., 2021a, 9, 151834–151840. 10.1109/ACCESS.2021.3126455.Search in Google Scholar

Koam A.N., Haider A., Ansari M.A., Pseudo-metric on KU-algebras. Korean J. Math., 2019, 27(1), 131–140. 10.11568/kjm.2019.27.1.131.Search in Google Scholar

Koam A.N.A., Ahmad A., Ibrahim M., Azeem M., Edge metric and fault-tolerant edge metric dimension of hollow coronoid. Mathematics, May 2021b, 9(12), 1405. 10.3390/math9121405.Search in Google Scholar

Mahapatra T., Ghorai G., Pal M., Fuzzy fractional coloring of fuzzy graph with its application. J. Ambient. Intell. Humanized Comput., 2020, 11, 5771–5784. 10.1007/s12652-020-01953-9.Search in Google Scholar

Moreno A.E., Yero I.G., Velazquez J.A.R., On the (k,t)-metric dimension of graphs. Comput. J., 2021, 64(5), 707–720. 10.1093/comjnl/bxaa009.Search in Google Scholar

Moscarini M., Computing a metric basis of a bipartite distance-hereditary graph. Theor. Comput. Sci., 2021, 900, 20–24. 10.1016/j.tcs.2021.11.015.Search in Google Scholar

Nadeem M.F., Azeem M., Khalil A., The locating number of hexagonal Möbius ladder network. J. Appl. Math. Comput., 2020, 66, 149–165. 10.1007/s12190-020-01430-8.Search in Google Scholar

Nadeem M.F., Hassan M., Azeem M., Khan S.U.D., Shaik M.R., Sharaf M.A.F., et al., Application of resolvability technique to investigate the different polyphenyl structures for polymer industry. J. Chem., 2021, 2021, 1–8. 10.1155/2021/6633227.Search in Google Scholar

Pirzada S., Aijaz M., On graphs with same metric and upper dimension. Discret. Math. Algorithms Appl., 2021, 13(2), 2150015. 10.1142/S1793830921500154.Search in Google Scholar

Raza H., Hayat S., Imran M., Pan X.F., Fault-tolerant resolvability and extremal structures of graphs. Mathematics, 2019a, 7, 78–97. 10.3390/math7010078.Search in Google Scholar

Raza H., Hayat S., Pan X.F., On the fault-tolerant metric dimension of convex polytopes. Appl. Math. Comput., 2018, 339, 172–185. 10.1016/j.amc.2018.07.010.Search in Google Scholar

Raza H., Hayat S., Pan X.F., On the fault-tolerant metric dimension of certain interconnection networks. J. Appl. Math. Comput., 2019b, 60, 517–535. 10.1109/ACCESS.2020.3014883.Search in Google Scholar

Raza H., Liu J.B., Azeem M., Nadeem M.F., Partition dimension of generalized petersen graph. Complexity, Oct. 2021. 10.1155/2021/5592476.Search in Google Scholar

Shabbir A., Azeem M., On the partition dimension of tri-hexagonal alpha-boron nanotube. IEEE Access., Apr 2021, 9, 55644–55653. 10.1109/ACCESS.2021.3071716.Search in Google Scholar

Siddiqui H.M.A., Arshad M.A., Nadeem M.F., Azeem M., Haider A., Malik M.A., Topological properties of supramolecular chain of different complexes of N-salicylidene-l-valine. Polycycl. Aromatic Compd., 2022, 42(9), 6185–6198. 10.1080/10406638.2021.1980060.Search in Google Scholar

Siddiqui M.K., Imran M., Computing the metric and partition dimension of H-Naphtalenic and VC5C7 nanotubes. J. Optoelectron. Adv. Mater., 2015, 17, 790–794.Search in Google Scholar

Siddiqui M.K., Naeem M., Rahman N.A., Imran M., Computing topological indices of certain networks. J. Optoelectron. Adv. Mater., 2016, 18, 9–10. 10.1016/j.amc.2014.04.091.Search in Google Scholar

Singh P., Sharma S., Sharma S.K., Bhat V.K., Metric dimension and edge metric dimension of windmill graphs. AIMS Math., 2021, 6(9), 9138–9153. 10.3934/math.2021531.Search in Google Scholar

Slater P.J., Leaves of trees. Proceeding of the 6th Southeastern Conference on Combinatorics, Graph Theory, and Computing, Congressus Numerantium. 1975, vol. 14, p. 549–559.Search in Google Scholar

Ucar A., Findik M., Bingol H., Guler E., Ozcan E., Organometallic chiral Schiff base for enantio-selective fluorescent recognition of methionine. Chem. Pap., 2017, 71, 1855–1862. 10.1007/s11696-017-0179-7.Search in Google Scholar

Vetrik T., Ahmad A. Computing the metric dimension of the categorial product of graphs. Int. J. Comput. Math., 2017, 94, 363–371. 10.1080/00207160.2015.1109081.Search in Google Scholar

Wang H., Azeem M., Nadeem M.F., Rehman A.U., Aslam A., On fault-tolerant resolving sets of some families of ladder networks. Complexity, May 2021, 2021, 9939559. 10.1155/2021/9939559.Search in Google Scholar

Yu J., Jiang H.J., Zhou Y., Luo S.W., Gong L.Z. Sodium salts of anionic chiral cobalt(III) complexes as catalysts of the enantioselective Povarov reaction. Angew. Chem., 2015, 54, 11209–11213. 10.1002/anie.201504790.Search in Google Scholar PubMed

Received: 2022-08-23

Revised: 2022-12-10

Accepted: 2022-12-16

Published Online: 2022-12-31

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/mgmc-2022-0027

Keywords for this article

N-salicylidene-l-valine; complex 2, 3, 4; supramolecular chain in dialkyltin; resolving set; finite metric dimension; complex chemical structures

Creative Commons

BY 4.0

Finite vertex-based resolvability of supramolecular chain in dialkyltin

Article

Abstract

1 Introduction

2 Literature review

3 Preliminaries

Definition 1

Definition 2

4 Finite vertex-based resolvability of supramolecular chain in dialkyltin complex-2, C2,λ

Theorem 1

Theorem 2

5 Finite vertex-based resolvability of supramolecular chain in dialkyltin complex-3, C 3,λ

Theorem 3

Theorem 4

6 Finite vertex-based resolvability of supramolecular chain in dialkyltin complex-4, C 4,λ

Theorem 5

Theorem 6

7 Finite vertex-based resolvability of polyhedron generalized sheet of C 28, λ ∗

Theorem 7

8 Conclusion

References

Articles in the same Issue

Articles in the same Issue

Articles in the same Issue

4 Finite vertex-based resolvability of supramolecular chain in dialkyltin complex-2, C_2,λ

5 Finite vertex-based resolvability of supramolecular chain in dialkyltin complex-3, C _3,λ

6 Finite vertex-based resolvability of supramolecular chain in dialkyltin complex-4, C _4,λ