Home Physical Sciences Computation of edge- and vertex-degree-based topological indices for tetrahedral sheets of clay minerals
Article Open Access

Computation of edge- and vertex-degree-based topological indices for tetrahedral sheets of clay minerals

  • Al-Nashri Al-Hossain Ahmad , Ali Ahmad EMAIL logo and Muhammad Azeem
Published/Copyright: April 21, 2022
Download Article (PDF)
Main Group Metal Chemistry
From the journal Main Group Metal Chemistry Volume 45 Issue 1

Abstract

In terms of soil conditions, clay minerals infrequently occur as homogenous mixtures of single constituents, gatherings, stages, or types of minerals. Rather, they contain intricate arrays of essential minerals and rippling intermediates of numerous basic and synergistic mixtures. There is also the possibility that a discrete mineral grain is composed of more than one clay type or has sections that are intermediate amongst two chosen minerals. Such minerals are alluded to as inter-stratified or mixed-layer minerals. The structures of clay minerals are the most researched compound in contemporary materials science. Tetrahedral sheets of clay minerals (TSCM) are one of the most well-known structures concentrated in materials science. QSPR/QSAR of the TSCM compounds requires articulations for the topological characteristic of these substances. Topological descriptors are indispensable gadgets for exploring chemical substances to understand the basic geography or physical properties of such chemical structures. In this article, we determine the edge-vertex-degree and vertex-edge-degree topological indices for TSCM.

Keywords: tetrahedral sheets of clay minerals; topological descriptors; complex chemical networks; edge-vertex-degree; vertex-edge-degree

1 Introduction

Chemical graph theory aids the interpretation of a chemical graph’s nuclear assistant properties. Chemical graph theory is expected to play an important role in showcasing and organizing any constructed framework or component organize out. A chemical compound or graph is a graphical portrayal that includes atoms called vertices and atom-to-atom bonds known as edges. The topological number is a quantitative assessment of molecular composition, whereas a topological index corresponds to specified chemical and physical properties of concealed chemical molecules that are not represented numerically.

Numerous complexes have almost the same molecular formula but have different structures; this is referred to as an isomer. Combinatorics and graph theory are much more appropriate scientific gadgets for contemplating the distinction between these isomers in mathematical branches that are firmly identified with one another. Such divisions are used to display the structures of chemical mixtures, investigating their chemical and physical properties. Throughout chemical graph theory, an atom is initiated as a vertex and the bonds between them are regarded as edges, and the developed illustration is referred to as a chemical graph. Chemical graph theory is an incredibly interesting branch of graph theory and has innumerable advancements in science, medicine architecture, and so on. The research work by Shao et al. (2017, 2018a) contains two examples of topological descriptors that have been studied in pharmaceutical research and theoretical science. In the concept of quantitative structure–property relationships (QSPR)/quantitative structure–activity relationships (QSAR), researchers are curious in comprehending a compound’s network topology using certain numbers and boundaries derived given by the network’s atomic structure.

Clay mineral structures are the most studied chemical substance in modern materials engineering. Probably, one of the best structures largely focused in materials science is the clay mineral sheet of tetrahedral. Clay minerals are versatile earth-rich ceramics with a variety of appealing properties and chemical stability under adverse conditions. Clay minerals are a collection of hydrous aluminosilicates that dominate the mud-measured ( < 2 | x m ) portion of soils. Such minerals are chemically and structurally similar to the essential minerals that originate in the Earth’s crust; however, changes in the geometric arrangement of atoms and ions within their structures occur as a result of weathering. Indispensable minerals form at high temperatures and pressures and are typically formed from molten or trans-formative rocks (Barton, 2002).

All such minerals are relatively stable within the Earth, but alteration can occur when exposed to the bordering counties of the surface of the ground. While the safest chemical constituents (quartz, micas, and a few feldspars) can persist in soils, other less protected minerals (pyroxenes, amphiboles, and a large group of adornment minerals) are prone to disintegrate and erosional, resulting in the formation of ancillary minerals. The outcomes of entirely voluntary minerals are the culmination of either reconfiguration of the essential micronutrient framework (incongruent reaction) or neoformation via precipitation or recrystallization of fragmented individual components into a successively stable framework (congruent reaction). Such entirely voluntary minerals are frequently referred to as phyllosilicates even though, as the name implies (Greek: phyllon, leaf), leaf they have platy or flaky proclivity, and one of their primary core elements is an all-inclusive plate of SiO4 tetrahedral (Barton, 2002).

Researchers defined the Harmonic index in the articles (Ediz, 2017; Zhong, 2012), and the majority of research is accomplished only using the conventional degree notion. Chellali et al. (2017) lately launched innovative degree notions, namely “vertex-edge-degree and edge-vertex-degree.” The relationship between “classical degree-based” and “vertex-edge-degree and edge-vertex-degree” is shown by Horoldagva et al. (2019), Ediz (2018), Sahin and Ediz (2018), and Zhang et al. (2020), and it was discovered that the “vertex-edge-degree Zagreb index” has an instrumental growth than the “traditional Zagreb index.”

2 Motivation and methodology

Topological descriptors play an important role in theoretical science. A topological descriptor, also known as a connectivity index throughout the areas of materials graph theory, is a type of molecular graph attribute that is determined by the chemical graph of a complex mixture. Generally, topological descriptors are distinguished by the use of vertex degree theory. Structural attributes have been used to comprehend and generate numerical attributes for real-world system models. Wiener (1947) presented the possibility of topological descriptors since attempting to reach the paraffin limit. As the first topological descriptor, he presented the Wiener descriptor. In scientific and chemical writing, the most commonly used topological descriptors are Zagreb, Randić, and Wiener descriptors (Ediz et al., 2017; Gutman and Trinajstic, 1972). Empowered by such considerations, we begin to investigate edge-vertex- and vertex-edge degree-based topological descriptors.

In this manuscript, we studied the structure of tetrahedral sheets of clay minerals (TSCM) and encountered the accurate value of vertex-edge and edge-vertex-degree-based topological properties for TSCM. Particularly, we determined the exact values of harmonic vertex-edge-degree index (H ve), edge-vertex-degree Randić index, sum-connectivity vertex-edge-degree (X ve) index, vertex-edge-degree Randić index, geometric-arithmetic vertex-edge-degree (GA ve) index, atom-bond connectivity vertex-edge-degree (ABC ve) index, first and second vertex-edge-degree Zagreb α(β) index, and Zagreb edge-vertex-degree index, for chemical structure of TSCM. For the basics of all these definitions in related literature, see studies by Ahmad (2018), Anjum and Safdar (2019), Gao et al. (2018), Shao et al. (2018a, 2018b), Siddiqui et al. (2016), Shao et al. (2019), and Raza et al. (2021).

The methodology of this article is as follows: first, we explain the topological indices, clay minerals, and their importance and applications. Second, we study the structure of TSCM. Third, we determine the vertex-edge- and edge-vertex degree-based topological descriptor and its numeric numbers. Then, we discuss the analogies of our computed theorems for TSCM, and finally, we give the closing remarks.

3 Definitions and results

“Let E and V be the edge set and vertex set of a connected graph G = ( V , E ) . The degree of a vertex x 1 , denoted by ξ ( x 1 ) , is the number of edges that are incident to x 1 . The open neighborhood of a vertex x 1 , denoted by N ( x 1 ) , is the number of all vertices adjacent to x 1 . The closed neighborhood of x 1 , denoted by N [ x 1 ] , is the union of x 1 and N ( x 1 ) . The edge-vertex-degree, denoted by ξ e v ( e ) , of any edge e = x 1 x 2 ∈ E is the total number of vertices of the closed neighborhoods union of x 1 and x 2 . The vertex-edge-degree, denoted by ξ v e ( x 1 ) , of any vertex x 1 ∈ V is the number of different edges that are incident to any vertex from the closed neighborhood of x 1 . ” Chellali et al. (2017), Ediz (2018), Horoldagva et al. (2019), and Sahin and Ediz (2018) studied some vertex- and edge-degree-based topological descriptors which are available in the main body of our draft, particularly shown in Table 1. Furthermore, the basic definitions are also available in these basic research articles.

Table 1

The topological descriptors of vertex-edge-degree and edge-vertex-degree indices

χ ve ( G ) = ∑ x 1 x 2 ∈ E ( ξ ve ( x 1 ) + ξ ve ( x 2 ) ) − 1 2 Sum-connectivity vertex-edge-degree index
H ve ( G ) = ∑ x 1 x 2 ∈ E 2 ξ ve ( x 1 ) + ξ ve ( x 2 ) Harmonic index of vertex-edge-degree
G A ve ( G ) = ∑ x 1 x 2 ∈ E 2 ( ξ ve ( x 1 ) × ξ ve ( x 2 ) ) 1 2 ξ ve ( x 1 ) + ξ ve ( x 2 ) Geometric–arithmetic vertex-edge-degree index
A B C ve ( G ) = ∑ x 1 x 2 ∈ E ξ ve ( x 1 ) + ξ ve ( x 2 ) − 2 ξ ve ( x 1 ) × ξ ve ( x 2 ) 1 2 Atom–bond connectivity vertex-edge-degree index
R e v ( G ) = ∑ e 1 ∈ E ( ξ ve e 1 ) − 1 2 Randić edge-vertex-degree index
R ve ( G ) = ∑ x 1 x 2 ∈ E ( ξ ve ( x 1 ) × ξ ve ( x 2 ) ) − 1 2 Randić vertex-edge-degree index
M ve 2 ( G ) = ∑ x 1 x 2 ∈ E ( ξ ve ( x 1 ) × ξ ve ( x 2 ) ) Second Zagreb vertex-edge-degree index
M β ve 1 ( G ) = ∑ x 1 x 2 ∈ E ( ξ ve ( x 1 ) + ξ ve ( x 2 ) ) First Zagreb β vertex-edge-degree index
M α ve 1 ( G ) = ∑ x 1 ∈ V ( ξ ve x 1 ) 2 First Zagreb α vertex-edge-degree index
M e v ( G ) = ∑ e 1 ∈ E ( ξ e v e 1 ) 2 ZAGREB edge-vertex-degree index

4 Structure of TSCM

The properties that decide the formation of a mineral are derived from its chemical foundation, geometric arrangement of atoms and ions, and the electrical powers that dilemma them together. Silicon will quite often be found in geochemical arrangements since silicate minerals are so universal. Underneath the pH of 9 or 10, most solvent silicon is found as silicic acid, Si(OH)4 (Figure 1).

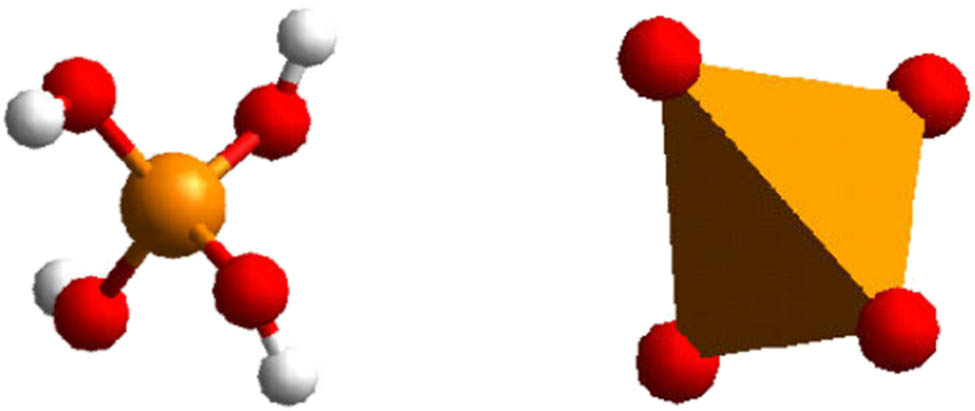
Figure 1 Tetrahedron.
Figure 1

Tetrahedron.

In whatsoever scenario, the phyllosilicate structure’s predominance of silicon and oxygen is logical. All silicate structures are found on the SiC > 4 tetrahedron. It has four O2 particles at the apexes of a conventional tetrahedron facilitated by one Si4+ particle in the middle (Figure 1). A hexagonal system called the tetrahedral sheet is formed by an interlocking array of these tetrahedral associated at three corners in a similar plane by shared oxygen anions. Figure 2 depicts the clay mineral sheet of tetrahedral TSCM p,q for p = 2 and q = 2.

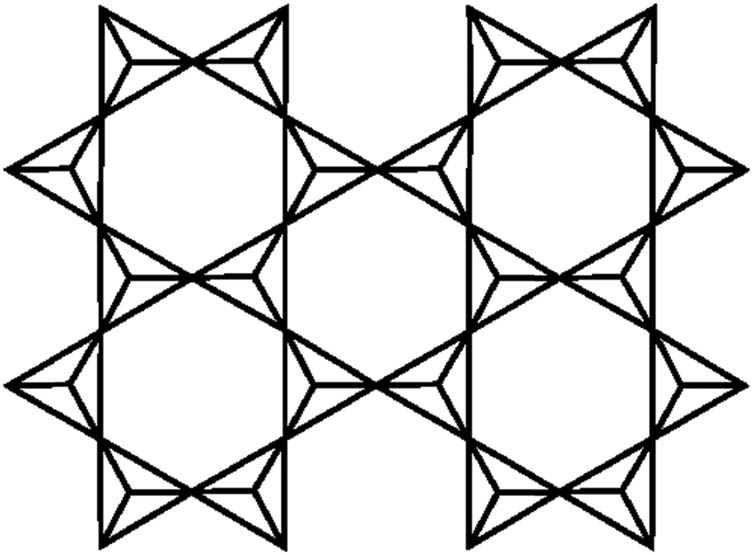
Figure 2 A clay mineral’s sheet of tetrahedral for p = q = 2.
Figure 2

A clay mineral’s sheet of tetrahedral for p = q = 2.

The graph TSCM p,q contains 10 p q + 7 p + q vertices and 24 p q + 12 p edges. The vertex partitions of TSCM p,q are V 3 = { x 1 ∈ V ( T S C M p , q ) : ξ ( x 1 ) = 3 } and V 6 = { x 1 ∈ V ( TSCM p , q ) : ξ ( x 1 ) = 6 } with | V 3 | = 4 p q + 6 p + 2 q and | V 6 | = 6 p q + p − q . The edge partitions based on the degree of vertices are E 3 , 3 = { x 1 x 2 ∈ E ( TSCM p , q ) : ξ ( x 1 ) = 3 , ξ ( x 2 ) = 3 } , E 3 , 6 = { x 1 x 2 ∈ E ( TSCM p , q ) : ξ ( x 1 ) = 3 , ξ ( x 2 ) = 6 } , and E 6 , 6 = { x 1 x 2 ∈ E ( TSCM p , q ) : ξ ( x 1 ) = 6 , ξ ( x 2 ) = 6 } with | E 3 , 3 | = 4 p + 2 q , | E 3 , 6 | = 12 p q + 10 p + 2 q and | E 6 , 6 | = 12 p q − 2 p − 4 q . The topological number is calculated for TSCM p,q , which are defined above.

5 Main results

This section contains the main results we determined. Particularly, harmonic vertex-edge-degree index (H ve), sum-connectivity vertex-edge-degree (X ve) index, Randić vertex-edge-degree and edge-vertex-degree index, geometric–arithmetic vertex-edge-degree (GA ve) index, atom–bond connectivity vertex-edge-degree (ABC ve) index, second Zagreb vertex-edge-degree β index, first Zagreb vertex-edge-degree α(β) index, and the Zagreb edge-vertex-degree index for TSCM p,q .

5.1 The edge-vertex-degree Zagreb index

Using Table 2 in M e v ( TSCM p , q ) = ∑ e 1 ∈ E ( ξ e v ( e 1 ) 2 , we obtain the Zagreb edge-vertex-degree index:

M e v ( TSCM p , q ) = 2700 p q + 666 p − 342 q

Table 2

Edge-vertex-degree of T S C M p , q

( ξ ( x 1 ) , ξ ( x 2 ) ) Edge-vertex-degree Frequency
( 3 , 3 ) 6 4 p + 2 q
( 3 , 6 ) 9 12 p q + 10 p + 2 q
( 6 , 6 ) 12 12 p q − 2 p − 4 q

5.2 The first vertex-edge-degree Zagreb α index

We compute the first vertex-edge-degree Zagreb α index using the values from Table 3 in the equation M αve 1 ( TSCM p , q ) = ∑ x 1 ∈ V ( ξ v e ( x 1 ) 2 . After simplification, we obtain:

M α v e 1 ( TSCM p , q ) = 6696 p q + 720 p − 1332 q + 72

Table 3

Edge-vertex-degree of T S C M p , q

ξ ( x 1 ) Vertex-edge-degree Frequency
3 15 8 p + 4 q
3 18 4 p q − 2 p − 2 q
6 24 2 p + 4
6 27 4 q − 8 + 4 p
6 30 4 − 5 q − 5 p + 6 p q

5.3 The first vertex-edge-degree Zagreb β index

Using the values from Table 4 in the equation M β ve 1 ( TSCM p , q ) = ∑ x 1 x 2 ∈ E ( ξ ve ( x 1 ) + ξ ve ( x 2 ) ) , after simple calculation, we obtain the first vertex-edge-degree Zagreb β index as follows:

M β v e 1 ( TSCM p , q ) = 1296 p q + 288 p − 180 q

Table 4

The TSCM p , q structure edge’s end vertices vertex-edge-degrees

( ξ ( x 1 ) , ξ ( x 2 ) ) Vertex-edge-degree Frequency
( 3 , 3 ) ( 15 , 15 ) 4 p + 2 q
( 3 , 6 ) ( 15 , 24 ) 8 p + 16
( 3 , 6 ) ( 15 , 27 ) 8 p + 8 q − 16
( 3 , 6 ) ( 18 , 27 ) 4 p + 4 q − 8
( 3 , 6 ) ( 18 , 30 ) 12 p q − 10 p − 10 q + 8
( 6 , 6 ) ( 24 , 24 ) 4
( 6 , 6 ) ( 24 , 27 ) 4 p
( 6 , 6 ) ( 27 , 27 ) 4 q − 6
( 6 , 6 ) ( 27 , 30 ) 8 p + 4 q − 12
( 6 , 6 ) ( 30 , 30 ) 12 p q − 14 p − 12 q + 14

5.4 The second vertex-edge-degree Zagreb index

We obtain the second vertex-edge-degree Zagreb index using the values from Table 4 in the equation M ve 2 ( TSCM p , q ) = ∑ x 1 x 2 ∈ E ( ξ ve ( x 1 ) × ξ ve ( x 2 ) ) . After simplification, it is as follows:

M v e 2 ( TSCM p , q ) = 17280 p q + 36 p − 4410 q + 522

5.5 The vertex-edge-degree Randić index

We acquire the vertex-edge-degree Randić index by using the values from Table 4 in the formula R ve ( TSCM p , q ) = ∑ x 1 x 2 ∈ E ( ξ ve ( x 1 ) × ξ ve ( x 2 ) ) − 1 2 . After simplification, it is as follows:

R ve ( TSCM p , q ) = 2 15 + 6 15 p q + 24 5 − 15 15 + 10 6 + 6 10 − 16 135 q + 30 10 + 24 5 + 10 6 − 9 15 + 15 2 − 27 135 p

5.6 The edge-vertex-degree Randić index

Using Table 2 in the equation R e v ( ( TSCM p , q ) ) = ∑ e 1 ∈ E ( ξ v e ( e 1 ) ) − 1 2 , we compute the edge-vertex-degree Randić index as follows:

R e v ( TSCM p , q ) = ( 4 + 2 3 ) p q + 2 6 − 3 + 10 3 p + 6 − 2 3 + 2 3 q

5.7 The vertex-edge-degree atom–bond connectivity index

Using values from Table 4 in the equation A B C ve ( TSCM p , q ) = ∑ x 1 x 2 ∈ E ξ ve ( x 1 ) + ξ ve ( x 2 ) − 2 ξ ve ( x 1 ) × ξ ve ( x 2 ) 1 2 , after simple calculation, we compute the vertex-edge-degree atom–bond connectivity index as follows:

A B C ve ( TSCM p , q ) = 2 690 15 + 2 58 5 p q + 23 9 2 + 2 370 15 − 690 9 + 2 27 258 + 8 15 7 + 4 22 9 − 7 15 58 p + − 2 58 5 + 16 9 2 + 4 15 7 + 2 27 258 + 8 27 13 − 690 9 q + 7 15 58 − 4 13 9 − 32 9 2 + 4 15 370 − 4 27 258 + 4 45 690

5.8 The geometric–arithmetic vertex-edge-degree index

We obtain the vertex-edge-degree geometric–arithmetic index using values from Table 4 in the equation G A ve ( TSCM p , q ) = ∑ x 1 x 2 ∈ E 2 ( ξ ve ( x 1 ) × ξ ve ( x 2 ) ) 1 2 ξ ve ( x 1 ) + ξ ve ( x 2 ) . It is as follows:

G A v e ( TSCM p , q ) = ( 3 15 + 12 ) p q + 24 7 5 − 5 / 2 15 + 8 / 5 6 + 24 19 10 − 6 q + 1232 247 10 + 24 7 5 + 8 / 5 6 − 5 / 2 15 + 48 17 2 − 10 p − 48 7 5 − 16 5 6 + 280 247 10 + 2 15 + 12

5.9 The vertex-edge-degree harmonic index

We obtain the vertex-edge-degree harmonic index using values from Table 4 in the equation H ve ( TSCM p , q ) = ∑ x 1 x 2 ∈ E 2 ξ ve ( x 1 ) + ξ ve ( x 2 ) . It is as follows:

H ve ( TSCM p , q ) = 9 10 p q + 4179073 5290740 p + 11771 71820 q + 823 31122

5.10 The sum-connectivity vertex-edge-degree index

We obtain the vertex-edge-degree sum-connectivity index using the values from Table 4 in the equation χ ve ( TSCM p , q ) = ∑ x 1 x 2 ∈ E ( ξ v e ( x 1 ) + ξ v e ( x 2 ) ) − 1 2 . It is as follows:

χ ve ( TSCM p , q ) = 3 + 2 15 5 p q + 4 21 42 + 8 39 39 − 5 3 6 + 4 15 5 + 4 51 51 + 2 30 15 + 8 57 57 − 7 15 15 p + − 2 15 5 + 4 21 42 + 30 15 + 4 15 5 + 2 6 9 − 5 3 6 q + 7 15 15 − 1 / 3 6 − 8 21 42 + 16 39 39 − 8 15 5 + 2 / 3 3

6 Numerical results and discussion of TSCM

In this section, we deliver quantitative examples for the edge-vertex-degree and vertex-edge-degree topological properties of TSCM. We acquired numerical valued tables utilizing various scores of p and q, for all the topological descriptors computed above in our main results section, for the TSCM (Tables 5 and 6).

Table 5

Numerical results for the Sections 5.1 to 5.5.

( p , q ) M e v M α v e 1 M β v e 1 M v e 2 R v e
( 2 , 2 ) 11448 25632 5400 60894 5.9682
( 3 , 3 ) 25272 58500 11988 142920 11.701
( 4 , 4 ) 44496 104760 21168 259506 19.267
( 5 , 5 ) 69120 164412 32940 410652 28.666
( 6 , 6 ) 99144 237456 47304 596358 39.898
( 7 , 7 ) 134568 323892 64260 816624 52.962
( 8 , 8 ) 175392 423720 83808 1071450 67.859
( 9 , 9 ) 221616 536940 105948 1360836 84.590
( 10 , 10 ) 273240 663552 130680 1684782 103.15
Table 6

Numerical results for the Sections 5.6 to 5.10.

( p , q ) R e v A B C v e G A v e H v e χ v e
( 2 , 2 ) 39.292 36.100 117.77 5.5340 18.135
( 3 , 3 ) 81.330 73.788 247.44 10.988 37.030
( 4 , 4 ) 138.30 124.58 424.34 18.242 62.489
( 5 , 5 ) 210.19 188.47 648.47 27.295 94.508
( 6 , 6 ) 297.02 265.46 919.85 38.149 133.09
( 7 , 7 ) 398.77 355.52 1238.5 50.803 178.23
( 8 , 8 ) 515.45 458.69 1604.31 65.257 229.95
( 9 , 9 ) 647.06 574.97 2017.4 81.510 288.20
( 10 , 10 ) 793.60 704.35 2477.7 99.564 353.04

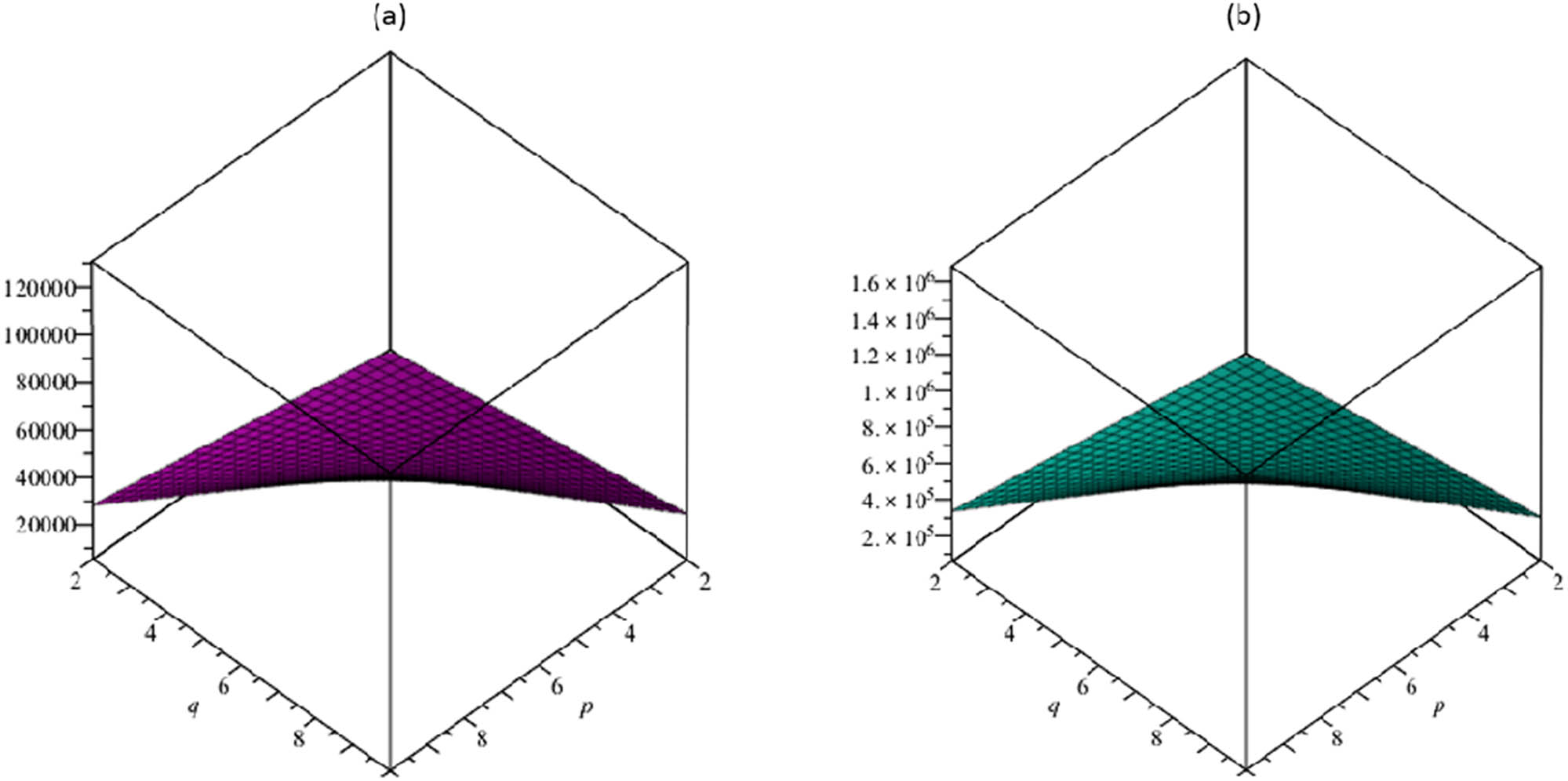
Furthermore, in Figures 3–7, based on the aforementioned numerical computation, we created the graphical depiction for the TSCM to study the behavior of the above-resulted topological descriptors.

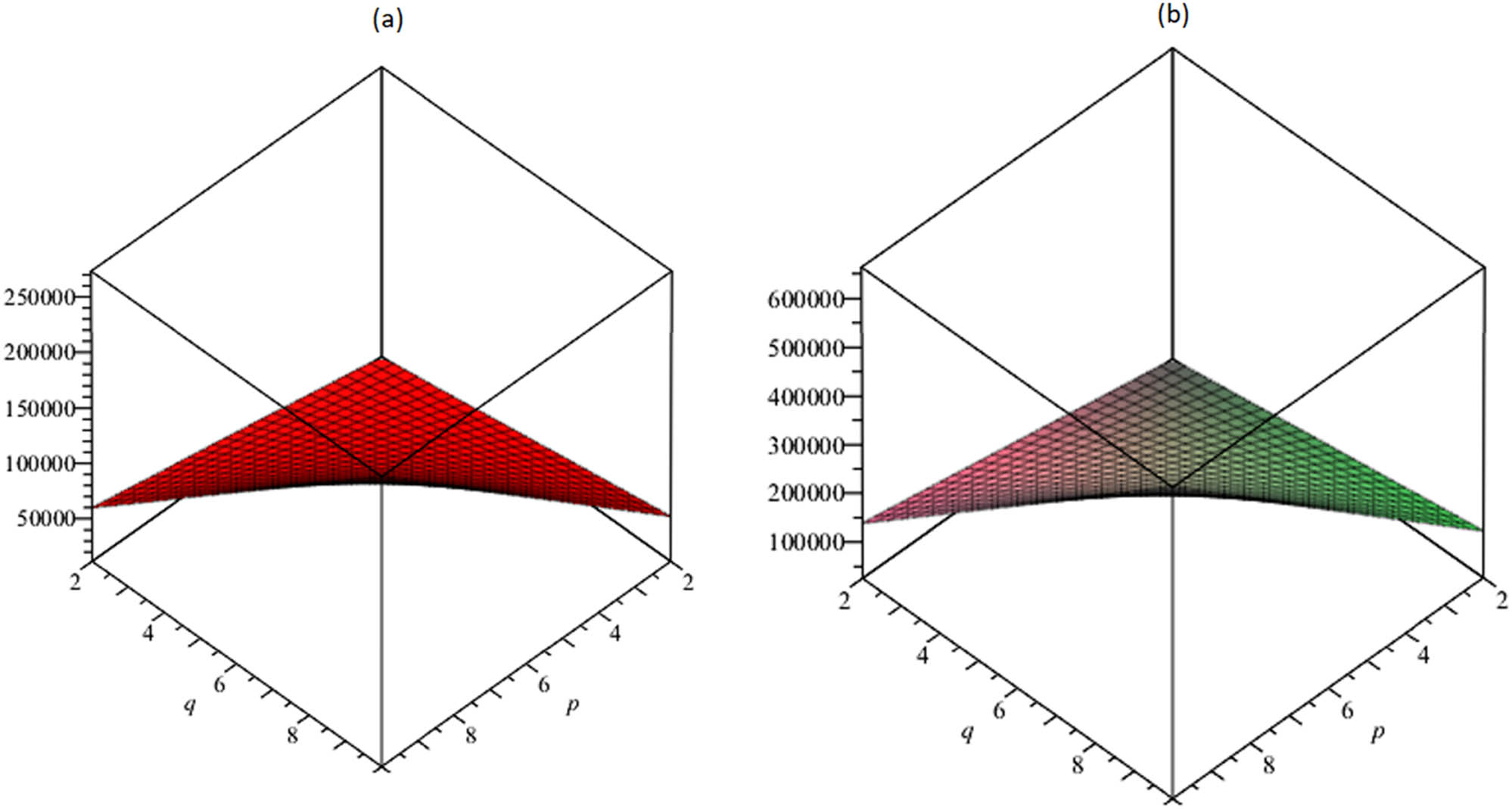
Figure 3 (a) The edge-vertex-degree Zagreb index M ev ; (b) the first vertex-edge-degree Zagreb α \alpha index M α v e 1 {M}_{\alpha ve}^{1} .
Figure 3

(a) The edge-vertex-degree Zagreb index M ev ; (b) the first vertex-edge-degree Zagreb α index M α v e 1 .

Figure 4 (a) The first vertex-edge-degree Zagreb β \beta index M β v e 1 {M}_{\beta ve}^{1} ; (b) the second vertex-edge-degree Zagreb index M v e 2 {M}_{ve}^{2} .
Figure 4

(a) The first vertex-edge-degree Zagreb β index M β v e 1 ; (b) the second vertex-edge-degree Zagreb index M v e 2 .

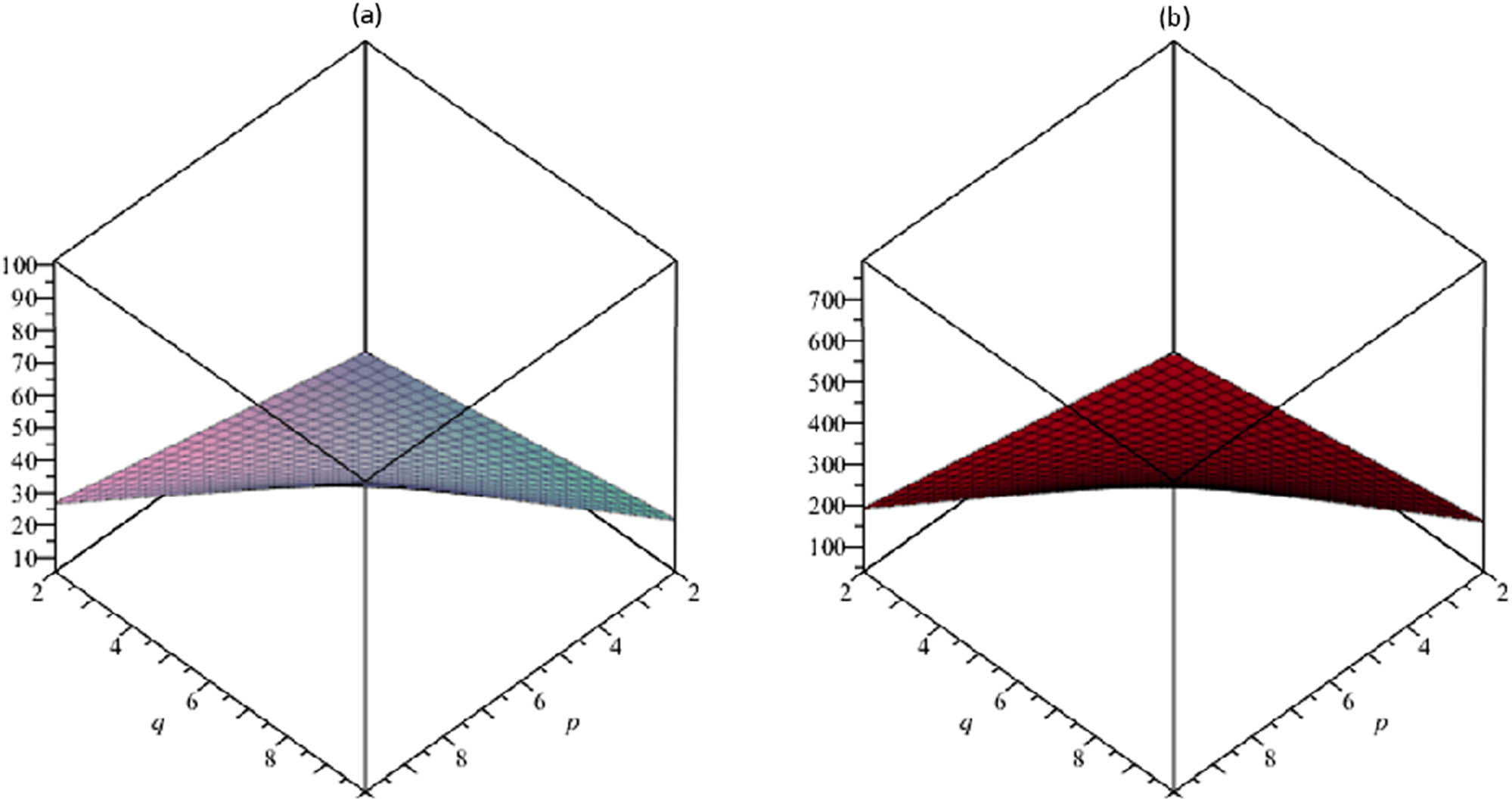
Figure 5 (a) The vertex-edge-degree Randić index R ve; (b) the edge-vertex-degree Randić index R ev .
Figure 5

(a) The vertex-edge-degree Randić index R ve; (b) the edge-vertex-degree Randić index R ev .

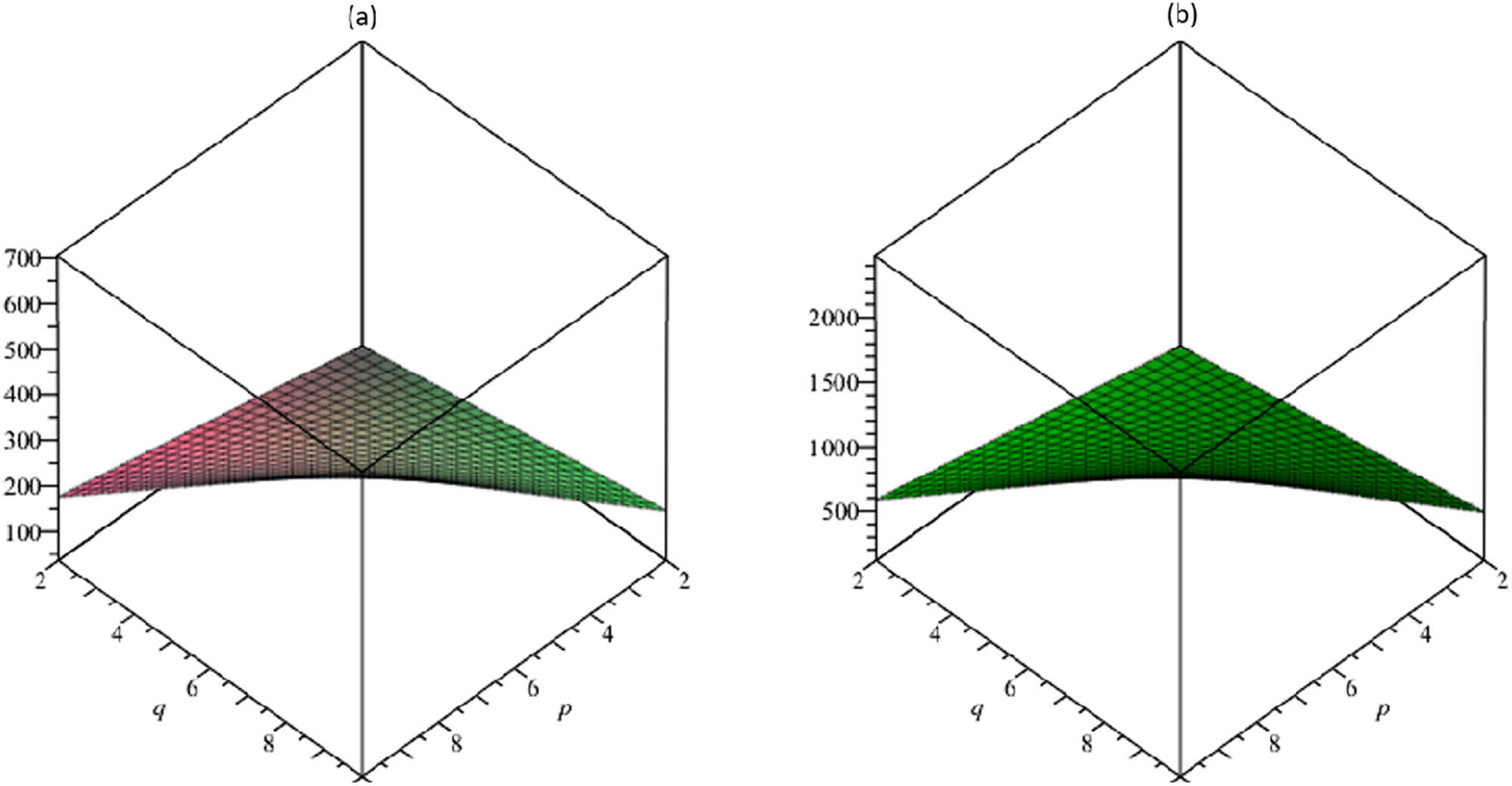
Figure 6 (a) The vertex-edge-degree atom–bond connectivity index ABC ve, (b) the geometric–arithmetic vertex-edge-degree index GA ve.
Figure 6

(a) The vertex-edge-degree atom–bond connectivity index ABC ve, (b) the geometric–arithmetic vertex-edge-degree index GA ve.

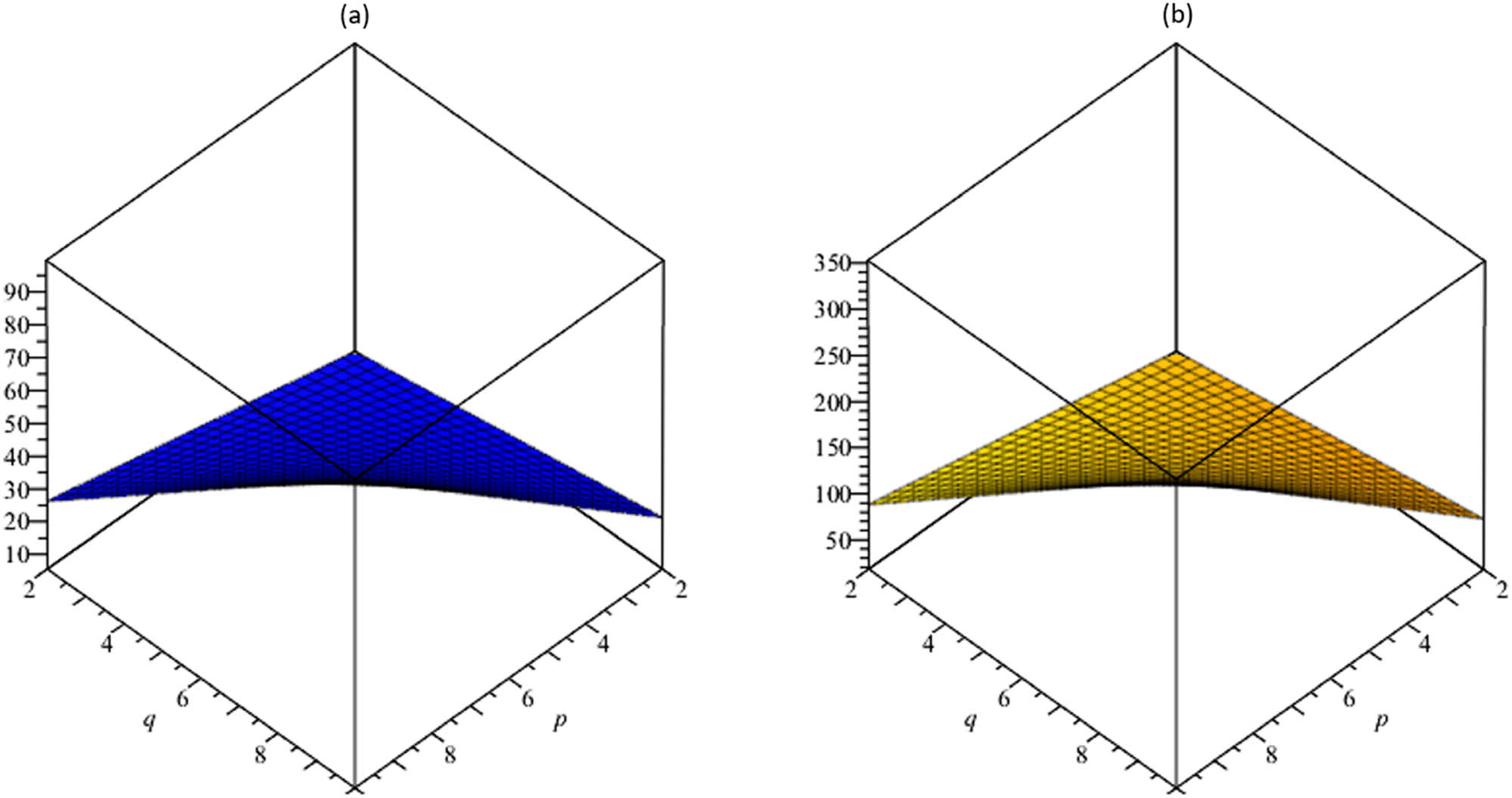
Figure 7 (a) The vertex-edge-degree harmonic index H ve; (b) the sum-connectivity vertex-edge-degree index χ ve {\chi }_{\text{ve}} .
Figure 7

(a) The vertex-edge-degree harmonic index H ve; (b) the sum-connectivity vertex-edge-degree index χ ve .

The resulting topological descriptors for the TSCM p,q increment as p and q rise as shown in Tables 5 and 6 and Figures 3–7.

Throughout the evaluation of the overall π -electron energy of molecules given by Gutman et al. (1975), Zagreb descriptors are implemented, and it is proved that boosting the attributes of p and q rises the total π-electron energy for TSCM p,q .

According to the research of isomer chemical compounds (Liu et al., 2019), automatic decision-making, computation of Kovats constants, and boiling point of molecules, the Randić descriptor is used. It can be observed that raising the quantities of p and q increases the quantities of the Randić characteristics for TSCM p,q .

The geometric–arithmetic descriptor outperforms the connectivity descriptor in terms of prediction power, and it is observed that the values of the GA descriptor increase for TSCM p,q as p and q increase.

The stability of linear and branched alkanes given in the research by Gao et al. (2017), also the strain energy of cycloalkanes, comparative to our computational ABC descriptor, provides a very good correlation. The ABC descriptor is increased for the underlying graph TSCM p,q with the increment of p and q.

7 Conclusion

Understanding the underlying topologies of graphs and networks requires the study of topological descriptors. Such studies have a wide spectrum of uses in the fields of cheminformatics, bioinformatics, and biomedicine, where various graph invariant-based assessments are used to deal with a variety of difficult strategies. Graph invariants are important tools for approximating and predicting the properties of biological and chemical compounds in the analysis of QSPRs⁄ and QSARs.

Rather, more importantly, we have indeed quantified results in this article for the edge-vertex-degree and vertex-edge-degree topological descriptors, namely, sum-connectivity vertex-edge-degree (X ve), vertex-edge-degree harmonic (H ve) index, geometric–arithmetic vertex-edge-degree (GA ve) index, atom–bond connectivity vertex-edge-degree (ABC ve) index, edge-vertex-degree Randić index, vertex-edge-degree Randić index, the second vertex-edge-degree Zagreb index, first vertex-edge-degree Zagreb β index, first vertex-edge-degree Zagreb α index, and Zagreb edge-vertex-degree index, for the TSCM.

Acknowledgement

We thank the anonymous reviewers for their careful reading of our manuscript and their many insightful comments and suggestions.

  1. Funding information: Authors state no funding is involved.

  2. Author contributions: Al-Nashri Al-Hossain Ahmad conceived of the presented idea and supervised the findings of this work. Ali Ahmad developed the theory and performed the computations. Muhammad Azeem verified the analytical methods and investigated them. All authors discussed the results and contributed to the final manuscript.

  3. Conflict of interest: Authors state there is no conflict of interest.

  4. Data availability statement: All data generated or analyzed during this study are included in this published article.

References

Ahmad A., On the degree based topological indices of benzene ring embedded in P-type-surface in 2D network. Hacet. J. Math. Stat., 2018, 47(1), 9–18.10.15672/HJMS.2017.443Search in Google Scholar

Anjum M.S., Safdar M.U., K Banhatti and K hyper-Banhatti indices of nanotubes. Eng. Appl. Sci. Lett., 2019, 21, 19–37.10.30538/psrp-easl2019.0013Search in Google Scholar

Barton C.D., Clay minerals, In: Rattan Lal, comp., ed. Encyclopedia of Soil Science. New York: Marcel Dekker, 2002, 187–192.10.1201/NOE0849338304.ch57Search in Google Scholar

Chellali M., Haynes T.W., Hedetniemi S.T., Lewis T.M., On vertex-edge-degrees and edge-vertex-degrees in graphs. Discret. Math., 2017, 340(2), 31–38.10.1016/j.disc.2016.07.008Search in Google Scholar

Ediz S., A new tool for QSPR researches: edge-vertex-degree Randić index. Celal Bayar Univ. J. Sci., 2017, 13(3), 615–618.10.18466/cbayarfbe.339313Search in Google Scholar

Ediz S., Farahani M.R., Imran M., On novel harmonic indices of certain Nanotubes. Int. J. Adv. Biotechnol. Res., 2017, 8(4), 277–282.Search in Google Scholar

Ediz S., On ve-degree molecular topological properties of silicate and oxygen networks, Int. J. Comput. Sci. Math., 2018, 9(1), 1–12.10.1504/IJCSM.2018.090730Search in Google Scholar

Gao W., Asif M., Nazeer W., The study of honeycomb derived network via topological indices, Open. J. Math. Anal., 2018, 2(2), 10–26.10.30538/psrp-oma2018.0014Search in Google Scholar

Gao W., Siddiqui M.K., Naeem M., Rehman N.A., Topological characterization of carbon graphite and crystal cubic carbon structures. Molecules, 2017, 22(9, 1496–1510.10.3390/molecules22091496Search in Google Scholar

Gutman I., Trinajstic N., Graph theory and molecular orbitals. iii. total π-electron energy of alternant hydrocarbons. Chem. Phys. Lett., 1972, 17(4), 535–538. 10.1016/0009-2614(72)85099-1.Search in Google Scholar

Gutman I., Ruscic B., Trinajstic N., Wilcox C.F., Graph theory and molecular orbitals. XII. Acyclic polyenes. J. Chem. Phys., 1975, 62(9), 3399–3405.10.1063/1.430994Search in Google Scholar

Horoldagva B., Das K.C., Selenge T.A., On vertex-edge-degree and edge-vertex-degree of graphs. Discret. Optim., 2019, 31, 1–7.10.1016/j.disopt.2018.07.002Search in Google Scholar

Liu J.B., Zhao J., He H., Shao Z., Valency-based topological descriptors and structural property of the generalized sierpinski networks. J. Stat. Phys., 2019, 177, 1131–1147.10.1007/s10955-019-02412-2Search in Google Scholar

Raza H., Nadeem M. F., Ahmad A., Asim M. A., Azeem M., Comparative study of valency-based topological indices for tetrahedral sheets of clay minerals. Curr. Org. Synth., 2021, 18(7), 711–718. 10.2174/1570179418666210709094729.Search in Google Scholar PubMed

Sahin B., Ediz S., On edge-vertex-degree and ve-degree topological indices. Iran. J. Math. Chem., 9(4)(2018), 263–277.Search in Google Scholar

Shao Z., Siddiqui M.K., Muhammad M.H., Computing Zagreb indices and Zagreb polynomials for symmetrical nanotubes, Symmetry, 2018a, 10(7), 244–260.10.3390/sym10070244Search in Google Scholar

Shao Z., Virk A.R., Javed M.S., Rehman M.A., Farahani M.R., Degree based graph invariants for the molecular graph of Bismuth Tri-Iodide, Eng. Appl. Sci. Lett., 2019, 2(1), 1–11.10.30538/psrp-easl2019.0011Search in Google Scholar

Shao Z., Wu P., Gao Y., Gutman I., Zhang X., On the maximum ABC index of graphs without pendent vertices, Appl. Math. Comput., 2017, 315, 298–312.10.1016/j.amc.2017.07.075Search in Google Scholar

Shao Z., Wu P., Zhang X., Dimitrov D., Liu J.B., On the maximum ABC index of graphs with prescribed size and without pendent vertices, IEEE Access., 2018b, 6, 27604–27616.10.1109/ACCESS.2018.2831910Search in Google Scholar

Siddiqui M.K., Imran M., and Ahmad A., On Zagreb indices, Zagreb polynomials of some nanostar dendrimers, Appl. Mathematics Computation, 2016, 280, 132–139.10.1016/j.amc.2016.01.041Search in Google Scholar

Wiener H., Structural determination of paraffin boiling points, J. Am. Chem. Soc., 1947, 69, 17–20.10.1021/ja01193a005Search in Google Scholar PubMed

Zhang J., Siddiqui M.K., Rauf A., Ishtiaq M., On ve-degree and edge-vertex-degree based topological properties of single walled titanium dioxide nanotube. J. Clust. Sci., 2020;32:821–32. 10.1007/s10876-020-01842-3.Search in Google Scholar

Zhong L., The harmonic index for graphs, Appl. Math. Lett., 2019, 25(3), 561–566.10.1016/j.aml.2011.09.059Search in Google Scholar
Received: 2021-12-31
Revised: 2022-03-30
Accepted: 2022-03-16
Published Online: 2022-04-21

© 2022 Al-Nashri Al-Hossain Ahmad et al., published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Embedded three spinel ferrite nanoparticles in PES-based nano filtration membranes with enhanced separation properties
  2. Research Articles
  3. Syntheses and crystal structures of ethyltin complexes with ferrocenecarboxylic acid
  4. Ultra-fast and effective ultrasonic synthesis of potassium borate: Santite
  5. Synthesis and structural characterization of new ladder-like organostannoxanes derived from carboxylic acid derivatives: [C5H4N(p-CO2)]2[Bu2Sn]4(μ3-O)2(μ2-OH)2, [Ph2CHCO2]4[Bu2Sn]4(μ3-O)2, and [(p-NH2)-C6H4-CO2]2[Bu2Sn]4(μ3-O)2(μ2-OH)2
  6. HPA-ZSM-5 nanocomposite as high-performance catalyst for the synthesis of indenopyrazolones
  7. Conjugation of tetracycline and penicillin with Sb(v) and Ag(i) against breast cancer cells
  8. Simple preparation and investigation of magnetic nanocomposites: Electrodeposition of polymeric aniline-barium ferrite and aniline-strontium ferrite thin films
  9. Effect of substrate temperature on structural, optical, and photoelectrochemical properties of Tl2S thin films fabricated using AACVD technique
  10. Core–shell structured magnetic MCM-41-type mesoporous silica-supported Cu/Fe: A novel recyclable nanocatalyst for Ullmann-type homocoupling reactions
  11. Synthesis and structural characterization of a novel lead coordination polymer: [Pb(L)(1,3-bdc)]·2H2O
  12. Comparative toxic effect of bulk zinc oxide (ZnO) and ZnO nanoparticles on human red blood cells
  13. In silico ADMET, molecular docking study, and nano Sb2O3-catalyzed microwave-mediated synthesis of new α-aminophosphonates as potential anti-diabetic agents
  14. Synthesis, structure, and cytotoxicity of some triorganotin(iv) complexes of 3-aminobenzoic acid-based Schiff bases
  15. Rapid Communications
  16. Synthesis and crystal structure of one new cadmium coordination polymer constructed by phenanthroline derivate and 1,4-naphthalenedicarboxylic acid
  17. A new cadmium(ii) coordination polymer with 1,4-cyclohexanedicarboxylate acid and phenanthroline derivate: Synthesis and crystal structure
  18. Synthesis and structural characterization of a novel lead dinuclear complex: [Pb(L)(I)(sba)0.5]2
  19. Special Issue: Theoretical and computational aspects of graph-theoretic methods in modern-day chemistry (Guest Editors: Muhammad Imran and Muhammad Javaid)
  20. Computation of edge- and vertex-degree-based topological indices for tetrahedral sheets of clay minerals
  21. Structures devised by the generalizations of two graph operations and their topological descriptors
  22. On topological indices of zinc-based metal organic frameworks
  23. On computation of the reduced reverse degree and neighbourhood degree sum-based topological indices for metal-organic frameworks
  24. An estimation of HOMO–LUMO gap for a class of molecular graphs
  25. On k-regular edge connectivity of chemical graphs
  26. On arithmetic–geometric eigenvalues of graphs
  27. Mostar index of graphs associated to groups
  28. On topological polynomials and indices for metal-organic and cuboctahedral bimetallic networks
  29. Finite vertex-based resolvability of supramolecular chain in dialkyltin
  30. Expressions for Mostar and weighted Mostar invariants in a chemical structure
https://doi.org/10.1515/mgmc-2022-0007
Keywords for this article
tetrahedral sheets of clay minerals; topological descriptors; complex chemical networks; edge-vertex-degree; vertex-edge-degree
Creative Commons
BY 4.0

Articles in the same Issue

  1. Embedded three spinel ferrite nanoparticles in PES-based nano filtration membranes with enhanced separation properties
  2. Research Articles
  3. Syntheses and crystal structures of ethyltin complexes with ferrocenecarboxylic acid
  4. Ultra-fast and effective ultrasonic synthesis of potassium borate: Santite
  5. Synthesis and structural characterization of new ladder-like organostannoxanes derived from carboxylic acid derivatives: [C5H4N(p-CO2)]2[Bu2Sn]4(μ3-O)2(μ2-OH)2, [Ph2CHCO2]4[Bu2Sn]4(μ3-O)2, and [(p-NH2)-C6H4-CO2]2[Bu2Sn]4(μ3-O)2(μ2-OH)2
  6. HPA-ZSM-5 nanocomposite as high-performance catalyst for the synthesis of indenopyrazolones
  7. Conjugation of tetracycline and penicillin with Sb(v) and Ag(i) against breast cancer cells
  8. Simple preparation and investigation of magnetic nanocomposites: Electrodeposition of polymeric aniline-barium ferrite and aniline-strontium ferrite thin films
  9. Effect of substrate temperature on structural, optical, and photoelectrochemical properties of Tl2S thin films fabricated using AACVD technique
  10. Core–shell structured magnetic MCM-41-type mesoporous silica-supported Cu/Fe: A novel recyclable nanocatalyst for Ullmann-type homocoupling reactions
  11. Synthesis and structural characterization of a novel lead coordination polymer: [Pb(L)(1,3-bdc)]·2H2O
  12. Comparative toxic effect of bulk zinc oxide (ZnO) and ZnO nanoparticles on human red blood cells
  13. In silico ADMET, molecular docking study, and nano Sb2O3-catalyzed microwave-mediated synthesis of new α-aminophosphonates as potential anti-diabetic agents
  14. Synthesis, structure, and cytotoxicity of some triorganotin(iv) complexes of 3-aminobenzoic acid-based Schiff bases
  15. Rapid Communications
  16. Synthesis and crystal structure of one new cadmium coordination polymer constructed by phenanthroline derivate and 1,4-naphthalenedicarboxylic acid
  17. A new cadmium(ii) coordination polymer with 1,4-cyclohexanedicarboxylate acid and phenanthroline derivate: Synthesis and crystal structure
  18. Synthesis and structural characterization of a novel lead dinuclear complex: [Pb(L)(I)(sba)0.5]2
  19. Special Issue: Theoretical and computational aspects of graph-theoretic methods in modern-day chemistry (Guest Editors: Muhammad Imran and Muhammad Javaid)
  20. Computation of edge- and vertex-degree-based topological indices for tetrahedral sheets of clay minerals
  21. Structures devised by the generalizations of two graph operations and their topological descriptors
  22. On topological indices of zinc-based metal organic frameworks
  23. On computation of the reduced reverse degree and neighbourhood degree sum-based topological indices for metal-organic frameworks
  24. An estimation of HOMO–LUMO gap for a class of molecular graphs
  25. On k-regular edge connectivity of chemical graphs
  26. On arithmetic–geometric eigenvalues of graphs
  27. Mostar index of graphs associated to groups
  28. On topological polynomials and indices for metal-organic and cuboctahedral bimetallic networks
  29. Finite vertex-based resolvability of supramolecular chain in dialkyltin
  30. Expressions for Mostar and weighted Mostar invariants in a chemical structure
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2026 De Gruyter Brill
Downloaded on 14.1.2026 from https://www.degruyterbrill.com/document/doi/10.1515/mgmc-2022-0007/html
Scroll to top button