Home Vibrations Analysis of Rectangular Plates with Clamped Corners
Article Open Access

Vibrations Analysis of Rectangular Plates with Clamped Corners

  • Mohammad A. Gharaibeh EMAIL logo and Amr M. Obeidat
Published/Copyright: September 2, 2018
Download Article (PDF)
Become an author with De Gruyter Brill
Submit Manuscript Author Information
Open Engineering
From the journal Open Engineering Volume 8 Issue 1

Abstract

This paper discusses the fundamental natural frequency of a thin elastic rectangular, isotropic and orthotropic, plates with clamped corners. Rayleigh’s method was used to analytically calculate the plate lowest natural frequency. In this solution, the vibration mode shape was assumed in a form that certifies the displacement as well as the rotational boundary conditions of the current problem. Finally, this paper provides useful information for evaluating the natural frequency of a plate with fixed corners with different mass attachments configurations.

1 Introduction

Rectangular elastic plates [1, 2] are widely used in engineering applications; e.g. in printed circuit boards and solar collecting panels. The exact solutions of free vibration of elastic plates are possible only for a few cases, particularly for plate structures with well-defined boundary conditions. However, real-life vibration problems may pose some difficulties in satisfying boundary conditions, such as plates having fixed (or clamped) corners. In these cases, only approximate solutions, using Rayleigh methods, are available [3].

In engineering applications, plates with clamped corners frequently appear in the fatigue life analysis of electronic printed circuit boards (PCBs). For the PCBs, the clamped constraint can arise from the fact that the elastic plate is clamped at each corner using threaded screws, washers and nuts to attach the plate structure to a base support. This type of attachment prevents both displacement and rotation of the structure at the support locations. This kind of problem has been thoroughly investigated using the analytical solution of the superposition method invented by Gorman [5, 6, 7, 8, 9, 10]. However, this analytical-type solution is very complicated and considered to be impractical.

A similar problem that has been investigated in literature is the vibration of elastic plate with pinned corners. The pinned-corner support boundary condition scheme, unlike the clamped corner scheme, only prevents displacements at the support locations, having no restriction on the rotation. Xiang-sheng [11] used Rayleigh method to analytically approximate the first resonant frequency of a plate having point-pinned supports at plate corners. Kim et al. [12, 13] used beam shape functions to solve for the deflections of plates with point supported at corners. Kerstens [14, 15] used a combination of Rayleigh-Ritz method and modal constraint method to obtain the free vibration problem of plates with such supports. As a powerful tool, the finite element analysis (FEA) has also been extensively used in the vibration analysis of plates with corner supports. Raju et al. [16] and Rao et al. [17] studied the natural frequencies of point-supported elastic plates using finite element method. Pitarresi and Kunz [18, 19] developed a simple technique using two-dimensional non-linear least-squares fit, and finite element simulations, to study the natural frequency of plates having point supports. Recently, Gharaibeh et al. [20, 21] employed the assumed mode method to evaluate the fundamental natural frequency of corner-supported plates using an electronic package.

In addition, elastic rectangular plates having corner supports may exist in many renewable energy and power generation systems such as concentrating solar power (CSP) systems, including solar dishes, parabolic trough solar collectors, and solar central receiver systems. The analysis and characteristics of vibrations of rectangular plates has been widely and extensively investigated based on various techniques. For example, Torabi et al. [22] studied the vibration characteristics of a rectangular plate having a circular central hole with point support, based on the Rayleigh-Ritz method, which is widely used, based on orthogonal polynomials and beam functions. Similarly, Li [23] employed the same approach to characterize vibrations of rectangular plates with general elastic boundary supports. Watkins et al. [24] computed normalized frequencies of elastically point-supported rectangular plates using Eigensensitivity analysis. Shahrjerdi et al. [25] used second-order shear deformation theory (SSDT) to study the vibration of solar-graded plates. Du et al. [26] employed Fourier series method for the in-plane vibration analysis of rectangular plates with elastically restrained edges.

The current work discusses the fundamental natural frequency of an elastic rectangular plate having fixed (or clamped) corners using the Rayleigh method. Both isotropic and orthotropic material systems were considered. In this paper, we first start by introducing the problem of the plate with clamped corners and resulting boundary conditions. This is followed by the use of the Rayleigh method in the system’s first natural frequency analysis. Subsequently, the careful selection of the mode shape function that satisfies the displacement and rotational boundary conditions of the problem is also presented. Finally, the natural frequency results for several geometric and mass attachment configurations are discussed in detail.

2 Description of the Problem

The plate under consideration in the present work is shown in Figure 1. The supports on the plate corners prevent both displacements and rotations at the support locations, and the edges are completely free elsewhere. The plate width is (a) and length is (b) with thickness (h). The complete set of boundary conditions can be described as:

Displacement

w0,0=wa,0=wa,b=w0,b=0(1)
Figure 1 Plate with clamped corners schematic.
Figure 1

Plate with clamped corners schematic.

Rotations

wx0,0=wxa,0=wxa,b=wx0,b=0(2a)
wy0,0=wya,0=wya,b=wy0,b=0(2b)

Moments

wxx0,y+νwyy0,y=0(3a)
wxxa,y+νwyya,y=0(3b)
wyyx,0+νwxxx,0=0(3c)
wyyx,b+νwxxx,b=0(3d)

Effective shear forces

wxxx0,y+(2−ν)wxyy0,y=0(4a)
wxxxa,y+(2−ν)wxyya,y=0(4b)
wyyyx,0+(2−ν)wxxyx,0=0(4c)
wyyyx,b+(2−ν)wxxyx,b=0(4d)

3 Natural Frequency Analysis by Rayleigh’s Method

As previously mentioned, the present work aims to produce an approximate analytical solution for calculating the first natural frequency of a plate with clamped corners using Rayleigh’s method. Therefore, it is essential to express the general energy of the system, which is composed of the potential and kinetic energies of the plate structure. Considering an isotropic plate having a constant thickness, the plate potential energy (V) can expressed as [27]:

V=D2∬Awxx+wyy2−2(1−ν)wxxwyy−wxy2dxdy(5)

where D = Eh312(1−ν) is the plate flexural rigidity; h, E and ν are the plate thickness, plate isotropic material modulus of elasticity, and Poisson’s ratio, respectively; w is the plate deflection in the transverse direction; wxx = ∂2w∂x2,wyy = ∂2w∂y2 and wxy = ∂2w∂x∂y.

The plate kinetic energy (T) is [27]:

T=ρh2∬Aw˙2dxdy(6)

where ρ is the mass per unit volume of the plate material; ẇ is the plate velocity in the lateral direction. The double integrals shown in Eq. (5) and Eq. (6) are evaluated over the plate surface area A.

The deflection of the plate, whose motion is harmonic, is:

wx,y,t=W(x,y)ei^ωt(7)

where î is the complex number î = −1,ω is the vibration circular frequency, and t is the time. The function W(x,y) is the plate mode shape. The proper selection of this mode function will be discussed later.

To use Rayleigh’s method, which is based on the energy conservation theorem, the maximum potential energy (Vmax) of the system must be equal to the kinetic energy (Tmax) of the system [8]:

Vmax=Tmax(8)

where,

Vmax=D2∬AWxx+Wyy2−2(1−ν)WxxWyy−Wxy2dxdy(9)
Tmax=ω2ρh2∬AW2dxdy(10)

Therefore, the first natural frequency of the plate is written as:

ω=Dρh∬AWxx+Wyy2−2(1−ν)WxxWyy−Wxy2dxdy∬AW2dxdy(11)

Considering orthotropic plate material system, the kinetic energy of the plate is still expressed as in Eq. (6) and Eq. (10) above. However, the potential energy is written as [28]:

V=12∬ADxwxx2+Dywyy2+2Dxνywxxwyy+4Dkwxy2dxdy(12)

where: Dx=Exh312(1−νxνy),Dy=Eyh312(1−νxνy)andDk=Gxyh312. The material parameters Ex, Ey and Gxy are the modulus of elasticity in x-direction, the modulus of elasticity in y-direction, and the shear modulus in xy plane, respectively. Also, νx and νy are Poisson’s ratio in xy and yx planes, respectively.

By applying Rayleigh’s method as shown previously, the natural frequency of the orthotropic plate can be expressed as:

ω=DxWxx2+DyWyy2+2DxνyWxxWyy+4DkWxy2dxdyρh∬AW2dxdy(13)

The accuracy of the calculated natural frequency of Eq. (11) and Eq. (13) greatly depends on the engineered selection of the mode shape function, W(x,y), to be discussed next.

4 Mode Shape Selection

As explained earlier, the proper selection of the mode shape in the Eq. (11) and Eq. (13) is very important. This mode function should be carefully selected in a mathematical form that satisfies the problem displacement as well as rotational boundary conditions. For the current analysis, the plate is fixed in all directions on the corners and free elsewhere. As formulated in Eq. (1) to Eq. (4), this type of constraint will result in zero displacements and rotations at the corners. Whereas the plate deflections and rotations on the edges are different from zero. Therefore, the mode shape of this problem can be formulated as:

Wx,y=C11−cos2πxa+C21−cos2πyb+C31−cos2πxa1−cos2πyb(14)

where a and b are the plate dimensions in x and y directions, respectively. Also, constants C1 and C2 are the deflections of the midpoints of the plate sides in x and y directions, respectively. The constant C3 represents the displacement of the plate center (x=a2,y=b2). All mode shape constants are independent, as well as unknown, and therefore need to be determined.

Obviously, the mode shape formulated in Eq. (14) completely satisfies the displacement as well as the rotation boundary conditions of Eq. (1) and Eq. (2). However, the satisfaction of the bending moment and shear forces of Eq. (3) and Eq. (4), respectively, are not adequately achieved. Here, if we can satisfy the bending moment and/or effective shear forces boundary conditions, we might be able to greatly increase the calculated natural frequency of Eq. (11) and (13). Furthermore, this can decrease the number of the independent constants of the mode shape function, Eq. (14), therefore achieving much simpler solution. Consequently, we aim to satisfy the shear forces conditions of Eq. (4), having y = 0 and x = 0, thus obtaining:

C1=β1C3(15)
C2=β2C3(16)

where β1 and β2 are constants depends on the plate aspect ratio ba, and Poisson’s ratio is defined as:

β1=ab2(2−ν)(17)
β2=ba2(2−ν)(18)

By applying Eq. (15) to Eq. (18), and into Eq. (14), the mode shape function can be modified to:

Wx,y=C3β11−cos2πxa+β21−cos2πyb+1−cos2πxa1−cos2πyb(19)

As can be clearly seen in Eq. (19), the number of independent constants in the mode shape are reduced from three to one (C3). This will result, as expected, in much simpler and accurate solution for the plate with clamped corners problem.

For the orthotropic plate analysis, the shear boundary conditions of the current plate problem become [28]:

wxxx0,y+2DxyDx−νywxyy0,y=0(20a)
wxxxa,y+2DxyDx−νywxyya,y=0(20b)
wyyyx,0+2DxyDy−DxDyνywxxyx,0=0(20c)
wyyyx,b+2DxyDy−DxDyνywxxyx,b=0(20d)

where Dxy = 2Dxνy + 2Dk.

Following the same procedure above, the mode shape constants of Eq. (19) are obtained as:

β1=ab22Dxy−DxνyDx(21)
β2=ba22Dxy−DxνyDy(22)

5 Results and Discussions

Plate with fixed corners with no mass attachments

To find an equation of the fixed-corners plate’s first natural frequency, and considering an isotropic plate system, we substitute Eq. (19), combined with Eq. (17) and Eq. (18), into Eq. (11) to obtain:

ω=λ2a2Dρh(23)

where a is the plate shortest length, and λ2 is the plate eigenvalue written as:

λ2=4π2S1+2ab2+S2ab4S(24)

where,

S=6β12+β22+12β1+β2+8β1β2+9(25a)
S1=2β12+4β1+3(25b)
S2=2β22+4β22+3(25c)

It important to mention that β1 and β2 of Eq. (25) are to be obtained from Eq. (17) and Eq. (18), respectively. As this eigenvalue is a function of β1 and β2, then it is a function of plate aspect ratio b/a and Poisson’s ratio ν only. Assuming that ν = 0.3, then the values of β1, β2 and λ2 for several plate aspect ratios are summarized in Table 1.

Table 1

Mode shape constants and isotropic plate eigenvalues for different plate aspect ratios (ν=0.3).

b/aβ1β2λ2
1.01.7001.70021.916
1.50.7563.82512.350
2.00.4256.8007.2033
2.50.27210.634.6175
3.00.18915.303.1940
3.50.13920.802.3370
4.00.10627.201.7831

To simplify the analysis, an empirical formula for calculating the plate eigenvalue as a function of the aspect ratio of the plate has been established. For this formula, the suggested general form is:

λ2=a11baa2(26)

where a1 and a2 are unknown constants that need to be determined. To determine such constants, a non-linear regression analysis using MINITAB is performed. Thus:

λ2=22.271ba1.66(27)

Eq. (27) was compared to the analytical solution data, as shown in Figure 2. From this comparison, it is found that the results of the curve-fitted equation are in agreement with the values of Table 1.

Figure 2 Plate eigenvalues for different plate geometries.
Figure 2

Plate eigenvalues for different plate geometries.

For an orthotropic plate, we substitute Eq. (19), combined with Eq. (21) and Eq. (22), into Eq. (13) to get:

ω=4π2a2DxyρhSxDxDxy+2ab2+SyDyDxyab4Sxy(28)

where:

Sxy=6β12+β22+12β1+β2+8β1β2+9(29a)
Sx=2β12+4β1+3(29b)
Sy=2β22+4β22+3(29c)

It important to mention that β1 and β2 of Eq. (29) are to be obtained from Eq. (21) and Eq. (22), respectively. This eigenvalue is a function of a/b, Ex, Ey, νx and νy.

Plate with fixed corners having mass attachments

After discussing the problem of a plate with fixed corners, we have a look at the problem of a plate with two mass attachment types:

  1. Case 1: Plate with fixed corners with a centrally placed mass.

  2. Case 2: Plate with fixed corners with edge-center-placed masses.

In the present analysis, only the isotropic plate material system was studied. The same procedure could be followed for orthotropic plate system.

For case 1, the concentrated mass (M) is mounted at the plate center point (x=a2,y=b2), as shown in Figure 3(a). For case 2, as depicted in Figure 3(b), four equal masses (the mass of each is M) are attached at the centers of the plate edges x=a2,y=0,x=a,y=b2,x=a2,y=b,x=0,y=b2.

Figure 3 Corner-clamped plate with mass attachments; (a) case 1, (b) case 2.
Figure 3

Corner-clamped plate with mass attachments; (a) case 1, (b) case 2.

This mass addition will have no effect on the structure’s potential energy. Generally, however, for a plate with attached mass (either for case 1 or case 2), the kinetic energy of the system could be expressed as:

T=ρh2∬Aw˙x,y2dxdy+M2∑i=1Nw2˙(ζi,ηi)(30)

where ẇ(ζi,ηi) are the velocities of the plate at the mass fix-up locations, and N is the total number of attached masses.

Following the previously described natural frequency analysis procedure, the system’s fundamental natural frequency is:

ω=λ2a2DαMa2+ρh(31)

where α is the reduced coefficient of the mass, and it is function of plate aspect ratio b/a, and Poisson’s ratio ν. Again, assuming that ν = 0.3, then the values of α for several plate aspect ratios, for both cases, are summarized in Table 2.

Table 2

Reduced coeficient of the mass for several plate aspect ratios for plate with center mass ν=0.3).

b/a1.01.52.02.53.03.54.0
αCase 14.3362.5911.7131.2671.0050.8350.716
αCase 26.8765.0214.2043.6163.1542.7852.486

It is important to mention at this point that this mass addition has no effect on the mode shape constants and plate eigenvalues, and their values are still equal to those listed in Table 1.

As done previously, a general equation to calculate the reduced coefficient of the mass, for both cases, was formulated. The suggested general form for this equation is:

α=c11bac2(32)

where c1 and c2 are coefficients determined using a nonlinear regression analysis as c1 = 4.35, c2 = 1.32 for case 1, and c1 = 6.85, c2 = 0.72 for case 2. A comparison between the fitted formula and the actual (analytical) data of α is shown in Figure 4. For both cases, the fitted formulas are in excellent match with the analytically derived data.

Figure 4 The reduced coefficient of the mass vs plate aspect ratio for (a) case 1 and (b) case 2.
Figure 4

The reduced coefficient of the mass vs plate aspect ratio for (a) case 1 and (b) case 2.

As a special configuration, we shall consider the mass (M) of the added mass (or masses) to be a function of the plate mass. Thus:

M=nbahρ(33)

where n is the plate mass fraction, and it can be any positive number: i.e., if n = 0.5 or n = 2, then the total added mass is half of the plate mass or double of it, respectively. Now, substitute Eq. (33) into Eq. (31), and after some simple mathematical manipulation we achieve:

ω=λ2a21nαba+1Dρh(34)

or:

ω=Λ2a2Dρh(35)

where Λ2 = λ21nαba+1 is the massed plate eigenvalue.

From Eq. (35) above, Λ2 is now function of b/a, ν and α, as well as n. Luckily, α is function of b/a (besides to ν), for both cases. Therefore, we can implicitly say that Λ2 is a function of b/a, ν and n only. As before, assuming ν = 0.3, Table 3 and Table 4 summarize the values of Λ2 for different b/a and n combinations for case 1 and case 2, respectively.

Table 3

Values of Λ2 at different b/a and n for case 1 (ν=0.3).

b/an
0.250.500.751.01.251.501.752.0
1.015.181412.313110.62839.48758.64968.00057.47857.047
1.58.79547.19876.24185.58695.10264.72574.42164.1696
2.05.28674.37333.81273.42393.13412.90732.72352.5706
2.53.44952.87262.51322.26192.07341.92541.80521.7049
3.02.41192.0171.76871.5941.46261.35911.27491.2046
3.51.77651.48961.30811.181.08341.00720.94510.8932
4.01.36121.14341.0050.90710.83320.77480.72720.6874

Table 4

Values of Λ2 at different b/a and n for case 2 (ν=0.3).

b/an
0.250.500.751.01.251.501.752.0
1.013.29110.40328.83247.80927.07526.51566.07075.7061
1.57.27375.65724.78964.22823.82693.52183.27963.0814
2.04.08993.15762.6652.34852.12321.95241.81711.7066
2.52.55741.96531.65551.45731.31661.21011.12591.0571
3.01.7411.33421.12250.98750.89180.81940.76220.7156
3.51.26060.96430.81070.71290.64360.59130.54990.5162
4.00.9550.72970.61310.53900.48660.44690.41570.3901

To establish a formula to calculate Λ2 as a function of the plate aspect ratio and of mass fraction factor, for both cases, a general non-linear form, which is a combination of Eq. (27) and Eq. (35), was selected as follows:

Λ2=a11baa21d1n1bad2+1(36)

Here, a1 and a2, for case 1 and case 2, are similar to those of Eq. (27). Also, d1 and d2 are two unknown coefficients. To obtain them, a multi-parametric fit was performed considering both case 1 and case 2. The resultant constant values are (d1 = 4.33, d2 = 0.29) and (d1 = 6.89, d2 = –0.26) for case 1 and case 2, respectively. Figure 5 shows a comparison between the analytically derived data and the fitted formulas for both mass attachment cases, for several plate aspect ratios. In conclusion, the Λ2 values for case 1 and case 2, from both solutions, are in a great agreement.

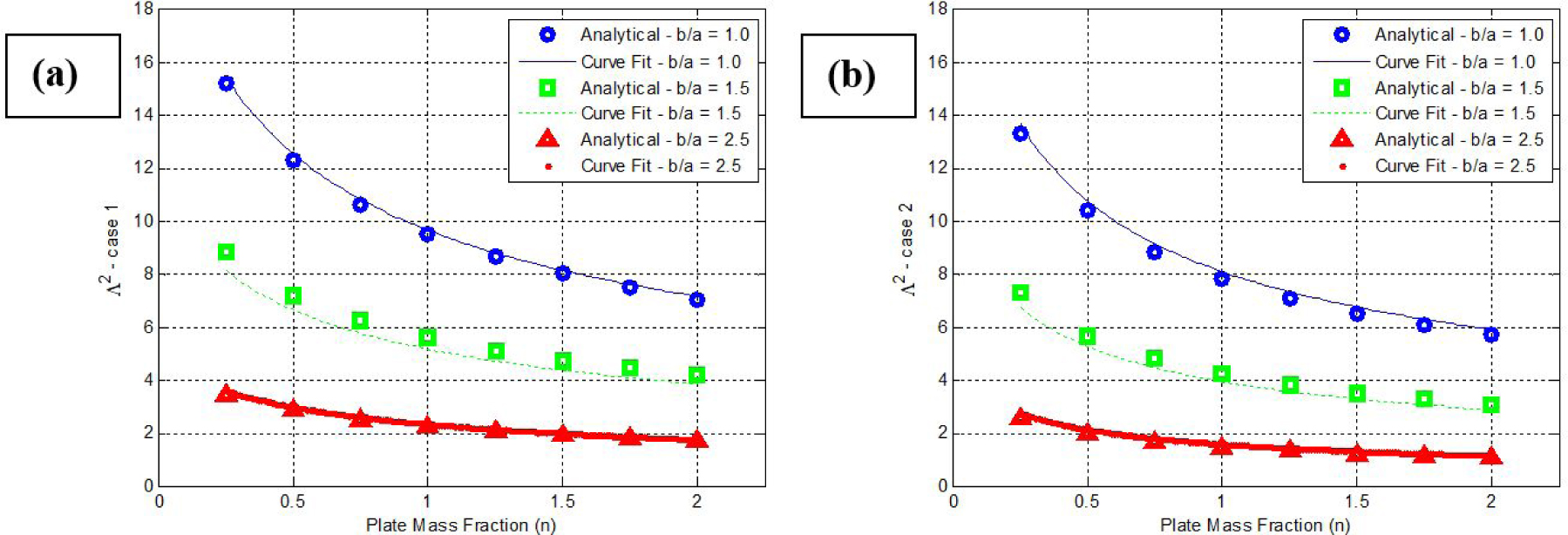
Figure 5 The massed plate eigenvalues (Λ2) vs. the plate mass fraction (n) at different b/a for (a) case 1 and (b) case 2.
Figure 5

The massed plate eigenvalues (Λ2) vs. the plate mass fraction (n) at different b/a for (a) case 1 and (b) case 2.

6 Conclusions

This paper has discussed the free vibration problem of plates with clamped corners. Rayleigh’s method was used to analytically approximate the fundamental natural frequency of the plate under study. From this approximation, the plate eigenvalue was obtained for several plate dimensions. In addition, two types of mass attachments, namely plate with centrally placed mass and plate with masses on the edges centers, were discussed. A special configuration considering the mass of the added masses as a function of the plate mass was also presented. Finally, this paper developed non-linear equations for calculating the plate eigenvalues for both massed and un-massed configurations.

References

[1] Leissa, A. W., Vibration of plates, 1969, NASA SP-160.Search in Google Scholar

[2] Leissa, A. W., The free vibration of rectangular plates, Journal of Sound and Vibration, 1973, 31(3), 257-293.10.1016/S0022-460X(73)80371-2Search in Google Scholar

[3] Rayleigh, J. W. S. B., The theory of sound, 1896, (Vol. 2). Macmillan.10.1063/1.3060230Search in Google Scholar

[4] Steinberg, D. S., Vibration analysis for electronic equipment, Second edition, 2000, John Wiley & Sons.Search in Google Scholar

[5] Gorman, D. J., Free vibration of orthotropic cantilever plates with point supports, Journal of Engineering Mechanics, 1995, 121(8), 851-857.10.1061/(ASCE)0733-9399(1995)121:8(851)Search in Google Scholar

[6] Singhal, R. K., and Gorman, D. J., Free vibration of partially clamped rectangular plates with and without rigid point supports, Journal of Sound and Vibration, 1997, 203(2), 181-192.10.1006/jsvi.1996.0878Search in Google Scholar

[7] Gorman, D. J., Accurate free vibration analysis of point supported Mindlin plates by the superposition method, Journal of Sound and Vibration, 1999, 219(2), 265-277.10.1006/jsvi.1998.1874Search in Google Scholar

[8] Gorman, D. J., and Singal, R. K., Analytical and experimental study of vibrating rectangular plates on rigid point supports, AIAA Journal, 1991, 29(5), 838-844.10.2514/3.10664Search in Google Scholar

[9] Gorman, D. J., A general analytical solution for free vibration of rectangular plates resting on fixed supports and with attached masses, Journal of Electronic Packaging, 1992, 114, 239.10.1115/1.2906424Search in Google Scholar

[10] Gorman, D. J., Vibration analysis of plates by the superposition method, 1999, (Vol. 3), World Scientific.10.1142/3967Search in Google Scholar

[11] Xiang-sheng, C., Vibrations of rectangular plates supported at corner points, Applied Mathematics and Mechanics, 1989, 10(8), 751-757.10.1007/BF02019300Search in Google Scholar

[12] Kim, C. S., and Dickinson, S. M., The flexural vibration of rectangular plates with point supports, Journal of Sound and Vibration, 1987, 117(2), 249-261.10.1016/0022-460X(87)90537-2Search in Google Scholar

[13] Kim, C. S., Young, P. G., and Dickinson, S. M., On the flexural vibration of rectangular plates approached by using simple polynomials in the Rayleigh-Ritz method, Journal of Sound and Vibration, 1990, 143(3), 379-394.10.1016/0022-460X(90)90730-NSearch in Google Scholar

[14] Kerstens, J. G. M., Vibration of a rectangular plate supported at an arbitrary number of points, Journal of Sound and Vibration, 1997, 65(4), 493-504.10.1016/0022-460X(79)90899-XSearch in Google Scholar

[15] Kerstens, J. G. M., Vibration of complex structures: the modal constraint method, Journal of Sound and Vibration, 1981, 76(4), 467-480.10.1016/0022-460X(81)90264-9Search in Google Scholar

[16] Raju, I. S., and Amba-Rao, C. L., Free vibrations of a square plate symmetrically supported at four points on the diagonals, Journal of Sound and Vibration, 1983, 90(2), 291-297.10.1016/0022-460X(83)90537-0Search in Google Scholar

[17] Rao, G. V., Raju, I. S., and Amba-Rao, C. L., Vibrations of point supported plates, Journal of Sound and Vibration, 1973, 29(3), 387-391.10.1016/S0022-460X(73)80292-5Search in Google Scholar

[18] Pitarresi, J. M., and Kunz, R. J., A simple technique for the rapid estimation of the optimal support locations for a vibrating plate, Journal of Vibration and Acoustics, 1992, 114(1), 112-118.10.1115/1.2930224Search in Google Scholar

[19] Kunz, R. J., and Pitarresi, J. M., Analytical and Experimental Optimization of Support Locations for Vibrating Printed Circuit Boards,” In Ninth Annual International Electronics Packaging Conference, San Diego, California, 1989, (pp. 11-13).Search in Google Scholar

[20] Gharaibeh, M. A., Finite element modeling, characterization and design of electronic packages under vibration, 2015, PhD Dissertation, State University of New York At Binghamton.Search in Google Scholar

[21] Gharaibeh, M. A., Su, Q. T., and Pitarresi, J. M., Analytical Solution for Electronic Assemblies Under Vibration, Journal of Electronic Packaging, 2016, 138(1), 011003.10.1115/1.4032497Search in Google Scholar

[22] Torabi, K. and Azadi, A.R., Vibration analysis for rectangular plate having a circular central hole with point support by Rayleigh-Ritz method, Journal of Solid Mechanics, 2014, 6(1), 28-42.Search in Google Scholar

[23] Li W.L., Vibration analysis of rectangular plates with general elastic boundary supports, Journal of Sound and Vibrations, 2004, 273(3), 619-635.10.1016/S0022-460X(03)00562-5Search in Google Scholar

[24] Watkin, R.J. and Barton, O., Characterizing the vibration of an elastically point supported rectangular plate using eigensensitivity analysis, Thin-Walled Structures, 2009, 48, 327-333.10.1016/j.tws.2009.11.005Search in Google Scholar

[25] Shahrjerdi A., Mustafa F., Bayat M., and Majid D.L.A., Free vibration analysis of solar functionally graded plates with temperature-dependent material properties using second order shear deformation theory, Journal of Mechanical Science and Technology, 2011, 25 (9), 2195-2209.10.1007/s12206-011-0610-xSearch in Google Scholar

[26] Du J., Li W., Jin G., Yang T., and Liu, Z., An analytical method for the in-plane vibration analysis of rectangular plates with elastically restrained edges, Journal of Sound and Vibrations, 2007, 306, 908-927.10.1016/j.jsv.2007.06.011Search in Google Scholar

[27] Timoshenko, S., and Woinowsky-Krieger, S., Theory of plates and shells, 1959, Mc-Graw Hill.Search in Google Scholar

[28] Lekhnitskii, S. G., Anisotropic plates (No. FTD-HT-23-608-67), 1957, Foreign Technology Div Wright-Patterson Afb Oh.Search in Google Scholar

Received: 2017-09-23
Accepted: 2018-08-06
Published Online: 2018-09-02

© 2018 Mohammad A. Gharaibeh and Amr M. Obeidat, published by De Gruyter

This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 License.

Articles in the same Issue

  1. Regular Article
  2. Real-scale comparison between simple and composite raw sewage sampling
  3. 10.1515/eng-2018-0017
  4. The risks associated with falling parts of glazed facades in case of fire
  5. Implementation of high speed machining in thin-walled aircraft integral elements
  6. Evaluating structural crashworthiness and progressive failure of double hull tanker under accidental grounding: bottom raking case
  7. Influence of Silica (SiO2) Loading on the Thermal and Swelling Properties of Hydrogenated-Nitrile-Butadiene-Rubber/Silica (HNBR/Silica) Composites
  8. Statistical Variations and New Correlation Models to Predict the Mechanical Behavior and Ultimate Shear Strength of Gypsum Rock
  9. Analytic approximate solutions to the chemically reactive solute transfer problem with partial slip in the flow of a viscous fluid over an exponentially stretching sheet with suction/blowing
  10. Thermo-mechanical behavior simulation coupled with the hydrostatic-pressure-dependent grain-scale fission gas swelling calculation for a monolithic UMo fuel plate under heterogeneous neutron irradiation
  11. Optimal Auxiliary Functions Method for viscous flow due to a stretching surface with partial slip
  12. Vibrations Analysis of Rectangular Plates with Clamped Corners
  13. Evaluating Lean Performance of Indian Small and Medium Sized Enterprises in Automotive Sector
  14. FPGA–implementation of PID-controller by differential evolution optimization
  15. Thermal properties and morphology of polypropylene based on exfoliated graphite nanoplatelets/nanomagnesium oxide
  16. A computer-based renewable resource management system for a construction company
  17. Hygrothermal Aging of Amine Epoxy: Reversible Static and Fatigue Properties
  18. The selected roof covering technologies in the aspect of their life cycle costs
  19. Influence of insulated glass units thickness and weight reduction on their functional properties
  20. Structural analysis of conditions determining the selection of construction technology for structures in the centres of urban agglomerations
  21. Selection of the optimal solution of acoustic screens in a graphical interpretation of biplot and radar charts method
  22. Subsidy Risk Related to Construction Projects: Seeking Causes
  23. Multidimensional sensitivity study of the fuzzy risk assessment module in the life cycle of building objects
  24. Planning repetitive construction projects considering technological constraints
  25. Identification of risk investment using the risk matrix on railway facilities
  26. Comparison of energy parameters of a centrifugal pump with a multi-piped impeller in cooperation either with an annular channel and a spiral channel
  27. Influence of the contractor’s payment method on the economic effectiveness of the construction project from the contractor’s point of view
  28. Special Issue Automation in Finland
  29. Diagnostics and Identification of Injection Duration of Common Rail Diesel Injectors
  30. An advanced teaching scheme for integrating problem-based learning in control education
  31. A survey of telerobotic surface finishing
  32. Wireless Light-Weight IEC 61850 Based Loss of Mains Protection for Smart Grid
  33. Smart Adaptive Big Data Analysis with Advanced Deep Learning
  34. Topical Issue Desktop Grids for High Performance Computing
  35. A Bitslice Implementation of Anderson’s Attack on A5/1
  36. Efficient Redundancy Techniques in Cloud and Desktop Grid Systems using MAP/G/c-type Queues
  37. Templet Web: the use of volunteer computing approach in PaaS-style cloud
  38. Using virtualization to protect the proprietary material science applications in volunteer computing
  39. Parallel Processing of Images in Mobile Devices using BOINC
  40. “XANSONS for COD”: a new small BOINC project in crystallography
  41. Special Issue on Sustainable Energy, Engineering, Materials and Environment
  42. An experimental study on premixed CNG/H2/CO2 mixture flames
  43. Tidal current energy potential of Nalón river estuary assessment using a high precision flow model
  44. Special Spring Issue 2017
  45. Context Analysis of Customer Requests using a Hybrid Adaptive Neuro Fuzzy Inference System and Hidden Markov Models in the Natural Language Call Routing Problem
  46. Special Issue on Non-ferrous metals and minerals
  47. Study of strength properties of semi-finished products from economically alloyed high-strength aluminium-scandium alloys for application in automobile transport and shipbuilding
  48. Use of Humic Sorbent from Sapropel for Extraction of Palladium Ions from Chloride Solutions
  49. Topical Issue on Mathematical Modelling in Applied Sciences, II
  50. Numerical simulation of two-phase filtration in the near well bore zone
  51. Calculation of 3D Coordinates of a Point on the Basis of a Stereoscopic System
  52. The model of encryption algorithm based on non-positional polynomial notations and constructed on an SP-network
  53. A computational algorithm and the method of determining the temperature field along the length of the rod of variable cross section
  54. ICEUBI2017 - International Congress on Engineering-A Vision for the Future
  55. Use of condensed water from air conditioning systems
  56. Development of a 4 stroke spark ignition opposed piston engine
  57. Development of a Coreless Permanent Magnet Synchronous Motor for a Battery Electric Shell Eco Marathon Prototype Vehicle
  58. Removal of Cr, Cu and Zn from liquid effluents using the fine component of granitic residual soils
  59. A fuzzy reasoning approach to assess innovation risk in ecosystems
  60. Special Issue SEALCONF 2018
  61. Brush seal with thermo-regulating bimetal elements
  62. The CFD simulation of the flow structure in the sewage pump
  63. The investigation of the cavitation processes in the radial labyrinth pump
  64. Testing of the gaskets at liquid nitrogen and ambient temperature
  65. Probabilistic Approach to Determination of Dynamic Characteristics of Automatic Balancing Device
  66. The design method of rubber-metallic expansion joint
  67. The Specific Features of High-Velocity Magnetic Fluid Sealing Complexes
  68. Effect of contact pressure and sliding speed on the friction of polyurethane elastomer (EPUR) during sliding on steel under water wetting conditions
  69. Special Issue on Advance Material
  70. Effect of thermo-mechanical parameters on the mechanical properties of Eurofer97 steel for nuclear applications
  71. Failure prediction of axi-symmetric cup in deep drawing and expansion processes
  72. Characterization of cement composites based on recycled cellulosic waste paper fibres
  73. Innovative Soft Magnetic Composite Materials: Evaluation of magnetic and mechanical properties
  74. Statistical modelling of recrystallization and grain growth phenomena in stainless steels: effect of initial grain size distribution
  75. Annealing effect on microstructure and mechanical properties of Cu-Al alloy subjected to Cryo-ECAP
  76. Influence of heat treatment on corrosion resistance of Mg-Al-Zn alloy processed by severe plastic deformation
  77. The mechanical properties of OFHC copper and CuCrZr alloys after asymmetric rolling at ambient and cryogenic temperatures
https://doi.org/10.1515/eng-2018-0030
Creative Commons
BY-NC-ND 4.0

Articles in the same Issue

  1. Regular Article
  2. Real-scale comparison between simple and composite raw sewage sampling
  3. 10.1515/eng-2018-0017
  4. The risks associated with falling parts of glazed facades in case of fire
  5. Implementation of high speed machining in thin-walled aircraft integral elements
  6. Evaluating structural crashworthiness and progressive failure of double hull tanker under accidental grounding: bottom raking case
  7. Influence of Silica (SiO2) Loading on the Thermal and Swelling Properties of Hydrogenated-Nitrile-Butadiene-Rubber/Silica (HNBR/Silica) Composites
  8. Statistical Variations and New Correlation Models to Predict the Mechanical Behavior and Ultimate Shear Strength of Gypsum Rock
  9. Analytic approximate solutions to the chemically reactive solute transfer problem with partial slip in the flow of a viscous fluid over an exponentially stretching sheet with suction/blowing
  10. Thermo-mechanical behavior simulation coupled with the hydrostatic-pressure-dependent grain-scale fission gas swelling calculation for a monolithic UMo fuel plate under heterogeneous neutron irradiation
  11. Optimal Auxiliary Functions Method for viscous flow due to a stretching surface with partial slip
  12. Vibrations Analysis of Rectangular Plates with Clamped Corners
  13. Evaluating Lean Performance of Indian Small and Medium Sized Enterprises in Automotive Sector
  14. FPGA–implementation of PID-controller by differential evolution optimization
  15. Thermal properties and morphology of polypropylene based on exfoliated graphite nanoplatelets/nanomagnesium oxide
  16. A computer-based renewable resource management system for a construction company
  17. Hygrothermal Aging of Amine Epoxy: Reversible Static and Fatigue Properties
  18. The selected roof covering technologies in the aspect of their life cycle costs
  19. Influence of insulated glass units thickness and weight reduction on their functional properties
  20. Structural analysis of conditions determining the selection of construction technology for structures in the centres of urban agglomerations
  21. Selection of the optimal solution of acoustic screens in a graphical interpretation of biplot and radar charts method
  22. Subsidy Risk Related to Construction Projects: Seeking Causes
  23. Multidimensional sensitivity study of the fuzzy risk assessment module in the life cycle of building objects
  24. Planning repetitive construction projects considering technological constraints
  25. Identification of risk investment using the risk matrix on railway facilities
  26. Comparison of energy parameters of a centrifugal pump with a multi-piped impeller in cooperation either with an annular channel and a spiral channel
  27. Influence of the contractor’s payment method on the economic effectiveness of the construction project from the contractor’s point of view
  28. Special Issue Automation in Finland
  29. Diagnostics and Identification of Injection Duration of Common Rail Diesel Injectors
  30. An advanced teaching scheme for integrating problem-based learning in control education
  31. A survey of telerobotic surface finishing
  32. Wireless Light-Weight IEC 61850 Based Loss of Mains Protection for Smart Grid
  33. Smart Adaptive Big Data Analysis with Advanced Deep Learning
  34. Topical Issue Desktop Grids for High Performance Computing
  35. A Bitslice Implementation of Anderson’s Attack on A5/1
  36. Efficient Redundancy Techniques in Cloud and Desktop Grid Systems using MAP/G/c-type Queues
  37. Templet Web: the use of volunteer computing approach in PaaS-style cloud
  38. Using virtualization to protect the proprietary material science applications in volunteer computing
  39. Parallel Processing of Images in Mobile Devices using BOINC
  40. “XANSONS for COD”: a new small BOINC project in crystallography
  41. Special Issue on Sustainable Energy, Engineering, Materials and Environment
  42. An experimental study on premixed CNG/H2/CO2 mixture flames
  43. Tidal current energy potential of Nalón river estuary assessment using a high precision flow model
  44. Special Spring Issue 2017
  45. Context Analysis of Customer Requests using a Hybrid Adaptive Neuro Fuzzy Inference System and Hidden Markov Models in the Natural Language Call Routing Problem
  46. Special Issue on Non-ferrous metals and minerals
  47. Study of strength properties of semi-finished products from economically alloyed high-strength aluminium-scandium alloys for application in automobile transport and shipbuilding
  48. Use of Humic Sorbent from Sapropel for Extraction of Palladium Ions from Chloride Solutions
  49. Topical Issue on Mathematical Modelling in Applied Sciences, II
  50. Numerical simulation of two-phase filtration in the near well bore zone
  51. Calculation of 3D Coordinates of a Point on the Basis of a Stereoscopic System
  52. The model of encryption algorithm based on non-positional polynomial notations and constructed on an SP-network
  53. A computational algorithm and the method of determining the temperature field along the length of the rod of variable cross section
  54. ICEUBI2017 - International Congress on Engineering-A Vision for the Future
  55. Use of condensed water from air conditioning systems
  56. Development of a 4 stroke spark ignition opposed piston engine
  57. Development of a Coreless Permanent Magnet Synchronous Motor for a Battery Electric Shell Eco Marathon Prototype Vehicle
  58. Removal of Cr, Cu and Zn from liquid effluents using the fine component of granitic residual soils
  59. A fuzzy reasoning approach to assess innovation risk in ecosystems
  60. Special Issue SEALCONF 2018
  61. Brush seal with thermo-regulating bimetal elements
  62. The CFD simulation of the flow structure in the sewage pump
  63. The investigation of the cavitation processes in the radial labyrinth pump
  64. Testing of the gaskets at liquid nitrogen and ambient temperature
  65. Probabilistic Approach to Determination of Dynamic Characteristics of Automatic Balancing Device
  66. The design method of rubber-metallic expansion joint
  67. The Specific Features of High-Velocity Magnetic Fluid Sealing Complexes
  68. Effect of contact pressure and sliding speed on the friction of polyurethane elastomer (EPUR) during sliding on steel under water wetting conditions
  69. Special Issue on Advance Material
  70. Effect of thermo-mechanical parameters on the mechanical properties of Eurofer97 steel for nuclear applications
  71. Failure prediction of axi-symmetric cup in deep drawing and expansion processes
  72. Characterization of cement composites based on recycled cellulosic waste paper fibres
  73. Innovative Soft Magnetic Composite Materials: Evaluation of magnetic and mechanical properties
  74. Statistical modelling of recrystallization and grain growth phenomena in stainless steels: effect of initial grain size distribution
  75. Annealing effect on microstructure and mechanical properties of Cu-Al alloy subjected to Cryo-ECAP
  76. Influence of heat treatment on corrosion resistance of Mg-Al-Zn alloy processed by severe plastic deformation
  77. The mechanical properties of OFHC copper and CuCrZr alloys after asymmetric rolling at ambient and cryogenic temperatures
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 17.9.2025 from https://www.degruyterbrill.com/document/doi/10.1515/eng-2018-0030/html
Scroll to top button