A coupled hygro-elastic 3D model for steady-state analysis of functionally graded plates and shells

Salvatore Brischetto; Domenico Cesare

doi:10.1515/cls-2022-0216

Artikel Open Access

A coupled hygro-elastic 3D model for steady-state analysis of functionally graded plates and shells

Salvatore Brischetto und Domenico Cesare

Veröffentlicht/Copyright: 3. Oktober 2023

Veröffentlicht von

Veröffentlichen auch Sie bei De Gruyter Brill

Manuskript einreichen Informationen für Autor*innen

Aus der Zeitschrift Curved and Layered Structures Band 10 Heft 1

Abstract

This 3D coupled hygro-elastic model proposes the three-dimensional (3D) equilibrium equations associated with the 3D Fick diffusion equation for spherical shells. The primary unknowns of the problem are the displacements and the moisture content. This coupled 3D exact shell model allows to understand the effects of the moisture field in relation with the elastic field on stresses and deformations in different plates and shells. This model is specifically developed for configurations including functionally graded material (FGM) layers. Four different geometries are analyzed using an orthogonal mixed curvilinear reference system. The main advantage of this reference system for spherical shells is the degeneration of the equations to those for simpler geometries. The solving method is the exponential matrix method in the thickness direction. The closed-form solution is possible because of simply supported sides and harmonic forms for displacements and moisture content. The moisture content amplitudes are directly applied at the top and bottom outer faces through steady-state hypotheses. The final system is based on a set of coupled homogeneous second-order differential equations. The moisture field effects are evaluated for the static analysis in terms of displacement, strain, and stress components. After preliminary validations, used to better understand how to properly define the calculation of the curvature-related terms and FGM properties, four new benchmarks are proposed for several thickness ratios, geometrical data, FGM configurations, and moisture values imposed at the external surfaces. From the results, it is clear the accordance between the uncoupled hygro-elastic model and this new coupled hygro-elastic model when the 3D Fick diffusion law is employed. Both effects connected with the thickness layer and the embedded material are included in the 3D hygro-elastic analyses proposed. The 3D coupled hygro-elastic model is simpler than the uncoupled one because the 3D Fick diffusion law does not have to be separately solved.

Keywords: three-dimensional exact model; coupled hygro-elastic shell model; 3D Fick diffusion law; functionally graded materials; moisture content

1 Introduction

In the framework of aerospace structural analyses, the external environmental conditions become extremely important to be analyzed. Severe temperature and humidity gradients are the classic conditions where these aircraft and spacecraft usually operate [1–4]. In particular, modern aerospace structures can have problems concerning the absorption of humidity from the external air. This phenomenon can create irreversible damages related to the debonding and the mechanical degradation of composite materials, with severe problems related to the safety of aircraft structures. For these reasons, the use of FGMs, whose peculiarity is the continuous variation of its own mechanical, thermal and hygroscopic properties along a given direction, can be relevant. These peculiarities of the FGMs can strongly mitigate all the aforementioned possible damages typical of composite materials.

The scientific and technical literature fulfills various features related to hygro-elastic models for plates and shells embedding FGM layers. Numerical and analytical models (1D, 2D, and 3D approaches) are deeply discussed in this section to better understand the originality of the new proposed model. In all the discussed papers, the moisture field is involved. Two different sections are proposed: in the first one, all the numerical models are deeply described; meanwhile, in the second one, analytical models are shown.

In the context of numerical models, Aria and Friswell [5] showed a hygro-thermal investigation of functionally graded (FG) sandwich microbeams based on Eringen nonlocal elasticity theory where motion equations are derived using Hamilton principle and the first order shear deformation theory (FSDT). The finite element (FE) procedure is based on a five-noded beam element. In the study by Garg et al. [6], the bending analysis of sandwich FGM beams under combined hygrothermomechanical loadings was evaluated. The study was carried out using a FE based on a high order zigzag theory (HOZT). Li and Tang [7] proposed three-directional FGMs to carry out the composition of slender beams. The nonlinear governing equations were developed using the principle of minimum for potential energy. Liu and Mohammadi [8] proposed the bending response of FG nanobeams under hygrothermomechanical loadings. The nonlocal strain gradient theory (NSGT) was implemented to consider both hardening and softening impacts on the system response. Nguyen et al. [9] discussed the hygro-thermal effects on vibration and buckling analyses of FG beams. This work was based on equations of motion obtained from Lagrange equations using a higher-order shear deformation theory. Tang and Ding [10] showed the nonlinear hygro-thermal dynamics of a bi-directionally FG beam where material and hygro-thermal properties gradually change along both thickness and length directions. Dastjerdi et al. [11] proposed a quasi three-dimensional approach for the bending analysis of plates embedding FGMs with porosities. The bending equations were developed using Hamilton principle, and the solution was obtained using a semi-analytical polynomial method. Lee and Kim [12] showed the postbuckling behaviors of FGM plates in hygrothermal environments. The model was based on the FSDT and the von Karman strain-displacement relations, and it was developed using the FE method and the Newton–Raphson technique. Sobhy [13] gave out the bending analysis of sandwich-curved beams with graphene platelets/aluminum (GPLs/Al) nanocomposite face sheets and aluminum honeycomb. The differential quadrature method (DQM), based on a new shear and normal deformation curved beam theory, was employed. Sobhy also [14] presented a three-dimensional asymmetric bending analysis of solid circular and annular plates, made of aluminum matrix reinforced with uniformly distributed GPLs, lying on an elastic medium with different boundary conditions. In-plane magnetic field, transverse external loads, thermal loads, and humid conditions were included. Zhao et al. [15] presented the dynamic analysis of GPL sandwich shallow shells reinforced with FG porous and embedding shape memory alloy (SMA) wires under hygrothermal loadings with general boundary conditions. Dai et al. [16] showed a mechanical model to investigate the coupling between temperature and moisture for a porous FG-carbon nanotube reinforced composite rotating annular plate with variable thickness. Numerical results were achieved by combining the DQM, the Runge–Kutta method, and the Newmark method. Saadaftar and Aghaie-Khafri [17] proposed a rotating FGM cylindrical shell with imperfect surfaces and piezoelectric layers subjected to an axisymmetric hygro-thermo-electro-mechanical loading. The Fourier series expansion method through the longitudinal direction and the DQM along the thickness direction were used to solve governing differential equations. Nie et al. [18] showed the hygro-thermo-electro-mechanical coupling problem of FG piezoelectric structures using the edge-based smoothed point interpolation method (ES-PIM). The basic equations for these structures were derived in the multi-physical field. The resolution of the coupled problem was obtained via ES-PIM and FE method under different hygrothermal conditions.

In the case of exact analytical models, Akbarzadeh and Chen [19] showed analytical solutions for hygrothermal stresses in 1D FG piezoelectric media where material properties varied through the thickness direction. The media were subjected to an external constant magnetic field. Governing equations were written in a unified form in cylindrical and spherical coordinates. Ebrahimi and Barati [20] presented an hygro-thermo-mechanical vibration analysis of FG size-dependent nanobeams exposed to various hygro-thermal loadings. The analysis was performed via a semi-analytical differential transform method. Three hygro-thermal loadings types (uniform, linear, and sinusoidal) were investigated. Ebrahimi and Barati also [21] proposed a study where the combined effects of moisture and temperature on free vibration characteristics of FG nanobeams resting on elastic foundation were investigated. Different refined beam theories, including shear deformations, were involved. Jouneghani et al. [22] investigated the bending behavior of FG nanobeams with internal porosity and subjected to a hygro-thermo-mechanical loading. Eringen nonlocal theory was applied for the numerical study considering a uniform porosity within the nanobeam. The bending response of porous FG Bernoulli–Euler nanobeams under hygrothermomechanical loadings was analyzed by Penna et al. [23]. The governing equations of the problem associated with the local/nonlocal stress and strain-driven gradient models of elasticity were derived using the principle of virtual work. Wang et al. [24] investigated the influence of hygrothermomechanical coupling loadings on buckling behaviors of porous bidirectional FG Timoshenko nanobeams. The governing equations and boundary conditions were derived using a two-phase local strain gradient theory/NSGT employing the principle of virtual work. A hygro-thermal stress analysis of rotating FG graphene/metal sandwich cylindrical shells embedding an auxetic honeycomb core was proposed the study by Allam et al. [25]. The simply supported sandwich shell was spinning about its axial axis with a constant angular speed. Arshid et al. proposed in [26] a study about the vibrational behavior of three-layered cylindrical shells embedding graphene nanoplatelets reinforced composite core and piezo-electro-magnetic face sheets. The whole structure was rested on the visco-Pasternak foundation, and it was exposed to hygro-magneto-electro-thermal loads. Karimiasl et al. [27] investigated the post-buckling behaviors of doubly curved composite shells in a hygro-thermal environment employing multiple scales perturbation methods. Three-phase composite shells with polymer/carbon nanotube/fiber and polymer/GPL/fiber and SMA/matrix were taken into consideration according to the Halpin–Tsai model. Zidi et al. [28] investigated the bending response of an FGM plate resting on elastic foundation and subjected to hygrothermomechanical loadings. Zenkour and Radwan [29] investigated the effects of moisture and temperature on the bending analysis of FG porous plates resting on two-parameter elastic foundation. The effects of transverse normal and shear strains were taken into account. Tang et al. [30] proposed a study where the influence of the hygrothermal effects on center deflections, fundamental natural frequencies, and vibration deflection amplitudes for shells were discussed to understand the service life of polymer matrix composites during operating conditions. In the study by Mudhaffar et al. [31], the bending behavior of an advanced FG ceramic-metal plate subjected to a hygrothermomechanical load and resting on a viscoelastic foundation was studied using a simple higher-order integral shear deformation theory.

All the proposed exact models are related to 1D or 2D theories. For this reason, a 3D hygro-elastic model was developed by Brischetto and Torre in [32] to understand the behavior of shells embedding FGM layers when external moisture conditions were imposed. The present work can be seen as a general extension of the works presented by Brischetto in [33–35] where the mechanical and free vibration analyses of FGM shells were proposed. In the present article, the important novelty with respect to the 3D hygro-elastic shell model proposed by Brischetto and Torre in [32,36] is the full coupling between the displacement field and the hygroscopic field. Therefore, the moisture content profile is directly obtained from the solution of the system, and it is not “a priori” defined. A similar procedure was already used by the authors in [37,38] in the case of full coupling between the displacement field and the thermal field for the 3D bending analysis of composite and FG plates and shells, and in the study by Brischetto and Cesare [39] for the case of full coupling between the displacement field and the hygroscopic field for the 3D bending analysis of classical multilayered composite plates and shells. The Fick diffusion equation [40,41] coupled with 3D equilibrium equations gives a system in mixed curvilinear orthogonal coordinates [42,43]. The system is solved via the exponential matrix method [44,45].

This article is organized in a section containing the theoretical formulation of the 3D coupled hygro-elastic model, a section about results (divided into preliminary validations and new benchmarks) and a section about conclusions where the achieved results are summarized.

2 3D coupled hygro-elastic model for FGM shells

The 3D formulation for full coupled exact hygro-elastic analyses of FGM plates and shells is here presented. This formulation allows hygro-elastic analyses of several geometries such as cylinders, plates, cylindrical panels, and spherical shells. The differences between these four geometries are highlighted in Figure 1. Figure 1 indicates also the mixed curvilinear orthogonal reference system with the origin point located in the left corner. The directions α and β are along to the in-plane curved sides, and they lie on the surface Ω 0 , defined as the middle and reference surface. Ω 0 surface will be used for the calculation of all the geometrical parameters. The thickness direction z is normal to the Ω 0 surface and directed upside and towards the top surface. A coupled formulation is possible because the three displacement components u , v , and w , and the scalar moisture content ℳ are the four unknown primary variables of the problem.

Figure 1

Geometries in the mixed curvilinear orthogonal reference system.

2.1 Geometrical and constitutive equations

Geometrical relations written in matrix form are here proposed for the coupled 3D hygro-elastic model. The matrix equation is:

(1) ε k = ε u k − ε ℳ k = ( Δ k ( z ) + G k ( z ) ) u k − η k ( z ) ℳ k ,

where ε k is the 6 × 1 hygro-mechanical strain vector, ε u k is the 6 × 1 strain vector related to the 3 × 1 displacement vector u k , ε ℳ k is the 6 × 1 strain vector related to the scalar moisture content ℳ k , Δ k ( z ) is the 6 × 3 matrix containing differential geometrical terms, G k ( z ) is the 6 × 3 matrix containing algebraic geometrical and curvature terms, and η k ( z ) is the 6 × 1 vector containing hygrometric expansion coefficients.

Each k FGM layer has elastic and hygroscopic properties that are functions of the z coordinate. Isotropic FGM layers are analyzed. Therefore, material reference system ( 1 , 2 , 3 ) is coincident with the structural reference system ( α , β , z ). The extended forms of the previous matrices and vectors are as follows:

(2) ε k = ε α α k ε β β k ε z z k γ β z k γ α z k γ α β k , Δ k ( z ) = 1 H α ( z ) ∂ ∂ α 0 0 0 1 H β ( z ) ∂ ∂ β 0 0 0 ∂ ∂ z 0 ∂ ∂ z 1 H β ( z ) ∂ ∂ β ∂ ∂ z 0 1 H α ( z ) ∂ ∂ α 1 H β ( z ) ∂ ∂ β 1 H α ( z ) ∂ ∂ α 0 , G k ( z ) = 0 0 1 H α ( z ) R α 0 0 1 H β ( z ) R β 0 0 0 0 − 1 H β ( z ) R β 0 − 1 H α ( z ) R α 0 0 0 0 0 , u k = u k v k w k , η k ( z ) = η α k ( z ) η β k ( z ) η z k ( z ) 0 0 0 .

R α and R β are the radii of curvature in the α and β in-plane directions, respectively; they are constant values. H α ( z ) and H β ( z ) coefficients introduce the curvature shell terms. They are defined, for each direction, as follows:

(3) H α ( z ) = 1 + z R α = 1 + z ˜ − h ⁄ 2 R α , H β ( z ) = 1 + z R β = 1 + z ˜ − h ⁄ 2 R β , H z = 1 .

The curvature shell terms are linear functions of the thickness coordinate z or z ˜ . h is the total thickness of the structure and it is always considered as constant. The z coordinate varies in the range between − h ⁄ 2 and h ⁄ 2 ; z ˜ is in the range between 0 and h .

The moisture content ℳ is defined as follows:

(4) ℳ = W − W d W d = W d + W c − W d W d = W c W d = ∫ V c ⋅ d V ∫ V ρ d ⋅ d V = c V ρ d V = c ρ d ,

where W d is the mass of the dry material in kg, W c is the mass of the moisture present in the material in kg, W is the mass of the moist material in kg (that is the sum of W d and W c ), V is the volume of the structure in m 3 , c is the moisture concentration in kg/m 3 , and ρ d is the density of the dry material in kg/m 3 . Therefore, ℳ is in nondimensional or in percentage form.

Stresses are linked with strains via the 3D Hooke law written for a generic k FGM layer:

(5) σ k = C k ( z ) ε k

where the stress vector is σ k = ( σ α α k σ β β k σ z z k σ β z k σ α z k σ α β k ) T and the elastic coefficient matrix C k ( z ) has 6 × 6 dimension. The substitution of Eq. (1) into Eq. (5) gives:

(6) σ k = C k ( z ) ε k = C k ( z ) [ ( Δ k ( z ) + G k ( z ) ) u k − η k ( z ) ℳ k ] = C k ( z ) ( Δ k ( z ) + G k ( z ) ) u k − C k ( z ) η k ( z ) ℳ k = M k ( z ) u k − ξ k ( z ) ℳ k ,

where M k ( z ) indicates the pure mechanical coefficients and it has dimension 6 × 3 ; ξ k ( z ) includes the hygro-elastic coupling coefficients in the structural reference system:

(7) ξ α k ( z ) ξ β k ( z ) ξ z k ( z ) 0 0 0 = C 11 k ( z ) C 12 k ( z ) C 13 k ( z ) 0 0 0 C 12 k ( z ) C 22 k ( z ) C 23 k ( z ) 0 0 0 C 13 k ( z ) C 23 k ( z ) C 33 k ( z ) 0 0 0 0 0 0 C 44 k ( z ) 0 0 0 0 0 0 C 55 k ( z ) 0 0 0 0 0 0 C 66 k ( z ) η α k ( z ) η β k ( z ) η z k ( z ) 0 0 0 .

In Eq. (6), the six stress components are linked with displacements u , v , w , and the moisture content ℳ that are unknown variables of this formulation.

2.2 3D equilibrium equations for spherical shells

The equilibrium equations and the 3D Fick diffusion equation for spherical shells are the basic equations of the present coupled formulation. The set of three equilibrium equations for spherical shells written in the matrix form using the mixed curvilinear orthogonal coordinates ( α , β , z ) is as follows:

(8) H β ( z ) ∂ ∂ α σ α α k σ α β k σ α z k + H α ( z ) ∂ ∂ β σ α β k σ β β k σ β z k + H α ( z ) H β ( z ) ∂ ∂ z σ α z k σ β z k σ z z k + H β ( z ) R α × σ α z k σ β z k σ z z k − − σ α z k 0 σ α α k + H α ( z ) R β σ α z k σ β z k σ z z k − 0 − σ β z k σ β β k ,

where σ α k = σ α α k σ α β k σ α z k is the vector whose stress components are applied on the face perpendicular to α axis; σ β k = σ α β k σ β β k σ β z k is the vector whose stress components are applied on the face perpendicular to β axis; σ z k = σ α z k σ β z k σ z z k is the vector whose stress components are applied on the face perpendicular to z axis; σ 1 k = − σ α z k 0 σ α α k is the vector for the stress components that considers the R α correction; σ 2 k = 0 − σ β z k σ β β k is the vector for the stress components that considers the R β correction.

The final compact form is:

(9) H β ( z ) σ α k , α + H α ( z ) σ β k , β + H α ( z ) H β ( z ) σ z k , z + H β ( z ) R α ( σ z k − σ 1 k ) + H α ( z ) R β ( σ z k − σ 2 k ) = 0 ,

where subscripts α , β , and, z indicate the partial derivatives ∂ ∂ α , ∂ ∂ β , and ∂ ∂ z , respectively.

Eq. (9) is coupled with the 3D Fick diffusion equation for spherical shells in steady-state conditions:

(10) D 1 * k ( z ) ∂ 2 ℳ ∂ α 2 + D 2 * k ( z ) ∂ 2 ℳ ∂ β 2 + D 3 * k ( z ) ∂ 2 ℳ ∂ z 2 = 0 ,

where the diffusion coefficients D 1 * k ( z ) , D 2 * k ( z ) and D 3 * k ( z ) for each k layer are defined as follows:

(11) D 1 * k ( z ) = D 1 k ( z ) H α 2 ( z ) , D 2 * k ( z ) = D 2 k ( z ) H β 2 ( z ) , D 3 * k ( z ) = D 3 k ( z ) .

D 1 k ( z ) , D 2 k ( z ) , and D 3 k ( z ) are the three diffusion coefficients in the mixed curvilinear reference system depending on z in the case of FGM layers. In Eq. (10), the diffusion coefficients take into account the curvature of the geometry along in-plane directions. For the plate cases, the D i * k ( z ) diffusion coefficients degenerate in D i k ( z ) because curvatures are not involved.

2.3 Solution procedure

The resolution of this coupled hygro-elastic problem in a closed form needs the imposition of the Navier conditions for all the main unknowns u k , v k , w k , and ℳ k . These impositions can be written as follows:

(12) u k ( α , β , z ) v k ( α , β , z ) w k ( α , β , z ) ℳ k ( α , β , z ) = U k ( z ) 0 0 0 0 V k ( z ) 0 0 0 0 W k ( z ) 0 0 0 0 M k ( z ) × cos ( α ¯ α ) sin ( β ¯ β ) sin ( α ¯ α ) cos ( β ¯ β ) sin ( α ¯ α ) sin ( β ¯ β ) sin ( α ¯ α ) sin ( β ¯ β ) .

Using the Navier form for the unknowns, the boundary conditions are simply-supported sides for all the investigated structures. The capital letters proposed in Eq. (12) are the amplitudes of the unknowns. The α ¯ and β ¯ coefficients depend on the a and b dimensions and on the half-wave numbers m and n in the in-plane directions:

(13) α ¯ = m π a , β ¯ = n π b .

All the primary variables expressed in Eq. (12) are 3D variables because they are functions of α , β , and z .

Substituting the primary variables written in the harmonic forms as in Eq. (12), the geometrical relations as in Eq. (1) and the constitutive equations as in Eq. (5) into the governing Eqs. (9) and (10), a global set of four second-order differential equations is obtained. It can be properly transformed into a first-order differential equation system by redoubling the number of unknowns (as stated in [44] and [45]). After all these manipulations, the set of first-order differential equations can be written in a compact matrix form as follows:

(14) D ( z ) k X k ′ ( z ) = A k ( z ) X k ( z ) ,

where

D k ( z ) = A 6 k ( z ) 0 0 0 0 0 0 0 0 A 12 k ( z ) 0 0 0 0 0 0 0 0 A 19 k ( z ) 0 0 0 0 0 0 0 0 J 7 k ( z ) 0 0 0 0 0 0 0 0 A 6 k ( z ) 0 0 0 0 0 0 0 0 A 12 k ( z ) 0 0 0 0 0 0 0 0 A 19 k ( z ) 0 0 0 0 0 0 0 0 J 7 k ( z ) ,

(15) X k ( z ) = U k ( z ) V k ( z ) W k ( z ) M k ( z ) U k ′ ( z ) V k ′ ( z ) W k ′ ( z ) M k ′ ( z ) , X k ′ ( z ) = U k ( z ) V k ( z ) W k ( z ) M k ( z ) U k ′ ( z ) V k ′ ( z ) W k ′ ( z ) M k ′ ( z ) ′ ,

A k ( z ) = 0 0 0 0 A 6 k ( z ) 0 0 0 0 0 0 0 0 A 12 k ( z ) 0 0 0 0 0 0 0 0 A 19 k ( z ) 0 0 0 0 0 0 0 0 J 7 k ( z ) − A 1 k ( z ) − A 2 k ( z ) − A 3 k ( z ) − J 1 k ( z ) − A 4 k ( z ) 0 − A 5 k ( z ) 0 − A 7 k ( z ) − A 8 k ( z ) − A 9 k ( z ) − J 2 k ( z ) 0 − A 10 k ( z ) − A 11 k ( z ) 0 − A 13 k ( z ) − A 14 k ( z ) − A 15 k ( z ) − J 3 k ( z ) − A 16 k ( z ) − A 17 k ( z ) − A 18 k ( z ) − J 4 k ( z ) 0 0 0 − ( J 5 k ( z ) + J 6 k ( z ) ) 0 0 0 0 .

X k ( z ) is the 8 × 1 redoubled unknown vector containing displacements, moisture content amplitudes, and related first order derivatives along z direction (stated with the superscript ′ ). Eq. (14) is valid for each k physical layer. Coefficient matrices in Eq. (14) depend on z due to the curvature terms H α ( z ) and H β ( z ) , and elastic and hygroscopic terms for FGMs. To solve the system in Eq. (14), the coefficients must be constant. Introducing a number of L fictitious layers in each physical layer k along the thickness direction, H α ( z ) , H β ( z ) , D k ( z ) , and A k ( z ) can be exactly calculated in the middle points of these layers, and the values become constant within each of it. A generic fictitious layer is indicated with j and goes from 1 to F = L × P (where P is the total number of physical layers). The system in Eq. (14) has now constant coefficients, and it can be rewritten as follows:

(16) X j ′ = A * j X j ,

where A * j = D j − 1 A j . The exponential matrix method, proposed in [44,45], is employed and the solution of the problem in Eq. (16) is:

(17) X t j = e ( A * j z ˜ j ) X b j = A * * j X b j .

The unknown amplitude vector X t j at the top of the j fictitious layer can be obtained from the unknown amplitude vector X b j at the bottom of the same j fictitious layer. The exponential matrix is computed referring to the thickness value h j . The exponential matrix can be expanded and calculated in correspondence of h j for each fictitious layer:

(18) A * * j = e ( A * j h j ) = I + A * j h j + A * j 2 2 ! h j 2 + A * j 3 3 ! h j 3 + ⋯ + A * j N N ! h j N .

I is the 8 × 8 identity matrix.

Further relationships must be included for interlaminar continuity conditions. They are useful to link the top of the j fictitious layer and the bottom of the j + 1 fictitious layer. These interlaminar continuity conditions must be imposed for displacements u , v , and w , moisture content ℳ , and transverse shear/normal stresses σ α z , σ β z , and σ z z and transverse normal moisture flux g z in the z direction. The interlaminar continuity conditions in the compact form is expressed as follows:

(19) x b j + 1 = u b j + 1 v b j + 1 w b j + 1 ℳ b j + 1 = x t j = u t j v t j w t j ℳ t j ,

(20) σ n b j + 1 = σ β z b j + 1 σ α z b j + 1 σ z z b j + 1 = σ n t j = σ β z t j σ α z t j σ z z t j ,

(21) g z b j + 1 = g z t j .

The interlaminar continuity conditions expressed in Eq. (19) can be easily imposed directly for the amplitudes U j , V j , W j , and ℳ j . It is possible to obtain an amplitude form of Eqs. (19)–(21) taking into account the constitutive relations in Eq. (5) and the harmonic forms in Eq. (12). This amplitude form can be rewritten as follows:

(22) U V W M U ′ V ′ W ′ M ′ b j + 1 = 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 T 1 0 T 2 0 T 3 0 0 0 0 T 4 T 5 0 0 T 6 0 0 T 7 T 8 T 9 τ 1 0 0 T 10 0 0 0 0 0 0 0 0 τ 2 j + 1 , j U V W M U ′ V ′ W ′ M ′ t j ⇒ X b j + 1 = T j + 1 , j X t j ,

where T j + 1 , j is the transfer matrix that links the bottom of the j + 1 layer with the top of the j layer.

The boundary conditions for simply supported sides are satisfied for harmonic forms:

(23) ℳ = 0 , w = v = 0 , σ α α = 0 for α = 0 , a ,

(24) ℳ = 0 , , w = u = 0 , σ β β = 0 for β = 0 , b .

Load boundary conditions are imposed on the external faces as follows:

(25) σ z z = 0 , σ α z = 0 , σ β z = 0 , ℳ = ℳ ext for z = ± h ⁄ 2 .

The matrix forms of Eq. (25) are as follows:

(26) − C 13 F H α t F α ¯ − C 23 F H β t F β ¯ C 13 F H α t F R α + C 23 F H β t F R β − λ z F 0 0 C 33 F 0 0 − C 44 F H β t F R β C 44 F H β t F β ¯ 0 0 C 44 F 0 0 − C 55 F H α t F R α 0 C 55 F H α t F α ¯ 0 C 55 F 0 0 0 0 0 0 1 0 0 0 0 U V W M U ′ V ′ W ′ M ′ t F = 0 0 0 M t ,

(27) − C 13 1 H α b 1 α ¯ − C 23 1 H β b 1 β ¯ C 13 1 H α b 1 R α + C 23 1 H β b 1 R β − λ z 1 0 0 C 33 1 0 0 − C 44 1 H β b 1 R β C 44 1 H β b 1 β ¯ 0 0 C 44 1 0 0 − C 55 1 H α b 1 R α 0 C 55 1 H α b 1 α ¯ 0 C 55 1 0 0 0 0 0 0 1 0 0 0 0 U V W M U ′ V ′ W ′ M ′ b 1 = 0 0 0 M b ,

and they can be further compacted as follows:

(28) B t F X t F = P t ,

(29) B b 1 X b 1 = P b .

Superscript F indicates the last fictitious layer and superscript 1 is the first fictitious layer. Vectors P t and P b include the impositions related to the mechanical load in the three directions α , β , and z and the moisture content. Assuming a classical hygro-elastic stress analysis, the mechanical loads in α , β , and z directions are set equal to zero.

It is possible to write X t F in terms of X b 1 to directly link the top of the last fictitious layer with the bottom of the first one. This operation can be achieved introducing recursively Eq. (22) into Eq. (17):

(30) X t F = ( A * * F T F , F − 1 A * * F − 1 T F − 1 , F − 2 … A * * 2 T 2 , 1 A * * 1 ) X b 1 = H m X b 1 .

Eq. (30) defines the 8 × 8 matrix H m for structures embedding FGM layers. Introducing Eq. (30) into Eq. (28):

(31) B t F H m X b 1 = P t .

Eqs. (29) and (31) can be now compacted in an unique equation as follows:

(32) B t F H m B b 1 X b 1 = P t P b ⇒ E X b 1 = P .

Matrix E has 8 × 8 dimension independently by the number of fictitious layers employed and layer-wise approach. Vector P contains all the load impositions, both mechanical and hygroscopic ones, at the top and at the bottom of the structure. The system in Eq. (32) is formally the same shown in the previous studies by Brischetto [32–34] even if the 3D Fick diffusion equation is added to equilibrium relations.

This mathematical formulation is implemented in a Matlab code to evaluate stresses, strains, and displacements along the thickness direction for all the structures presented in the next section and including different FGM configurations (sandwich and single-layered ones).

Once the unknown vector at the bottom of the first fictitious layer ( j = 1 ) is computed, Eqs. (17) and (22) can be recursively applied to obtain the trends of all the variables through the z direction of the structures.

3 Results

This 3D coupled hygro-elastic shell model here developed is indicated with the acronym 3D-u- ℳ that clearly indicates the employed primary variables (displacement vector and scalar moisture content) . This new model is also compared with past 3D uncoupled hygro-elastic shell models where the moisture content profile is separately defined. These models are indicated as 3D( ℳ a ) when the moisture content profile is a priori assumed as linear through the entire thickness direction, 3D( ℳ c , 1D) when the moisture content profile is separately calculated by solving the 1D version of the Fick diffusion equation, and 3D( ℳ c , 3D) when the moisture content profile is separately calculated by solving the 3D version of the Fick diffusion equation.

This section is splitted in two different parts: the first subsection is devoted to the validation of the 3D coupled hygro-elastic model for FGM shells by means of comparisons with the past 3D( ℳ c , 3D) model and the 3D solid finite element model by Patran and Nastran in the study by Brischetto and Torre [32]. This assessment subsection is very important because it is useful to understand the number of fictitious layers F that must be used to properly account for effects of the shell curvatures and FGM variable properties. In addition, the order of the expansion N for the exponential matrix must be also defined to obtain accurate results. In the second subsection, four new benchmarks are presented. They are useful to understand all the potentiality of the model because they consider different parameters such as the thickness ratio, the FGM configuration, the moisture content at the external surfaces, and the geometry. In both subsections, the FGM is composed by two phases: the metallic one is Monel (70Ni30Cu) and the ceramic one is Zirconia. The hygro-elastic properties of these two materials are clearly shown in Table 1.

Table 1

Mechanical and hygroscopic properties for the two PVR and for benchmarks (B)

FGM properties
K m [GPa]	227.24
G m [GPa]	65.55
η m 1 %	2 × 1 0 ‒ 3
D m kg ms	1 0 ‒ 9
K c [GPa]	125.83
G c [GPa]	58.077
η c 1 %	1 0 ‒ 3
D c kg ms	1 0 ‒ 10

The volume fraction of the ceramic phase for all the cases proposed (both assessments and benchmarks) is:

(33) V c = z ˜ FGM h FGM p ,

where z ˜ FGM is the local thickness coordinate of the FGM layer, p is the exponential coefficient, and h FGM is the total dimension in the z direction of the FGM layer. The FGM layer is completely in Monel for V c = 0 , and it is completely in Zirconia for V c = 1 .

Bulk and shear moduli of the FGM layer vary in the thickness direction following the Mori-Tanaka model:

(34) K − K m K c − K m = V c 1 + ( 1 − V c ) K c − K m K m + 4 3 G m , G − G m G c − G m = V c 1 + ( 1 − V c ) G c − G m G m + f m ,

where f m = G m ( 9 K m + 8 G m ) 6 ( K m + 2 G m ) .

The moisture expansion coefficient η , written according to the Hatta and Taya model, is a function of the bulk modulus as follows:

(35) η − η m η c − η m = 1 K − 1 K m 1 K c − 1 K m ,

and the moisture diffusion coefficient D can be computed using:

(36) D − D m D c − D m = V c 1 + ( 1 − V c ) k c − k m 3 k m ,

where the dependence on V c is clear. The material data employed in this section were proposed by Reddy and Cheng in [46].

3.1 Comparisons for validations

Two preliminary validation results (PVRs) are proposed for this new three-dimensional general exact coupled hygro-elastic shell model (3D-u- ℳ ). A square plate and a cylindrical shell panel are analyzed for several thickness ratios, moisture content profiles and lamination schemes. For these validation cases, the 3D-u- ℳ model is compared with the 3D( ℳ c , 3D) model and the 3D FE model via Patran and Nastran (for the details about these models, see [32]). Table 2 shows all the data used for the assessment cases. When N = 3 and F = 300 , the 3D-u- ℳ model obtains the same results as the 3D( ℳ c , 3D) presented by Brischetto and Torre in [32], but some differences occur with respect to the 3D FE analysis. The results obtained by the Patran and Nastran model are always the same for each number of fictitious layers F because the 3D solid FE model does not use fictitious layer discretization.

Table 2

Moisture contents, geometrical data, and lamination configurations for the two PVR

	PVR1	PVR2
	Square plate	Cylindrical shell
a [m]	100	1
b [m]	100	π 3 R β
h [m]	25, 10, 2	0.2, 0.01
R α [m]	∞	∞
R β [m]	∞	10
ℳ t [%]	+1.0	+1.0
ℳ b [%]	+0.5	+0.5
m	1	1
n	1	1
p	2.0	2.0
Configuration	Single FGM layer	Single FGM layer

The first preliminary validation results (PVR1) propose a simply supported square plate composed by a single FGM layer. The hygro-elastic material properties are presented in Table 1, and the geometrical parameters are given in the first column of Table 2. Table 3 shows the results of the conducted analyses for different numbers of fictitious layers F and different thickness ratios a ⁄ h . Transverse normal displacement w , in-plane displacement u , and in-plane normal stress σ α α are analyzed. There is a clear convergence of results for the increasing number of fictitious layers F . For the majority of the cases, a number of 200 fictitious layers is sufficient for both the 3D uncoupled model and for the 3D coupled model (both using the 3D Fick diffusion equation).

Table 3

Preliminary validation results (PVR1), square plate embedding a single FGM layer. Moisture content applied at the external surfaces. The reference solutions are the 3D uncoupled analytical model and the 3D FE model via Patran and Nastran proposed by Brischetto and Torre [32]

F →		10	50	100	200	300
w [ 10 ‒ 4 m] at z ˜ = h , α = a ⁄ 2 , and β = b ⁄ 2
a ⁄ h = 4	3D FEM [32]	143.3	143.3	143.3	143.3	143.3
	3D( ℳ c , 3D) [32]	151.0	141.9	141.6	141.5	141.5
	3D-u- ℳ	152.0	142.0	141.6	141.5	141.5
σ α α [Pa] at z ˜ = 0 , α = a ⁄ 2 , and β = b ⁄ 2
a ⁄ h = 4	3D FEM [32]	‒ 751,662	‒ 751,662	‒ 751,662	‒ 751,662	‒ 751,662
	3D( ℳ c , 3D) [32]	‒ 75,532	‒ 75,561	‒ 75,551	‒ 75,548	‒ 75,548
	3D-u- ℳ	‒ 76,106	‒ 75,573	‒ 75,554	‒ 75,549	‒ 75,549
u [ 10 ‒ 4 m] at z ˜ = h ⁄ 2 , α = a ⁄ 2 , and β = 0
a ⁄ h = 10	3D FEM [32]	‒ 226.0	‒ 226.0	‒ 226.0	‒ 226.0	‒ 226.0
	3D( ℳ c , 3D) [32]	‒ 227.3	‒ 225.8	‒ 225.7	‒ 225.7	‒ 225.7
	3D-u- ℳ	‒ 227.4	‒ 225.8	‒ 225.8	‒ 225.8	‒ 225.8
σ α α [Pa] at z ˜ = h , α = a ⁄ 2 , and β = b ⁄ 2
a ⁄ h = 10	3D FEM [32]	‒ 63,825	‒ 63,825	‒ 63,825	‒ 63,825	‒ 63,825
	3D( ℳ c , 3D) [32]	‒ 87,250	‒ 68,062	‒ 65,359	‒ 63,979	‒ 63,515
	3D-u- ℳ	‒ 87,228	‒ 68,063	‒ 65,360	‒ 63,980	‒ 63,516
u [ 10 ‒ 4 m] at z ˜ = 0 , α = a ⁄ 2 , and β = 0
a ⁄ h = 50	3D FEM [32]	‒ 236.8	‒ 236.8	‒ 236.8	‒ 236.8	‒ 236.8
	3D( ℳ c , 3D) [32]	‒ 235.9	‒ 236.8	‒ 236.8	‒ 236.9	‒ 236.9
	3D-u- ℳ	‒ 235.9	‒ 236.9	‒ 236.9	‒ 236.9	‒ 236.9
σ α α [Pa] at z ˜ = h ⁄ 2 , α = a ⁄ 2 , and β = b ⁄ 2
a ⁄ h = 50	3D FEM [32]	‒ 105,149	‒ 105,149	‒ 105,149	‒ 105,149	‒ 105,149
	3D( ℳ c , 3D) [32]	‒ 114,035	‒ 107,338	‒ 106,457	‒ 106,013	‒ 105,865
	3D-u- ℳ	‒ 96,097	‒ 103,761	‒ 104,669	‒ 105,119	‒ 105,269

The second preliminary validation results (PVR2) show a simply supported cylindrical shell embedding a single FGM layer. The hygro-elastic material properties are collected in Table 1, and the geometrical parameters are given in the second column of Table 2. Table 4 proposes results for different numbers of fictitious layers F and for two different thickness ratios: a thick configuration and a thin configuration. Transverse and in-plane displacements are analyzed and the reference solutions are the same seen in PVR1. The same conclusions seen for PVR1 are confirmed. For a number of fictitious layers F = 200 and order of expansion N = 3 for the exponential matrix, the 3D-u- ℳ model is coincident with the reference solution for both thickness ratios because these two different 3D analytical models take into account the same effects but in a different way.

Table 4

Preliminary validation results (PVR2), cylindrical shell embedding a single FGM layer. Moisture content applied at the external surfaces. The reference solutions are the 3D uncoupled analytical model and the 3D FE model via Patran and Nastran proposed by Brischetto and Torre [32]

F →		10	50	100	200	300
w [ 10 ‒ 6 m] at z ˜ = h , α = a ⁄ 2 , and β = b ⁄ 2
R β ⁄ h = 50	3D FEM [32]	411.97	411.97	411.97	411.97	411.97
	3D( ℳ c , 3D) [32]	417.06	398.20	397.51	397.34	397.31
	3D-u- ℳ	417.80	398.20	397.52	397.35	397.31
w [ 10 ‒ 6 m] at z ˜ = h ⁄ 2 , α = a ⁄ 2 , and β = b ⁄ 2
R β ⁄ h = 50	3D FEM [32]	279.92	279.92	279.92	279.92	279.92
	3D( ℳ c , 3D) [32]	285.49	268.05	267.42	267.26	267.23
	3D-u- ℳ	286.30	268.06	267.42	267.26	267.23
u [ 10 ‒ 6 m] at z ˜ = h , α = a ⁄ 2 , and β = 0
R β ⁄ h = 50	3D FEM [32]	‒ 538.01	‒ 538.01	‒ 538.01	‒ 538.01	‒ 538.01
	3D( ℳ c , 3D) [32]	‒ 539.7	‒ 531.1	‒ 530.8	‒ 530.7	‒ 530.7
	3D-u- ℳ	‒ 539.9	‒ 531.1	‒ 530.8	‒ 530.7	‒ 530.7
u [ 10 ‒ 6 m] at z ˜ = 0 , α = a ⁄ 2 , and β = 0
R β ⁄ h = 50	3D FEM [32]	‒ 380.50	‒ 380.50	‒ 380.50	‒ 380.50	‒ 380.50
	3D( ℳ c , 3D) [32]	‒ 379.6	‒ 381.7	‒ 381.8	‒ 381.8	‒ 381.8
	3D-u- ℳ	‒ 379.2	‒ 381.8	‒ 381.9	‒ 381.9	‒ 381.9
w [ 10 ‒ 6 m] at z ˜ = h , α = a ⁄ 2 , and β = b ⁄ 2
R β ⁄ h = 1,000	3D FEM [32]	10,128	10,128	10,128	10,128	10,128
	3D( ℳ c , 3D) [32]	10,149	10,064	10,061	10,060	10,060
	3D-u- ℳ	10,149	10,064	10,061	10,061	10,061
w [ 10 ‒ 6 m] at z ˜ = h ⁄ 2 , α = a ⁄ 2 , and β = b ⁄ 2
R β ⁄ h = 1,000	3D FEM [32]	10,123	10,123	10,123	10,123	10,123
	3D( ℳ c , 3D) [32]	10,144	10,059	10,056	10,055	10,055
	3D-u- ℳ	10,144	10,059	10,056	10,056	10,056
u [ 10 ‒ 6 m] at z ˜ = h , α = a ⁄ 2 , and β = 0
R β ⁄ h = 1,000	3D FEM [32]	‒ 520.37	‒ 520.37	‒ 520.37	‒ 520.37	‒ 538.01
	3D( ℳ c , 3D) [32]	‒ 521.1	‒ 517.9	‒ 517.8	‒ 517.8	‒ 517.8
	3D-u- ℳ	‒ 521.1	‒ 518.0	‒ 517.8	‒ 517.8	‒ 517.8
u [ 10 ‒ 6 m] at z ˜ = 0 , α = a ⁄ 2 , and β = 0
R β ⁄ h = 1,000	3D FEM [32]	‒ 202.42	‒ 202.42	‒ 202.42	‒ 202.42	‒ 202.42
	3D( ℳ c , 3D) [32]	‒ 202.5	‒ 202.0	‒ 201.9	‒ 201.9	‒ 201.9
	3D-u- ℳ	‒ 202.5	‒ 202.0	‒ 202.0	‒ 202.0	‒ 202.0

After these PVRs, a number of F = 300 fictitious layers (that is overbundant with respect to F = 200 ) and an order of expansion for the exponential matrix N = 3 are fixed for all the future new benchmarks proposed in the next section.

3.2 New benchmarks

Four benchmark cases are here proposed. They take into account different characteristics for each case to have a global overview of all the peculiarities. The proposed four benchmarks consider the geometries given in Figure 1. The results obtained in this subsection consider different lamination schemes, FGM properties, and external moisture content impositions. N = 3 is used as the order of expansion for the exponential matrix, and F = 300 is the number of fictitious layers involved in each benchmark. This choice about N and F has been deeply discussed in the previous subsection. The new 3D coupled hygro-elastic model (3D-u- ℳ ) is compared with 3D uncoupled models presented by Brischetto and Torre in [32] (3D( ℳ c , 3D), 3D( ℳ c , 1D), and 3D( ℳ a )). Now, some reference results have been corrected because of some residual errors in [32]. All the geometrical features involved in the four benchmarks are collected in Table 5. The results discussed in this subsection can be used as test cases for scientists involved in the developing of 2D or 3D analytical/numerical models to evaluate the effects of the moisture content in these types of structures. The material data for the four benchmarks are given in Table 1.

Table 5

Moisture contents, geometrical data, and lamination configurations for the four Benchmarks (B). t can assume the values 5, 2.5, 1, 0.2, and 0.1

	B1	B2	B3	B4
	Square plate	Cylinder	Cylindrical shell	Spherical shell
a [m]	10	30	30	π 3 R α
b [m]	10	2 π R β	π 3 R β	π 3 R β
h [m]	t	t	t	t
R α [m]	∞	∞	∞	10
R β [m]	∞	10	10	10
ℳ t [%]	+1.0	+1.0	+1.0	+1.0
ℳ b [%]	0.0	0.0	0.0	0.0
m	1	1	0	2
n	1	2	2	2
p	1.0	2.0	0.5	0.5
Scheme	Single FGM layer	Single FGM layer	Sandwich with FGM core	Sandwich with FGM core

The first benchmark (B1) considers a square plate with a single FGM layer and simply supported sides. The top of the structure is fully ceramic, and the bottom is fully metallic. All the data used for the hygroelastic analysis are presented in the first column of Table 5. Several thickness ratios are considered to evaluate the effects of geometrical parameters. The thickness ratios vary from a ⁄ h = 2 to a ⁄ h = 100 . The moisture content is directly imposed at the external surfaces in harmonic form. In Figure 2, it is possible to see how the bulk modulus and the volume fraction of the ceramic phase vary across the thickness direction of the material. The trend adopted for the volume fraction of the ceramic phase is linear and p = 1 is the exponent used in Eq. (33). In Table 6, moisture content, displacements, stresses and strains are proposed. The results for the thick plate highlight the accordance between the 3D-u- ℳ and the 3D( ℳ c , 3D) because both consider the three-dimensional nature of the problem, taking into account both the material and the thickness layer effects. For this reason, these two solutions show the most accurate results. Due to the fact that the 3D( ℳ c , 1D) considers only the material effect and the 3D( ℳ a ) discards both material and thickness layer effects, the results proposed by these two models are not correct for the thick cases. For what concerns the thin configuration, as the thickness layer effect vanishes, even the 3D( ℳ c , 1D) is reliable as the 3D-u- ℳ and the 3D( ℳ c , 3D); the only discrepancies are proposed by the 3D( ℳ a ) because it assumes a moisture content profile always linear. In Figure 3, it is possible to visualize the four moisture content profiles for a moderately thick case and a moderately thin one. It is possible to clearly see the differences involved for the moderately thick structure case among the u- ℳ coupled profile, the calculated ( ℳ c , 3D) profile and the calculated ( ℳ c , 1D) profile. For the moderately thin structure case, only the assumed linear profile ( ℳ a ) is wrong because it does not take into account both material and thickness layer effect. Figure 4 shows the trend along the z direction of two displacement components, the moisture content calculated with this new 3D coupled model, and stresses. All the variables are continuous along the thickness direction because this is a peculiarity of the FGMs, and it also demonstrates the correct implementation of the continuity conditions in the model. The transverse normal stress σ z z and the transverse shear stress σ β z satisfy the external mechanical loading boundary conditions: they equal zero at both the external faces because no external mechanical loads act on them.

$Figure 2 Benchmark 1 (B1), bulk modulus, and volume fraction of the ceramic phase for a square plate embedding a single FGM layer ( p = 1.0 p=1.0 ).$

Figure 2

Benchmark 1 (B1), bulk modulus, and volume fraction of the ceramic phase for a square plate embedding a single FGM layer ( p = 1.0 ).

Table 6

Benchmark 1 (B1), square plate embedding a single FGM layer. 3D uncoupled hygro-elastic models [32] vs the 3D coupled hygro-elastic model

a ⁄ h	2	4	10	50	100
ℳ [ ‒ ] at z ˜ = + 4 h ⁄ 5 , α = a ⁄ 2 , and β = b ⁄ 2
3D( ℳ a ) [32]	0.8000	0.8000	0.8000	0.8000	0.8000
3D( ℳ c , 1D) [32]	0.5595	0.5595	0.5595	0.5595	0.5595
3D( ℳ c , 3D) [32]	0.4351	0.5197	0.5525	0.5592	0.5594
3D-u- ℳ	0.4352	0.5197	0.5526	0.5592	0.5594
v [ 10 ‒ 3 m] at z ˜ = + 4 h ⁄ 5 , α = a ⁄ 2 , and β = 0
3D( ℳ a ) [32]	‒ 2.094	‒ 2.089	‒ 2.087	‒ 2.086	‒ 2.086
3D( ℳ c , 1D) [32]	‒ 1.454	‒ 1.461	‒ 1.462	‒ 1.462	‒ 1.462
3D( ℳ c , 3D) [32]	‒ 1.148	‒ 1.362	‒ 1.445	‒ 1.462	‒ 1.462
3D-u- ℳ	‒ 1.148	‒ 1.363	‒ 1.445	‒ 1.462	‒ 1.463
w [ 10 ‒ 3 m] at z ˜ = + h ⁄ 2 , α = a ⁄ 2 , and β = b ⁄ 2
3D( ℳ a ) [32]	1.226	2.661	6.791	34.07	68.16
3D( ℳ c , 1D) [32]	1.103	2.405	6.144	30.83	61.68
3D( ℳ c , 3D) [32]	1.008	2.336	6.113	30.83	61.67
3D-u- ℳ	1.008	2.337	6.113	30.83	61.68
σ zz [ 10 3 Pa] at z ˜ = + h ⁄ 5 , α = a ⁄ 2 , and β = b ⁄ 2
3D( ℳ a ) [32]	‒ 5,915	‒ 982.6	‒ 127.7	‒ 4.879	‒ 1.218
3D( ℳ c , 1D) [32]	‒ 1,197	44.77	26.65	1.217	0.3054
3D( ℳ c , 3D) [32]	515.5	173.0	30.09	1.222	0.3057
3D-u- ℳ	515.5	173.0	30.09	1.222	0.3057
σ α α [ 10 6 Pa] at z ˜ = + h , α = a ⁄ 2 , and β = b ⁄ 2
3D( ℳ a ) [32]	‒ 7.939	‒ 34.86	‒ 43.94	‒ 45.68	‒ 45.73
3D( ℳ c , 1D) [32]	‒ 63.24	‒ 3.08	‒ 89.55	‒ 90.74	‒ 90.78
3D( ℳ c , 3D) [32]	‒ 90.78	‒ 90.95	‒ 90.83	‒ 90.79	‒ 90.79
3D-u- ℳ	‒ 90.78	‒ 90.95	‒ 90.83	‒ 90.79	‒ 90.79
γ β z [ 10 ‒ 6 ] at z ˜ = + h ⁄ 3 , α = a ⁄ 2 , and β = 0
3D( ℳ a ) [32]	‒ 173.7	‒ 57.29	‒ 18.35	‒ 3.489	‒ 1.741
3D( ℳ c , 1D) [32]	‒ 39.06	3.440	4.709	1.072	0.5379
3D( ℳ c , 3D) [32]	19.67	12.49	5.321	1.076	0.5384
3D-u- ℳ	19.67	12.49	5.324	1.077	0.5386

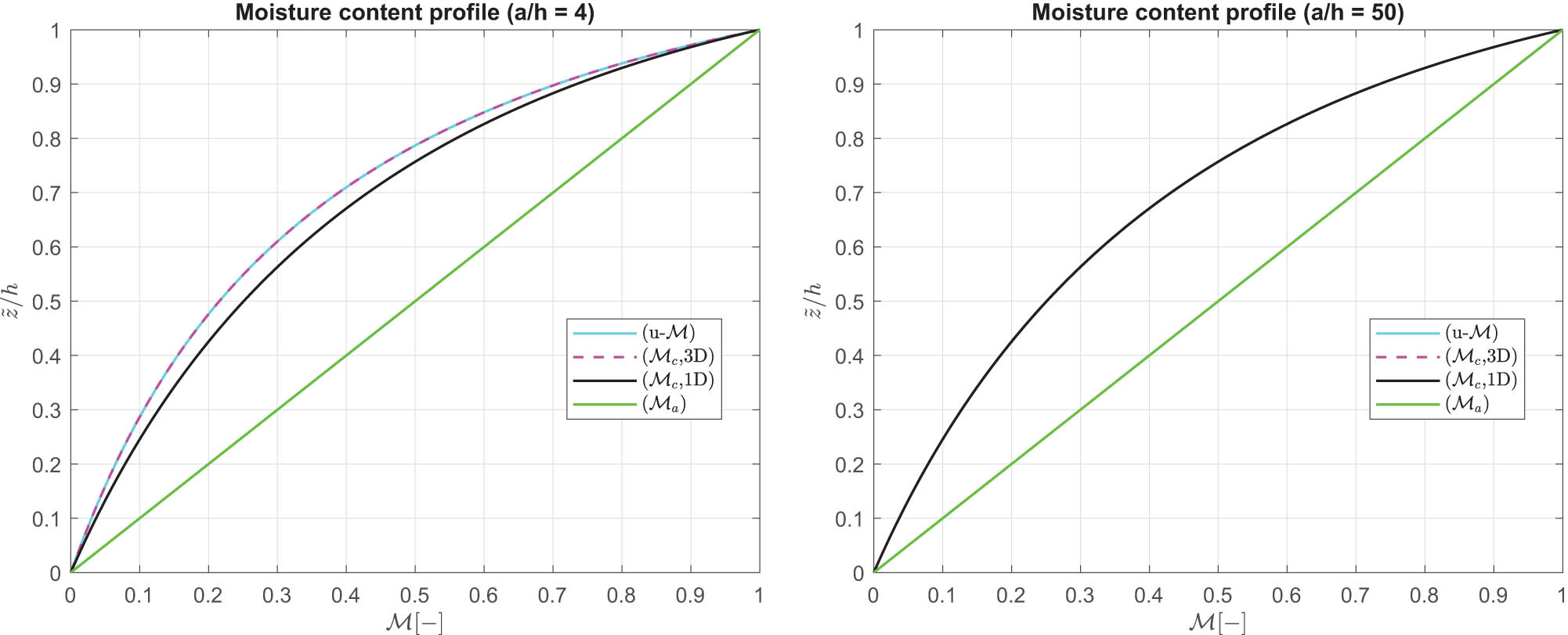
$Figure 3 Benchmark 1 (B1), moisture content profile ℳ ( α , β , z ) {\mathcal{ {\mathcal M} }}\left(\alpha ,\beta ,z) at α = + a ⁄ 2 \alpha =+a/2 and β = + b ⁄ 2 \beta =+b/2 for a moderately thick ( a ⁄ h = 4 a/h=4 ) and a moderately thin ( a ⁄ h = 50 a/h=50 ) configuration. Square plate embedding a single FGM layer ( p = 1.0 p=1.0 ).$

Figure 3

Benchmark 1 (B1), moisture content profile ℳ ( α , β , z ) at α = + a ⁄ 2 and β = + b ⁄ 2 for a moderately thick ( a ⁄ h = 4 ) and a moderately thin ( a ⁄ h = 50 ) configuration. Square plate embedding a single FGM layer ( p = 1.0 ).

$Figure 4 Benchmark 1 (B1), displacement components, moisture content profile, and stress components for a thick ( a ⁄ h = 2 a/h=2 ) square plate embedding a single FGM layer ( p = 1.0 p=1.0 ). Maximum values: u u in (0, b b /2); w w , ℳ {\mathcal{ {\mathcal M} }} , σ z z {\sigma }_{zz} , and σ α α {\sigma }_{\alpha \alpha } in ( a a /2, b b /2); σ β z {\sigma }_{\beta z} in ( a a /2, 0).$

Figure 4

Benchmark 1 (B1), displacement components, moisture content profile, and stress components for a thick ( a ⁄ h = 2 ) square plate embedding a single FGM layer ( p = 1.0 ). Maximum values: u in (0, b /2); w , ℳ , σ z z , and σ α α in ( a /2, b /2); σ β z in ( a /2, 0).

The second benchmark (B2) is about a closed cylinder with a single FGM layer and simply supported sides. The metallic and ceramic phases and related mechanical and hygroelastic properties are the same seen in B1 and in Table 1. The geometrical data of the structure are shown in the second column of Table 5. Different thickness ratios are considered to better understand the effects of geometrical parameters. The thickness ratio varies from R α ⁄ h = 2 to R α ⁄ h = 100 . The FGM law (Eq. (33)) has exponent p = 2 . In Figure 5, it is possible to see the bulk modulus and the volume fraction trend. In Table 7, results are shown to compare the 3D( ℳ c , 3D) model, the 3D( ℳ c , 1D) model, the 3D( ℳ a ) model, and the new 3D-u- θ model. The conclusions for both thin and thick structures are the same seen in the first benchmark. In Figure 6, the moisture content profile is given for a moderately thin and a moderately thick case. For the closed cylinder case, the differences among the ( ℳ c , 1D) profile, ( ℳ c , 3D) profile, and the u- ℳ profile are also small for the moderately thick case. Only the ( ℳ a ) profile is always incorrect because the hypothesis of linear profile is not true due to the material and thickness layer effects. Figure 7 shows some variables of interest to understand the main peculiarities of this case. All the variables presented are continuous: it means the correctness of the continuity conditions. The continuous trends of these variables are a specific characteristic of the FGMs. In addition, as no mechanical loads are applied, the stress σ z z is zero at the top and bottom surfaces.

$Figure 5 Benchmark 2 (B2), bulk modulus and volume fraction of the ceramic phase for a circular cylinder embedding a single FGM layer ( p = 2.0 p=2.0 ).$

Figure 5

Benchmark 2 (B2), bulk modulus and volume fraction of the ceramic phase for a circular cylinder embedding a single FGM layer ( p = 2.0 ).

Table 7

Benchmark 2 (B2), closed cylinder embedding a single FGM layer. 3D uncoupled hygro-elastic models [32] vs the 3D coupled hygro-elastic model

R β ⁄ h	2	4	10	50	100
ℳ [ ‒ ] at z ˜ = + h ⁄ 2 , α = a ⁄ 2 , and β = b ⁄ 2
3D( ℳ a ) [32]	0.5000	0.5000	0.5000	0.5000	0.5000
3D( ℳ c , 1D) [32]	0.2627	0.2627	0.2627	0.2627	0.2627
3D( ℳ c , 3D) [32]	0.2439	0.2577	0.2619	0.2627	0.2627
3D-u- ℳ	0.2439	0.2577	0.2619	0.2627	0.2627
u [ 10 ‒ 3 m] at z ˜ = + h ⁄ 3 , α = a ⁄ 2 , and β = 0
3D( ℳ a ) [32]	‒ 6.095	‒ 6.688	‒ 6.975	‒ 7.079	‒ 7.089
3D( ℳ c , 1D) [32]	‒ 3.725	‒ 4.096	‒ 4.253	‒ 4.298	‒ 4.302
3D( ℳ c , 3D) [32]	‒ 3.541	‒ 4.043	‒ 4.244	‒ 4.298	‒ 4.302
3D-u- ℳ	‒ 3.541	‒ 4.043	‒ 4.244	‒ 4.298	‒ 4.302
w [ 10 ‒ 3 m] at z ˜ = + h ⁄ 2 , α = a ⁄ 2 , and β = b ⁄ 2
3D( ℳ a ) [32]	14.96	15.14	14.73	14.33	14.27
3D( ℳ c , 1D) [32]	9.600	9.488	9.056	8.715	8.667
3D( ℳ c , 3D) [32]	9.187	9.372	9.037	8.714	8.667
3D-u- ℳ	9.187	9.372	9.037	8.714	8.667
σ zz [ 10 6 Pa] at z ˜ = + 2 h ⁄ 3 , α = a ⁄ 2 , and β = b ⁄ 2
3D( ℳ a ) [32]	4.442	4.370	2.346	0.5349	0.2716
3D( ℳ c , 1D) [32]	7.308	5.035	2.383	0.5161	0.2605
3D( ℳ c , 3D) [32]	7.578	5.055	2.384	0.5161	0.2605
3D-u- ℳ	7.578	5.055	2.384	0.5161	0.2605
σ β β [ 10 6 Pa] at z ˜ = + h , α = a ⁄ 2 , and β = b ⁄ 2
3D( ℳ a ) [32]	12.32	‒ 16.61	‒ 39.44	‒ 52.85	‒ 54.56
3D( ℳ c , 1D) [32]	‒ 69.19	‒ 91.24	‒ 107.7	‒ 117.1	‒ 118.3
3D( ℳ c , 3D) [32]	‒ 75.45	‒ 92.77	‒ 107.9	‒ 117.1	‒ 118.3
3D-u- ℳ	‒ 75.46	‒ 92.77	‒ 107.9	‒ 117.1	‒ 118.3
γ α β [ 10 ‒ 6 ] at z ˜ = 0 , α = 0 , and β = 0
3D( ℳ a ) [32]	516.7	292.5	119.2	23.61	11.78
3D( ℳ c , 1D) [32]	390.8	209.0	82.62	16.12	8.025
3D( ℳ c , 3D) [32]	381.8	207.4	82.50	16.11	8.025
3D-u- ℳ	381.8	207.4	82.50	16.11	8.025

$Figure 6 Benchmark 2 (B2), moisture content profile ℳ ( α , β , z ) {\mathcal{ {\mathcal M} }}\left(\alpha ,\beta ,z) at α = + a ⁄ 2 \alpha =+a/2 and β = + b ⁄ 2 \beta =+b/2 for a moderately thick ( R β ⁄ h = 4 {R}_{\beta }/h=4 ) and a moderately thin ( R β ⁄ h = 50 {R}_{\beta }/h=50 ) configuration. Circular cylinder embedding a single FGM layer ( p = 2.0 p=2.0 ).$

Figure 6

Benchmark 2 (B2), moisture content profile ℳ ( α , β , z ) at α = + a ⁄ 2 and β = + b ⁄ 2 for a moderately thick ( R β ⁄ h = 4 ) and a moderately thin ( R β ⁄ h = 50 ) configuration. Circular cylinder embedding a single FGM layer ( p = 2.0 ).

$Figure 7 Benchmark 2 (B2), displacement components, moisture content profile, and stress components for a thick ( R β ⁄ h = 2 {R}_{\beta }/h=2 ) circular cylinder embedding a single FGM layer ( p = 2.0 p=2.0 ). Maximum values: v v in ( a a /2, 0); w w , ℳ {\mathcal{ {\mathcal M} }} , σ β β {\sigma }_{\beta \beta } , and σ z z {\sigma }_{zz} in ( a a /2, b b /2); σ α β {\sigma }_{\alpha \beta } in (0,0).$

Figure 7

Benchmark 2 (B2), displacement components, moisture content profile, and stress components for a thick ( R β ⁄ h = 2 ) circular cylinder embedding a single FGM layer ( p = 2.0 ). Maximum values: v in ( a /2, 0); w , ℳ , σ β β , and σ z z in ( a /2, b /2); σ α β in (0,0).

The third benchmark (B3) proposes a sandwich cylindrical shell panel with simply supported sides. The material configuration has a bottom face in Monel (thickness h f = 0.1 h ), a top face in Zirconia (thickness h f = 0.1 h ), and a center core in FGM (thickness h c = 0.8 h ). For this sandwich configuration, the volume fraction of the ceramic phase V c of the core is 0 at the bottom (full metallic constituent) and 1 at the top (full ceramic constituent); it varies with continuity from 0 to 1 in the FGM core. The exponent p adopted for the FGM law is 0.5. The volume fraction V c and the bulk modulus trends can be seen in Figure 8. The mechanical and hygroscopic properties are the same used for B1 and B2. The geometrical characteristics are shown in the third column of Table 5. Table 8 shows results for the four different models and for different R α ⁄ h ratios (from thick to thin case). Even for the sandwich configuration, the thick cases ( R α ⁄ h = 2 and R α ⁄ h = 4 ) show the accordance between the 3D( ℳ c , 3D) model and the 3D-u- ℳ model. The reason is to be sought in the caption of the thickness effect that is crucial for thick structures. The 3D( ℳ c , 1D) cannot grasp the thickness layer effect but only the material layer effect that is not so much influent for these configurations. The 3D( ℳ a ) model is always inadequate for thick structures because the moisture content profile assumed as linear is not the actual one. For the thin structure case, as the thickness layer effect is less important, the 3D( ℳ c , 1D) model is similar to the 3D( ℳ c , 3D) and the 3D-u- ℳ models. These conclusions can also be seen in Figure 9 where the moisture content profiles are computed for a moderately thick and a moderately thin configuration. In Figure 10, six variables are proposed: two displacements, the moisture content profile calculated with the 3D-u- ℳ model, and two stresses. Even for the sandwich case, all the variables are continuous as a consequence of the continuous variation in the thickness direction of the FGM properties. In addition, the transverse shear stress σ α z fulfills the external load conditions because no mechanical loads are applied at the external surfaces.

$Figure 8 Benchmarks 3 and 4 (B3–B4), bulk modulus and volume fraction of the ceramic phase for a sandwich cylindrical shell panel and a sandwich spherical shell panel embedding a FGM core ( p = 0.5 p=0.5 ).$

Figure 8

Benchmarks 3 and 4 (B3–B4), bulk modulus and volume fraction of the ceramic phase for a sandwich cylindrical shell panel and a sandwich spherical shell panel embedding a FGM core ( p = 0.5 ).

Table 8

Benchmark 3 (B3), sandwich cylindrical shell panel embedding a FGM core. 3D uncoupled hygro-elastic models [32] vs the 3D coupled hygro-elastic model

R β ⁄ h	2	4	10	50	100
ℳ [ ‒ ] at z ˜ = + h ⁄ 2 , α = a ⁄ 2 , and β = b ⁄ 2
3D( ℳ a ) [32]	0.5000	0.5000	0.5000	0.5000	0.5000
3D( ℳ c , 1D) [32]	0.2263	0.2263	0.2263	0.2263	0.2263
3D( ℳ c , 3D) [32]	0.1100	0.1813	0.2178	0.2260	0.2263
3D-u- ℳ	0.1100	0.1813	0.2178	0.2260	0.2263
u [ 10 ‒ 6 m] at z ˜ = + 3 h ⁄ 4 , α = 0 , and β = b ⁄ 2
3D( ℳ a ) [32]	0.000	0.000	0.000	0.000	0.0000
3D( ℳ c , 1D) [32]	0.000	0.000	0.000	0.000	0.0000
3D( ℳ c , 3D) [32]	0.000	0.000	0.000	0.000	0.0000
3D-u- ℳ	0.000	0.000	0.000	0.000	0.0000
w [ 10 ‒ 5 m] at z ˜ = + h ⁄ 2 , α = a ⁄ 2 , and β = b ⁄ 2
3D( ℳ a ) [32]	52.486	111.71	313.64	1670.1	3364.9
3D( ℳ c , 1D) [32]	50.442	116.57	318.37	1653.2	3320.1
3D( ℳ c , 3D) [32]	47.154	113.37	316.31	1652.8	3319.8
3D-u- ℳ	47.154	113.37	316.31	1652.8	3319.8
σ zz [ 10 3 Pa] at z ˜ = + h ⁄ 4 , α = a ⁄ 2 , and β = b ⁄ 2
3D( ℳ a ) [32]	‒ 14157	‒ 1173.1	66.489	47.729	26.056
3D( ℳ c , 1D) [32]	‒ 1629.3	321.95	‒ 77.335	‒ 43.159	‒ 23.078
3D( ℳ c , 3D) [32]	2422.9	480.71	‒ 83.679	‒ 43.275	‒ 23.094
3D-u- ℳ	2422.9	480.71	‒ 83.679	‒ 43.275	‒ 23.094
σ β β [ 10 3 Pa] at z ˜ = 0 , α = 0 , and β = 0
3D( ℳ a ) [32]	10,924	61,711	44,781	42,437	42,487
3D( ℳ c , 1D) [32]	11,090	‒ 15,730	‒ 23,684	‒ 24,007	‒ 23,851
3D( ℳ c , 3D) [32]	‒ 16,516	‒ 23,828	‒ 24,986	‒ 24,058	‒ 23,864
3D-u- ℳ	‒ 16,516	‒ 23,828	‒ 24,986	‒ 24,058	‒ 23,864
γ α z [ 10 ‒ 8 ] at z ˜ = + h ⁄ 3 , α = 0 , and β = b ⁄ 2
3D( ℳ a ) [32]	0.000	0.000	0.000	0.000	0.0000
3D( ℳ c , 1D) [32]	0.000	0.000	0.000	0.000	0.0000
3D( ℳ c , 3D) [32]	0.000	0.000	0.000	0.000	0.0000
3D-u- ℳ	0.000	0.000	0.000	0.000	0.0000

$Figure 9 Benchmark 3 (B3), moisture content profile ℳ ( α , β , z ) {\mathcal{ {\mathcal M} }}\left(\alpha ,\beta ,z) at α = + a ⁄ 2 \alpha =+a/2 and β = + b ⁄ 2 \beta =+b/2 for a moderately thick ( R β ⁄ h = 4 {R}_{\beta }/h=4 ) and a moderately thin ( R β ⁄ h = 50 {R}_{\beta }/h=50 ) configuration. Sandwich cylindrical shell panel embedding a FGM core ( p = 0.5 p=0.5 ).$

Figure 9

Benchmark 3 (B3), moisture content profile ℳ ( α , β , z ) at α = + a ⁄ 2 and β = + b ⁄ 2 for a moderately thick ( R β ⁄ h = 4 ) and a moderately thin ( R β ⁄ h = 50 ) configuration. Sandwich cylindrical shell panel embedding a FGM core ( p = 0.5 ).

$Figure 10 Benchmark 3 (B3), displacement components, moisture content profile, and stress components for a thick ( R β ⁄ h = 2 {R}_{\beta }/h=2 ) sandwich cylindrical shell panel embedding a FGM core ( p = 0.5 p=0.5 ). Maximum values: u u in (0, b b /2); w w , ℳ {\mathcal{ {\mathcal M} }} , σ α α {\sigma }_{\alpha \alpha } , and σ β β {\sigma }_{\beta \beta } in ( a a /2, b b /2); σ α z {\sigma }_{\alpha z} in (0, b b /2).$

Figure 10

Benchmark 3 (B3), displacement components, moisture content profile, and stress components for a thick ( R β ⁄ h = 2 ) sandwich cylindrical shell panel embedding a FGM core ( p = 0.5 ). Maximum values: u in (0, b /2); w , ℳ , σ α α , and σ β β in ( a /2, b /2); σ α z in (0, b /2).

The last benchmark (B4) considers a sandwich spherical shell panel with simply supported sides. The sandwich lamination, the thickness values of the three layers, and the FGM law are the same seen in B3 (see also Figure 8). The hygro-elastic properties are given in Table 1, and the geometrical data are proposed in the fourth column of Table 5. Table 9 presents some results for different thickness ratios and for different variables. The considerations discussed for the B3 are the same. In Figure 11, it is possible to see the moisture content profile for a moderately thick and a moderately thin sandwich spherical shell configuration. It may be easily noted the fact that the ( ℳ c , 1D) profile has an important difference with respect to the ( ℳ c , 3D) and u- ℳ profiles because it does not take into account some important effects acting on this case. For what concerns the moderately thin case, the ( ℳ c , 1D) is sufficiently accurate. In the end, Figure 12 shows six variables in the thickness direction. The correct imposition of the continuity conditions are confirmed. The transverse shear stress σ β z and the transverse normal stress σ z z satisfy the load boundary conditions because no mechanical loads are applied at the external surfaces.

Table 9

Benchmark 4 (B4), sandwich spherical shell panel embedding a FGM core. 3D uncoupled hygro-elastic models [32] vs the 3D coupled hygro-elastic model

R β ⁄ h	2	4	10	50	100
ℳ [ ‒ ] at z ˜ = + h ⁄ 2 , α = a ⁄ 2 , and β = b ⁄ 2
3D( ℳ a ) [32]	0.5000	0.5000	0.5000	0.5000	0.5000
3D( ℳ c , 1D) [32]	0.2263	0.2263	0.2263	0.2263	0.2263
3D( ℳ c , 3D) [32]	0.0664	0.1492	0.2097	0.2256	0.2262
3D-u- ℳ	0.0664	0.1492	0.2097	0.2256	0.2262
v [ 10 ‒ 6 m] at z ˜ = + h ⁄ 3 , α = 0 , and β = b ⁄ 2
3D( ℳ a ) [32]	‒ 472.2	‒ 348.1	‒ 161.6	165.5	116.4
3D( ℳ c , 1D) [32]	‒ 146.8	‒ 97.22	22.91	166.0	104.0
3D( ℳ c , 3D) [32]	8.931	‒ 41.05	30.36	165.9	104.0
3D-u- ℳ	8.931	‒ 41.05	30.36	165.9	104.0
w [ 10 ‒ 6 m] at z ˜ = + h ⁄ 2 , α = a ⁄ 2 , and β = b ⁄ 2
3D( ℳ a ) [32]	451.5	909.6	2,454	6,323	6,380
3D( ℳ c , 1D) [32]	348.0	763.5	1,972	4,188	3,983
3D( ℳ c , 3D) [32]	293.3	694.9	1,926	4,182	3,981
3D-u- ℳ	293.3	694.9	1,926	4,182	3,981
σ zz [ 10 3 Pa] at z ˜ = + h ⁄ 3 , α = a ⁄ 2 , and β = b ⁄ 2
3D( ℳ a ) [32]	‒ 42,890	‒ 5394.8	‒ 488.01	586.86	426.57
3D( ℳ c , 1D) [32]	‒ 8096.9	2494.6	897.29	620.14	390.30
3D( ℳ c , 3D) [32]	7524.4	3999.2	932.31	619.62	390.19
3D-u- ℳ	7524.3	3999.2	932.31	619.62	390.19
σ β z [ 10 3 Pa] at z ˜ = + 2 h ⁄ 3 , α = 0 , and β = b ⁄ 2
3D( ℳ a ) [32]	28,381	15,367	7733.1	‒ 439.9	‒ 755.8
3D( ℳ c , 1D) [32]	11,029	4217.1	1656.3	‒ 1,591	‒ 1,171
3D( ℳ c , 3D) [32]	1946.1	1388.9	1339.1	‒ 1593	‒ 1,171
3D-u- ℳ	1946.0	1388.9	1339.1	‒ 1,593	‒ 1,171
ε α α [ 10 ‒ 6 ] at z ˜ = + h , α = a ⁄ 2 , and β = b ⁄ 2
3D( ℳ a ) [32]	89.66	‒ 50.19	‒ 57.30	‒ 160.8	‒ 276.8
3D( ℳ c , 1D) [32]	‒ 156.0	‒ 294.3	‒ 326.1	‒ 476.0	‒ 566.4
3D( ℳ c , 3D) [32]	‒ 369.0	‒ 384.8	‒ 346.3	‒ 476.9	‒ 566.6
3D-u- ℳ	‒ 369.0	‒ 384.8	‒ 346.3	‒ 476.9	‒ 566.6

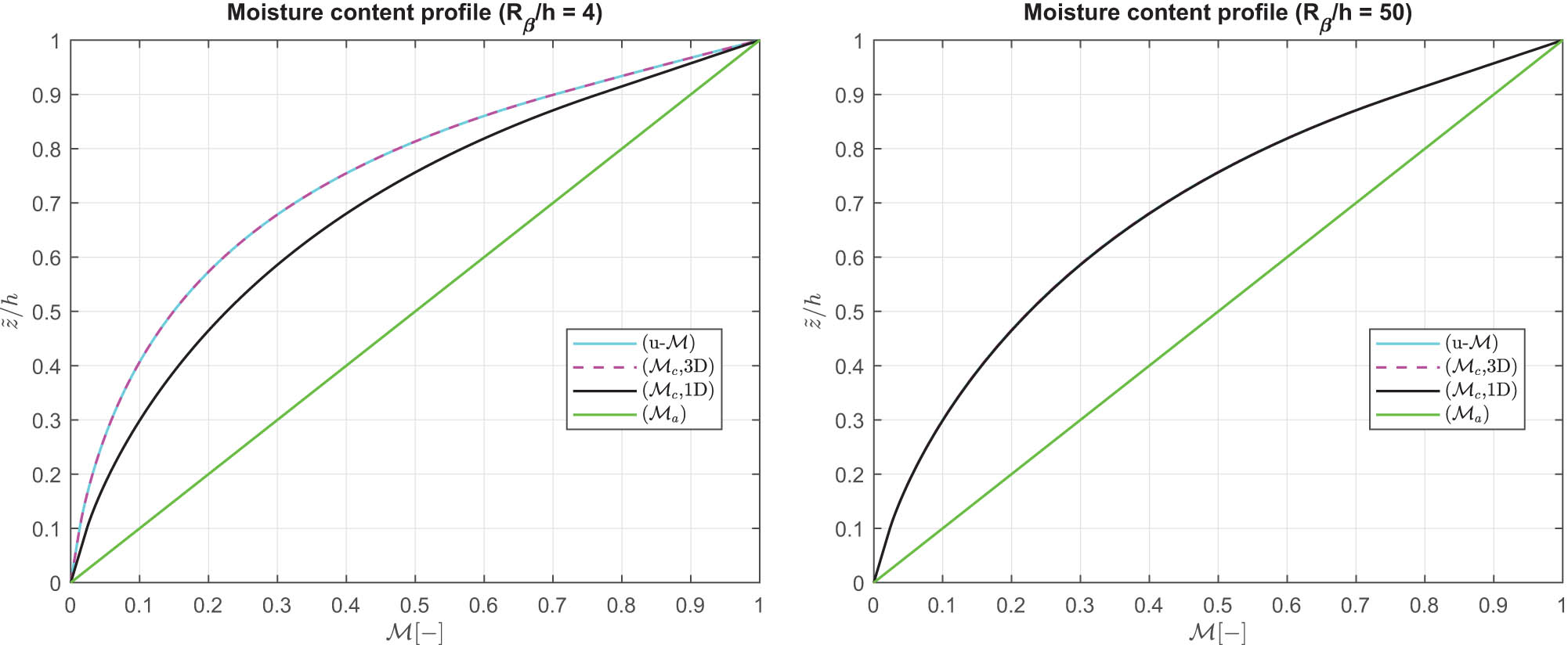
$Figure 11 Benchmark 4 (B4), moisture content profile ℳ ( α , β , z ) {\mathcal{ {\mathcal M} }}\left(\alpha ,\beta ,z) at α = + a ⁄ 2 \alpha =+a/2 and β = + b ⁄ 2 \beta =+b/2 for a moderately thick ( R β ⁄ h = 4 {R}_{\beta }/h=4 ) and moderately thin ( R β ⁄ h = 50 {R}_{\beta }/h=50 ) configuration. Sandwich spherical shell panel embedding a FGM core ( p = 0.5 p=0.5 ).$

Figure 11

Benchmark 4 (B4), moisture content profile ℳ ( α , β , z ) at α = + a ⁄ 2 and β = + b ⁄ 2 for a moderately thick ( R β ⁄ h = 4 ) and moderately thin ( R β ⁄ h = 50 ) configuration. Sandwich spherical shell panel embedding a FGM core ( p = 0.5 ).

$Figure 12 Benchmark 4 (B4), displacement components, moisture content profile and stress components for a thick ( R β ⁄ h = 2 {R}_{\beta }/h=2 ) sandwich spherical shell panel embedding a FGM core ( p = 0.5 p=0.5 ). Maximum values: u u in (0, b b /2); w w , ℳ {\mathcal{ {\mathcal M} }} , σ β β {\sigma }_{\beta \beta } , and σ z z {\sigma }_{zz} in ( a a /2, b b /2); σ β z {\sigma }_{\beta z} in ( a a /2,0).$

Figure 12

Benchmark 4 (B4), displacement components, moisture content profile and stress components for a thick ( R β ⁄ h = 2 ) sandwich spherical shell panel embedding a FGM core ( p = 0.5 ). Maximum values: u in (0, b /2); w , ℳ , σ β β , and σ z z in ( a /2, b /2); σ β z in ( a /2,0).

4 Conclusion

A full coupled hygro-elastic 3D exact shell model for the static analysis of FGM structures has been shown. The moisture content along the thickness direction is evaluated in steady-state conditions. The moisture content profile is a primary variable of the problem together with the displacement components. The 3D Fick diffusion equation for spherical shells allows a moisture content profile that takes into account both thickness layer and material layer effects. The coupled system is solved in a closed form using the exponential matrix method and a layer wise approach. Different results, in terms of displacements, stresses, and moisture content profiles, have been discussed for several thickness ratios, geometrical properties, FGM configurations (sandwich or single layer), and moisture content impositions. These analyses showed a very comforting match between the past 3D uncoupled model that separately solved the 3D Fick diffusion equation and the present 3D full coupled model. The main advantage of this new coupled formulation is the introduction of both thickness and material layer effects using a simpler and more elegant mathematical formulation having a faster convergence: in fact, a reduced number of fictitious layers F is requested in comparison with the uncoupled 3D model.

Funding information: This research received no external funding.
Author contributions: Methodology, S.B.; software, S.B.; validation, D.C.; formal analysis, D.C.; investigation, D.C.; data curation, S.B.; writing – original draft, D.C.; writing – review and editing, S.B. All authors have read and agreed to the published version of the manuscript.
Conflict of interest: The authors declare no conflict of interest.

References

[1] Bouadi H. Hygrothermal effects on complex moduli of composite laminates [dissertation]. Gainesville (FL): University of Florida; 1998.Suche in Google Scholar

[2] Vodicka R. Accelerated environmental testing of composite materials. DSTO - Aeronautical and Maritime Research Laboratory. DSTOTR-0657. Commonwealth of Australia: Melbourne; 1997. Suche in Google Scholar

[3] Tabrez S, Mitra M, Gopalakrishnan S. Modeling of degraded composite beam due to moisture absorption for wave based detection. CMES - Comput Model Eng Sci. 2007;22(1):77–90. Suche in Google Scholar

[4] Gawin D, Sanavia L. A unified approach to numerical modeling of fully and partially saturated porous materials by considering air dissolved in water. CMES - Comput Model Eng Sci. 2009;53(3):255–302. Suche in Google Scholar

[5] Aria AI, Friswell MI. Computational hygro-thermal vibration and buckling analysis of functionally graded sandwich microbeams. Compos Part B. 2019;165:785–97. 10.1016/j.compositesb.2019.02.028Suche in Google Scholar

[6] Garg A, Chalak HD, Belarbi MO, Zenkour AM. Hygro-thermo-mechanical based bending analysis of symmetric and unsymmetric power-law, exponential and sigmoidal FG sandwich beams. Mechanics Adv Mater Struct. 2022;29(25):4523–45. 10.1080/15376494.2021.1931993Suche in Google Scholar

[7] Li Y, Tang Y. Application of Galerkin iterative technique to nonlinear bending response of three-directional functionally graded slender beams subjected tohygro-thermal loads. Compos Struct. 2022;115481:290. 10.1016/j.compstruct.2022.115481Suche in Google Scholar

[8] Liu B, Mohammadi R. Effects of nonlinear hygro-thermo-mechanical loading on the bending response of nanobeams using nonlocal strain gradient theory. Waves Random Complex Media. 2022:1–17. 10.1080/17455030.2022.2072529Suche in Google Scholar

[9] Nguyen TK, Nguyen BD, Vo TP, Thai HT. Hygro-thermal effects on vibration and thermal buckling behaviors of functionally graded beams. Compos Struct. 2017;176:1050–60. 10.1016/j.compstruct.2017.06.036Suche in Google Scholar

[10] Tang Y, Ding Q. Nonlinear vibration analysis of a bi-directional functionally graded beam under hygro-thermal loads. Compos Struct. 2019;225:111076. 10.1016/j.compstruct.2019.111076Suche in Google Scholar

[11] Dastjerdi S, Malikan M, Dimitri R, Tornabene F. Nonlocal elasticity analysis of moderately thick porous functionally graded plates in a hygro-thermal environment. Compos Struct. 2021;255:112925. 10.1016/j.compstruct.2020.112925Suche in Google Scholar

[12] Lee CY, Kim JH. Hygrothermal postbuckling behavior of functionally graded plates. Compos Struct. 2013;95:278–82. 10.1016/j.compstruct.2012.07.010Suche in Google Scholar

[13] Sobhy M. Differential quadrature method for magneto-hygrothermal bending of functionally graded graphene/Al sandwich-curved beams with honeycomb core via a new higher-order theory. J Sandw Struct Mater. 2021;23:1662–700. 10.1177/1099636219900668Suche in Google Scholar

[14] Sobhy M. 3-D elasticity numerical solution for magneto-hygrothermal bending of FG graphene/metal circular and annular plates on an elastic medium. Eur J MechA Solids. 2021;88:104265. 10.1016/j.euromechsol.2021.104265Suche in Google Scholar

[15] Zhao J, Hu J, Wang T, Li H, Guan J, Liu J, et al. A unified modeling method for dynamic analysis of GPLs-FGP sandwich shallow shell embedded SMA wires with general boundary conditions under hygrothermal loading. Eng Struct. 2022;250:113439. 10.1016/j.engstruct.2021.113439Suche in Google Scholar

[16] Daia T, Yanga Y, Daia HL, Tang H, Lina ZY. Hygrothermal mechanical behaviors of a porous FG-CRC annular plate with variable thickness considering aggregation of CNTs. Compos Struct. 2019;215:198–213. 10.1016/j.compstruct.2019.02.061Suche in Google Scholar

[17] Saadatfar M, Aghaie-Khafri M. Hygrothermal analysis of a rotating smart exponentially graded cylindrical shell with imperfect bonding supported by an elastic foundation. Aerosp Sci Technol. 2015;43:37–50. 10.1016/j.ast.2015.02.012Suche in Google Scholar

[18] Nie B, Ren S, Li W, Zhou L, Liu C. The hygro-thermo-electro-mechanical coupling edge-based smoothed point interpolation method for the response of functionally graded piezoelectric structure under hygrothermal environment. Eng Anal Bound Elem. 2021;130;29–39. 10.1016/j.enganabound.2021.05.004Suche in Google Scholar

[19] Akbarzadeh AH, Chen ZT. Hygrothermal stresses in one-dimensional functionally graded piezoelectric media in constant magnetic field. Compos Struct. 2013;97:317–31. 10.1016/j.compstruct.2012.09.058Suche in Google Scholar

[20] Ebrahimi F, Barati MR. Small-scale effects on hygro-thermo-mechanical vibration of temperature-dependent nonhomogeneous nanoscale beams. Mech Adv Mater Struct. 2017;24:924–36. 10.1080/15376494.2016.1196795Suche in Google Scholar

[21] Ebrahimi F, Barati MR. A unified formulation for dynamic analysis of nonlocal heterogeneous nanobeams in hygro-thermal environment. Appl Phys A. 2016;122:792. 10.1007/s00339-016-0322-2Suche in Google Scholar

[22] Jouneghani FZ, Dimitri R, Tornabene F. Structural response of porous FG nanobeams under hygro-thermo-mechanical loadings. Compos Part B. 2018;152:71–8. 10.1016/j.compositesb.2018.06.023Suche in Google Scholar

[23] Penna R, Feo L, Lovisi G. Hygro-thermal bending behavior of porous FG nano-beams via local/nonlocal strain and stress gradient theories of elasticity. Compos Struct. 2021;263:113627. 10.1016/j.compstruct.2021.113627Suche in Google Scholar

[24] Wang S, Kang W, Yang W, Zhang Z, Li Q, Liu M, et al. Hygrothermal effects on buckling behaviors of porous bi-directional functionally graded micro-/nanobeams using two-phase local/nonlocal strain gradient theory. Eur J Mech/A Solids. 2022;94;104554. 10.1016/j.euromechsol.2022.104554Suche in Google Scholar

[25] Allam MNM, Radwan AF, Sobhy M. Hygrothermal deformation of spinning FG graphene sandwich cylindrical shells having an auxetic core. Eng Struct. 2022;251:113433. 10.1016/j.engstruct.2021.113433Suche in Google Scholar

[26] Arshid E, Soleimani-Javid Z, Amir S, DinhDuc N. Higher-order hygro-magneto-electro-thermo-mechanical analysis of FG-GNPs reinforced composite cylindrical shells embedded in PEM layers. Aerosp Sci Tech. 2022;126:107573. 10.1016/j.ast.2022.107573Suche in Google Scholar

[27] Karimiasla M, Ebrahimia F, Akgözb B. Buckling and post-buckling responses of smart doubly curved composite shallow shells embedded in SMA fiber under hygro-thermal loading. Compos Struct. 2019;223:110988. 10.1016/j.compstruct.2019.110988Suche in Google Scholar

[28] Zidi M, Tounsi A, Houari MSA, Bedia EAA, AnwarBég O. Bending analysis of FGM plates under hygro-thermo-mechanical loading using a four variable refined plate theory. Aerosp Sci Tech. 2014;34:24–34. 10.1016/j.ast.2014.02.001Suche in Google Scholar

[29] Zenkour AM, Radwanc AF. Bending response of FG plates resting on elastic foundations in hygrothermal environment with porosities. Compos Struct. 2019;213:133–43. 10.1016/j.compstruct.2019.01.065Suche in Google Scholar

[30] Tang H, Dai HL, Du Y. Effect of hygrothermal load on amplitude frequency response for CFRP spherical shell panel. Compos Struct. 2022;281:114978. 10.1016/j.compstruct.2021.114978Suche in Google Scholar

[31] Mudhaffar IM, Tounsi A, Chikh A, Al-Osta MA, Al-Zahrani MM, Al-Dulaijan SU. Hygro-thermo-mechanical bending behavior of advanced functionally graded ceramic metal plate resting on a viscoelastic foundation. Structures. 2021;33:2177–89. 10.1016/j.istruc.2021.05.090Suche in Google Scholar

[32] Brischetto S, Torre R. 3D stress analysis of multilayered functionally graded plates and shells under moisture conditions. Appl Sci. 2022;12:512. 10.3390/app12010512Suche in Google Scholar

[33] Brischetto S. A general exact elastic shell solution for bending analysis of funcionally graded structures. Compos Struct. 2017;175:70–85. 10.1016/j.compstruct.2017.04.002Suche in Google Scholar

[34] Brischetto S. A 3D layer-wise model for the correct imposition of transverse shear/normal load conditions in FGM shells. Int J Mech Sci. 2018;136:50–66. 10.1016/j.ijmecsci.2017.12.013Suche in Google Scholar

[35] Brischetto S. Exact elasticity solution for natural frequencies of functionally graded simply-supported structures. CMES - Comput Model Eng Sci. 2013;95:391–430. Suche in Google Scholar

[36] Brischetto S, Torre R. 3D hygro-elastic shell model for the analysis of composite and sandwichstructures. Compos Struct. 2022;285:115162. 10.1016/j.compstruct.2021.115162Suche in Google Scholar

[37] Brischetto S, Torre R, Cesare D. Three dimensional coupling between elastic and thermal fields in the static analysis of multilayered composite shells. CMES Comput Model Eng Sci. 2023;136:2551–94. 10.32604/cmes.2023.026312Suche in Google Scholar

[38] Brischetto S, Cesare D, Torre R. A layer-wise coupled thermo-elastic shell model for three-dimensional stress analysis of functionally graded material structures. Technologies. 2023;11:35. 10.3390/technologies11020035Suche in Google Scholar

[39] Brischetto S, Cesare D. Hygro-elastic coupling in a 3D exact shell model for bending analysis of layered composite structures. J Compos Sci. 2023;7:1–27. 10.3390/jcs7050183Suche in Google Scholar

[40] Özişik MN. Heat conduction. New York (NY), USA: John Wiley & Sons, Inc; 1993. Suche in Google Scholar

[41] Povstenko Y. Fractional thermoelasticity. Cham, Switzerland: Springer International Publishing; 2015. 10.1007/978-3-319-15335-3Suche in Google Scholar

[42] Moon P, Spencer DE. Field Theory Handbook. Including Coordinate Systems, Differential Equations and Their Solutions. Berlin, Germany: Springer-Verlag; 1988. 10.1007/978-3-642-83243-7Suche in Google Scholar

[43] Mikhailov MD, Özişik MN. Unified analysis and solutions of heat and mass diffusion. New York (NY), USA: Dover Publications Inc.; 1984. Suche in Google Scholar

[44] Boyce WE, DiPrima RC. Elementary differential equations and boundary value problems. New York (NY), USA: John Wiley & Sons, Ltd.; 2001. Suche in Google Scholar

[45] Open document. Systems of differential equations. [Internet]. http://www.math.utah.edu/gustafso/. [Accessed on 30 May 2013].Suche in Google Scholar

[46] Reddy JN, Cheng ZQ. Three-dimensional thermomechanical deformations of functionally graded rectangular plates. Eur J Mech/A Solids. 2001;20:841–55. 10.1016/S0997-7538(01)01174-3Suche in Google Scholar

Received: 2023-07-12

Accepted: 2023-08-27

Published Online: 2023-10-03

This work is licensed under the Creative Commons Attribution 4.0 International License.

Artikel in diesem Heft

https://doi.org/10.1515/cls-2022-0216

Schlagwörter für diesen Artikel

three-dimensional exact model; coupled hygro-elastic shell model; 3D Fick diffusion law; functionally graded materials; moisture content

Creative Commons

BY 4.0