MD-based study on the deformation process of engineered Ni–Al core–shell nanowires: Toward an understanding underlying deformation mechanisms

1 Introduction

In light of high thermal and electrical conductivity, strength–weight ratio, Young’s modulus, and thermal stability, core–shell nanostructures have been of great interest in aerospace industries and stable chemical and medical catalysts in recent years [1]. To construct such nanostructures, a core is situated in a certain position, with the shell being deposited on the core [1]. The core–shell interface in such nanostructures is crucial, as with nanocomposites, since its strength strongly affects the properties of the nanostructure [2,3,4,5,6]. Research has recently shown that molecular dynamics (MD) is an efficient method to identify the nature of the interface and its effects on the properties of nanowires, composites, and core–shell structures. It also allows for effectively monitoring crystalline defects in microstructures at an atomic scale [7,8]. As important defects in crystalline structures, dislocations, stacking faults, and twins are the major explanations for plastic deformation within metals under mechanical loading [9,10]. Several factors, for example, strain rate, sample geometry, loading type, and temperature, are involved in crystalline defects [11,12]. However, the nature of the interface is a crucial determinant of mechanical behavior in core–shell nanostructures. Ke and Mastorakos [13] and Abdulkareem-Alsultan et al. [14] studied semi-coherent and coherent Cu/Ni and Au/Ni core–shell nanostructures. It was found that misfit dislocations in structures with a semi-coherent interface were the major cause of dislocation emission in the shell structure. However, the semi-coherent interface could be an obstacle to the transmission of dislocations from the shell into the core. A review of the literature indicates that core–shell structures are not limited to metals. Shang et al. [15] and Alsultan et al. [16] studied an Al₂O₃ ceramic shell for an Al core. Despite the incoherent core–shell interface, it was found that the O atoms of the ceramic shell and their bonding to the Al atoms of the core created a diffusional interface that enhanced the ductility of the Al₂O₃/Al core–shell structure. It should be noted that diffusion is very sensitive to temperature and time. Lee et al. [17] and Lim et al. [18] investigated Cu/Ag core–shell nanoparticles and observed that the diffusion of atoms in the core–shell interface was substantially dependent on the core and shell melting points. Samsonov et al. [19] discussed this phenomenon in detail. They found that the interface of a core–shell structure was destabilized for synthetic reasons at low temperatures, while interface instability at high temperatures arose from thermodynamic factors.

The shell structure can be not only crystalline structures (metals) but also non-crystalline structures (ceramics), as Pourboghrat et al. [20] and Feng et al. [21] reported for an Si–Au core–shell structure. They showed that an Si shell with an amorphous structure could enhance the yield strength of the system above that of the Au nanowire. However, the self-healing of the core–shell structure declined under cyclic loads. This was attributed to the change in the crystalline defects of the core from twins into perfect dislocations.

Apart from the influence of the shell microstructure on the mechanical properties of a shell–core structure, researchers [22,23,24,25] reported that the shell thickness would strongly affect the mechanical properties. They implemented tensile tests on Cu/Ag core–shell nanostructures of different core and shell thicknesses. It was observed that no certain thickness could be applied to improve all the mechanical properties, and the optimal yield strength, ultimate tensile strength, and elasticity modulus would occur at different thicknesses. Ozdemir Kart et al. [26] and Cherukara et al. [27] evaluated Al–Cu core–shell structures and observed that dislocation tangling in the core–shell interface was the main parameter enhancing mechanical properties.

In addition to the formation of crystalline defects, the density of crystalline defects is also very important during the stages of plastic deformation. For example, the stacking fault region can be removed or expanded. Also, dislocations can slip and facilitate the plastic deformation acceleration [28,29,30,31,32,33]. As mentioned, the plastic deformation of core–shell structures is significantly dependent on the interface area [34,35,36]. Also, the presence of impurities or voids can affect thermal conductivity, mechanical properties, and other physical or mechanical properties of core–shell structures [37,38].

According to previous studies [39,40,41,42,43,44,45], magnetic properties, structural stability at high temperatures, and mechanical properties of core–shell structures are strongly dependent on the crystal defects in the microstructures of these materials. Therefore, the identification of crystal defects and the modification of the microstructure can determine the mentioned properties. Some of the crystal defects can be removed during the production process, and some can be removed after production by processes such as annealing.

Since Ni has high thermal resistance, Ni–Al core–shell nanostructures are considered to be heat-resistant nanostructures. Researchers [26,46,47] recently studied the effects of heat on the stability of Ni–Al core–shell structures with different core and shell thicknesses by LAMMPS software. They analyzed the crystalline structure and diffusion layer of the annealed core–shell microstructure at different temperatures. However, a review of the literature indicates that temperature has rarely been examined as a parameter with substantial effects on the mechanical properties and deformation mechanisms of such structures. The present work subjected Ni–Al core–shell samples to the uniaxial tensile test at 300 K using MD. Then, the samples were subjected to tests at the same strain rate and different temperatures to evaluate the role of the temperature in the deformation mechanism. The remainder of the study is organized as follows: Section 2 describes the MD simulations and sample development; Section 3 provides and discusses the results at different temperatures; and Section 4 concludes the study.

2 MD setup

As previous studies investigated the effects of the core and shell thicknesses, this study assumed the same core and shell thickness. The core–shell nanowire samples consisted of a cylindrical Al core with a diameter of 5 nm and a length of 10 surrounded by an Ni shell with a thickness of 5 nm and a length of 10 nm was assumed, as shown in Figure 1. The samples and tensile test simulations were implemented using the LAMMPS code [46]. The interactions of Al–Al, Ni–Ni, and Ni–Al particles in the force and energy fields were simulated using an EAM potential function [23]. This function has been demonstrated to be very efficient in the mechanical evaluation of Al–Ni systems through the identification and examination of dislocations and defect areas in the layout [21,27]. This study calculated initial velocities using the Maxwell–Boltzmann distribution at the given temperatures. Furthermore, the velocity Verlet algorithm was employed to integrate the motion equations [24,47].

Figure 1

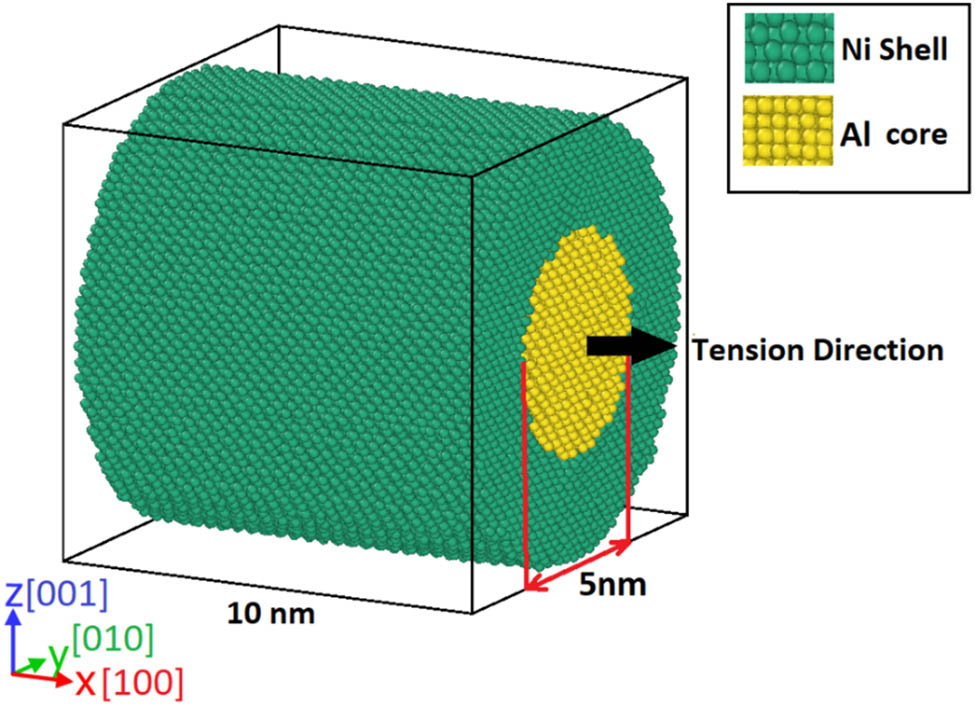
Ni–Al core–shell nanowire construction step. Taken from OVITO software.

It was required to relax the samples before the tensile test. The samples were relaxed using the NPT ensemble at ambient temperature for 100 ps using a time step of 1 fs.

As seen in Figure 2, the values of the total energy of the system tend to the steady-state trend showing our method works successfully during the equilibration stage. Another parameter, which can help us to make sure about simulation protocols, is monitoring temperature fluctuations. As shown in Figure 3, temperature was successfully kept constant at 300 K during relaxation before applying uniaxial tensile test.

Figure 2

Total energy fluctuations during relaxation stage.

Figure 3

Temperature fluctuation during relaxation stage.

Periodic boundary conditions were applied in all three directions. Once they had been relaxed, the samples in accordance with the literature were stretched at a constant engineering strain of 5 × 10⁸ s⁻¹ in the x-direction [4,25]. The pressure was controlled to be zero in the y- and z-directions to implement uniaxial tensile testing.

The dislocations were identified via the dislocation extraction algorithm (DXA) developed by Stukowski [5]. To measure the stress concentration in the crystalline defects and Ni–Al interface, von Mises stress analysis was used. The common neighbor analysis (CNA) was adopted to differentiate the structures. The images were obtained and analyzed using OVITO [5].

As mentioned, the CNA was used to characterize the local structural environment of atoms within the crystal structures. The structural types are encoded as integer values, which are 1 for face-centered cubic (FCC); 2 for hexagonal close-packed (HCP); 3 for body-centric cubic; 4 for icosahedral structures; and 5 for free surfaces, sample edges, and other unknown structures. In this technique, a threshold distance criterion is used to determine whether a pair of atoms is bonded or not. The input cutoff radius for any crystal lattice can be chosen using the following equations [30,31]:

In these equations, a 0 stands for the lattice parameter of the unit cell.

Centro-symmetry parameter (CSP) was defined for the specified atom i as follows:

where N is the number of nearest neighbors of atom i equal to 12 for the FCC metals. Also, R ⃗ i and R ⃗ i + N / 2 are vectors from the central atom to a particular pair of nearest neighbors in the crystal lattice. This analysis helped us to study crystalline defects.

3 Results and discussion

In this section, we aim to study the mechanical behavior of Ni–Al core–shell structures. This step is followed by a quantitative and qualitative analysis of samples to evaluate microstructural changes during the mechanical tests. Subsequently, CNA and DXA analysis tools were utilized to explore the main sintering mechanisms governing the process.

3.1 Mechanical properties of Ni–Al core–shell nanowires

To investigate the mechanical properties, the Ni–Al core–shell sample was subjected to a uniaxial tensile test at 300 K, as shown in Figure 4. According to Figure 4, the length of sample increases as strain increased, with the sample showing ductile deformation behavior. Figure 5 plots the tensile stress–strain curve of the sample. As can be seen, the elastic region was almost linear, and the stress declined after the yielding of the sample. In the plastic region, the stress was independent of the strain. The CNA results are shown for different points in the elastic and plastic regions. The core and shell systems had a completely FCC structure below the yield stress. This structure is shown by green atoms. At the strain of 0.05, a step appeared in the elastic region; the first defect in the layout of atoms occurred, with FCC changing into HCP. These areas are represented by red atoms. As the strain increased to the plastic level, more defect areas appeared in the sample. Defects are very common in FCC metals due to the low stacking fault energy (SFE) [6,28]. The sample underwent completely ductile deformation – no brittle fracture was detected. The plastic deformation process is discussed in detail below. Table 1 provides the yield stress and elasticity modulus of the sample. It is worth mentioning that the linear slope of the stress–strain curve was assumed to represent the elasticity modulus.

Figure 4

Illustration of uniaxial tension steps of Ni–Al core–shell nanowire at different strains: (a) ε = 0, (b) ε = 0.02, (c) ε = 0.05, (d) ε = 0.08, (e) ε = 0.2, and (f) ε = 0.3.

Figure 5

Evaluation of crystalline structural changes before and after yielding point.

Table 1

Yield strength and elastic modulus of the sample obtained in the present work

Sample	Yield strength (GPa)	Elastic modulus (GPa)
Ni–Al core–shell	3.57	67

3.2 Plastic deformation of Ni–Al core–shell nanowires and underlying mechanisms

Research has shown that the plastic deformation of single-crystal FCC structures arises from active slip systems based on edge and screw dislocations. To further evaluate this phenomenon, Figure 6 shows different plastic deformation stages of the sample. As can be seen, edge dislocations occurred in the Ni–Al interface before plastic deformation (Figure 6a). As the stress rose above the plastic limit, defects appeared between the dislocations within Al, as shown in Figure 6b. At larger strains, edge and screw dislocations were emitted into Ni, as shown in Figure 6c and d. Figure 6e–h illustrates the process from another angle. Tian et al. [29] argued that SFE was lower in Al than in Ni. Therefore, defects were expected to form in Al and be emitted into Ni. As a result, the plastic deformation of Ni–Al nanowires can be concluded to stem from dislocation slips. As such, dislocations nucleated in the Ni–Al interface. Research has shown that dislocation would nucleate from free surfaces, grain boundaries, and impurities [30,31,32]. This is mainly explained by the stress concentration in these areas and reduced SFE [33]. To further evaluate the cause of dislocations in the Ni–Al interface, the stress distribution of the interface was analyzed. According to Figure 7a, the atoms in the interface had larger stresses than the atoms in the core and those at larger distances from the interface. Based on Figure 7b, the interface is a potential candidate for the appearance of dislocations and crystalline defects. Earlier works reported that dislocations had a lower energy barrier in areas with stress concentration, which facilitated dislocation emission [16,34,35]. The stress concentration in the interface arises from a lattice mismatch. For a lattice constant of 3.499 in Ni and 4.056 in Al, the lattice mismatch is obtained to be 15%, which is very large. Hence, the interface is assumed to be semi-coherent, and a high density of dislocations is expected to appear in the interface [37,38]. This is illustrated in Figure 7b. Once the deformation mechanism of the Ni–Al core–shell nanostructure had been evaluated at ambient temperature, the effects of the temperature on dislocations and defect areas as important determinants of plastic deformation in the nanostructure were explored.

Figure 6

DXA analysis results presenting the dislocation density and stacking fault areas in Ni–Al core–shell nanowire at the different strains. (a) ε = 0, (b) ε = 0.08, (c) ε = 0.15, (d) ε = 0.25, and (e–h) the other views at the same strains.

Figure 7

The interfacial region of Ni/Al nanowire sample. (a) Stress concentration shown by von Mises stress distribution map and (b) perfect dislocations detected by DXA analysis.

Figure 8a and b depicts the crystalline structure of the samples at 300 and 600 K, respectively. The green atoms represent FCC areas, while the red ones stand for HCP in the stacking fault structure. Figure 8c and d compares the dislocation distributions at 300 and 600 K, respectively. As can be seen, an increase in the temperature reduced dislocation forest areas. As the temperature rose, many dislocations having the opposite sign eliminated each other, diminishing dislocation entanglement. The red circles represent the entangled dislocations. As can be seen, dislocation recovery was facilitated at a higher temperature, increasing the mobility of the remaining dislocations, and reducing the mechanical properties.

Figure 8

CSP analysis and comparison of crystalline defects at the temperatures of 300 and 600 K: (a and b) the stacking fault areas and (c and d) dislocation entanglements.

4 Conclusion

This study evaluated the mechanical properties and plastic deformation mechanism of Ni/Al core–shell structures using MD. It was observed that the crystalline structure remained perfect in the elastic deformation, whereas stacking faults and dislocations nucleated from the Ni–Al interface above the yield point. Therefore, the interface became a source of dislocation emission due to stress concentration. The crystalline defect density increased as the stress increased. The dislocations were entangled as they increased in number, leading to dislocation entanglement areas that would impede the movement of dislocations and enhance mechanical properties. A rise in the temperature from 300 to 600 K decreased dislocation entanglement areas due to the activation of dislocation recovery mechanisms, diminishing the mechanical properties at higher temperatures. For the next step, the aim will be to study the effects of pre-existing crystalline defects on the mechanical properties of such core–shell structures. For this purpose, importing voids and inclusions inside the shell region, several defect concentrations will be systematically analyzed.