Abstract
The paper analyzes the effect of positive trend inflation in the framework of a standard New Keynesian model with Calvo price setting and capital accumulation. We are building on the work of Carlstrom and Fuerst (Carlstrom, Charles T., and Timothy S. Fuerst. 2005. “Investment and Interest Rate Policy: A Discrete-Time Analysis.” Journal of Economic Theory 123: 4–20.) and Ascari and Ropele (Ascari, Guido, and Tiziano Ropele. 2007. “Optimal Monetary Policy under Low Trend Inflation.” Journal of Monetary Economics 54 (8): 2568–2583., Ascari, Guido, and Tiziano Ropele. 2009. “Trend Inflation, Taylor Principle, and Indeterminacy.” Journal of Money, Credit and Banking 48 (1): 1557–1584.) who separately considered effects of capital accumulation and trend inflation in a similar context. It is shown that the simultaneous presence of positive trend inflation and capital accumulation greatly affect the determinacy property of equilibrium under this setup. Namely, in the presence of positive trend inflation the determinacy region shrinks, and it is virtually impossible to produce a determinate equilibrium with the Taylor-type rule given a steady state of inflation of more than 5%. Even for a moderate value of 2.5%, the design of the rule that ensures the uniqueness of the equilibrium requires detailed knowledge of the parameters of an economy. We also show that for a large set of plausible parameters, the standard Taylor rule leads to indeterminacy. Alternative monetary policy rules such as interest rate smoothing, output growth targeting and price level targeting are also analyzed. It is shown that the latter improves the determinacy of the model solution, and the best way to guarantee the determinate equilibrium is to use price level targeting in the policy rule.
Acknowledgments
We are grateful to Yuriy Gorodnichenko, Konstantin Styrin and Oleg Zamulin for helpful comments and suggestions. We would also like to thank two anonymous referees, the editor Luisa Lambertini and seminar participants at New Economic School, European Economic Association meeting 2010, Asian Meeting of Econometric Society 2011 and Econometric Society Australasian meeting 2011.
Appendix
New-Keynesian Phillips curve
Given the aggregate production function the demand for the specific good Yi,t is given by
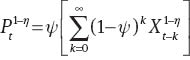
where Xt stands for the reset price. Let
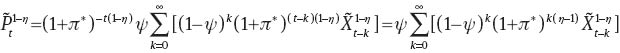
or equivalently in logs:
The reset price Xt is the solution of the following maximization problem:
subject to the sequence of demand constraints:
where C(Yt,i)=MCtYt is a real cost function of the firm i and MCt are real marginal costs which are the same for all firms due to constant returns to scale property of the production.
Solution of the problem is given by
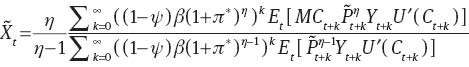
In logs
Therefore
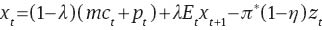
and
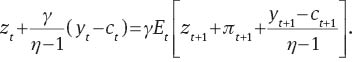
From equation (47) one gets
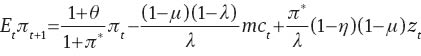
where (51) is a New-Keynesian Phillips curve, which reduces to the standard one by setting π*=0.
Steady-state values
From (46) one can get
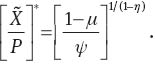
Equation (48) leads to
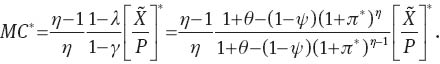
The output-capital ratio can be reduced from the demand for capital equation:
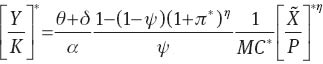
while the consumption-capital ratio is given by
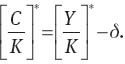
Equilibrium system
The equilibrium is given by a system of 10 equations with 10 variables
Production function
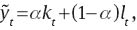
Relative price dispersion:
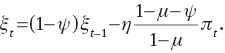
Capital accumulation equation
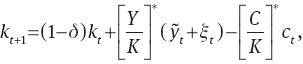
Labor demand
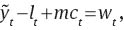
Labor supply
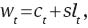
Demand for capital
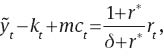
Euler equation
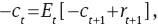
Phillips curve
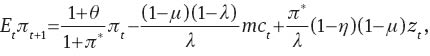
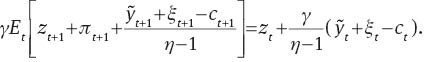
Monetary policy rule and Fisher’s parity
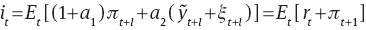
or
The system can be reduced to six intertemporal equations with two predetermined and four endogenous variables. Therefore, unique equilibrium requires that four eigenvalues of the resulting system be greater than one in absolute value. If the number of such eigenvalues is <4 then the equilibrium is indeterminant.
Matrix notation
Let X1=[k, c, r, π, z, ξ]′ and X2=[y, l, w, mc]′.
J1X1=J2X2
where
The system of intertemporal equations can be written as Et[J4X1t+1+J5X2t+1]= J6X1t+J7X2t, where
where
Let
where
References
Ascari, Guido. 2004. “Staggered Prices and Trend Inflation: Some Nuisances.” Review of Economic Dynamics 7: 642–667.10.1016/j.red.2004.01.002Suche in Google Scholar
Ascari, Guido, and Tiziano Ropele. 2007. “Optimal Monetary Policy under Low Trend Inflation.” Journal of Monetary Economics 54 (8): 2568–2583.10.1016/j.jmoneco.2007.06.024Suche in Google Scholar
Ascari, Guido, and Tiziano Ropele. 2009. “Trend Inflation, Taylor Principle, and Indeterminacy.” Journal of Money, Credit and Banking 48 (1): 1557–1584.10.1111/j.1538-4616.2009.00272.xSuche in Google Scholar
Bils, Mark, and Peter J. Klenow. 2004. “Some Evidence on the Importance of Sticky Prices.” Journal of Political Economy 112 (5): 947–985.10.1086/422559Suche in Google Scholar
Calvo, Guillermo. 1983. “Staggered Prices in a Utility-Maximizing Framework.” Journal of Monetary Economics 12 (3): 383–398.10.1016/0304-3932(83)90060-0Suche in Google Scholar
Carlstrom, Charles T., and Timothy S. Fuerst. 2005. “Investment and Interest Rate Policy: A Discrete-Time Analysis.” Journal of Economic Theory 123: 4–20.10.1016/j.jet.2004.05.002Suche in Google Scholar
Christiano, Lawrence J., Martin Eichenbaum, and Charles Evans. 2005. “Nominal Rigidities and the Dynamic Effects of a Shock to Monetary Policy.” Journal of Political Economy 113 (1): 1–45.10.1086/426038Suche in Google Scholar
Cogley, Timothy, and Argia M. Sbordone. 2008. “Trend Inflation, Indexation and Inflation Persistence in the New Keynesian Phillips Curve.” American Economic Review 98 (5): 2101–2126.10.1257/aer.98.5.2101Suche in Google Scholar
Coibion, Olivier, and Yuriy Gorodnichenko. 2011. “Monetary Policy, Trend Inflation and the Great Moderation: An Alternative Interpretation.” American Economic Review 101 (1): 341–370.10.1257/aer.101.1.341Suche in Google Scholar
Dupor, Bill. 2001. “Investment and Interest Rate Policy.” Journal of Economic Theory 98: 81–113.10.1006/jeth.2000.2765Suche in Google Scholar
Gali, Jordi. 2008. Monetary Policy, Inflation and the Business Cycle: An Introduction to the New Keynesian Framework. Princeton NJ: Princeton University Press.Suche in Google Scholar
Gorodnichenko, Yuriy, and Matthew D. Shapiro. 2007. “Monetary Policy when Potential Output is Uncertain: Understanding the Growth Gamble of the 1990s.” Journal of Monetary Economics 54 (4): 1132–1162.10.1016/j.jmoneco.2006.03.004Suche in Google Scholar
Hansen, Gary D. 1985. “Indivisible Labor and the Business Cycle.” Journal of Monetary Economics 16 (3): 309–327.10.1016/0304-3932(85)90039-XSuche in Google Scholar
Hornstein, Andreas, and Alexander L. Wolman. 2005. “Trend Inflation, Firm-Specific Capital, and Sticky Prices.” Federal Reserve Bank of Richmond Economic Quarterly 91 (4): 57–83.Suche in Google Scholar
Nakamura, Emi, and Jon Steinsson. 2008. “Five Facts about Prices: A Reevaluation of Menu Cost Models.” The Quarterly Journal of Economics 123 (4): 1415–1464.10.1162/qjec.2008.123.4.1415Suche in Google Scholar
Schmitt-Grohe, Stephanie, and Martin Uribe. 2007. “Optimal Simple and Implementable Monetary and Fiscal Rules.” Journal of Monetary Economics 54 (6): 1702–1725.10.1016/j.jmoneco.2006.07.002Suche in Google Scholar
Smets, Frank, and Raf Wouters. 2003. “An Estimated Dynamic Stochastic General Equilibrium Model of the Euro Area.” Journal of the European Economic Association 1 (5): 1123–1175.10.1162/154247603770383415Suche in Google Scholar
Walsh, Carl E. 2003. “Speed Limit Policies: The Output Gap and Optimal Monetary Policies.” American Economic Review 93 (1): 265–278.10.1257/000282803321455278Suche in Google Scholar
Woodford, Michael. 2003. Interest and Prices: Foundations of a Theory of Monetary Policy. Princeton NJ: Princeton University Press.10.1515/9781400830169Suche in Google Scholar
Yun, Tack. 2003. “Nominal Price Rigidity, Money Supply Endogeneity, and Business Cycles.” Journal of Monetary Economics 37 (2–3): 345–370.Suche in Google Scholar
©2015 by De Gruyter
Artikel in diesem Heft
- Frontmatter
- Advances
- Consumption composition and macroeconomic dynamics
- Evaluating linear approximations in a two-country model with occasionally binding borrowing constraints
- Contributions
- The bank lending channel and monetary policy rules for Eurozone banks: further extensions
- Investment lags and macroeconomic dynamics
- The zero lower bound: frequency, duration, and numerical convergence
- What drives endogenous growth in the United States?
- Environmental policy and economic growth: the macroeconomic implications of the health effect
- US household deleveraging following the Great Recession – a model-based estimate of equilibrium debt
- Price-level instability and international monetary policy coordination
- Households forming macroeconomic expectations: inattentive behavior with social learning
- Topics
- Complementarity and transition to modern economic growth
- Trend inflation and monetary policy rules: determinacy analysis in New Keynesian model with capital accumulation
- Discussions
- Preface to “Reflections on Macroeconometric Modeling” by Ray C. Fair
- Reflections on macroeconometric modeling
Artikel in diesem Heft
- Frontmatter
- Advances
- Consumption composition and macroeconomic dynamics
- Evaluating linear approximations in a two-country model with occasionally binding borrowing constraints
- Contributions
- The bank lending channel and monetary policy rules for Eurozone banks: further extensions
- Investment lags and macroeconomic dynamics
- The zero lower bound: frequency, duration, and numerical convergence
- What drives endogenous growth in the United States?
- Environmental policy and economic growth: the macroeconomic implications of the health effect
- US household deleveraging following the Great Recession – a model-based estimate of equilibrium debt
- Price-level instability and international monetary policy coordination
- Households forming macroeconomic expectations: inattentive behavior with social learning
- Topics
- Complementarity and transition to modern economic growth
- Trend inflation and monetary policy rules: determinacy analysis in New Keynesian model with capital accumulation
- Discussions
- Preface to “Reflections on Macroeconometric Modeling” by Ray C. Fair
- Reflections on macroeconometric modeling

