Abstract
Photometric study and light curve modeling for the systems V0876 Lyr, V3660 Oph, and V0988 Mon were carried out by means of their first charge-coupled device observations and the Wilson–Devinney code based on model atmospheres by Kurucz (1993. In: Milone, E. (Ed.), Light curve modeling of eclipsing binary stars. New York: Springer-Verlag. p. 93). The accepted models reveal physical parameters that show that all the primary components of the studied systems are more massive and hotter than the secondary ones. The systems V0876 Lyr and V0988 Mon were classified as over contact, with mass ratios of 0.8940 and 0.3904, respectively, while the system V366Oph was classified as detached, with a mass ratio of 0.1181. The evolutionary state of the system components was investigated, and their spectral types were adopted. Both components of the system V0876 Lyr and secondary components of the systems V3660 Oph and V0988 Mon show lower radii and luminosities than expected for Zero Age Main Sequence (ZAMS). Secondary components of the system, V3660 Oph and V0988 Mon, deviated from ZAMS and the Terminal-age Main Sequence (TAMS) with a higher radius and luminosity than expected for ZAMS and TAMS.
1 Introduction
Physical properties and geometrical configurations are the main factors used to classify eclipsing binary systems. Roche geometry specifies the binary component shapes according to the degree of filling of the Roche lobe. A unique photometric and spectroscopic observation of the eclipsing binary is the target of light curve modeling and orbital solutions, which reveal essential characteristics of stars, such as their masses, radii, and luminosities. The stellar structure and evolutionary status of eclipsing binary components can be studied by means of the estimated physical parameters from their light curve modeling and orbital solutions. Since the systems V0876 Lyr, V3660 Oph, and V0988 Mon were discovered some years ago, the current study is the first orbital solution for them, which is considered an important source of their fundamental stellar properties and information. Based on the degree of filling the Roche lobe, the morphologies of the binary components are defined and classified according to Roche geometry (Prša 2019). So their classifications are important, and their first physical and absolute parameters are needed to be estimated in order to investigate the system evolution state (Yilmaz et al., 2017).
The structure of the study is as follows: Section 2 deals with the basic information about the studied systems and the light minima derived from their observations; Section 3 is devoted to the light curve modeling. In Section 4, we discuss the evolutionary status of the studied systems. A summary of the results and conclusion are outlined in Section 5.
2 Observations
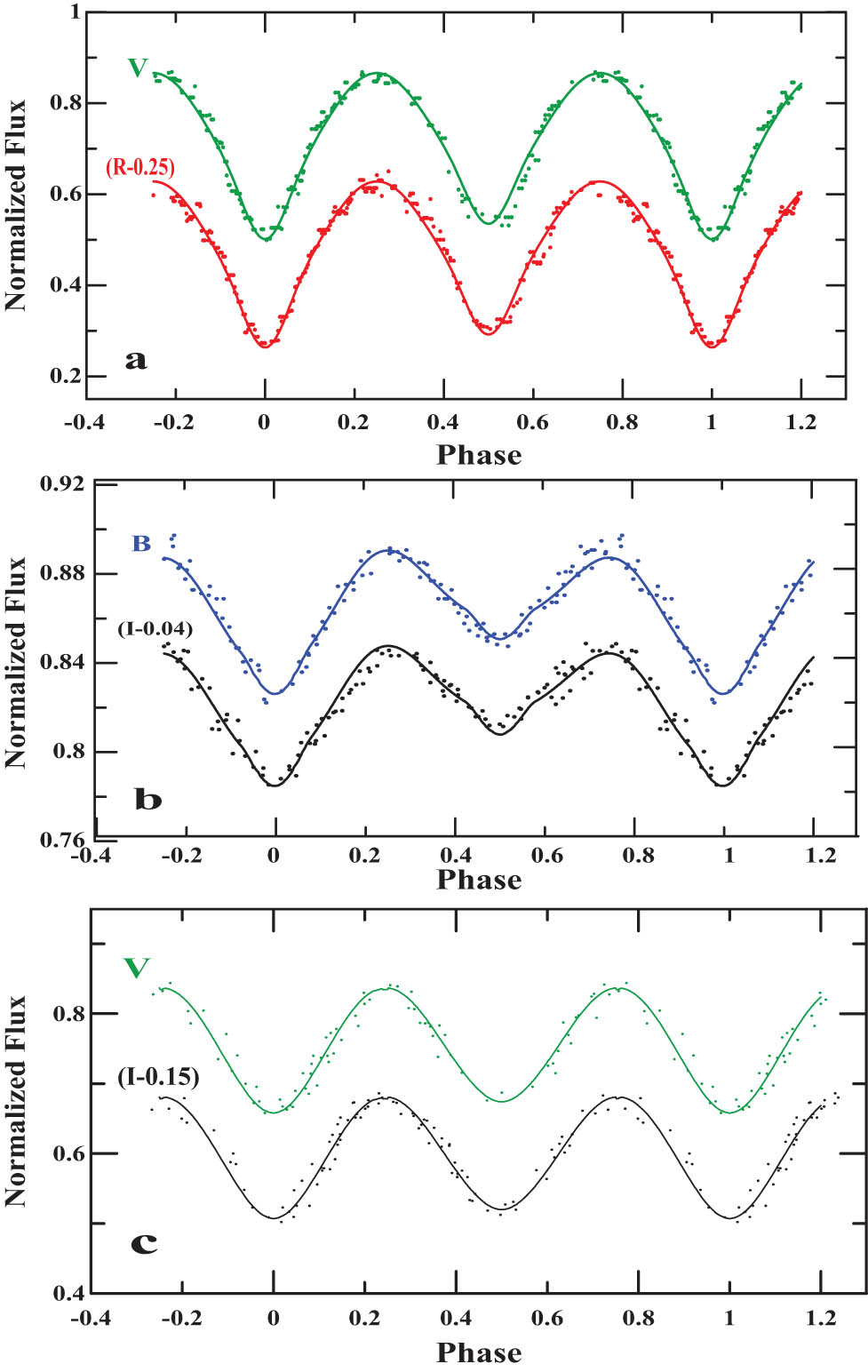
The system V0876 Lyr (P = 0d.39781) was reported as a W UMa system on May 12, 2015, in the field of view of KIC 2835289 by Gazeas (2017). The first complete light curves were observed in visual and red filters (Bessel) pass bands. The ephemeris employed by Gazeas (2017), represented by Eq. (1) in Table 1, was utilized to determine each phase of all observational data. The variability of the systems V3660 Oph (P = 0d.68932) and V0988 Mon (P = 0d.44408) was discovered for the first time by Liakos and Niarchos (2010, 2011) during their observations for the systems V456 Oph and HO Mon, respectively. The systems V3660 Oph and V0988 Mon were classified as Beta Lyrae types and W UMa types, respectively. Observations of the system V3660 Oph were carried out from 2007 to 2009 in BI (Bessel) pass bands; the stars GSC 1025-01618 and GSC 1025-00331 were used as comparison and check stars, respectively. The system V0988 Mon was observed during January–March 2011 using the stars USNO-A2.0 0900-04404074 and USNO-A2.0 0900-04404538 as comparison and check stars, respectively. All the charge-coupled device (CCD) observations of the three systems were carried out at the Gerostathopoulion Observatory of the University of Athens using a 40 cm Cassegrain telescope equipped with ST-8XMEi and ST-10XME CCD cameras and a BVRI Bessell photometric filters. The second and third equations listed in Table 1, which represented the ephemeris adopted by Liakos and Niarchos (2010, 2011), were used to calculate the individual phases of all observational data of the systems V3660 Oph and V0988 Mon, respectively. We searched for additional light curves from other sources to add to our photometric study, but we could not, because most of the databases did not include the studied systems in their programs, and the existing data are not suitable for photometric investigations. Using the Minima V2.3 Package (Nelson 2009), we determined the times of minima of eclipsing binary light curves. The program uses different algorithms, depending on the accuracy of the observation. As the observed light curves of the studied systems show sparseness around the minima and maxima, we applied the Fourier fit algorithm of the Minima V2.3 Package (Nelson 2009), which fits a five-term Fourier series (of cosine terms) to the data; the time of minima is one of the parameters. A total of 19 new times of minima were estimated from the observed light curves of the studied systems. Table 2 shows the new minima for the systems together with their epochs (E) and observed Julian date-calculated Julian date (O-C), which are computed using ephemeris listed in Table 1 for each system. Figure 1a–c displays the observed light curves for the systems V0876 Lyr, V3660 Oph, and V0988 Mon, respectively.
Ephemeris equations for studied systems
| Star name | Ephemeris |
|---|---|
| V0876 Lyr | Min I = HJD 2457907.5396 + 0.39781 E |
| V3660 Oph | Min I = HJD 2455014.5046 + 0.68932 E |
| V0988 Mon | Min I = HJD 2455603.4260 + 0.44408 E |
Light minima for the systems V0876 Lyr (Gazeas 2017), V3660 Oph (Liakos and Niarchos 2010), and V0988 Mon (Liakos and Niarchos 2011)
| Star name | Heliocentric Julian Date | Error | Min | Filter | E | (O-C) |
|---|---|---|---|---|---|---|
| V0876 Lyr | 2457155.4836 | 0.0003 | I | V | −1,887 | −0.0949 |
| 2457155.4844 | 0.0002 | I | R | −1,887 | −0.0951 | |
| 2457156.4800 | 0.0005 | II | V | −1884.5 | −0.0958 | |
| 2457156.48001 | 0.0003 | II | R | −1884.5 | −0.0958 | |
| 2457157.4700 | 0.0003 | I | V | −1,882 | −0.1020 | |
| 2457157.4719 | 0.0002 | I | R | −1,882 | −0.1001 | |
| 2457158.4669 | 0.0004 | II | V | −1879.5 | −0.1014 | |
| 2457158.4658 | 0.0004 | II | R | −1879.5 | −0.1025 | |
| 2457159.4581 | 0.0004 | I | V | −1,877 | −0.1064 | |
| 2457159.4594 | 0.0003 | I | R | −1,877 | −0.1051 | |
| V3660 Oph | 2455013.4807 | 0.0130 | II | B | −1.5 | 0.0101 |
| 2455013.4738 | 0.0110 | II | I | −1.5 | 0.0032 | |
| 2455014.5242 | 0.0060 | I | B | 0 | 0.0196 | |
| 2455014.5085 | 0.0059 | I | I | 0 | 0.0039 | |
| 2455015.5435 | 0.0132 | II | I | 1.5 | 0.0049 | |
| V0988 Mon | 2455630.3165 | 0.0275 | II | V | 60.5 | 0.0237 |
| 2455630.2990 | 0.0016 | II | I | 60.5 | 0.0062 | |
| 2455632.2912 | 0.0006 | I | V | 65 | 0.0000 | |
| 2455632.2962 | 0.0007 | I | I | 65 | 0.0050 |

Observed light curves for the systems. (a) V0876 Lyr, (b) V3660 Oph, and (c) V0988 Mon.
To comprehend the structure evolution of W UMa systems, it is essential to examine both the light curve variation and the orbital period of these systems. A relationship between orbital period changes and light curve variations was predicted during the same cycle (Applegate 1992). A Fourier series fit was applied to the observed light curves to estimate the light level difference in magnitude between both maxima D max (Max I–Max II) and minima D min (Min I–Min II) of the observed light curves of the studied systems. The amplitudes (depths) of the primary A p and secondary A s minima for each observed light curve of the studied systems are also calculated and listed in Table 3, where
Light curve characteristic for the systems
| Star name | Filter | D max (mag) | D min (mag) | A p (mag) | A s (mag) |
|---|---|---|---|---|---|
| V0876 Lyr | V | 0.0183 ± 0.0008 | 0.0470 ± 0.0019 | 0.5367 ± 0.0219 | 0.4898 ± 0.0200 |
| R | −0.0053 ± 0.0002 | 0.0548 ± 0.0022 | 0.5169 ± 0.0211 | 0.4621 ± 0.0189 | |
| V3660 Oph | B | 0.0011 ± 0.0001 | 0.0313 ± 0.0013 | 0.0785 ± 0.0032 | 0.0472 ± 0.0019 |
| I | 0.0019 ± 0.0001 | 0.0422 ± 0.0017 | 0.0776 ± 0.0032 | 0.0354 ± 0.0015 | |
| V0988 Mon | V | 0.0059 ± 0.0002 | 0.0482 ± 0.0020 | 0.2736 ± 0.0112 | 0.2255 ± 0.0092 |
| I | −0.0138 ± 0.0006 | 0.0279 ± 0.0011 | 0.2547 ± 0.0103 | 0.2269 ± 0.0093 |
The estimated values shown in Table 3 can be used in conjunction with any future measurements to track the system’s light curve variation and study how predictions by Applegate (1992) can be applied to the studied systems.
3 Photometric solution
The two primary modules of the Wilson–Devinney (WD) binary star modeling algorithm provide a comprehensive package for simulating binary stars and their eclipses (Wilson et al., 2020). The light curve generation module generates synthetic light and radial velocity curves based on the entered initial five main parameters (temperature of system components T 1, T 2, orbit inclination i, mass ratio q, and surface potentials Ω1, Ω2) for the studied system to get the best fit; the differential corrections module handles differential corrections, performing final parameter adjustments of synthetic light curves (at minimum residuals), velocity curves, and eclipse timings by the least squares criterion. WD offers options for detailed reflection and nonlinear (logarithmic law) limb darkening, adjustment of spot parameters, and an optional provision for spots to drift over the surface. The temperatures of both eclipsing binaries components can likewise be estimated via absolute flux solutions under suitable circumstances. Photometric analysis on the observed light curves of the systems under study was performed using the WD binary star modeling code (Wilson et al., 2020), which is based on model atmospheres by Kurucz (1993). The color index (B-V) for the systems V3660 Oph and V0988 Mon and (J-H) for the system V0876 Lyr found in SIMBAD (http://simbad.u-strasbg.fr/simbad/) were utilized to calculate the temperature of the primary star (T 1). To determine the relevant temperature for each color index, the temperature relation of Tokunaga’s (2000) color index was applied. We examined each individual observation of the observed light curves in each band. For the convective envelopes (T eff < 7,500 K), gravity darkening (A 1, A 2) and bolometric albedo (g 1, g 2) exponents were used; therefore, we adopted A 1 = A 2 = 0.5 (Rucinski 1969) and g 1 = g 2 = 0.32 (Lucy 1967). The bolometric limb darkening was adopted using Van Hamme’s (1993) tables and the logarithmic law for extinction coefficients. According to fill factor (f), which is defined as 0 < f < 1, f = 0, and f < 0, respectively, the eclipsing binaries are categorized as contact, semi-detached, and detached binary (Vinod Prasad et al., 2013). The formula for the fill-out factor (f) is f = (Ωin − Ω1,2)/(Ωin − Ωout), where Ω1,2 denotes the surface potentials of stars 1 (primary) and 2 (secondary), respectively, while Ωin and Ωout are the inner and outer Lagrangian surface potentials. The surface potentials of the primary and secondary binaries in contact binaries are identical to the surface potential (Ω) of the common envelope for the binary system, meaning that Ω1 = Ω2 = Ω. If the primary and secondary components of semi-detached binaries fill their Roche lobe, then Ω1 = Ωin and Ω2 = Ωin, respectively, for detached binaries, Ω1,2 > Ωin.
Adjustable parameters through the light curve solution are: the temperature of the primary component (T 1) and secondary one (T 2), the orbital inclination (i), the mass ratio (q), the surface potentials (Ω1, Ω2), for Mode 3 in WD code, Ω1 = Ω2 = Ω, and the monochromatic luminosity of the primary star (L 1). The relative brightness of the secondary star was calculated from stellar atmosphere models. Because the studied systems have no reported radial velocity curves and do not have previous photometric studies, the q-search method can be used to determine the ideal starting points for the mass ratios (q) for the systems under study. This technique, based on a series of assumed mass ratios (q) with values using the adopted mode for each system, was used to accomplish the test solutions. The sum of the squared deviations for each value of assumed q for all systems under consideration Σ(O-C)2 is plotted in Figure 2a–c for each value of q for which a convergent solution has been achieved. The modeling procedure makes use of the computed minima of Σ(O-C)2 for the initial values of q for each system.

q-search of the binary systems: (a) V0876 Lyr. (b) V3660 Oph. (c) V0988 Mon.
The studied systems were discovered some years ago, and the used observations are the only CCD ground-based observations. Therefore, we searched on some databases (Kepler, TESS, ZTF, and Gaia Satellite DR3) to download any complete light curves to compare the results from many sources. Some of the databases included incomplete light curves with missing parts around the phases of minimum and maximum, which are not suitable for photometric analysis; in addition, the studied systems are not included in the observation area of some of the databases.
A set of photometric parameters was downloaded from Gaia satellite DR3 data (Gaia Collaboration et al., 2016, 2023) for the studied systems, such as apparent magnitudes in different passbands, color indexes to calculate the distances to each star, and component temperatures, which can be used as initial values in constructing the models and estimating physical and absolute parameters.
The light curves of the systems V0876 Lyr and V0988 Mon were used in the WD code’s Mode 3 (over contact mode), whereas those for the system V3660 Oph was used in the WD code's Mode 2 (detached).
The parameters that best describe the observed light curves were estimated through trials. After multiple iterations, the best photometric fitting was attained, demonstrating that all systems under study have hotter primary components than secondary ones. The constructed model for the system V3660 Oph includes a cool spot located on the surface of the secondary component. The parameters stated in Table 4 are revealed by the acceptable models, while Figure 3a–c shows the observed light curves of the systems alongside with the synthetic ones. The spectral types of system components are adopted and listed in Table 4 in accordance with the established models (Popper 1980).
Orbital solution parameters for the systems V0876 Lyr, V3660 Oph, and V0988 Mon
| Parameter | V0876 Lyr | V3660 Oph | V0988 Mon |
|---|---|---|---|
| i (°) | 73.42 ± 0.22 | 51.64 ± 0.25 | 54.50 ± 0.67 |
| g 1 = g 2 | 0.32 | 0.32 | 0.32 |
| A 1 = A 2 | 0.5 | 0.5 | 0.5 |
| q (M2/M1) | 0.8940 ± 0.0046 | 0.1181 ± 0.0008 | 0.3904 ± 0.0063 |
| Ω1 | Ω1 = Ω2 = 3.4166 ± 0.0083 | 2.1017 ± 0.0050 | Ω1 = Ω2 = 2.5161 ± 0.0136 |
| Ω2 | 2.1052 ± 0.0064 | ||
| T 1 (K) | 5372±4 | 7125 ± 15 | 5185 ± 17 |
| T 2 (K) | 5187±5 | 6316 ± 35 | 5035 ± 22 |
| Ωin | 3.5756 | 2.0131 | 2.6584 |
| Ωout | 3.0809 | 1.9364 | 2.4198 |
| r 1 pole | 0.3872 ± 0.0035 | 0.5010 ± 0.0037 | 0.4626 ± 0.0109 |
| r 1 side | 0.4116 ± 0.0046 | 0.5461 ± 0.0054 | 0.5020 ± 0.0157 |
| r 1 back | 0.4546 ± 0.0078 | 0.5605 ± 0.0061 | 0.5412 ± 0.0231 |
| r 2 pole | 0.3686 ± 0.0037 | 0.1739 | 0.3108 ± 0.0162 |
| r 2 side | 0.3908 ± 0.0048 | 0.1784 | 0.3292 ± 0.0209 |
| r 2 back | 0.4358 ± 0.0085 | 0.1929 | 0.3933 ± 0.0528 |
| Spot A of star 2 | |||
| Spot latitude | 90 ± 3.67 | ||
| Spot longitude | 190 ± 7.76 | ||
| Spot radius | 43.45 ± 1.152 | ||
| Temp. factor | 0.6921 ± 0.0023 | ||
| ∑ (O-C)2 | 0.07652 | 0.00231 | 0.24766 |
Observed and synthetic light curves for the systems: (a) V0876 Lyr. (b) V3660 Oph. (c) V0988 Mon.
Binnendijk (1970) subcategorizes the W UMa systems into A-type and W-type, which can be classified according to their spectral types as A9-F8 (A-type) and F7-M5 (W-type) groups. Eaton (1983) suggested that the presence (W-type) or absence (A-type) of magnetic spots can be used to distinguish between the two types of W UMa systems. According to the adopted spectral types, the systems V0876 Lyr and V0988 Mon can be classified as W UMa systems of W-type. The relation r 1 + r 2 = 0.75 should be met for contact systems, according to Kopal (1959); hence, using the mean values of r 1 and r 2 in Table 4 for the systems V0876 Lyr and V0988 Mon, we have r 1 + r 2 = 0.8162 for the system V0876 Lyr and 0.8463 for the system V0988 Mon. Based on the calculated values, the systems V0876 Lyr and V0988 Mon are contact binary with degrees of overcontact of f = 32.17 and 59.64%, respectively, and their components overfill their respective Roche lobes. A three-dimensional geometrical structure based on the computed parameters of the systems shown in Figure 4 was created using the software Binary Maker 3.03 (Bradstreet and Steelman 2002).
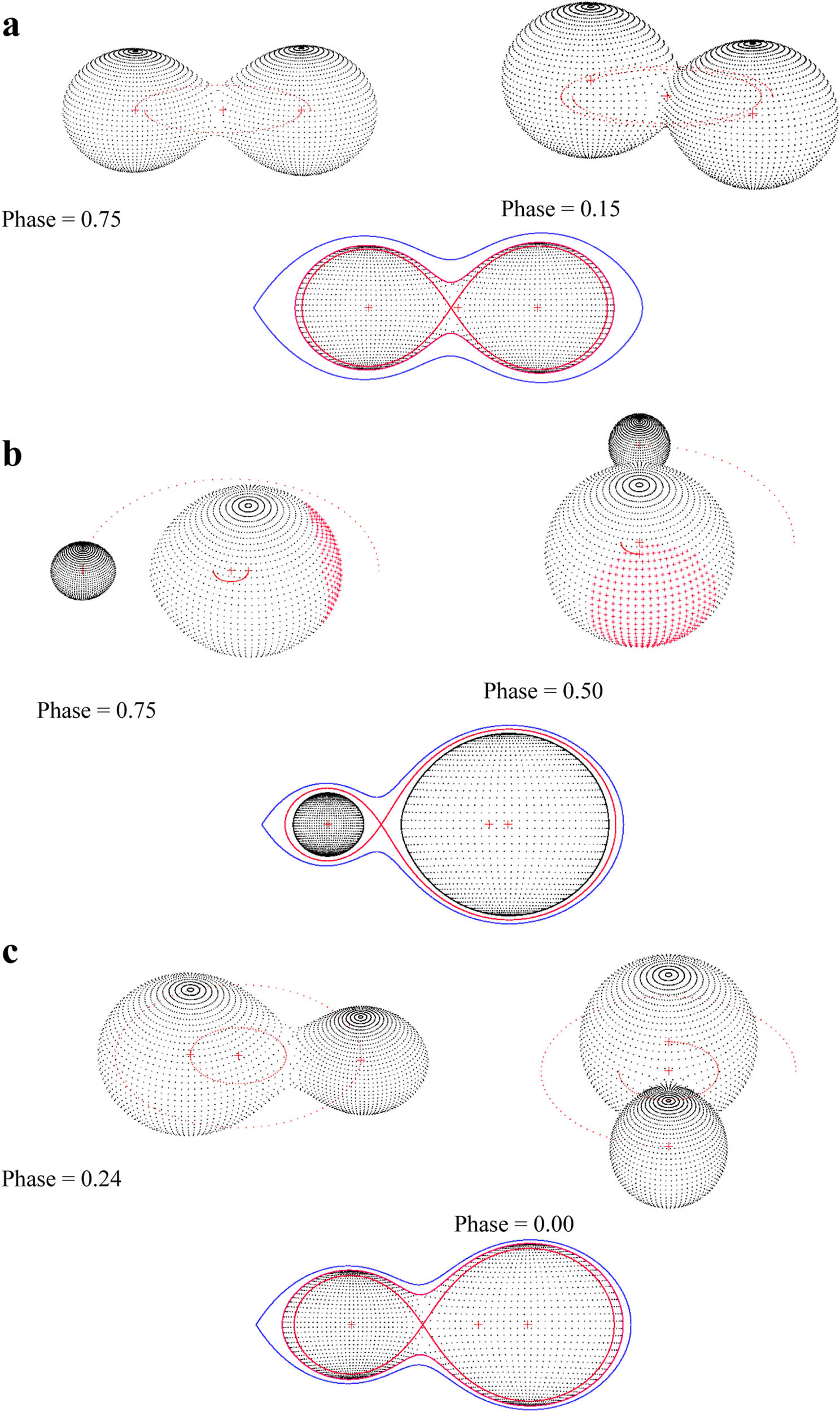
Geometric structure of the binary systems: (a) V0876 Lyr. (b) V3660 Oph. (c) V0988 Mon.
The distance (using the equation d = 10(m−M v+5)/5) was calculated using the photometric and absolute properties of each system, where m and M v are the apparent and absolute magnitudes, respectively. Current distance equation is a function of the absolute magnitude (M v), which is affected by estimated radius and luminosity by the adopted models (see Equations in Section 4). As radius and luminosity for both components of the system V876 Lyr (S1, S2) and secondary components (S2) of the system V366 Oph are lower than expected for Zero Age Main Sequence (ZAMS) stars, as seen in Figure 5a and b (Section 4), their estimated distances showed a reasonable difference than that calculated for the same systems by Gaia satellite DR3, while a comparable distance value to Gaia satellite DR3 for the system V988 Mon is estimated, and the primary component of this system showed a good fit for the luminosity and radius for ZAMS (Table 5). Assuming the Gaia distance, the luminosities would be lower by 34% and 35.8% for the systems V876 Lyr and V366 Oph, respectively, while for the system V988 Mon, it is 8.8% of the values in Table 5. Lower or higher radius and luminosity than expected for ZAMS can be attributed to an energy transfer from the primary to the secondary components of the systems through the shared convective envelope, as proposed by Lucy (1973), also the studied systems are detached and over contact systems, where the secondary star can temporarily be far out of thermal equilibrium, which may explain why it is so under luminous for its mass. Also calculations based on ground-based observations and our estimation of the mean system color index and interstellar reddening can be a little bit inaccurate because we do not know the phase at which the measurements were made, so we cannot be sure that they refer to the maximum light.

Positions of the components (S1, S2) of the systems V0876 Lyr, V3660 Oph, and V0988 Mon on the theoretical: (a) M–L diagram and (b) M–R diagram of Girardi et al., (2000) model.
Absolute physical parameters for the systems V0876 Lyr, V3660 Oph, and V0988 Mon
| Element | Star name | ||
|---|---|---|---|
| V0876 Lyr | V3660 Oph | V0988 Mon | |
| M 1 (M ⊙) | 1.3300 ± 0.0543 | 2.1870 ± 0.0893 | 1.4660 ± 0.0599 |
| M 2 (M ⊙) | 1.1900 ± 0.0486 | 0.2582 ± 0.0105 | 0.5722 ± 0.0234 |
| R 1 (R ⊙) | 0.9763 ± 0.0399 | 1.6345 ± 0.0667 | 1.1742 ± 0.0479 |
| R 2 (R ⊙) | 0.9309 ± 0.0380 | 0.5543 ± 0.0226 | 0.8057 ± 0.0329 |
| T 1 (T ⊙) | 0.9297 ± 0.0380 | 1.2331 ± 0.0503 | 0.8974 ± 0.0366 |
| T 2 (T ⊙) | 0.8977 ± 0.0367 | 1.0931 ± 0.0446 | 0.8714 ± 0.0356 |
| L 1 (L ⊙) | 0.7112 ± 0.0290 | 6.1688 ± 0.2518 | 0.8928 ± 0.0365 |
| L 2 (L ⊙) | 0.5620 ± 0.0229 | 0.4381 ± 0.0179 | 0.3738 ± 0.0153 |
| M bol_1 | 5.1200 ± 0.2090 | 2.7745 ± 0.1133 | 4.8731 ± 0.1989 |
| M bol_2 | 5.3756 ± 0.2195 | 5.6461 ± 0.2305 | 5.8184 ± 0.2375 |
| M V_1 | 5.4063 ± 0.2207 | 2.8613 ± 0.1168 | 5.2277 ± 0.2134 |
| M V_2 | 5.7294 ± 0.2339 | 5.7496 ± 0.2347 | 6.2382 ± 0.2547 |
| Sp. Type | (G7)1, (K0)2 | (F1)1, (F7)2 | (K0)1, (K1)2 |
| Distance (pc) | 1186 ± 48.42 | 757 ± 30.90 | 1180 ± 48.17 |
| Gaia distance_GSP-Phot (pc) | 2492 ± 101.74 | 1235 ± 50.42 | 980 ± 40.01 |
| Gaia Parallax (mas) | 0.3834 ± 0.0282 | 0.7623 ± 0.0162 | 0.1914 ± 0.0899 |
Note: 1 and 2 refer to primary and secondary components, respectively.
4 Evolutionary state of the systems
Physical parameter determinations for eclipsing binary systems are based on spectroscopic observation (radial velocity curves) of these systems. Star evolution can be inferred from fundamental star properties, including mass, radius, brightness, and chemical composition. For more precise understanding of evolution, stars with well-defined properties are particularly significant. In the present study, we used empirical parameter relationships between mass and orbital period by Latkovic et al., (2021) for estimating the mass of the primary components of the more massive star in the studied systems. Using the mass ratio from the light curve solution, we obtained the mass of the other companion star. Then, we computed the radius (
The computed physical parameters show that in all systems under study, the primary components have a greater mass than the secondary ones.
We looked into the evolutionary status of the studied systems using the physical parameters mentioned in Table 5. According to the evolutionary tracks calculated by Girardi et al., (2000) for both Zero Age Main Sequence (ZAMS) and Terminal-age Main Sequence (TAMS) with metallicity Z = 0.019, we plotted the components of the systems on the mass-luminosity (M–L) and mass-radius (M–R) relations along with the systems’ components in Figure 5a and b. Both components of the system V876 Lyr (S1, S2) and secondary components (S2) of the systems V366 Oph and V988 Mon show lower radius and luminosity than expected for ZAMS. Secondary components of the system, V366 Oph and V988 Mon, deviated from ZAMS and TAMS with a higher radius and luminosity than expected for ZAMS and TAMS. According to Lucy (1973), energy transfer from the primary to the secondary component of the system V0988 Mon occurs through the shared convective envelope, which clarifies the differences in the secondary components’ placements on the mass-radius (M–R) and mass-luminosity (M–L) relations. The non-rotating evolutionary models of Ekström et al., (2012) were used to assign the studied systems’ components to the (Teff–L) diagram, which is depicted in Figure 6. At a solar metallicity of z = 0.014, all of the systems’ components are shown to be on the expected tracks in the diagram. Figure 7 shows the mass-effective temperature (M–Teff) relation for intermediate and low mass stars, according to Malkov (2007). All the primary components of the systems under study, as well as the secondary component of system V0876 Lyr, indicated a good fit; however, there is a deviation for the secondary components of systems V0988 Mon and V3660 Oph. As shown in Figure 7, it is obvious that the same components behave in a similar way in terms of mass-luminosity and mass-radius relationships, as in Figure 5. As suggested by Lucy (1973), we explained this pattern as an energy transfer from the primary to the secondary components of the systems via the common convective envelope.
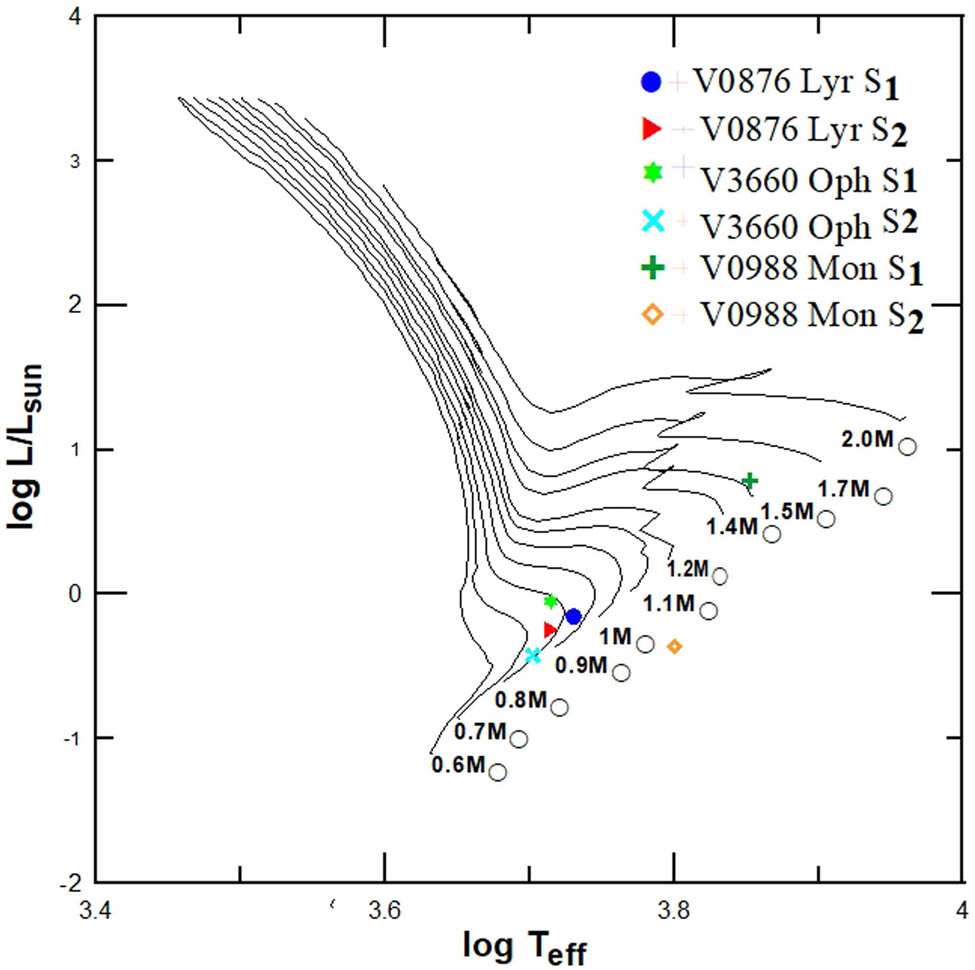
Positions of the components (S1, S2) of the systems V0876 Lyr, V3660 Oph, and V0988 Mon on the Teff–L diagram of Ekström et al., (2012).

Positions of the components (S1, S2) of the systems V0876 Lyr, V3660 Oph, and V0988 Mon on M–Teff diagram by Malkov (2007).
5 Discussion and conclusion
Photometric study and evolutionary state for the systems V0876 Lyr, V3660 Oph, and V0988 Mon were carried out using their first observed complete light curves. A total of 19 new times of minima were estimated from the observed light curves of the studied systems using a five-term Fourier series (of cosine terms) method. Orbital solution was calculated, absolute and physical parameters were estimated based on the accepted models for all systems. Primary components in all systems are hotter and more massive than the secondary ones. The accepted model for the system V3660 Oph includes a cool spot located on the surface of the secondary component. The spectral type for each system component was adopted based on the estimated absolute parameters. Uncertainties play a main role in constructing acceptable models, which reveal absolute parameters describing the observed light curves. In WD code, through the iteration process for estimating each parameter, the suggested correction in the parameter by the program should be less than the standard deviation to accept the parameter value; otherwise, we repeat the calculation. Uncertainties are affected in WD code by the efficiency of the input data (smooth or scatter data), and there is a condition in the program that should be marked if the light curves have scattering points to take into account during the run process. The evolutionary state of the studied systems has been investigated to explore their behavior in M–R and M–L relations. Components of the system V876 Lyr (S1, S2) and secondary components (S2) of the systems V366 Oph and V988 Mon show lower radius and luminosity than expected for ZAMS. Secondary components of the system, V366 Oph and V988 Mon, deviated from ZAMS and TAMS with a higher radius and luminosity than expected for ZAMS and TAMS. The same components behave similarly in terms of the mass–effective temperature (M–Teff) relation for intermediate and low mass stars. Lower or higher radius and luminosity, than expected for ZAMS and TAMS, can be attributed to an energy transfer from the primary to the secondary components of the systems through the shared convective envelope, as proposed by Lucy (1973), also the studied systems are detached and over contact systems, where the secondary star can temporarily be far out of thermal equilibrium, which may explain why it is so under luminous for its mass.
As the studied systems do not have any historical data or previous studies, we consider the results presented in this research to be preliminary. Spectroscopic observations of the studied systems are needed to compute precise mass ratios and, hence, follow their evolutionary status carefully.
Acknowledgements
This research has made use of NASA’s ADS and AAVSO databases and the available online material from the IBVS. Our sincere thanks to Dr. Gazeas, K., Dr. Liakos, A., and Dr. Niarchos, P., for making their photometric observations available.
-
Funding information: The authors state no funding involved.
-
Author contributions: All authors have accepted responsibility for the entire content of this manuscript and consented to its submission to the journal, reviewed all the results and approved the final version of the manuscript. MSA wrote and edited the manuscript; MME carried out the calculations and modeling.
-
Conflict of interest: Authors state no conflict of interest.
References
Applegate JH. 1992. A mechanism for orbital period modulation in close binaries. Astrophys J. 385:621.10.1086/170967Suche in Google Scholar
Binnendijk L. 1970. The orbital elements of W Ursae Majoris systems. Vistas Astron. 12:217. 10.1016/0083-6656(70)90041-3.Suche in Google Scholar
Bradstreet DH, Steelman DP. 2002. Binary Maker 3.0 – An interactive graphics-based light curve synthesis program written in Java. In American Astronomical Society Meeting Abstracts, Vol. 201. p. 75–02.Suche in Google Scholar
Ekström S, Georgy C, Eggenberger P, Meynet G, Mowlavi N, Wyttenbach A, et al. 2012. Grids of stellar models with rotation. I. Models from 0.8 to 120 M⊙ at solar metallicity (Z = 0.014). Astron Astrophys. 537:A146. 10.1051/0004-6361/201117751.Suche in Google Scholar
Eaton JA. 1983. Chromospheric emission of W Ursae Majoris-type stars and its relation to the structure of their common envelopes. Astrophys J. 268:800. 10.1086/161002.Suche in Google Scholar
Flower P. 1996. Transformations from theoretical Hertzsprung-Russell diagrams to color-magnitude diagrams: Effective temperatures, B-V colors, and bolometric corrections. Astrophys J. 469:355.10.1086/177785Suche in Google Scholar
Gaia Collaboration, Brown AGA, Vallenari A, et al. 2016. Gaia Data Release 1. Summary of the astrometric, photometric, and survey properties. Astron Astrophys. 595:A2. 10.1051/0004-6361/201629512.Suche in Google Scholar
Gaia Collaboration, Vallenari A, Brown AGA, et al. 2023. Gaia Data Release 3. Summary of the content and survey properties. Astron Astrophys. 674:A1. 10.1051/0004-6361/202243940.Suche in Google Scholar
Gazeas K. 2017. Reports on new discoveries, IBVS, 6200, Vol. 62.Suche in Google Scholar
Girardi L, Bressan A, Bertelli G, Chiosi C. 2000. Evolutionary tracks and isochrones for low- and intermediate-mass stars: From 0.15 to 7 Msun, and from Z = 0.0004 to 0.03. Astron Astrophys Suppl. 141:371. 10.1051/aas:2000126.Suche in Google Scholar
Kopal Z. 1959. Close binary systems. London: Chapman and Hall Ltd.Suche in Google Scholar
Kurucz R. 1993. In: Milone, E. (Ed.), Light curve modeling of eclipsing binary stars. New York: Springer-Verlag. p. 93.10.1007/978-1-4612-2742-7_8Suche in Google Scholar
Latkovic O, Ceki A, & Lazarevic S. 2021. Statistics of 700 Individually Studied W UMa Stars. Astrophys J Suppl Ser. 254:10. 10.3847/1538-4365/abeb23.Suche in Google Scholar
Liakos A, Niarchos P. 2010. Photometric elements for five newly discovered variable stars. Peremennye Zvezdy Prilozhenie. 10:9.Suche in Google Scholar
Liakos A, Niarchos P. 2011. Discovery of Three W UMa Type Eclipsing Binaries. Peremennye Zvezdy Prilozhenie. 11:26.Suche in Google Scholar
Lucy L. 1967. Gravity-darkening for stars with convective envelopes. Z für Astrophysik. 65:89.Suche in Google Scholar
Lucy LB. 1973. The common convective envelope model for W Ursae Majoris systems and the analysis of their light curves. Astrophys Space Sci. 22:381. 10.1007/BF00647433.Suche in Google Scholar
Malkov OY. 2007. Mass-luminosity relation of intermediate-mass stars. Mon Not RAS. 382:1073. 10.1111/j.1365-2966.2007.12086.x.Suche in Google Scholar
Nelson R. 2009. https://www.variablestarssouth.org/resources/bob-nelsons-software-tools/software-by-bob-nelson.Suche in Google Scholar
Popper D. 1980. Stellar masses. Ann Rev Astron Astrophys. 18:115. 10.1146/annurev.aa.18.090180.000555.Suche in Google Scholar
Prša A. 2019. Modeling and analysis of eclipsing binary stars: The theory and design principles of PHOEBE. IOP ebooks. Bristol, UK: IOP Publishing. ISBN: 978-0-7503-1288-2.Suche in Google Scholar
Rucinski SM. 1969. The proximity effects in close binary systems. II. The bolometric reflection effect for stars with deep convective envelopes. Acta Astron. 19:245.Suche in Google Scholar
Tokunaga A. 2000. Allen’s Astrophysical Quantities. 4th ed. New York: AIP Press, Springer.Suche in Google Scholar
Torres G. 2010. On the use of empirical bolometric corrections for stars. Astron J. 140:1158.10.1088/0004-6256/140/5/1158Suche in Google Scholar
Van Hamme W. 1993. New limb-darkening coefficients for modeling binary star light curves. Astron J. 106:2096. doi: 10.1086/116788.Suche in Google Scholar
Vinod Prasad J, Pandey B, Manoj K, Patel A, Srivastava A. 2013. BVRI photometric and polarimetric studies of W UMa type eclipsing binary FO Hydra. N Astr. 20:52.10.1016/j.newast.2012.10.001Suche in Google Scholar
Wilson RE, Devinney EJ, Van Hamme W. 2020. WD: Wilson-Devinney binary star modeling. Astrophys Source Code Library. record ascl:2004.004.Suche in Google Scholar
Yilmaz M, Nelson R, Senavci H, Izaci D, Ozavci I, Gumus D. 2017. Light curve and orbital period analysis of VX lac. Rev Mex Astron Astrofis. 53:29–36.Suche in Google Scholar
© 2024 the author(s), published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Artikel in diesem Heft
- Research Articles
- A generalized super-twisting algorithm-based adaptive fixed-time controller for spacecraft pose tracking
- Retrograde infall of the intergalactic gas onto S-galaxy and activity of galactic nuclei
- Application of SDN-IP hybrid network multicast architecture in Commercial Aerospace Data Center
- Observations of comet C/1652 Y1 recorded in Korean histories
- Computing N-dimensional polytrope via power series
- Stability of granular media impacts morphological characteristics under different impact conditions
- Intelligent collision avoidance strategy for all-electric propulsion GEO satellite orbit transfer control
- Asteroids discovered in the Baldone Observatory between 2017 and 2022: The orbits of asteroid 428694 Saule and 330836 Orius
- Light curve modeling of the eclipsing binary systems V0876 Lyr, V3660 Oph, and V0988 Mon
- Modified Jeans instability and Friedmann equation from generalized Maxwellian distribution
- Special Issue: New Progress in Astrodynamics Applications - Part II
- Multidimensional visualization analysis based on large-scale GNSS data
- Parallel observations process of Tianwen-1 orbit determination
- A novel autonomous navigation constellation in the Earth–Moon system
Artikel in diesem Heft
- Research Articles
- A generalized super-twisting algorithm-based adaptive fixed-time controller for spacecraft pose tracking
- Retrograde infall of the intergalactic gas onto S-galaxy and activity of galactic nuclei
- Application of SDN-IP hybrid network multicast architecture in Commercial Aerospace Data Center
- Observations of comet C/1652 Y1 recorded in Korean histories
- Computing N-dimensional polytrope via power series
- Stability of granular media impacts morphological characteristics under different impact conditions
- Intelligent collision avoidance strategy for all-electric propulsion GEO satellite orbit transfer control
- Asteroids discovered in the Baldone Observatory between 2017 and 2022: The orbits of asteroid 428694 Saule and 330836 Orius
- Light curve modeling of the eclipsing binary systems V0876 Lyr, V3660 Oph, and V0988 Mon
- Modified Jeans instability and Friedmann equation from generalized Maxwellian distribution
- Special Issue: New Progress in Astrodynamics Applications - Part II
- Multidimensional visualization analysis based on large-scale GNSS data
- Parallel observations process of Tianwen-1 orbit determination
- A novel autonomous navigation constellation in the Earth–Moon system

